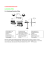MZI - Interferometrie und Polarisation mit dem Mach

MZI - Interferometrie und Polarisation mit dem Mach-Zehnder-Interferometer
Fakultät für Physik der Ludwig-Maximilians-Universität München – Grundpraktika
(21. SEPTEMBER 2011)
Ziele:
Nähere Betrachtung von Interferenz mit Hilfe der MachZehnder-Interferometers. Überblick über einige Polarisationsvorgänge von Licht und deren Anwendungen.
Untersuchung der Interferenz von polarisiertem Licht.
Teilversuche:
1. Mach-Zehnder-Interferometer
Aufbau und Justage des Mach-ZehnderInterferometers. Beobachtung des Interferenzbildes auf dem Schirm.
2. Wellenlänge eines Lasers
Mit Hilfe des Abstandes der Intensitätsmaxima
lässt sich die Wellenlänge des verwendeten Laserlichtes bestimmen.
3. Bestimmung der Brechzahl von Luft
In einem der beiden Strahlengänge des MachZehnder-Interferometers wird eine luftgefüllte
Küvette eingebracht. Nach dem Erzeugen eines
Unterdrucks in der Küvette, wird wieder Luft hineingelassen. Dabei beobachtet man das Interferenzbild und bestimmt aus der Verschiebung des
Interferenzbildes und der dazugehörigen Druckdifferenz die Brechzahl von Luft.
4. Beobachtung von Polarisationsphänomenen
(a) Bestätigung der Existenz des Brewsterwinkels
(b) Nachweis der Polarisation des Himmelblaus
(c) Untersuchung der Doppelbrechung eines
Kalkspats
5. Quantenradierer
Das Mach-Zehnder-Interferometer wird durch
drei Polarisationsfilter zum Quantenradierer erweitert. Je nach Stellung der Polarisationsfilter ergibt sich ein anderes Bild auf dem Schirm. Diese
werden gedeutet.
Stichwortliste:
siehe Text unter Rekapitulation
I.
THEORETISCHE GRUNDLAGEN
I.1.
Wellen, Interferenz, Kohärenz
Licht ist eine elektromagnetische Welle; Wellen sind
Schwingungen, die sich im Raum fortbewegen. Eine
physikalische Schwingung bezeichnet einen in der Zeit
periodischen Verlauf einer physikalischen Größe. Beschreibt die Schwingung einen sinusförmigen Verlauf,
so nennt man sie eine harmonische Schwingung. Ihre
maximale Auslenkung heißt Amplitude. Eine elektromagnetische Welle lässt sich durch ein sich ausbreiten~
des schwingendes elektrisches Feld (E-Feld)
und ein da~
zu senkrecht schwingendes magnetisches Feld (H-Feld)
beschreiben. Da Felder gerichtete physikalische Größen
sind, ist es sinnvoll, sie durch Vektoren auszudrücken.
Per Konvention betrachtet man bei elektromagneti~ der elektrischen Feldstärke.
schen Wellen den Vektor E
~ lässt sich, falls notwendig, hieraus bestimmen. Eine
H
harmonische elektromagnetische Welle kann im Reellen
wie folgt beschrieben werden:
E(reell) (x, t) = Ê(reell) cos(kx − ωt + ϕ)
E = elektrische Feldstärke, Ê = Amplitude, k = 2π/λ =
Kreiswellenzahl mit λ = Wellenlänge, ω = 2πf = 2π/T
Kreisfrequenz mit f = Frequenz und T = Schwingungsdauer, ϕ = Phasenwinkel.
Mathematisch vorteilhafter ist allerdings die komplexe
Schreibweise (vgl. AMG) einer harmonischen elektromagnetischen Welle:
E(x, t) = |Ê| exp(i(kx − ωt + ϕ))
= |Ê| exp(iϕ) exp(i(kx − ωt))
= Ê exp(i(kx − ωt)) .
(1)
Hierbei stellt Ê = |Ê| exp(iϕ) die komplexe Amplitude dar. Durch diese Schreibweise wird die reelle, physikalisch beobachtbare Größe um eine zweite Dimension
erweitert. Auf diese Weise erleichtert man sich spätere
Rechnungen, da die reelle Amplitude und ihre Phasenlage in einer komplexen Zahl, einem zweikomponentigen
Vektor zusammengefasst sind.
Betrachtet man das Argument der Exponentionalfunktion, so sieht man, dass sich dieses u. a. mit der
Zeit ändert. Diese Änderung entspricht einer Rotation um den Ursprung der Ebene. Damit sind auch
Real- und Imaginärteil der komplexen Zahl einer Änderung unterzogen. Betrachtet man nur den Realteil in
Gl. (1), so ergibt sich wieder die Wellengleichung vor
der Überführung ins Komplexe
Re {E(x, t)} = Ê(reell) cos(kx − ωt + ϕ) .
2
Abbildung 1: Überlagerung des Zeitanteils zweier Wellen am Ort x = 0. Amplitude und Phase der resultierenden Welle
ergeben sich aus dem Zeigerdiagramm.
Überlagerung von Wellen und Interferenz
Treffen an einem Raumpunkt zwei Wellen aufeinander,
spricht man von Überlagerung der Wellen. Das Superpositionsprinzip sagt aus, dass sich die Wellenfunktionen zweier Wellen mit gleicher Schwingungsrichtung addieren1 . Für gleiche Wellenzahl und Frequenz gilt:
+ |Ê2 | exp(i(kx − ωt + ϕ2 ))
= [|Ê1 | exp(iϕ1 ) + |Ê2 | exp(iϕ2 )]
· exp(i(kx − ωt))
= Ê exp(i(kx − ωt))
(2)
Bei Betrachtung der Gl. (2) erkennt man, dass sich
die Überlagerung von Wellen durch die Überführung
ins Komplexe auf eine einfache Addition von komplexen Zahlen reduzieren lässt. Um diese Erleichterung
einschätzen zu können, stelle man sich diese Addition im Reellen vor, welche schnell auf eine Vielzahl von
Sinus- und Cosinustermen anwächst und auf unhandliche Additionstheoreme angewiesen ist.
Die komplexe Amplitude der resultierenden Welle ist
die Summe der komplexen Amplituden der Einzelwellen: Ê = Ê1 + Ê2 . Graphisch wird sie durch vektorielle
Addition von Ê1 und Ê2 in der komplexen Ebene konstruiert, was in Abb. 1 dargestellt ist. Dabei entsprechen die phasenverschobenen Cosinuskurven dem Realteil Re {E} der komplexen Wellenfunktion und stellen
1
|Ê|2 = |Ê1 + Ê2 |2 = (Ê1 + Ê2 )(Ê1 + Ê2 )∗
= [Ê1 exp(iϕ1 ) + Ê2 exp(iϕ2 )]
E1 (x, t) + E2 (x, t) = |Ê1 | exp(i(kx − ωt + ϕ1 ))
= (Ê1 + Ê2 ) exp(i(kx − ωt))
das physikalische Geschehen dar.
Das Maximum des Realteils ist die Länge des Vektors
in der Gaußschen Zahlenebene. Aus diesem Grund ist
die Amplitude der resultierenden Welle der Betrag |Ê|
der komplexen Amplitude. Damit ergibt sich:
Im Vakuum gilt das Superpositionsprinzip für elektromagnetische Wellen, soweit man weiß, uneingeschränkt. In Materie
kann es zu Abweichungen, d.h. nichtlinearen Effekten kommen.
2
= |Ê1 | + |Ê2 |
2
· [Ê1 exp(−iϕ1 ) + Ê2 exp(−iϕ2 )]
+ |Ê1 ||Ê2 |[exp(i(ϕ1 −ϕ2 )) + exp(−i(ϕ1 −ϕ2 ))]
= |Ê1 |2 + |Ê2 |2 + 2|Ê1 ||Ê2 | cos ∆ϕ
(3)
Dieses Ergebnis liefert eine Abbhängigkeit der physikalischen Amplitude von der Phasendifferenz ∆ϕ =
ϕ2 − ϕ1 der sich überlagernden Wellen. Es kann auch
durch Anwendung des Cosinussatzes auf das von den
drei Zeigern in Abb. 1 gebildete Dreieck erhalten werden.
Die Überlagerung von Wellen gleicher Wellenlänge heißt
Interferenz. In einem durch Überlagerung erzeugten
Wellenfeld treten Gebiete mit großer und Gebiete mit
kleiner resultierenden Amplitude auf. Bei sichtbarem
Licht ergibt sich so ein aus helleren und dunkleren Gebieten bestehendes Interferenzmuster. Für die Intensität, die proportional zum Quadrat der Amplitude ist
(I ∝ |Ê|2 ), folgt aus Gl. (3) für Wellen gleicher Schwingungsrichtung die Beziehung:
p
(4)
I = I1 + I2 + 2 I1 I2 cos ∆ϕ
Als Interferenz kann man auch die Abweichung von der
Additivität der Intensitäten
definieren. Diese entspricht
√
dem Summanden 2 I1 I2 cos ∆ϕ, der deshalb auch gelegentlich als Interferenzterm bezeichnet wird und von
der Phasenverschiebung ∆ϕ abhängig ist. Bei ∆ϕ = 0
3
hat der Term ein Maximum, während er bei ∆ϕ = 180◦
minimal wird. Man spricht darum bei ∆ϕ = 0 von konstruktiver und bei ∆ϕ = 180◦ von destruktiver Interferenz. Allerdings ist Interferenz bei beliebigen Lichtquellen nicht immer zu beobachten, da sich die Phasenverschiebung ∆ϕ so schnell ändern kann, dass es aufgrund
der Trägheit vieler Registrierinstrumente (insbesondere des menschlichen Auges) nicht mehr bemerkt wird.
Deshalb muss eine weitere Bedingung gegeben sein, um
Interferenz beobachten zu können.
Interferenz möglich
gerade keine Interferenz mehr möglich
Kohärenz
Die notwendige Voraussetzung für ein beobachtbares Interferenzbild ist die zeitliche Konstanz der Phasenverschiebung. Ist dies bei zwei sich überlagernden Wellen
der Fall, so spricht man von kohärenten Wellen. Diese Eigenschaft einer konstanten Phasendifferenz nennt
man Kohärenz. Sie ist dann ideal gegeben, wenn zwei
Erregungszentren je einen Wellenzug unendlicher Länge
abstrahlen. Natürliches Licht stammt aber meist aus einer Vielzahl von angeregten Atomen, die nur während
der Relaxation kurzfristig und in der Regel statistisch
unabhängig Licht emmitieren. Die Längen dieser emittierten Wellenzüge betragen unter Umständen nur wenige Zentimeter, und die Phasenlagen von unterschiedlichen Wellenzügen sind statistisch unabhängig. Bei einer
solchen Lichtquelle ist also nicht mit beobachtbarer Interferenz zu rechnen und erst recht nicht zwischen zwei
solcher Lichtquellen.
Doch kann unter bestimmten Gegebenheiten trotzdem
Interferenz beobachtet werden. Wird z. B. ein Wellenzug durch einen Strahlteiler in zwei Teilwellenzüge zerlegt, welche danach verschiedene Wege durchlaufen,
besitzen diese durch die Apparatur festgelegte Laufzeiten. Unterscheiden sich diese Laufzeiten, so ergibt
sich eine konstante Phasendifferenz zwischen den Wellenzügen. Bei Wellenzügen endlicher Länge muss allerdings gewährleistet sein, dass diese sich im Vereinigungspunkt überlappen. Dies ist der Fall, wenn der
Laufzeitunterschied maximal so groß ist, dass die Wegdifferenz der Teilstrahlen kleiner als die Wellenzuglänge
ist. Dies nennt sich zeitliche Kohärenz. Dazu darf die
apparaturbedingte Differenz der optischen Wege nicht
größer sein als die Länge des Wellenzugs. Der maximale
Weglängenunterschied, bei dem Interferenz möglich ist,
heißt Kohärenzlänge. Welche Fälle auftreten können,
zeigt Abb. 2.
Der Laser ist eine Lichtquelle, die Strahlung mit besonders großer Kohärenzlänge aussendet. Sein Licht kann
eine Kohärenzlänge bis zu einigen Kilometern erreichen.
Die Ursache hierfür liegt in der Funktionsweise des Lasers, auf die an dieser Stelle nicht näher eingegangen
wird. Aufgrund dieser besonderen Eigenschaften ist er
aus Interferenzversuchen kaum mehr wegzudenken.
Rekapitulation
1. Wie kann man eine Welle komplex darstellen?
Interferenz unmöglich
Abbildung 2: Wellenzüge mit verschiedenen Wegdifferenzen:
die zeitliche Kohärenzbedingung.
2. Was bedeutet das geometrisch?
3. Wie sieht eine Überlagerung von Wellen im komplexen Zeigerdiagramm aus?
4. Welchen Einfluss hat die Phasenverschiebung auf
die resultierende Amplitude?
5. Wie hängt die Amplitude mit der Intensität zusammen?
6. Was ist Interferenz?
7. Was versteht man unter Kohärenz?
8. Gibt es eine Möglichkeit mit inkohärenten Wellen
ein beobachtbares Interferenzmuster zu erzeugen?
I.2.
Das Mach-Zehnder-Interferometer
Eine gute Möglichkeit, Interferenz zu beobachten bietet das Mach-Zehnder-Interferometer (MZI, s. Abb. 3),
das 1891/92 von dem Österreicher Ludwig Mach und
dem Schweizer Ludwig Zehnder unabhängig voneinander entwickelt wurde.
Einfallendes Licht wird durch einen Strahlteiler und
einen Spiegel in zwei Strahlen aufgeteilt. Nach Durchlaufen der beiden Strecken werden die Strahlen mit einem zweiten Strahlteiler und Spiegel wieder überlagert.
Da ein Laserstrahl ein paralleles Lichtbündel ist, wird
dieser durch die Linse in ihrem Brennpunkt vereinigt.
Wird der zweite Spiegel so ausgerichtet, dass die Teilstrahlen einen kleinen Winkel einschließen, so ergeben
sich durch die Linse zwei punktförmige Lichtquellen (L1
und L2). Von diesen punktförmigen Lichtquellen gehen
Lichtwellen aus, die Teilen von Kugelwellen entsprechen
(Huygen’sches Prinzip).
4
Abbildung 3: Anordnung der Komponenten des Mach-Zehnder-Interferometers.
Abbildung 4: Zur Herleitung des Interferenzmusters von zwei punktförmigen Lichtquellen.
I.3.
Das Interferenzbild
Man betrachte zunächst zwei punktförmige Lichtquellen, die kohärentes Licht emittieren. Da diese in alle
Raumrichtungen strahlen, ergeben sich von ihnen ausgehende Kugelwellen.
Zur Untersuchung der Struktur des Interferenzmusters
werde an dieser Stelle angenommen, dass die von den
Lichtquellen L1 und L2 ausgehenden Wellen mit gleicher Phase starten.
Die Differenz des Weges, den die Wellen zu einem Punkt
des Wellenfeldes zurücklegen, nennt man Gangunterschied. In einem Punkt P , der von L1 den Abstand r1
und von L2 den Abstand r2 hat, ist der Gangunterschied
der beiden Wellen r2 −r1 . Betrachtet man die Menge aller Punkte mit gleichem Gangunterschied in der Ebene,
so liegen diese auf einer Hyperbel. Beim Übergang zum
dreidimensionalen Raum wird aus der Hyperbel dann
ein zweischaliges Rotationshyperboloid mit L1 , L2 als
Brennpunkten und der Verbindungslinie von L1 und L2
als Rotationsachse.
Im hier verwendeten Koordinatensystem (Abb. 4) steht
die z-Achse senkrecht auf dem Schirm (der in der x-yEbene liegt) und bei z = −a durchstößt sie den Mittelpunkt zwischen L1 und L2 . In einem genügend kleinen Gebiet um den so definierten Koordinatenursprung
werden zur x-Achse parallele Interferenzstreifen beobachtet. Für Licht der Wellenlänge λ tritt ein Maximum
der Helligkeit (helle Streifen) auf, wenn gilt:
r2m − r1m = mλ
I.4.
mit m = 0, ±1, ±2, . . .
(5)
Bestimmung der Wellenlänge eines Lasers
Man kann das Mach-Zehnder-Interferometer benutzen,
um die Wellenlänge eines Lasers zu bestimmen. Ist die
Interferenz konstruktiv, so beträgt der Gangunterschied
gerade ein Vielfaches der Wellenlänge, siehe Gl. (5). Da
die konstruktive Interferenz in Form der Intensitätsmaxima zu lokalisieren ist, lässt sich, durch die Messung
der Abstände ym der hellen Streifen zur nullten Ordnung, die Wellenlänge λ bestimmen (vgl. Abb. 4). Für
ym gilt
2
2
r1m
= (ym + g/2)2 + a2 und r2m
= (ym − g/2)2 + a2 .
5
Einsetzen in Gl. (5) ergibt unter Berücksichtigung von
(r2m − r1m )(r2m + r1m ) =
2
r2m
−
I.5.
Elektromagnetische Wellen in Materie
2
r1m
1.
Die optische Weglänge
folgendes Ergebnis:
mλ = p
4ym g/2
p
(ym − g/2)2 + a2 + (ym + g/2)2 + a2
Ist der Abstand a >> (ym ± g/2), kann man die Klammern unter den Wurzeln vernachlässigen und es gilt folgende Näherung:
∼ ym g
(6)
λ=
ma
Den Abstand g, der punktförmigen Lichtquellen, direkt
zu messen, ist experimentell schwierig, da die Lage der
Brennpunkte nur schwer zugänglich ist. Er kann aber
auf experimentell leicht zugängliche Größen zurückgeführt werden:
Zunächst wird die Linse aus dem Strahlengang entfernt.
Es besteht dann folgender Zusammenhang der in Abb. 5
dargestellten Größen:
tan(α/2) =
g0
2a0
mit g 0 = Abstand der Lichtpunkte auf dem Schirm, a0
= Abstand vom 2. Strahlenteiler zum Schirm.
Elektromagnetische Wellen breiten sich mit Lichtgeschwindigkeit aus. Diese ist im Vakuum am größten
und wird mit c0 bezeichnet. Durchläuft eine elektromagnetische Welle Materie, so löst sie in dieser eine
frequenzgleiche Welle aus. Jedoch breitet sich eine elektromagnetische Welle in Materie langsamer aus als im
Vakuum (Lichtgeschwindigkeit in Materie c1 ), was zur
Folge hat, dass die Wellenlänge sich verkürzt. Man erkennt dies aus dem Zusammenhang λ = c/f . Wenn die
Frequenz f konstant ist und sich die Ausbreitungsgeschwindigkeit c ändert, so muss sich die Wellenlänge λ
ebenfalls ändern, damit die Gleichung erfüllt ist.
Aus der Definition des Brechungsindex n = c0 /c1 folgt
mit obigem Zusammenhang n = λ0 /λ1 . Da die Lichtgeschwindigkeit im Vakuum größer ist als in Materie
(c0 > c1 ), ist auch die Wellenlänge im Vakuum größer,
als in Materie (λ0 > λ1 ).
Läuft ein Lichtstrahl also durch Materie, so fallen auf
eine Strecke s eben so viele Wellenlängen, wie im Vakuum auf die Strecke n · s (vgl. Abb. 7). Die Strecke n · s
wird als optische Weglänge bezeichnet.
2.
Bestimmung der Brechzahl von Luft
Mit Hilfe des Mach-Zehnder-Interferometers kann man
die Brechzahl von Luft bestimmen. Lässt man im MachZehnder-Interferometer einen der beiden Strahlbündel
durch eine mit Luft gefüllte Küvette laufen, in welcher
ein geringerer Druck als außerhalb herrscht, so ergibt
sich aufgrund der verschiedenen optischen Weglängen
ein Gangunterschied. Der Grund hierfür liegt in der
Proportionalität der Abweichung ∆n = n − 1, der
Brechzahl n eines Gases von der des Vakuums (n = 1),
zur Gasdichte ρ, solange diese hinreichend klein ist.
∆n = n − 1 = aρ
n = aρ + 1
Abbildung 5: Strahlenverlauf ohne Linse.
Daraufhin bringt man die Linse wieder in den Strahlengang. Es ergibt sich der in Abb. 6, links dargestellte
Strahlenverlauf. Da der Querschnitt der Strahlenbündel
groß im Verhältnis zur Linsengröße ist, kann man die
Strahlen als Mittelpunktstrahlen auffassen. Diese Näherung erreicht man durch eine Parallelverschiebung der
Stahlenbündel (s. Abb. 6, rechts).
Die Parallelverschiebung erhält auch den Winkel α. Mit
der Brennweite f der Linse lässt sich nun der Abstand
g der Lichtquellen wie folgt bestimmen:
g
= f tan(α/2)
2
Für Luft gilt bei Raumtemperatur und einem Druck
von 1 bar in guter Näherung die ideale Gasgleichung:
Damit ergibt sich schließlich folgende Formel für die
Wellenlänge:
Daher besteht ein linearer Zusammenhang zwischen der
Brechzahl n und dem Druck p:
λ∼
=
ym f g 0
maa0
(7)
pV =
m
RT
M
p = Druck, V = Volumen, m = Masse, M = molare Masse,
R = allgemeine Gaskonstante, T = absolute Temperatur.
Aus dieser folgt nach Umformung:
ρ=
m
M
=
p
V
RT
n=a
M
p+1
RT
(8)
6
Abbildung 6: Vereinigung von zwei Parallelstrahlbündeln zu zwei punktförmigen Lichtquellen.
Abbildung 7: Elektromagnetische Welle: oben in Materie,
unten im Vakuum.
man Luft in die Küvette einströmen lässt. ∆p ist hierbei die Differenz von dem in der Küvette vorherrschendem Druck zum aktuellen Atmosphärendruck (∆p =
pKüvette − pAtmosphäre ).
Trägt man ∆p gegen ∆m auf, erhält man nach Gl. (9)
eine Gerade mit der Steigung RT λ0 /aM s, aus welcher
man die Größe aM/RT ermitteln kann. Der Wert für n
ergibt sich somit aus Gl. (8).
Der Literaturwert n0 wird üblicherweise für den Normaldruck p0 = 101325 Pa (= 760 mm Hg) und die Temperatur T0 = 288 K angegeben. Um den Messwert n
mit dem Literaturwert zu vergleichen, kann man ihn
wie folgt umrechnen:
p
M
T M
p0 + 1 =
a
p0 + 1
RT0
T RT0 p
T p0 M
T p0
=
a
p+1 =
(n − 1) + 1 (10)
T0 p RT
T0 p
n0 = a
Da innerhalb der Küvette in einem der Strahlengänge
ein geringerer Druck als in der Umgebung herrscht,
ändert sich dort die Brechzahl der Luft. Die optische
Weglänge des Teilstrahls, welcher die Küvette passiert,
unterscheidet sich dementsprechend von der optischen
Weglänge des anderen Teilstrahls. Die Differenz der optischen Weglängen ergibt ∆ns, wobei ∆n die Differenz
der Brechzahlen und s die Länge der Küvette ist. Aus
den verschiedenen optischen Weglängen folgt ein Gangunterschied der beiden Teilstrahlen. Am Ort der Interferenzstreifen ist der Gangunterschied ein ganzzahliges
Vielfaches mλ0 der Wellenlänge des Laserlichtes (vgl.
Abschnitt I.3). Also gilt
∆ns = ∆mλ0 .
Ändert sich der Druck um ∆p, so ändert sich n um ∆n.
Dies hat eine Änderung der optischen Weglänge zur Folge und durch diese Änderung der optischen Weglänge
verschieben sich die Streifen des Interferenzbildes. Zählt
man die an einem Fixpunkt auf dem Schirm vorbeilaufenden Streifen, so erhält man ∆m Stück, denn jeder
Streifen entspricht einem Gangunterschied von mλ0 .
Daraus folgt mit Gl. (8):
RT λ0
∆m
(9)
aM s
Aus praktischen Gründen ist es einfacher, zuerst die
Küvette zu evakuieren und anschließend die Verschiebung der Interferenzstreifen zu beobachten, während
∆p =
Rekapitulation
1. Wie ist ein Mach-Zehnder-Interferometer (MZI)
aufgebaut?
2. Wie kommt es zum Interferenzmuster von zwei
punktförmigen Lichtquellen?
3. Welche Rolle spielt dabei der Gangunterschied?
4. Wie kann man mit dem MZI die Wellenlänge eines
Lasers bestimmen?
5. Was versteht man unter der optischen Weglänge?
6. Welche Möglichkeit bietet das MZI zur Bestimmung der Brechzahl von Luft?
I.6.
Polarisation
Mit dem Mach-Zehnder-Interferometer ist es möglich
durch eine geringe Modifikation ein Experiment aus der
Quantenphysik durchzuführen. Um dieses Experiment
nachvollziehen zu können, ist das Verständnis der Polarisation von Wellen notwendig.
7
Elektromagnetische Wellen sind transversal, bei ihnen
~=E
~ ×H
~ den Energiebeschreibt der Poyntingvektor S
transport sowie die Ausbreitungsrichtung. Eine Eigenschaft von Transversalwellen ist, dass sie sich polarisieren lassen2 .
Bei natürlichem Licht sind die Schwingungsrichtungen der Wellenzüge statistisch verteilt. Es ist jedoch
möglich, Wellenzüge bestimmter Schwingungsrichtungen aus dem Licht zurückzuhalten. Dieser Vorgang heißt
Polarisation. Eine Welle nennt man linear polarisiert,
wenn ihre Auslenkungen nur eine Richtung senkrecht
zur Ausbreitungsrichtung annehmen. Man unterscheidet lineare von elliptischer Polarisation, wobei auf letztere hier nicht näher eingegangen wird. Im Folgenden werden drei ausgewählte Polarisationsmechanismen
vorgestellt.
1.
Polarisation durch Streuung
Den Effekt der Polarisation durch Streuung kann
man beobachten, wenn z. B. Licht auf kleine Partikel
trifft. Streuung an einem Partikel bedeutet, dass dieses
durch eine ankommende elektromagnetische Welle zum
Schwingen angeregt wird und diese selbst wieder abstrahlt. Oft ist das streuende Partikel ein Hertzscher Dipol, dann strahlt es in Schwingungsrichtung keine Welle
ab, sondern nur rechtwinklig dazu (s. Abb. 8). Dies bedeutet aber gleichfalls, dass die Welle dementsprechend
polarisiert ist.
2.
Polarisation durch Reflexion
Jeder Lichtstrahl, der an einem durchsichtigen Dielektrikum (z. B. Glas, Wasser, Kunststoff, Lacke, Luft,
...) reflektiert wird, ist danach je nach Einfallswinkel teilweise oder sogar vollständig linear polarisiert
(vgl. OPT). Der Vorgang der vollständigen Polarisation
durch Reflexion wurde von dem schottischen Physiker
David Brewster näher untersucht. Er stellte fest, dass
bei vollständiger Polarisation der reflektierte und der
transmitierte Strahl rechtwinklig aufeinander stehen.
Das Licht streut an den Teilchen der Materie3 , welche
als Dipol keine Welle in Schwingungsrichtung abstrahlen können. Dies bedeutet, dass der reflektierte Strahl
vollständig polarisiert ist. Da man weiß, dass reflektierter und transmittierter Strahl einen rechten Winkel einschließen, kann man eine Formel für den Einfallswinkel αB bestimmen. Er wurde, nach seinem Entdecker,
Brewsterwinkel benannt und folgt der Beziehung
n2
tan αB =
(11)
n1
n1 = Brechungsindex des an das Dielektrikum grenzenden
Mediums, n2 = Brechungsindex des Dielektrikums.
Der Formel kann man entnehmen, dass der Brewsterwinkel eine materialspezifische Größe ist.
Abb. 9 zeigt den Vorgang der Polarisation durch Reflexion. Der reflektierte Strahl ist polarisiert, nämlich
senkrecht zur Einfallsebene – der Ebene, in der einfallender und reflektierter Strahl verlaufen.
maximale
Abbildung 9: Polarisation durch Reflexion im Brewsterwinkel.
3.
Abbildung 8: Polarisation durch Streuung. Elektromagnetische Welle streut an einem Objekt.
2
Im Gegensatz dazu lassen sich Longitudinalwellen nicht polarisieren. Bei dieser Art von Wellen fallen Schwingungs- und
Ausbreitungsrichtung zusammen (z. B. Schall).
Polarisation durch Doppelbrechung
Ein weiteres Phänomen der Polarisation ist die Doppelbrechung. Sie tritt bei anisotropen Materialien auf,
wie z. B. im Kalkspat (Calcit, CaCO3 ). Diese haben die
Eigenschaft, dass sich elektromagnetische Wellen innerhalb des Materials nicht in allen Schwingungsichtungen gleich schnell ausbreiten. Gründe hierfür liegen in
3
Das Licht streut auch an den Teilchen der Luft, jedoch ist aufgrund der höheren Dichte der Effekt bei Materie stärker.
8
der E-Feldvektor aber senkrecht zu den Ketten, so wird
das Licht durchgelassen.
Rekapitulation
1. Was ist Polarisation? Was kann man polarisieren?
2. Leiten Sie die Formel für den Brewsterwinkel her!
Abbildung 10: Polarisation durch Doppelbrechung. Kalkspat
als anisotropes Medium.
3. Welchen Zusammenhang gibt es zwischen Polarisation und
Polarisationsfolie?
Reflexion?
der Gitterstruktur des Materials. Beim Eintritt eines
Lichtstrahls in ein solches Medium, wird dieser in zwei
Komponenten aufgespalten, da diese sich unterschiedlich schnell durch das Material bewegen. Diese Komponenten schwingen in zwei senkrecht aufeinander stehenden Ebenen und sind somit senkrecht zueinander
polarisiert. Einer der Teilstrahlen gehorcht dem Brechungsgesetz. Diesen nennt man ordentlichen Strahl (oStrahl), während der andere dies nicht tut und dementsprechend außerordentlicher Strahl (ao-Strahl) genannt
wird (s. Abb. 10). Im Allgemeinen verlaufen diese Komponeten räumlich getrennt voneinamder. Eine Ausnahme ergibt sich, wenn der Lichtstrahl parallel zur sogn.
optischen Achse des Mediums eintritt. In diesem Fall
verlaufen die Teilstrahlen räumlich ungetrennt.
4.
Polarisationsfolie
Eine Polarisationsfolie (s. Abb. 11, vgl. auch OPT) besteht z. B. aus langkettigen ausgerichteten Kohlenwasserstoffmolekülen. Die Ausrichtung wird durch das Dehnen des Materials in eine bestimmte Richtung während
des Herstellungsprozesses erreicht. Die Folie wird bei
optischen Frequenzen leitend, wenn sie während der
Herstellung in eine jodhaltige Lösung getaucht wurde.
Fällt auf die Molekülketten Licht, dessen Vektor des
Abbildung 11: Funktionsweise der Polarisationsfolie. Die
Molekülketten liegen waagerecht.
~ parallel zu den Ketten schwingt,
elektrischen Feldes E
dann werden elektrische Ströme entlang der Ketten induziert, und die Lichtenergie wird absorbiert. Schwingt
Streuung?
Doppelbrechung?
I.7.
Interferenz polarisierter Wellen und
Quantenradierer
Der Quantenradierer besteht aus einem Mach-ZehnderInterferometer, in dessen Strahlengänge 1 und 2 jeweils
ein Polarisationsfilter gebracht wird (s. Abb. 12).
Richtet man deren Transmissionsrichtungen senkrecht
zueinander aus, so verschwindet das Interferenzmuster.
Bringt man nun einen weiteren Polarisationsfilter, dessen Transmissionsrichtung um 45◦ zu den beiden anderen verdreht ist, an die Stelle, wo die beiden Strahlengänge wieder vereint sind, erscheint das Interferenzmuster wieder.
Hierfür gibt es zwei verschiedene Erklärungen, von denen eine aus der modernen Quantenphysik stammt.
Erklärung im Wellenmodell
Die Grundlage für Interferenz ist die Überlagerung von kohärenten Wellen. Polarisiertes Licht kann
auch inkohärent sein, was Interferenzerscheinungen
unmöglich macht. Bringt man jeweils einen Polarisator
in den Strahlengang der Teilstrahlen des Mach-ZehnderInterferometers und richtet die Transmissionsrichtungen der Polarisationsfilter parallel aus, so ergibt sich,
die im oberen Teil von Abb. 13 dargestellte Situation.
Die hindurchgelassenen Schwingungskomponenten sind
darunter dargestellt, und zwar nur die Projektionen auf
die z-Achse, in beliebiger zeitlicher Reihenfolge. Für
jedes Strahlenbündel ergibt sich eine statistische Verteilung dieser Schwingungskomponenten, und da beide
Verteilungen genau gleich sind, interferieren die Teilwellen paarweise miteinander. Im Versuch wird dementsprechend ein strukturiertes Interferenzbild beobachtet.
Dagegen erscheint bei untereinander senkrechten Polarisatoren (Abb. 13, unten) auf dem Schirm eine helle Fläche ohne Interferenzmuster. Man könnte argumentieren, dass aufeinander senkrechte Polarisationsrichtungen nicht miteinander interferieren, da sie sich
nicht gegenseitig beeinflussen können – jede der beiden
Schwingungen hat schließlich in Richtung der jeweils
9
Abbildung 12: Der Quantenradierer – das Mach-Zehnder-Interferometer mit Polarisatoren in den Strahlengängen.
anderen die Komponente null. Dann müsste aber nach
Drehung der Schwingungsrichtung der einen Welle um
90◦ (z. B. durch eine optisch aktive Substanz) das Interferenzbild wieder erscheinen, was aber nicht geschieht.
Vielmehr sind die beiden Teilbündel nach dem Durchgang durch die senkrecht gestellten Polarisatoren völlig
inkohärent. Die einzelnen Wellenzüge des ursprünglichen Lichtbündels werden nämlich in ihre Komponenten senkrecht und parallel zur Polarisatorachse zerlegt,
wobei nur die jeweils parallelen Anteile durchgelassen
werden. Damit haben die Teilbündel aber keinerlei Korrelation mehr miteinander. Man betrachte zur Illustration vor allem den unteren Teil von Abb. 13, in dem die
zu den jeweiligen Polarisationsachsen parallelen Komponenten separat dargestellt sind. Man erkennt hier keinen statistischen Zusammenhang.
Bringt man einen dritten Polarisator in den Strahlengang (s. Abb. 12) und richtet dessen Transmissionsrichtung parallel zur z-Achse aus, so erscheint das Interferenzmuster wieder. Die vorher auf die ±45◦-Achsen projizierten Schwingungskomponenten, werden nun auf die
z-Achse projiziert und haben somit wieder die gleiche
Verteilung der Schwingungskomponenten; die Kohärenz
der Teilwellen ist wiederhergestellt.
Alternative Erklärung
Der alternativen Erklärung aus der modernen Quentenphysik verdankt der Quantenradierer seinen Namen. Sie
erhalten diese Erklärung in Form eines Artikels bei Ihrem Versuchsbetreuer.
Rekapitulation
1. Was ist der Quantenradierer und wie ist er aufgebaut?
2. Mit welchen Beobachtungen ist zu rechnen?
3. Wie beeinflussen die senkrecht zueinander stehenden Polarisationsfilter die Kohärenz der Teilwellen?
4. Was bewirkt der dritte Polarisationsfilter?
10
Abbildung 13: Zur Demonstration der Inkohärenz der aus unpolarisiertem Licht ausgesiebten zueinander senkecht linear
polarisierten Teilwellen. Im unteren Teil sind die Schwingungsrichtungen völlig unkorreliert.
II.
TECHNISCHE GRUNDLAGEN
II.1.
Strahlenteiler und Spiegel
Ein Strahlenteiler wird verwendet um einen Lichtstrahl
in zwei Teilstrahlen zu zerlegen. In diesem Versuch ist
der Strahlenteiler aus einer beschichteten Glasscheibe
im 45◦ -Winkel zum Strahl konstruiert. Trifft der Lichtstrahl auf die Glasscheibe, so wird ein Teil des Strahls
reflektiert. Der andere Teil passiert die Scheibe und
trifft auf den Spiegel, der diesen vollständig reflektiert
(s. Abb. 14). Um die relative Lage der Teilstrahlen zueinander beeinflussen zu können, lässt sich der Spiegel
in horizontaler und vertikaler Ebene kippen. Hierzu die-
nen die an ihm befindlichen Schrauben.
II.2.
Justierhilfe
Der Versuchsaufbau des Mach-Zehnder-Interferometers
muss sehr genau justiert werden, um Interferenz beobachten zu können. Da man die Laserstahlen nur sieht,
wenn sie von einem Objekt reflektiert werden, ist es
nicht ganz einfach sie auszurichten. Um dies zu vereinfachen, bietet es sich an, eine Justierhilfe zu verwenden. Abb. 15 zeigt eine Möglichkeit sie zu konstruieren.
Hierbei ist ein Blech mit Hilfslinien und -bohrungen an
einem Standfuß befestigt. Stellt man diese Justierhilfe in den Strahlengang, so lassen sich die Teilstrahlen
11
Abbildung 16: Ansicht der Luftküvette von oben.
II.4.
Abbildung 14: Prinzip der im Versuch verwendeten Baugruppe, bestehend aus Strahlenteiler und Spiegel.
Küvette
Die Küvette ist ein Zylinder mit transparenten Stirnflächen, der evakuiert werden kann (Abb. 16). Hierzu
besitzt sie einen Anschluss mit Ventil, an den eine Pumpe angeschlossen werden kann. Ein weiterer Anschluss
(ohne Ventil) dient der Verbindung mit einem Druckmessgerät. Die Länge der Küvette beträgt s = 339 mm.
sichtbar machen und an den Hilfslinien der Schablone
ausrichten. Sind die Teilstrahlen korrekt ausgerichtet,
so passieren sie die Schablone durch die dafür vorgesehenen Löcher. Da die Löcher etwas kleiner als der Querschnitt der Laserstrahlen sind, leuchten die Ränder der
Löcher auf, wenn die Strahlen sie passieren.
II.5.
Quecksilbermanometer
Das Quecksilbermanometer besteht aus einem Glasrohr
in U-Form, welches mit Quecksilber befüllt ist. Das
rechte Ende des Glasrohres ist nach oben geöffnet, so
dass der Atmosphärendruck auf die rechte Quecksilbersäule im Rohr wirken kann. Das linke Ende lässt
sich über einen Schlauch an eine Küvette anschließen, womit der Innendruck der Küvette auf die linke
Quecksilbersäule wirkt. Sind Atmosphären- und Küvettendruck gleich groß, so ist die Höhendifferenz der
Quecksilbersäulen null, ansonsten lässt sich die Differenz der Drücke direkt an der Differenz der Höhen der
Quecksilbersäulen ablesen. Aus Sicherheitgründen ist
das Quecksilbermanometer auf der rechten Seite durch
einen Gummipfropfen und auf der linken Seite durch
ein angeflanschtes Metallendstück verschlossen.
III.
Abbildung 15: Justierhilfe zur leichteren Ausrichtung der
Teilstrahlen.
II.3.
Linse
Die im Versuch verwendete Linse ist Teil eines Mikroskopobjektivs, das an einem rechtwinkligem Stativ befestigt ist. Die Brennweite der Linse beträgt
f = 4,34 mm und ist durch eine schwarze Linie auf
weißem Grund gekennzeichnet.
VERSUCHSDURCHFÜHRUNG
Vorbemerkung: Einen Großteil der Versuchszeit
werden Sie für den Aufbau des Interferometers
verwenden (Teilversuch 1). Dies ist ein
anspruchsvoller optischer Aufbau und nicht zu
vergleichen mit Versuchen wie z.B. OPT, LIN
und OIN aus Ihrem ersten Grundpraktikum. Es
dauert lange, bis die Strahlengänge optimal
verlaufen und ein brauchbares Interferenzbild
erscheint, was nicht ungewöhnlich für ein
interferometrisches Experiment ist. Dabei
werden Sie lernen, beim Experimentieren mit
Überlegung, Geduld und Präzision vorzugehen.
12
III.1.
III.5.
Mach-Zehnder-Interferometer
Bauen Sie das Mach-Zehnder-Interferometer (MZI) auf.
• Beobachten, skizzieren und beschreiben Sie die Interferenzerscheinung!
Quantenradierer
Bauen Sie den Quantenradierer auf und beobachten sie
das Interferenzmuster mit und ohne den dritten Polarisationsfilter.
• Beschreiben Sie ihre Beobachtungen!
III.2.
Wellenlänge des Lasers
IV.
Messen Sie die notwendigen Größen zur Bestimmung
der Wellenlänge des Laserlichtes!
IV.1.
III.3.
AUSWERTUNG
Mach-Zehnder-Interferometer
Brechzahl von Luft
Messen Sie die notwendigen Größen zur Bestimmung
der Brechzahl von Luft mit Hilfe des MZI.
Notieren Sie, während des Einströmens der Luft, bei
einigen äquidistanten Werten von ∆m, die Differenz
∆p zwischen Atmosphären- und Küvettendruck. Die
Druckdifferenz entspricht dem Höhenunterschied der
Quecksilbersäulen des Quecksilbermanometers. Den aktuellen Atmosphärendruck können Sie am Quecksilberbarometer im Raum 326 ablesen.
III.4.
Polarisation
Beobachten und beschreiben Sie bitte qualitativ mindestens eines der folgenden Phänomene (im Laborprotokoll)! Hilfsmittel bzw. Versuchsaufbauten zeigt Ihnen
Ihr Praktikumsbetreuer.
keine
IV.2.
Wellenlänge des Lasers
Bestimmen Sie mit Ihren Messdaten die Wellenlänge
des Laserlichtes (mit Berechnung der Messabweichung
nach Gaußs), und vergleichen Sie Ihr Ergebnis mit der
Herstellerangabe.
IV.3.
Bestimmen Sie mit Ihren Messdaten die Brechzahl von
Luft und vergleichen Sie diese mit dem Literaturwert!
IV.4.
3. Untersuchen Sie die Doppelbrechung eines Kalkspats!
Polarisation
keine
1. Bestätigen Sie die Existenz des Brewsterwinkels!
2. Weisen Sie die Polarisation des Himmelsblau
nach!
Brechzahl von Luft
IV.5.
Quantenradierer
Erklären Sie ihre Beobachtungen!