Lineare Regression in R, Teil 2 - WWZ

Lineare Regression in R, Teil 2
Christian Kleiber
Abt. Quantitative Methoden, WWZ, Universität Basel
28. Oktober 2009
1
Vorbereitungen
Zur Illustration betrachten wir wieder den Datensatz CASchools.
Laden des Paketes und der Daten:
R> library("AER")
R> data("CASchools")
Wie schon diskutiert müssen die benötigten Variablen zunächst erzeugt werden:
R> CASchools$stratio <- with(CASchools, students/teachers)
R> CASchools$score <- with(CASchools, (read + math)/2)
2
Testen allgemeiner linearer Hypothesen
Tests zur Überprüfung von Hypothesen des Typs H0 : βj = 0 wurden bereits besprochen. Manchmal will man Hypothesen von allgemeinerer Form testen.
Angenommen, wir wollen im Modell
score = β0 + β1 stratio + β2 english + ui
geschätzt mit
R> fm2 <- lm(score ~ stratio + english, data = CASchools)
die Hypothese H0 : β1 = β2 testen, oder äquivalent H0 : β1 − β2 = 0, d.h. die Koeffizienten
zu stratio und english sind gleich (keine inhaltlich sinnvolle Hypothese, nur eine Illustration).
Solche Hypothesen können mit der Funktion linear.hypothesis() aus dem Paket car getestet
werden. (Dieses Paket muss i.a. erst installiert werden. Wenn Sie aber schon AER installiert haben,
wurde car bereits automatisch mitinstalliert; es wird beim Laden von AER auch automatisch
mitgeladen).
Die einfachste Möglichkeit besteht nun in der Nutzung einer Formelschreibweise:
R> linear.hypothesis(fm2, "str = english", vcov = sandwich)
oder alternativ
R> linear.hypothesis(fm2, "str - english", vcov = sandwich)
Im zweiten Fall wird also von der Funktion verstanden, dass die “rechte Seite” der Hypothese Null
ist.
Lineare Regression in R, Teil 2
2
Unser Problem lässt sich aber noch etwas allgemeiner (und damit transparenter!) formulieren: In
Matrixform ist eine allgemeine lineare Hypothese von der Form
Rβ = r
(1)
wobei β der (k + 1) × 1 Vektor der Regressionskoeffizienten, R eine q × (k + 1) Matrix und r ein
q × 1 Vektor sind.
Die Funktion linear.hypothesis() kann auch mit dieser Formulierung umgehen, sie benötigt
dafür eine hypothesis.matrix (die Matrix R aus (1)), und rhs (der Vektor r auf der rechten
Seite von (1)). In unserem Fall reduziert sich die Matrix R zu einem (Zeilen-)Vektor, da wir nur
eine einzelne lineare Hypothese testen, und die rechte Seite ist ein Skalar.
Eine weitere Möglichkeit des Tests ist deshalb gegeben durch den Funktionsaufruf
R> linear.hypothesis(fm2, hypothesis.matrix = c(0, 1, -1), rhs = 0)
Linear hypothesis test
Hypothesis:
stratio - english = 0
Model 1: score ~ stratio + english
Model 2: restricted model
1
2
Res.Df
RSS
417 87245
418 87526
Df Sum of Sq
-1
F Pr(>F)
-281 1.34
0.25
Das Ergebnis von linear.hypothesis() ähnelt dem von anova(): man erhält die zu vergleichenden Modelle mit Freiheitsgraden, Fehlerquadratsummen und zugehöriger F -Statistik. Demnach
kann die Hypothese zu den üblichen Signifikanzniveaus nicht verworfen werden.
Bei Verdacht auf Heteroskedastie kann man solche lineare Hypothesen wie oben auch gleich mit
einer Eicker-White-Kovarianzmatrix testen:
R> linear.hypothesis(fm2, hypothesis.matrix = c(0, 1, -1), rhs = 0, vcov = sandwich)
Linear hypothesis test
Hypothesis:
stratio - english = 0
Model 1: score ~ stratio + english
Model 2: restricted model
Note: Coefficient covariance matrix supplied.
1
2
Res.Df
417
418
Df
F Pr(>F)
-1 1.09
0.3
Die heteroskedastie-robuste Version führt also bei den üblichen Signifikanzniveaus zur gleichen
Testentscheidung.
3
Formeln
R bietet eine flexible Formelmethode an, um Regressionsmodelle zu spezifizieren. Dabei haben
allerdings die Grundrechenarten eine neue Bedeutung, bspw. bedeutet wie schon gesehen y ~x + z
Regression von y auf x und z (aber eben nicht auf x + z):
c
Christian Kleiber
U Basel, HS 2009
Lineare Regression in R, Teil 2
3
R> fm2 <- lm(score ~ stratio + english, data = CASchools)
Analog bedeutet "-" Weglassen von Regressoren. Ein Modell mit nur dem Regressor stratio
ergibt sich bspw. aus fm2 unter Verwendung der Funktion update() über
R> fm1 <- update(fm2, . ~ . - english, data = CASchools)
Die Grundrechenarten werden insb. gebraucht, um Interaktionsterme kompakt zu spezifizieren.
Ein Modell mit Interaktionen zwischen den metrischen Regressoren stratio und english wird
spezifiziert durch:
R> fmint1a <- lm(score ~ stratio + english + stratio:english, data = CASchools)
oder kompakter durch
R> fmint1b <- lm(score ~ stratio * english, data = CASchools)
Dabei ist stratio:english der Interaktionsterm selbst, und stratio * english steht für eine
Regression auf die angegebenen Regressoren und sämtliche Interaktionsterme.
Besonders elegant (aber anfangs etwas gewöhnungsbedürftig) ist die Formelschreibweise im Zusammenhang mit Faktoren (qualitativen Variablen):
Sei dazu a eine kategoriale Variable (Faktor) mit k Stufen. Im Ökonometrie-Jargon würde man
dazu k − 1 Dummies einführen, der Vorteil der R-Version ist, dass man nur eine einzige Variable
verwalten muss und diese Dummies im Hintergrund automatisch erzeugt werden. Damit kann
man insb. sehr schnell die Referenzkategorie wechseln. Tabelle 1 zeigt einige Möglichkeiten, mit
Faktoren und einer metrischen Variablen x sehr kompakt Interaktionen zu spezifizieren.
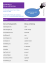
Tabelle 1: Formeln in Regressionsmodellen.
Formel
y ~ a + x
y ~ a * x
y ~ a + x + a:x
y ~ a / x
y ~ a + x %in% a
Beschreibung
Modell ohne Interaktion: identische Steigungen bzgl.
x, aber unterschiedliche Achsenabschnitte bzgl. a.
Modell mit Interaktion: der Term a:x erzeugt
die Differenz der Steigungen bzgl. der Referenzkategorie.
Modell mit Interaktion: gleiche ŷi wie oben,
aber Koeffizienten hierarchisch kodiert. Explizite
Steigung für jede Kategorie von a.
Ein Beispiel zu Interaktionen zwischen einem Faktor und einem metrischen Regressor (um die
Möglichkeiten der Formelsprache deutlicher zu machen, wird der Faktor noch etwas aufbereitet):
R>
R>
R>
R>
henglish <- I(CASchools$english >= 10)
henglish <- factor(henglish, labels = c("no", "yes"))
fmint2 <- lm(score ~ stratio * henglish, data = CASchools)
coeftest(fmint2, vcov = sandwich)
t test of coefficients:
(Intercept)
stratio
henglishyes
stratio:henglishyes
c
Christian Kleiber
Estimate Std. Error t value Pr(>|t|)
682.246
11.811
57.76
<2e-16
-0.968
0.586
-1.65
0.10
5.639
19.421
0.29
0.77
-1.277
0.962
-1.33
0.19
U Basel, HS 2009
Lineare Regression in R, Teil 2
4
Hier wird henglish durch einen logischen Vergleich erzeugt: die Aussage english >= 10 ist für
einen gegebenen Schulbezirk entweder wahr oder falsch, somit entsteht ein Vektor mit diesen Einträgen. Er wird nun in einen Faktor verwandelt, dessen Ausprägungen "no" bzw. "yes" sind. Die
Referenzkategorie des Faktors enspricht dabei "no". Will man die Regression mit der Referenzkategorie "yes" durchführen, definiert man die Kategorien um. Am einfachsten geht dies mit der
Funktion relevel():
R> henglish <- relevel(henglish, ref = "yes")
R> fmint3 <- lm(score ~ stratio * henglish, data = CASchools)
R> coeftest(fmint3, vcov = sandwich)
t test of coefficients:
(Intercept)
stratio
henglishno
stratio:henglishno
4
Estimate Std. Error t value Pr(>|t|)
687.885
15.417
44.62
<2e-16
-2.245
0.763
-2.94
0.0034
-5.639
19.421
-0.29
0.7717
1.277
0.962
1.33
0.1854
Regression mit transformierten Variablen
Wie oben beschrieben haben die Grundrechenarten in Formeln eine spezielle Bedeutung. Will man
sie verwenden, um Regressoren zu transformieren, muss man deshalb einen Operator benutzen,
nämlich I(). Ein quadratischer Term im Regressor income wird bspw. spezifiziert über
R> fmquad <- lm(score ~ income + I(income^2), data = CASchools)
Transformationen, die keine Grundrechenarten enthalten, brauchen das I() nicht, deshalb genügt
z.B. für Logarithmen einfach
R> fmlinlog <- lm(score ~ log(income), data = CASchools)
Wird nun der transformierte Regressor selbst wieder mit einer Grundrechenart transformiert, muss
I() wieder verwendet werden:
R> fmlinlogquad <- lm(score ~ log(income) + I(log(income)^2), data = CASchools)
5
Visualisierung von Regressionsergebnissen
Zur Beurteilung der Anpassung ist es hilfreich, Graphiken zu erzeugen. Hier ein Beispiel für die
Regression fmlinlog:
R> plot(score ~ income, data = CASchools, pch = 20,
+ xlim = c(0, 60), ylim = c(600, 730))
R> grid <- seq(5, 55, by = 0.1)
R> lines(grid, coef(fmlinlog)[1] + coef(fmlinlog)[2] * log(grid),
+ col = "slategrey", lwd = 2)
R> legend("topleft", "linlog", col = "slategrey", lwd = 2, bty = "n")
c
Christian Kleiber
U Basel, HS 2009
720
Lineare Regression in R, Teil 2
5
linlog
●
●
680
●
●
●
●●
●● ● ●● ●● ●● ●
●●
● ● ●●
●
●● ●● ● ●●
● ●●
● ●●
●● ●●
● ●
●
●●
●●● ●●
●
●
●●●
● ●
●● ●●
●●
●
●●● ● ●
●●
●● ●
●
●
●●
●
●
●●●
● ●
●● ●
●
●
●
●●●
●
●
●●
●●
●
●
●●
●●
●●
●
●●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●●● ● ● ●
● ●●●
●
●●●●●
●
●
●●●
●
●
●●
●●
●
●
●●●
● ● ●●
●
●
●●
●
●●
●●
●
●
●
●
●
●
●
●●●●
●●●
●
●●
●
●
●●
●
●●●
●●●
●
●
●●●
●
●
● ●
● ●●
●●
●
●●
●
●
●
●
●
●
●
●
●
●
●●●
●
● ●●●
●●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
● ●●
●●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
● ●●
●
●
●●
●
●
●
●
●
●
●
●●●
●●
●
●
●
●
●
●●
●
●●
●
●
●●●
●
●
●
●
●
●
●
●
●●
●
●●● ●
●
●● ●● ●
●
●
●● ●
●●
●●●
●● ●
● ●
● ●●●
●
●●●●
● ●
●
●
● ● ●
600
640
score
●
0
10
20
●
●
●
●●
●
●
●
● ●
●
30
●
●
●
●
●
●
●
●
●
40
50
60
income
Dabei wird zunächst ein Vektor von Stützstellen (grid, hier eine Folge von Werten beginnend mit 5 und endend mit 55, bei einer Schrittweite von 0.1) erzeugt, in denen die Funktion
dann mit den geschätzten Regressionskoeffizienten ausgewertet wird (coef(fmlinlog)[1] + coef(fmlinlog)[2]*log(grid)), diese beiden Vektoren werden schliesslich in der Form plot(x,
y) gegeneinander abgetragen. Da die Punkte als Kurve zu einer bestehenden Graphik hinzugefügt
werden sollen, wird dabei aber nicht die Funktion plot(), sondern lines() verwendet.
c
Christian Kleiber
U Basel, HS 2009