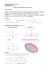a origem da computação - Afiliados

para o professor
Matemática
A origem da computação
propostas pedagógicas
CONTEXTUALIZAÇÃO
A
palavra “computador” não trás
para quem a diz, lê ou escreve
nenhuma referência à sua etimologia,
apesar de estar ainda em sua forma
original. Vem de “computar”, que remete a contar, calcular. O usuário do
computador no século XXI não asso-
propostas de atividades
O
artigo pode ser abordado sob duas
perspectivas. A primeira diz respeito aos limites para a tecnologia. Quais
são eles? Quão distante estão os primeiros computadores dos modelos de uso
doméstico atuais? Quais as diferenças
técnicas entre tais máquinas? Um ponto
de partida pode ser uma reflexão sobre
o comentário publicado na revista americana Popular Mechanics em 1949, que
afirmava: “no futuro, os computadores
não pesarão mais do que 1,5 toneladas.”
A segunda é levar o aluno de encontro à
realidade dos computadores humanos.
Para isso, é possível efetuar diversos procedimentos, que mostram o quanto de
trabalho se poupa ao apertar a tecla Enter. São procedimentos que, além de melhorarem a destreza aritmética, possibilitam aos estudantes visualizar aplicações
cia mais a invenção com o seu propósito original justamente por ela tê-lo ultrapassado. O artigo de MartIn
Campbell-Kelly tem, portanto, esse
mérito. Ao recapitular a origem da
computação e fazer uma breve retrospectiva ilustrada da fase moderna,
para conceitos como logaritmos que,
embora superadas, permitem conhecer
o quanto eles contribuíram para o avanço
científico (ver roteiro sugerido na edição
8 de Aula Aberta). Nessa perspectiva, é
possível também explorar o conceito da
recursividade (tão importante quanto ignorado no ensino médio), que ajuda a
desmitificar aparatos “mágicos” como as
calculadoras, que aparentemente têm na
memória todas as respostas possíveis.
plo, definir as progressões aritméticas e
geométricas usando princípios recursivos. Para isso, basta definir os valores do
primeiro termo e da razão; o que diferencia essas sequências é a operação realizada para se obter o termo seguinte (adição da razão ao termo anterior em um
caso, e multiplicação no outro). Tal definição permite estabelecer a condição para
que três termos consecutivos formem
uma dessas sequências e o cálculo do
termo geral de cada uma delas.
Assinale para os estudantes que em muitas linguagens de programação uma função pode chamar a si própria (uma característica das funções recursivas). O
processo recursivo baseia-se na recorrência válida para uma sequência: a obtenção dos termos seguintes ocorre a
partir dos anteriores e de um padrão previamente definido. É possível, por exem-
1
competências e habilidades segundo a matriz de referência do enem
MATEMÁTICA E SUAS TECNOLOGIAS
n Competência de área 5
H1 - Reconhecer, no contexto social,
diferentes significados e representações
dos números e operações - naturais,
inteiros, racionais ou reais.
H2 - Identificar padrões numéricos ou
princípios de contagem.
H3 - Resolver situação-problema
envolvendo conhecimentos numéricos.
H5 - Avaliar propostas de intervenção na
realidade utilizando conhecimentos numéricos.
CIÊNCIAS HUMANAS E SUAS
TECNOLOGIAS
n Competência de área 4
H16 - Identificar registros sobre o papel das
técnicas e tecnologias na organização do
trabalho e/ou da vida social.
n Competência de área 1
64 SCIENTIFIC AMERICAN BRASIL aula aberta
o estudante é apresentando a uma
máquina paradoxalmente tão familiar
quanto desconhecida.
H19 - Identificar representações algébricas que
expressem a relação entre grandezas.
H21 - Resolver situação-problema cuja
modelagem envolva conhecimentos algébricos.
Movimentações financeiras Uma
aplicação interessante da recursividade, para examinar com a classe,
é a variação do saldo em uma capitalização composta. Por exemplo, se
um capital C é depositado em um fundo com taxa mensal i, a sequência
de saldos pode ser obtida de a1 = C
e an = an-1 + an-1 . i = an-1 . (1 + i) . É possível, com isso, mostrar a diferença entre
as capitalizações simples e composta
e associar cada uma delas às progressões aritméticas e geométricas. A recursividade, no caso, ilustra o conceito
de “juros sobre juros” da capitalização
composta. É possível, ainda, ampliar as
movimentações financeiras estudadas.
A variação do saldo se um depósito D é
feito periodicamente é dada por a1 = C e
an = an-1 . (1 + i)+ D . Repare como a definição recursiva simplifica bastante o
entendimento do conceito, acrescentan-
do somente o depósito em relação à movimentação anterior. Outra possibilidade
é a evolução da dívida S em P parcelas
iguais, com a1 = S e an = an-1 . (1 + i) – P.
Pode-se variar inserindo tempo de carência ou pagamento de entrada, por
exemplo. Para dar conta de movimentações financeiras com prazos longos,
recomenda-se o uso de planilhas eletrônicas (Microsoft Excel e BrOffice
Calc são adequados). A grande vantagem que a recursividade traz nesses casos é a compreensão da variação de cada movimentação, o que
não acontece quando aplica-se as fórmulas algébricas. O uso de recursos
computacionais ilustra bem os benefícios da tecnologia discutidos anteriormente. Ainda, movimentações financeiras são (ou deveriam ser!) de
interesse de membros de uma sociedade de consumo tal qual a nossa.
de abscissa k, tem valor 2k. De modo genérico, o coeficiente angular da reta tangente à curva em um ponto de certa função f(x) é dado pelo valor numérico da
derivada f´(x) para a abcissa desejada.
No caso das funções polinomiais f(x) =
anxn, a derivada é dada por f’(x) = n .anxn1
, regra que pode ser aplicada a cada
um dos termos xn dessas funções . No
caso, f(x) = x2 – 2 e f´(x) = 2x. Em x = 4,
a reta tangente tem coeficiente angular
f’(4) = 2 . 4 = 8 . Assim, a equação da reta
tangente é dada por y = 8x + b. Como (4;
14) pertence à reta, 14 = 8 . 4 + b => b = –
18. Logo, a equação dessa reta é y = 8x
– 18 , cuja raiz é 2,25. Assim, se a1 = 4, a2
= 2,25. Observe a representação da reta
e dos valores no gráfico abaixo. Cada
novo valor obtido será mais próximo do
valor desejado, e essa convergência é
com frequência bastante rápida. Repetindo o processo e aproximando alguns
valores, conforme a precisão desejada, a
nova reta tangente será y = 4,5x – 7,04,
com raiz a3 = 1,56. Após 5 etapas, obtêm-se a5 = 1,41. É importante destacar para
os alunos a associação entre o funcionamento de calculadoras com procedimentos semelhantes. Afinal, elas não têm
todas as respostas salvas na memória.
Um bom exercício é implantar o processo recursivo em uma planilha eletrônica
e, com isso, obter resultados com maior
precisão. É necessário enfatizar que a dificuldade operacional que enfrentamos
não é compartilhada pelos computadores digitais, mas só é possível utilizar um
computador após ser programado por
seres humanos. Cabe, aqui, uma discussão entre o emprego de máquinas substituindo funcionários e a necessidade de
mão-de-obra qualificada para colocar
tais máquinas em funcionamento.
2
Método de Newton-Raphson para
calcular raízes Processos recursivos
também foram importantes para a obtenção de raízes de funções e, com isso, a
obtenção de parte da dízima de números irracionais. Um dos primeiros métodos conhecidos foi desenvolvido por
Newton e aperfeiçoado por Raphson e
envolve conceitos de Cálculo para sua
aplicação. No entanto, é possível apresentar a recursividade para um caso específico. Por exemplo, vamos calcular o
valor aproximado de 2. Se x = 2, então x2 = 2 => x2 – 2 = 0. Ou seja, o número desejado anula a função f (x) = x2 – 2,
cujo gráfico é ilustrado abaixo. Aplicando
a lei da função, percebe-se que x = 4 não
é o valor desejado: f(4) = 16 – 2 = 14. A
grande idéia aqui foi obter o valor seguinte a ser testado calculando a abscissa
do ponto onde a reta tangente à parábola no ponto (4; 14) intercepta o eixo das
abscissas. A informação que precisa ser
dada aos alunos (e pode ser ilustrada esboçando algumas situações) é de que o
coeficiente angular dessa reta, no ponto
SUGESTÕES DE LEITURA
MAOR, Eli. e: a história de um número. Rio de Janeiro. Record. 2003 (capítulos 1, 2 e 3).
DU SAUTOY, Marcus. A música dos números primos. Rio de Janeiro. Jorge Zahar Editor. 2003 (capítulos 8, 9 e 10).
CÓSER FILHO, Marcelo Salvador. Aprendizagem de matemática financeira no Ensino
Médio: uma proposta de trabalho a partir das planilhas eletrônicas. Porto Alegre. UFRGS.
2008. (Disponível em http://www.lume.ufrgs.br/).
Roteiro sugerido por Marcelo Salvador Cóser Filho, professor de Matemática do Colégio Monteiro Lobato e do Curso Anglo,
em Porto Alegre. É licenciado em Matemática e mestre em Ensino de Matemática pela UFRGS.
SCIENTIFIC AMERICAN BRASIL aula aberta
65