Modelo de elétrons livres em um metal dEE h mV dEEg )2(8 )( = 1 )2
Transcrição
Modelo de elétrons livres em um metal dEE h mV dEEg )2(8 )( = 1 )2
Modelo de elétrons livres em um metal Vamos considerar e– em um poço 3D (limites da rede cristalina) Número de estados (caso anterior x 2, pois 2 estados de spin em cada nível): 8 V ( 2m 3 )1/ 2 1/ 2 g ( E ) dE = E dE 3 h Ocupação dos estados (distribuição de Fermi): f (E) = 1 α e e E / kT +1 = 1 e ( E − E F ) / kT +1 , com E F = −αkT Então a ocupação dos estados de energia do gás de e–, fica: 8 V ( 2m 3 )1/ 2 E 1/ 2 dE n( E ) = f ( E ) g ( E ) dE = h3 e ( E − E F ) / kT + 1 Normalização: se T = 0 K ⇒ estados populados só até EF ⇒ ⇒ f(E) = 1, se E < EF e f(E) = 0, se E > EF. FNC0376 - Física Moderna 2 Aula 16 1 1,0 1/2 E 0,8 = 0,6 n(E) X 0,4 0,2 0,0 0,0 0,2 0,4 0,6 0,8 1,0 E f(E) = 1, se E < EF e f(E) = 0, se E > EF. Assim: EF 8 V ( 2m 3 )1/ 2 N = ∫ n( E ) dE = 3 h 0 ⇒ E F (0) = h 3N 8m V 2 EF 16 V ( 2m 3 )1/ 2 3 / 2 EF ⇒ 3 ∫0 E dE = 3h 1/ 2 2/3 Expressão define EF em T = 0 K FNC0376 - Física Moderna 2 Aula 16 2 h 2 3N E F (0) = 8m V 2/3 h 2 3ρ = 8m 2/3 com ρ = N/V . Excelente aprox. para kT << EF (até milhares de K, para metais comuns, veja tabela na próxima transparência). Vemos então que, à medida que mais partículas são adicionadas ao sistema, EF cresce. Se a temperatura estiver ligeiramente acima de 0 K, EF deixa de ser a energia do último estado ocupado e é definida como a energia em que n(E) = ½; à medida que T aumenta, EF diminui. Para temperaturas suficientemente altas, EF < 0, implicando que todos os estados, em média, têm menos de ½ partícula. FNC0376 - Física Moderna 2 Aula 16 3 A energia total do sistema, em T = 0 K, é: EF 3 1/ 2 E F 3 1/ 2 ( 2 ) 8 V ( 2m ) 16 V m 3/ 2 5/ 2 E dE E E = ∫ n( E ) EdE = = F (0) 3 3 ∫ 5h h 0 0 16 V ( 2m 3 )1/ 2 3 / 2 3 Mas N = EF ⇒ E = NE F 3 3h 5 Notem que, mesmo em T = 0 K, o último férmion adicionado, aquele com energia EF, tem velocidade dada por: - de condução em um metal No caso de 1 e 1 2 EF 2 mv F = EF ⇒ v F = típico (EF ~ 5 eV) a velocidade de Fermi é da 2 m ordem de 106 m/s (a 0 K!). A temperatura de Fermi é definida como: TF = EF /k. FNC0376 - Física Moderna 2 Aula 16 4 Parênteses termodinâmico Lembrando de 1 dos limites de validade da distribuição de Maxwell-Boltzmann: λ << d. Sendo λ o comprimento de onda de de Broglie da partícula. Podemos então definir o comprimento de onda térmico de de Broglie, como aquele associado ao momento médio de uma partícula em equilíbrio térmico no sistema, cuja energia cinética é 3kT/2: λ= h 2 mkT Consideremos um sistema com um número grande de partículas, com energia total E, em equilíbrio térmico à temperatura T. Suponhamos que esse sistema seja um gás e que ele seja comprimido, lentamente, reduzindo seu volume em dV. Isso provoca um aumento nos níveis de energia, pois diminuímos o tamanho da caixa. Assim, um nível εi passa a εi + dεi e as partículas nesse estado ganham energia dεi. O ganho total do sistema será: dE = ∑ ni dε i i Esse ganho de energia veio do trabalho realizado para comprimir o sistema. Se uma das arestas do cubo for reduzida de dL por uma força F, teremos: dW = – FdL. FNC0376 - Física Moderna 2 Aula 16 5 A força F é necessária para se opor à pressão do gás. Assim, F = PA. Substituindo na expressão do trabalho: dW = – PAdL = – PdV. Como o trabalho deve ser igual ao aumento de energia do sistema, temos: − PdV = dE = ∑ ni dε i ⇒ P = −∑ ni i i dε i dV Os níveis de energia de uma caixa cúbica são dados por: ( ) 2 2 h −2 / 3 ⇒ = C V ε n1n2n3 = n12 + n22 + n32 ε i i 2mL2 −2 / 3 dε i dCiV −2 / 3 C V 2 2 2 εi −5 / 3 i Assim: = = − CiV =− =− dV dV 3 3 V 3V Dessa forma, para um gás ideal, seja ele clássico, fermiônico ou bosônico, temos: dε i 2 1 2E onde E é a energia total média do gás. = P = −∑ ni niε i = ∑ 3V dV 3 V i i No caso de um gás clássico (Boltzmann) a energia média, por partícula, é: 3 ε = kT 2 FNC0376 - Física Moderna 2 Aula 16 6 A energia total do sistema é: E = N ε ⇒ PV = NkT = nRT que nos remete à conhecida expressão da lei dos gases ideais. Nós vimos que as distribuições quânticas se reduzem à clássica quando α é muito grande. Podemos escrever as funções de distribuição como: 1 f( )= α e e kT = −α e e − −α kT ±1 1± e e − kT com o sinal de cima valendo para férmions e o de baixo para bósons. A distribuição de Boltzmann é obtida fazendo o denominador igual a 1, o que −α − é equivalente a e e kT << 1 Vamos tentar uma aproximação um pouco melhor e fazer uma expansão binomial (para x << 1): 1 = 1m x + x2 L 1± x −α Nesse caso a distribuição fica: f ( ) = e e − kT − −α kT 1 m e e + L A partir desse resultado, seguindo um caminho um pouco trabalhoso, pode-se mostrar que a lei dos gases pode ser escrita como: FNC0376 - Física Moderna 2 Aula 16 7 N λ3 PV = NkT 1 ± + L 5/ 2 V 2 No caso da energia média, por partícula, do sistema, temos: E 3 N λ3 ε = = kT 1 ± + L 5/ 2 N 2 V 2 Substituindo o valor do comprimento de onda térmico: E 3 1 N h3 ε = = kT 1 ± 5 / 2 + L 3/ 2 N 2 2 V (2 mkT ) + – férmions bósons Daí pode-se perceber que a energia média de um gás de férmions é um pouco superior à de um gás ideal, enquanto à de um gás de bósons é um pouco menor. Valor do termo de correção é boa indicação da necessidade, ou não, de se usar as distribuições quânticas. Se o termo de correção << 1 a distribuição de Boltzmann (e os resultados decorrentes dela) são OK. FNC0376 - Física Moderna 2 Aula 16 8 FNC0376 - Física Moderna 2 Aula 16 9 FNC0376 - Física Moderna 2 Aula 16 10

















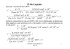 O resultado de que B12 = B21 é muito interessante, pois mostra que os
processos de emissão e absorção (estimulados) só dependem das
características físicas do átomo.
O resultado de que B12 = B21 é muito interessante, pois mostra que os
processos de emissão e absorção (estimulados) só dependem das
características físicas do átomo.



