Tabela Derivadas e integrais
Transcrição
Tabela Derivadas e integrais
Prof. Joaquim Rodrigues TABELA DE DERIVADAS E INTEGRAIS 01) DERIVADAS Se f ( x) = x , então f ′( x) = 1 INTEGRAIS ∫ 1 dx = 1 ∫ dx = ∫ dx = x + c 02) Se f ( x) = ax , então f ′( x) = a ∫ adx = a ∫ dx = ax + c 03) Se f ( x) = x n , então f ′( x) = n ⋅ x n − 1 04) Se f ( x) = log a x , então f ′( x) = 05) n ∫ x dx = 1 x ⋅ ln a x n +1 + c , n ≠ −1 n +1 1 ∫ x ⋅ ln a dx = log a x+c ∫ x dx = ln x + c 06) 1 x x Se f ( x) = a , então f ′( x) = a x ⋅ ln a 07) Se f ( x) = e x , então f ′( x) = e x 08) Se f ( x) = sen x , então f ′( x) = cos x 09) Se f ( x) = cos x , então f ′( x) = − sen x 10) Se f ( x) = tg x , então f ′( x) = sec 2 x 11) Se f ( x) = ctg x , então f ′( x) = − csc 2 x 12) Se f ( x) = sec x , então f ′( x) = tg x ⋅ sec x 13) Se f ( x) = csc x , então f ′( x) = −ctg x ⋅ csc x ∫ e dx = e + c ∫ cos x dx = sen x + c ∫ sen x dx = − cos x + c ∫ sec x dx = tg x + c ∫ csc x dx = −ctg x + c ∫ sec x ⋅ tg x dx = sec x + c ∫ csc x ⋅ ctg x dx = − csc x + c 14) Se f ( x) = arc tg x , então f ′( x) = 15) 16) 17) 18) 1 Se f ( x) = ln x , então f ′( x) = x ∫ a dx = x ( ) x 2 2 1 1+ x2 1 Se f ( x) = arc sen x , então f ′( x) = 1− x2 1 Se f ( x) = arc cos x , então f ′( x) = − 1− x2 Se f ( x) = ln x + x 2 + 1 , então f ′( x) = ax +c ln a 1 ∫1+ x ∫ ∫− 1 1+ x2 1 1+ x 1 Se f ( x) = ⋅ ln , então f ′( x) = 1− x 1− x2 2 2 dx = arc tg x + c 1 1− x2 1 dx = arc sen x + c dx = arc cos x + c 1− x2 1 2 ∫ 1 + x 2 dx = ln x + x + 1 + c 1 1 1+ x ∫ 1 − x 2 dx = 2 ⋅ ln 1 − x + c Regra do produto: Se f ( x) = u ⋅ v , então f ′( x) = u ′v + uv ′ Regra de L’Hospital Seja lim f ( x) = 0 e lim g ( x) = 0 e se existe Regra do quociente: u ′ ⋅ v − u ⋅ v′ u Se f ( x) = , então: f ′ ( x) = . v v2 f ′( x) f ( x) lim , então existe lim e daí temos: x → a g ( x) x → a g ′( x ) f ( x) f ′( x) lim = lim x → a g ( x) x → a g ′( x ) Regra da cadeia: f ( x) = g [h ( x)] ⇒ f ′( x) = g ′ [h ( x)] ⋅ h ′ ( x) x→a x→a Prof. Joaquim Rodrigues INTEGRAÇÃO POR PARTE: ∫ f ( x) ⋅ g ′( x) dx = f ( x) ⋅ g ( x) − ∫ f ′( x) ⋅ g ( x) dx PRODUTOS NOTÁVEIS 1. ( A + B) 2 = A 2 + 2 AB + B 2 2. ( A − B) 2 = A 2 − 2 AB + B 2 3. A 2 − B 2 = ( A + B)( A − B) 4. 5. 6. 7. ( A + B) 3 = A 3 + 3 A 2 B + 3 AB 2 + B 3 ( A − B) 3 = A3 − 3 A 2 B + 3 AB 2 − B 3 A 3 − B 3 = ( A − B)( A 2 + AB + B 2 ) A 3 + B 3 = ( A + B)( A 2 − AB + B 2 ) EXPOENTES INTEIROS 1. a m ⋅ a n = a m + n am 2. = a m − n ( a ≠ 0 e m ≥ n) n a ( ) PRINCIPAIS BASES DOS LOGARITMOS 1. LOG A = LOG 10 A 2. LN A = LOG e A , onde e = 2 , 71 COLOGARITMO: COLOG B A = − LOG B A ARCOS NOTÁVEIS 30º 45º sen 1 2 2 2 cos 3 2 2 2 tg 3 1 3 60º 3 2 1 2 3 n 3. a m = a m ⋅ n 4. (a ⋅ b) n = a n ⋅ b n a a 5. = n (b ≠ 0) b b CICLO TRIGONOMÉTRICO 0o 90º 180º 270º sen 0 1 0 −1 cos 1 0 0 −1 EXPOENTES FRACIONÁRIOS 1. n a ⋅ n b = n a ⋅ b Vale lembrar que π rad → 180° n 2. 3. n a n b n =n n a b am = a (b ≠ 0) m n FÓRMULA DA EQUAÇÃO DE 2º GRAU Dado Ax 2 + Bx + C = 0 , então x= 360º 0 1 − B ± B 2 − 4 AC 2A LOGARITMOS 1. LOG K A + LOG K B = LOG K (AB ) A 2. LOG K A − LOG K B = LOG K B n 3. LOG K A = n ⋅ LOG K A MUDANÇA DE BASE LOG K A LOG B A = LOG K B IDENTIDADES FUNDAMENTAIS 1. sen 2 x + cos 2 x = 1 sen x 2. tg x = cos x cos x 3. cot g x = sen x 1 4. sec x = cos x 1 5. cos sec x = sen x FÓRMULAS PARA O ARCO DOBRO 1. sen 2a = 2 sen a ⋅ cos a cos 2a = cos 2 a − sen 2 a 2. cos 2a = 1 − 2 sen 2 a cos 2a = 2 cos 2 a − 1
Documentos relacionados
trabalho 1 - WordPress.com
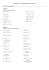 ∫ cos (ln x) ⋅ x dx
∫ sen x ⋅ cos x dx
∫ tg x ⋅ sec x dx
∫ cos 7 x dx
∫ cos x dx
∫ cos (ln x) ⋅ x dx
∫ sen x ⋅ cos x dx
∫ tg x ⋅ sec x dx
∫ cos 7 x dx
∫ cos x dx




