Introdução à radiação solar

UNIVERSIDADE DO VALE DO RIO DOS SINOS
UNISINOS
Programa de Pós-Graduação em Engenharia Mecânica
Introdução à radiação solar
Mario H. Macagnan
São Leopoldo 2010
- 11.1. O Sol
O Sol é a estrela mais próxima da Terra, constituído de matéria gasosa, principalmente
hidrogênio, a altíssima temperatura. Possui um diâmetro de 1,39x109 m e se encontra, em média,
a 1,5x1011 m da Terra.
O Sol possui uma temperatura efetiva de corpo negro de aproximadamente 5762 K. Sua
estrutura, bastante complexa, pode ser considerada como composta de diversas regiões: o núcleo,
interior, a zona convectiva, a fotosfera, a camada de reversão, a cromosfera e a corona, de acordo
com a Figura 1.
Figura 1. Estrutura do Sol.
A região interna, o núcleo, é a parte mais densa e quente. Sua temperatura varia de
15x106 K até 40x106 K e a densidade é 100 vezes a da água (100.000-150.000 kg/m3). Acima do
núcleo se encontra o interior, que contém praticamente toda a massa do Sol. Estas duas partes
funcionam como um reator nuclear e se constituem na fonte de quase toda a energia produzida.
Esta energia é transferida para a superfície e irradiada para o espaço através de sucessivos
processos de radiação e convecção com suas respectivas emissões, absorções e re-irradiações.
A superfície do Sol, chamada fotosfera, é a fonte da maior parte da radiação visível que
alcança a Terra. Está formada por gases não homogêneos de baixa densidade responsáveis pela
formação, entre outros fenômenos, das manchas solares.
Próximo à fotosfera se encontra a camada de reversão que se estende por centenas de
quilômetros. Esta camada contém vapor de quase todos os elementos familiares da crosta
terrestre. Acima desta camada, entendendo-se a uma distância de aproximadamente 2500 km está
a cromosfera a qual, juntamente com a camada de reversão, forma a atmosfera solar, composta
principalmente de hidrogênio e hélio.
A camada externa do Sol, corona, está composta por gases de densidade muito baixa e
alta temperatura.
2
Em função destes gradientes de temperatura e densidade se pode apreciar que o Sol não é,
de fato, um radiador de corpo negro a uma temperatura fixa.
1.2. Geometria Sol-Terra
A relação Sol-Terra é mostrada esquematicamente na Figura 2.
Figura 2. Relação entre Sol e Terra.
A Terra gira ao redor do Sol descrevendo uma órbita elíptica na qual o Sol ocupa um dos
focos, tal como se vê na Figura 3.
Equinócio de outono
20/21 março
δ = 0°
Solstício de inverno
21/22 junho
δ = 23.45°
1 UA
≈ 0,983 UA
≈ 1,017 UA
1 UA
Solstício de verão
21/22
dezembro
órbita elíptica
Equinócio de primavera
22/22 setembro
δ = 0°
Figura 3. Movimento da Terra ao redor do Sol.
O plano que contém esta órbita é chamado eclíptica e o tempo que a Terra tarda em
percorrê-la é um ano. A excentricidade desta órbita é tal que a distância entre o Sol e a Terra
varia 1,7%. Esta excentricidade pode ser calculada da seguinte maneira:
3
Eo = 1, 00011 + 0, 034221cos Γ + 0, 00128senΓ + 0, 000719 cos 2 Γ + 0, 000077 sen2 Γ (1)
onde Eo é chamado fator de correção da excentricidade da órbita terrestre. Nesta equação Γ, em
radianos, é chamado ângulo do dia e é representado por:
Γ = 2π (d n − 1) / 365 (2)
onde dn é o número do dia do ano no calendário Juliano, variando de 1 (1° de janeiro) até 365
(31 de dezembro). Outra equação mais simples é dada da seguinte maneira:
[(
)]
Eo = 1 + 0,033 cos 2πd n / 365 (3)
e que pode ser utilizada na maioria das aplicações de engenharia.
A uma distância de uma unidade astronômica (UA), que é a distância média entre o Sol e
a Terra e que equivale a 1 UA = 1,496x108 km, o Sol subentende um ângulo de 32'.
A Terra, por sua vez, gira ao redor de um eixo central, chamado eixo polar, completando
uma volta por dia (sucessão dia-noite). Este eixo gira ao redor da normal ao plano da eclíptica
com um ângulo constante e igual a 23,45°, conforme pode ser observado na Figura 4.
Figura 4. Movimento da Terra ao redor de seu eixo.
Desta forma, e de acordo com a Figura 5, o ângulo formado entre o plano equatorial e a
linha que une os centros da Terra e do Sol muda continuamente (sucessão das estações do ano).
Este ângulo é conhecido como declinação solar, δ, e pode ser estimado pela seguinte equação,
com um êrro inferior a 3':
δ = 0, 006918 − 0, 399912 cos Γ + 0. 070257 senΓ − 0, 006758 cos 2 Γ
+0, 000907 sen2 Γ − 0, 002697 cos 3Γ + 0, 00148sen3Γ
(4)
sendo δ dado em radianos. Este ângulo vale zero nos equinócios de primavera e outono, 23,45°
no solstício de inverno e -23,45° no solstício de verão.
Durante um dia (24h) a variação máxima da declinação (que acontece nos equinócios) é
menor que 0,5° podendo-se considerar, portanto, como constante ao longo do dia.
4
Figura 5. Esfera celeste mostrando o caminho aparente do Sol e o ângulo de declinação solar.
Esta expressão, da mesma forma que a equação (1) leva em conta que a velocidade
angular da Terra no seu passo sobre a eclíptica é, de acordo com a lei de Kepler, variável. Isto é,
os planetas percorrem áreas iguais em tempos iguais. Para a maioria das aplicações de
engenharia, a aproximação de que a Terra gira ao redor do Sol numa órbita circular e com
velocidade constante é suficiente. Desta forma, a declinação solar pode ser determinada pela
seguinte expressão (este mesmo raciocínio produziu a equação (3)):
 360

d n + 284) , em graus (5)
(
 365

δ = 23,45 sen
1.2.1. Hora solar
A hora solar é o tempo especificado em todas as relações envolvendo a posição do Sol
em um determinado momento. Está baseado no movimento angular aparente do Sol através do
céu, onde o meio dia solar é a hora em que o Sol cruza o meridiano do observador.
A hora solar não coincide com a hora oficial do lugar (hora do relógio). Para calcular-la é
necessário aplicar dois fatores de correção: o primeiro é um fator constante que considera a
diferença de longitude entre o meridiano do observador e o meridiano no qual a hora oficial está
baseada e considerando que o Sol leva quatro minutos para cruzar 1° de longitude. O segundo
fator de correção é chamado equação do tempo, o qual considera a perturbação na taxa de
rotação da Terra, a qual afeta o tempo que o Sol cruza o meridiano do observador.
A hora solar (também chamada tempo solar verdadeiro) está relacionada com a hora
oficial da seguinte maneira:
TSV = TO ± 4(Lst − Lloc ) + Et (6)
onde TO é a hora oficial, Lst é a longitude padrão, Lloc é a longitude local e Et a equação do
tempo. Deve ser notado que a correção de longitude é positiva se a longitude local está à leste da
longitude padrão e negativa se está à oeste.
A equação do tempo, Et, é mostrada na Figura 6 e é calculada pela seguinte equação:
5
Et = (0,000075 + 0,001868 cos Γ − 0,032077 senΓ − 0,014615 cos 2Γ
− 0,04089sen2Γ)(229,18)
(7)
Nesta equação, o termo entre parênteses da esquerda representa a equação do tempo e o
termo multiplicador da direita a conversão para minutos.
Figura 6. Variação anual da equação do tempo.
1.2.2. Posição do Sol em relação à uma superfície horizontal
Uma forma de representação clássica do céu consiste em imaginar uma esfera com a
Terra fixa no seu centro, tal como se mostra na Figura 5.
Esta esfera é chamada esfera celeste e cada um de seus pontos representa uma direção do
céu vista desde a Terra. A intersecção desta esfera com o plano do equador terrestre define o
equador celeste e os pontos de intersecção com os eixos polares definem os pólos celestes.
O movimento da Terra ao redor do Sol pode ser descrito, desta maneira, como o
movimento do Sol ao redor da Terra seguindo o maior círculo que forma um ângulo de 23,45°
com o equador celeste (a eclíptica). Desta forma, o Sol descreve diariamente e ao redor da Terra,
um círculo cujo diâmetro varia dia a dia, sendo máximo nos equinócios e mínimos nos solstícios,
de acordo com a representação da Figura 7.
Figura 7. Caminho do Sol através do céu visto por um observador no ponto de intersecção dos
eixos.
6
Figura 8. Esfera celeste e coordenadas do Sol relativas a um observador na Terra, no ponto O.
Para calcular a radiação solar que atinge uma superfície horizontal na Terra, é necessário
estabelecer algumas relações geométricas entre a posição do Sol no céu e as coordenadas desta
superfície na Terra. Para isto, utilizaremos a Figura 8 como referência.
A vertical (normal) de um lugar (observador) na Terra intersecta a esfera celeste em dois
pontos, chamados zênite e nadir. O ângulo que forma esta reta com o plano do equador celeste é
chamado latitude geográfica, φ, sendo positiva ao norte e negativa ao sul deste plano.
O horizonte do observador é o círculo máximo na esfera celeste cujo plano passa através
do centro da Terra, normal a uma linha unindo o centro da Terra e o zênite. O ângulo de zênite,
referido como θz à partir de agora, é o ângulo entre o zênite local e a linha que une o observador
e o Sol. A altitude solar, α, (também chamada elevação solar) é a altura angular do Sol acima do
horizonte celeste do observador. Este ângulo nada mais é que o complemento do ângulo de
zênite.
O ângulo de azimute solar, γs, é o ângulo (no zênite local) entre o plano do meridiano do
observador e o plano do círculo máximo que passa através do zênite e o Sol. Este ângulo é
positivo à oeste e negativo à leste (sul igual a zero), variando assim entre 0° e ±180°.
O ângulo horário, ω, é o ângulo (medido no pólo celeste) entre o meridiano do
observador e o meridiano do Sol, valendo 0° ao meio-dia (TSV) e desde aí, muda 15° por hora.
Considera-se esse ângulo negativo pela manhã e positivo pela tarde.
Para uma dada posição geográfica e na ausência de uma atmosfera refrativa, as relações
geométricas entre o Sol e uma superfície horizontal são as seguintes:
cos θ z = sin δ sin φ + cos δ cos φ cos ω = sin α (8)
cos γ s = (sin α sin φ − sin δ ) / cos α cos φ (9)
onde θz é o ângulo de zênite, em graus; α é a altitude solar (α = 90-θz); ω é o ângulo horário,
meio-dia igual a zero e manhãs negativo; γs é o ângulo de azimute solar, sul zero e leste negativo
e δ é a declinação solar, positiva ao norte, em graus.
7
Estes ângulos podem ser visualizados de uma forma mais simples na Figura 9.
Figura 9. Definição dos ângulos de zênite e azimute.
Para encontrar ωs, o ângulo de nascimento do Sol, basta resolver a equação (8) para cos
θz = 0. Desta maneira:
cos ω s = − sin φ sin δ / cos φ cos δ (10a)
ω s = cos −1 (− tan φ tan δ ) (10b)
Deve-se notar que o ângulo de nascimento do Sol é igual ao ângulo do pôr-do-sol,
excetuando-se o sinal. O número de horas de sol do dia, Nd, é igual a 2ωs e da equação (10):
Nd =
2
cos−1 ( − tan φ tanδ ) (11)
15
1.2.3. Posição do Sol para superfícies arbitrariamente inclinadas
Na maioria das aplicações práticas da energia solar é necessário determinar a posição do
Sol com respeito a uma superfície inclinada. A orientação desta superfície se descreve mediante
seu ângulo de inclinação, β, em relação à horizontal e o ângulo de azimute da superfície, γ, que é
o afastamento, em relação ao meridiano local, da projeção da normal da superfície no plano
horizontal. Estes ângulos são representados na Figura 10.
8
Figura 10. Posição do Sol relativa a uma superfície inclinada.
Nesta figura também está representado θs, chamado ângulo de incidência, formado pela
normal à superfície e o vetor Sol-Terra. Este ângulo é calculado da seguinte maneira:
cos θ s = sin δ sin φ cos β − sin δ cos φ sin β cos γ + cos δ cos φ cos β cos ω
(12a)
+ cos δ sin φ sin β cos γ cos ω + cos δ sin β sin γ sin ω
ou
cosθ s = cos β cosθ z + sinβsinθ z cos( γ s − γ ) (12b)
Para uma superfície orientada ao equador, a equação (12a) pode ser simplificada
utilizando-se a representação da Figura 11.
Figura 11. Demonstração da equivalência entre os ângulos θz e θs.
9
Essa figura mostra que uma superfície localizada em uma latitude φ e inclinada β graus
da horizontal e orientada ao equador é paralela a uma superfície horizontal localizada em uma
latitude (φ-β), isto é, o ângulo θs em uma latitude φ é igual ao ângulo θz em uma latitude (φ-β).
Da equação (12a) resulta que:
cosθ s = sinδsin( φ − β ) + cosδ cos( φ − β ) cosω (13a)
Para manter a convenção de sinais para o hemisfério sul, essa expressão é escrita como:
cos θ s = senδsen(φ + β ) + cos δ cos(φ + β ) cos ω (13b)
Da mesma forma que encontramos o ângulo de nascimento do Sol, ωs, para uma
superfície horizontal, podemos encontrar ωs', chamado ângulo de nascimento do sol para uma
superfície inclinada. Isto é obtido da equação (13) fazendo-se θs=90°. Para o hemisfério norte:
ωs ' = cos−1 [ − tanδ tan( φ − β ) ] (14a)
e para o hemisfério sul:
ω s ' = cos −1 [− tan δ tan (φ + β )] (14b)
Desta equação se podem considerar três casos particulares:
i) nos equinócios, δ=0 e da equação (14):
ω s' = π / 2
Ou seja, o ângulo de nascimento do sol é independente da latitude e da inclinação.
ii) durante o verão, δ<0, resultando em ωs > ωs'. Isto significa que o Sol surge antes para uma
superfície horizontal que para uma superfície inclinada.
iii) durante o inverno, δ>0, resultando, matematicamente, que o Sol surge para uma superfície
inclinada antes que para uma horizontal. Como isto não é possível fisicamente, estabelece-se
uma expressão geral para ωs'. Para o hemisfério norte:
{
}
{
}
ω s ' = min cos −1 (− tan δ tan φ ), cos −1 [− tan δ tan (φ − β )] (15a)
e para o hemisfério sul:
ω s ' = min cos −1 (− tan δ tan φ ), cos −1 [− tan δ tan (φ + β )] (15b)
onde min sigunifica o valor mínimo.
10
- 22. A constante solar e sua distribuição espectral
2.1. Introdução
A constante solar é a taxa da energia solar total, em todos os comprimentos de onda, fora
da atmosfera terrestre, incidente em uma superfície de área unitária em exposição normal aos
raios do Sol, a uma distância de 1 UA (distância média Terra-Sol). Sua determinação exata bem
como sua distribuição espectral são extremamente importantes não só para aplicações extraatmosféricas (satélites, naves espaciais, etc.) como para aplicações terrestres.
A determinação do valor da constante solar é estudada extensivamente desde o princípio
do século passado, primeiramente através de medidas ao nível do solo e posteriormente
extrapoladas para condições no topo da atmosfera, levando-se em consideração a atenuação dos
raios do Sol pelos diversos componentes constituintes da atmosfera e mais recentemente
utilizando satélites. O valor recomendado pela Organização Meteorológica Mundial foi obtido do
valor médio de oito medidas da constante solar, realizadas entre 1969 e 1980. Este valor é:
-2
ou
Isc = 1367Wm
Isc=4921 kJm-2h-1
com um desvio padrão de 1, 7Wm2 e um desvio máximo de ±7 Wm-2.
2.2. Distribuição espectral da irradiancia solar extraterrestre
O espectro da radiação solar extraterrestre cobre um intervalo de comprimentos de onda
desde 0,2 até 25µm. A intensidade da radiação varia com o comprimento de onda, conforme foi
comentado anteriormente, devido principalmente às diferenças de temperatura de cada região do
Sol. Esta relação funcional entre intensidade e comprimento de onda é chamada distribuição
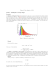
espectral. O espectro solar extraterrestre no intervalo de comprimentos de onda de 0,2 a 2,3µm é
mostrado na Figura 12.
Esta distribuição espectral é muito similar a do espectro de um corpo negro a 5900 K,
também representado na mesma figura. Na Tabela 1 é apresentada a distribuição do espectro
solar extraterrestre em diferentes bandas de cores. Aproximadamente a metade da energia solar
se encontra na região do visível e quase a mesma quantidade se encontra no infravermelho.
Desta forma, aproximadamente 95% da energia so Sol está dentro do intervalo 0,3-2,4 µ
m, 1,2% no intervalo < 0,3 µm e 3,6% no intervalo > 2,4 µm.
2.3. Irradiação solar extraterrestre
Aqui se discutirá o valor integrado da radiação solar extraterrestre em todos os
comprimentos de onda. Antes, porém, se definiram alguns conceitos relacionados à terminologia
da radiação solar. Estes conceitos são:
11
i) Radiância, Wm-2sr-1: é a taxa de energia por unidade de área e por unidade de ângulo sólido
normal a esta área;
ii) Irradiância, Wm-2: taxa na qual a energia radiante incide em uma superfície, por unidade de
área desta superfície;
iii) Irradiação, Whm-2 ou Jm-2: energia incidente por unidade de área, numa superfície, obtido
por integração da irradiância em um tempo especificado (geralmente uma hora ou um dia).
Figura 12. Distribuição espectral da radiação extraterrestre AM0 e distribuição espectral de um
corpo negro a 5900 K.
Tabela 1. Divisão do espectro solar em bandas de cores e regiões de energia.
Cor
Violeta
Azul
Verde
Amarelo
Laranja
Vermelho
λ, µm
0,390 - 0,455
0,455 - 0,492
0,492 - 0,577
0,577 - 0,597
0,597 - 0,622
0,622 - 0,770
Irradiância, Wm-2
108,85
73,63
160,00
35,97
43,14
212,82
Porcentagem da Isc
7,96
5,39
11,70
2,63
3,16
15,57
Ultravioleta
Visível
Infravermelho
< 0,4
0,390 - 0,770
> 0,770
109,81
634,40
634,40
8,03
46,4
46,4
iv) Radiação direta: radiação solar recebida do Sol sem nenhum tipo de dispersão pela atmosfera
terrestre.
12
v) Radiação difusa: radiação solar recebida do Sol após sua direção ter sido alterada devido à
dispersão pela atmosfera. Também chama radiação do céu.
vi) Radiação global ou total: soma da radiação direta mais a difusa recebida por uma superfície.
2.3.1. Irradiação extraterrestre em superfície horizontais
A. Radiação horária
A irradiância extraterrestre, Ion, em uma superfície normal aos raios do Sol é:
I&on = I&sc E o (16)
Pela observação da Figura 13, a irradiância pode ser determinada da seguinte relação:
I&o = I&on cosθ z , Wm-2 (17)
onde θz é o ângulo de zênite do Sol.
A irradiação dIo durante um curto período de tempo dt será dado por:
dI o = I sc Eo cos θ z dt (18)
onde dt está em horas e Isc, a constante solar, em unidades de energia. O tempo, em horas, pode
ser convertido em ângulo horário da seguinte maneira:
2π
dω
Ω = velocidade de rotação da Terra =
=
24 h dt
em tôrno ao seu eixo
resultando em
 12 
dt =  dω
π 
Figura 13. Relação entre a irradiância direta normal e a horizontal.
13
A equação (18) se reduz a:
 12 
dI o =   I sc Eo ( sinδsinφ + cosδ cos φ cosω ) dω (20)
π 
Desta forma, a radiação para um período de uma hora pode ser obtida. Integrando a
equação (20) para um período definido pelos ângulos horários ω1 e ω2, que definem a hora,
teremos:
ω2
12
Io =
I sc E o ∫ω ( sinδsinφ + cos δ cos φ cos ω )dω (21)
π
1
cujo resultado é:
Io =
12
π
[
]
I sc Eo cosδ cos φ ( sinω2 − sinω1 ) + (ω2 − ω1 ) sinδsinφ (22)
com ω1 e ω2 dados em radianos (ω1 < ω2).
Outra forma de resolver é considerando a i-ésima hora à partir do meio-dia e ωi o ângulo
horário na metade desta hora. Assim:
Io =
12
π
ωi +π / 24
I sc Eo ∫ω −π / 24 ( sinδsinφ + cosδ cos φ cosω )dω (23)
i
ou


 24   π 
I o = I sc Eo  sinδsinφ +  sin  cosδ cos φ cosωi  (24)
 π   24 


mas como
 24   24 
  sen  = 0,9972 ≈ 1
π  π 
podemos reescrever a equação (22) como:
I o = I sc Eo ( sinδsinφ + cosδ cos φ cosωi ) (25)
A Figura 14 apresenta valores de Io para dias característicos (solstícios e equinócio) para
Porto Alegre - RS (latitude 30°01' S) e São Luis - MA (latitude 2°32' S).
A irradiação extraterrestre diária em uma superfície horizontal, Ho, desde o nascer-dosol, ns, até o pôr-do-sol, ps, é calculada da seguinte maneira:
Ho = ∫n I o dt (26)
ps
s
e considerando a simetria do dia:
Ho = 2 ∫0 I o dt (27)
ps
14
Assumindo Eo e δ constantes ao longo do dia e convertendo o tempo dt em ângulo
horário, obtemos:
Ho =
24
π
I sc Eo ∫o ( sinδsinφ + cosδ cos φ cosω )dω (28)
ps
ou
Ho =
24
π
[( 180)ws (senδsenφ ) + (cos δ cos φsenws )] (29)
I sc Eo π
sendo ws dado em graus.
Na Tabela 2 se pode encontrar os valores de Ho para os doze meses do ano e para
algumas latitudes (hemisfério sul). Esta tabela foi construída utilizando-se dias médios de cada
mês, de acordo com a Tabela 3. O dia médio é aquele que apresenta valores de Ho idênticos ao
valor médio mensal, Ho.
Figura 14.Variação diurna da irradiação extraterrestre horária em uma superfície horizontal para
(a) Porto Alegre - RS e (b) São Luis - MA. Os valores estão em Whm-2.
B. Radiação diária
2.3.2. Irradiação extraterrestre em superfícies inclinadas
Da mesma forma que para uma superfície horizontal, serão derivadas expressões para o
cálculo da irradiação extraterrestre em superfícies inclinadas.
2.3.2.1. Irradiação para superfícies inclinadas voltadas ao equador
A. Irradiação horária
De acordo com a Figura 15, a irradiancia extraterrestre incidente em uma superfície
inclinada β graus, Ioβ, e voltada ao equador é:
I&oβ = I&on cos θ s (30)
onde θs é o ângulo de incidência.
15
Tabela 2. Variação da irradiação extraterrestre diária em uma superfície horizontal, Ho (MJm-2).
Mês
Jan
Fev
Mar
Abr
Mai
Jun
Jul
Ago
Set
Out
Nov
Dez
Media
Latitude (Sul)
15°
30°
45°
40,87 43,04 42,89
39,83 39,57 36,84
37,14 33,85 28,28
32,99 27,08 19,45
28,92 21,42 12,91
26,76 18,68 10,02
27,57 19,76 11,19
30,89 24,29 16,28
35,03 30,62 24,16
38,42 36,95 33,07
40,28 41,66 40,66
40,91 43,80 44,44
34,97 31,73 26,68
0°
36,32
37,53
37,90
36,75
34,78
33,50
33,89
35,56
37,07
37,34
36,47
35,74
36,07
60°
41,05
32,07
20,83
10,75
4,47
2,15
3,07
7,66
16,09
27,16
37,83
43,61
20,56
90°
43,32
27,06
5,49
0,00
0,00
0,00
0,00
0,00
0,69
17,86
37,96
47,66
15,00
Tabela 3. Dias médios e declinações características (irradiação extraterrestre diaria idêntica ao
valor médio mensal).
Mês
Jan
Fev
Mar
Abr
Mai
Jun
Jul
Ago
Set
Out
Nov
Dez
Data
17
14
15
15
15
10
18
18
18
19
18
13
δ, graus
-20,84
-13,32
-2,40
+9,46
+18,78
+23,04
+21,11
+13,28
+1,97
-9,84
-19,02
-23,12
Número do dia, dn
17
45
74
105
135
161
199
230
261
292
322
347
A irradiação Ioβ entre os ângulos horários ω1 e ω2 é dada por:
I oβ =
12
π
I sc Eo ∫ω [ sinδsin( φ − β ) + cosδ cos( φ − β ) cosω ]dω (31)
ω2
1
Para uma hora completa, sendo ωi o ângulo horário na metade desta hora, temos:
I oβ = I sc Eo [ sinδsin( φ − β ) + cosδ cos( φ − β ) cosωi ] (32)
ou
I oβ =
12
π
[
]
I sc Eo cosδ cos( φ − β ) ( sinω2 − sinω1 ) + ( ω2 − ω1 ) sinδsin( φ − β ) (33)
16
Figura 15. Irradiação em uma superfície inclinada voltada ao equador.
B.
Irradiação diária
Hoβ :
Integrando-se a equação (31) entre ωns e ωps obtém-se a irradiação extraterrestre diária,
Hoβ =
24
π
ω =ω s ,ω s '
I sc Eo ∫0
[ sinδsin( φ − β ) + cosδ cos( φ − β ) cosω ]dω (34)
O limite de integração, tal como foi comentado anteriormente, deve ser o valor mínimo
entre ωs e ωs'. Desta forma:
 24 
Hoβ =   I sc Eo [ωs ' sinδsin( φ − β ) + cosδ cos( φ − β ) sinωs ' ] (35)
π 
onde
ωs ' = min{ωs ,cos−1 [ − tanδ tan( φ − β )] } (36)
com ωs' (e obviamente ωs) em radianos.
2.3.2.2. Irradiação extraterrestre em uma superfície inclinada e arbitrariamente orientada
A. Irradiação horária
A irradiação extraterrestre horária em uma superfície arbitrariamente orientada, Ioβγ é
calculada da mesma maneira que Ioβ, utilizando-se para θs a equação (12a).
B. Irradiação diária
A irradiação extraterrestre diária, Hoβγ, pode ser obtida da seguinte expressão:
17
H oβγ =
12
π
ω ps
I sc E o ∫ω cos θdω (37)
ns
Através das expressões para ωns e ωps vistas anteriormente, se pode calcular Hoβγ como:
 12 
H oβγ =   I sc Eo cos(P1 − P2 + P3 + P4 + P5 ) (38)
π 
onde
(
P1 = cos βsenδsenφ ω ns − ω ps π
180
)
(
P2 = senδ cos φsenβ cos γ ω ns − ω ps π
180
)
P3 = cos φ cos δ cos β senω ns − senω ps
P4 = cos δ cos γ sen φ sen β sen ω ns − sen ω ps
P5 = cos δsenβsenγ cos ω ns − cos ω ps
onde
indica o valor absoluto.
2.4. Cálculo de r&b , rb , rb , Rb e Rb
i) A relação entre a irradiância em uma superfície inclinada e aquela em uma superfície
horizontal, na ausência da atmosfera terrestre é chamada r&b . De acordo com as Eq. (17) e (30),
temos:
I&o = I&on cos θ z (39)
I&oβ = I&on cos θ s
(40)
e obviamente, da definição acima:
I&oβ cos θ s
r&b = & =
Io
cos θ z
(41)
ii) Da mesma forma, rb é a relação entre a radiação horária em uma superfície inclinada em
relação àquela numa superfície horizontal, na ausência da atmosfera terrestre. Esta relação é
escrita como:
18
rb =
I oβ
Io
ωi + π / 24
=
I sc E o ∫ω −π / 24 cos θ s dω
i
ωi + π / 24
I sc E o ∫ω −π / 24 cos θ z dω
(42)
i
Como já foi comentado anteriormente, uma boa aproximação para as integrais acima
pode ser obtida estimando-se cos θs e cos θz para o intervalo médio da hora.. Assim:
rb =
I oβ
Io
≈
cos θ s
cos θ z
(43)
Deve tomar-se cuidado para as horas perto do nascer ou do pôr-do-sol, quando o valor de
rb muda rapidamente, aproximando-se de zero ou infinito, porque tanto o numerador quanto o
denominador da equação acima são números muito pequenos.
iii) A relação entre a radiação horária média mensal em uma superfície inclinada em relação a
incidente em uma superfície horizontal, na ausência da atmosfera terrestre é chamada de rb . Esta
definição é análoga à (ii) exceto que δ é estimado em δc (a declinação para um dia médio do mês
- Tabela 3).
iv) A relação entre a radiação diária em uma superfície inclinada e aquela em uma superfície
horizontal, também na ausência da atmosfera terrestre é chama Rb. e é dada pela seguinte relação:
Rb =
H oβ
Ho
(44)
v) Nos equinócios, δ=0 e ωs=ωs´=π/2. Desta forma, temos:
r&b = rb = Rb =
cos( φ − β )
cos φ
19
(45)
-3Radiação solar disponível na superfície terrestre
3.1 Introdução
A medida da radiação solar disponível na superfície da Terra é essencial para um grande
número de aplicações além, naturalmente, dos sistemas solares onde é fundamental. Esta
informação também é utilizada para estimar o rendimento energético de edificações, modelos
climáticos, agricultura, etc. A medida da radiação solar em alguns pontos da superfície terrestre
permite o desenvolvimento de modelos empíricos que possibilitam a predição da energia solar
disponível em muitos outros lugares que não dispõem destas medidas.
Nesta seção comentaremos os instrumentos utilizados para medir a radiação solar, a
classificação destes instrumentos e os métodos de calibração. Posteriormente se tecerá alguns
comentários sobre a situação mundial atual das medidas da radiação solar.
A medida da radiação solar é efetuada, basicamente, por dois tipos de aparelhos: os
pirheliômetros e os piranômetros.
O pirheliômetro é o instrumento utilizado para a medida do fluxo de radiação solar direta,
em incidência normal. Este instrumento é geralmente acoplado a um sistema para o seguimento
do Sol.
O piranômetro é o instrumento que efetua medidas da radiação solar proveniente de todo
o hemisfério celeste, onde se inclui a parte difusa e a parte direta proveniente do disco solar. Este
instrumento também pode ser utilizado em posição inclinada e neste caso recebe uma parte da
radiação refletida pelo solo.
Este instrumento quando provido de um disco ou anel de sombra pode medir a radiação
difusa (dentro de um ângulo sólido de 2π sr) excetuando o ângulo sólido donde está o Sol.
Naturalmente, quando utiliza um anel de sombra, este dispositivo oculta, além do Sol, uma
fração do hemisfério do céu. Esta fração da radiação difusa ocultada dever ser somada à leitura
deste instrumento.
3.2. Sensores de radiação
Os sensores destes instrumentos podem ser classificados da seguinte maneira:
calorimétricos, termomecânicos, termoelétricos e fotoelétricos. A seguir se faz uma breve
descrição de cada um deles.
3.2.1. Sensores calorimétricos
Nos instrumentos calorimétricos, a energia radiante incide em um metal de alta
condutividade recoberto com uma pintura negra não seletiva de alta absortância. Esta energia
radiante é convertida em calor que pode ser medido de várias maneiras:
i) o calor é retirado por um fluído em circulação e sua variação de entalpia é medida. Esta
variação de entalpia é a indicação do fluxo solar incidente.
20
ii) o calor origina uma variação de entalpia do metal absorvedor (sensor) e da mesma forma que
o método anterior, esta variação de entalpia pode ser facilmente medida.
iii) a diferença de temperatura através de um transdutor é mantida constante por meio de
aquecimento adicional requerido entre a face exposta e a sombreada. O fluxo de radiação é então
proporcional à diferença do aquecimento elétrico nas duas faces.
3.2.2. Sensores termomecânicos
Estes sensores atuam pelo princípio termomecânico, onde o fluxo de energia é medido
através da curvatura de uma lâmina bimetálica. Neste sistema, duas lâminas metálicas com
distintas propriedades de dilatação térmica são rigidamente mantidas unidas. Uma extremidade
desta união de lâminas está fixa enquanto a outra é livre. Uma lâmina está recoberta com uma
tinta preta de alta absortância e a outra recoberta com uma tinta branca de alta refletância. A
lâmina negra é exposta à radiação solar e a outra é mantida na sombra. Estas duas lâminas estão
isoladas uma da outra para impedir o fluxo de calor entre elas. Devido à diferença de temperatura
entre elas e aos diferentes coeficientes de dilatação, estas lâminas se curvam. Esta distorção é
transmitida ótica ou mecanicamente à um indicador.
3.2.3. Sensores termolétricos
Estes sensores consistem de dois fios metálicos diferentes com suas extremidades
conectadas. Quando estas duas extremidades se encontram à temperaturas diferentes (uma
exposta à radiação solar e a outra sombreada) acontece a geração de uma força eletromotriz
(fem), de acordo com a representação da Figura 16a. A fem gerada é proporcional à diferença de
temperatura e depende do tipo de material de cada fio. Para baixas temperaturas costuma-se
utilizar um par de cobre-constantan.
Como a fem de um único par é muito baixa, se conectam um grande número de junções
termopares em série, tal como se mostra na Figura 16b. Este arranjo é chamado termopilha.
Figura 16. Configurações de sensores termoelétricos.
Nestas termopilhas, as juntas quentes são pintadas de preto e as juntas frias de branco.
Para manter condições estáveis é necessário que as junções frias estejam à temperatura constante.
Isto foi obtido fazendo-se com que as junções frias estejam unidas termicamente, mas
21
eletricamente isoladas em uma placa de latão (ver Figura 16d). A inércia térmica desta placa
absorve as variações de temperatura de curto período provocadas pelas correntes de ar. Este
dispositivo é chamado termopilha de Moll. Utiliza termopares de manganês-constantan
conectados a pinos de cobre. Estes pinos estão em contato térmico com a placa de latão mas
isolados eletricamente.
3.2.4. Sensores fotoelétricos
Estes sensores convertem parte da radiação solar incidente diretamente em eletricidade, a
qual é proporcional à intensidade da radiação. Geralmente, o sensor utilizado é do tipo
fotovoltaico, sendo o mais comum a célula de silício ou fotodiodos, operados em curto circuito,
tal como é mostrado na Figura 17.
Figura 17. Sensor fotovoltaico: (a) curvas características de uma célula de silício, (b) célula solar
com uma resistência.
Uma célula de silício responde quase instantaneamente à qualquer variação da radiação
solar (tempo de resposta aproximadamente igual a 10 µs). A linearidade entre corrente e radiação
incidente, G, é alcançada dimensionando-se a resistência suficientemente pequena, tal que a
queda de tensão através da resistência esteja abaixo da tensão de circuito aberto de ≈ 0,6 Volts.
Além disso, não apresentam sensibilidade à inclinação e tem um fator de resposta bastante alto,
não necessitando amplificação do sinal de saída.
Como desvantagem, apresentam seletividade espectral (mais forte somente nas regiões do
vermelho e no infravermelho próximo ). Também, sua sensibilidade angular em sensores
desprovidos de camada antireflexiva pode ser importante. Entretanto, isto acontece para ângulos
de incidência maiores que 60°, onde os níveis de irradiância já são menores.
3.3. Medida da irradiância direta: pirheliômetros
A radiação direta normal é medida com um pirheliômetro. Este aparelho consiste de um
sensor localizado em uma extremidade de um tubo telescópico e o lado oposto consiste na
abertura, geralmente com um campo de visão reduzido. Um desenho esquemático deste aparelho
é mostrado na Figura 18.
22
Figura 18. Detalhe de um pirheliômetro (a) e o sistema de seguimento (b).
A relação geométrica entre sensor e abertura define o campo de visão do instrumento e
são as seguintes, de acôrdo com a Figura 19.
(ângulo de abertura) = tan-1 R/L
zp (ângulo de inclinação) = tan-1[(R-r)/L]
z (ângulo limite) = tan-1[(R+r)/L]
zo
Figura 19. Geometria da limitação do campo de visão de um pirheliômetro.
Neste caso, o campo de visão é 2 zo. Os valores de ângulos recomendados pela World
Meteorological Organization (WMO) são: zo=2,5° (5x10-3 sr) e zp= 1°.
Do exposto, fica óbvio que este aparelho necessita utilizar um dispositivo preciso para o
seguimento do Sol.
3.3.1. Classificação dos pirheliômetros
A classificação dos pirheliômetros, de acôrdo com o guia da WMO de 1983 é descrita na
Tabela 4.
23
Tabela 4. Classificação dos pirheliômetros, segundo a WMO (1983).
Classificação do
instrumento
Pirheliômetro absoluto
Pirheliômetro padrão de
referência
Pirheliômetro 1a classe
(tipo termopilha)
Pirheliômetro 2a classe
Usos principais
padrão primário
padrão secundário
a)padrão secundário
b) rêdes
c) testes
rêdes
Precisão em um Campo de visão
ano, %
± 0,1
5°
± 0,5
± 1,0
6°
± 2,0
-
Os pirheliômetros absolutos atualmente aceitos pela WMO são todos do tipo cavidade.
São auto-calibráveis eletricamente e a irradiância pode ser determinada em unidades absolutas de
calor. Sua calibração depende somente das dimensões, arranjo dos componentes e da medida
elétrica. Estes aparelhos apresentam uma exatidão melhor que ± 0,3%.
Estes radiômetros absorvem radiação em um receptor cônico e determinam o fluxo de
calor radiante por substituição elétrica. A vantagem de utilizar-se um cone em relação à uma
superfície plana pode ser compreendida através da Figura 20.
Figura 20. Absortância efetiva de (a) superfície plana e (b) superfície cônica.
Dependendo do ângulo de abertura do cone, a radiação que entra é refletida nas paredes
antes de escapar, ao contrário do que acontece numa superfície plana. Em cada incidência deste
raio uma fração αs será absorvida e pode ser provado que a cavidade terá uma absortância efetiva
αc, maior que αs. O valor de αc aumenta a medida que diminui a abertura do cone. Além disso,
uma pintura especular destas paredes aumentará a absortância em relação a uma pintura fosca.
Uma vista esquemática deste aparelho é apresentada na Figura 21.
Os dois cones invertidos (e opostos) contém as superfícies absorvedoras do radiômetro.
Os cones re-irradiam para o elemento sensitivo do detetor, uma termopilha ou termômetro de
resistência de platina.
As juntas frias de ambos absorvedores e as termopilhas de compensação estão em contato
com uma bacia de calor (A) e a cavidade de compensação é "vista"por um corpo-negro. O cone
absorvedor (posterior) e o cilindro são envolvidos por um aquecedor elétrico.
O receptor e a cavidade de compensação estão montados em um tubo colimador, o qual
limita o campo de visão do aparelho.
24
Em operação, o aquecedor do cone posterior é ajustado para produzir o mesmo sinal do
detector quando iluminado pelo Sol. A irradiância é calculada simplesmente como a potência por
unidade de área do absorvedor.
Figura 21. Diagrama de um pirheliômetro absoluto do tipo cavidade.
3.3.2. Pirheliômetros de campo (redes)
Os instrumentos absolutos ou padrões de referência, não são utilizados para medidas
rotineiras de irradiância direta normal. Para isto, são utilizados os intrumentos de campo, que
possuem uma precisão inferior mas são muito mais fáceis de operar.
Entre os instrumentos de campo fabricados os dois mais populares são: pirheliômetro de
incidência normal (NIP), da Eppley e o actinômetro da Kipp&Zonen.
O instrumento Eppley NIP possui um elemento sensor tipo termopilha multijunção,
recoberto com uma pintura 3M Velvet Black. O tubo colimador tem um campo de visão de 5°
43'30" cujo interior também está pintado de negro. Este tubo é preenchido com ar sêco à pressão
atmosférica. A outra extremidade do tubo possui uma janela de cristal de quartzo de 1 mm de
espessura. A resposta do sensor é estabilizada através de um circuito de compensação de
temperatura.
O pirheliômetro fabricado pela Kipp&Zonen, o actinômetro, possui um elemento sensor
do tipo termopilha de Moll, composta de 46 tiras de constantan-manganês. O tubo colimador
possui um ângulo de abertura de 10°12’ e é construído em um bloco maciço de cobre (para
minimizar os efeitos da flutuação da temperatura ambiente) com diafragmas internos.
3.3.3. Escalas pirheliométricas
Um instrumento cujo comportamento tenha sido determinado com um alto grau de
precisão é chamado pirheliômetro absoluto. Geralmente, um grupo de amostras de instrumentos
é calibrado contra o instrumento absoluto e é utilizado para contrôle da estabilidade do
instrumento absoluto. Tais instrumentos são chamados pirheliômetros padrões ou padrões de
referência e podem ser ou não do mesmo tipo do instrumento absoluto.
Para fins meteorológicos é necessário padronizar os instrumentos de medida da radiação
solar e para isto é fundamental adotar-se uma escala padrão de radiação. Antes de 1956 existiam
duas escalas padrão, conhecidas como escala Ångström (ÅS 1905) e a escala Smithsonian (SS
1913), aplicadas independentemente uma da outra.
25
Em 1956, a Comissão Internacional de Radiação, reunida em Davos, Suiça, adotou uma
nova escala, conhecida como International Pyrheliometric Scale de 1956 (IPS 1956). Esta nova
escala mudou as duas anteriores da seguinte maneira:
i) as medias realizadas de acôrdo com a escala Ångström deveriam ser incrementadas em 1,5%,
ou seja:
IPS 1956 = 1,015 (ÅS 1905)
ii) as medidas realizadas de acôrdo com a escala Smithsonian deveriam ser diminuidas em 2%
ou:
IPS 1956 = 0,98 (SS 1913)
A nova escala estava baseada na hipótese que a diferença total entre as duas escalas era de
3,5%. A partir de 1959 (IPC I) foram realizadas, a cada cinco anos, em Davos, uma comparação
de instrumentos. Durante a IPC III (1970) foram introduzidos os primeiros pirheliômetros do tipo
cavidade elétrica e foi notado que a IPS 1956 estava aproximadamente 2% abaixo das medidas.
Desta comparação foi criada a World Radiometric Reference (WRR), 2,2% acima da IPS 1956,
isto é:
WRR = 1,022 (IPS 1956)
3.4. Medida da irradiância global: piranômetros
Os piranômetros são os instrumentos utilizados para medida da radiação solar global
(direta + difusa). Possuem um campo de visão hemisférico (2π sr) e os elementos sensores mais
utilizados são termoelétricos, termomecânicos ou fotovoltaicos. Ao contrário dos pirheliômetros,
os elementos sensores são planos.
Os piranômetros mais utilizados consistem de um receptor pintado de preto conectado à
junção quente de uma termopilha que por sua vez está montada em um casco isolado. O sensor
está envolto por um ou dois hemisférios de cristal. A principal finalidade destes hemisférios de
cristal é, primeiro evitar efeitos transientes causados por resfriamento convectivo do sensor e
segundo, excluir as radiações de onda larga do céu e da terra. No caso de dois hemisférios, as
trocas de radiação no infravermelho acontecem entre o hemisfério externo (+ frio) e o interno (+
quente), como também entre o interno e o sensor, minimizando desta maneira a troca directa no
infravermelho entre o hemisfério externo e o sensor quente. Na Figura 22 se representa um
piranômetro com dois hemisférios.
As pinturas pretas dos sensores são bons receptores difusos da radiação solar e
espectralmente não seletivos e desta forma não exibem dependência angular significativa. Estas
pinturas se alteram com a exposição constante do instrumento o que explica a propensão de
alguns piranômetros em exibir uma crescente dependência angular com o tempo.
Em geral, os piranômetros são menos sensíveis que os pirheliômetros à variação da
distribuição espectral da energia do Sol. Como resultado, os piranômetros do tipo fotovoltaico
(célula de silício) tem sido cada vez mais utilizados para a medida da irradiância solar. Embora
os sensores fotovoltaicos "nus"sejam sensíveis ao ângulo de incidência da iluminação, a
utilização de difusores (Teflon) ou camadas anti reflexivas ajudam a diminuir significativamente
os desvios da lei do coseno.
26
Figura 22. Foto de um piranômetro de um piranômetro.
O uso destes sensores para a medida da irradiância solar hemisférica está baseado na
suposição de que a distribuição da resposta espectral cobre aproximadamente 85% da energia
representada pela distribuição espectral da energia solar AM 1,5. Entretanto, a presença de
camadas de nuvens, neblina ou poluição, que afetam desproporcionalmente regiões da resposta
espectral das células solares (isto é, a região do infravermelho é menos sensível à tais condições
atmosféricas) resultará em erros de medida da irradiância global. Da mesma maneira, as células
solares não medem acuradamente a distribuição de energia rica de infravermelho e elevada massa
de ar (primeiras e últimas horas do dia). Por último, embora a resposta destas células não seja
afetada pela inclinação do sensor, variações na irradiância espectral em função da fração do
hemisfério do céu incluído pode resultar em erros de 5% ou mais (caso em que o sensor for
calibrado horizontalmente, em condições de céu claro, e que quando inclinado "veja"o Sol, um
céu nublado e a radiação refletida pelo solo).
Além desses dois tipos de piranômetros (termopilhas e fotovoltaicos) ainda se pode
encontrar operando em algumas estações meteorológicas, os piranômetros bimetálicos tipo
Robitzsch, também chamados actinógrafos.
A popularidade deste instrumento reside principalmente na sua simplicidade além de
possuir um registrador incorporado na sua estrutura, o que é particularmente útil para operação
em regiões remotas. Apesar das muitas modificações realizadas neste instrumento desde a data
do primeiro projeto (1932), ele não é recomendado para realizar qualquer medida com exceção
de totais diários e "com a reserva de que, mesmo com um fator de calibração variando de mes a
mes, estes totais diários terão uma incerteza nunca inferior a 5-10%".
Estes instrumentos funcionam com o principio bimetálico, descrito anteriormente.
Através de um mecanismo, a extremidade livre está conectada a uma pena que registra o valor da
radiação em uma tira de papel montada em um cilindro movido por um relógio, realizando uma
rotação em 24 horas ou em 7 dias.
Pelo próprio principio bimetálico, este sistema é extremamente sensível à temperatura.
Além disso, a constante de calibração varia muito com o ângulo de incidência, pois o sensor se
curva com a temperatura, deixando de ser plano. Desta forma a constante de calibração é função
dos ângulos de azimute e zênite. No modelo Robitzsch-Feuss, a calibração do instrumento pode
diminuir até 40% quando o ângulo de incidência aumenta de 10° a 70°, obrigando a adoção de
correções diárias.
Outro grave problema é a grande inércia térmica destes instrumentos, que possuem um
tempo de resposta (a 98%) extremamente lento, podendo chegar de 10-15 min, dependendo do
tipo.
27
Para finalizar, é necessário comentar que a integração do valor diário é realizada
manualmente, utilizando-se um planímetro, processo este que pode introduzir mais erro na
medida final.
3.4.1. Classificação dos piranômetros
Segundo a World Meteorological Organization (WMO) os piranômetros são
classificados1 em: padrão secundário, piranômetros de primeira classe e segunda classe. Esta
classificação é apresentada na Tabela 5.
Tabela 5. Classificação dos piranômetros, segundo a WMO.
Especificação
Tempo de resposta (a 95%)
Zero offset
Não-estabilidade
Não-linearidade
Resposta coseno (60°)
[desvio máx. entre 60° e 80°]
Resposta azimutal
Seletividade espectral
Resposta a temperatura
Resposta à inclinação
Padrão
secundário
15 s
± 10Wm-2
± 0,8%
± 0,5%
± 1%
[± 3%]
± 3%
± 3%
2%
± 0,5%
1ª clase
2ª classe
30 s
± 15Wm-2
± 1,5%
± 1%
± 2%
[± 5%]
± 5%
± 5%
4%
± 2%
60 s
± 40Wm-2
± 3%
± 3%
± 5%
[± 10%]
± 10%
± 10%
8%
± 5%
Na primeira coluna desta tabela estão listados os chamados problemas em piranometria.
Podem ser descritos resumidamente como:
a) Efeitos do ângulo de incidência: os desvios devido aos erros de coseno e azimute
(resposta coseno e azimutal) são simplesmente duas descrições de um mesmo efeito, que é o
desvio da lei do coseno de Lambert, para ângulos de incidência maiores que 0°.
Figura 23. Resposta coseno de um piranômetro medida em dois planos ortogonais, passando pelo
eixo do aparelho.
28
Geralmente se descreve a resposta coseno como o desvio da lei do coseno em dois planos
ortogonais, passando pelo eixo do piranômetro enquanto a resposta azimutal é descrita como o
desvio da lei de Lambert num dado ângulo de incidência, quando um piranômetro montado
horizontalmente é girado 360°. Estes dois efeitos são mostrados nas Figuras 23 e 24.
Figura 24. Resposta azimutal para um piranômetro em um dado ângulo de incidência.
Para dois piranômetros típicos, as respostas coseno e azimutal são mostradas nas Figuras
25 e 26.
Figura 25. Resposta azimutal, em coordenadas polares, de um piranômetro Eppley PSP, em
termos da resposta em incidência normal.
29
Figura 26. Resposta coseno de um piranômetro Eppley PSP.
b) Resposta à inclinação: a sensibilidade de um piranômetro de 2ª classe (com setores
segmentados, tipo star) pode variar entre 13-15% devido à inclinação do aparelho. Acredita-se
que este efeito se deva ao resfriamento da junção quente da termopilha devido a um aumento da
transferência de calor convectiva.
Em piranômetros Eppley PSP este erro é muito pequeno, tal como se vê na Figura 27.
Para inclinações até 45°, o valor gira em torno a 0,5-2%.
Figura 27. Variação na resposta de um piranômetro Eppley PSP em função da inclinação com a
horizontal.
c) Resposta à temperatura: apesar da maioria dos piranômetros atuais possuirem um
circuito de compensação de temperatura, este sistema não é efeitivo em toda a faixa de
temperaturas ambientes. A Figura 28 mostra a dependência da temperatura na constante de
calibração do instrumento.
30
Figura 28. Dependência da temperatura na constante de calibração de um piranômetro Eppley
PSP.
d) Não-linearidade: a linearidade assume que a constante de calibração do instrumento é
linear dentro da faixa de irradiâncias de interesse. Para os modelos Eppley PSP, a não-linearidade
é muito pequena entre 200 e 1000 Wm-2.
e) Seletividade espectral: talvez sejam os erros mais difíceis de tratar. Em princípio, todos
os materiais conhecidos mudam suas características de refletividade ou espectrais após um
periodo de exposição ao Sol. Isto é o que acontece com as superfícies absorvedoras dos
pirheliômetros e piranômetros.
Também, a cor característica da luz usada na comparação/calibração de instrumentos
afetará suas leituras relativas mesmo para uma leve diferença da característica espectral.
As características dos piranômetros mais utilizados são descritas na Tabela 6, de acôrdo
com Zerlaut2:
31
Tabela 6. Características dos piranômetros.
Fabricante
Modelo
Resposta
coseno (70°)
Eppley Labs
Eppley Labs
Eppley Labs
Kipp&Zonen
Kipp&Zonen
Phillip Shenk
Swissteco
Eko
LiCor
Hollis Obs.
8-48
PSP
SCP
CM6
CM11
T-8101
SS-85
MS-42
200SB
TR-201
±2a
1c
0
f
<3
±2
f
≈5
≈3
1,5
Sensibilidade a Resposta
temp.(-20/+40°) inclinação, %
±1,5
±1
e
-5
±1
≈2
≈1
≈3,5
f
≈1,5
<0,5b
<0,5
0
f
<0,5
1
f
Tempo de
resposta,
1/e, s
5
1
≈1
3
5
20
5
Intervalo
espectral, nm
Linearidade
até 1000 Wm-2
285-2800
285-2800
<285->2800
305-2800
305-2800
300-3000
280-2900
0,99
0,995
>0,995
0,985
0,995
0,99
f
f
≈0,1
≈0,1
400-1100
400-1100
>0,99
0,99
f
1,5
0
0
a. Valores medidos > 2%
b. Valor estabelecido para todos os instrumentos com número de série ≥ 15007
c. Em sensores mais antigos pode estar na ordem de 8%
d. Até 2% / ano para números de séries mais altas
e. Não aplicável
f. Desconhecido
g. Mostra a irradiância integrada
32
f
Variação da Sensibilidad
estabilidade
e
(%, por ano)
11-12
d
8-10
f
0,1-0,15
f
11-12
f
5-6
15
≈3
f
16
f
7-8
≈1
8×10-3µA
g
<2
3.5. Outras medidas de radiação solar
Além das medidas normais de radiação solar (global, difusa e direta), se dispõe de
instrumentos capazes de medir a intensidade da radiação em determinados comprimentos de
onda. Entre os mais utilizados se encontram os instrumentos para medida da intensidade da
radiação solar no infravermelho e no ultravioleta.
3.5.1. Medidas de radiação de infravermelho
O único instrumento atualmente fabricado é o radiômetro Eppley PIR, derivado do
modelo PSP. Para eliminar a radiação solar de ondas curtas, utiliza um hemisfério de silício,
recoberto com seleneto de telúrio-zinco. Esta cobertura corta a radiação em 4 µm e é transparente
até 50 µm, limite de corte do hemisfério de silício.
3.5.2. Medida de radiação de ultravioleta
Um dos poucos instrumentos comercialmente disponíveis para medida da radiação no
ultravioleta é o modelo Eppley TUVR. Este aparelho consiste de uma célula fotoelétrica de
selênio e um par de filtros de corte que isolam a fração ultravioleta do espectro solar, que varia
entre 295 nm e 385 nm. Uma janela difusa de quartzo opaco é utilizada tanto para reduzir o fluxo
de radiação como melhorar a resposta coseno. Infelizmente, estes instrumentos apresentam
variações na ordem de 10 a 15% por ano devido à exposição prolongada, requerendo calibrações
frequentes (até três vezes por ano).
3.5.3. Medidas de duração da luz do Sol (insolação)
A duração da luz do Sol é definida como o intervalo de tempo no qual o disco solar não é
obstruído por nuvens. É, talvez, o tipo de medida de radiação mais antiga e inúmeros dispositivos
foram desenvolvidos nos últimos 160 anos para este fim. Estas medidas são importantes por duas
razões: a duração da luz solar, ou percentagem da luz solar possível, é um dos parâmetros
primários para a caracterização do clima em uma determinada região. A segunda é que este dado
pode ser utilizado para a estimativa do fluxo total de radiação solar numa superfície horizontal
para locais onde as medidas piranométricas não são efetuadas.
A popularidade destes instrumentos reside na sua simplicidade, conveniência e baixo
custo. A quantidade medida por estes registradores é o tempo, geralmente expresso em décimos
de hora (0,1 hora) na qual a intensidade da radiação solar direta é suficiente para ativar o
registrador.
Talvez o instrumento mais conhecido seja o registrador Campbell-Stokes, que consta
basicamente de uma esfera de vidro que atua como uma lente esférica para concentrar os raios de
sol em uma superfície côncava, o foco, onde se coloca uma tira de papel. Quando a intensidade
da radiação ultrapassa certo nível, o papel queima produzindo uma marca.
Estes instrumentos, entretanto, apresentam graves problemas de precisão. Um deles é que
não são suficientemente sensíveis para responder à baixas intensidades de radiação, como ocorre
nos primeiros minutos do amanhecer e nos últimos do entardecer. Outro problema é a dificuldade
para definir o limite inferior preciso do fluxo de irradiância direta que marcará legivelmente a tira
de papel. Em condições extremas de céu claro, atmosfera seca e uma tira de papel seca, este nível
estaria em torno de 70 Wm-2 enquanto numa situação oposta, o nível aumenta num fator de 4.
Um nível médio estaria em torno a 210 Wm-2.
Figura xx. Registrador Campbell-Stokes.
3.5.4. Medida da radiação através de satélites
A quantidade de radiação solar alcançando a superfície terrestre exibe grandes variações
espaciais, devido principalmente à diferenças geográficas nas características das nuvens. Devido
à restrições logísticas, existe uma impossibilidade de operar rede de monitoramento da radiação
solar em uma densidade compatível com esta complexidade espacial.
A maneira para contornar este problema está sendo a estimativa da radiação solar à partir
de dados obtidos por satélites meteorológicos. Os satélites oferecem a vantagem de uma ampla
cobertura geográfica (em muitos casos, global) com alta resolução espacial e temporal
(geralmente uma hora). Nenhum outro sistema de observação pode oferecer tais vantagens.
Entretanto, existe uma série de problemas associados com o uso de dados de satélite para estimar
o fluxo de radiação na superfície da terra. Na Figura 29 se apresentam alguns destes problemas.
Figura 29. Problemas associados com o monitoramento e modelamento da radiação solar baseada
em satélites.
34
Os primeiros trabalhos nesta área foram desenvolvidos na década de 70 e foram
realizados por Hanson3 e Vonder Haar4 . Estes pesquisadores utilizaram dados do satélite NOAA
(National Oceanic and Atmospheric Administration), de órbita polar, com uma única passagem
diária pela Terra.
Desta forma não foi incluido nestes modelos o efeito das variações diurnas da cobertura
de nuvens, que é o primeiro modulador da radiação solar que atinge a superfície da Terra. Esta
dificuldade foi contornada posteriormente por Tarpley5 que utilizou imagens de satélites
geoestacionários (por ex., GOES, LANDSAT, etc.). Estes dados possuem alta resolução
temporal (30 min) e espacial (≈ 2Km em uma latitude de 45°), permitindo, desta forma, a
avaliação das variações da cobertura de nuvens.
Os sensores dos satélites (radiômetros de varredura no visível e no infra-vermelho)
detectam a radiancia que emerge do sistema terra-atmosfera.
Os modelos disponíveis atualmente (físicos ou estatísticos) ainda apresentam erros
significativos, entre 3 e 30%, dependendo da cobertura de nuvens. Só como exemplo, podemos
citar o modelo abaixo, dado pela seguinte equação:
K ↓ = I sc cos θ ( a − bSR )
onde K ↓ é a irradiância na superfície terrestre, SR é a refletância normalizada medida pelo
satélite, a e b são coeficientes de regressão e θ é o ângulo de zênite local.
3.6. Calibração de instrumentos
A calibração de um instrumento significa a determinação de suas características e do fator
a ser utilizado para converter o seu sinal de saída em um valor de radiação solar (constante de
calibração). Geralmente, a constante de calibração de um instrumento é obtida para uma
temperatura nominal (25°C) e a transferência de calibração realizada em dias muito claros e com
intensidade de radiação acima de 800 Wm-2.
3.6.1. Transferência de calibração de pirheliômetros de referência para pirheliômetros de campo
A transferência de calibração de pirheliômetros de referência para pirheliômetros de
campo está regulada pela norma ASTM E816. Esta norma está limitada para pirheliômetros com
campo de visão entre 5 e 6°. Para a calibração de pirheliômetros de referência secundários, o
padrão primário necessita ser um radiômetro absoluto do tipo cavidade auto-calibrável, traçável
diretamente à WRR através de participação em uma IPC (V ou VI). Um pirheliômetro de
referência secundário calibrado desta maneira pode ser usado para calibrar pirheliômetros para
uso em campo. Padrões de referência primários ou secundários nunca devem ser utilizados como
pirheliômetros de campo, pois a exposição ao Sol necessita ser limitada somente à casos de
calibrações ou inter-comparações.
As medidas entre os pirheliômetros devem ser realizadas simultaneamente, com sistemas
de seguimento idênticos. Devem tomar-se medidas a cada 30 s durante 10 minutos para produzir
um conjunto de 21 medidas. Cinco conjuntos de medidas devem ser tomados para cada um dos
três dias, e isto deve ser realizado sempre no intervalo de 2 horas antes e depois do meio-dia
(TSV). A constante do instrumento é obtida simplesmente dividindo a tensão de saída do
instrumento de teste pela irradiância determinada pelo pirheliômetro de referência.
35
Esta norma também discute problemas tais como condições do céu, comparação entre
instrumentos de diferentes aberturas e resposta espectral.
3.6.2. Calibração de piranômetros
O único método de calibração outdoor de piranômetros de referência primário envolve a
comparação com um pirheliômetro absoluto de cavidade ou um pirheliômetro de incidência
normal.
A transferência de calibração pode ser realizada limitando-se o campo de visão do
piranômetro usando-se um tubo que obstrui o céu, deixando somente o disco solar ou por um dos
dois métodos de disco de sombra, que oculta o sol.
a) Método do tubo colimador
Um tubo colimador típico consta de um invólucro pintado internamente de negro, com as
mesmas relações geométricas do tubo do pirheliômetro e alinhado corretamente com o sensor do
piranômetro. Neste caso, a transferência do fator de calibração é direta, desde que a inclinação e
a abertura do tubo colimador sejam idênticas ao pirheliômetro de referência.
As desvantagens decorrentes deste método são:
- diferença de resposta do piranômetro devido ao aquecimento solar induzido pelo tubo
colimador
- desalinhamento ótico entre o tubo e o sensor do piranômetro
- interações óticas entre o(s) domo(s) e o casco do piranômetro
b) Método da sombra intermitente
Este é o método de calibração tradicional de piranômetros. A comparação é indireta e é
feita dividindo-se a diferença entre a tensão do piranômetro nas condições alternadas de sombra e
exposição ao sol pela irradiância medida com o pirheliômetro de referência. Na Figura 30 se
esboça este método.
Figura 39. Método da sombra intermitente.
36
Apesar do largo uso deste método, existe considerável controvérsia sobre ele,
principalmente no que se refere a tempo de resposta. Na calibração, a tensão Vs da sequência
sombreada representa a irradiância difusa (com a componente direta removida), a tensão Vu da
sequência sem sombra menos Vs é equivalente a tensão da componente direta e a constante é
obtida como:
k=
Vu − V s
(46)
I b cos θ z
onde k é a constante do instrumento em µVW-1m-2, Ib é a radiação direta normal e θz é o ângulo
de zênite.
Na prática, a sequência sombra-exposição varia desde menos de 1 min cada (para o
modelo Eppley) até 6 min para os outros modelos. Este tempo depende da constante de tempo do
piranômetro (termodinâmica do equipamento) e pode variar em função da temperatura.
c) Método da soma dos componentes
Este método, apresentado na Figura 31, substitui o método da sombra intermitente.
Necessita a utilização de um pirheliômetro de referência para medir a componente direta e um
piranômetro, bem caracterizado e continuamente sombreado, para medir a componente difusa.
Figura 31. Método da soma dos componentes.
A constante do aparelho é obtida como:
k=
Vt
(47)
I s + I b cos θ z
onde Vt é a tensão do instrumento testado, Is é a irradiância medida pelo piranômetro
continuamente sombreado, Ib é a irradiância direta medida pelo pirheliômetro e θz é o ângulo de
zênite.
A vantagem deste método é a facilidade de operação e a possibilidade de calibrar vários
instrumentos ao mesmo tempo. A calibração deve ser efetuada somente quando a irradiância
difusa for inferior a 20% da total e neste caso a incerteza do método está na ordem de 0,6%.
37
3.7. Rêdes de monitoramento de radiação solar
Os dados de radiação solar medidos pelas diversas redes de monitoramento podem ser
utilizados em uma infinidade de aplicações. Somente para ilustração, podemos citar:
- tecnologias de conversão da energia solar (fotovoltaica, sistemas solares térmicos ativos
e passivos e biomassa)
- meteorologia (transferência radiativa, física atmosférica, etc.)
- climatologia (efeito estufa, efeitos de urbanização, etc.)
- agricultura (evapotranspiração, fotossíntese, etc.)
- medicina (pesquisa sobre câncer de pele, etc.)
- materiais (degradação de polímeros, coberturas reflexivas, etc.)
Entretanto, para a maioria das necessidades, a consulta de uma base de dados se vê
frustrada pelo conflito entre a informação desejada e a disponível. Entre os problemas mais
usuais podemos citar:
- dificuldade de acesso público às bases de dados existentes
- formato de armazenamento (material impresso, fitas magnéticas, disquetes, etc.)
- tipo de medidas (global horizontal, global inclinada, direta normal, difusa, etc.)
- exatidão dos dados (a maioria dos dados são estimativas baseadas em observações de
nuvens, além de ausência de calibração sistemática, instrumentos inadequados, etc.)
- frequência dos dados (minutos, horas, dias, meses, etc.)
- período de registro (os dados são suficientes para representar todos os critérios de
projeto?)
- dados relacionados (vento, temperatura, pressão, cobertura de nuvens, etc. )
Numerosos esforços foram realizados para a construção e manutenção de bases de dados
meteorológicos em todo o mundo. Talvez do maior deles resultou a construção da National Solar
Radiation Network, dos Estados Unidos, a mais de 80 anos. Com o interesse despertado pelas
energias renováveis, na década de 70, esta base foi submetida a um laborioso processo de
reabilitação. Deste processo resultou a criação de uma base de dados horários de radiação solar
global horizontal de 26 estações de observação, combinados com outros dados meteorológicos de
interesse da comunidade científica. Esta base de dados é conhecida com o nome de SOLMET, e
pode ser obtida diretamente ao National Climatic Data Center. Dos dados diários de 27 estações,
resultou a criação da base conhecida como SOLDAY. Estas duas bases facilitaram o
modelamento dos dados de radiação com outras variáveis climatológicas, e os modelos
resultantes permitiram criar uma base de dados de radiação solar para 222 estações onde não
haviam registros destes dados. Esta base de dados é conhecida como ERSATZ. A partir de 1977,
foi criada uma nova rede meteorológica com 38 estações que utilizaram novos modelos de
radiômetros e com disponibilidade de fundos para executar cuidadosas e periódicas recalibrações
destes instrumentos. Durante o período 1981-1985, restrições governamentais fizeram com que a
manutenção e a recuperação dos dados destas estações, paulatinamente, chegassem a níveis
inaceitáveis e finalmente, em 1985, foram desativadas.
A partir de 1986, e com novos fundos, estas estações foram progressivamente melhoradas
e foram instalados equipamentos automáticos de coleta e transmissão destes dados possibilitando
a volta ao funcionamento em 1988.
Além desta rede, os Estados Unidos contam ou contaram com outras redes especiais,
controladas por outros órgãos. A que mais se destaca é a rede formada por oito universidades que
38
monitoraram, com elevada qualidade e resolução (frequência de 1 minuto), dados de diversos
radiômetros e instrumentos meteorológicos. A base de dados resultante abrange o período 19791983.
Na América do Norte, também o Canada possui uma rêde muito importante de medida da
radiação solar administrada pelo Canadian Atmospheric Environment Service. Esta rêde, menos
extensa que a dos Estados Unidos, se caracteriza pela elevada qualidade dos dados medidos.
Na Europa, diversos países possuem redes meteorológicas que coletam sistematicamente
dados horários de radiação solar (global horizontal, difusa e direta normal). Estas redes, em geral,
possuem um número reduzido de estações mas que, em função do espaço territorial ser também
menor, possuem uma boa abrangência. Contudo, a disseminação destas informações é ainda
muito restrita. Tanto é possível conseguir-se dados de radiação solar de um país sem qualquer
ônus, como alguns podem pedir valores proibitivos.
O trabalho mais abrangente feito na Europa sobre dados de radiação solar é o projeto
EUFRAT6 e nada mais é que uma ação conjunta para preparar dados climatológicos que sirvam
como dados de entrada para as ferramentas de projeto de sistemas solares (basicamente radiação
e temperatura). No final, foram reunidos dados de 37 localidades de 9 países mas com um
número médio de 3 anos.
No Brasil, as medidas de radiação solar estão a cargo do Centro Nacional de Radiação
Solar (CERAS) do Instituto Nacional de Meteorologia (INEMET), pertencentes ao Ministério da
Agricultura. Os dados de radiação solar medidos pelas estações meteorológicas pertencentes a
esta rêde começaram a ser publicados à partir de 1978, no ‘Boletim Trimestral de Radiação
Solar’. Até o ano de 1984, o Laboratório de Energia Solar possui todos os volumes deste boletim.
Os dados pertencentes a algumas estações já foram colocados em forma informatizada,
permitindo o estudo e caracterização da energia solar nestes locais. Na Tabela 7 se apresenta uma
lista destas estações, juntamente com informações da latitude, longitude e altitude acima do nível
do mar, bem como do período de tempo correspondente.
Tabela 7. Relação das estações meteorológicas pertencentes ao CERAS com dados
informatizados.
Cidade
U.F.
Latitude
Longitude
Altitude (m)
1º mês
Ult. mês
Belém
Belo Horizonte
Boa Vista
Brasília
Carolina
Curitiba
Manaus
Porto Alegre
Rio de Janeiro
Salvador
São Paulo
PA
MG
RR
DF
MA
PR
AM
RS
RJ
BA
SP
1.45 S
19.93 S
2.82 N
15.78 S
7.33 S
25.43 S
3.13 S
30.02 S
22.92 S
13.00 S
23.50 S
48.47 W
43.93 W
60.65 W
47.93 W
47.47 W
49.27 W
60.02 W
51.22 W
43.17 W
38.52 W
46.62 W
24.00
850.23
90.00
1158.40
192.83
923.50
59.50
46.97
5.32
51.41
792.06
mai/78
mar/79
nov/80
jan/78
fev/78
jan/78
jun/78
jan/78
fev/78
jan/78
jan/78
dez/88
mar/88
ago/87
mar/88
dez/87
mar/88
mar/88
mar/88
mar/88
mar/88
dez/87
Além destas, foram publicados dados de:
- Bom Jesus da Lapa (BA) - jan/78-mar/81
- Campo Grande (MS) - ago/78-mar/88
- Cuiabá (MT) - jul/78-mar/88
39
- Floriano (PI) - mai/78-set/87
- Fortaleza (CE) - mai/78-mar/88
- Foz do Iguaçu (PR) - jan/78-fev/81
- Parque Nacional (GO) - jan/84-mar/88
- Petrolina (PE) - jan/78-mar/88
- Rio Verde (GO) - jan/84-ago/87
- São Luis (MA) - mai/78-fev/88
- São Luis Gonzaga (RS) - jan/84-mar/88.
- Bagé (RS) - jan/84-mar/88
- Caravelas (BA) - jan/78-out/87
que posteriormente sofrerão o mesmo processo de informatização.
No Brasil também existem inúmeras redes regionais de monitoramento de dados
climatológicos e algumas delas medem a radiação solar global. Entre estas está a rede do
Instituto de Pesquisas Agronômicas (IPAGRO) da Secretaria da Agricultura do Estado do Rio
Grande do Sul. Esta rede está composta de 22 estações espalhadas por todo o estado e os dados
de radiação solar e outras variáveis climatológicas são publicados nos boletins ¨Observações
Meteorológicas no Estado do Rio Grande do Sul¨. Na Tabela 8 é apresentada a relação das
estações pertencentes a esta rede.
Tabela 8. Relação das estações meteorológicas pertencentes ao IPAGRO.
Estações
Bagé
Encruzilhada do S.
Erexim
Farroupilha
Gauiba
Ijuí
Jaguarão
Júlio de Cast.
Osório
Passo Fundo
Quaraí
Rio Grande
Santa Maria
Santana do Liv.
Santo Augusto
São Borja
São Gabriel
Taquari
Tramandaí
Uruguaiana
Vacaria
Veranópolis
Altitude
214
420
760
702
46
448
11
514
32
709
100
16
153
210
380
99
109
76
3
74
955
705
Latitude
31°20’14”
30°32’35”
27°37’45”
29°14’30”
30°05’52”
28°23’17”
32°33’32”
29°13’26”
29°40’49”
28°15’41”
30°23’17”
32°01’02”
29°41’24”
30°53’18”
27°54’16”
28°39’44”
30°20’27”
29°48’15”
29°56’22”
29°45’23”
28°30’09”
28°56’14”
40
Longitude
54°05’59”
52°31’20”
52°16’33”
51°26’20”
51°39’08”
53°54’50”
53°23’20”
53°40’45”
50°13’56”
52°24’45”
56°26’53”
52°09’32”
53°48’42”
55°31’56”
53°45’14”
56°00’44”
54°19’01”
51°49’30”
50°30’12”
57°05’37”
50°56’12”
51°33’11”
Período
1957-77
1959-77
1966-77
1964-77
1968-77
1964-77
1966-77
1957-77
1959-77
1966-77
1967-77
1957-77
1964-77
1967-77
1970-77
1957-77
1965-77
1964-77
1961-72
1964-77
1966-77
1957-77
Nestas estações, para a medida da radiação solar são utilizados os actinógrafos tipo
Robitzsch-Fuess e para as medidas de insolação heliógrafos tipo Campbell-Stokes.
Estes dados permitiram a construção de mapas solarimétricos mensais para o estado do
Rio Grande do Sul, tal como se vê na Fig. 32 para os meses de junho (inverno) e dezembro
(verão).
Nestes mapas, a irradiação diária média mensal é representada por isolinhas, traçadas
considerando-se, além dos valores de irradiação em cada uma das estações, as zonas climáticas e
o relevo do estado. Os valores da irradiação estão expressos em MJm-2dia-1 .
Figura 32. Mapas com isolinhas de radiação para o estado do Rio Grande do Sul.
41
- 4A atmosfera terrestre
A radiação originada do Sol é atenuada, antes de alcançar o solo, pela atmosfera terrestre,
que pode ser classificada em dois tipos bastante amplos: (i) atmosfera sem nuvens e (ii)
atmosfera com nuvens. Neste capítulo, os constituintes de uma atmosfera sem nuvens são
descritos.
A radiação máxima recebida pela Terra é em condições de atmosfera sem nuvens e céu
claro. A maioria dos equipamentos de conversão solar são projetados para operar nestas
condições ou quando o nível de radiação estiver acima de um determinado patamar. Como
valores altos de radiação também podem causar muitos problemas (agricultura, arquitetura, etc.)
a correta determinação destes níveis máximos é muito importante.
A estrutura vertical da atmosfera terrestre, como é representada esquematicamente na
Figura 33, é dividida em um número de esferas concêntricas: troposfera, estratosfera, mesosfera,
termosfera, etc. e é descrita por uma atmosfera padrão.
Figura 33. Representação esquemática da atmosfera terrestre (estratificação).
Existe uma acentuada variação de temperatura em cada uma destas esferas, tal como se vê
na Figura 34. Já a densidade e a pressão diminuem continuamente. Para efeitos práticos, os
valores ao nível do mar da pressão, temperatura e densidade são os seguintes:
- Pressão: 1013,25 mbares; 760 mm Hg ou 101,325 kPa
- Temperatura: 288 K ou 15°C
- Densidade: 1225 kg m-3
42
Figura 34. Variação da temperatura e pressão atmosférica com a altitude geográfica.
A atmosfera terrestre consiste principalmente de nitrogênio molecular e oxigênio
molecular. Ar seco limpo contém aproximadamente 78% de nitrogênio, 21% de oxigênio, 1% de
argônio e 0,03% de dióxido de carbono, em volume. Além disso, a atmosfera terrestre contém
vapor d’água e matéria particulada (aerossóis) tais como pó, fuligem, gotas d’água e cristais de
gelo, componentes estes que são extremamente variáveis tanto no tempo como no espaço. Desta
forma, para determinar a transmitância da atmosfera à radiação solar, a atmosfera total da terra é
geralmente dividida em três grupos: moléculas de ar seco, vapor d’água e aerossóis. A radiação
solar que penetra a atmosfera terrestre é atenuada por cada um destes grupos, diferentemente.
4.1. Ar seco limpo
A composição e concentração real dos constituintes do ar seco variam com a localização
geográfica, elevação e estação do ano. A concentração de alguns gases, tais como dióxido de
carbono, ozônio, monóxido de carbono e metano podem ser altamente variáveis. Estes gases não
são distribuídos homogeneamente, tanto no espaço como no tempo. Estas variações são função
da atividade industrial e rural do lugar, do meio ambiente e da natureza dinâmica da atmosfera.
A dissociação do oxigênio molecular (O2) pela radiação solar ultravioleta, começa à partir
de 90 km, na direção vertical. Desta forma, a medida que a altitude aumenta, a concentração de
O2 diminui e a concentração de oxigênio atômico (O) aumenta. Como o nitrogênio molecular é
mais difícil de dissociar, a concentração de nitrogênio atômico (N) permanece muito baixa,
mesmo em altas altitudes. A partir de 600 km, o hélio torna-se o principal constituinte, e a
aproximadamente 2.000 km, os principais constituintes da atmosfera são o hélio ionizado, o
hidrogênio ionizado e elétrons.
Todas as moléculas de ar “exaurem” a energia solar através do espalhamento (dispersão),
a qual acontece em todos os comprimentos de onda, o que caracteriza um processo continuo. As
moléculas de ar também absorvem a radiação solar, só que seletivamente, em determinados
comprimentos de onda. Os absorvedores mais importantes do ar seco são o ozônio, o dióxido de
carbono, oxigênio, óxidos de nitrogênio, nitrogênio e combinações de hidrocarbonetos.
Na alta atmosfera, o ozônio é formado principalmente pela radiação solar. No solo, ele é
formado através da decomposição do óxido de nitrogênio que penetra na atmosfera através da
fumaça de indústrias ou pela queima de florestas.
Em volta do equador, a quantidade média de ozônio está em torno a 0,24 cm (CNTP) e
este valor aumenta com a latitude. Nas regiões polares, a quantidade medida de ozônio é de 0,46
cm (CNTP). A distribuição vertical do ozônio varia com a latitude e a estação do ano. Está
43
concentrado principalmente entre 10 e 35 km de altitude e o perfil desta distribuição está
representado na Figura 35.
Figura 35. Variação da concentração de ozônio em função da altitude geográfica.
4.2. Vapor d’água
A água existe na atmosfera em três estados: gás, líquido e sólido (gêlo). A água em estado
gasoso é chamada vapor d’água e sua quantidade pode ser definida de duas maneiras. A relação
de mistura, Mr e a água precipitável, w´. A relação de mistura é a relação entre a massa de vapor
d’água presente e a massa de ar sêco, em um volume unitário. A água precipitável é a quantidade
total de vapor d’água na direção zenital, entre a superfície da terra e o topo da atmosfera. Assim,
água precipitável pode ser escrita como:
w′ =
1 ∞
∫ M dz (48)
g 0 r
onde z é a altura vertical e g a aceleração da gravidade. Desta equação, as unidades de w´ são
massa por unidade de área. Entretanto, água precipitável é geralmente descrita como a espessura
de água líquida que seria formada se todo o vapor, na direção zenital, se condensasse na
superfície de uma área unitária. Como 1 cm corresponde a 1g cm-2 de água precipitável, a
equação acima ainda pode ser usada. A Tabela 9 contém valores médios anuais de Mr e w´, em
intervalos de 2 km de altitude.
Desta tabela, é evidente que aproximadamente metade da água precipitável está
concentrada nos primeiros 2 km acima do nível do mar. Além de 12 km, a quantidade de água
precipitável é praticamente inexistente.
A quantidade de água precipitável é altamente variável, principalmente com a estação do
ano. Uma atmosfera muito seca pode conter apenas 1 mm de água precipitável enquanto uma
muito úmida pode conter até 40 mm.
44
Tabela 9. Relação de mistura, Mr (ppm) e água precipitável, w´ (µm) (valores medios anuais).
Altitude,
km
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
31
Relação de mistura Agua precipitável, w´, µm
média, Mr, ppm
6300
11224
3800
5206
1900
2057
90
710
270
150
37
22
17
8
10
4
9
3
13
3
18
4
27
4
38
4
58
4
86
5
128
2
150
Total
19,41 mm
Muitos países publicam mapas de contorno com médias mensais de água precipitável. Na
ausência destes mapas, podem-se utilizar correlações entre água precipitável e a pressão parcial
do vapor d’água, ou temperatura de orvalho ou ainda umidade relativa. Algumas destas
correlações são:
w ′ = 0,125 exp( 0,295 p v1/ 2 − 0,803) (49)
onde w´ está em centímetros e pv (a pressão parcial do vapor a nível do solo) em milibares.
w ′ = 0,1 exp( 2 ,2572 + 0,054544t d ) (50)
onde w´ está em centímetros e td é a temperatura de orvalho em °C. Geralmente, o valor da água
precipitável obtida destas equações necessita ser reduzida para condições padrão, isto é, pressão
de 1013,25 mbares e temperatura de 273 K. A fórmula para realizar esta redução é a seguinte:
3/ 4
 p   273 1/ 2
 (51)
 
w = w ′
 1013,25   T 
onde w é a água precipitável reduzida, em centímetros, p é a pressão da estação em mbares e T a
temperatura ambiente, em Kelvin. Outra equação, que não necessita correção é:
w = 0,493
φ r ps
45
T
(52)
onde w é a água precipitável reduzida, em centímetros, φr é a umidade relativa em frações de um,
T é a temperatura ambiente em graus K e ps é a pressão parcial do vapor d’água no ar saturado
que pode ser obtida por:
p s = exp( 26,23 − 5416 / T ) (53)
4.3. Aerossóis
Aerossol é uma pequena partícula sólida ou líquida que permanece em suspensão no ar e
se move com este. Obviamente, chuva, neve e granizo não são aerossóis. Ao contrário das
moléculas dos gases atmosféricos permanentes, as partículas suspensas na atmosfera apresentam
uma considerável diversidade em volume, tamanho, distribuição, forma e composição. Estas
partículas podem ser tanto de origem terrestre (fumaça industrial, pólen, erupções vulcânicas,
tormentas de areia, incêndios florestais e queimadas agrícolas) como de origem marinha (cristais
de sal, etc.).
A chuva é o principal limpador dos pós secos na atmosfera. A chuva reduz o número de
partículas de aerossóis, mas aumenta o tamanho daquelas que permanecem. Consequentemente, a
turbidância (no sentido ótico) permanece inalterada imediatamente após uma chuva.
Uma atmosfera que contém aerossóis é chamada atmosfera turva. A turbidância é um
parâmetro ótico da atmosfera e pode ser grosseiramente relacionado com a visibilidade
horizontal, que na realidade é uma medida subjetiva. A presença de aerossóis na atmosfera pode
ser quantificada por um destes três parâmetros:
- número de partículas de pó por centímetro cúbico
- turbidância atmosférica
- visibilidade
4.4. Caminho ótico relativo e massa ótica relativa
Quando a radiação monocromática atravessa um meio, cada molécula (ou partícula)
atenua a energia. A atenuação é função do tipo e do número de moléculas encontradas no
caminho de um raio solar. O número de moléculas atingidas por um raio solar antes que ele atinja
o solo está relacionado com a distância percorrida pelo raio.
A densidade multiplicada pelo caminho percorrido representa a massa de uma substância
em uma coluna de seção unitária; isto também pode ser chamado de massa ótica. A massa ótica
real pode ser escrita como:
∞
mact = ∫ ρds (54)
0
onde ds é o caminho geométrico do raio de luz do sol e ρ é a densidade da substância em ds.
Como a refração é dependente do comprimento de onda, o caminho ótico varia com o
comprimento de onda e, consequentemente, a equação acima somente se aplica à radiação
monocromática. Quando o sol está no zênite, a trajetória da luz é uma linha reta e ds é igual a
altura de um elemento dz, onde z é a distância ao longo da direção vertical. Assim, a massa ótica
real na direção vertical é dada por:
46
∞
mact , v = ∫ ρdz (55)
0
A massa ótica relativa, mr, é definida como a relação entre o caminho ótico numa
trajetória obliqua e o caminho ótico na direção vertical (direção zenital). Assim:
∞
∫ ρds
mr =
0
∞
∫ ρdz
(56)
0
Como a atenuação é feita por diferentes moléculas, a equação acima deve ser resolvida
separadamente para cada um dos componentes atenuadores. Ignorando a curvatura da terra e
assumindo uma atmosfera não-refrativa e completamente homogênea, tal como se vê na Figura
36(a), a massa ótica relativa, aplicada para todos os constituintes da atmosfera, é dada por:
mr′ = sec θ z (57)
(a)
(b)
Figura 36. Trajetória de um raio de sol através da atmosfera terrestre. (a) atmosfera planoparalela não-refrativa e (b) atmosfera refrativa esférica de densidade variável.
O erro nesta equação, devido à curvatura da terra e a refração da atmosfera real ter sidos
desprezados é 0,25% para θz =60° e aumenta para 10% para θz =85°.
4.5. Massa de ar ótica relativa
Para resolver a Equação (56), a variação de densidade de uma atmosfera real é necessária.
Baseado em uma atmosfera padrão, Kasten7 apresentou uma tabela de massas de ar e a seguinte
equação, que aproximava sua tabela:
[
mr = = cos θ z + 0,50572( 96,07995 − θ z )
47
]
−1, 6364 −1
(58)
com θz dado em graus. Esta fórmula tem uma exatidão superior a 0,1% para ângulos de zênite
menores que 86° e um erro máximo de 1,25% para θz =89,5°. Os valores de massa de ar para
alguns ângulos de zênite são dados na Tabela 10.
Tabela 10. Valores de massa de ar.
θz,, graus
0
30
60
65
70
75
80
85
86
87
88
89
90
Massa de ar ótica
mr (Kasten)
mr´=secθz
1,00
1,00
1,15
1,15
2,00
1,99
2,37
2,35
2,92
2,90
3,86
3,81
5,76
5,58
11,47
10,32
14,34
12,34
19,11
15,22
28,65
19,54
57,30
26,31
36,51
∞
A equação acima é aplicável para uma pressão padrão de 1013,25 mbares no nível do
mar; para outras pressões é comum modificá-la, seguindo a seguinte aproximação:
 p 
 (59)
ma = mr 
 1013,25 
Em geral, a correção da pressão necessita ser aplicada para estações a 2000 m de altitude
ou mais ou quando a diferença entre a pressão padrão e a pressão local for maior que 20 mbares.
A pressão acima do nível do mar pode ser obtida através de:
p
= exp( −0,0001184z ) (60)
po
onde z e a altitude da estação, em metros acima do nível do mar.
48
-5Estimativa da radiação solar média
A melhor fonte de informação para a estimativa da radiação média incidente são,
obviamente, os dados medidos de radiação. Na ausência destes dados assim como dados de
locais próximos com climatologia semelhante, é possível usar relações empíricas para estimar a
radiação solar incidente.
5.1. Correlação entre irradiação global diária média mensal e insolação (horas de brilho de
sol)
É óbvio que, quanto maior for o número de horas de brilho de sol (insolação), maior será
a radiação incidente e vice-versa, existindo uma relação direta entre estes dois valores. A longo
prazo, a radiação global diária média mensal pode ser estimada através da insolação, dado este
medido em muitos lugares do mundo utilizando o registrador (Heliógrafo) Campbell-Stokes.
A equação original se deve a Ångstrom8 e relaciona a irradiação diária média mensal com
a irradiação de um dia claro para o local em questão e a fração de horas de sol possível. Assim:
H
) ) n
=a+b
(61)
Hc
Nd
onde H é a irradiação global horizontal
diária média mensal, Hc é irradiação diária horizontal em
) )
um dia perfeitamente claro, a e b são constantes empíricas obtidas através de regressão, n é o
número medido de horas de sol e N d é o número teórico de horas de sol, calculado com a
Equação (11), para um dia médio do mês.
) )
Para Estocolmo, Ångstrom encontrou valores) de a e b de 0,25 e 0,75, respectivamente.
)
De acordo com a Equação (61), é óbvio que a + b =1, pois para dias muito claros, n / N d =1.
Entretanto, devido a problemas inerentes aos registradores Campbell-Stokes, n / N d nunca é igual
a 1. Consequentemente, para condição de céu claro e com este tipo de coeficiente, a radiação é
subestimada.
Do exposto acima, fica claro que a soma destes coeficientes deve ser diferente da
unidade. Além disso, este tipo de correlação sofre outro problema. A dificuldade em definir-se
um dia perfeitamente claro, Hc . Para solucionar este problema, este tipo de equação foi
modificada por Prescott9 , basendo-a na radiação extraterrestre, Ho, quantidade que pode ser
facilmente calculada. Assim:
H
n
=a+b
(62)
Ho
Nd
Geralmente, os valores de a se encontram numa faixa entre 0,17 e 0,32 enquanto b varia
entre 0,37 e 0,69. Examinando vários valores publicados de a e b, Rietveld10 encontrou que a está
relacionado linearmente e b hiperbolicamente ao valor médio de n / N d , tal que:
49
 n 
a = 0,1 + 0,24
 (63a)
 Nd 
e
N
b = 0,38 + 0,08 d
 n

 (63b)

Substituindo estas duas equações em (62), obtém-se:
H
n
= 0,18 + 0,62
(64)
Ho
Nd
Esta equação pode ser aplicável em qualquer parte do mundo, porém volta-se a salientar
que estas correlações somente são aplicáveis para médias de longo prazo. Para o Rio Grande do
Sul, Berlato11, utilizando valores de irradiação global horizontal diária media mensal e insolação
medida por 17 estações pertencentes ao Serviço de Ecologia Agrícola da Secretaria de
Agricultura, no período de 1955-1965, encontrou valores de a e b iguais a 0,23 e 0,46,
respectivamente.
5.2. Correlação entre a irradiação global diária media mensal com a cobertura de nuvens
Na busca de outros estimadores de radiação solar, principalmente para cobrir a carência
de estações de medidas, a variável cobertura de nuvens leva vantagem em relação à insolação,
porque estes valores são medidos em muitas estações pelo mundo com uma melhor distribuição
geográfica que esta.
A correlação entre irradiação solar e a fração do céu coberto por nuvens é perfeitamente
conhecida e a correlação linear proposta é na seguinte forma:
H
&& (65)
= a&& − bC
Ho
onde C é a fração média mensal do céu obstruído pela presença de nuvens (durante o período
diurno, obviamente). De acordo com Black12, a forma final da correlação é:
H
= 0,803 − 0,340C − 0,458C 2 , para C ≤ 0,8 (66)
Ho
5.3. Estimativa da irradiação global horária média mensal, em superfície horizontal
Em muitas situações de projeto, é necessário utilizar valores horários de radiação global e
difusa de longo prazo. Como se pode imaginar, a disponibilidade de tais dados é bastante
reduzida. Para isso, foram desenvolvidas relações que permitem, a partir de valores medidos ou
estimados da radiação global diária media mensal, H , obter os dois valores horários desejados.
Na Figura 37(a), está representada a variação diurna da irradiação global horária média
mensal, I , medida em Montreal. A área de cada uma destas curvas corresponde ao valor diário
H . Para qualquer estação, a forma desta figura será equivalente. Considerando agora a Figura
37(b), onde se representa a variação diurna da irradiação extraterrestre horária, I o , também para
50
Montreal e cuja área representa o valor de H o . Pode-se notar a semelhança existente entre as
duas figuras, a qual leva a consideração de que as relações I / H e I o / H o sejam idênticas. A
partir desta constatação, Whillier13 desenvolveu uma relação entre valores horários e diários da
irradiação direta, I b / H b , a qual pode ser escrita da seguinte maneira:
∫
∫
1h
Ib
=
Hb
τ b (ω )I&sc E o cosθ z dω
1dia
τ b (ω )I&sc E o cosθ z dω
(67)
onde
τb =
Ib
(68)
Io
é chamada de transmitância atmosférica para a radiação direta. Assumindo-se que τ b seja
constante ao longo de um dia, a Equação (67) se reduz a:
Ib
Io
π ( 24 / π ) sen( π / 24) cos ω i − cos ω s
(69)
=
=
Hb H o 24
sen ω s − ( π / 180)ω s cos ω s
que nada mais é que a relação entre a Equação (24) e a Equação (29). Como na maioria das vezes
Hb não é conhecido, impedindo, portanto de determinar I b , mas que a sua vez possui variação
diurna semelhante a I , utiliza-se a relação I / H em substituição à relação I b / H b . A
discrepância existente entre esta aproximação teórica e os dados medidos é que a transmitância
não é constante ao longo do dia. Posteriormente, Collares-Pereira e Rabl14 desenvolveram uma
expressão matemática para a relação I / H , com a seguinte forma:
rh ( ω , ω s ) =
cos ω i − cos ω s
I
π
&&&
=
(
a + b&&& cos ω i )
(70)
H 24
sen ω s − ω s cos ω s
onde
&&&
a = 0,409 + 0,5016 sen( ω s − 1,047) (71a)
e
b&&& = 0,6609 − 0,4767 sen( ω s − 1,047) (71b)
E da mesma forma, para o cálculo da irradiação difusa horária, temos:
rd ( ω , ω s ) =
Id
(72)
Hd
e cuja expressão matemática é dada por:
rd ( ω , ωs ) =
π cosωi − cosωs
(73)
24 sen ωs − ωs cosωs
51
(a)
(b)
Figura 37. Variação diurna da irradiação global horária media mensal em Montreal (a) e variação
diurna da irradiação extraterrestre horária, também para Montreal (b).
5.4. Distribuição estatística da irradiação global em superfície horizontal
A irradiação solar na superfície terrestre, ao contrário da irradiação extraterrestre, não
pode ser determinada analiticamente, devido principalmente à presença das nuvens. O efeito das
nuvens pode ser caracterizado por duas variáveis: o índice de claridade (que é a transmitância da
atmosfera) Kt e a fração difusa Kd , definidos como:
Kt =
H
(74)
Ho
52
e
Kd =
Hd
(75)
H
sendo H a irradiação global diária em superfície horizontal e Hd a irradiação difusa diária,
também em superfície horizontal. Uma vez conhecidos estes dois valores, a irradiação na
superfície terrestre pode ser calculada. No entanto, nenhum destes dois valores pode ser estimado
com confiança.
Entretanto, estudando-se a distribuição estatística de ocorrências passadas, se pode
construir um modelo de probabilidade, capaz de estimar a probabilidade que um valor de Kt ou
Kd para um evento futuro esteja dentro de certos limites especificados.
Os estudos da distribuição estatística de Kt foram realizados por Liu e Jordan15 que
geraram a função distribuição F(Kt ) para um número de conjuntos de eventos separados, cada
conjunto consistindo de dados de um determinado local e um determinado mês do ano. Eles
encontraram uma importante regra que governa as funções F(Kt ): se dois conjuntos de eventos
possuem o mesmo valor médio de Kt (isto é, K t ), eles gerarão funções F(Kt ) aproximadamente
idênticas. Esta regra implica que se pode definir uma função universal de duas variáveis F(Kt,
K t ) da seguinte forma: dado um grande conjunto de eventos, cada um tendo um índice de
claridade correspondente, com seu valor médio K t , então F(Kt, K t ) é a probabilidade que um
evento tenha seu índice de claridade menor que Kt*.
Estas funções de distribuição estão mostradas na Figura 38.
Figura 38. Distribuição fracional de tempo da irradiação global diária em função do índice de
claridade.
Assim, por esta figura, para um local com K t de 0,6, aproximadamente 19% dos dias
terão Kt igual ou menor que 0,40, por exemplo.
Uma equação analítica que ajusta bastante bem esta distribuição foi proposta por
Hollands e Huget16. A função densidade de probabilidade foi aproximada por uma distribuição
Gama modificada, na seguinte forma:
P( K t , K t ) = C
(K
tmax
− Kt )
K tmax
53
exp( λK t ) (76)
onde C e λ são funções de Ktmax e K t . Substituindo esta equação naquela que define o valor
esperado (media) de uma variável aleatória:
Ktmax
∫ K P (K , K )dK
Kt =
t
t
t
(77)
t
0
obtém-se:
C=
(e
λ2 K tmax
λKtmax
(78)
− 1 − λK tmax )
Substituindo a Equação (78) em (76) elimina-se C e substituindo a expressão resultante
para P( K t , K t ) em (77), obtém uma relação entre K t e λ:
Kt =
 2


λKtmax
) + 2K tmax e λKtmax 
 λ + K tmax (1 − e

(e
λKtmax
− 1 − λK tmax )
(79)
Esta relação implícita pode ser aproximada pela seguinte equação:
λ=
(2ϑ − 17,519 exp(− 1,3118ϑ ) − 1062 exp(− 5,0426ϑ )) (80)
K t max
onde
ϑ = K tmax ( K tmax − K t ) (81)
O valor fixado para Ktmax é aquele que permite um melhor ajuste com a curvas de Liu e
Jordan, e o valor proposto na literatura é igual a 0,864.
A equação de F(Kt, K t ) obtida é:
F ( Kt , Kt ) =
C
K tmax λγ 1
[ e (1 − γ K ) − 1] (83)
λKt
1
onde
γ1 =
λ
(84)
(1 + λKtmax )
As curvas resultantes são apresentadas na Figura 39.
54
t
Figura 39. Distribuição da fração de tempo F(Kt, K t ).
5.5. Estimativa da irradiação difusa diária em uma superfície horizontal
Em um dia nublado, a radiação global recebida é um indicador da nebulosidade e deveria
ser também uma indicação da quantidade de radiação difusa. Em um local, o parâmetro Kt é um
indicador da claridade diária. Da mesma forma, se pode definir um novo parâmetro, Kd, definido
como:
Kd =
Hd
(85)
H
e que fornece uma indicação da quantidade de radiação difusa. Desta forma, conhecido o valor de
Kd, seria possível estimar o valor de Hd, a irradiação difusa diaria. Esta estimativa pode ser
facilmente realizada através de correlações existentes entre Kt e Kd. Deve-se tomar cuidado, no
entanto, que os valores estimados não são para dias individuais mas sim para valores medios de
dias aleatoriamente escolhidos.
A seguir, e nas próximas seções, se mostrarão algumas correlações mais utilizadas. Para
valores diários de radiação, uma das correlações mais empregadas é a de Collares-Pereira e
Rabl14, que pode ser escrita como:
H d  0,99, para K t ≤ 0,17
=
(86)
H 1,188 − 2,272K t + 9,473K t2 − 21,856K t3 + 14,648K t4 , para 0,17 < K t ≤ 0,8
Outra correlação, que também apresenta bons resultados, é aquela proposta por Erbs e
outros17, que introduziram um efeito sazonal, com equações diferentes para o inverno e para o
resto do ano. As equações propostas são:
 para ω s < 1,4208

2
3
4
 = 1,0 − 0,2727K t + 2,4495K t − 11,9514K t + 9,3879K t ; para K t < 0,715
H d  = 0,143; para K t ≥ 0,715
=
(87)
H  para ω s ≥ 1,4208
 = 1,0 − 0,2832K t − 2,5557K t2 + 0,8448K t3 ; para K t < 0,722

 = 0,175; para K t ≥ 0,722
55
onde ωs é o ângulo de nascimento do sol, em radianos. Uma representação gráfica destas duas
equações pode ser vista na Figura 40.
Figura 40. Variação da fração difusa diária, Kd , em função do índice de claridade.
Pode-se notar desta figura que, sob condições muito nubladas (Kt →0), a radiação global
é composta principalmente de radiação difusa. Já para dias muito claros (Kt >0,7),
aproximadamente 20% da radiação diária é difusa.
Figura 41. Variação da fração difusa diária H d / H o , em função do índice de claridade.
Outra maneira mais instrutiva de estudar esta situação é através da correlação de H / H o
com H d / H o . Esta correlação é mostrada na Figura 41. Fica evidente desta figura a existência de
três situações: céu muito nublado, parcialmente nublado e céu claro. Durante dias muito
nublados, a radiação difusa é igual à radiação global. Em dias parcialmente nublados, a radiação
difusa corresponde de 20 a 35% do valor da radiação extraterrestre. E em dias muito claros, a
radiação difusa é aproximadamente metade daquela para dias parcialmente nublados.
56
5.6. Estimativa da irradiação difusa diária média mensal em uma superfície horizontal
A estimativa da irradiação difusa diária média mensal permite, através da utilização do
método de Collares-Pereira e Rabl, a determinação de valores horários, tanto da radiação global
como da difusa. Existem muitas equações de correlação que permitem determinar este valor.
Entre estas, podemos destacar a equação de Liu e Jordan15, cuja forma final é:
Hd
= 1,39 − 4 ,027 K t + 5,531K t2 − 3,108K t3 , para 0,3 < K t < 0,7 (88)
H
Outra equação, desenvolvida por Page18, foi baseada em uma análise de regressão de
dados de 10 estações, localizadas entre latitudes de 40°N e 40°S, resultando a seguinte equação
linear:
Hd
= 1,00 − 1,13K t (89)
H
Uma outra equação, também desenvolvida por Collares-Pereira e Rabl14, com a
diferença de que os coeficientes variam com a estação do ano. A equação é:
Hd
= 0,775 + 0,347( π / 180) ( ω s − 90) − 0,505 + 0,261( π / 180) ( ω s − 90) cos 2( K t − 0,9) (90)
H
[
] [
]
onde ωs é o ângulo de nascimento do sol, em graus, valendo 90° de fevereiro a abril e de agosto a
outubro, 80° de maio a julho e 100° de novembro a janeiro.
Estas equações estão representadas na Figura 42.
Figura 42. Relação entre a radiação difusa diária e a radiação global diária media mensal.
Além destas, se encontra na literatura outras equações de regressão para estimar a
componente difusa utilizando principalmente como parâmetros a relação, já vista antes, entre o
número de horas de sol medido e o número máximo de horas de sol, n / N d . Entre estas, a
equação linear proposta por Iqbal19:
57
 n 
Hd
= C − D
 (91)
H
 Nd 
onde C e D são constantes, obtidas por análise de regressão com dados medidos. Como valores
aproximados, pode-se utilizar, para C e D, 0,791 e 0,635, respectivamente.
Todos os métodos anteriores necessitam para estimar o valor da componente difusa o
valor da radiação global, H . Se multiplicarmos a Equação 62 pela Equação 91 acima, poderemos
remover esta restrição. Assim:
2
 n 
Hd
n
= C1 + C 2
+ C3
 (92)
Ho
Nd
 Nd 
e de acordo com Iqbal19 , os coeficientes podem ser obtidos por análise de regressão, indicando
os valores de:
2
 n 
Hd
n
= 0,163 + 0,478
− 0,655
 (93)
Ho
Nd
 Nd 
Todas as equações vistas até agora são dependentes do local, ou seja, elas são válidas
somente para o local ou região onde os parâmetros índice de claridade e número de horas de sol
foram medidos. Estes parâmetros não representam adequadamente todos os fatores
climatológicos envolvidos, necessitando-se também variáveis como propriedades óticas do céu e
da cobertura do terreno. Locais de maiores latitudes são geralmente caracterizados por maiores
massas de ar e albedo (ambos aumentam a fração da radiação difusa). Contudo é muito difícil
separar o efeito da latitude dos outros parâmetros. De qualquer forma, o clima local possui um
efeito dominante diante da latitude e que deve ser apropriadamente considerado.
5.7. Estimativa da irradiação difusa horária em superfícies horizontais
Quando se trata de simulações matemáticas de processos de energia solar, valores de
radiação global e difusa para horas individuais são necessárias. Até agora estudamos os casos de
valores médios, tanto de estimativas diárias como horárias. Naturalmente, para estimarem-se
valores individuais de radiação difusa, obrigatoriamente deveremos possuir valores individuais
de radiação global.
A quantidade de radiação difusa depende tanto da altitude solar como da cobertura de
nuvens. Sob condições de céu muito claro e para uma dada atmosfera, a altitude solar é o
parâmetro governante. O efeito das nuvens aumenta à medida que aumenta a parcela do céu
coberta por elas e da distribuição geométrica das mesmas em relação aos raios solares.
Para calcular a fração difusa foram desenvolvidas correlações estatísticas relacionando kd,
definido como Id/I, ou seja a relação entre a irradiação difusa horária e a irradiação global
horária, e o índice de claridade horário kt, definido como a relação I/Io , isto é, a relação entre a
irradiação global horária e a irradiação extraterrestre, também horária e em superfície horizontal.
A correlação entre estas duas variáveis é bastante evidente, tal como se pode comprovar
analisando-se a Figura 43.
58
Figura 43. Relação entre kd, e kt,.
Entretanto, pode-se notar a existência de uma grande dispersão dos valores de kd, em
torno de um mesmo valor de kt,. Por exemplo, para valores intermediários de kt,=0,5, os valores
da fração difusa variam desde 0,26 até 0,84. Isto, na verdade, leva a pensar-se na existência de
outras variáveis climáticas que afetam esta correlação. Entre as possíveis variáveis, a massa de ar
ou o ângulo de elevação solar parecem os mais evidentes.
A seguir, segue uma série de equações de correlação que visam determinar o valor da
fração difusa a partir, principalmente, do índice de claridade e da elevação solar.
A correlação de Orgill e Hollands20 é dada da seguinte forma:
1,0 − 0,249 k t ; para 0 ≤ k t < 0,35
Id 
= 1,577 − 1,84 k t ; para 0,35 ≤ k t ≤ 0,75 (94)
I 
 0,177 ; para k t > 0,75
A correlação de Erbs e outros17 é dada da seguinte forma:
1,0 − 0,09 k t ; para k t ≤ 0,22
Id 
=  0,9511 − 0,1604 k t + 4 ,388k t2 − 16,638k t3 + 12 ,336k t4 ; para 0,22 < k t ≤ 0,80 (95)
I 
 0,165 ; para k t > 0,80
A correlação de Reindl e outros21 consiste de um trabalho muito mais elaborado uma vez
que fizeram exaustivas comparações buscando encontrar as variáveis climatológicas que mais
influenciam a determinação da fração difusa e que diminuam o erro associado aos modelos do
tipo Liu e Jordan. Entre as muitas variáveis pesquisadas podemos citar: temperatura ambiente,
temperatura de bulbo úmido, umidade relativa, altitude solar, massa de ar, índice de claridade,
etc. As quatro variáveis climatológicas que resultaram mais interessantes foram, por ordem de
importância: o índice de claridade kt , o seno da altitude solar sen α, a temperatura ambiente Ta , e
59
a umidade relativa φr . Como nem a temperatura ambiente e nem a umidade relativa são dados
facilmente obtidos por nós, nos limitaremos a apenas duas correlações:
1,020 − 0,254 k t + 0,0123 sen α ; para k t ≤ 0,30 (I)
Id 
= 1,4 − 1,749 k t + 0,177 sen α ; para 0,3 < k t < 0,78 (II)
I 
0,486k t − 0,182 sen α ; para k t ≥ 0,78 (III)
Para a equação (I) existe a restrição kd ≤ 1,0; para a equação (II) kd ≤ 0,97 e kd ≥ 0,1 e para
a equação (III) kd ≥ 0,1. As restrições impostas eliminam a possibilidade de resultados incorretos
que, de outra forma, podem aparecer através das diversas combinações das variáveis envolvidas.
Estes mesmos autores também propuseram um modelo mais simples, do tipo Liu e Jordan, dado
da seguinte forma:
1,020 − 0,248k t ; para k t ≤ 0,30
Id 
= 1,45 − 1,67 k t ; para 0,3 < k t < 0,78 (96)
I 
0,147 ; para k t ≥ 0,78
e a única restrição imposta é na primeira equação, que deve obrigatoriamente ser < 1,0.
Por último, o modelo proposto por Maxwell22 que calcula na realidade a fração direta, kb ,
definida como a relação entre a irradiação direta normal e a irradiação extraterrestre, também
normal. Este modelo necessita como dados de entrada somente kt e m. É chamado “quase-físico”
porque considera o parâmetro físico kbc , isto é, valor máximo de kb , definido como o valor
máximo de kb para uma dada massa de ar. O modelo é dado da seguinte maneira:
Se kt ≤ 0,60
a = 0,512 − 1,56k t + 2,286k t2 − 2,222k t3
b = 0,370 + 0,962k t
(97)
c = −0,280 + 0,932k t − 2,048k t2
Se kt > 0,60
a = −5,743 + 21,77k t − 27,49k t2 + 11,56k t3
b = 41,40 − 118,5k t + 66,05k t2 + 31,90k t3
(98)
c = −47,01 + 184,2k t − 222,0k t2 + 73,81k t3
A variação de kb está dada por:
∆k b = a + b exp(cm) (99)
e a fração direta se determina mediante:
k b = k bc − ∆k b (100)
onde
k bc = 0,886 − 0,122 m + 0,0121m2 − 0,000653m3 + 0,000014 m4 (101)
60
e desta maneira, a irradiação direta (normal) pode ser calculada como:
I b = I o k b (102)
Como a irradiância difusa é a diferença entre a global e a direta:
I d = I − I b cosθ z (103)
e dividindo-se os dois lados da equação por I, resulta:
Id
I cosθ z
= kd = 1 − b
(104)
I
I
61
-6Albedo
6.1. Introdução
Quando energia radiante incide em uma superfície, ela pode ser parcialmente absorvida,
refletida ou transmitida. As propriedades de uma superfície ou material associadas com estas três
funções são chamadas de absortividade, refletividade e transmissividade. As frações da energia
incidente total associada com estas propriedades são chamadas absortância, refletância e
transmitância. Quando a fonte de radiação incidente é o sol, o termo albedo é costumeiramente
usado em lugar de refletância.
A determinação do valor exato do albedo é muito importante para a determinação da
radiação total em uma edificação ou em um dispositivo de coleta de radiação solar e,
principalmente, em estudos que tratam do balanço térmico na atmosfera. Mas, apesar disto, sua
exata determinação ainda é matéria de estudo principalmente pela dificuldade em definir as
características de uma superfície que cobre uma grande área, possivelmente excetuando-se uma
área de água.
De uma maneira muito simples, o albedo ρ pode ser definido como:
ρ=
radiação refletida por uma superfície
(105)
radiação incidente em uma superfície
Com respeito às propriedades reflexivas da superfície, duas características limites podem
ser encontradas e que são chamadas: difusa e especular. Uma superfície perfeitamente difusa
(também chamada Lambertiana) é aquela na qual a intensidade da radiação que deixa a superfície
é distribuída uniformemente em todas as direções. Assim, considerando a Figura 44(a), a
radiação refletida hemisfericamente e a intensidade difusa correspondente estão relacionadas pela
igualdade:
I&ρ = πi (106)
onde I& é a irradiância (global, difusa ou direta), ρ é o albedo e i é a intensidade uniforme de
radiação refletida. Tal superfície também pode ser chamada de refletora difusa.
Figura 44. Reflexão pelo solo: (a) reflexão difusa isotrópica e (b) reflexão difusa anisotrópica.
62
Quando a reflexão não é perfeitamente difusa, como é mostrado na Figura 44(b), id , a
intensidade anisotrópica refletida está relacionada com a radiação total refletida da seguinte
maneira:
I&ρ = ∫0 i d dω cos Φ (107)
⊗
onde dω é o ângulo sólido relacionado com a intensidade da radiação refletida e ⊗ indica que a
integração deve ser realizada em todo hemisfério.
Superfícies que são uniformes com respeito ao comprimento de onda da radiação
incidente são chamadas superfícies especulares e estão representadas na Figura 45.
Figura 45. Reflexão especular: (a) perfeitamente especular e (b) bi direcionalmente especular.
A radiação que chega está contida dentro de um ângulo sólido dωi e incide em um ângulo
Φi em relação a normal da superfície. Toda intensidade refletida está contida dentro de um
ângulo sólido dωr tal que:
dω i = dω r e Φi = Φr (108)
Além disso, as intensidades incidentes e refletidas estão no mesmo plano que contém a
normal à superfície.
Uma superfície que não é perfeitamente especular é ilustrada na Figura 45(b), onde
qualquer uma das seguintes condições pode acontecer:
dω i ≠ dω r , Φi ≠ Φr , ψ ≠ 0 (109)
onde ψ é o azimute da radiação refletida.
Esta superfície é muito importante nas aplicações de energia solar e o albedo associado é
chamado refletância bidirecional. Por exemplo, em dias de céu claro, o albedo do mar, lagos,
gelo ou campos com folhas brilhantes, geralmente se comporta com natureza bidimensional.
Além do aspecto direcional, o albedo é também fortemente dependente da distribuição
espectral da radiação incidente. Por exemplo, o papel branco desta página possui um albedo
muito grande para a região do visível do espectro solar embora ela absorva quase toda a radiação
em comprimentos de ondas maiores, tais como as que emanam do corpo do leitor. Portanto, ela
possui uma baixa refletância para a radiação de ondas largas.
63
Quanto à relação entre albedo espectral e altitude solar podemos ainda fazer algumas
considerações: para um solo descoberto (de vegetação), o albedo espectral aumenta com o
comprimento de onda e com o decréscimo da altitude solar até um valor de 10° e a partir daí, o
valor diminui. Para o caso de coberturas vegetais, especialmente para folhas muito verdes, o
albedo espectral exibe algumas características seletivas peculiares. O albedo é geralmente baixo
na região do visível e alta na região do infra-vermelho. A característica seletiva se deve à
presença da banda de absorção da clorofila, perto de λ=0,65µm, onde o albedo é mínimo.
Também, o albedo aumenta com o decréscimo da altitude solar e é mínimo no meio-dia.
Para o caso de superfícies aquáticas, o albedo é dependente do ângulo de incidência e do
índice de refração da água. Quando a altitude solar diminui, o albedo aumenta. Na Figura 46 se
apresenta alguns valores de albedo em função da altitude solar, de acordo com Paltridge e
Platt22.
Figura 46. Variação angular do albedo para várias coberturas de solo.
O albedo global geralmente é medido utilizando-se dois piranômetros, um colocado atrás
do outro, e ambos montados em uma posição horizontal, a poucos metros acima da superfície
que se quer medir. O piranômetro apontado para o céu mede a radiação global incidente e o
outro, apontado para a superfície, mede a energia refletida.
Na Tabela 11, se apresenta alguns valores de albedo global para diversas superfícies.
Tabela 11. Albedo de coberturas naturais.
Coberturas
Grama verde
Areia fina e clara
Floresta verde
Neve fresca
Asfalto
Cimento
Água
64
Albedo, ρ
0,26
0,37
0,03-0,10
0,82-0,98
0,15
0,25
x
- 7Fator de forma
Para o cálculo da irradiação refletida pelo solo (ou albedo) se utiliza a aproximação de
que a reflexão seja isotrópica. Na realidade, esta aproximação acontece ou quando a radiação
global é composta principalmente de radiação difusa ou quando o solo seja um refletor difuso
perfeito, tal como um piso de concreto. Além disso, também se considera que as refletâncias,
tanto da radiação difusa como da radiação direta, sejam iguais.
Para encontrar esta fração, utilizaremos o fator de forma entre um coletor plano inclinado
e o solo e entre um coletor plano inclinado e o céu, que nos será útil posteriormente, quando se
calculará a irradiação difusa recebida por uma superfície inclinada. Considere-se a Figura 47 que
mostra um coletor plano inclinado um ângulo β em relação à horizontal. O coletor se encontra no
centro de um hemisfério de raio unitário. A superfície deste hemisfério acima do solo é a porção
do domo do céu visto pelo coletor. A área sombreada na parte inferior desta figura é a projeção
do domo do céu vista pelo coletor na base deste hemisfério de raio unitário.
Figura 47. Projeção de uma superfície inclinada em um hemisfério unitário.
Seja Fc→s o fator de forma entre o coletor e o céu. Assim:
Fc → s =
Área sombr eada da figura
(110)
Área do cí rculo de raio unitá io
r
1
1
1
(
πr 2 ) + ( π cos β )
π (1 + cos β ) 1
2
2
2
=
=
= (1 + cos β ) (111)
π
2
πr 2
65
O fator de forma entre a superfície do coletor e o solo, Fc→g , pode ser obtido ou pelo
método do hemisfério unitário ou através da seguinte relação:
Fc → s + Fc → g = 1 (112)
E, portanto:
Fc → g =
1
(1 − cos β ) (113)
2
Desta forma, a irradiação refletida pelo solo é dada, utilizando-se a Equação 113, da
seguinte maneira:
Ir =
1
Iρ (1 − cos β ) (114)
2
A Equação 111 é utilizada quando se calcula a irradiação difusa recebida por uma
superfície inclinada, considerando esta mesma radiação distribuída uniformemente no hemisfério
celeste, ou seja, a suposição de isotropia. Desta forma, a equação resultante é dada por:
I dβ =
1
I ( 1 + cos β ) (115)
2 d
66
-8A natureza da radiação solar
Antes de entrarmos no cálculo da radiação solar em superfícies inclinadas, que será o
assunto tratado no próximo capítulo, é conveniente estudar, ainda que brevemente, a interação
entre a radiação solar e a atmosfera terrestre que originará a radiação solar recebida na superfície
da terra.
8.1. A componente direta
A distribuição espectral da radiação solar incidente na camada superior da atmosfera é
comparável àquela emitida por um corpo negro a aproximadamente 6000 K, como é mostrado na
Figura 48.
Figura 48. Distribuição espectral da radiação solar na camada superior da atmosfera e
distribuições típicas na superfície da Terra.
A principal diferença entre estas curvas ocorre na região do ultravioleta, causada
principalmente pelas transições eletrônicas que ocorrem na camada de gases do Sol. Quando a
radiação atravessa a atmosfera, ocorrem vários processos que mudam sua distribuição espectral.
As principais bandas de absorção se devem ao vapor d’água, na região do infra-vermelho e ao
ozônio, no ultra-violeta. Menores absorções se devem ao oxigênio, na região 0,6-0,7µm além de
pequenas bandas de absorção perto do infra-vermelho, devido ao dióxido de carbono.
A dispersão (ou espalhamento) da radiação, principalmente em comprimentos de ondas
curtas, é responsável pelo decréscimo nas regiões do visível e o UV próximo.
Entretanto, grande parte da radiação solar é transmitida diretamente e alcança a superfície
terrestre em feixes aproximadamente paralelos, como se comprova olhando diretamente para o
Sol. Este processo é regido pela lei de Bouguer-Lambert que, para uma atmosfera homogênea e
plano-paralela, pode ser escrita como:
67
E λ = E oλ exp( −τ λ m) (116)
onde Eoλ e Eλ são as intensidades monocromáticas incidente e transmitida, respectivamente, m é
a massa de ar, λ é o comprimento de onda e τλ é a espessura ótica da atmosfera, medida na
direção do zênite local e que, para uma altitude arbitrária z, está dada por:
τ z ,λ = ∫z B( λ, z )dz (117)
∞
onde B( λ, z ) é o coeficiente de atenuação. Como a atenuação se deve ao espalhamento e a
absorção, temos:
B = Be + Ba (118)
e
τ = τ e + τ a (119)
sendo que os sub índices e e a indicam espalhamento e absorção, respectivamente.
8.1.1. Caso de uma atmosfera clara
Para simplificar a discussão, é conveniente considerar a dispersão e a absorção em
separado, ainda que na atmosfera real estes dois efeitos aconteçam simultaneamente.
Para estudar o espalhamento, o modelo atmosférico mais simples é aquele composto de
um meio absorvedor no qual as partículas possuem um tamanho menor que o comprimento de
onda. Este critério se aplica principalmente às moléculas dos gases atmosféricos. Este tipo de
atmosfera é denominado de atmosfera de Rayleigh sendo que o coeficiente volumétrico de
espalhamento é dado por:
2
32π 3 ( n − 1)
Bλ =
(120)
N
3λ4
R
onde n é o índice de refração do meio e N é a densidade de partículas.
É importante destacar da equação anterior que em uma atmosfera clara, o rendimento de
espalhamento é dependente do comprimento de onda (λ-4 ), no sentido de que os comprimentos
de ondas curtas se espalham mais fortemente do que os comprimentos de ondas mais largas, isto
é, a quantidade de luz espalhada é proporcional à quarta potência de sua freqüência (ν4 ), de
modo que o azul (νa =7,5×1014 Hz) é dez vezes mais espalhado que o vermelho (νa =4,2×1014
Hz). Este fato, combinado com a sensibilidade espectral do olho humano e a distribuição
espectral da luz solar é o que dá lugar a cor azul do céu em um dia claro. Ainda como
curiosidade, se sabe que o vermelho e o verde são menos espalhados e se olharmos diretamente
para o Sol o veremos amarelado, que nada mais é que uma combinação das radiações verde e
vermelha, que foram pouco desviadas pelo espalhamento. Já ao amanhecer e ao entardecer, os
raios solares percorrem uma maior distância (massa de ar), fazendo com que o azul e o verde
sejam tão espalhados que não alcançam a superfície da Terra, sendo absorvidos antes. Esta é a
explicação da cor avermelhada do céu nestes instantes.
68
8.1.2. Caso de uma atmosfera túrbida
Existe na atmosfera (inclusive no caso de uma atmosfera natural clara) um número
suficiente de partículas de tamanho maior que as moléculas de ar (pó, aerossóis e partículas do
tipo não-Rayleigh) que produzem efeitos importantes na radiação.
O tamanho destas partículas, caracterizado por 2πr/λ (sendo r o raio da partícula), está
compreendido na faixa de 0,1λ<r<25λ, pelo que não se pode aplicar a elas a teoria do
espalhamento de Rayleigh. Em seu lugar, convém recorrer-se à teoria desenvolvida por Mie.
8.1.3. Caso de uma atmosfera nublada
As nuvens são fortes atenuadores da radiação direta, como é obvio, com exceção dos
cirros (nuvens altas) e os alto-estratos (nuvens medias) pouco espessos. Ainda que uma fração
significativa da luz solar incidente seja transmitida pelos cúmulos densos ou pelos estratos
nebulosos, a transmissão se realiza principalmente pela dispersão múltipla nas gotas de água, e
não por transmissão direta do raio original.
Com boa aproximação, as gotas d’água que constituem uma nuvem podem ser
consideradas como esferas transparentes e, neste caso, toda radiação do feixe original reaparece
como energia espalhada. Se for conhecida a distribuição de frequência do tamanho destas gotas e
o conteúdo de água líquida da nuvem, o coeficiente de atenuação da nuvem pode ser calculado
utilizando-se a teoria do espalhamento de Mie. Assim, para uma gota de raio r e de concentração
N, o coeficiente de atenuação Bc da nuvem é calculado como:
B c = Nr 2 f (λ / r ) (121)
onde f(λ/r) possui um valor aproximadamente constante e igual a 2 para a luz visível e raios
típicos de nuvens. Como exemplo, a Figura 49 mostra a transmissão da radiação solar direta em
função da espessura de diferentes tipos de nuvens.
Figura 49. Fração transmitida da radiação solar direta em função da espessura das nuvens.
69
8.2. A componente difusa
A energia que constitui a radiação difusa do céu é o resultado do espalhamento dos raios
solares incidentes em algum tipo de partícula, suspensa na atmosfera. Os tipos mais gerais de
espalhamento são aqueles produzidos por partículas de tamanho muito pequeno, comparado ao
comprimento de onda (Rayleigh) e os produzidos por partículas de tamanho comparável ou
maior que o comprimento de onda (Mie), tal como é representado na Figura 50. As moléculas
gasosas do ar, principalmente oxigênio e nitrogênio, são os maiores espalhadores de Rayleigh e
dominam a forma de espalhamento nos casos de atmosferas claras e livres de turbidância. Para
atmosferas túrbidas, as partículas de aerossóis espalham fortemente e o espalhamento de Mie
chega ser tão importante quanto o de Rayleigh em comprimentos de ondas no azul e no UV. No
visível longínquo e infra-vermeho, o processo de espalhamento em atmosferas turbidas está
dominado pelo espalhamento de Mie e para atmosferas fortemente contaminadas ou nubladas, o
espalhamento de Mie é o dominante em todos os comprimentos de onda.
Figura 50. Espalhamento da radiação eletromagnética; (a) espalhamento de Rayleigh e (b)
espalhamento de Mie.
8.2.1. Caso de uma atmosfera clara
As três linhas representadas na Figura 51 descrevem a intensidade da luz do céu em uma
atmosfera clara, de acordo com cálculos realizados por Coulson23, para três comprimentos de
onda, no caso de um local ao nível do mar e sem reflexão da superfície.
O forte brilho do horizonte é uma característica da luz do céu em comprimentos de onda
larga, enquanto que a atenuação da radiação espalhada, através do maior caminho ótico perto do
horizonte, produz um escurecimento no caso de comprimentos de ondas mais curtos.
8.2.2. Caso de uma atmosfera túrbida
O espalhamento pela neblina e outras partículas de aerossol tem um efeito importante na
intensidade da luz do céu, sendo mais pronunciado na região da auréola solar (área brilhante em
torno ao Sol). Isto pode ser observado na Figura 52, onde se vê o efeito do espalhamento frontal
muito forte na vizinhança do Sol devido as partículas de aerossol. A intensidade nesta zona é
quase o dobro para uma atmosfera túrbida que para uma atmosfera molecular (Rayleigh). Uma
turbidância em níveis mais baixos da atmosfera causa um pronunciado escurecimento do
horizonte.
70
Figura 51. Intensidade relativa da luz do céu, ao nível do mar, em uma atmosfera do tipo
Rayleigh para três comprimentos de ondas. O Sol está situado em um ângulo de zênite de 53,1°.
Figura 52. Intensidade relativa da luz do céu para uma atmosfera molecular (Rayleigh).
71
- 9Radiação solar incidente em superfícies inclinadas
9.1 Introdução
A determinação da radiação incidente em superfícies inclinadas é muito importante não
só para aqueles que projetam dispositivos para coletar a radiação solar (estimativa do potencial
solar, dimensionamento, etc.) como para os arquitetos (determinação da carga térmica e cálculo
de sombras em edificações, etc.) e para os agrônomos (estudo da vegetação em montanhas,
cálculo da evapo transpiração, etc.). Como a grande maioria das fontes de dados de radiação
solar dispõe somente de valores medidos em posição horizontal, tornam-se necessários métodos
adequados para a transposição destes valores para superfície inclinada. O procedimento consiste,
basicamente, na divisão da radiação global horizontal em três componentes e que são mostrados
na Figura 53:
a componente direta (proveniente do disco solar)
a componente difusa (proveniente do hemisfério celeste)
a componente de albedo (refletida pelo solo)
Desta forma, então, a radiação global em uma superfície inclinada será dada como:
I β = I bβ + I dβ + I rβ (121)
Figura 53. Radiação direta, difusa e de albedo incidentes em uma superfície inclinada.
72
Para um tratamento mais compreensível do problema, se utilizará primeiramente uma
escala de tempo horária. No final deste capítulo se inclui alguns comentários e formulações de
como abordar este problema em escalas de tempo diferentes da horária, tal como valores médios
mensais da radiação diária.
Para estes cálculos, é útil considerar que a irradiação ao longo de uma hora, dada em
kWhm-2 , coincide numericamente com a irradiância media durante esta hora, em kWm-2 e além
disso, supor que coincide com a irradiância no instante central desta hora.
Nas seguintes seções se desenvolve os procedimentos de cálculo de cada componente em
separado.
9.2. Radiação direta incidente em uma superfície inclinada
Supondo conhecido o valor da irradiação direta horizontal, o cálculo da irradiação direta
em uma superfície inclinada é obtido através de relações trigonométricas bastante simples. Seja
Ibh a irradiação direta horária horizontal, a irradiação direta em uma superfície inclinada β graus é
dada por:
 cos θ s 
I bβ = I bh 
 = I bh rb (122)
 cos θ z 
9.3. Radiação refletida pelo solo incidente em um plano inclinado - albedo
Como resultado da simplicidade e da falta de dados observados que sirvam como base
para aprimorar o algoritmo, a aproximação utilizada para calcular a radiação refletida por
superfícies dentro do campo de visão da superfície inclinada consiste na suposição de reflexão
isotrópica por uma superfície horizontal infinita em frente da superfície receptora inclinada.
Conforme foi visto nos capítulos 6 e 7, a reflexão pelo solo ou albedo, pode então ser
calculada pela seguinte relação:
Ir =
1
Iρ (1 − cos β ) (123)
2
sendo I a irradiação global horária em superfície horizontal, ρ o albedo e β a inclinação da
superfície.
Se a superfície adjacente não é horizontal, mas também inclinada um ângulo β+ , o último
termo na Equação 123 deve ser escrito como cos(β+β+).
Na realidade, reflexão isotrópica ocorre usualmente quando a radiação global é composta
principalmente de radiação difusa e/ou quando a cobertura do solo for um refletor perfeitamente
difuso, tal como um piso de concreto. Para a maioria das situações, a superfície exibe uma
refletância fortemente direcional e necessita-se modificar o algoritmo anterior. Uma destas
modificações foi àquela proposta por Temps e Coulson24, descrita pela seguinte equação:
Ir =

 θ z 
1
Iρ ( 1 − cos β ) 1 + sen 2  ( cos ∆ ) (124)
 2 
2

onde ∆=γ-γs . Contudo, os resultados apresentados por este algoritmo não foram muito
animadores. Para alguns tipos de superfícies refletoras, os erros produzidos são muito maiores
73
que aqueles produzidos pela simples suposição de isotropia, pelo que se desaconselha sua
utilização.
9.4. Distribuição angular da radiação difusa
A radiação difusa representa uma fração apreciável da radiação total, variando desde 1015% em climas com céus predominantemente claros até 60% em climas com céus cobertos,
freqüentes em países com latitudes superiores a 40° ou em regiões muito úmidas, como nos
países equatoriais.
A irradiância difusa do céu recebida por uma superfície qualquer está fisicamente
relacionada com a distribuição da irradiância no céu. Considere, por exemplo, uma superfície
horizontal elementar dA, na base de um hemisfério imaginário representando a abóboda do céu,
tal como se representa na Figura 54.
Figura 54. Coordenadas de uma pequena área na superfície de um hemisfério.
Assumindo-se que o céu está composto de superfícies elementares, de tal forma que uma
superfície dS propague energia radiante (solar) difusa em direção à superfície horizontal. Seja id a
intensidade (radiância) da radiação difusa associada com esta superfície dS. A taxa de energia
radiante alcançando a superfície dA, a partir de dS é dada por:
dI&d = i d dω cos φ (124)
onde id é a intensidade de radiação (Wm-2sr-1), dω é o ângulo sólido representado pela área dS
(sr) e φ é o ângulo de zênite da superfície dS (graus). Devido à que a intensidade é sempre
expressada em termos da uma área normal ao eixo do ângulo sólido, utiliza-se na equação
anterior cosφ.
Quando o Sol se encontra ocultado, a integração da Equação 124 nos dá a taxa total da
radiação difusa do céu recebida na superfície dA. Esta relação pode ser escrita como:
⊗
I&d = ∫ i d dω cos φ (125)
Se a intensidade for isotrópica, isto é, independente de sua posição no céu, a equação
anterior se reduz à:
I&d = πi d (126)
74
e devido a que I&d é disponível à partir de medidas ou estimado, id pode ser facilmente derivado e
o problema de calcular a radiação difusa do céu incidente em uma superfície inclinada pode ser
facilmente resolvido.
Sob condições de céus reais, a intensidade difusa não se distribui uniformemente e varia
com as condições do céu. Para uma determinação exata da radiação difusa do céu incidente em
um plano inclinado, é necessário que a distribuição de id no hemisfério do céu seja medida.
As primeiras publicações sobre medidas da distribuição espacial da radiação difusa e da
radiância no hemisfério celeste datam de 1922 e se devem a Kimball e Hand25 e posteriormente a
trabalhos de Moon e Spencer26, em 1942 e de Hopkinson27, em 1954.
A maioria destes estudos foi realizada utilizando-se medidas obtidas por radiômetros (ou
telescópios de varredura). Devido à constante de tempo destes radiômetros e o número de
medidas realizadas, uma varredura completa do hemisfério celeste pode durar muitos minutos,
durante os quais as condições do céu podem mudar rapidamente.
McArthur e Hay28 empregaram uma técnica fotográfica, utilizando lentes “olho-depeixe”. Em cima das fotos, realizaram avaliações densitométricas e construíram mapas de isoradiância, tal como se vê nas Figuras 55 e 56.
As figuras mostram que, para condições de céu claro, a intensidade de um elemento no
hemisfério do céu depende da posição deste elemento com respeito ao Sol e com respeito ao
zênite. As intensidades máximas ocorrem perto do Sol e no horizonte e as intensidades mínimas
à 90º do zênite solar.
A radiação vinda da região em torno ao disco solar é chamada radiação circunsolar ou
auréola solar e é causada pelo forte espalhamento frontal das partículas de aerossol. A extensão
desta região depende da turbidância atmosférica e do ângulo de zênite do Sol. De outro lado, o
aumento de intensidade perto do horizonte, chamado brilho do horizonte, é o resultado do
espalhamento devido a elevada massa de ar. Outra característica apresentada é a simetria da
intensidade da radiação difusa em relação à um plano que contém o Sol e o zênite do observador.
Estas observações são bastante evidentes observando-se a Figura 55.
Para o caso de um céu nublado, tal como é mostrado na Figura 56(a), a intensidade não é
completamente isotrópica em todo o hemisfério celeste. Se pode notar a existência de um
máximo à aproximadamente 90º do zênite solar.
Para o caso de um céu parcialmente nublado, como é mostrado na Figura 56(b), a
distribuição da intensidade da radiância difusa é altamente complexa. Isto deve-se principalmente
às fortes reflexões nas bordas das nuvens e das proprias formações das nuvens. Também se pode
ver a existência de grandes variações da intensidade desde o zênite solar até o horizonte.
Destas observações fica claro que para uma determinação rigorosa da radiação incidente
em um plano inclinado necessita-se de informações detalhadas da distribuição da intensidade da
radiação difusa do céu. Entretanto, estas medidas são raras. Além disso, outros parâmetros que
influenciam esta distribuição, tais como características das nuvens, turbidância e albedo, não são
medidos simultaneamente, não permitindo desta forma a generalização e o desenvolvimento de
métodos para estimar a distribuição da intensidade da radiação difusa.
9.5. Radiação difusa horária incidente em uma superfície inclinada
Para contornar a dificuldade em modelar a distribuição da radiação difusa no hemisfério
celeste, foram desenvolvidas várias aproximações empíricas que serão discutidas a seguir.
Basicamente se pode dizer que existem dois tipos de modelos simplificados para a descrição da
radiação difusa: os modelos não-direcionais e os direcionais. Os modelos não-direcionais,
determinados empiricamente a partir de medidas obtidas com sensores planos, não fornecem
nenhuma informação de existência de gradientes da radiância difusa no hemisfério do céu. Com
75
exceção do modelo isotrópico, o que fazem é estabelecer incrementos da radiância de
determinadas zonas do céu (circunsolar e horizonte). Os modelos direcionais, por sua vez, são
determinados através de medidas realizadas com instrumentos com campo de visão reduzido.
Estas medidas permitem mapear o hemisfério celeste para diferentes condições do céu e
diferentes posições do Sol.
Figura 55. Distribuições da radiância difusa (normalizada) para céus claros, com ângulos de
zênite solar, θz , no intervalo de 61º até 67,6º. As unidades são sr-1.
76
Figura 56. Distribuições da radiância difusa para (a) céu nublado e (b) céu parcialmente nublado.
A posição do Sol está indicada pelo ponto negro. As unidades são Wm-2sr-1.
9.5.1. Modelo isotrópico (ou modelo de Liu e Jordan29)
Considera que a radiação difusa é uniformemente distribuída no hemisfério celeste
(suposição de isotropia), como se representa na Figura 57. Assim, a irradiação difusa Idβ,
incidente em uma superfície inclinada pode ser determinada em função do campo de visão desta
superfície em relação ao hemisfério celeste:
I dβ = 0,5I d ( 1 + cos β ) (126)
onde Id é a irradiação difusa horizontal e β é a inclinação da superfície em relação à horizontal.
Figura 57. Descrição esquemática do modelo isotrópico.
77
9.5.2. Modelo de Temps e Coulson24
A partir do modelo isotrópico, introduziram modificações para considerar a anisotropia
da radiação difusa que se manifesta, de forma geral, como um aumento da intensidade perto do
horizonte e na região circunsolar, de acordo com o esquema da Figura 58.
Figura 58. Descrição esquemática do modelo de Temps e Coulson.
Observando que a intensidade da luz do céu é aproximadamente 40% maior perto do
horizonte do que no zênite e que o gradiente é mais pronunciado para baixos ângulos de elevação
solar, introduziram o fator:
β 
1 + sen 3  
2
na equação base, para representar esta distribuição. O aumento do brilho do céu perto do Sol foi
aproximado pelo fator:
1 + cos 2 θ s sen 3 θ z
onde θs e θz são, respectivamente, os ângulos de incidência e de zênite.
A equação que descreve a irradiação difusa em uma superfície inclinada fica, então,
como:


 β 
I dβ = 0,5I d ( 1 + cos β ) 1 + sen 3  (1 + cos 2 θ s sen 3 θ z )  (127)
 2 


9.5.3. Modelo de Klucher30
Em vista da incapacidade do modelo de Temps e Coulson para descrever a radiação
difusa em céus nublados ou parcialmente nublados, Klucher propôs uma função de ajuste neste
modelo. Esta função serve de modulação quando o céu passa de claro a nublado, e é dada por:
2
Id 
F = 1 −   (128)
I 
78
onde Id é a irradiação difusa horizontal e I é a irradiação global, também horizontal. Desta forma,
a equação para a irradiação difusa incidente em uma superfície inclinada é dada por:


 β 
I dβ = 0,5I d ( 1 + cos β )1 + F sen 3  ( 1 + F cos 2 θ s sen 3 θ z )  (129)
 2 


Desta forma, busca um equilíbrio entre o modelo isotrópico que é válido para céu
nublado e o modelo de Temps e Coulson, que é válido para céu claro. A descrição esquemática
deste modelo é mostrada na Figura 59. Deve-se notar que para condições de céu nublado F=0 e a
equação se reduz ao modelo isotrópico enquanto que quando F→0, se reduz ao modelo de
Temps e Coulson.
Figura 59. Descrição esquemática do céu para o modelo de Klucher.
9.5.3. Modelo de Hay e McKay31
Este modelo considera duas zonas no céu como fontes de radiação difusa: uma emitindo
isotropicamente e a outra, a parte circunsolar, emitindo direcionalmente, de acordo com o
esquema da Figura 60.
Figura 60. Descrição esquemática do céu para o modelo de Hay e McKay.
Este modelo assume que as componentes isotrópica e circunsolar são uma combinação
linear baseada na transmitância da radiação direta. Para isto, definem um índice de anisotropia,
κ, que nada mais é que um índice de transmissão da radiação direta:
79
κ=
I bn
(130)
I on
onde Ibn é a irradiação direta normal e Ion é a irradiação extraterrestre, também normal.
Assim, a parte a ser tratada como isotrópica é dada por:
I d∗β = 0,5I d ( (1 + cos β ) (1 − κ ) (131)
e a parte circunsolar,
 cosθ s 
I d×β = I d  κ
 (132)
 cosθ z 
Desta maneira, a irradiação difusa incidente em uma superfície inclinada é dada por:
 cosθ s

I dβ = I d κ
+ 0,5(1 − κ )(1 + cos β ) (133)
 cosθ z

Na ausência da irradiação direta, κ=0, o céu está completamente nublado e a equação
resultante é igual ao modelo isotrópico. Na ausência de atmosfera, toda radiação é direta, κ=1, e
a radiação difusa é considerada como direta, isto é, vem diretamente da posição do Sol. Neste
modelo não se considera o horizonte como fonte de radiação difusa.
9.5.4. Modelo de Perez32
Este modelo utiliza uma descrição geométrica da distribuição da radiação difusa no céu
bastante simples, de acordo com a representação da Figura 61.
Figura 61. Descrição esquemática do céu para o modelo de Perez.
Assume uma radiância constante sobre todo o céu exceto em um disco em torno ao Sol e
uma banda no horizonte, onde os valores da radiância difusa são incrementados. A magnitude
deste incremento é considerada como uma função de três parâmetros que descrevem a condição
do céu em cada instante, que se relacionam com a radiação difusa, a relação entre a radiação
direta e a difusa e o ângulo de zênite solar. São assim definidos:
80
• ângulo de zênite solar, θz
• ∆=(Id m)/Ion
• ε=(Id+Ibn)/Id
onde Id é a irradiação difusa horizontal, m a massa de ar, Ibn a irradiação direta normal e Ion a
irradiação extraterrestre, também normal. A forma deste modelo é dada pela equação:


 cosθ s 
I dβ = I d  0,5(1 + cos β ) (1 − F1 ) + F1 
 + F2 sen β  (134)
 cosθ z 


Os coeficientes F1 e F2 são obtidos através das equações empíricas:
F1 = F11 ( ε ) + F12 ( ε ) ∆ + F13 ( ε )θ z (135a)
F2 = F21 ( ε ) + F22 ( ε ) ∆ + F23 ( ε )θ z (135b)
onde θz é em radianos. Os valores de Fij , i=1...3;j=1...3, podem ser encontrados na Tabela 12.
Tabela 12. Coeficientes para o modelo de Perez.
Intervalo
1
2
3
4
5
6
7
8
ε
1,000 a 1,056
1,056 a 1,253
1,253 a 1,586
1,586 a 2,134
2,134 a 3,230
3,230 a 5,980
5,980 a 10,080
10,080 a ∞-
F11
-0,042
0,261
0,481
0,825
1,102
1,226
1,367
0,978
F12
0,550
0,559
0,460
0,187
-0,299
-0,451
-0,838
-0,812
F13
-0,044
-0,243
-0,354
-0,532
-0,586
-0,617
-0,655
-0,393
F21
-0,120
-0,019
0,077
0,172
0,350
0,444
0,431
0,335
F22
0,138
0,083
0,006
-0,050
-0,398
-0,949
-1,750
-2,160
F23
-0,034
-0,081
-0,116
-0,151
-0,171
-0,073
0,094
0,186
9.6. Irradiação difusa diária incidente em superfícies inclinadas
A seguir se apresentam as expressões correspondentes para totais diários da radiação
difusa.
9.6.1. Modelo isotrópico
Similar à Equação 126, o total diário da irradiação difusa em um plano inclinado pode ser
escrita como:
H dβ = 0,5H d ( 1 + cos β ) (136)
9.6.2. Modelo de Klucher
A expressão diária deste modelo é muito difícil de formular, em função basicamente de
sua relação entre ângulo de incidência e ângulo de azimute solar. Desta forma se pode escrever:


β
H dβ = ∑  0,5I d ( 1 + cos β )1 + F sen 3 
2


dia
81


( 1 + F cos2 θ s sen 3 θ z )  (137)


9.6.3. Modelo de Hay e McKay
A expressão diária deste modelo pode ser desenvolvida à partir da Equação 133. Se pode
mostrar que:
H dβ = H d
{[ ( H − H ) / H ] R
d
o
b
[
+ 0,5( 1 + cos β ) 1 − ( H − H d ) / H o
] } (138)
9.6.4. Modelo de Perez
Para este modelo e da mesma forma que para o modelo de Klucher, não é possível
desenvolver uma expressão para o total diário. Desta maneira:
 
dia 

 cosθ s 
H dβ = ∑  I d  0,5( 1 + cos β ) ( 1 − F1 ) + F1
 + F2 sen β  (139)
 
 cosθ z 

82
- 10 Geração de dados de radiação solar
10.1. Introdução
Pelo que vimos até agora, os métodos para estimar a radiação solar global incidente em
uma superfície qualquer são trabalhosos mas, em geral, fáceis de utilizar e os resultados obtidos
estão dentro de uma incerteza na mesma ordem de grandeza das medidas de radiação solar. Isto é
verdadeiro, obviamente, desde que se disponham destes dados de radiação solar.
Seguindo este raciocínio, a situação mais crítica quando ao erro desta estimativa seria o
caso de se dispor de apenas 12 valores de radiação solar (diária media mensal), um para cada
mês, estimados por alguns dos métodos já vistos e a partir daí, calcular os valores horários
(também médios mensais). Os resultados destes cálculos seriam uma série de valores horários de
radiação global, idênticos nos 30/31 dias de cada mês e além disso, simétricos em torno ao meiodia.
Para o estudo de desempenho e de dimensionamento de sistemas solares à longo-prazo,
este procedimento poderia ser adequado unicamente se a fração de energia fornecida via energia
solar (ou seja, a relação entre a parte solar e a energia total requerida) fosse pequena. Caso
contrário, quando a fração solar aumenta (aproximando-se de 100%) e, principalmente, quando
os custos de armazenamento se tornam muito elevados, como acontece em instalações
fotovoltaicas, o projetista é obrigado a trabalhar em níveis críticos. Nestes casos, os efeitos da
distribuição da radiação solar e de sua persistência tornam-se extremamente importantes. Isto
acontece devido a que a unidade de armazenamento geralmente encontra-se completa ou quase
completa, diminuindo a capacidade de amortecer os efeitos das condições variáveis da relação
energia fornecida/consumo.
Neste caso, a solução seria trabalhar diretamente com as sequências de dados de radiação
solar, em base horária ou mesmo diária, disponíveis para o local de interesse e além disso,
contendo um número estatisticamente significativo de dados. Segundo Klein e Beckman33, o
desempenho médio de sistemas solares em períodos de 10 anos, tendo probabilidade de perda de
carga igual ou menor que 0,01 (≈ 3,6 falhas/ano) pode variar muito de um período a outro e,
portanto, os resultados de simulações realizadas com sequências com este período de tempo não
podem ser considerados como estimativas realistas de seus desempenhos, havendo necessidade
de trabalhar com sequências muito maiores.
Como também vimos anteriormente, a disponibilidade de tais sequências (20 anos ou
mais) está restrita à poucos lugares no mundo. Para contornar este problema, utilizam-se
sequências de dados de radiação solar geradas artificialmente, através de modelos estatísticos
adequados que visam conservar certas características apresentadas pelas séries verdadeiras, tais
como média, desvio padrão, função densidade de probabilidade, autocorrelação, etc.
Os algoritmos desenvolvidos são então introduzidos nos programas de simulação,
permitindo que se gere sinteticamente sequências de dados de radiação solar do tamanho
desejado, além de trazer outras facilidades, como por exemplo, eliminar a necessidade de grandes
arquivos de dados e poupar espaço de memória e principalmente, diminuir o tempo de execução
destes programas.
A seguir serão descritos alguns destes métodos e comparados os resultados para algumas
aplicações específicas.
83
10.2. Geração estocástica de valores diários de irradiação global - descrição do problema
Na Figura 62 se apresenta uma sequência de irradiação global horizontal, H, recebida em
Porto Alegre no ano de 1983. Nesta mesma figura também se representa a irradiação
extraterrestre horizontal, Ho, também para Porto Alegre. Pode-se notar que a distribuição da
irradiação ao longo do ano apresenta uma tendência sazonal com flutuações diária superpostas.
Figura 62. Irradiação global diária horizontal , H, e irradiação extraterrestre diária horizontal, Ho,
em Porto Alegre, durante o ano de 1983.
Os componentes de baixa frequência (tendência determinística) podem ser eliminados
destas sequências de irradiação a fim de tornar sua distribuição independente da época do ano e
da latitude. Entre as técnicas utilizadas, a mais simples é a divisão da irradiação global horizontal
pela extraterrestre horizontal, resultando no já conhecido índice de claridade, Kt. Desta forma, o
resultado para esta série de 1983 pode ser vista na Figura 63.
Figura 63. Série de valores de Kt obtida para Porto Alegre, em 1983.
84
Deve-se salientar, entretanto, como pode ser visto na Figura 63, que a utilização deste
método não permite que a tendência sazonal seja completamente removida (a média de Kt
evidentemente não é zero).
Uma vez eliminada a componente determinística, a componente aleatória, que representa
o comportamento irregular do fenômeno natural devido principalmente à presença das nuvens e a
variabilidades destas no tempo e no espaço, pode ser aproximada através de modelos
probabilísticos adequados.
Os dois modelos de geração de dados mais utilizados, tanto pela simplicidade como pelo
número de parâmetros necessários são: o modelo ARMA e as Matrizes de Transição de Markov.
10.2.1. O modelo ARMA
O modelo ARMA (Auto Regressive Moving Average) é uma classe de modelo estatístico
estável desenvolvido por Box e Jenkins34. Este modelo estocástico linear está baseado na idéia de
que uma série de tempo onde os valores sucessivos são altamente dependentes pode ser
considerada como se fosse gerada de uma série de “choques” independentes ωt . Estes “choques”
são números aleatórios retirados de uma distribuição fixa, geralmente normal e tendo média zero
e variância σ2ω. Uma tal sequência de variáveis aleatórias ωt, ωt-1 , ωt-2 , ..., é chamada de
processo de ruído branco. Sua função de autocorrelação ρk tem a particularidade que:
1, k = 0
 0, k ≠ 0
ρk = 
onde k é o intervalo (lag) de tempo entre duas variáveis consecutivas.
Este modelo misto é formado, na verdade, pela aglutinação de outros dois modelos: o
modelo auto-regressivo (AR) e o modelo de média móvel (MA).
No modelo auto-regressivo (AR), o valor corrente do processo é expresso como um
agregado linear finito dos valores prévios do processo e de um choque ωt . Nestes modelos,
chamaremos zt o valor da variável no tempo t e zt-1 o valor da variável no tempo t-1. Além disso,
define-se:
~
zt = z t − µ (140)
onde µ é a média da população. Desta forma, poderemos definir um processo auto-regressivo
(AR) como:
~
zt = φ 1 ~
zt −1 + φ 2 ~
zt − 2 +...+ φ p ~
zt − p + ω t (141)
onde utiliza-se os símbolos φ1, φ2 , ..., φp para o conjunto finito de parâmetros ponderados. Este
modelo contém p+2 parâmetros desconhecidos (µ,φ1, φ2 , ..., φp e σ2ω) que necessitam ser
estimados através dos dados conhecidos.
No modelo da média móvel (MA), ~
zt é linearmente dependente de um número finito q de
valores prévios de ω.
~
zt = ω t − θ 1ω t −1 − θ 2 ω t − 2 −...−θ q ω t − q (142)
Este modelo contém q+2 parâmetros desconhecidos (µ,θ1, θ2 , ..., θp e σ2ω) que também
necessitam ser estimados através dos dados conhecidos.
85
O modelos misto auto-regressivo de média móvel de ordem p,q ou ARMA(p,q) é a
aglutinação dos dois modelos anteriores e pode ser escrito da seguinte maneira:
~
zt = φ 1 ~
zt −1 + ...+φ p ~
zt − p + ω t − θ 1ω t −1 −...−θ q ω t − q (143)
Este modelo emprega p+q+2 parâmetros desconhecidos.
Na prática, é quase sempre verdade que se pode obter uma representação adequada das
séries de tempo através de qualquer um destes modelos, nos quais p e q tomam valores iguais a
dois e inclusive menores. O uso do menor número possível de parâmetros para uma
representação adequada é conhecido como parcimônia.
Estes modelos descritos são modelos estacionários, os quais assumem que o processo
permanece em equilíbrio em torno à um nível médio constante e gaussianos (a distribuição da
variável aleatória é normal).
Seguindo-se o critério de estacionariedade e de normalidade, não seria possível aplicar
sobre uma série de tempo com valores de Kt nenhum dos modelos acima descritos, pois, como se
pode verificar pela análise da Figura 64, esta apresenta uma distribuição não-normal, com grande
assimetria à direita e também é uma série não estacionaria, pois o valor médio de Kt varia com o
tempo.
Figura 64. Distribuição de frequência dos valores de Kt em Porto Alegre.
Uma solução encontrada foi a de transformar Kt em uma nova variável com uma
distribuição gaussiana. No entanto, como a distribuição dos valores de Kt é uma função de seu
valor médio mensal K t , não é possível utilizar-se as técnicas convencionais de transformação
pois estas necessitariam que os parâmetros fossem determinados interativamente para cada mês e
para cada localidade, impossibilitando que se obtenha um modelo universal válido para qualquer
parte do mundo. Isto poderia ser conseguido incorporando-se a distribuição de Liu e Jordan, que
possibilitaria que um usuário, de qualquer parte, pudesse produzir as sequências de Kt
conhecendo somente os valores de K t .
Assim, as series produzidas teriam a variação mensal e a distribuição de probabilidades
corretas e também manteriam a relação entre os eventos diários.
86
A) O mapeamento gaussiano
Para corrigir a não-estacionariedade e o caráter não-gaussiano das séries de Kt ,
transforma-se Kt em uma nova variável aleatória gaussiana χ com estatísticas que são invariantes,
isto é, possuem a mesma média e a mesma variância para todos os meses. Se fj representa a
função de transformação mensal desconhecida que mapeia Kt em uma variável gaussiana χ,
então:
f j ( K t ) = χ (144)
O mapeamento entre χ e Kt e vice-versa tem de garantir que suas respectivas
probabilidades marginais não sejam alteradas. Este mapeamento é feito com a utilização de uma
transformação integral, assim definida: seja x uma variável aleatória tendo uma distribuição de
probabilidade contínua em Rx, com função densidade de probabilidade P(x) e função distribuição
F(x). A transformação integral:
y = F (x ) = ∫−∞ P (x )dx (145)
x
mapeia Rx no intervalo (0,1), isto é, a variável aleatória y é uniformemente distribuída no
intervalo (0,1) para qualquer valor de x.
Se g(z) representa a distribuição gaussiana padrão (média zero e desvio padrão unitário) e
P( K t , K t ) a função densidade de probabilidade de Kt, obtém-se as seguintes transformações:
1
χ
u = ∫−∞ g (z )dz =
2π
e
v = ∫kt
kt max
min
∫
χ
exp − z
−∞
2
/2
dz =
 χ 
1
1 + erf   (146)
2
 2 
P( K t , K t ) dK t = F ( K t , K t ) (147)
onde u é a função distribuição de χ e v a função distribuição de Kt e erf(x) é a função erro, onde
x = χ / 2.
Variáveis aleatórias que são transformadas por suas funções de distribuição fornecem
sempre uma variável transformada que é uniformemente distribuída em (0,1). Assim, tanto u
como v são uniformemente distribuídos no intervalo (0,1). Como u e v possuem a mesma função
distribuição e a transformação procurada exige que as probabilidades acumuladas sejam
mantidas, então u necessita ser igual a v. Então, a função de transformação fj fica:
 χ 
1
 = F ( K t , K t ) (148)
1 + erf 
2
 2 
onde F ( K t , K t ) é a função distribuição de Kt.. Resolvendo a Equação 148 para χ, tem-se:
χ = 2erf
−1
{2 F ( K , K ) − 1} = f
t
t
j
( K t ) (149)
A função distribuição F ( K t , K t ) pode ser obtida dos dados observados ou analiticamente,
conforme foi demonstrado no Capítulo 5, pela Equação 83.
87
B) Construção do modelo
A equação geral para um processo ARMA(p,q) é:
p
q
t =1
t =1
χ ( n) = ∑ φ t χ ( n − t ) + ω ( n) − ∑θ t ω ( n − t ) (150)
onde n e n-t são números de dias, sendo que n-t equivale à t dias precedentes ao dia n. χ(n) é o
valor de χ no dia e ω(n) é o valor no dia n de um número aleatório retirado de um conjunto de
números com distribuição normal de média zero e variância σω2.
Os parâmetros φt (t=1,2,...,p) e θt (t=1,2,...,q) são chamados parâmetros autoregressivos e
de média-móvel, respectivamente. A construção do modelo segue o procedimento aconselhado
por Box e Jenkins.
Identificação:
Este passo destina-se à determinar a classe do modelo, isto é, os valores de p e q para as
equações que representam o processo real. As principais ferrramentas para a identificação são as
funções de autocorrelação e de autocorrelação parcial. A função autocorrelação pode ser
calculada mediante a seguinte expressão:
N −k
rk =
∑( z
t =1
t
− z )( zt + k − z )
N
∑( z
t =1
t
− z)
2
(151)
onde N é o número de elementos da série, k é o intervalo entre as duas variáveis, zt e zt+k são os
valores das variáveis nos tempos t e t+k, respectivamente e z é o valor médio da série.
Esta equação, que estima o valor rk de ρk , o coeficiente de autocorrelação, mede a
direção e intensidade da relação estatística entre pares ordenados de observações de duas
variáveis aleatórias. É um número adimensional que toma valores entre -1 e +1. Um valor de -1
significa uma perfeita correlação negativa e um valor de +1 uma perfeita correlação positiva. Se
ρk=0, então não existe correlação.
A função autocorrelação parcial φ$kk , onde k é o intervalo de tempo considerado, é obtida
através da seguinte equação, onde rkk é o valor estimado de φ$kk :
k −1
rk − ∑ φ$k −1, j rk − j
φ$kk =
j =1
k −1
1 − ∑ φ$k −1, j r jh
(152)
j =1
Esta função mede como zt e zt+k estão relacionados, mas considerando os efeitos dos z´s
intermediários.
Comparando estas funções para as séries da variável χ obtidas pela transformação das
séries de Kt observadas, com as funções teóricas, Grahan et alii35 mostraram que o modelo
ARMA(1,0) descreve perfeitamente o processo real.
88
Estimativa dos parâmetros
Aqui, utilizando o critério da máxima probabilidade ou dos mínimos quadrados, estimase os valores dos parâmetros do modelo escolhido e verifica-se suas significâncias. No mesmo
trabalho de Grahan et alii35, o valor do parâmetro autoregressivo de primeira ordem φ1 , mostrou
ser bem significante, acima de 15 vezes seu erro padrão. Isto fortaleceu a escolha do modelo
ARMA(1,0) como o mais adequado.
Checagem
Após a utilização do modelo escolhido, testam-se os resíduos ω$( n) para verificar sua
independência e normalidade, através das funções de autocorrelação e de autocorrelação parcial.
Se os resíduos são brancos (independentes), as autocorrelações estimadas terão um erro padrão
de 1 / N .
C) Validação do modelo
Satisfeitos todos os requisitos, concluiu-se que um modelo ARMA(1,0) seria adequado
para a representação do processo real. Este modelo pode ser representado por:
χ (n) = φ1 χ ( n − 1) + ω( n) (153)
A variância do ruído, σω2 , não é uma quantidade independente pois está relacionada com
a variância de χ:
σω2
σχ =
(154)
1 − φ 12
2
Como foi assumido que a distribuição gaussiana de χ tem uma média igual a zero e
variância unitária, tem-se:
σω2 = 1 − φ 12 (155)
Os valores numéricos exatos dos coeficientes das funções de autocorrelação e de
autocorrelação parcial teóricas de um modelo ARMA(1,0) são determinados pelo valor de φ1 .
Para o intervalo 1, tanto o coeficiente de autocorrelação ρ1 como o coeficiente de autocorrelação
parcial φ11, são iguais a φ1. O valor deste coeficiente pode ser estimado, sem introduzir um erro
muito grande, pelo coeficiente de autocorrelação da amostra, r1.
Os números aleatórios ω(n) utilizados na Equação 153 podem ser gerados pelo método de
Box-Muller, obtidos em Press36 , o qual transforma um número aleatório uniformemente
distribuído em um número aleatório com distribuição normal de média zero e variância σω2.
O valor de χ(0) necessário para inicializar o processo é obtido gerando-se um número
aleatório entre zero e um. A função distribuição F ( K t , K t ) empregada para realizar o
mapeamento foi a de Hollands e Huget (Equação 83). O processo utilizado é:
89
1 1
 φ 1 χ ( n − 1) + ω ( n) 
F ( K t , K t ) =  + erf 
 (156)


2
2 2
onde a função erro é dada por:
erf (x ) =
2
π
x
∫e
−t2
dt (157)
0
que pode ser avaliada utilizando-se a função Gama incompleta P(α,x), pois estão relacionadas da
seguinte forma:
1

erf (x ) = P , x 2 , x ≥ 0 (158)
2

O algoritmo utilizado pode ser encontrado em Press36.
10.2.2. Processo de Markov
Para uma melhor visualização do que é o processo em si, se utiliza o seguinte exemplo:
considere um lago com folhas de nenúfares, tal como é descrito na Figura 65 e analisamos o
comportamento de uma rã neste lago.
Figura 65. Representação de um processo de Markov.
A rã necessita obrigatoriamente estar localizada em uma folha; ela nunca nada na água.
Ela tanto pode pular de uma folha a outra como permanecer no mesmo lugar.
Considera-se que o lago possua um número finito de folhas, N. Se n indica o número de
saltos realizados pela rã e s(n) o número da folha ocupada após o enésimo salto, a sequência:
s(0), s(1), s(2 ), ... , s(n ), s(n + 1)
especifica todo o itinerário da rã. Esta sequência é chamada de processo e o estado do processo é
o número da folha ocupada pela rã. Os saltos da rã de uma folha a outra representam um processo
de transição de estados. A quantidade s(n) representa o estado do processo após a enésima
transição.
90
A trajetória do processo, como se pode perceber, é aleatória. O comportamento estatístico
deste processo poderia ser descrito caso fosse conhecida a probabilidade condicional para todos
os valores de seus argumentos:
P{s(n + 1) = j s(n) = i , s(n − 1) = k ,..., s(0) = m} (159)
onde 1≤ (i,j,k,...,m) ≤ N.
Esta é a probabilidade de que cada estado será ocupado após a n+1 transição, fornecendo
a trajetória ou história de como são ocupados os estados no tempo n. Se esta probabilidade
condicional pudesse ser especificada arbitrariamente para todo valor de n, então o
comportamento do processo poderia ser extremamente complexo.
A) A suposição markoviana
Esta suposição diz que somente o último estado ocupado pelo processo é relevante na
determinação de seu comportamento. Com esta suposição a probabilidade condicional dada pela
Equação 159 torna-se:
P{s(n + 1) = j s(n) = i } (160)
Assim, a probabilidade de transição de cada estado depende somente do estado
presentemente ocupado. Como é muito difícil encontrar sistemas físicos que apresentem tão
pouca ¨memória¨, a questão a colocar é se o modelo de Markov pode ser útil ou não na descrição
de tais sistemas.
B) Probabilidades de transição
Para definir um processo de Markov é necessário especificar para cada estado no
processo e para cada tempo de transição a probabilidade de fazer a próxima transição para um
outro estado, dadas estas condições. Para isto, é necessário especificar a probabilidade
condicional, dada pela Equação 160, para todo 1≤ i,j ≤ N e para n=0,1,2,...
Definindo-se a probabilidade de transição pij:
pij = P{s(n + 1) = j s(n) = i }, 1 ≤ i , j ≤ N , n = 0,1,2, ... (161)
A probabilidade de transição pij é a probabilidade que o processo presentemente no
estado i ocupará o estado j após a próxima transição. Como cada probabilidade de transição pij é
uma probabilidade, ela necessariamente precisa satisfazer a condição:
0 ≤ pij ≤ 1, para 1 ≤ i,j ≤ N (162)
Deve-se notar que as probabilidades do mesmo estado ser ocupado após uma transição,
isto é, as probabilidade pii , i=1,2,...,N não são necessariamente zero. Visto que o processo
precisa ocupar um dos N estados após uma transição:
91
N
∑p
j =1
ij
= 1, para i = 1,2, ... , N (163)
As N2 probabilidades de transição que descrevem um processo de Markov são
convenientemente representadas por uma matriz N×N, chamada matriz de probabilidades de
transição P, com elementos pij:
{ }
P = pij
p11
p21
=
.
pN 1
p12
p22
.
pN 2
... p1N
... p2 N
(164)
...
.
... p NN
As entradas na matriz P necessitam satisfazer as exigências impostas pelas Equações 162
e 163. A matriz cujos elementos estão na faixa (0,1) e cujas linhas soma à unidade é chamada de
matriz estocástica.
C) Construção das matrizes
Utilizando-se o fato de que a função distribuição de Kt possui uma forma associada
somente com o valor médio mensal desta variável, como foi anteriormente mostrado, derivou-se
uma biblioteca de matrizes, cada uma correspondendo a um intervalo estreito de valores médios
de Kt à partir de dados observados disponíveis. Estas matrizes podem, então, ser usadas para a
geração de sequências de valores de diários de radiação para qualquer local.
O procedimento foi dividir a amplitude dos valores de Kt para o período em observação
em n intervalos iguais (estados) e avaliar a probabilidade pij de que, se Kt tem um certo valor
num dia, correspondente ao estado i, no dia seguinte terá um valor correspondente ao estado j.
Desta forma é gerada uma matriz quadrada (n×n) chamada Matriz de Transição de Markov
(MTM), já que ela contém implicitamente a memória do que acontece no intervalo de tempo de
um dia e descreve qual a probabilidade de acontecer qualquer transição de um valor para o
próximo. Como o valor de Kt precisa estar necessariamente em um dos estados possíveis no
próximo dia, é preciso que, para cada linha da matriz ∑ pij = 1.
j
O procedimento é o seguinte:
a) os estados são numerados de 1 até n.
b) cada valor na sequência é colocado em seu estado e é obtida então uma sequência de estados
como, por exemplo, (4,7,3,6,5,...).
c) são formados pares ordenados, tais como (4,7), (7,3), (3,6), (6,5), etc. tomando-se todos os
pares contíguos de estados.
d) cada par é um evento que é adicionado a todos os outros eventos iguais em cada posição da
matriz, produzindo um histograma bidimensional, normalizado à unidade para cada linha,
dividindo-se pelo número de eventos na linha.
É útil observar que o estado estacionário de uma MTM (n×n) é um vetor cujos
componentes são n valores discretos da função distribuição correspondente ao período associado.
92
Outra observação básica é que a forma da função distribuição para um período tal como um mês
parece ser idêntica para todos os meses tendo o mesmo valor de K t . Visto que esta função
distribuição é o estado estacionário de uma MTM mensal, parece razoável esperar que para cada
valor de K t corresponde uma e somente uma MTM mensal.
Nas Tabela 13 a 22 se apresentam a biblioteca de matrizes de transição de 10×10 e na
Tabela 23 os valores de Ktmin e Ktmax associados a cada uma delas.
Tabela 13. Matriz de Transição de Markov para K t ≤ 0,30.
Tabela 14. Matriz de Transição de Markov para 0,30 < K t ≤ 0,35.
Tabela 15. Matriz de Transição de Markov para 0,35 < K t ≤ 0,40.
Tabela 16. Matriz de Transição de Markov para 0,40 < K t ≤ 0,45.
93
Tabela 17. Matriz de Transição de Markov para 0,45 < K t ≤ 0,50.
Tabela 18. Matriz de Transição de Markov para 0,50 < K t ≤ 0,55.
Tabela 19. Matriz de Transição de Markov para 0,55 < K t ≤ 0,60.
Tabela 20. Matriz de Transição de Markov para 0,60 < K t ≤ 0,65.
94
Tabela 21. Matriz de Transição de Markov para 0,65 < K t ≤ 0,70.
Tabela 22. Matriz de Transição de Markov para K t > 0,70.
Tabela 23. Valores máximos e mínimos de Kt para cada uma das dez classes definidas.
Classe
Ktmin
Ktmax
1
0,031
,705
2
0,058
0,694
3
0,051
0,753
4
0,052
0,753
5
0,028
0,807
6
0,053
0,856
7
0,044
0,818
8
0,085
0,846
9
0,010
0,842
10
0,319
0,865
D) Geração das sequências de radiação solar
O procedimento de geração das sequências de radiação solar à partir das Matrizes de
Transição de Markov é descrito a seguir. Os únicos parâmetros necessários são os valores médios
mensais de Kt.
a) seleciona-se uma MTM em função do valor de K t , com seus valores associados de Ktmin e
Ktmax.
b) o estado i é escolhido tomando-se no começo de cada mês o valor de Kt do último dia do mês
anterior, Kt+, (exceto para o primeiro dia do primeiro mês, para o qual toma-se o valor médio do
95
mês anterior) e portanto, uma linha da matriz. Este estado é obtido verificando-se em que
intervalo h = ( K tmax − K tmin ) / n se encontra o valor de Kt+ .
c) gera-se um número aleatório R entre 0 e 1, distribuído uniformemente.
d) os elementos pi1, pi2, pi3, ..., pij são somados até que sua soma seja maior que R, determinandose j, o próximo estado de Kt, isto é, o estado no qual Kt estará no próximo dia. A maneira mais
simples de encontrar o novo valor de Kt consiste em atribuir-lhe o valor médio do intervalo
correspondente ao estado j. Uma outra maneira seria fazer uma interpolação linear dentro do
intervalo.
e) o segundo dia da sequência pertence, então, ao estado j. Repete-se os passos c) e d).
Como o valor médio de Kt de uma sequência gerada pode desviar-se um pouco do valor
médio mensal K t usado como entrada, devido principalmente ao pequeno tamanho da sequência,
pode-se gerar várias sequências mensais até que a média destas esteja tão próxima ao valor de K t
quanto se deseje, tipicamente dentro de um limite tal como K t ( observado ) − K t ( gerado ) ≤ 0,01.
10.3. Geração estocástica de valores horários de irradiação global
Estudando a distribuição dos valores de kt para cada ângulo de elevação Aguiar e
Collares-Pereira37 constataram que a variância destas distribuições muda com o tempo solar,
principalmente para valore de Kt > 0,45 e para as primeiras e últimas horas do dia. Também
mostraram que a forma destas distribuições é similar à uma gaussiana. Para aplicar às séries de kt
modelos de cadeias de Markov necessita-se transformar estas variáveis em outras, estacionárias e
homogêneas no tempo, atuando-se não só na media como na variância da série. O modelo assim
proposto por estes autores é denominado TAG - Time-dependent Autoregressive Gaussian.
Como a função gaussiana se estende indefinidamente em ambos os lados do valor médio,
esta função foi truncada em zero e um valor máximo, chamado kcs ou seja, um valor máximo de
kt, obrigando desta forma que esta variável permanece entre estes limites físicos.
Como a variável kt, é não-estacionária e homogênea no tempo, se define uma nova
variável y, através do procedimento usual de normalização:
y (t ) =
k t (t ) − k tm (K t , t )
(165)
σ (K t , t )
onde ktm é a media horária, em função da hora do dia (1 a 24) e σ o desvio padrão de kt, em
função dos valores diários de Kt e da hora. Como kt, é normalmente distribuído, ktm e σ
caracterizam completamente sua distribuição.
À variável y pode então aplicar-se o modelo ARMA de primeira ordem:
y (t ) = φ 1 y( t − 1) + r (166)
onde φ1 é o coeficiente de autocorrelação de primeira ordem, também associado ao valor diário
Kt :
φ 1 = 0,38 + 0,06 cos( 7,4K t − 2,5) (167)
A função ktm é parametrizada da seguinte maneira:
96
k tm (t ) = λ + ξ exp{− κ / sen α } (168)
onde
λ = −0,19 + 1,12K t + 0,24e −8K
ξ = 0,32 − 1,6( K t2 − 0,5)
2
t
(169)
κ = 0,19 + 2,27K t2 − 2,51K t3
O desvio padrão σ foi ajustado aos valores calculados e é representado pela seguinte
equação:
σ ( K t , t ) = A exp{B(1 − sen α ) } (170)
onde
{
A = 0,14 exp −20( K t − 0,35)
2
B = 3( K t − 0,45) + 16K t5
2
} (171)
O valor da variável aleatória gaussiana r deverá possuir média zero e desvio padrão:
σ ′ = (1 − φ 12 )
0 ,5
(172)
Uma forma fácil de obter-se a variável aleatória gaussiana é retirando um número
aleatório uniformemente distribuído z e aplicando a seguinte transformação:
[
r = σ ′ z 0,135 − (1 − z )
0 ,135
] / 0,1975 (173)
Do processo inverso à normalização obtém-se o novo valor de kt :
k t (t ) = ktm ( Kt , t ) + σ ( Kt , t ) y( t ) (174)
Para certificar-se que o valor encontrado de kt esteja dentro de limites físicos aceitáveis,
compara-se o valor encontrado com valor máximo permitido, dado por:
k cs (t ) = 0,88 cos{π ( t − 12,5) / 30} (175)
O processo de geração necessita então comparar, para cada valor gerado de kt, se kt >0 e
se kt < kcs . Uma vez encontrado todos os valores de kt para um determinado dia, compara-se o
valor diário encontrado Kt’ com o valor de partida, Kt , de tal forma que:
Kt′ − K t
Kt
< ε (176)
97
onde ε é o máximo erro permitido. Caso isso não se satisfaça, reinicia-se o processo para aquele
dia.
Bibliografia consultada
1. M. Iqbal, An introduction to solar radiation. Academic Press, Toronto, 390p, 1983.
2. J. A. Duffie e W. A. Beckman, Solar engineering of thermal process. John Wiley & Sons,
New York, 762p, 1980.
3. A. A. M. Sayigh, Ed, Solar energy engineering. Academic Press, Orlando, 506p, 1977.
4. J. T. McMullan, R. Morgan e R. B. Murray, Energy resources and supply. John Wiley & Sons,
Chichester, 508p, 1976.
5. A. B. Meinel e M. P. Meinel, Aplicaciones de la energía solar. Editorial Reverté, Barcelona,
699p, 1982.
6. R. L. Hulstrom, Ed., Solar resources. The MIT Press, Cambridge, 408p, 1989.
Referências
1. World Meteorological Organization, "WMO Commission for Instruments and Methods of
Observation, Abridge Final Report of the 9th Session". Secretariat of WMO, Geneva, 1985.
2. G. Zerlaut, “Solar radiation instrumentation”, Capitulo 5, in Solar Resources, Ed. R.L
Hulstrom, The MIT Press, Cambridge, 408 p, 1989.
3. K.J. Hanson, Studies of cloud and satellite parameterization of solar radiation at the earth´s
surface. Proc. Miami Conf. on Remote Sensing. U.S. Dept. of Commerce, 133-148, 1971
4. T.H. Vonder Haar, Solar insolation microclimate determined using satellite data. Solar Energy
Data Workshop, NOAA NSF-RA-N-74-062, 143-148, 1973.
5. J.D. Tarpley, Estimating incident solar radiation at the Earth´s surface from geostationary
satellite data. J. Appl. Meteor. 18, 1172-1181, 1979.
6. B. Bourges, Ed. Project Eufrat - Final Scientific Report. Contract EN3S-0111-F. Commission
of the European Communities, 1990.
7. F. Kasten e A.T. Young, Revised optical air mass tables and approximation formula. Applied
Optics 28, 4735-4738, 1989.
8. A. Ångstrom, Solar and terrestrial radiation, Quarterly J. of the Royal Meteorology Soc. 50,
121-126, 1924.
9. J.A. Prescott, Evaporation from a water surface in relation to solar radiation. Trans. R. Soc. S.
Aust. 64, 114-118, 1940.
10. M.R. Rietveld, A new method for estimating the regression coefficients in the formula
relating solar radiation to sunshine. Agr. Meteorol. 19, 243-252, 1978.
11. M. Berlato, Radiação global no Estado do Rio Grande do Sul, Agronomia Sulriograndense
V, 115-131, 1971.
98
12. J.N. Black, The distribution of solar radiation over the earth´s surface. Arch. Meteorol.
Geophys. Bioklimatol. 7, 165-189, 1956.
13. A. Whillier, The determination of hourly values of total solar radiation from daily
summation. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 7, 197-204, 1956.
14. B.Y.H. Liu e R.C. Jordan, The interrelationship and characteristic distribution of direct,
diffuse and total solar radiation. Solar Energy 4, 1-19, 1960.
15. M. Collares-Pereira e A. Rabl, The average distribution of solar radiation correlations
between diffuse and hemispherical and between daily and hourly insolation values. Solar Energy
22, 155-164, 1979.
16. D.G. Erbs, S.A. Klein e J.A. Duffie, Estimation of the diffuse radiation fraction for hourly,
daily and monthly-average global radiation. Solar Energy 28, 293-302, 1982.
17. J.K. Page, The estimation of monthly mean values of daily total short-wave radiation on
vertical and inclined surfaces from sunshine records for latitudes 40°N-40°S. Proc. U.N. Conf.
New Sources Energy, Paper no. S98, Vol. 4, 378-390, 1961.
18. M. Iqbal, Correlation of average diffuse and beam radiation with hours of brigh sunshine.
Solar Energy 23, 169-173, 1979.
19. J.F. Orgill e K.G.T. Hollands, Correlation equation for hourly diffuse radiation on a
horizontal surface. Solar Energy 19, 357-359, 1977.
20. D.T. Reindl, W.A. Beckman e J.A. Duffie, Diffuse fraction correlations. Solar Energy 45, 17, 1990.
21. E.L. Maxwell, A quasi-physical model for converting hourly global horizontal to direct
normal insolation. SERI/TR-215-3087, 1987.
22. G.W. Paltridge e C.M.R. Platt, Radiative processes in meteorology and climatology.
Elsevier, New York, 1976.
23. K.L. Coulson, Solar and terrestrial radiation. Academic Press, New York, 322p, 1975.
24. R.C. Temps e K.L. Coulson, Solar radiation incidente upon slopes of different orientations.
Solar Energy 19, 179-184, 1977.
25. H.H. Kimball e I.F. Hand, Daylight illumination on horizontal, vertical and sloping surfaces.
Monthly Weather Review 50, 615-628, 1922
26. P. Moon e D.E. Spencer, Illumination from a non-uniform sky. Trans. Illum. Eng. Soc. 37,
707-726, 1942.
27. R.G. Hopkinson, Measurements of sky luminance distribution at Stockholm. J. of the Opt.
Soc. of Am. 44, 455-459, 1954.
28. L.J. McArthur e J.E. Hay, A technique for mapping the distribution of diffuse solar radiation
over the sky hemisphere. J. of Appl. Meteo. 20, 421-429, 1981.
29. B.Y.H. Liu e R.C. Jordan, Daily insolation on surfaces tilted toward the ecuator. ASHRAE
Journal 3, 53-59, 1961.
30. T.M. Klucher, Evaluation of models do predict insolation on tilted surfaces. Solar Energy 23,
111-114, 1979.
31. J.E. Hay e D.C. McKay, Estimating solar irradiance on inclined surfaces: a review and
assessment of methodologies. Int. J. Solar Energy 3, 203-240, 1985.
32. R. Perez, R. Seals, P. Ineichen, R. Stewart e D. Meniccucci, A new simplifie version of the
Perez diffuse irradiance model for tilted surfaces. Solar Energy 39, 221-231, 1987.
33. S.A. Klein. e W.A. Beckman, Loss-of-load probabilities for stand-alone photovoltaic
systems. Solar Energy 39, 499-512, 1987.
34.G.E.P. Box e G.M. Jenkins, Time series analysis, forecasting and control. San Francisco,
Holden-Day, 575p, 1976.
35. V.A. Grahan, K.G.T. Hollands e T.E. Unny, A time series model for Kt with application to
global synthetic weather generation. Solar Energy 40, 83-92, 1988.
99
36. W.H. Press, Numerical recipes; the art of scientific computing. New York, McGraw-Hill,
312p, 1987.
37. R. Aguiar e M. Collares-Pereira, TAG: a time-dependente, autoregressive, gaussian model
for generating systhetic hourly radiation. Solar Energy 49, 167-174, 1992.
100