Aula 04
Transcrição
Aula 04
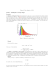
Parte III O Universo Homogêneo II: Breve História Térmica do Universo Equação de estado e temperatura G Se kT >> mc2: relativístico ⇒ p ≈ ρ/3 G Se kT << mc2: não relativístico ⇒ p<<ρ Pressão e Densidade • Densidade de Energia: g g 3 ρ= f ( p) E ( p)d p = 3 ∫ 3 ∫ ( 2π ) e ( 2π ) função de distribuição (“probabilidade”) Energia 1 m2 + p 2 / T ±1 m2 + p 2 d 3 p Fermi-Dirac Energia Bose-Einstein • Pressão: p= g ( 2π ) 3 ∫ p2 1 g 3 f ( p) d p= 3E ( p ) 3 ( 2π )3 ∫ e 1 m2 + p 2 / T p2 2 2 ±1 m + p Equilíbrio, m = 0 d3 p Densidade de energia e expansão do Universo: partículas com massa ∝ a −4 = (1 + z ) 4 r ∝ a −3 = (1 + z )3 Observação: Exemplo ao lado para neutrinos 1+ z Uma História do Universo Cabum!! Recombinação plasma Ocorre a 0.26eV em vez de 13.6eV! nb η := nγ matéria neutra Figura retirada de http://blueox.uoregon.edu/~karen/astro123/lectures/lec20.html 6 × 10−10 Recombinação Quando a temperatura cai abaixo dos 3.000K os elétrons ficam presos aos núcleos ¾ O Universo passa a ser transparente ¾ A luz se propaga livremente Figura retirada de http://blueox.uoregon.edu/~karen/astro123/lectures/lec21.html A Radiação Cósmica de Fundo “Fotosfera” vista da nossa galáxia Esperamos ver: Corpo negro, com desvio para o vermelho z ~ 1000 Intensidade [10-4 ergs cm-2 s-1 sr-1 cm] O Espectro da Radiação Cósmica de Fundo espectro térmico com T = 2.725 ± 0.002 K barras de erro de 100σ Ωγ h 2 = 2.47 ×10−5 Comprimento de onda [cm-1] Radiação Cósmica de Fundo I Mapa da Radição Cósmica: Contraste: 1× G G G G 400× Época do desacoplamento entre matéria e radiação (em torno de 380.000 anos após o “Big-Bang”). T0 = 2.725 ± 0.002. Desvio para o vermelho, z = 1089. Universo primordial altamente homogêneo. Dipolo: ∆T = 3.346 ± 0.017 mK ⇒ vgal = 360 Km/s Nucleossíntese: Alquimia no Universo Primordial Produção de 7Li, 3He, D, 4He z ~ 104, 3MeV,T ~ 1010 K - 109 K, 1s a 3min “DBB” Figura retirada de http://blueox.uoregon.edu/~karen/astro123/lectures/lec20.html Produção de elementos leves Universo dominado pela radiação: • H = H(T) • taxa de interações = f(T) • depende apenas de h = nb/ng Universo dominado pela radiação: a ∝ t1/ 2 a& 1 H= = a 2t Figura: Kepler Oliveira, Maria de Fátima Saraiva Astronomia e Astrofísica, http://astro.if.ufrgs.br/ Abundância de Elementos Leves Produção de 7Li, 3He, D, 4He Todos com o mesmo η! D é o melhor “bariômetro” Ωb 0, 04 Independente da matéria escura Assimetria Matéria/Anti-Matéria G G G G No universo primordial: equilíbrio entre partículas e anti-partículas (eqüipartição) T ~ 175 MeV (t ~ 10-5 s “DBB”): Meio quark-glúon ⇒ Hadronização Aniquilação ⇒ Universo dominado por píons Aniquilação produz fótons: n−n η= = 6 × 10−10 n ¾ Assimetria de 1 parte em 109! Relíquias Térmicas Frias e Matéria Escura Γ << H −1 → desacoplamento ΩX ∝ σ −1 A (independente da massa) Alguns Marcos da História do Universo kT (radiação) 2 x 10-4 eV Evento Hoje 10-3 eV 1 eV 10 eV 300 keV Formação das Galáxias Recombinação do H (desacoplamento matéria-radiação) Dominação pela matéria Formação dos elementos leves (He4, He3, D e Li) 0.5 MeV 100 MeV Fim da era leptônica (aniquilação e+ e-) Fim da era hadrônica e início da era leptônica 1000 GeV 1015 GeV Transição de fase eletrofraca Bariossíntese? Grande Unificação? 1019 GeV Fim da era quântica? Inflação? (nucleossíntese) (hadronização, aniquilação hádron anti-hádron) Parte IV O Universo Perturbado A radiação cósmica de fundo G G G Desacoplamento matériaradiação, z = 1089. Universo primordial altamente homogêneo. Resultados obtidos pelo COBE: ∆ρ ∆T −2 −3 −5 → ≈ 10 − 10 ≈ 10 ρ T Î Flutuações lineares Perturbações Lineares G G G G Perturbações dentro do raio de Hubble: Análise newtoniana Notas do Curso Fora do raio de Hubble: tratamento relativístico Antes do desacoplamento: equações de Boltzmann Após: basicamente gravitação Espectro de Potência da Radiação Cósmica de Fundo T2 (θ 2 , φ2 ) T1 (θ1 , φ1 ) T1T2 = ∑ almYlm (θ , φ ) alm 2 1/ 2 ≡ Cl Espectro de Potência Segundo o WMAP3 O Universo é quase plano! Ω k = 1 − Ω m − Ω? Polarização da RCF Espectro da Polarização Resultados da análise linear Necessidade de Matéria Escura I I I I Matéria bariônica: só pode se aglomerar depois de tdec (~ 380.000 anos) e para r > λJ CDM se aglomera a partir de teq (~ 56.000 anos) Bárions seguem os poços de potencial da matéria escura Amortecimento de Silk diminui amplitude de perturbações nos bárions Resultados da análise linear Necessidade de Matéria Escura Efeito Sachs-Wolfe Integrado G G G Efeito acumulado dos desvios gravitacionais: τ 0 ∂φ δ TISW dτ = 2∫ τ dec ∂τ T Evolução linear, EdS: φ = const. Efeito tardio: I Correlação entre radiação cósmica de fundo e estrutura em grande escala! Energia escura Estatística: Função de Correlação G Contraste de densidade: r r n(r ) − n (r ) r δ obs ( r ) = r n (r ) G r δ ( r1 ) Função de correlação: r r r ξ ( r12 ) = δ ( r1 ) δ ( r2 ) Sobredensidade de pontos próximo de uma partícula aleatória G Espectro de potência: transformada de Fourier r δ ( r2 ) Espectro de Potência: Energia Escura Forma das flutuações primordiais Matéria escura Massa dos neutrinos Quantidade de bárions Max Tegmark, http://www.hep.upenn.edu/~max/ Dados e Teoria P Espectro de Potência: k I I I I Tegmark, et al., ApJ 606, 702 (2004) Forma das flutuações primordiais Matéria escura Massa dos neutrinos Quantidade de bárions Exemplo (do SDSS): Ω m = 0.30 ± 0.03 k 205.443 galáxias do SDSS Flutuações em Todas as Escalas
Documentos relacionados
Radiação Cósmica de Fundo - Departamento de Física da UEFS
 presenciar um forno microondas em funcionamento: ao colocar um alimento neste aparelho, em poucos
instantes e de forma rápida, está pronto para ser digerido. Ou então, falar em um telefone móvel (o...
presenciar um forno microondas em funcionamento: ao colocar um alimento neste aparelho, em poucos
instantes e de forma rápida, está pronto para ser digerido. Ou então, falar em um telefone móvel (o...