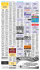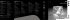Ajuste de uma função pelo Método dos Mínimos-Quadrados

Ajuste de uma função
pelo
Método dos Mínimos-Quadrados
O Método dos Mínimos-Quadrados é um método estatístico de tratamento de dados que
permite obter os parâmetros de uma função que a aproximam o mais possível dos pontos
experimentais. Nas figura 1a e 1b mostram-se duas situações em que as funções teóricas
Δl =
AM =
€
g
m
K
(1)
A0
(2)
2
(4π 2 f 02 − 4π 2 f a2 ) + 16π 2λ2 f a2
se aproximam claramente dos pontos experimentais.
€
a)
b)
Figura 1: a) Ajuste da função (1) a um conjunto de dados experimentais; b) ajuste da
função (2) a um conjunto de dados experimentais.
Observando os gráficos é fácil de verificar que as curvas teóricas não passam por todos
os pontos experimentais. Existem pontos com ordenadas superiors às curvas teóricas e
pontos com ordenadas inferiores. No caso do gráfico da figura 1a poderiamos ter obtido
um ajuste idêntico se tivessemos colocado os pontos num gráfico em papel milimétrico e
MO-Lab – MMQ.doc (Versão 6.3.5-1)
1
de seguida desenhado uma recta que se aproximasse o mais possível de todos os pontos
simultaneamente. No caso do gráfico da figura 1b já seria mais dificil desenhar a curva
teórica porque é uma curva que não depende linearmente da variável independente.
Numericamente o problema resume-se a encontrar o valor do declive da recta no
caso do figura 1a e dos valores de A0 , λ, f a que permitem traçar a melhor curva (2) no
caso da figura 1b.
O caso da recta da figura 1a é mais fácil porque existe uma solução analítica. O
€
caso da figura 1b só tem um solução numérica obtida iterativamente.
Figura 2: Detalhe da qualidade do ajuste de uma recta a um conjunto de pontos
experimentais.
O ajuste de uma recta pelo método dos mínimos quadrados é muita vezes designado por
regressão linear e numericamente pode ser expresso da seguinte forma:
1. Para cada ponto experimental calcula-se a diferença entre a ordenada
experimental
e
o
valor
da
função
calculado
para
a
abcissa
correspondente Δy = y exp − f (x i ) . Se a função for uma recta então f (x) = a + bx e
Δy = y exp − a − bx i
€
MO-Lab – MMQ.doc (Versão 6.3.5-1)
€
€
2
2. Calcula-se a soma dos quadrados dessas diferenças para todos os pontos
experimentais tendo em conta o erro experimental de cada ponto, εy exp
2
 y − f (x ) 
N y
− a − bx i 
i
Q2 ( a,b) = ∑  exp
 = ∑  exp

i=1
i=1
 εy exp

 €εy exp

2
N
(3)
Note-se que quanto maior for o erro experimental de um ponto εy exp menor sera a
contribuição desse ponto para o resultado final.
€
€
3. O resultado dessa soma, Q2 ( a,b) , é uma função de duas variáveis a e b, a
ordenada na origem e o declive, respectivamente. Os valores de a e b que
interessam são aqueles para os quais a função Q2 ( a,b) tem o valor mínimo. Essa
€
situação corresponde à ideia intuitiva de que a curva passa próximo de todos os
pontos simultaneamente. Os valores de a e b que correspondem a esse mínimo
€
obtêm-se calculando
 ∂Q 2
=0

 ∂a2
 ∂Q = 0
 ∂b
(4)
(o facto de termos uma função de 2 variáveis não consitui problema uma vez que
€
basta calcular cada uma das derivadas assumindo que tudo o resto é constante).
Para termos a certeza que os valores de de a e b que satisfazem (4) corrspondem a
um mínimo de (3) as segundas derivadas têm de ser positivas. Podemos
anticipadamente ter essa certeza porque (3) é uma função quadrática.
O sistema (4) tem solução analítica e os valores a e b que o satisfazem são
MO-Lab – MMQ.doc (Versão 6.3.5-1)
3

y
y x
x i2
x
∑ ε 2 ∑ ε 2exp − ∑ ε 2 i ∑ εexp2 i

y exp
y exp
y exp
y exp
a =
2

2


1
xi
xi

∑ ε 2 ∑ ε 2 − ∑ ε 2 

y exp
y exp

y exp 

y exp x i
y
1
x

− ∑ 2 i ∑ 2exp
∑
∑
2
2

εy exp
εy exp
εy exp εy exp
b =
2
1
x i2 
xi 

∑ ε 2 ∑ ε 2 − ∑ ε 2 

y exp
y exp

y exp 

(5)
As incertezas experimentais também se propagam ao declive e à ordenada na origem e
podem-se calcular através das expressões
€

x2

∑ ε2 i

y exp
σ a =
2

2
1
x
x
i
i

∑ ε 2 ∑ ε 2 − ∑ ε 2 

y exp
y exp

y exp 

1

∑ ε2

y exp
σ b =
2
2


1
xi
xi 
∑ ε 2 ∑ ε 2 − ∑ ε 2 

y exp
y exp

y exp 

(6)
No caso de uma função não linear nos parametros de ajuste o sistema (4) equação
€
pode não ter solução analítica e os valores dos parâmetros de ajuste têm de ser obtidos
numericamente de forma iterativa.
Nos casos mais simples em que as funções de ajuste são rectas e temos poucos
pontos experimentais (5) e (6) podem ser calculados com uma simples máquina de
calcular. No entanto facilmente nos deparamos com a necessidade de utilizar programas
informáticos de tratamento de dados.
MO-Lab – MMQ.doc (Versão 6.3.5-1)
4
MO-Lab – MMQ.doc (Versão 6.3.5-1)
5