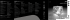Uma versão em PDF

Função de Green para a equação de onda
Anteriormente mostramos que, no calibre de Lorentz, dadas as fontes ρ e J, tudo o que temos a fazer para
encontrar os potenciais escalar e vetorial é resolver a equação diferencial
1 ∂ 2 Ψ (r, t)
c2
∂t2
∇2 Ψ (r, t) −
=
f (r, t) ,
onde o par ordenado (Ψ, f ) representa um elemento qualquer do conjunto
4π
4π
4π
(φ, −4πρ) , Ax , − Jx , Ay , − Jy , Az , − Jz
.
c
c
c
Queremos encontrar, primeiramente, uma solução particular dessa equação. Para isso, utilizamos a função
de Green G (r, t, r0 , t0 ), que, por denição, satisfaz
∇2 G (r, t, r0 , t0 ) −
1 ∂2
G (r, t, r0 , t0 )
c2 ∂t2
= δ (3) (r − r0 ) δ (t − t0 ) .
Podemos fazer a transformada de Fourier sobre a variável t em ambos os membros dessa equação para obter
∇2 g (r, ω, r0 , t0 ) +
ω2
g (r, ω, r0 , t0 )
c2
=
exp (iωt0 ) (3)
δ (r − r0 ) ,
2π
onde usamos a representação integral da função delta de Dirac, isto é,
δ (t − t0 )
=
e denimos
1
2π
ˆ
0
0
G (r, t, r , t )
ˆ
+∞
dω exp [−iω (t − t0 )]
−∞
+∞
dω exp (−iωt) g (r, ω, r0 , t0 ) .
=
−∞
Como explicaremos mais adiante, ao invés de resolvermos a equação diferencial acima, vamos modicá-la:
2
∇2 gη (r, ω, r0 , t0 ) + (k0 + iη) gη (r, ω, r0 , t0 )
=
exp (iωt0 ) (3)
δ (r − r0 ) ,
2π
onde denimos
k0
=
ω
,
c
que assume valores positivos e negativos, como ω. Podemos agora tomar a transformada de Fourier com relação
à variável r e obter
2
−k 2 g η (k, ω, r0 , t0 ) + (k0 + iη) g η (k, ω, r0 , t0 )
onde utilizamos
(3)
0
(r − r )
=
gη (r, ω, r0 , t0 )
=
δ
e denimos
=
exp (−ik · r0 + iωt0 )
ˆ
1
3
(2π)
d3 k exp [ik · (r − r0 )]
ˆ
d3 k exp (ik · r) g η (k, ω, r0 , t0 ) .
Logo,
g η (k, ω, r0 , t0 )
=
exp (−ik · r0 + iωt0 )
h
i
4
2
(2π) −k 2 + (k0 + iη)
1
4
(2π)
,
e, portanto,
ˆ
gη (r, ω, r0 , t0 )
d3 k
=
exp [ik · (r − r0 ) + iωt0 ]
h
i.
4
2
(2π) −k 2 + (k0 + iη)
Notemos que se não tivéssemos modicado a equação original e, portanto, equivalentemente tomado η = 0, a
integral acima não convergiria e não poderíamos encontrar uma função de Green pelo presente método. No
entanto, a função de Green, no caso modicado, ca
ˆ
0
0
Gη (r − r , t − t )
+∞
dω exp (−iωt) gη (r, ω, r0 , t0 )
=
−∞
ˆ
ˆ
+∞
d3 k
=
exp [ik · (r − r0 ) − iω (t − t0 )]
h
i ,
4
2
(2π) −k 2 + (k0 + iη)
dω
−∞
ou ainda,
ˆ
ˆ
+∞
exp (ik · r − iωt)
i
h
4
2
−∞
(2π) −k 2 + (k0 + iη)
ˆ +∞
ˆ
1
exp (ik · r)
= −
dω
exp
(−iωt)
d3 k
4
2.
(2π) −∞
k 2 − (k0 + iη)
Gη (r, t)
d3 k
=
dω
Em coordenadas polares,
ˆ
ˆ
exp (ik · r)
d3 k
2
k 2 − (k0 + iη)
ˆ
∞
∞
0
0
k2
exp (ik · r)
dθk senθk
0
=
π
dϕk
0
ˆ
ˆ
2π
k 2 dk
=
2 dk
k 2 − (k0 + iη)
2
k 2 − (k0 + iη)
ˆ π
2π
dϕk
dθk senθk exp (ik · r) .
ˆ
0
0
Se escolhermos o eixo z do espaço dos vetores de onda k como sendo paralelo ao vetor r, teremos
ˆ
d k
ˆ
exp (ik · r)
3
k 2 − (k0 + iη)
2
∞
=
0
ˆ
∞
=
=
k 2 − (k0 + iη)
2πk 2
k 2 − (k0 + iη)
0
ˆ
ˆ
k2
∞
2πk 2
dϕk
0
ˆ
2 dk
π
dθk senθk exp (ikr cos θk )
0
π
dθk senθk exp (ikr cos θk )
0
ˆ
1
2 dk
du exp (ikru)
k 2 − (k0 + iη)
−1
ˆ
2π ∞
k
[exp (ikr) − exp (−ikr)] dk,
2
ir 0 k − (k0 + iη)2
0
=
2 dk
ˆ
2π
onde utilizamos a substituição u = cos θk . Como temos
ˆ
0
∞
ˆ
k
k2
− (k0 + iη)
2
exp (−ikr) dk
0
−
=
−∞
k
k2
2
− (k0 + iη)
exp (ikr) dk,
podemos escrever
ˆ
3
d k
exp (ik · r)
k2
2
− (k0 + iη)
=
2π
ir
ˆ
+∞
−∞
k exp (ikr)
k2
Os polos dessa integral são dados por
Z±
= ± (k0 + iη) .
com k0 dado acima, isto é,
k0
=
2
ω
.
c
2 dk.
− (k0 + iη)
Consideremos a integral no plano complexo:
˛
C
Z exp (irZ)
dZ,
(Z − Z+ ) (Z − Z− )
onde o contorno é fechado sobre o semi-plano complexo superior.
Quando η → 0+ (veja a gura acima), temos
˛
C
Z exp (irZ)
dZ
(Z − Z+ ) (Z − Z− )
3
Z+ exp (irZ+ )
Z+ − Z−
= πi exp (ik0 r) .
=
2πi
Quando η → 0− (veja a gura acima), temos
˛
C
Z exp (irZ)
dZ
(Z − Z+ ) (Z − Z− )
=
πi exp (−ik0 r) .
Mas, com o contorno fechado sobre o semi-plano complexo superior,
ˆ
+∞
−∞
˛
k exp (ikr)
2 dk
k 2 − (k0 + iη)
=
C
Z exp (irZ)
dZ
(Z − Z+ ) (Z − Z− )
e, portanto,
ˆ
+∞
−∞
k exp (ikr)
2 dk
k 2 − (k0 + iη)
= πi exp (±ik0 r) .
Com esses resultados, podemos concluir que
ˆ
d3 k
exp (ik · r)
k 2 − (k0 + iη)
=
2
2π 2
exp (±ik0 r)
r
e, portanto,
G± (r, t)
=
=
=
=
ˆ
+∞
2π 2
exp (±ik0 r)
r
(2π) −∞
ˆ +∞
ω 1
− 2
dω exp (−iωt) exp ±i r
8π r −∞
c
ˆ +∞
h
i
1
r
− 2
dω exp −iω t ∓
8π r −∞
c
1 r
−
δ t∓
.
4πr
c
−
1
4
dω exp (−iωt)
4
Assim, também temos
1
1
|r − r0 |
0
G± (r − r , t − t ) = −
δ t−t ∓
4π |r − r0 |
c
1
1
|r − r0 |
0
= −
δ t −t±
.
4π |r − r0 |
c
0
0
Há, portanto, duas soluções possíveis para o problema:
ˆ
Ψ± (r, t)
=
ˆ
+∞
dt0 G± (r − r0 , t − t0 ) f (r0 , t0 )
d3 r0
ˆ
−∞
3 0
ˆ +∞
|r − r0 |
d r
0
0
dt δ t − t ±
f (r0 , t0 )
|r − r0 | −∞
c
|r−r0 |
0
ˆ
f r ,t ∓ c
1
d3 r 0
.
= −
4π
|r − r0 |
1
= −
4π
Para os campos eletromagnéticos especicamente de distribuições de cargas e correntes dadas, sendo esses
campos nulos no caso de termos as fontes também nulas, entendemos que esses campos são causados pelas
fontes. Nesse caso, utilizaremos as soluções retardadas e não as avançadas, isto é,
ˆ
φ (r, t)
d3 r 0
=
|r−r0 |
0
ρ r ,t − c
|r − r0 |
e
A (r, t)
=
1
c
ˆ
0
J r ,t −
d3 r 0
5
|r −
|r−r0 |
c
r0 |
.