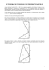TRIGONOMETRIA

Matemática - Trigonometria
129
Semelhança
TRIGONOMETRIA
1. SEMEL
EMELHANÇA
Texto e contexto
O
bservando objetos, podemos perceber que alguns deles possuem uma característica comum: têm a
mesma forma.
Por exemplo, ao compararmos bolas utilizadas em diversas práticas esportivas, como futebol, basquete,
tênis, verificamos que elas possuem a mesma forma esférica, diferenciando-se pela medida do seu raio.
Para serem semelhantes, os objetos devem apresentar a mesma
forma e manterem uma proporcionalidade entre suas medidas lineares.
Consideremos os cilindros ao lado.
10 cm
7 cm
Observe que a razão entre as alturas e entre os diâmetros são iguais.
7 = 3,5 = 0,7
10 5
5 cm
3,5
Disponível em: <www.lmc.ep.usp.br>.
Acesso em: 28 set. 2012.
Como a razão entre as medidas lineares são iguais e os cilindros têm a mesma forma, eles são
semelhantes.
Através do teorema de Thales ou da semelhança de triângulos, a proporcionalidade foi um dos
conceitos geométricos mais úteis desde a antiguidade.
Usando semelhança de triângulos, Thales de Mileto causou grande admiração no Egito ao calcular a
altura de uma pirâmide.
THALES E A PIRÂMIDE DE QUÉOPS
Por volta do ano 600 a.C., Thales de Mileto, um dos sete sábios
da antiguidade, surpreendeu o faraó Amasis por ter-se oferecido
para determinar a altura da pirâmide de Quéops.
Para demonstrar o seu método, Thales procedeu do seguinte
modo: foi até a extremidade da sombra projetada pela grande
pirâmide e cravou seu bastão no solo bem na vertical. A altura da
pirâmide e sua sombra são os lados de um triângulo retângulo, e
isso também acontece com o bastão e a sua sombra.
A grande pirâmide
Co
mp
da rimen
bas to
e
Bastão
H
H
=
b+s
c
d
⇒ H = (b + s) . c
d
c
b
s
d
Por semelhança de triângulos, Tales deduziu a relação H = (b + s) . c , que permite calcular a altura H
d
da pirâmide, conhecendo-se as medidas de b (metade da base da pirâmide), s (comprimento da sombra da
pirâmide), c (altura do bastão) e d (comprimento da sombra do bastão).
Thales tinha consciência de que o método que acabara de utilizar era geral e podia ser empregado em
muitas outras situações.
Matemática - Trigonometria
130
Semelhança
Portanto, para medir distâncias inacessíveis, podemos aplicar a semelhança de triângulos, como na
determinação da altura de prédios, árvores, torres, etc., usando como referência suas sombras.
Saiba mais
THALES DE MILETO
Disponível em: <www.iep.utm.edu>. Acesso em: 28 dez. 2012.
Thales de Mileto nasceu em torno de 624 a.C. em Mileto, Ásia Menor (agora Turquia), e morreu em torno
de 547 a.C. também em Mileto. É descrito em algumas lendas como homem de negócios, mercador de sal,
defensor do celibato ou estadista da visão, mas a verdade é que pouco se sabe sobre sua vida. As obras
de Tales não conseguiram sobreviver até nossos dias, mas, com base em tradições, pode-se reconstruir
algumas ideias.
Viajando muito pelos centros antigos de conhecimento
deve ter obtido informações sobre Astronomia e Matemática
aprendendo Geometria no Egito. Na Babilônia, sob o
governo de Nabucodonosor II, entrou em contato com as
primeiras tabelas e instrumentos astronômicos e diz-se que
em 585 a.C. conseguiu predizer o eclipse solar que ocorreria
neste ano, assombrando seus contemporâneos e é nesta
data que se apoiam para indicar aproximadamente o ano
em que nasceu, pois na época deveria contar com quarenta
anos, mais ou menos. Calcula-se que tenha morrido com 78
anos de idade.
Thales é considerado o primeiro filósofo e o primeiro dos
sete sábios, discípulo dos egípcios e caldeus, e recebe o
título comumente de “primeiro matemático’’ verdadeiro,
tentando organizar a Geometria de forma dedutiva. Acreditase que durante sua viagem à Babilônia estudou o resultado
que chega até nós como “Teorema de Thales”. A ele também
se devem outros quatro teoremas fundamentais: “um circulo
é bissectado por um diâmetro’’, “os ângulos da base de
um triângulo isósceles são iguais”, “os pares de ângulos
opostos formados por duas retas que se cortam são iguais”,
e “se dois triângulos são tais que dois ângulos e um lado são
iguais respectivamente a dois ângulos e um lado do outro,
então, eles são congruentes”.
Thales foi mestre de um grupo de seguidores de suas ideias, chamado “Escola Jániá’’ e foi o primeiro
homem da História a quem se atribuem descobertas matemáticas especificas e, como disse Aristóteles, “para
Thales a questão primordial não era o que sabemos, mas como sabemos’’.
Disponível em: <www.somatematica.com.br>. Acesso em: 28 set. 2012.
1.1 Semelhanças de triângulos
Vamos analisar a seguinte situação-problema.
A sombra de uma torre vertical, projetada pelo Sol sobre um chão plano, mede 8 m. Nesse mesmo
instante, a sombra de um bastão vertical de 0,8 m de altura mede 0,4 m. Qual é a altura dessa torre?
Problemas como esse poderão ser resolvidos com a aplicação da semelhança de triângulos.
Definição:
Dois triângulos são semelhantes se, e somente se, possuem os três ângulos ordenadamente congruentes
e os lados homólogos (Homo = mesmo, logos = lugar) proporcionais.
Matemática - Trigonometria
131
Semelhança
Consideramos os triângulos ABC e DEF:
A
D
b
c
e
f
B
a
C
E
d
F
Â≡D
a b c
B ≡ E e = = = K (Constante ou razão de
d e f
proporcionalidade)
C≡F
∆ABC ∼ ∆DEF ⇔
Busca
Congruência (≡)
Semelhança (∼)
1.2 Casos de semelhança
1o caso: AA (ângulo, ângulo)
Dois triângulos são semelhantes se possuem dois ângulos ordenadamente congruentes.
A
D
c
b
a
B
C
 ≡ D ∆ABC ∼ ∆DEF
B ≡E
e
f
E
d
F
2o caso: LAL (lado, ângulo, lado)
Dois triângulos são semelhantes se possuem dois lados proporcionais aos homólogos de outro e o
ângulo compreendido entre esses lados são congruentes.
A
D
c
B
a
b
C
f
E
d
c = b =K
∆ABC ∼ ∆DEF
f e
Â≡D
e
F
3o caso: LLL (lado, lado, lado)
Dois triângulos são semelhantes se possuem lados homólogos proporcionais.
A
b
D
C
c
a
B
f
E
d
e
F
a b c
= = = K ⇒ ∆ABC ∼ ∆DEF
d e f
Vamos voltar ao problema proposto na introdução.
Façamos um modelo matemático da situação apresentada.
H
(Torre)
Raios
Solares
0,8 m
(Bastão)
8 m (Sombra)
Raios
Solares
0,4 m (Sombra)
Matemática - Trigonometria
132
Semelhança
Considerando que a torre e o bastão formam um ângulo reto com o plano horizontal, pelo caso AA
temos dois triângulos semelhantes. Fazendo a razão entre as alturas e as sombras temos: H = 8
0,8 0,4
Dividindo os denominadores por 0,4, fica:
H = 8 → usando a propriedade fundamental das proporções.
2
1
H = 16 m
Portanto, a altura da torre é de 16 metros.
1.3 Relações métricas no triângulo retângulo
Vamos relembrar os elementos do triângulo retângulo a seguir:
BÂC = 90o, portanto, o ∆ABC é retângulo.
A
BC = a : hipotenusa (lado oposto ao ângulo reto).
c
b
AC = b : cateto.
h
AB = c : cateto.
n
m
AD = h : altura relativa à hipotenusa.
B
D
C
BD = n : projeção ortogonal do cateto c sobre a hipotenusa.
a
DC = m : projeção ortogonal do cateto b sobre a hipotenusa.
Podemos relacionar esses elementos através da semelhança entre os triângulos.
Observe o triângulo retângulo a seguir:
A
β
B
α
A soma dos ângulos internos do ∆ABC é 180º, logo:
 + B + C = 180o
90º + α + β = 180o
α + β = 90o
α
β
D
C
Veja que os ângulos α e β devem ser agudos já que a soma entre eles resulta em 90o . Quando a soma
de dois ângulos resulta em 90o, eles serão ângulos complementares.
Portanto, α é o complemento de β, ou β é o complemento de α.
Ao projetarmos a altura relativa à hipotenusa, obtemos os triângulos BDA e ADC, semelhantes entre
si e semelhantes ao triângulo ABC pelo caso AA.
A
A
c
B
α
b
a
c
β
C
β h
αn
B
D
A
α
h
D
b
m
β
C
Relações métricas
∆ABC ∼ ∆ABD:
BC = AC ⇒ a = b ⇒
c h
AB
AD
a.h=b.c
O produto entre a hipotenusa e a sua altura relativa é igual ao produto dos catetos.
AB = BC ⇒ c = a ⇒
n c
BD AB
c2 = a . n
∆ABC ∼ ∆ADC:
AC = BC ⇒ b = a ⇒
b2 = a . m
b
m
CD AC
O cateto ao quadrado é igual ao produto da hipotenusa pela projeção ortogonal desse cateto.
Matemática - Trigonometria
133
Semelhança
∆ABD ∼ ∆ADC:
AD = BD ⇒ h = n ⇒
m h
CD AD
h2 = m . n
A altura relativa à hipotenusa ao quadrado é igual ao produto entre as projeções ortogonais dos catetos.
Somando membro a membro as relações b2 = a . m e c2 = a . n, fica:
2
b2 + c2 = am + an
+ b 2 = a . m ⇒ 2 2 a(m + n) ⇒
b +c =
c =a.n
a
A soma dos quadrados dos catetos
é igual ao quadrado da hipotenusa.
Esta relação é conhecida como
Teorema de Pitágoras.
b2 + c2 = a2
Pitágoras de Samos foi um filósofo e matemático grego
que nasceu em Samos entre cerca de 571 a.C. e 570 a.C.
e morreu em Metaponto entre cerca de 497 a.C. ou 496
a.C. A sua biografia está envolta em lendas.
Imagem disponível em: <http://mathsmusings.blogspot.com.br>. Acesso em: 28 out. 2012.
Exemplo 1
Determine o valor de x, y, z e w no triângulo ao lado.
Para obter o valor de x, apliquemos o Teorema de Pitágoras:
x
z
a2 = b2 + c2 ⇒ 52 = 42 + x2 ⇒ 25 -16 = x2
x2 = 9 ⇒
4
y
w
5
x=3
Para obter y (altura relativa), vamos usar a relação a . h = b . c:
5 . y = 3 . 4 ⇒ y = 12 ⇒ y = 2,4
5
Como z e w são as projeções ortogonais dos catetos, vamos usar as relações b2 = a . m e c2 = a . n:
42 = 5 . w ⇒ 16 = w ⇒
5
z = 1,8
32 = 5 . z ⇒ 9 = z ⇒
5
w = 3,2
ou
z + 3,2 = 5 ⇒ z = 1,8
Saiba mais
MANIA DE PITÁGORAS
Elisha Scott Loomis, professor de Matemática em Cleveland, Ohio (Estados Unidos), era realmente um
apaixonado pelo Teorema de Pitágoras. Durante 20 anos, de 1907 a 1927, colecionou demonstrações desse
teorema, agrupou-as e as organizou num livro, ao qual chamou The Pythagorean Proposition (A Proposição
de Pitágoras). A primeira edição, em 1927, continha 230 demonstrações. Na segunda edição, publicada
em 1940, esse número foi aumentado para 370 demonstrações. Depois do falecimento do autor, o livro foi
reimpresso, em 1968 e 1972, pelo National Council of Teachers of Mathematics daquele país.
O Professor Loomis classifica as demonstrações do teorema de Pitágoras em basicamente dois tipos:
provas “algébricas” (baseadas nas relações métricas nos triângulos retângulos) e provas “geométricas”
(baseadas em comparações de áreas). Ele se dá ao trabalho de observar que não é possível provar o
teorema de Pitágoras com argumentos trigonométricos, porque a igualdade fundamental da Trigonometria,
cos2 x + sen2 x = 1, já é um caso particular daquele teorema.
Como sabemos, o enunciado do teorema de Pitágoras é o seguinte: “A área do quadrado cujo lado é a
hipotenusa de um triângulo retângulo é igual à soma das áreas dos quadrados que têm como lados cada
um dos catetos”. Se a, b são as medidas dos catetos e c é a medida da hipotenusa, o enunciado equivale a
afirmar que a2 + b2 = c2.
Matemática - Trigonometria
134
Semelhança
Documentos históricos mostram que os egípcios e os babilônios, muito antes dos gregos, conheciam
casos particulares desse teorema, expressos em relações como:
32 + 42 = 52 e 12 + 3
4
2
= 1
1 2
.
4
O fato de o triângulo de lados 3, 4 e 5 ser retângulo foi (e ainda é) útil aos agrimensores. Há também um
manuscrito chinês, datado de mais de mil anos antes de Cristo, em que se encontra a seguinte afirmação:
“Tome o quadrado do primeiro lado e o quadrado do segundo e some-os; a raiz quadrada dessa soma é a
hipotenusa”. Outros documentos antigos mostram que, na Índia, bem antes da era Cristã, sabia-se que os
triângulos de lados 3, 4, 5, ou 5, 12, 13, ou 12, 35, 37 eram retângulos.
O que parece certo, todavia, é que nenhum desses povos sabia demonstrar o teorema. Tudo indica que
Pitágoras foi o primeiro a prová-lo. (Ou alguém da sua Escola o fez, o que dá no mesmo, pois o conhecimento
científico, naquele grupo, era propriedade comum.)
A mais bela prova
Qual foi a demonstração dada por Pitágoras? Não se sabe ao certo, pois ele não deixou trabalhos escritos.
A maioria dos historiadores acredita que foi uma demonstração do tipo “geométrico”, isto é, baseada na
comparação de áreas. Não foi a que se encontra nos “Elementos” de Euclides, e que é, ainda hoje, muito
encontrada nos livros de Geometria, pois tal demonstração parece ter sido concebida pelo próprio Euclides.
A demonstração de Pitágoras poderia ter decorrido destas figuras:
a
b
c
c
a
b
a
b
b
c
a
Do quadrado que tem a + b como lado, retiremos 4 triângulos iguais ao dado. Se fizermos isso como na
figura à esquerda, obteremos um quadrado de lado c. Mas se a mesma operação for feita como na figura
à direita, restarão dois quadrados, de lados a e b respectivamente. Logo, a área do quadrado de lado c é a
soma das áreas dos quadrados cujos lados medem a e b.
James Abram Garfield, presidente dos Estados Unidos durante apenas 4 meses (pois foi assassinado em
1881), era também general e gostava de Matemática. Ele deu uma prova do teorema de Pitágoras baseada
na figura a seguir.
b
c
a
c
a
b
A área do trapézio com bases a, b e altura a + b é igual à semissoma das bases vezes a altura. Por outro
lado, a mesma área é também igual à soma das áreas de 3 triângulos:
a + b (a + b) = a2 + ab + b2 = ab + c2 , implicando a2 + b2 = c2.
2
2
2
2
Essa é, provavelmente, a mais bela demonstração do teorema de Pitágoras. Entretanto, no livro de Loomis,
ela aparece sem maior destaque, como variante de uma das provas dadas, não sendo sequer contada entre
as 370 numeradas.
Baseado no artigo Mania de Pitágoras. Euclides Rosa, RPM 02. (Adaptado)
1
Uma demonstração é conhecida como a prova mais
curta. Baseando-se na semelhança entre os triângulos da figura
ao lado, tente provar o Teorema de Pitágoras.
a
b
m
n
c
Matemática - Trigonometria
135
Semelhança
4
Para saber mais sobre Semelhança de
triângulos, acesse:
• <http://www6.ufrgs.br/espmat/geonoplano/
conteudo32.html>.
• <http://www6.ufrgs.br/espmat/disciplinas/
geotri/modulo3/problema_triggeo.html>.
(FUVEST) No triângulo acutângulo ABC, a base
AB mede 4 cm e a altura relativa a essa base
também mede 4 cm. MNPQ é um retângulo
cujos vértices M e N pertencem ao lado AB, P
pertence ao lado BC e Q ao lado AC.
Determine o perímetro do retângulo MNPQ
em cm.
C
Exercícios de sala
Q
2
Na figura, determine o valor dos elementos a,
b, c e d.
A M
P
N
B
B
D
a
c
b
C
3
24
7
A
(UNICAMP) Uma rampa de inclinação constante,
como a que dá acesso ao Palácio do Planalto
em Brasília, tem 4 metros de altura na sua
parte mais alta. Uma pessoa, tendo começado
a subi-la, nota que, após caminhar 12,3 metros
sobre a rampa, está a 1,5 metro de altura em
relação ao solo.
a) Faça uma figura ilustrativa da situação
descrita.
b) Calcule quantos metros a pessoa ainda
deve caminhar para atingir o ponto mais alto da
rampa.
5
(UEL-ADAPTADO) Para medir a altura de
um edifício, um engenheiro utilizou o seguinte
procedimento: mediu a sombra do prédio,
obtendo 10,0 metros. Em seguida, mediu sua
própria sombra que resultou em 0,5 metros.
Sabendo que sua altura é de 1,8 metro, ele
pôde calcular a altura do prédio.
Determine a altura desse prédio em metros.
Matemática - Trigonometria
136
Semelhança
6
(UFG-ADAPTADO) Uma fonte luminosa a
25 cm do centro de uma esfera projeta sobre
uma parede uma sombra circular de 28 cm de
diâmetro, conforme figura a seguir.
Exercícios propostos
8
7 cm
Fonte
luminosa
25 cm
28 cm
d
(FAAP-ADAPTADO) Um crítico de arte, olha,
através de uma câmara escura que tem 50 cm
de comprimento, para um quadro pendurado de
3 metros de altura, cuja base está a 1,20 metros
acima do solo, conforme a figura a seguir:
Sabendo que o raio da esfera mede 7 cm,
qual a medida, em cm, da distância (d) do
centro da esfera até a parede?
15 cm
3m
x
1,20 m
50 cm
Sabendo-se que o quadro fornece uma
imagem de 15 cm. A distância “x” da câmara
ao quadro (em metros) é:
a) 15
b) 3
c) 8
d) 12
e) 10
7
(FUVEST-ADAPTADO) Um banco de altura
regulável, cujo assento tem forma retangular, de
comprimento 40 cm, apoia-se sobre duas barras
iguais, de comprimento 60 cm (ver figura 1). Cada
barra tem três furos, e o ajuste da altura do banco
é feito colocando-se o parafuso nos primeiros, ou
nos segundos, ou nos terceiros furos das barras
(visão lateral do banco, na figura 2).
40 cm
40 cm
25 cm
60 cm
5 cm
5 cm
25 cm
Figura 1
Figura 2
9
(UFMG) Em determinada hora do dia, o sol projeta
a sombra de um poste de iluminação sobre o piso
plano de uma quadra de vôlei. Neste instante, a
sombra dele mede 16 m. Simultaneamente, um
poste de 2,7 m, que sustenta a rede, tem sua
sombra projetada sobre a mesma quadra.Neste
momento, essa sombra mede 4,8 m.
A altura do poste de iluminação é de:
a) 8,0 m.
b) 8,5 m.
c) 9,0 m.
d) 7,5 m.
10 (VUNESP) A sombra de um prédio, num terreno
plano, numa determinada hora do dia, mede
15 m. Nesse mesmo instante, próximo ao prédio,
a sombra de um poste de altura 5 m mede 3 m.
Sol
Determine a menor altura que pode ser obtida.
prédio
poste
5
15
3
A altura do prédio, em metros, é:
a) 25. b) 29.
c) 30.
d) 45.
e) 75.
Matemática - Trigonometria
137
Semelhança
11 (UNIRIO) Numa cidade do interior, à noite,
surgiu um objeto voador não identificado, em
forma de disco, que estacionou a 50 m do solo,
aproximadamente. Um helicóptero do exército,
situado a aproximadamente 30 m acima do
objeto, iluminou-o com um holofote, conforme
mostra a figura a seguir. Sendo assim, pode-se
afirmar que o raio do disco voador mede, em
metros, aproximadamente:
48 m
N
16 m
50m
sombra
16m
b) 3,5
c) 4,0
d) 4,5
e) 5,0
12 (VUNESP) Um observador situado num ponto
O, localizado na margem de um rio, precisa
determinar sua distância até um ponto P,
localizado na outra margem, sem atravessar
o rio. Para isso marca, com estacas, outros
pontos do lado da margem em que se encontra,
de tal forma que P, O e B estão alinhados entre
si e P, A e C também. Além disso, OA é paralelo
a BC, OA = 25 m, BC = 40 m e OB = 30 m,
conforme a figura.
A
12 m
rio
B
r
14 (FUVEST) Um lateral L faz um lançamento
para um atacante A, situado 32 m à sua frente
em uma linha paralela à lateral do campo de
futebol. A bola, entretanto, segue uma trajetória
retilínea, mas não paralela à lateral e, quando
passa pela linha de meio do campo, está a uma
distância de 12 m da linha que une o lateral
ao atacante. Sabendo-se que a linha de meio
do campo está à mesma distância dos dois
jogadores, a distância mínima que o atacante
terá que percorrer para encontrar a trajetória da
bola será de:
P
O
Q
A distância do chão aos olhos do observador
é 1,8 m e o segmento PQ = 61,6 m.
O comprimento da parte do para-raios que o
observador não consegue avistar é:
a) 16 m.
c) 8 m.
e) 3 m.
b) 12 m .
d) 6 m.
30m
a) 3,0
M
P
32 m
A
L
C
A distância, em metros, do observador em
O até o ponto P, é:
a) 30
b) 35
c) 40
d) 45
e) 50
13 (UFF) Um prédio com a forma de um
paralelepípedo retângulo tem 48 m de altura.
No centro da cobertura desse prédio e
perpendicularmente a essa cobertura, está
instalado um para-raios. No ponto Q sobre
a reta r — que passa pelo centro da base do
prédio e é perpendicular ao segmento MN —
está um observador que avista somente uma
parte do para-raios (ver a figura a seguir).
a) 18,8 m.
b) 19,2 m.
c) 19,6 m.
d) 20 m.
e) 20,4 m.
15 (UEL) Após um tremor de terra, dois muros
paralelos em uma rua de uma cidade ficaram
ligeiramente abalados. Os moradores se
reuniram e decidiram escorar os muros
utilizando duas barras metálicas, como mostra
a figura a seguir. Sabendo que os muros têm
alturas de 9 m e 3 m, respectivamente, a que
altura do nível do chão as duas barras se
interceptam? Despreze a espessura das barras.
Matemática - Trigonometria
138
Semelhança
a)
b)
c)
d)
e)
1,50m
1,75m
2,00m
2,25m
2,50m
9m
3m
16 (UFSCAR) A hipotenusa do triângulo retângulo
ABC está localizada sobre a reta real, conforme
indica a figura.
B
A
-4
D
x
C
7
Se x > 0 e a medida da altura BD relativa
ao lado AC do triângulo ABC é 2 6 , então x é o
número real:
a) 2 3 .
b) 4.
c) 3 2 .
d) 5.
e) 3 3 .
17 (ENEM) A rampa de um hospital tem, na sua
parte mais elevada, uma altura de 2,2 metros.
Um paciente, ao caminhar sobre a rampa,
percebe que se deslocou 3,2 metros e alcançou
uma altura de 0,8 metro.
A distância, em metros, que o paciente
ainda deve caminhar para atingir o ponto mais
alto da rampa é
a) 1,16 metro.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.
Matemática - Trigonometria
139
Trigonometria
2. TRIGONOMETRIA
Texto e contexto
UM POUCO DA HISTÓRIA DA TRIGONOMETRIA
A origem da trigonometria é incerta. Entretanto, pode-se dizer que
o início do desenvolvimento da trigonometria se deu principalmente
devido aos problemas gerados pela Astronomia, Agrimensura e
Navegações, por volta do século IV ou V a.C., com os egípcios e os
babilônios. É possível encontrar problemas envolvendo a cotangente
no Papiro Rhind e também uma notável tábua de secantes na tábula
cuneiforme babilônica Plimpton 322.
Papiro Rhind, Museu de Londres.
O astrônomo Hiparco de Nicéia, ganhou o direito
Hiparco, em grego Hipparkhos, foi um
de ser chamado “o pai da Trigonometria” pois, na
astrônomo, construtor, cartógrafo e
segunda metade do século II a.C., fez um tratado
matemático grego da escola de Alexandria
nascido em 190 a.C. em Nicéia, na Bitínia,
em doze livros em que se ocupou da construção do
hoje Iznik, na Turquia.
que deve ter sido a primeira tabela trigonométrica,
Nascimento: 190 a.C., İznik
incluindo uma tábua de cordas. Evidentemente,
Falecimento: 120 a.C., Rodes
Hiparco fez esses cálculos para usá-los em seus
estudos de Astronomia. Hiparco foi uma figura de transição entre a astronomia babilônica e a obra de
Ptolomeu. As principais contribuições à Astronomia atribuídas a Hiparco se constituíram na organização de
dados empíricos derivados dos babilônios, bem como na elaboração de um catálogo estrelar, melhoramentos
em constantes astronômicas importantes — duração do mês e do ano, o tamanho da Lua, o ângulo de
inclinação da eclítica — e, finalmente, a descoberta da precessão dos equinócios.
Disponível em: <http://ecalculo.if.usp.br>. (Adaptado) Acesso em: 28 out. 2012.
2.1 Trigonometria no triângulo retângulo
2.1.1 Introdução
de proporcionalidade é o ponto de partida da trigonometria.
O conceito
Como vimos na unidade anterior, é da semelhança de triângulos que desenvolveremos métodos para
a medição de distâncias inacessíveis aos instrumentos mais comuns para medir comprimentos.
A palavra trigonometria é de origem grega e significa medida dos triângulos (tri = três, gonos = ângulos,
metron = medir). Há campos da matemática, como a geometria e a análise, que usam a trigonometria.
Atualmente, a trigonometria encontra aplicações na eletricidade, na acústica, na mecânica, na
engenharia civil, na topografia, na música, na astronomia e em outras áreas do conhecimento.
Exemplo concreto
Suponhamos que desejemos medir a altura de uma torre, como ilustrado na Figura 1.
Não tendo um instrumento para medir a altura da torre, podemos usar a semelhança de triângulos
retângulos e medidas de ângulos para obtermos essa altura.
Consideremos o modelo matemático (Figura 2):
Q
Figura 1
O
Observador
Q
Figura 2
P
O
P
Matemática - Trigonometria
140
Trigonometria
Suponhamos que o ângulo de visão do observador esteja no ponto O. Os
pontos P e Q (sendo o ponto Q o topo da torre) formam uma perpendicular com
o segmento de reta OP (OP é um segmento paralelo ao solo).
Utilizando um instrumento chamado teodolito, podemos medir o ângulo POQ.
Luneta capaz de girar
no plano horizontal e
vertical, com escalas
em que se pode ler o
ângulo de giro.
O ângulo de giro da luneta fornece o ângulo POQ. Se soubermos as medidas do segmento OP e do
ângulo POQ, podemos obter a medida inacessível do segmento PQ, através da semelhança de triângulos.
Podemos fazer a medição de uma figura em escala. Vamos supor que a distância do observador até
a torre seja de 100 m (segmento OP) e o ângulo POQ seja de 30º. Em uma folha, fazemos um desenho
arbitrário com o cateto O’P’ = 10 cm e, usando um transferidor, construímos o triângulo O’P’Q’. Com
uma régua, medimos o cateto PQ obtendo 5,8 cm.
Q
Q
h
O
30º
5,8 cm
P
100 m
30º
10 cm
O
P
O triângulo menor O’P’Q’ é semelhante ao original, pois tem os mesmos ângulos. Então, temos
h = 100 m ⇒ h = 58 m.
5,8 cm 10 cm
Assim o segmento PQ no mundo real mede aproximadamente 58 metros.
Para termos a altura da torre, basta somarmos a altura do observador aos 58 metros.
Nesse exemplo, observamos que são semelhantes os triângulos retângulos que têm um ângulo agudo em comum.
Por essa semelhança, podemos usar medidas arbitrárias para os lados do triângulo na certeza de que
a razão entre esses lados é a mesma que a no mundo real. Essas razões, que são denominadas de razões
trigonométricas, dependem apenas dos ângulos do triângulo e não das medidas dos lados como poderemos
constatar na unidade a seguir.
2.2 Razões trigonométricas
Dado um triângulo ABC, retângulo em A, em que o ângulo ABC é igual a α (0º < α < 90º), tracemos a
partir dos pontos C1, C2, C3, etc. da semirreta BC, perpendiculares A1C1, A2C2, A3C3, etc. à semirreta AB.
C
C1
B
A
B
α
A1
C2
A2
C3
A3
C
A
Os triângulos ABC, A1BC1, A2BC2, A3BC3, etc. são semelhantes por terem os mesmos ângulos. Então:
A1C1 = A2C2 = A3C3 = ...
BC1
BC2
BC3
I
Estas razões dependem apenas do ângulo α, e não dos comprimentos envolvidos.
Na relação I, fixando o ângulo α, a razão entre o cateto oposto a α e a hipotenusa são diretamente proporcionais.
Essa razão é denominada seno do ângulo α.
Busca
sen α =
A1C1
BC1
sen α = seno do ângulo α.
Matemática - Trigonometria
141
Trigonometria
Voltando aos triângulos semelhantes, vemos que as relações
A1B = A2B = A3B = ...
II
BC1
BC2
BC3
A1C1 = A2C2 = A3C3 = ...
III
A1B
A2B
A3B
também dependem apenas do ângulo α.
Na relação II, fixando o ângulo α, a razão entre o cateto adjacente a α e a hipotenusa são diretamente
proporcionais.
Busca
Essa razão é denominada cosseno do ângulo α.
cos α = cosseno do ângulo α.
cos α = A1B
BC1
Na relação III, fixando o ângulo α, a razão entre o cateto oposto a α e o cateto adjacente a α são
diretamente proporcionais.
Busca
Essa razão é denominada tangente do ângulo α.
tg α = tangente do ângulo α.
tg α = A1C1
A1B
Reforçamos que essas definições só fazem sentido devido à semelhança entre os triângulos retângulos,
em que é conhecida a medida do ângulo agudo α. Por esse fato, as razões são sempre as mesmas não
dependendo das medidas dos lados envolvidos.
Exemplo 1
Considere o triângulo ABC, reto em A.
Calcule:
a) sen α
b) cos α
c) tg α
C
26
x
A
24
α
B
Resolução:
Inicialmente, devemos obter a medida do lado AC, para isso, basta aplicar o Teorema de Pitágoras.
262 = 242 + x2
676 = 576 + x2
100 = x2 ⇒ x = 10
cateto oposto a α
hipotenusa
10
5
sen α =
=
26 13
a) sen α =
cateto adjacente a α
hipotenusa
24 12
cos α =
=
26 13
b) cos α =
cateto oposto a α
cateto adjacente a α
10
5
tg α =
=
24 12
c) tg α =
2.3 Tabela de razões trigonométricas
Vimos que as razões trigonométricas dependem apenas do ângulo α, e não das medidas dos lados do
triângulo. Portanto, podemos obter uma tabela de razões trigonométricas para ângulos agudos, os quais
variam de 1º a 89º, usando valores arbitrários nos triângulos semelhantes.
Se não tivermos uma tabela com esses valores, podemos usar uma calculadora que utilizam métodos
numéricos baseados nas séries de Taylor das funções trigonométricas.
A seguir, mostramos uma tabela para as principais razões trigonométricas.
Matemática - Trigonometria
142
Trigonometria
Ângulo
sen
cos
tg
46°
0,7193
0,6947
1,0355
1°
2°
3°
4°
5°
6°
7°
8°
9°
10°
11°
12°
13°
14°
15°
16°
17°
18°
19°
20°
21°
22°
23°
24°
25°
26°
27°
28°
29°
30°
31°
32°
33°
34°
35°
36°
37°
38°
39°
40°
41°
42°
43°
44°
45°
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3990
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
0,9998
0,9994
0,9986
0,9976
0,9962
0,9945
0,9925
0,9903
0,9877
0,9848
0,9816
0,9781
0,9744
0,9703
0,9659
0,9613
0,9563
0,9511
0,9455
0,9397
0,9336
0,9272
0,9205
0,9135
0,9063
0,8988
0,8910
0,8829
0,8746
0,8660
0,8572
0,8480
0,8387
0,8290
0,8192
0,8090
0,7986
0,7880
0,7771
0,7660
0,7547
0,7431
0,7314
0,7193
0,7071
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
47°
0,7314
0,6820
1,0724
48°
0,7431
0,6691
1,1106
49°
0,7547
0,6561
1,1504
50°
0,7660
0,6428
1,1918
51°
0,7771
0,6293
1,2349
52°
0,7880
0,6157
1,2799
53°
0,7986
0,6018
1,3270
54°
0,8090
0,5878
1,3764
55°
0,8192
0,5736
1,4281
56°
0,8290
0,5592
1,4826
57°
0,8387
0,5446
1,5399
58°
0,8480
0,5299
1,6003
59°
0,8572
0,5150
1,6643
60°
0,8660
0,5000
1,7321
61°
0,8746
0,4848
1,8040
62°
0,8829
0,4695
1,8807
63°
0,8910
0,4540
1,9626
64°
0,8988
0,4384
2,0503
65°
0,9063
0,4226
2,1445
66°
0,9135
0,4067
2,2460
67°
0,9205
0,3907
2,3559
68°
0,9272
0,3746
2,4751
69°
0,9336
0,3584
2,6051
70°
0,9397
0,3420
2,7475
71°
0,9455
0,3256
2,9042
72°
0,9511
0,3090
3,0777
73°
0,9563
0,2924
3,2709
74°
0,9613
0,2756
3,4874
75°
0,9659
0,2588
3,7321
76°
0,9703
0,2419
4,0108
77°
0,9744
0,2250
4,3315
78°
0,9781
0,2079
4,7046
79°
0,9816
0,1908
5,1446
80°
0,9848
0,1736
5,6713
81°
0,9877
0,1564
6,3138
82°
0,9903
0,1392
7,1154
83°
0,9925
0,1219
8,1443
84°
0,9945
0,1045
9,5144
85°
0,9962
0,0872
11,4301
86°
0,9976
0,0698
14,3007
87°
0,9986
0,0523
19,0811
88°
0,9994
0,0349
28,6363
89°
0,9998
0,0175
57,2900
Matemática - Trigonometria
143
Trigonometria
Exemplo 2
B
Neste triângulo, determine a medida dos catetos.
15
y
Resolução:
36º
Analisando essa figura, devemos utilizar as razões trigonométricas
A
x
C
para obtermos, pelo menos, um dos catetos.
Como foi dada a medida da hipotenusa, usaremos, em relação ao ângulo de 36º, a razão seno para
obter y ou a razão cosseno para obtermos x.
y
sen 36º =
⇒ y = 15 . sen 36º
15
Da tabela, temos que sen 36º ≅ 0,5878, então:
y = 15 . 0,5878 ⇒ y = 8,817
De forma análoga
cos 36º =
x
⇒ x = 15 . cos 36º
15
Da tabela, temos que cos 36º ≅ 0,8090, então:
x = 15 . 0,8090 ⇒ x = 12,135
Portanto, os catetos x e y medem, respectivamente, 12,135 e 8,817. Observamos que ao obtermos um
dos catetos, poderíamos ter obtido o outro cateto pelo Teorema de Pitágoras.
Exemplo 3
Uma rampa tem 10 m de comprimento, e sua parte mais alta está a 6 m do solo. Qual é o ângulo de
inclinação (de subida) dessa rampa?
Resolução:
Nossa meta é determinar o ângulo de subida θ.
Ao representar um modelo da rampa, obtém-se o ângulo θ, pela
razão seno.
6
sen θ =
⇒ sen θ = 0,6
10
10 m
6m
θ
Procurando na tabela o valor mais próximo de 0,6 para o seno, encontramos 0,6018, portanto
θ ≅ 37º.
2.4 Ângulos Notáveis
Existem alguns ângulos que podem ser obtidos algebricamente, e suas razões trigonométricas podem ser
determinadas com precisão, sem a necessidade de arredondamentos ou aproximações.
Devido a essas particularidades, esses ângulos são frequentes nos exercícios e, por esse motivo, faremos
um estudo mais detalhado de suas razões trigonométricas.
• Ângulo de 45º
Consideremos o triângulo retângulo isósceles ABC, com catetos de medida unitária.
B
a
45º
A
a 2
a
45º
C
AB = AC = a
BC = a 2 (Pitágoras)
 = 90º
B = C = 45º
Prezado leitor,
Agradecemos o interesse em nosso
material. Entretanto, essa é somente
uma amostra gratuita.
Caso haja interesse, todos os materiais
do Sistema de Ensino CNEC estão
disponíveis para aquisição através
de nossa loja virtual.
loja.cneceduca.com.br