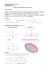Apostila - Completa 05/08/16

ÍNDICE
CONTEÚDO
Página
Análise Combinatória
Binômio de Newton
Cálculo Algébrico
Equação da Circunferência
Equações do 2° grau
Equações Exponenciais
Equações Irracionais
Equações Modulares
Equações Polinomiais
Estatística
Fatoração de Polinômios
171
191
58
370
62
101
64
120
396
209
65
Funções
Função afim (1° grau)
Função definida por mais de uma sentença
Função Exponencial
Função Logarítmica
Função quadrática (2° grau)
72
85
112
102
107
92
Geometria Analítica
Geometria Espacial de Posição
345
296
Geometria Espacial ( Prismas )
Geometria Plana
306
234
Logaritmos
Matemática Comercial
Matemática Financeira
Matrizes, Determinantes e Sistemas Lineares
Números Complexos
Números Inteiros
Números Irracionais
Números Naturais
Números Racionais
Números Reais
Poliedros
Polinômios
105
40
137
146
381
25
33
10
26
34
302
391
Probabilidade
Progressões
Provas ENEM
Sistemas de Numeração
Teoria dos Conjuntos
Teoria Elementar dos Números
198
125
400
21
4
10
Translação e Rotação de Eixos
Trigonometria
113
277
1
CALENDÁRIO 2016
ANOTAÇÕES
2
HORÁRIO DE ESTUDO
3
TEORIA DOS CONJUNTOS
CONCEITOS PRIMITIVOS
A idéia de conjunto é a mesma de coleção, conforme
mostram os exemplos a seguir.
Exemplos
a) Uma coleção de revistas é um conjunto. Cada
revista é um elemento desse conjunto.
b) Os alunos de sua sala de aula formam um
conjunto. Você é um elemento desse conjunto.
* Em geral, um conjunto é denotado por uma letra
maiúscula do alfabeto; e o elemento de um conjunto, é
denotado por uma letra minúscula do alfabeto.
REPRESENTAÇÃO DE UM CONJUNTO
Tabular (enumeração dos elementos)
Os elementos do conjunto são representados entre
chaves e separados por vírgulas.
Exemplo: Quando um elemento a pertence a um
conjunto B, indicamos:
aB
Quando um elemento c não pertence a um
conjunto B, indicamos:
cB
SUBCONJUNTOS
Um conjunto B é subconjunto de um conjunto A se,
e somente se, todo elemento de B pertence a A.
Notação: B  A ( B está contido em A )
A  B ( A contém B)
Exemplo
Se B = {1, 2, 3} e A = {1, 2, 3, 4, 5} , então B  A
ou A  B, já que todo elemento de B também é
elemento de A. Neste caso , B é subconjunto de A.
* Todo conjunto é subconjunto dele mesmo.
TIPOS ESPECIAIS DE CONJUNTOS
Exemplo:
A = {a, e, i, o, u}
Conjunto Unitário
Por uma propriedade
É o conjunto que possui um único elemento.
O conjunto é descrito por uma ou mais propriedades:
Exemplo: A = {x / x é uma vogal}
Por um diagrama de Venn-Euler (lê-se: "Ven-óiler")
A representação de um conjunto por uma diagrama de
Venn é aquela em que os elementos são simbolizados por
pontos interiores a uma região plana, delimitada por uma
linha fechada que não se entrelaça.
A
.a
.e
.i .o
.u
Conjunto Vazio
É todo conjunto que não tem elementos.
Representamos o conjunto vazio por { } ou  .
Conjunto Universo (U)
É um conjunto que contém todos os elementos do
contexto no qual estamos trabalhando e também
contém todos os conjuntos desse contexto. O conjunto
universo é representado por uma letra U.
Conjunto das Partes
RELAÇÃO DE PERTINÊNCIA
É a relação existente entre o elemento e o conjunto do
qual pertence.
Notação: Pertence  
Não pertence  
Dado um conjunto A qualquer, pode-se obter um
outro conjunto, cujos elementos são todos os possíveis
subconjuntos do conjunto A. Este conjunto,
representado por P(A), é denominado conjuntos das
partes de A.
Se um conjunto A qualquer possui N
elementos,então P(A) terá 2n elementos:
n(A) = n

n(P(A)) = 2n
4
Exercício resolvido
1. ( UEPI ) Seja o conjunto A = { 0, {0}, 1, {1}, {0, 1} }. É
correto afirmar que:
a) 0  A
b) { 0, 1 }  A
c) { 0, 1 }  A
d) Os elementos de A são 0 e 1
e) O número de subconjuntos de A é 22 = 4
União De Conjuntos
Dados os conjuntos A e B, define-se como união
dos conjuntos A e B ao conjunto representado
por A  B , formado por todos
pertencentes a A ou B, ou seja:
os
elementos
A  B  {x / x  A ou x B}
A
B
A B
Exemplo
Se A = {a, e, i} e B = {i, o, u} , temos que : AUB= {a,
e, i, o, u}
Exemplo
Obtenha o conjunto das partes do conjunto A= {2; 5; 6}:
n
3
P(A) = 2
P(A) = 2
Diferença De Conjuntos
Dados os conjuntos A e B, define-se como diferença
entre A e B (nesta ordem) ao conjunto representado
por A  B , formado por todos os elementos
pertencentes a A, mas que não pertencem a B, ou
seja :
A  B  {x / x  A , x B}
P(A) = 8 subconjuntos
A
B
São eles:
P(A) = {{2}; {5}; {6}; {2; 5}; {2; 6}; {5; 6}; {2; 5; 6}; { }}
A B
OPERAÇÕES COM CONJUNTOS
Interseção De Conjuntos
Dados os conjuntos A e B, define-se como conjunto
representado por A  B , formado por todos os elementos
pertencentes a A e B, simultaneamente, ou seja:
A  B  {x / x  A e x B}
A
B
A B
Exemplo: A = {x, y, z, w} e B= {a, b, x, y}, temos que :


A  B  z, w
Conjunto Complementar
O complemento do conjunto B contido no conjunto
B
A, denotado por C A , é a diferença entre os conjuntos
A e B, ou seja, é o conjunto de todos os elementos
que pertencem ao conjunto A e não pertencem ao
conjunto B.
CBA = A – B = {x / x  A e x  B}
Exemplo
Se A = {1, 2, 3, 8, 9,} e B = {2, 3, 4, 7, 9} , temos que :
A  B  2, 3, 9
A
CBA
B
5
Exemplo
Se A={1, 2, 3} e B={1, 2, 3, 4, 5}, então
NÚMERO DE ELEMENTOS DA UNIÃO DE
CONJUNTOS
CBA = B – A = {4, 5}
Com dois conjuntos
B
Observe que, no exemplo acima, não existe C A , pois para
n( A  B)  n( A)  n(B)  n( A  B)
B
existir C A ,B deveria estar contido em A.
A
Complementar em relação ao universo U
A B
Quando tivermos um conjunto universo U previamente
fixado, indicaremos o complementar de A em relação a
U simplesmente por
A
em vez de
A B
BA
CUA .
B
EXERCÍCIOS
AB
01.Se A = {2, 3, 6, 7, 8}, B = {1, 2, 3, 6, 8,9} e C = {0, 4, 6,
8}, então determine :
Exercício resolvido
a) A – (B ∩ C)
01. Em uma classe de 48 alunos, cada aluno
apresentou um trabalho sobre ecologia, tendo sido
indicado dois livros sobre esse assunto. O livro A foi
consultado por 26 alunos e o livro B por 28 alunos.
Pergunta-se:
a) Quantos alunos consultaram os dois livros?
b) (A – B) ∩ (C – A)
b) Quantos alunos consultaram apenas o livro A?
Resolução:
nA  B   os dois livros
n( A)  leram o livro A
n(B)  leram o livro B
n( A  B)  ?
c) (A ∩ C ) ( B – C )
a) solução
nA  B  n( A)  n(B)  n( A  B)
48  26  28  n( A  B)
n( A  B)  54  48  6
b) solução
26 alunos consultaram o livro A, porém 6 leram A e B,
logo os que leram apenas o livro a será:
26 - 6 = 20
6
Com três conjuntos
Para completar o conjunto A, devemos Ter:
300  (30  40  25 )  300  95  205
n( A  B  C)  n( A )  n(B)  n(C)  n( A  B)
 n( A  C)  n(B  C)  n( A  B  C)
Da mesma forma:
n(B)  135  250  135  115
n(C)  130  200  130  70
Respostas de:
a) 205 lêem apenas o jornal A
b) nA  B  n( A)  n(b)  n( A  B)
nA  B  300  250  70  480
Exercício resolvido
01. Desejando verificar qual o jornal preferido pela
população de uma cidade, foi apresentado o resultado de
uma pesquisa:
c) 205  30  115  150  500
d) 205  30  115  150  70  25  65  40  700
Pergunta-se:
Júlio César Oliveira
a) Quantas pessoas lêem apenas o jornal A?
b) Quantas pessoas lêem o jornal A ou B?
c) Quantas pessoas não lêem o jornal C?
d) Quantas pessoas foram consultadas?
Solução:
Vamos recorrer aos diagramas, observe:
U
A
B
30
205
115
40
25
65
EXERCÍCIOS
01. Uepi – PI
O número de subconjuntos de A = {1, 2, 3, 4}, exceto
o conjunto vazio é:
a) 15
b) 16
c) 25
d) 31
e) 63
02. PUC - MG
Se A = { {}, , {0} }, podemos afirmar que:
A) {}  A
B) {0}  A
C) {} = 
D) { {0},  }  A
E) { {0},  }  A
70
C
150
A  B  C  40 (ver tabela )
Na região complementar colocamos 150 (não leram
nenhum dos 3 jornais)
Como n( A  B)  70 e já foram colocados 40 leitores,
restam 30 para completar ( A  B) . Da mesma forma:
n( A  C)  40  65  40  25
n(B  C)  40  105  40  65
03. PUC – MG
Seja o conjunto A = { x, y, {x} } e as proposições:
(I) x  A
(II) {x}  A
(III) {x}  A
(IV)   A
A) Apenas (I) e (II) são verdadeiras
B) Apenas (II) e (IV) são verdadeiras
C) Todas as proposições são falsas
D) Todas as proposições são verdadeiras
7
04. UFLA
Se n é o número de subconjuntos não-vazios do conjunto
formado por cinco algarismos ímpares, então, n vale:
a) 63
b) 24
c) 31
d) 32
05. UFLA
Considere o conjunto A = {1, 2, 5, 8, {5}, {1, 2} }. Então a
alternativa correta é:
a) 1  A, 5  A, {5}  A, {1, 5}  A
b) 5  A, {5}  A, {5}  A, {{5}}  A
c) {1, 2}  A, {1, 2, 5}  A, 8  A, {8}  A
d) 1  A, 2  A, 8  A, {1, 2, 8}  A
e)   A,   A, {1, 2, 5}  A, {}  A
06.(PUC-MG) Em um grupo de n crianças, 80 receberam a
vacina de Sabin, 58 receberam a vacina contra sarampo,
36 receberam as duas vacinas e 15% não foram
vacinadas. O valor de n é:
a) 117
b) 120
c) 135
d) 143
e) 179
07. PUC – MG
Se A = { , 3, {3}, {2, 3} }, então:
A)
B)
C)
D)
E)
{2, 3}  A
2A
A
3A
{3}  A
08. UFOP – MG
Sejam os conjuntos A, B, e C, apresentados no diagrama
abaixo:
C
A
B
A) (A – B)  (A – C)
B) (A  B)  (A – B) = 
C) (A  B  C)  (A – B)
D) (A – C)  (A – B)
E) A  B  A
09. UFJF
10.(ESAF/AFC) Considere dois conjuntos, A e B, onde
A = {X1, X2, X3, X4} e B = {X1, X5, X6, X4}. Sabendose que a operação Ψ é definida por AΨB = (A–B)U(B–
A), então a expressão (AΨB)ΨB é dada por:
A) { X1, X5, X4}
B) { X1, X2}
C) { X1, X2, X3, X4}
D) {X4, X6, X5}
E) {X1, X6}
11. (Esaf - ANEEL) X e Y são dois conjuntos não
vazios. O conjunto X possui 64 subconjuntos. O
conjunto Y, por sua vez, possui 256 subconjuntos.
Sabe-se, também, que o conjunto Z  X  Y possui 2
elementos. Desse modo, conclui-se que o número de
elementos do conjunto P = Y – X é igual a:
A) 4
B) 6
C) 8
D) vazio
E) 1
12.(F.C.C.-SP) Se A  {{ }, 3, {3}, {2,3}} , então
A) {2, 3}  A
B) 2  A
C) { }  A
D) 3  A
E) {3}  A
13.(Cesgranrio) Em uma universidade são lidos dois
jornais A e B . Exatamente 80% dos alunos lêem o
jornal A ; e 60% , o jornal B .Sabendo que todo aluno é
leitor de pelo menos um dos jornais , o percentual de
alunos que lêem ambos é :
A) 48%
B) 140%
C) 60%
D) 80%
E) 40%
14.
(UFMG) Em uma escola , 5000 alunos
inscreveram-se para cursar as disciplinas A e B .
Desses alunos , 2825 matricularam-se na disciplina A e
1027 na disciplina B . por falta de condições
8
acadêmicas , 1324 alunos não puderam matricular-se em
nenhuma das disciplinas . O número de alunos
matriculados , simultaneamente , nas duas disciplinas, é :
A) 156
B) 176
C) 297
D) 1027
E) 1798
15.(UFMG) Em uma pesquisa de opinião, foram obtidos
estes dados:
- 40% dos entrevistados lêem o jornal A.
- 55% dos entrevistados lêem o jornal B.
- 35% dos entrevistados lêem o jornal C.
- 12% dos entrevistados lêem os jornais A e B.
- 15% dos entrevistados lêem os jornais A e C.
- 19% dos entrevistados lêem os jornais B e C.
- 7% dos entrevistados lêem os três jornais.
- 135 pessoas entrevistadas não lêem nenhum dos três
jornais.
Considerando-se esses dados, é CORRETO afirmar que
o número total de entrevistados foi
A) 1 200.
B) 1 500.
C) 1 250.
D) 1 350
16.(UESC) No diagrama de Venn, a região sombreada
representa o conjunto:
18. (FASA - 2015) Dos pacientes que tomam certo
medicamento, um quarto apresenta insônia ou
taquicardia como efeitos colaterais, sendo que os que
têm insônia são três vezes mais numerosos que
aqueles com taquicardia.
Se 5% dos pacientes apresentam ambos os
problemas,então a porcentagem que tem apenas
insônia é
01) 22,5%
02) 17,5%
03) 12%
04) 7%
05) 2,5%
GABARITO
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
A
E
D
C
B
B
E
B
A
C
B
E
E
B
B
01
A
02
01) C  (B – A)
02) C – (A  B  C)
03) C – (A  B)
04) C  B  A


05) C  B   A
17.(CFO/PM 2009)Sejam C, F e O os conjuntos tais que:
Os elementos do conjunto O são:
A) {3,4,6,8,9,10}
B) {1,2,9,10}
C) {3,4,6,8,9}
D) {9,10}
9
TEORIA ELEMENTAR DOS NÚMEROS
1. O CONJUNTO DOS NÚMEROS NATURAIS ( )
A idéia de número natural surgiu da necessidade de
contar objetos. Tal fato deu origem, inicialmente, aos
números 1, 2, 3, 4, 5, ...e, posteriormente, ao número zero.
Portanto, chamamos conjunto dos
naturais o conjunto
IN = {0, 1, 2, 3, 4, 5, ...}
números
n
an
a
   n ,b0
b
b
Aplicação:
Simplifique a expressão
34  62  50  28 34  (2  3)2  1 28 34  22  32.28



2
82  3 4
26.34
23  34
 

2 3
10
6
2 .3
6
4
 24  32
O conjunto dos números naturais não-nulos é
representado por IN*. Logo
DIVISÃO COM RESTO ( DIVISÃO EUCLIDIANA )
IN* = {1, 2, 3, 4, 5, ...}
Definida em IN, a divisão com resto, então sejam a
 IN e b  IN com b  0. Dividir a por b é encontrar
dois números q  IN e r  IN tais que:
Propriedades
P1. A soma de dois números naturais quaisquer é um
numero natural.
P2. O produto de dois números naturais quaisquer é um
numero natural.
POTENCIAÇÃO EM
Sendo an, n  IN, definimos a potenciação em IN da
seguinte maneira:
a0 = 1, a  0
a1 = a
I.
II.
III.
a
r
(b.q) + r = a
b
q
onde r < b
O número “a” é o dividendo, “b” é o divisor, “q” é o
quociente e “r” é o resto da divisão.
Observe que o resto “r” deve ser menor que o divisor
“b”.
Exemplo:
 Na divisão de 34 (dividendo) por 5 (divisor), o
quociente é 6 e o resto é 4.
porque 6 . 5 + 4 = 34 e 4 < 5.
an  a
a

a 
...
a , n  2


n fatores
Se an = b, o número a é denominado base, o número n
é o expoente e o resultado b é a potência.
Não se define 00.
Exemplos:
 53 = 5. 5. 5 =125
 271 = 27
 160 = 1
 27 = 2 . 2. 2. 2. 2. 2. 2 =128
A potenciação possui algumas
importantes, que apresentamos a seguir.
Se na divisão de a por b  0 encontramos r = 0,
concluímos que a = b . q, que temos uma divisão
exata e ainda, que a é divisível por b.
Dizemos, então, que a divisão de a por b é exata
ou, Podemos afirmar ainda, neste caso, que a é
múltiplo de b e que b é divisor de a.
a bq
propriedades
a é múltiplo de b
b é divisor de a
O maior resto possível de uma divisão exata será
sempre o Divisor menos uma unidade.
CRITÉRIOS DE DIVISIBILIDADE
a a a
m
am
a
n
n
m n
 a mn , com a  0
a   a
mn
a  b
n
São critérios que nos permite verificar se um
número é divisível por outro sem precisarmos efetuar
grandes divisões.
Por 2: Se termina em número par.
mn
Por 3: Se a soma dos algarismos é múltiplo de 3.
 a b
n
n
10
Por 15: Um número será divisível por 15 quando for, ao
mesmo tempo, divisível por 3 e por 5.
Por 4: Se seus dois últimos algarismos é 00 ou é um
múltiplo de 4.
Por 5: Se termina em 0 ou em 5.
Por 6: Se é divisível por 2 e por 3.
TEOREMA 1
Se dividirmos uma soma e cada uma das parcelas
pelo mesmo número, a soma dará o mesmo resto que
a soma dos restos das parcelas.
Exemplo:
Por 7: Separa-se o algarismo das unidades do restante,
então a diferença entre esse número e o dobro do
algarismo das unidades, tem que ser divisível por 7.
TEOREMA 2
Se dividirmos o produto de vários fatores e cada um
deles pelo mesmo número, o produto dará o mesmo
resto que o produto dos fatores.
Exemplo:
Por 8: Se seus três últimos algarismos é 000 ou formar
um número divisível por 8.
Por 9: Se a soma dos algarismos resultar em um
número divisível por 9.
Por 10: Se terminar em 0.
Por 11: A diferença entre as somas dos algarismos de
ordem ímpar e de ordem par resulta em um no divisível
por 11 os números iguais.
Dado um número a  IN, convencionaremos
representar por D(a) o conjunto dos divisores de a.
Para determinar todos os divisores de um número
natural não nulo é uma tarefa às vezes um pouco
complexa, principalmente para números maiores.
Iremos ver alguns processos de determinação mais
adiante.
Vejamos alguns exemplos simples em que basta
efetuar divisões elementares:
D(12) = {1, 2, 3, 4, 6, 12}
D(14) = {1, 2, 7 , 14)
D(17) = {1, 17}
NÚMEROS PRIMOS
Sendo n  IN tal que n  0 e n  1, dizemos que n
é um número:
a) Primo se possui apenas os divisores triviais (1
e n);
Por 12: Um número será divisível por 12 quando for, ao
mesmo tempo, divisível por 3 e por 4.
Pode-se afirmar que, se n é um número primo, ele
possui apenas 4 divisores inteiros distintos ( 1, – 1,
n, – n )
b) Composto se, além dos divisores triviais (1 e
n), possui pelo menos um divisor próprio.
11
Todo número composto pode ser decomposto em um
produto de números primos.
Ex.: 12 = 2 . 2 . 3
Exemplos:

2 tem apenas os divisores naturais 1 e 2, portanto 2
é primo.

23 tem apenas os divisores naturais 1 e 23, portanto
23 é primo.

10 tem os divisores 1, 2, 5 e 10, portanto 10 é
composto.
 Quando um número natural n, n > 1, não é primo
dizemos que ele é composto.
 Existem infinitos números primos.
Atenção:
1 não é um número primo, porque ele tem apenas um
divisor que é ele mesmo.
TEOREMA FUNDAMENTAL DA ARITMÉTICA
Todo número composto é igual a um produto de
números primos.
Quando escrevemos um número composto como um
produto de números primos, nós dizemos que o número
dado foi decomposto em seus fatores primos ou, ainda,
que o número foi fatorado.
COMO ACHAR OS DIVISORES DE UM NÚMERO
Na prática determinamos todos os divisores de
um número utilizando os seus fatores primos.
Vamos determinar, por exemplo, os divisores de
72:
1º Fatoramos o número 72.
Exemplo: Decompor em fatores primos os números 72,
540 e 1800.
Solução:
2º Traçamos uma linha e escrevemos o 1 no alto,
porque ele é divisor de qualquer número.
Regra: Coloque à direita do traço vertical o menor número
primo que divide o número dado. Continue procedendo do
mesmo modo com os quocientes obtidos, até encontrar o
quociente 1.
3º Multiplicamos sucessivamente cada fator primo
pelos divisores já obtidos e escrevemos esses produtos
ao lado de cada fator primo(desconsiderando os
valores repetidos).
Quando um número termina em zeros, podemos
cancelá-los e substituí-los pelo produto 2n x 5n, onde n é a
quantidade de zeros cortados. Observe:
12
4º Os divisores já obtidos não precisam ser repetidos.
Então o conjunto dos divisores de 72 é
Qual comprimento deve possuir cada uma das partes?
D(72) = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}
QUANTIDADE DE DIVISORES DE UM NÚMERO
Será que é possível descobrir quantos divisores tem
um número sem determinar antes quais são eles?
Isso é possível e é outra interessante aplicação da
fatoração.
Exemplo:
D(12) = {1, 2, 3, 4, 6, 12}
Vamos descobrir quantos são os divisores POSITIVOS
de 72 (já sabemos, contando, que são 24). O processo,
cuja demonstração utiliza noções elementares de cálculo
combinatório, é o seguinte:
1°) Fatoramos o número:
Para responder a estas pergunta, devem-se encontrar
os divisores de 12, 18 e 24?
72 = 23 x 32
2°) Tomamos apenas os expoentes da fatoração: 3 e 2.
3°) Adicionamos 1 (um) a cada expoente:
3 + 1 = 4;
2 + 1 = 3;
4°) Multiplicamos os resultados obtidos: 4 x 3 = 12
Conclusão: o número 72 possui 12 divisores (positivos
ou naturais), conforme já havíamos descoberto por mera
contagem.
Obs.: O número 72 possui 24 divisores INTEIROS.
REGRA GERAL DE DIVISIBILIDADE
Sejam a e b dois números, decompostos em seus
fatores primos. O número a será divisível por b se ele
contiver todos os fatores primos de b, com expoentes
maiores ou iguais.
D(18) = {1, 2, 3, 6, 18}
D(24) = {1, 2, 3, 4, 6, 8, 12, 24}
D(12) ∩ M(18) ∩ M(24) = {6}
Observe que 6 é o maior divisor comum entre 12, 18
e 24. Logo, cada tora deve possuir comprimento igual
a 6 m para que todas fiquem no maior tamanho
possível.
O máximo divisor comum entre dois ou mais
números naturais não nulos (números diferentes de
zero) é o maior número que é divisor ao mesmo tempo
de todos eles.
PROCESSOS PRÁTICOS PARA DETERMINAR O
MDC
I) Regra da decomposição simultânea
Escrevemos os números dados, separamos uns dos
outros por vírgulas, e colocamos um traço vertical ao
lado do último.
No outro lado do traço colocamos o menor dos
fatores primos que for divisor de todos os números de
uma só vês.
O mdc será a multiplicação dos fatores primos que
serão usados.
Exemplo
Exemplos:
MÁXIMO DIVISOR COMUM (MDC)
Analise a seguinte situação: deseja-se dividir 3 toras
de madeira, que medem respectivamente 12m, 18m e
24m, em partes iguais e com maior tamanho possível.
13
M(5) = {x  IN / x = 5n} = {5.0, 5.1, 5.2, 5.3, 5.4, ...)=
{ 0, 5, 10, 15, 20, ...}
M(7) = {x  IN / x = 7n} = {7.0, 7.1, 7.2, 7.3, 7.4, ...} =
{0, 7, 14, 21, 28, ...}
MÍNIMO MÚLTIPLO COMUM (MMC)
II) Divisões sucessivas
O cálculo do m.d.c. de dois números pelo processo das
divisões sucessivas obedece às seguintes regras:
1) Divide-se o maior número pelo menor.
2) Divide-se o número menor pelo primeiro resto.
3) Divide-se o primeiro resto pelo segundo resto, e assim
sucessivamente, até se obter uma divisão exata.
O mínimo múltiplo comum entre dois ou mais
números naturais não nulos(números diferente de
zero), é o menor número que é múltiplo de todos eles.
Analise a seguinte situação:
Três navios fazem o mesmo percurso entre dois
portos: o primeiro de 8 em 8 dias. O segundo de 12 em
12 dias e o terceiro de 16 em 16 dias.
Tendo saído juntos em certo dia do mês, após quantos
dias sairão juntos novamente?
Para responder a essa pergunta, devem-se
encontrar os múltiplos de 8, 12 e 16.
4) O último divisor é o m.d.c. procurado.
M(8) = {0, 8,16, 24, 32, 40,48, ....}
Exemplo: Calcular o m.d.c de 78 e 54.
M(12) = {0, 12, 24, 36, 48, 60, ...}
M(16) = {0, 16, 32, 48, 64, 80, .... }
M(8) ∩ M(12) ∩ M(16) = {48}
Logo, após 48 dias esses navios sairão juntos
novamente.
NÚMEROS PRIMOS ENTRE SI
Regra da decomposição simultânea
Dois números naturais a e b são ditos primos entre si
ou relativamente primos, se e somente se, o MDC(a, b) =
1.
Devemos saber que existe outras formas de calcular
o mmc, mas vamos nos ater apenas a decomposição
simultânea.
Exemplo: Verifique se 4 e 15 são primos entre si.
OBS: Esta regra difere da usada para o MDC, fique
atento as diferenças.
D(4) = {1, 2, 4) e D(15) = {1, 3, 5, 15}
Como o único divisor comum de 4 e 15 é 1 então 4 e
15 são primos entre si.
É claro que, sendo a e b primos entre si, MDC (a, b) =
1, já que 1 é o único divisor comum.
MÚLTIPLOS DE UM NÚMERO
Dado um número a IN, convencionaremos
representar por M (a) o conjunto dos múltiplos de a e por
D (a) o conjunto dos divisores de a.
Na prática, para obter os múltiplos de um número a  0,
basta multiplicar cada número natural não nulo por a.
Assim, sendo n uma variável natural não nula, podemos
escrever, por exemplo:
Exemplos:
MMC (18, 25, 30) = 720
1º: Escrevemos os números dados, separados por
vírgulas, e colocamos um traço vertical a direita dos
números dados.
2º: Abaixo de cada número divisível pelo fator primo
colocamos o resultado da divisão. Os números não
divisíveis pelo fator primo são repetidos.
3º: Continuamos a divisão até obtermos resto 1 para
todos os números.
14
Observe:
2°) Calculando o MDC
Fatores comuns: 2, 3, 5 com os menores expoentes:
3
2 . 3 . 5 = 120
3°) Calculando o MMC
Fatores comuns e não comuns: 2, 3, 5, 7
maiores expoentes: 25 . 32 . 52 . 7 = 50400
com os
Logo, MDC (1200, 480, 2520) = 120 e
MMC (1200, 480, 2520) = 50400
RELAÇÃO ENTRE MMC E MDC
MMC(a, b) x MDC(a, b) = a x b
Exemplo:
Propriedade: Observe, o mmc (10, 20, 100) , note que o
maior deles é múltiplo dos menores ao mesmo tempo,
logo o mmc entre eles vai ser 100.
Exemplos:
mmc (150, 50 ) = 150, pois 150 é múltiplo de 50 e dele
mesmo.
MDC (12, 20) = 4 e MMC (12, 20) = 60 observe que,
de fato, 4 x 60 = 12 x 20 = 240.
**CURIOSIDADES
Números PRIMOS GÊMEOS
São aqueles que tem diferença 2.
Ex.: 3 e 5, 11 e 13, 59 e 61, 137 e 139, etc.
mmc (4, 12, 24) = 24, pois 24 é múltiplo de 4, 12 e dele
mesmo.
Números PRIMOS EM SEGUNDO GRAU
CALCULANDO MDC E MMC PELA FATORAÇÃO
São os quadrados dos números primos e que tem
apenas três divisores naturais
O cálculo do MDC e do MMC de dois ou mais números
torna-se extremamente simples quando eles se
apresentam na forma fatorada, ou seja, decompostos em
fatores primos.
4 →1, 2, 4
9 →1, 3, 9
25 →1, 5, 25
Basta usar a seguinte regra geral:
MDC - tomam-se apenas os fatores comuns com os
menores expoentes.
MMC - tomam-se tanto os fatores comuns como os não
comuns com os maiores expoentes.
Exemplos:
Calcular o MDC e o MMC de 1200, 480 e 2520
1°) Fatoramos os três números.
1200 = 24 . 3 . 52
480 = 25 . 3 . 5
3
2
2520 = 2 . 3 . 5 . 7
Números AMIGOS OU AMIGÁVEIS
Se um é a soma dos divisores próprios do outro
(divisores próprios são todos divisores positivos do
números,
exceto o próprio número).
Ex.: 220 e 284
Números PERFEITOS
Um número é perfeito se o seu ciclo é de
comprimento 1(um) ou seja, é aquele cuja soma dos
seus divisores próprios é igual a si mesmo.
6→1+2+3=6
15
EXERCÍCIOS
01. (CESGRANRIO) Se a2 = 996, b3 = 997 e c4 = 998, então
12
(abc) vale:
A) 9912
21/2
B) 99
C) 9928
88
D) 99
99
E) 99
02 . ( PUC – MG ) Na divisão do número natural P pelo
número natural m o quociente é 13 e o resto, 5. O
menor valor de P é :
a) 44
b) 57
c) 83
d) 13
03. (UFMG) Na divisão de dois inteiros positivos, o
quociente é 16 e o resto é o maior possível. Se a soma do
dividendo e do divisor é 125, o resto é:
A) 4
B) 5
C) 6
D) 7
E) 8
04. ( PUC – MG ) Os números M e N são inteiros
positivos. Na divisão de M por N o quociente é 17 e o
resto, o maior possível. Se M – N = 407, o resto é:
a) 24
b) 23
c) 21
d) 18
e) 16
05. ( UFMG) Um número é da forma 3a7b. Sabendo-se
que este número é divisível por 25 e por 9, os
algarismos a e b são, respectivamente:
a) 0 e 8
b) 3 e 7
c) 6 e 5
d) 3 e 5
e) N.d.a
06. ( ETF – RJ ) Qual o menor número que se deve
subtrair de 21.316 para se obter um número que seja
divisível por 5 e por 9 ?
a) 31
b) 1
c) 30
d) 42
e) 41
07. (UNIMONTES PAES/2007 ) Se no número m498n, m
é o algarismo da dezena de milhar e n o algarismo das
unidades e m498n é divisível por 45, então m + n vale:
A) 6
B) 7
C) 8
D) 9
08. (UNIMONTES) Um número de seis algarismos é
formado pela repetição de uma classe, por exemplo:
256256 ou 678678. Qualquer número dessa forma é
sempre divisível por
A) 13, somente.
B) 1010.
C) 11, somente.
D) 1001
09. ( UFU – MG ) São dados os conjuntos :
 D = divisores positivos de 24
 M = múltiplos positivos de 3
 S= DM
 N = números de subconjuntos de S.
Portanto, N é igual a:
a) 64
b) 16
c) 32
d) 8
e) 4
10. ( Unimontes / PAES – 2004 ) Dados os conjuntos
A = { x  N / x = 3n, n  N } e B = { x  N–{0} /
18
=
x
n, n  N } , tem-se que AB é igual ao conjunto:
a) [3, 18 ]
b) Vazio
c) { x  N / 3 ≤ x ≤ 18 }
d) { 3, 18, 6, 9 }
11. ( Fuvest) O número de divisores positivos de 360
é:
a) 18
b) 22
c) 24
d) 26
e) 30
12. ( PUC – MG ) O número 2a . 3b tem oito divisores.
Se a.b = 3, então a + b é igual a:
a) 1
b) 2
c) 3
d) 4
e) 60
a
b
13. (UFMG) O número N = 2 . 3 . c divide o número
3600. Suponha que a, b e c sejam números inteiros,
positivos, c seja um número primo maior que 3 e N
com 16 divisores. Então, a + b – c será igual a:
a) - 2
b) - 1
c) 0
d) 1
e) 2
16
14. (UFMG) A soma de todos os divisores do número 105
é:
a) 15
b) 16
c) 120
d) 121
e) 192
15.( Unimontes – MG ) Entre os números 20 e 35,
quantos são os números que têm apenas quatro divisores
no conjunto dos números inteiros?
a) 4
b) 3
c) 5
d) 6
16. (UFMG) Sabe-se que o número 213 – 1 é primo. Seja n
= 217 – 16. No conjunto dos números naturais, o número
de divisores de n é
a) 5
b) 8
c) 6
d) 10
17. ( UFMG ) Sabe-se que os meses de janeiro, março,
maio, julho, agosto, outubro e dezembro têm 31 dias. O
dia 31 de março de um certo ano ocorreu numa quartafeira. Então, 15 de outubro do mesmo ano foi:
a) quinta-feira
b) terça-feira
c) quarta-feira
d) sexta-feira
18. ( UFMG ) Seja N o menor número inteiro pelo qual se
deve multiplicar 2520 para que o resultado seja um
quadrado de um número natural. Então, a soma dos
algarismos de N é:
a) 9
b) 7
c) 8
d) 10
19. ( FCC ) Sejam os números A = 23. 32. 5 e B = 2. 33.
52 . O MDC e o MMC entre A e B valem
respectivamente :
2
3
3
2
a) 2. 3 . 5 e 2 . 3 . 5
2
2
2
b) 2. 5 . 5 e 2 . 3 . 5
3
3
2
c) 2. 3. 5 e 2 . 3 . 5
2
2
2
d) 2 . 3 . 5 e 2. 3 . 5
e) 23. 32. 52 e 2. 33. 52
20. (UFU-MG) Se o máximo divisor comum entre os
números 144 e (30)P é 36, em que p é um inteiro
positivo, então o expoente p é igual a:
A) 1
B) 3
C) 4
D) 2
21. ( Fuvest ) Sejam a e b o máximo divisor comum
e o mínimo múltiplo comum de 360 e 300,
respectivamente. Então o produto a.b vale :
4
4
3
a) 2 . 3 . 5
5
2
b) 2 . 3 . 52
5
3
3
c) 2 . 3 . 5
6
3
2
d) 2 . 3 . 5
6
4
e) 2 . 3 . 52
22. (UFU) Os irmãos José e Maria visitam
regularmente seu avô Pedro. José visita-o a cada 8
dias e Maria a cada 6 dias, ambos, rigorosamente, sem
nunca falharem. Se José e Maria visitaram
simultaneamente o avô no primeiro dia do ano de 2004,
quantas vezes mais eles fizeram a visita simultânea até
o dia 31 de dezembro de 2006?
Obs.: Considere cada ano com 365 dias.
A) 48
B) 44
C) 46
D) 45
23. ( CFTPR ) Três vendedores encontraram-se num
certo dia na cidade de Medianeira - PR e jantaram
juntos. O primeiro vendedor visita esta cidade a cada 6
dias, o segundo a cada 8 dias e o terceiro a cada 5
dias. Estes três vendedores marcaram de jantar juntos
novamente no próximo encontro. Este, deverá
acontecer após:
a) 480 dias.
b) 120 dias.
c) 48 dias.
d) 80 dias.
e) 60 dias.
24. ( UEL – PR ) Em 1982 ocorreu uma conjunção
entre os planetas Júpiter e Saturno, o que significa que
podiam ser vistos bem próximos um do outro quando
avistados da Terra. Se Júpiter e Saturno dão uma volta
completa ao redor do Sol aproximadamente a cada 12
e 30 anos, respectivamente, em qual dos anos
seguintes ambos estiveram em conjunção no céu da
Terra?
a) 1840
b) 1852
c) 1864
d) 1922
e) 1960
25. ( UERJ ) Dois sinais luminosos fecham juntos num
determinado instante. Um deles permanece 10
segundos fechado e 40 segundos aberto, enquanto o
outro permanece 10 segundos fechado e 30 segundos
aberto.
O número mínimo de segundos necessários, a partir
daquele instante, para que os dois sinais voltem a
fechar juntos outra vez é de:
a) 150
b) 160
17
c) 190
d) 200
d) 4
e) 5
26. ( FGV – SP ) Seja x o maior número inteiro de 4
algarismos que é divisível por 13 e y o menor número
inteiro positivo de 4 algarismos que é divisível por 17. Se a
diferença entre x e y é igual a K, a soma dos algarismos
de K é:
a) 26
b) 27
c) 28
d) 29
e) 30
31. (CFO/PM 2007) No alto de uma torre de uma
emissora de televisão, duas luzes "piscam" com
freqüências diferentes. A primeira "pisca" 15 vezes por
minuto e a segunda "pisca" 10 vezes por minuto. Se
num certo instante as luzes piscam simultaneamente,
após quantos segundos elas voltarão a piscar
simultaneamente?
A. ( ) 12
B. ( ) 10
C. ( ) 20
D. ( ) 15
27. (UESB) Um paciente deve tomar três medicamentos
distintos, em intervalos de 2:00h, 2:30h e 3:20h
respectivamente. Se esse paciente tomou os três
medicamentos às 7:00h, então deverá voltar a tomar os
três, ao mesmo tempo, às
(01) 10:00h
(02) 12:50h
(03) 15:00h
(04) 16:30h
(05) 17:00h
28. (CFO/PM 2005) Duas pessoas, fazendo exercícios
diários, partem simultaneamente de um mesmo ponto e,
andando, contornam uma pista oval que circunda um
jardim. Uma dessas pessoas dá uma volta completa na
pista em 12 minutos. A outra, andando mais devagar, leva
20 minutos para completar a volta. Depois de quantos
minutos essas duas pessoas voltarão a se encontrar no
ponto de partida?
A. ( ) 30 minutos.
B. ( ) 45 minutos.
C. ( ) 60 minutos.
D. ( ) 240 minutos.
29.( UECE)
Dois relógios tocam uma música
periodicamente, um deles a cada 60 segundos e o outro a
cada 62 segundos. Se ambos tocaram, juntos, às 10
horas, que horas estarão marcando os relógios quando
voltarem a tocar juntos, pela primeira vez após as 10
horas ?
a) 10 horas e 31 minutos
b) 11 horas e 02 minutos
c) 13 horas e 30 minutos
d) 17 horas
30. (UPE-PE) Neto e Rebeca fazem diariamente uma
caminhada de duas horas em uma pista circular. Rebeca
gasta 18 minutos para completar uma volta, e Neto, 12
minutos para completar a volta. Se eles partem do mesmo
ponto P da pista e caminham em sentidos opostos, podese afirmar que o número de vezes que o casal se encontra
no ponto P é
a) 1
b) 2
c) 3
32. (UFTM) Márcia fabrica trufas de chocolate, que são
vendidas em embalagens com 5, 8 ou 12 unidades.
Renata, uma de suas vendedoras, possui em seu
estoque 793 trufas, que serão todas vendidas em
embalagens do mesmo tipo. Porém, ela ainda não
decidiu qual das três embalagens irá utilizar. Nessas
condições, a menor quantidade de trufas que Márcia
deverá acrescentar ao estoque de Renata de modo
que, independentemente do tipo de embalagem
utilizada, não sobre nenhuma trufa no estoque depois
da confecção das embalagens, é igual a
a) 7.
b) 11.
c) 23.
d) 39.
e) 47.
33. (UFMG) No sítio de Paulo, a colheita de laranjas
ficou entre 500 e 1500 unidades. Se essas laranjas
fossem colocadas em sacos com 50 unidades cada
um, sobrariam 12 laranjas e, se fossem colocadas em
sacos com 36 unidades cada um, também sobrariam
12 laranjas. Assim sendo, quantas laranjas sobrariam
se elas fossem colocadas em sacos com 35 unidades
cada um?
A) 4
B) 6
C) 7
D) 2
34. ( EEAer ) Três rolos de arame farpado têm,
respectivamente, 168 m, 264 m e 312 m. Deseja-se
cortá-los em partes de mesmo comprimento, de forma
que, cada parte, seja a maior possível. Qual o número
de partes obtidas e o comprimento, em metros de cada
parte?
a) 21 e 14
b) 23 e 16
c) 25 e 18
d) 31 e 24
35. ( FEI – SP ) Em uma sala retangular de piso plano
nas dimensões 8,80 m por 7,60 m deseja-se colocar
ladrilhos quadrados iguais, sem necessidade de
18
recortar nenhuma peça. A medida máxima do lado de
cada ladrilho é:
a) 10 cm
b) 20 cm
c) 30 cm
d) 40 cm
e) 50 cm
36. ( PUC / MG – 2001 ) Uma praça retangular, de 110 m
de comprimento por 66 m de largura é contornada por
fileiras de palmeiras igualmente espaçadas. A distância
entre uma palmeira e a seguinte é a mesma e a maior
possível. Se em cada vértice da praça existe uma
palmeira, o número total de palmeiras contornando a
praça é :
110
a) 16
b) 18
66
c) 22
d) 24
41. (FIP-2010) Observe a figura abaixo, que descreve
as dimensões oficiais possíveis para um campo de
futebol:
37. ( UFMG ) Sejam a, b e c números primos distintos,
em que a > b. O máximo divisor comum e o mínimo
múltiplo comum de m = a2.b.c2 e n = a.b2 são,
respectivamente, 21 e 1764. Pode-se afirmar que a + b
+c é:
a) 9
b) 10
c) 12
d) 42
e) 62
38. (UFU-MG) Se p é um número natural primo e a soma
de todos os divisores positivos de p2 é igual a 31, então p
é igual a:
a) 5
b) 7
c) 13
d) 3
39. (FIP-2009) Numa competição de arremesso de disco,
o vencedor conseguiu 61 m. O segundo colocado, 58m.
De quanto foi o lançamento do terceiro colocado,
sabendo-se que a diferença entre o seu lançamento e o
lançamento do segundo colocado foi duas vezes a
diferença entre o segundo colocado e o primeiro?
A) 56m
B) 52m
C) 54m
D) 50m
40. (FIP-2009) Suponha que uma pessoa esteja
percorrendo uma pista em forma do polígono ABCDEFGHI
da figura abaixo. Saindo do ponto A, no sentido horário, ao
caminhar, ela irá contando quantos lados já percorreu. Em
qual dos vértices (A, B, C, ...) ela estará quando disser
555.555.555.555.555?
Segundo o projeto, o comprimento do campo pode
variar de 90 a 120 metros, e a largura de 45 a 90
metros. Admitindo que o comprimento seja um múltiplo
de 10, e a largura seja um múltiplo de 5, de quantos
modos possíveis pode ser construído o campo?
A) 80
B) 60
C) 120
D) 40
42. (FIP-2010) Pensando em contribuir com uma
alimentação mais saudável para a sua família, um
professor da rede Pitágoras está planejando uma horta
em um espaço retangular de 1,56m por 84cm,
disponível em seu quintal. Ele inicia o preparo da horta
dividindo o comprimento e a largura do terreno em
partes iguais, todas de mesma medida inteira, quando
expressas em centímetros. Dessa maneira, esse
professor formou, na superfície do terreno, um
quadriculado composto por quadrados congruentes, de
modo que as medidas das arestas de cada quadrado
tivessem o maior valor possível. Sua intenção é plantar,
no centro de cada quadrado obtido, uma única muda.
Nessas condições, a quantidade máxima de mudas
que pode ser plantada é:
19
A) 480 passos
B) 240 passos
C) 120 passos
D) 80 passos
GABARITO
A) 91
B) 76
C) 120
D) 144
43. (FIP-2011) Um grupo de estudantes se preparava para
as provas do vestibular das FIPMoc. Ao estudar o assunto
CONJUNTOS, em Matemática, eles observaram que o
número de subconjuntos de um conjunto era dado por 2n.
Se P e Q são conjuntos que possuem um único elemento
em comum e se o número de subconjuntos de P é igual ao
dobro do número de subconjuntos de Q, então o número
de elementos do conjunto P união Q é o:
1) D
2) C
3) C
4) B
5) D
6) A
7) A
8) D
9) B
10) D
11) C
12) D
13) B
14) E
15) B
16) D
17) D
18) B
19) A
20) D
21) C
22) D
23) B
24) D
25) D
26) E
27) 5
28) C
29) A
30) C
31) A
32) E
33) D
34) D
35) D
36) A
37) C
38) A
39) B
40) A
41) D
42) A
43)B
44) C
45) B
A) triplo do número de elementos de P.
B) dobro do número de elementos de Q.
C) triplo do número de elementos de Q.
D) dobro do número de elementos de P.
44 .(FIP-2012) Os números primos são verdadeiras
estrelas da matemática - eles só podem ser divididos por
eles mesmos (com resultado igual a um) ou por um (com
resultado igual a ele mesmo), sem nenhuma outra
possibilidade de se conseguir um número inteiro. O mais
célebre desses números é o 2, mas o maior deles foi
descoberto no ano passado por Martin Nowak, professor
da Universidade de Harvard, nos Estados Unidos. O
25 964 951
número é dado pela notação 2
– 1 e tem mais de
sete milhões de dígitos, o equivalente ao número total de
letras publicadas em mais de 61 edições de Galileu.
Considere um número natural N, dado por N = 251 929 902 –
225 964 951.
A quantidade de divisores naturais do número N é:
A) 12 982 476
B) 25 964 952
C) 51 929 904
D) 103 859 804
45 .(FIP-2013) Numa prova de aquecimento, o atleta
Bruno Lins sai correndo e, após dar 200 passos, o atleta
UsainBolt parte em seu encalço. Enquanto Bolt dá 3
passos, Lins dá 11 passos; porém, 2 passos de Bolt
valem 9 de Lins. É correto afirmar que, para alcançar
Bruno Lins, UsainBolt deverá dar
20
SISTEMAS DE NUMERAÇÃO
A ORIGEM DO SISTEMA DE NUMERAÇÃO
Para entender como surgiram os números, é preciso
ter uma idéia de como o homem, desde a época mais
remota, vivia e quais eram suas necessidades. Naquele
tempo, o homem, para alimentar-se, caçava, pescava e
colhia frutos; para morar, usava cavernas; para defenderse, usava paus e pedras. Portanto o homem precisava
contar. Quantos peixes havia? Quantas espigas de milho?
Quantos dias faltavam para a caça de pássaros antes das
chuvas? Quantas ovelhas havia no rebanho? Essas
necessidades de sobrevivência levaram-no a fazer
comparações entre as “coisas” que tinham ou queriam
com os dedos das mãos. Segundo alguns autores, o
surgimento da primeira máquina de calcular deve-se às
contagens nos dedos das mãos.
NOSSO SISTEMA DE NUMERAÇÃO
O Brasil, assim como a maioria dos países, utiliza o
sistema de numeração indo-arábico, que é decimal. A
palavra “decimal” origina-se do latim decem, que significa
dez, ou seja, os agrupamentos são sempre feitos de dez
em dez. Por isso, é usualmente chamado de sistema
numérico decimal. A denominação indo-arábico deve-se
ao fato de seus símbolos e suas regras terem sido
inventados pela antiga civilização hindu e aperfeiçoados e
divulgados
pelos árabes. A seguir, as principais características desse
sistema:
1) Utiliza apenas 10 símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9,
com os quais é possível representar qualquer número.
Esses símbolos são chamados algarismos.
200 + 30 + 5 (princípio aditivo)
Ou seja,
2 ×100 + 3 ×10 + 5 ×1 (princípio multiplicativo)
No princípio aditivo, o número é obtido pela adição
dos valores posicionais.
No princípio multiplicativo, cada algarismo escrito
imediatamente à esquerda de um outro algarismo vale
dez vezes o valor posicional deste.
Assim, cada grupo de dez unidades forma uma
dezena. Cada grupo de dez dezenas forma uma
centena. Cada grupo de dez centenas forma um
milhar. Cada grupo de dez unidades de milhar
forma uma dezena de milhar. Cada grupo de dez
dezenas de milhar forma uma centena de milhar. E
assim por diante. Dessa forma, todo número pode ser
representado utilizando potências de dez. Este tipo de
representação do número é chamado de notação
exponencial.
BASES DIFERENTES DE 10
Quando se precisa contar uma grande quantidade
de coisas, separam-se os objetos em grupos, pois isto
facilita a contagem. Por exemplo, contar as dúzias de
ovos é uma forma de agrupar: agrupar de 12 em 12. Os
fabricantes agrupam um determinado número de
unidades em cada embalagem. Por exemplo: as
barrinhas de drops vêm com o mesmo número de
balas, as cartelas dos medicamentos vêm com o
mesmo número de comprimidos. Até a medição do
tempo é feita por meio de grupamentos de 60 em 60 –
sistema sexagesimal. Exemplo: Uma hora tem 60
minutos e um minuto tem 60 segundos. Dessa forma,
tem-se:
2) Tem base 10, ou seja, os agrupamentos são feitos de
dez em dez.
3) É um sistema posicional, isto é, um mesmo símbolo
representa valores diferentes dependendo da posição que
ocupa no numeral.
Exemplo: no número 32 524, o primeiro algarismo “2”
(contando a partir da direita) vale vinte unidades, enquanto
o segundo vale duas mil unidades.
4) Obedece aos princípios aditivo e multiplicativo.
O número 235, por exemplo, significa:
Portanto é possível usar qualquer número como
base para criar um sistema numérico posicional. Regra:
obtém-se o valor do número, multiplicando o valor
de cada algarismo pela base elevada à posição
ocupada por ele (a partir da posição zero),
somando-se todas as parcelas.
Outro sistema não decimal bastante utilizado é o
sistema binário – sistema numérico posicional de
21
base dois que usa apenas os algarismos “um” e “zero”. A
grande maioria dos componentes de circuitos elétricos
podem assumir apenas um dentre dois estados. Por
exemplo: interruptores ou transistores podem estar
fechados ou abertos; capacitores podem estar carregados
ou descarregados; lâmpadas podem estar acesas ou
apagadas. Foi estabelecido que um desses estados
representa o “um” (lâmpada acesa, por exemplo) e que o
outro representa o “zero” (lâmpada apagada, por
exemplo). O algarismo do sistema binário é chamado de
dígito binário, oriundo do inglês binary digit, cuja contração
produz bit. O bit é a menor unidade de dado (ou
informação) que pode ser armazenada em um
computador.
O processo de conversão das grandezas do mundo
real em quantidades expressas no sistema binário chamase “digitalização”.
O sistema binário funciona de modo parecido a um
interruptor, como mostra a Figura
MUDANÇA DE BASE
1° caso: Dado um número numa base não-decimal,
passá-lo para a base decimal.
Nesse caso, é só indicar o valor posicional de cada
algarismo, em seguida, efetuar as operações indicadas.
Exemplo
Escrever 1203(4) na base dez.
1203(4) =
2° caso: Dado um número na base decimal, passá-lo
para uma base não-decimal .
Como proceder para fazer o caminho inverso,ou
seja, escrever 99 na base 4? Vejamos
Se desejar representar, neste sistema numérico, o número
oito mediante um conjunto de lâmpadas, onde uma
lâmpada acesa representa o algarismo “1” e uma lâmpada
apagada o algarismo “0”, tem-se as 3 lâmpadas da
esquerda para direita apagadas e 1 acesa
a) Dividir o número 99 pela nova base, no caso 4, temse:
b) Dividir o quociente obtido (24) pela nova base (4).
Continuar dividindo cada novo quociente obtido pela
base, até que se obtenha quociente menos que a base.
Em seguida, destacar os restos encontrados e o último
quociente obtido:
1 000(dois) = 1×23 + 0×22 + 0×21 + 0×20 = 8
Já foi demonstrado como escrever um número em uma
determinada base para a base 10. Agora, será
demonstrado como fazer o processo inverso. A maneira
mais simples consiste em fazer divisões sucessivas pela
base. As divisões serão feitas com o número e com
cada um dos quocientes inteiros encontrados. O
processo termina quando o quociente for igual a zero.
Os restos das divisões, escritos na ordem inversa em
que aparecem, darão a representação do número na
base escolhida. Observe como fica transformando o
número oito na base 10 para a base 2.
c) Para a representação de 99 na base quatro, tomase, ordenadamente, o último quociente e os restos das
divisões, do último até o primeiro.
Assim, 99 = 1203(4)
22
MUDANÇA DA BASE 10 PARA HEXADECIMAL (base
16)
Os números binários sendo cada vez mais longos, foi
necessário introduzir uma nova base: a base
hexadecimal. A base hexadecimal consiste em contar
numa base 16, é por isso que, além dos 10 primeiros
números, decidiu-se acrescentar as 6 primeiras letras : 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Decimal
Hexa
Decimal
Hexa
0
0
8
8
1
1
9
9
2
2
10
A
3
3
11
B
4
4
12
C
5
5
13
D
6
6
14
E
7
7
15
F
82, parágrafo 3º da Constituição Mineira de ( 10101 )2
de setembro de 1989. Ao digitar o texto acima, o
digitador se distraiu e colocou o dia das duas datas na
base 2. Escrevendo esses dias na base 10,
encontramos respectivamente :
a) 28 e 21
b) 26 e 20
c) 24 e 30
d) 24 e 21
03.(F.C.Chagas) Num sistema de numeração de base
4, faz-se a contagem do seguinte modo: 1, 2, 3, 10, 11,
12, 13, 20, 21, 22, 23, 30...
O número 42 ( quarenta e dois ) no sistema de base 4
é composto de:
a) 4 algarismos iguais.
b) 3 algarismos iguais.
c) 2 algarismos iguais.
d) 3 algarismos distintos.
e) 2 algarismos distintos.
04.( Unimontes) A tábua da multiplicação abaixo está
incompleta.
Exemplo
Para mudar 1069 para a base 16, devemos realizar a
divisão de 1069 por 16.
Após realizar a divisão iremos substituir por letras os
restos ou o quociente, quando forem superiores a 9.
Então 1069 = 42D.
EXERCÍCIOS
01. (UNIMONTES) O numeral na base três, que
representa o número de pontos do quadro abaixo, é
a) 123.
b) 1203.
c) 1023.
d) 3203.
02.( PAES / UNIMONTES ) Em 1962, através da Lei
2615 de ( 11000 )2 de maio de 1962, foi criada a
Fundação Norte-Mineira de Ensino Superior ( FUNM ) de
cuja transformação resultou a Universidade Estadual de
Montes Claros ( UNIMONTES ), de acordo com o artigo
05.(F.G.V) Qualquer número pode ser representado na
base "2" como a soma de fatores que indicam
potências crescentes de 2, da direita para esquerda,
aparecendo o símbolo "1" se 2 elevado aquela
potência está presente na composição de número e o
símbolo "0" se 2 elevado aquela potência não está
presente na composição do número.
Por exemplo: O número 5 é representado por (101),
2
1
0
pois 5 = 1.(2 ) + 0.( 2 ) + 1.( 2 )
O número 9 pode ser representado por (1001), pois
9 = 1.( 23 ) + 0.( 22 ) + 0 .( 21 ) + 1.( 20 )
Utilizando os números a seguir, (10010)2 e (1010)2
representados na base "2", somando-os e
apresentando o resultado na base "2" teremos:
a) (11000)
b) (11100)
c) (11011)
d) (11101)
e) (11111)
23
06.(Escola Técnica Federal - RJ) Escrevendo o número
324 num sistema de base 3 obtemos:
a) 110000
b) 101110
c) 122010
d) 210010
e) 112110
07. ( PUC – MG ) Se A = 10023, B = 2214 e C = 10012, o
valor A + B – C, na base 6 é:
a) 114
b) 121
c) 141
d) 212
e) 221
08.( CEFET – MG ) Seja x = ( 1001) 2e
valor de ( x + y ) 16 é :
a) 5C
b) 5E
c) 46
d) 92
e) 125
y = ( 123 ) 8. O
caractere padronizado em uma tabela chamada de
ASCII. Veja o exemplo abaixo:
Quando o computador recebe o sinal elétrico acima, ele
reconhece a letra “e” minúscula.
De acordo com parte da tabela ASCII abaixo, o sinal
elétrico indicado corresponde ao símbolo:
a)
b)
c)
d)
e)
Y
Z
[
\
]
09.( UFLA – MG ) Dois números
a
e
b, são
representados em uma base x por 100 e 102,
respectivamente. O produto a.b é representado na base
5 por 344. A base x é:
a) 3
b) 2
c) 5
d) 7
e) 9
GABARITO
10.(UNIMONTES) No sistema de numeração em base 5, a
contagem é feita assim: 1, 2, 3, 4, 10, 11, 12, 13, 14, 20,
21, ... O número 69, na base 10, quando descrito em base
5, é um número formado por
A) 3 dígitos consecutivos.
B) 2 dígitos consecutivos.
C) 2 dígitos não consecutivos.
D) 3 dígitos não consecutivos.
11. (UNIMONTES) Um número de 3 dígitos tem, da
esquerda para a direita, os dígitos h, t e u, sendo h > u.
Quando o número com os dígitos em posição reversa é
subtraído do número original, o dígito da unidade da
diferença é 4. Então, os dois dígitos seguintes, da direita
para a esquerda, são
A) 9 e 5.
B) 5 e 4.
C) 5 e 9.
D) 4 e 5.
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
B
D
B
B
B
A
C
A
A
A
A
C
12. O computador trabalha convertendo pulsos elétricos
em números binários onde cada conjunto binário de oito
dígitos é chamado de BYTE e cada dígito desse número é
chamado de BIT. Cada BYTE pode ser convertido para o
sistema decimal e esse número corresponde a um
24
O CONJUNTO DOS NÚMEROS INTEIROS ( )
Lembrete:
1º: Zero é maior que qualquer número negativo.
O conjunto Z = {....-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5....}.
2º: Menos um é o maior número negativo.
Observe que este conjunto é formado por números
negativos, zero e números positivos. Vale lembrar que
zero é um número nulo ou neutro, não é negativo e nem
positivo.
No seu dia a dia você já dever ter deparado com números
inteiros; quando temos um crédito temos um número
positivo, um débito é um número negativo, temperaturas
acima de zero são positivas, abaixo de zero são negativas,
se você prestar atenção ao seu redor vai encontrar muitos
números negativo e positivos.
3º: Zero é menor que qualquer número positivo.
4º: Qualquer número positivo é maior que qualquer
número negativo.
NÚMEROS OPOSTOS OU SIMÉTRICOS
Observe na reta numérica que a distancia do -3 até o
zero é a mesma do +3 até o zero, estes números são
chamados de opostos ou simétricos.
Como subconjuntos de Z, destacamos:
Logo: - 3 é oposto ou simétrico do + 3.
a. o conjunto dos inteiros não negativos
POTENCIAÇÃO DE NÚMEROS INTEIROS
Z + = {0, + 1, +2, +3, +4, ...} = IN
b. o conjunto dos inteiros positivos
Z 
= {+1, +2, +3, +4, ... } = IN*
c. o conjunto dos inteiros não positivos
Z –= {0, –1 , –2, –3, –4, ...}
d. o conjunto dos inteiros negativos
Z 
= {–1, –2. –3, –4, ... }
Exemplos:
a) (+3)2 = (+3) x (+3) = + 9
b) (-2)5 = (-2) x (-2) x (-2) x (-2) x (-2) = - 32
**Importante:
(-2)2 = (-2) x (-2) = 4 é diferente de
- 22 = -(2) x (2) = - (4) = - 4
No primeiro caso tanto o sinal quanto ao número
estão ao quadrado e no segundo caso apenas o
número está elevado ao quadrado.
Propriedades
P1. A soma de números inteiros quaisquer é um número
inteiro.
P2. A diferença de dois números inteiros quaisquer é um
número inteiro.
P3. O produto de dois números inteiros quaisquer é um
número inteiro.
EXERCÍCIOS
01.( Unimontes – PAES) Se n é um número inteiro
positivo, podemos afirmar que:
a)
b)
c)
d)
n2 + n
n2 + n
n2 – 1
n2 – 1
é sempre um número par.
é sempre um número ímpar.
é sempre um número par.
é sempre um número ímpar.
RETA NUMÉRICA INTEIRA
GABARITO
01. A
Observe que a reta tem uma seta que indica a ordem de
crescimento dos números, eles estão crescendo da
esquerda para a direita, -7 é menor que -6, 0 é maior que 1 e assim em diante.
25
O CONJUNTO DOS NÚMEROS RACIONAIS ( )
O conjunto dos Números Racionais (Q) é formado por
a
todos os números que podem ser escritos na forma
b
onde a e b  Z e b  0 (1º Mandamento da Matemática:
NÃO DIVIDIRÁS POR ZERO)
São racionais por exemplo:



12
12

 4
3
3
( inteiro )
13
13

 3,25 ( Decimal exato )
4
4
8
8

 2,6666... ( Dízima periódica )
3
3
que a fração é aparente. Observe que uma fração
aparente é, na verdade, um número inteiro.
Exemplos:
6
15
 3; 
 5
2
3
SIMPLIFICANDO FRAÇÕES
Uma fração pode ser simplificada dividindo-se
numerador e denominador pelo seu máximo divisor
comum
Exemplos:
15 15  5 3


20 20  5 4
(MDC (15, 20) = 5)
3
é irredutível, pois o único
4
divisor comum do numerador e do denominador é 1.
Dizemos que a fração
Podemos definir, portanto, o conjunto Q dos números
racionais da seguinte forma
OPERAÇÕES EM Q
Propriedades
As operações com número racionais segue as
mesmas regras de operação das frações.
P1. A soma de dois números racionais quaisquer é um
número racional.
Adição e Subtração
P2. A diferença de dois números racionais quaisquer é um
número racional.
P3. O produto de dois números racionais quaisquer é um
número racional.
P4. O quociente de dois números racionais quaisquer,
sendo o divisor diferente de zero, é um número racional.
TIPOS DE FRAÇÃO
a) Fração própria
É aquela cujo numerador é menor que o denominador
Exemplos:
3 2 1
,
,
5 7 4
b) Fração imprópria
É aquela cujo numerador é maior que o denominador.
Exemplos:
7 3 5
,
,
5 2 4
Reduzem-se as frações ao mesmo denominador. Para
isso devemos encontrar o mmc dos denominadores,
criarmos uma mesma seqüência de fração com o novo
denominador e numerador igual ao resultado da divisão
do novo denominador pelo velho multiplicado pelo
numerador velho.
Exemplo
2 3
 
3 4
O mmc(3,4) = 12 então
12

12

Dividindo-se 12 por 3 e multiplicando-se por 2, depois
dividindo-se 12 por 4 e multiplicando-se por 3, então
teremos:
8
9
17


12 12
12
Inverso De Um Número Racional
Chama–se inverso de um número racional
a
≠ 0 o
b
b
≠ 0 , obtido do primeiro
a
invertendo-se numerador e denominador.
número racional
Obs.:Se o numerador é múltiplo do denominador, dizemos
26
Potenciação De Frações – Expoente Inteiro
Negativo
a
Sendo
≠ 0 um numero racional, definimos a
b
potenciação com expoente inteiro negativo da seguinte
forma:
Exemplos:

3
5
O inverso de
é
.
5
3

O inverso de 
8
7
é  .
7
8
n
n
a) Não se define o inverso de 0 (zero):
a
 
b
b) O produto de um racional pelo seu inverso e igual
a 1.
Observe que basta tomar o inverso da base e elevar
ao expoente natural simétrico.
Observe que:
De fato:
a b ab
 
1
b a ab
Exemplos:
**O inverso de um numero racional a pode ser indicado
1
–1
por
sendo a  0 ou por a .
a
Exemplo:
7
O inverso de
é:
13
1
 1
a x     x
a
a
 2
 
 3
3
 33   27   27
 3
   
8
8
 2
23
3
0 – 5 não se define. Pois não existe o inverso de 0.
A partir desta definição, o inverso de um número
1
racional x  0 pode ser indicado por
ou x –1.
x
1
13 13
 1 
7
7
7
13
x
Observe que:
b
   , com n  IN
a
a  IR *
x  IR
OPERAÇÕES COM OS NÚMEROS DECIMAIS
Multiplicação
As operações elementares com números decimais
obedecem a regras simples, conforme veremos a
seguir.
Multiplicam-se os numeradores e os denominadores
obtendo-se assim o resultado.
Adição e subtração de decimais
3 2
6
. 
5 7
35
Divisão
Deve-se multiplicar a primeira pelo inverso da segunda
Colocamos vírgula debaixo de vírgula e efetuamos a
operação normalmente.
Exemplos:
 31,45 + 2,137
31,45
+ 2,137
33,587
3 2
3 7
21
: 
. 
5 7
5 2
10
Potenciação de frações
Para se elevar uma fração a um expoente natural, elevamse numerador e denominador a esse expoente.

6,4 – 3,158
6,400
+ 3,158
3,242
Exemplos:
2

32
9
3
   2 
25
5
5
3

(2) 3
8
 2

  
3
27
3
 3
Multiplicação de decimais
Efetuamos normalmente a multiplicação e
separamos, no produto, um número de casas decimais
igual à soma do número de casas decimais de cada um
dos dois fatores.
27
Exemplo:
 Vamos efetuar 2,3 . 0,138
Encontrando a Fração Geratriz de uma Dízima
Periódica
0,138  3 casas decimais
2,3  1 casa decimal
414
+ 267 .
0,3174  4 casas decimais

Dízima periódica simples
Divisão de decimais
Transformamos o divisor em inteiro, multiplicando
dividendo e divisor por uma potência de dez adequada
efetuamos a divisão normalmente e separamos, no
quociente, um número de casas decimais igual ao numero
de casas decimais utilizadas no dividendo (incluindo os
zeros que tenham sido acrescentados)
Devemos adicionar a parte decimal à parte inteira.
Deve-se lembrar que a parte decimal será
transformada em uma fração cujo numerador é o
período da dízima e o denominador é um número
formado por tantos noves quantos sãos os algarismos
do período.
Exemplos:
Exemplos:
 Dividir 32,4 por 0,008
32,4  0,008 = 32400  8 = 4050
Dízima periódica composta
FRAÇÃO GERATRIZ DE UMA DÍZIMA PERIÓDICA
Conforme você já estudou, todo número racional
(Conjunto Q), resulta da divisão de dois números inteiros,
a divisão pode resultar em um número inteiro ou decimal.
Convém lembrar que temos decimais exatos.
Exemplo: 2,45; 0,256; 12,5689;
12,5689
Temos também decimais não exatos (dízima periódica)
Exemplos: 2,555555.... ; 45,252525....;
456,12454545; 7,4689999....
Devemos adicionar à parte inteira, uma fração cujo
numerador é formado pelo anti-período, seguindo de
um período, menos o anti-período, e cujo denominador
é formado de tantos noves quantos são os algarismos
do período seguidos de tantos zeros quanto são os
Algarismos do ante-período.
Exemplos:
Parte inteira = 0
Período = 7(implica que temos um nove)
Anti-período = 1 (implica em um 0)
0,123123123...;
Você deve saber, que em uma dízima periódica a parte
decimal que repete, recebe o nome de período, a parte
que não repete é chamada de anti-período, a parte não
decimal é a parte inteira.
Parte inteira = 2
Período = 5 (implica um nove)
Anti-período = 003 (implica três zeros)
Exemplo:
28
Exercício Resolvido
as raízes definidas em IR.
m
1.
2.
3.
4.
an 
n
n
a
n
b
m
n
n m
a
b
n
 a
n
am
(m  Z e n  IN*)
a  n b  n ab
5.
6.
n
b0
 n am
a  n m a
am 
n p
am p
A simplificação de um radical consiste em reduzir
seu radicando à expressão mais simples possível. Um
radical em que o índice e o expoente do radicando têm
um divisor comum pode ser simplificado.
Exemplo:
6
16  6 2 4  6:2 2 4:2  3 22  3 4
RADICIAÇÃO NO CONJUNTO DOS RACIONAIS

A Radiciação é o ato de extrair a raiz de um número,
lembrando que temos raiz quadrada, raiz cúbica, raiz
quarta, raiz quinta e etc...
Radiciação é a operação inversa da potenciação. Sendo:
Se o radicando ou os fatores que o compõem
possuem expoentes maiores que ou iguais ao índice do
radical, ele pode também ser simplificado.
Exemplo:

Sendo a  Q e n  IN*, definimos a raiz enésima de a
 a  da seguinte forma:
5 162  5 2.3 4  5 3 4 . 2  5.3 2. 2  45 2
A redução de radicais ao mesmo índice é importante
na multiplicação e na divisão de radicais. Para reduzir
radicais ao mesmo índice, utilizamos a propriedade 6,
tomando como índice comum o MMC dos índices dos
radicais dados.
n
n  par e a  0
n  ímpar
n
a  b  bn  a e b  0
n
a  b  bn  a
Lembrando que:
Se o índice é um número maior que 1 (n > 1), se este
for igual a dois (raiz quadrada "não escrevemos este valor,
o local do índice fica vazio ou seja fica entendido que ali
está o número 2"), se for igual a 3 (raiz cúbica "este valor
deve aparecer no índice"), etc...
Exemplos:
2
9  3 porque 3 = 9 e 3 > 0


8
0 0

4
81 3
81
3
3
 porque   
e 0
16 2
2
2
16
 
4
Para trabalhar com radicais, utilizamos a definição
potência de expoente fracionário e as propriedades da
radiciação, conformes iremos ver a seguir, onde supomos
Exemplos:

Reduza ao mesmo índice os radicais
ab , 34 ab2 e
6
a 5b
Os índices são 2, 4 e 6, cujo MMC é 12. Temos:
2
ab  12 (ab)6
34 ab2  312 (ab2 )3
6
 
a5b  12 a5b
2
Obtemos então:
12
a 6b 6 , 312 a 3b 6 e
12
a10 b 2
Operações Com Radicais
A adição e a subtração de radicais semelhantes
resulta sempre em um radical. Basta aplicar a
propriedade distributiva da multiplicação em relação à
adição. Esse procedimento é denominado redução de
radicais semelhantes.
29
Exemplos:
d)
3 5 5

3 5 
3
11
11 5
  3  1   5 
5
4
4
4
4

7 , 3 e 2
5
15 5
2) ( PUC – MG) Em uma caixa há m pirulitos. Depois
2
do total de pirulitos
7
dessa caixa e a criança B retira 11 pirulitos, ainda
2
restam na caixa,
de m. O valor de m é :
5
a) 25
b) 30
c) 35
d) 40
que a criança A
De maneira geral, a adição e a subtração de radicais
se efetuam simplificando-se os radicais (se possível) e
reduzindo-se, em seguida, os radicais semelhantes acaso
existentes.
A multiplicação e a divisão de radicais se efetuam da
seguinte forma:
1º- Reduzem-se os radicais ao mesmo índice;
2°- Aplicam-se as propriedades 2 e 3.
Exemplos:



3 2  2 5  3.2. 2. 5  6 10

 3 2. 5  6 22 .6 53  6 22.53  6 500
A potenciação de radicais é efetuada utilizando-se a
propriedade 4 e simplificando-se, em seguida, a expressão
obtida.
Exemplo:

3 2 
3
4
 3 4  3 2 4  81.3 23.2  1623 2
A radiciação de radicais é efetuada introduzindo-se o
coeficiente no radicando e aplicando-se, em seguida, a
propriedade 5 .
Exemplos:


5 65
3
23 5 
3
23.5  6 40
retira
2
2
2
3) ( Fatec – SP ) Se A = (–3) – 2 , B = – 3 + (–2)
2
e
2
C = (–3 –2) , então C + A × B é igual a
a) –150
b) –100
c) 50
d) 10
e) 0
4) ( Fuvest – SP ) Qual desses números é igual a
0,064 ?
2
a) ( 1/80 )
2
b) ( 1/8 )
c) ( 2/5 )3
d) ( 1/800 )2
e) ( 8/10 )3
3 2 3
5) ( UNIP ) Simplificando-se a expressão [(2 ) ] ,
obtém-se:
a) 66
b) 68
c) 28
d) 218
e) 224
6) ( UEL – PR ) Se x e y são números reais, então
a única alternativa correta é:
EXERCÍCIOS
1) ( PAES – 2006 ) Considere as figuras abaixo na ordem
dada.
 
x
a) 3
b)
c)
d)
e)
y
 3x
y
(2x . 3y)2 = 22x . 32y
x
x y
xy
xy
xy
(2 – 3 ) = 2 – 3 = –1
x
x
x
5 +3 =8
3 . 2x = 6x
9
7) ( PUC – MG ) O resultado da expressão {[2 : (2 .
2 3 –3
As frações representadas pelas regiões assinaladas
nessas figuras são, respectivamente:
a)
b)
c)
4
, 1 e 1
3
15 10
3
2
4
,
e
7
5 15
7
, 2 e 1
3
15 5
2 ) ] } / 2 é:
a) 1/5
b) 1/4
c) 1/3
d) 1/2
2 8
8) ( CFTCE ) O valor da expressão [(0, 5) ] .
 1  2 
  
 64  
3
como uma só potência de 2 é:
30
a)
b)
c)
d)
e)
2 16
18
2
20
2
22
2
2 24
b) 2.49 2 11
c)
–1
0
9) ( UFJF ) A soma 3.10 + 3.10 + 3.10
é igual a:
16) ( PUC – SP ) O valor da expressão
27000. 1
30
3
 2  1   2  1
2
2
 3 2 é:
3
c) 3001,01
d) 3001,3
e) 3003,3
a) 2 2
2
3
b) 3 3
2
10) ( Fuvest – SP ) O valor de ( 0,2 ) + ( 0,16 ) é
1
0,0264
0,0336
0,1056
0,2568
0,6256
c)
62
1
d) 3 2
1
e) 2 6
11) ( PUC – RJ ) O maior número a seguir é:
17) ( PUC – SP ) Considere o número p =
a) 3 31
b) 8 10
c)16 8
d) 81 6
e) 243 4
2
12) ( UFG – GO ) O número
a)
b)
8
4
c)
18  6
d)
e)
10  2
0
quando a 
2
18) ( PUC / MG ) A seguir, estão três afirmativas sobre
números reais :
I - O número 2,3235666... é racional.
a 3 .b 2 . c
,
d
II- O número
1
, b = – 2, c = 4 e d = – 8 é :
2
k
t
p
,
7 pode ser escrito na forma
q
na qual p e q são inteiros, com q  0.
III – O valor de m =
–8
–4
–2
– 1/4
– 1/8
2k
14) ( Izabela Hendrix – BH ) Se 2 = x e 2 = y, então 2
 32
é – 1 ou 1.
3
O número de afirmativas corretas é:
a) 0
b) 1
c) 2
d) 3
1
+ 3t
é:
a) 2x + 3y
b) x.y
c) x + y
d) x2. y3
e) x3. y2
19) ( Unimontes / PAES) Se a =  3  64 e b = 16 4 ,
então a única alternativa CORRETA é:
a) a + b =
1,2222...
15) ( PUC – MG ) O produto 2
51
a) 2. 2
9
2m
, em
n
2
 1
que m    + 0,3 e n = 4 –   . O valor de
3
2
“p” é tal que:
a) 0 < p < 1
b) 1 < p < 2
c) 2 < p < 3
d) 3 < p < 4
e) 4 < p < 5
18  8  2 é igual a:
13) ( Unaerp – SP ) O valor da expressão
a)
b)
c)
d)
e)
2 16
e) 2.25 2 12
a) 303,3
a)
b)
c)
d)
e)
45
d) 2.30 2
3
b)
2.
0,133333...
.2
9
2
b) a = b
c) a : b = 2
é igual a :
d) a.b = 1
8
31
20) ( Unimontes / PAES) Se a e b são números reais
26) (PUC –MG) Calcule o valor da expressão:
positivos, m e n são números naturais não nulos,
então, das afirmações abaixo, a única INCORRETA é:
a)
n
a.n b  n a.b
b)
m
a  n b  mn a  b
c) (am )n . (bn)m = (a.b)mn
a 

  am n.b m n
 bm 


m
d)
27) (Unimontes) Qual o valor de a + b, se a
b
3
,
444
...
fração irredutível
?
1,222...
n
A) 42/9
B) 21/9
C) 21
D) 42
21) ( PAES / UNIMONTES ) Os números a e b estão
representados na reta.
–1
a
0
b
é a
1
GABARITO
O número a + b está :
a) à direita de 1
b) entre 0 e b
c) à esquerda de –1
d) entre –1 e 0.
22) (UFOP) O valor simplificado da expressão
é:
A) 1,7
B) 2
C) -3,025
D) -4
7
5
23) (UNIMONTES) A terça parte da soma 3 + 9
é igual
a
9
3
A) 3 + 9
7
2
B) 3 + 9
9
5
C) 3 + 3
6
5
d) 3 + 3
24) (CTSP-2009)(FUVEST) Dividir um número por 0,0125
equivale a multiplicá-lo por:
A. 8
B. 80
C. 1/8
D. 1/125
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
C
C
E
C
D
B
D
C
E
B
A
E
A
D
C
E
B
B(V F F)
C
B
B
B
A
B
B
7/3
D
25)
32
O CONJUNTO DOS NÚMEROS IRRACIONAIS (
)
A radiciação nem sempre e possível no conjunto Q dos
números racionais. Observe que, por exemplo,
3
 8  2  Q;
36
6
 Q
25 5
Pode–se provar, no entanto, que raízes do tipo
3
5,
5
racionalização de denominadores.
O processo geral consiste em multiplicar numerador e
denominador por um fator conveniente, denominado
fator racionalizante.
1º- O denominador é um radical simples
2,
3
, etc. não são racionais. Isso quer dizer que, por
4
exemplo, não existe número racional cujo quadrado é 2,
não existe número racional cujo cubo é 5, e assim por
diante.
Números como esses são chamados números
irracionais.
Escritos na forma decimal, os números irracionais, não
são exatos nem periódicos. De fato, usando uma
simples calculadora, encontramos
O fator racionalizante é um radical com o mesmo
índice que o denominador e com radicando tal que, ao
se efetuar a multiplicação, a raiz obtida no
denominador seja exata.
Exemplo:

6
6

2
2
2

6 2
 3 2
2

2
a b
2º- O denominador é do tipo
2 = 1,414213562...
3
Duas expressões do tipo a  b e a  b
são ditas conjugadas. É importante observar que
5 = 1,709975947...
3
= 0,944087511...
4
 a  b  a  b   a  b
5
Os números irracionais não provém necessariamente
da radiciação. São também irracionais, por exemplo, os
números

 = 3.141592654... (importante no estudo do círculo)

e = 2.71828182... (importante no estudo dos
logaritmos)

0,303303330...
Essa
identidade
nos
permite
denominadores do tipo a  b . O fator racionalizante
é o conjugado do denominador.
Exemplo:
6
5 1

6
5 1
5 1

5 1

Exemplo:
3
3  2 1
P1. A soma de um número racional com um número
irracional é um número irracional.

P2. A diferença entre um número racional e um número
irracional, em qualquer ordem, é um número irracional.
 


 3

 3  2  1 
2  1  3  2  1
3

 3
3 3  2 1
 3  2 1
2
2
6 3
42 6

3 6  3 42 6 3 2 2 3  6


4
42 6
42 6
P3. O produto de um número racional, não-nulo,por um
número irracional é um número irracional.
P4. O quociente de um número racional, não-nulo, por um
número irracional é um número irracional.
Quando um radical ou uma expressão com radicais
aparece como denominador de uma fração, é possível as
vezes encontrar uma fração equivalente cujo denominador
não contém radical. Tal procedimento é chamado

6 5 1 3 5 1

5 1
2
Às vezes, a racionalização deve ser feita por partes.
Propriedades
RACIONALIZAÇÃO DE DENOMINADORES
racionalizar
3
3º- o denominador é do tipo
a 3b
As identidades notáveis, nos permitem escrever:
 a  b .
3
3
3
a 2  3 ab  3 b 2   a  b

33
 a  b .
3
3
3
 Intervalo fechado:
a 2  3 ab  3 b 2   a  b

Em cada caso, a segunda expressão entre parênteses é o
fator racionalizante.
Exemplo:
2
3
3 1

2
3
3 1

3
32  3 3  1
3
3  3 1
2
3



2 3 9  3 3 1

3 1
 3 9  3 3 1
O CONJUNTO DOS NÚMEROS REAIS (IR)
Acrescentando ao conjunto dos números racionais os
números irracionais, obtemos o conjunto IR dos números Reais.
Portanto, IR = Q U {irracionais}
Podendo ser representado da seguinte maneira pelo
diagrama de VENN:
Notação: [a, b] = {x  IR / a ≤ x ≤b}
A este intervalo pertencem todos os números
compreendidos entre a e b ,inclusive a e b .
 Intervalo aberto:
Notação: ]a, b[ = { x  IR / a < x < b }
A este intervalo pertencem todos os números
compreendidos entre a e b , excluindo a e b.
 Intervalo fechado à esquerda e aberto à
direita:
Notação: [a, b[ = { x  IR / a ≤ x < b }
A este intervalo pertencem todos os números
compreendidos entre a e b , incluindo a e não incluindo
b.
 Intervalo aberto à esquerda e fechado à
direita:
O EIXO REAL
A cada ponto de uma reta pode-se associar um único
número real e a cada número real pode-se associar um
único ponto dessa reta.
Notação: ]a, b] = { x  IR / a < x ≤ b }
A este intervalo pertencem todos os números
compreendidos entre a e b , exceto a e incluindo b.
 Intervalos indicados pelo símbolo∞
(infinito):
Notação: ]a, +∞[ = { x  IR / x > a }
Notação: ]-∞, a[ = { x  IR / x < a }
INTERVALOS REAIS
Os intervalos reais são subconjuntos dos números
reais . Serão caracterizados por desigualdades, sendo a e
b números reais, com a < b, temos:
Notação: [a, +∞[ = { x  IR / x ≥ a }
Notação: ]-∞, a] = { x  IR / x ≤ a }
34
EXERCÍCIOS
Notação : ]-∞, ∞[ = IR
 Não esqueça!!!!!
Os números reais a e b são denominados extremos dos
intervalos.
O intervalo é sempre aberto na indicação do
infinito.
MÓDULO DE UM NÚMERO REAL
Chama-se módulo ou valor absoluto de um número
inteiro “x” a distância desse número até o zero na reta
numérica.
Sendo x  IR, definimos de módulo ou valor absoluto
de x e indicamos por x , através da relação:
 x, se x  0
,
x 
 x se x  0
ou seja: um número real positivo tem como módulo o
próprio número. Já um número real negativo terá como
módulo o oposto a esse número.
Exemplos:
O módulo de +177 é 177 e indica-se |+177| = 177.
O módulo de − 79 é 79 e indica-se |−79| = 79.
01. (PUC-SP) Seja x um número natural que, ao ser
dividido por 9, deixa resto 5 e, ao ser dividido por 3,
deixa resto 2. Sabendo que a soma dos quocientes é 9,
podemos afirmar que x é igual a:
A) 28
B) 35
C) 27
D) 33
E) 23
02. Analise as sentenças abaixo:
I. todo número primo admite apenas 2 divisores.
II. 1 é primo.
III. se a e b são primos distintos, então a e b são
primos entre si.
IV. se a e b são primos entre si, então a e b são
primos.
São falsas
A) apenas I e III
B) apenas II e IV
C) apenas I e II
D) apenas I, II e IV
E) apenas III e IV
03. O número 45a4, onde a é o algarismo das dezenas,
é divisível por 12. A soma dos possíveis valores de a é:
A) 9
B) 10
C) 12
D) 15
E) 16
04.(UFMG) O produto de um inteiro positivo a de três
algarismos por 3 é um número terminado em 721. A
soma dos algarismos de a é:
A) 12
B) 13
C) 14
D) 15
E) 16
Propriedades envolvendo módulo
Admitiremos, sem demonstrar, algumas propriedades
dos módulos:
1. Para todo x
IR, temos |x| ≥ 0 e |x| = 0 ⇔ x = 0
2. Para todo x
IR, temos |x| = |−x|
3. Para todo x
IR, temos |x2| = |−x2| = x2
4. Para todo x e y
1
IR, temos |x|−|y| ≤ |x − y|
1
1
5
(UNB) A expressão
é equivalente a:
3
 1
1
1
5
3
2
2
3
1
3
1
4
1
06.
IR, temos |x.y| = |x|.|y|
5. Para todo x e y IR, temos |x+y||≤|x|+|y|
6. Para todo x e y
05. (UFMG) O número de 3 algarismos divisível, ao
mesmo tempo, por 2, 3, 5, 6, 9, 11 é:
A) 330
B) 660
C) 676
D) 990
E) 996
A)
B)
C)
D)
35
1 1
07. A expressão   
3
a:
A)
B)
C)
D)
E)
8
–3
5
4
2
08.
A)
B)
C)
D)
E)
(PUC) O valor de
0,222...
0,333...
0,444...
0.555...
0,666...
6
1
3

   0,4 
5

1
 2 1
  
3 5
0
é igual
C) 2 2  2 3
D) 2 2  3
E) 2 3  2
14.(Bombeiros-MG) Considere os números reais a, b
c
b
e c tais que : a  b  c,
0 e
 0 Nessas
b
a
condições podemos afirmar que:
2
A) a > 0 e b < 0
2
B) b < 0 e a > 0
C) a2 > 0 e a < 0
D) c2 > 0 e c < 0
0,444... é:
09. (USP) Sela a a fração geratriz da dízima 0,1222...
b
com a e b primos entre si. Nestas condições, temos:
A) ab = 990
B) ab = 900
C) a – b = 8
D) a + b = 110
E) b – a = 79
10. (UFMG) Efetuando as operações indicadas na
expressão 1 0,01 0,12  0,142  0,04 obtemos:
3
A)
B)
C)
D)
E)
0,220
0,226
0,296
0,560
0,650
11.
A)
B)
C)
D)
E)
(UFMG) O valor de 10–2 . [(–3)2 – (–2)3]  3  0,001 é:
–17
– 1,7
– 0,1
0,1
1,7
12. (FUVEST) O valor da expressão
A)
2
B)
1
2 2
2 1
2
C) 2
D)
1
2
é:
15. (Bombeiros-MG) Sejam p e q dois números
primos. Sabe-se que a soma dos divisores naturais de
p2 é 133, e que a soma dos divisores naturais de 2q é
18. O valor de p + q é:
A) 10
B) 7
C) 18
D) 16
16. (CFO/PM) Duas pessoas, fazendo exercícios
diários, partem simultaneamente de um mesmo ponto
e, andando, contornam uma pista oval que circunda um
jardim. Uma dessas pessoas dá uma volta completa na
pista em 12 minutos. A outra, andando mais devagar,
leva 20 minutos para completar a volta. Depois de
quantos minutos essas duas pessoas voltarão a se
encontrar no ponto de partida?
A) 30 minutos.
B) 45 minutos.
C) 60 minutos.
D) 240 minutos.
17.(CFO/PM) No alto de uma torre de uma emissora de
televisão, duas luzes "piscam" com freqüências
diferentes. A primeira "pisca" 15 vezes por minuto e a
segunda "pisca" 10 vezes por minuto. Se num certo
instante as luzes piscam simultaneamente, após
quantos
segundos
elas
voltarão
a
piscar
simultaneamente?
A) 12
B) 10
C) 20
D) 15
18.(BNB-ACEP)Sejam x e y números reais dados por
suas representações decimais
2 1
E)
A) 2 2
B) 3 2  3
13. (FGV-SP) Simplificando-se a expressão
1
3 2

2
3 2
obteremos:
Pode-se afirmar que:
A) x + y = 1
B) x – y = 8 / 9
36
C) xy = 0,9
D) 1 / ( x + y ) = 0,9
E) xy = 1
19.(IBGE-UFRJ) Três de cada oito moradores de um
edifício são do sexo feminino; se, nesse edifício, há doze
moradores do sexo feminino, então o número de
moradores do sexo masculino é igual a:
A) 12
B) 16
C) 20
D) 30
E) 36.
20. (UFMG) Na representação dos números reais por
pontos da linha reta, a unidade de comprimento esta
dividida em três partes iguais. como na figura.
O valor de
24. (EPCAR) Qual das proposições abaixo e falsa?
a) Todo numero real e racional.
b) Todo numero natural e inteiro.
c) Todo numero irracional e real.
d) Todo numero inteiro e racional.
e) Todo numero natural e racional.
GABARITO
A B
é:
A B
1
9
1
B)
3
C) 1
D) 3
E) 9
A)
21.(PUC –MG) Na reta real da figura, estão representados
os números 0, a, b e 1. O ponto P que corresponde ao
b
número
está:
a
a) à esquerda de 0
b) entre 0 e a
c) entre a e b
d) entre b e 1
e) à direita de 1
22. (PASES) O número
( ) –1 é um numero irracional
( ) √64 é um numero inteiro
( ) 2/7 é um numero racional
( ) – 0,6666... é um numero irracional
( )7 Z
( )1 Q
( ) √3 R
( )2∉Z
( )–1∉I
( ) √8 ∉ N
( ) 6/2 N
( ) 72 N
( ) 0,7777... Z
é:
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
E
B
B
E
D
A
A
E
E
A
B
A
B
C
D
C
A
D
C
A
E
A
V,F,V,V,F,V,V,V,F,V,V,V,V,F
A
a) racional menor do que 7
b) irracional maior do que 3
c) irracional menor do que 3
d) racional maior do que 12
e) racional entre 7 e 12
23.Coloque V ou F conforme a sentença seja verdadeira
ou falsa, respectivamente:
( ) 4 é um numero natural
37
QUESTÕES DO ENEM
01. (ENEM-2009) No calendário utilizado atualmente, os
anos são numerados em uma escala sem o zero, isto é,
não existe o zero. A era cristã se inicia no ano 1 depois de
Cristo (d.C.) e designa-se o ano anterior a esse como ano
1 antes de Cristo (a.C). Por essa razão, o primeiro século
ou intervalo de 100 anos da era cristã terminou no dia 31
de dezembro do ano 100 d.C., quando haviam decorrido
os primeiros 100 anos após o início da era. O século II
começou no dia 1º de janeiro do ano 101 d.C., e assim
sucessivamente.
Como não existe o ano zero, o intervalo entre os anos
de 50 a.C. e 50 d.C., por exemplo, é de 100 anos. Outra
forma de representar anos é utilizando-se números
inteiros, como fazemos astrônomos. Para eles, o ano 1ª.C.
corresponde ao ano 0, o ano 2 a.C. ao ano –1, e assim
sucessivamente. Os anos depois de Cristo são
representados pelos números inteiros positivos, fazendo
corresponder o número 1 ao ano 1 d.C.
Considerando o intervalo de 3a.C a 2 d.C., o quadro
que relaciona as duas contagens descritas no texto é
segundo por 9, e assim sucessivamente); em seguida,
calcula-se o resto r da divisão da soma dos resultados
das multiplicações por 11, e se esse resto r for 0 ou 1,
d1 é zero, caso contrário d1 = (11 – r). O dígito d2 é
calculado pela mesma regra, na qual os números a
serem multiplicados pela sequência dada são contados
a partir do segundo algarismo, sendo d1 o último
algarismo, isto é, d2 é zero se o resto s da divisão por
11 das somas das multiplicações for 0 ou 1, caso
contrário, d2 = (11 – s). Suponha que João tenha
perdido seus documentos, inclusive o cartão de CPF e,
ao dar queixa da perda na delegacia, não conseguisse
lembrar quais eram os dígitos verificadores,
recordando-se apenas que os nove primeiros
algarismos eram 123.456.789. Neste caso, os dígitos
verificadores d1 e d2 esquecidos são, respectivamente,
A) 0 e 9.
B) 1 e 4. C) 1 e 7.
D) 9 e 1.
E) 0 e 1.
03. (ENEM-2013) Em um certo teatro, as poltronas são
divididas em setores. A figura apresenta a vista do
setor 3 desse teatro, no qual as cadeiras escuras estão
reservadas e as claras não foram vendidas.
A razão que representa a quantidade de cadeiras
reservadas do setor 3 em relação ao total de cadeiras
desse mesmo setor é
02. (ENEM-2009) Para cada indivíduo, a sua inscrição no
Cadastro de Pessoas Físicas (CPF) é composto por um
número de 9 algarismos e outro número de 2 algarismos,
na forma d1d2, em que os dígitos d1 e d2 são
denominados dígitos verificadores. Os dígitos verificadores
são calculados, a partir da esquerda, da seguinte maneira:
os 9 primeiros algarismos são multiplicados pela
sequência 10, 9, 8, 7, 6, 5, 4, 3, 2 (o primeiro por 10, o
03. (ENEM-2013) O ciclo de atividade magnética do Sol
tem um período de 11 anos. O início do primeiro ciclo
registrado se deu no começo de 1755 e se estendeu
até o final de 1765.
Desde então, todos os ciclos de atividade magnética do
Sol têm sido registrados.
Disponível em: http://g1.globo.com. Acesso em: 27 fev. 2013.
No ano de 2101, o Sol estará no ciclo de atividade
magnética de número
A) 32. B) 34. C) 33.
D) 35.
E) 31.
38
04.(ENEM/2009) A música e a matemática se encontram
na representação dos tempos das notas musicais,
conforme a figura seguinte.
GABARITO
01. B
02. A
03. A
04. D
05. D
06. E
Um compasso é uma unidade musical composta por
determinada quantidade de notas musicais em que a
soma das durações coincide com a fração indicada como
fórmula do compasso. Por exemplo, se a fórmula de
compasso for
1
, poderia ter um compasso ou com duas
2
semínimas ou uma mínima ou quatro colcheias, sendo
possível a combinação de diferentes figuras.
Um trecho musical de oito compassos, cuja fórmula é
3
,
4
poderia ser preenchido com
a) 24 fusas.
b)3 semínimas.
c)8 semínimas.
d)24 colcheias e 12 semínimas.
e)16 semínimas e 8 semicolcheias.
05.(ENEM/2010) O gráfico a seguir apresenta o gasto
militar dos Estados Unidos, no período de 1988 a 2006.
Almanaque Abril 2008. Editora Abril.
Com base no gráfico, o gasto militar no início da guerra no
Iraque foi de
a) U$ 4.174.000,00.
b) U$ 41.740.000,00.
c) U$ 417.400.000,00.
d) U$ 41.740.000.000,00.
e) U$ 417.400.000.000,00.
39
MATEMÁTICA COMERCIAL
SISTEMA LEGAL DE UNIDADE DE MEDIDA
GRANDEZA
Intuitivamente, podemos chamar de grandeza qualquer
entidade que pode ser medida numericamente.
Vamos analisar as seguintes afirmações:
a) "O tempo gasto em uma viagem foi de 6 horas;
b) "O comprimento da bandeira do Atlético é 3
metros;
c) "A temperatura máxima de hoje foi de 39 graus".
Uma medida de uma grandeza é constituída de um
número real e uma unidade de medida.
Por questões práticas, as unidades de medida das
principais grandezas são convencionadas e adotadas
universalmente. Essa providência facilita a comunicação,
pois estabelece padrões que uniformizam a linguagem.
MEDINDO ÁREAS
A área é uma grandeza que mede a extensão de
uma superfície limitada.
No sistema métrico decimal, a unidade fundamental
de área é o metro quadrado (símbolo m2).
Na verdade, toda medida de área é obtida a partir
do produto de 2 medidas de comprimento. Observe:
5m.8m
medidas de comprimento
Múltiplos
Unidade padrão
Submúltiplos
Unidade
Quilômetro
Hectômetro
Decâmetro
Metro
Decímetro
Centímetro
Milímetro
símbolo
km
hm
dam
m
dm
cm
mm
Valor
1 000 m
100 m
10 m
1m
0,1 m
0,01 m
0,001 m
Na seqüência em que as unidades aparecem no
quadro (da maior para a menor), podemos dizer que cada
unidade de comprimento vale 10 vezes a unidade
seguinte.
Em função disso, é muito prático utilizar-se o número
decimal na medida de um comprimento. Ao escrevermos,
por exemplo
35,472m
O algarismo 5, que se encontra imediatamente antes
da vírgula, é o que de fato corresponde à unidade "metro".
Poderíamos escrever, então:
35,472m = 3 dam 5 m 4 dm 7 cm 2 mm
2
40 m
medida de área
O metro quadrado admite também seus múltiplos e
submúltiplos, todos derivados das unidades de
comprimento. Veja o quadro a seguir.
Múltiplos
MEDINDO COMPRIMENTOS
O comprimento é a grandeza que mede a extensão
de um segmento ou a distância entre dois pontos. É uma
das grandezas chamadas fundamentais.
No sistema métrico decimal, a unidade fundamental de
comprimento é o metro (símbolo m).
No quadro a seguir, apresentamos os múltiplos e
submúltiplos do metro com os símbolos e valores
respectivos.
=
Unidade
padrão
Unidade
Quilômetro
quadrado
Hectômetro
quadrado
Decâmetro
quadrado
Metro quadrado
Símbolo
valor
km
2
10 m
6
2
hm
2
10 m
4
2
dam2
m2
102 m2
1 m2
Decímetro
dm2
10–2 m2
quadrado
Centímetro
Submúltiplos
cm2
10–4 m2
quadrado
Milímetro
mm2
10–6 m2
quadrado
Observe que, para o caso de medidas de área,
cada unidade vale 100 vezes a unidade seguinte. De
fato, temos por exemplo:
1 dam2 = l dam . 1 dam = 10m . 10m = 100m 2
Em função disso, a mudança de unidades de área
no sistema decimal se efetua deslocando a vírgula de 2
em 2 casas decimais. Observe, por exemplo, o quadro
a seguir, em que escrevemos uma mesma medida de
área em diferentes unidades.
MEDINDO VOLUMES E CAPACIDADES
O volume é uma grandeza que mede o espaço
ocupado por um corpo.
No sistema métrico decimal, a unidade padrão de
3
volume é o metro cúbico (símbolo m ).
Uma medida de volume é obtida, na prática, a partir
do produto de 3 medidas de comprimento. Por
exemplo:
2 m . 5 m . 6 m = 60 m3
Observe, no quadro a seguir, os múltiplos e
submúltiplos do metro cúbico.
Unidade
Símbolo Valor
Quilômetro
km3
109 m3
cúbico
Múltiplos
Hectômetro
hm3
106 m3
cúbico
40
Unidade
padrão
Submúltiplos
Decâmetro
cúbico
dam
Metro cúbico
m3
3
3
10 m
3
como unidade-referência, já que os nomes das demais
unidades derivam do grama. Observe:
1 m3
3
Decímetro cúbico
dm
Centímetro
cúbico
cm
Milímetro cúbico
mm
3
3
–3
10
m3
10–6
m3
10–9
m3
Ao trabalhar com medidas de volume, observe que
cada unidade vale 1000 vezes a unidade seguinte. Veja o
porquê no seguinte exemplo:
1dam3 = 1dam . 1dam . 1dam = 10m . 10m . 10m =
1000m3
Como conseqüência, a mudança de unidades de
volume se processa deslocando a vírgula de 3 em 3 casas
decimais. No quadro a seguir, escrevemos uma mesma
medida de volume em quatro unidades diferentes.
A capacidade é uma grandeza associada ao volume.
Ao dizermos que um recipiente tem uma determinada
capacidade, queremos dizer, na verdade, que ele
comporta um certo volume em seu interior.
Desta forma, se uma lata está cheia de água, a
grandeza volume está associada à água, ao passo que a
grandeza capacidade está associada à lata que contém a
água.
É tão sutil essa diferença que, na prática, podemos
utilizar as mesmas unidades para medir volumes e
capacidades.
Além das unidades já vistas para o volume, utilizamos
com freqüência a unidade litro (símbolo  ), com a
seguinte definição:
3
1l = 1 dm
O litro possui múltiplos e submúltiplos, sendo o principal
o mililitro (símbolo m l), correspondente a um milésimo do
litro. Temos então:
1 ml = 0,001 l = 0,001 dm3 = 1 cm3
Temos ainda o decalitro (1 da l = 10l), o hectolitro (1 hl
= 100l) e o quilolitro (1 kl = 1000l) como múltiplos do litro
e o decilitro (1dl = 0,1l) e o centilitro (1cl = 0,01l) como
submúltiplos do litro.
MEDINDO A MASSA
A massa é uma grandeza padrão associada à inércia
de um corpo. No sistema métrico decimal, a unidade
fundamental é o
quilograma (símbolo Kg). Um
quilograma é a massa de 1 dm 3 (1 litro) de água em
determinadas condições ideais.
Podemos considerar o grama (símbolo g), no entanto,
Unidade
Símbolo
Valor
quilograma
Kg
1000 g
hectograma
Hg
100 g
decagrama
Dag
10 g
Grama
G
1g
decigrama
Dg
0,1 g
centigrama
Cg
0,01 g
miligrama
MG
0,001 g
Para medir massas de valor mais elevado,
utilizamos também a tonelada (símbolo t), assim
definida:
1 t = 1.000 kg = 1.000.000 g
A transformação de unidades de massa é efetuada
da mesma forma utilizada para as unidades de
comprimento. Basta observar, no quadro anterior, que
cada unidade de massa vale 10 vezes a unidade
seguinte.
MEDINDO O TEMPO
O tempo é uma grandeza fundamental, como o
comprimento e a massa. A unidade fundamental de
tempo é o segundo (símbolo s). Seus múltiplos
principais são o minuto (símbolo min) e a hora (símbolo
h), com os seguintes valores:
1 min = 60 s
1 h = 60 min = 3600 s
O dia equivale a 24h, o mês comercial equivale a 30
dias e o ano equivale a 12 meses.
Para intervalos de tempo menores que o segundo,
utilizam-se o décimo de segundo, o centésimo de
segundo, etc.
É importante observar que as unidades de medida
de tempo não fazem parte do sistema métrico decimal.
Em vista disso, os números decimais não são os mais
adequados para representar medidas de tempo,
excetuando-se obviamente medidas menores que o
segundo, conforme acabamos de mencionar.
Veja como interpretar medidas de tempo expressas
na forma decimal ou fracionária.
Exemplos:
 Vamos interpretar o tempo t = 6,8h. Temos:
6,8h = 6h e 0,8 da hora
= 6h 48min

 6h e 0,8.60min =
Vejamos, agora o significado de t =
17
min.
3
41
Dividindo (com resto) 17 por 3,
17
2

v
d
280km
280km


 80km / h
t 3h30 min
3,5h
3
5
17
2
5
3
3
2
17
Então
min = 5 min e
do minuto =
3
3
2
= 5 min e
.60s = 5 min 40s.
3
PROPORÇÃO
Proporção, é uma igualdade entre duas razões.
Dados os números racionais a, b, c e d, diferentes
de zero, dizemos que eles formam, nessa ordem uma
proporção quando a razão de a para b for igual a razão
de c para d.
RAZÃO
Sendo a e b dois números reais com b  0, chamamos
a
razão de a para b o quociente
.
b
Exemplo:
6
 A razão do número real 6 para o número real 8 é
8
= 0,75.
Sendo os Termos de uma Razão:
A razão entre duas medidas de uma mesma grandeza
é sempre um número real "puro" (sem unidade). Esse
número nos leva, na prática, a uma comparação entre as
duas medidas.
Exemplos:
 Um segmento AB mede 36 cm e um outro segmento
AB
CD mede 1,44 m. Vamos calcular as razões
e
CD
CD
.
AB
AB 36cm 36cm
1


  0,25
CD 1,44m 144cm 4
CD 1,44m 144cm


4
AB 36cm
36cm
A última razão 4 obtida significa que o segmento AB
cabe 4 vezes no segmento CD, ou seja, CD = 4 AB.
A razão entre duas grandezas distintas define, muitas
vezes, outras grandezas importantes.

Se um automóvel percorreu 280 km em 3h 30min, sua
velocidade escalar média foi
Costuma-se ler: a está para b assim como c está
para d.
Podemos dizer também, neste caso, que os
números a e c são proporcionais aos números b e d.
Numa proporção, o produto dos extremos é igual ao
produto dos meios. Em símbolos,
Exemplo
Numa maquete, a altura de um edifício é igual a 80
cm. Se a maquete foi construída na escala 1:40, vamos
calcular a altura real do edifício.
Sendo x a altura real do edifício, temos:
80cm
1
 x = 40 .80 cm = 3200 cm = 32 m

x
40
QUESTÕES
01.(Enem )No depósito de uma biblioteca há caixas
contendo folhas de papel de 0,1 mm de espessura, e
em cada uma delas estão anotadas 10 títulos de livros
diferentes. Essas folhas foram empilhadas formando
uma torre vertical de 1 m de altura.
Qual a representação, em potência de 10,
correspondente à quantidade de títulos de livros
registrados nesse empilhamento?
2
A) 10
4
B) 10
C) 105
D) 106
7
E) 10
02.(ENEM) Os calendários usados pelos diferentes
povos da terra são muito variados. O calendário
islâmico, por exemplo, é lunar, e nele cada mês tem
sincronia com a fase da lua. O calendário maia segue
o ciclo de Vênus, com cerca de 584 dias, e cada 5
ciclos de Vênus corresponde a 8 anos de 365 dias da
42
terra.
MATSSURA, Oscar. Calendário e o fluxo do tempo.
Scientific
American
Brasil.
Disponível
em:
http://www.uol.com.br Acesso em: 14 out. 2008 (adaptado)
Quantos ciclos teria, em Vênus, um período terrestre
de 48 anos?
(A) 30 ciclos.
(B) 40 ciclos.
(C) 73 ciclos.
(D) 240 ciclos.
(E) 384 ciclos.
03(ENEM) Pneus usados geralmente são descartados de
forma inadequada, favorecendo a proliferação de insetos e
roedores e provocando sérios problemas de saúde
pública. Estima-se que, no Brasil, a cada ano, sejam
descartados 20 milhões de pneus usados. Como
alternativa para dar uma destinação final a esses pneus, a
Petrobras, em sua unidade de São Mateus do Sul, no
Paraná, desenvolveu um processo de obtenção de
combustível a partir da mistura dos pneus com xisto. Esse
procedimento permite, a partir de uma tonelada de pneu,
um rendimento de cerca de 530 kg de óleo.
Disponível em: http://www.ambientebrasil.com.br. Acesso
em 3 out. 2008 (adaptado)
Considerando que uma tonelada corresponde, em média,
a cerca de 200 pneus, se todos os pneus descartados
anualmente fossem utilizados no processo de obtenção de
combustível pela mistura com xisto, seriam então
produzidas
(A) 5,3 mil toneladas de óleo.
(B) 53 mil toneladas de óleo.
(C) 530 mil toneladas de óleo.
(D) 5,3 milhões de toneladas de óleo.
(E) 530 milhões de toneladas de óleo.
04.(ENEM) No monte do Cerro Amazones, no deserto do
Atacama, no Chile, ficará o maior telescópio da superfície
terrestre, o Telescópio Europeu Extremamente Grande
(E – ELT). O E–ELT terá um espelho primário de 42m de
diâmetro, “O maior olho do mundo voltado para o céu”.
Ao ler o texto em sala de aula, a professora fez uma
suposição de que o diâmetro do olho humano mede
aproximadamente 2,1cm.
Qual a razão entre o diâmetro do olho humano, e o
diâmetro do espelho primário do telescópio citado?
a) 1:20;
b) 1:100;
c) 1:200;
d) 1:1000;
e) 1:2000.
06.(Unimontes)Um artesão faz um trabalho em 10
dias. O mesmo trabalho é feito por outro artesão em 15
dias. Se os dois trabalhassem juntos, quantos dias
gastariam para fazer o trabalho?
A) 6 dias.
B) 5 dias.
C) 12 dias e 12 horas.
D) 9 dias.
07. (UFMG) As dimensões de uma caixa retangular são
3cm, 20mm e 0,07m. O volume dessa caixa, em
mililitros, é
A) 0,42
B) 4,2
C) 42
D) 420
E) 4200
08. (UFOP) Na planta de uma casa, escala 1:100, a
área de uma sala retangular, com dimensões de 5m
por 6m, é:
2
A) 0,3 cm
2
B) 3 cm
C) 15 cm2
2
D) 30 cm
E) 150 cm2
09.(UFMG) Na maqueta de um prédio, feita na escala
1:1000, a piscina com a forma de um cilindro circular
reto, tem a capacidade de 0,6 cm 3. O volume, em litros,
dessa piscina será:
A) 600
B) 6.000
C) 60.000
D) 600.000
E) 6.000.000
10.(PUC) Um elevador pode levar 20 adultos ou 24
crianças. Se 15 adultos já estão no elevador, quantas
crianças podem ainda entrar ?
A) 5
B) 6
C) 7
D) 8
E) 9
11.(ENEM) A figura a seguir mostra as medidas reais
de uma aeronave que será fabricada para utilização por
companhias de transporte aéreo. Um engenheiro
precisa fazer o desenho desse avião em escala de
1:150.
05.(PUC-MG) Um caminhão pode carregar 52 sacos de
areia ou 416 tijolos. Se forem colocados no caminhão 30
sacos de areia, o número de tijolos que ele ainda pode
carregar é:
A) 144
B) 156
C) 176
D) 194
43
Para o engenheiro fazer esse desenho em uma folha de
papel, deixando uma margem de 1 cm em relação às
bordas da folha, quais as dimensões mínimas, em
centímetros, que essa folha deverá ter?
A) 2,9 cm × 3,4 cm.
B) 3,9 cm × 4,4 cm.
C) 20 cm × 25 cm.
D) 21 cm × 26 cm.
E) 192 cm × 242 cm.
12.Se dois carteiros, de igual capacidade de produção,
entregam uma certa quantidade de cartas em 5 horas, em
quanto tempo três carteiros, de mesma capacidade de
produção que os anteriores, entregarão a mesma
quantidade de cartas?
A. 3h 40min
B. 3h 33min
C. 3h 20min
D. 3h 10min
E. 3h
13. (UFMG) Se, para encher um tanque, uma torneira A
gasta 3 h, e outra, B, gasta 7 horas, ambas abertas ao
mesmo tempo levam:
A) 1 h 50 min.
B) 2 h 06 min
C) 2 h 10 min
D) 2 h 20 min
E) 2 h 30 min
14. (UFMG) Dois operários, juntos, realizam uma tarefa
em 5 horas. Sabendo que, trabalhando isoladamente. o
primeiro gasta a metade do tempo do segundo.
concluímos que o primeiro operário, sozinho, realiza a
tarefa em
A) 6 h 40 min
B) 7 h 10 min
C) 7 h 50 min
D) 7 h 30 min
E) 8 h 10 min
15. (CESGRANRIO) Uma torneira enche um tanque em 4
horas. O ralo do tanque pode esvaziá-lo em 3 horas.
Estando o tanque cheio, abrimos, simultaneamente a
torneira e o ralo. Então o tanque,
A) nunca se esvazia.
B) esvazia-se em 1 hora.
C) esvazia-se em 4 horas.
D) esvazia-se em 7 horas.
E) esvazia-se em 12 horas.
GABARITO
01.
02.
03.
04.
05.
06.
C
A
B
E
C
A
07.
08.
09.
10.
11.
12.
13.
14.
15.
C
D
D
B
D
C
B
D
E
GRANDEZAS DIRETAMENTE PROPORCIONAIS
Suponhamos duas grandezas x e y, relacionadas
entre si. Suponhamos que x 1, x2, x3, x4, ... sejam
medidas da grandeza x. e y1, y2, y3, y4, ... as medidas
correspondentes da grandeza y.
Dizemos que as grandezas x e y são diretamente
proporcionais ou simplesmente proporcionais se e
somente se
x1 x 2 x 3 x 4



 ...  k
y1 y 2 y 3 y 4
A constante k é chamada constante de
proporcionalidade das duas grandezas. Temos então,
genericamente:
x
 k ou x = ky
y
Exercício resolvido:
Dividir o número 72 em três partes diretamente
proporcionais aos números 3, 4 e 5.
Resolução:
Indicamos por A, B e C as partes procuradas,
temos que: A  3p , B  4p , C  5p e A  B  C  72 e
sendo assim,
3 p  4 p  5 p  72
 12 p  72
 p6
e portanto, as três partes procuradas são 18, 24 e 30.
GRANDEZAS INVERSAMENTE PROPORCIONAIS
Suponhamos, novamente, duas grandezas x e y,
relacionadas entre si. Sejam x 1, x2, x3, x4, ... medidas
da grandeza x e y1, y2, y3, y4, ... as medidas
correspondentes da grandeza y.
Dizemos que as grandezas x e y são inversamente
proporcionais se e somente se
x1.y1 = x2.y2 = x3.y3 = x4.y4 = ... = k
Considerando genericamente as duas grandezas.
k
x . y = k ou x 
y
44
Exemplo
Uma herança de R$ 288.200,00 deve ser dividida entre
três herdeiros, em partes inversamente proporcionais às
suas idades: 3 anos, 6 anos e 9 anos. Vamos encontrar a
parte que cabe a cada um.
Chamando x, y e z as partes respectivas, temos:
x  y  z  288.200

3x  6y  9z  p
p
p
p
; y  ; z
3
6
9
p p p
   288.200  6p + 3p + 2p = 5 187 600
3 6 9
x
 11 p = 5 187 600
 p = 471 600
05. Três amigos fazem um bolão para jogar na Mega
Sena. Um entra com R$ 10,00, o outro com R$ 20,00 e
o terceiro com R$ 30,00. Se ganharem um prêmio de 6
milhões de reais, eles será dividido em partes
proporcionais às quantias jogadas. Nesse caso, quanto
receberá cada um?
06.Dividir o número 260 em partes inversamente
proporcionais aos números 2, 3 e 4.
07.Luciana guardou em uma caixa todas as suas
bijuterias, num total de 94 peças. Sabendo que a
quantidade de pulseiras, a de colares e a de anéis que
Luciana possui é inversamente proporcional aos
números 3, 4 e 5, respectivamente, calcule quantas
bijuterias de cada tipo há nessa caixa.
471600
 157200
3
471600
y
 78600
6
471600
z
 52400
9
x
QUESTÕES
01. (Unimontes) Um pai tinha R$800,00. Com essa
quantia, pagou uma dívida correspondente a
08. Os números da sequência 12, 10, 16 são
proporcionais aos da sequência 18, 15, 24? Justifique.
7
do que
20
tinha, e o restante repartiu entre seus três filhos, em partes
inversamente proporcionais às suas respectivas idades
que são 3, 8 e 12 anos. Quanto recebeu o filho mais
velho?
A) R$320,00.
B) R$120,00.
C) R$160,00.
D) R$80,00.
02. (Unimontes) Se a idade de três crianças é
diretamente proporcional a 6, 3 e 15, e se a idade da
primeira com o dobro da idade da segunda e o triplo da
idade da terceira é 38 anos, então as idades são
A)1, 2 e 3.
B)2, 4 e 6.
C) 4, 2 e 10.
D)4, 6 e 10.
03.(Correios) Dividindo-se R$ 3.375,00 em partes A, B e
C, proporcionais respectivamente, a 3, 5 e 7, a parte
correspondente a C é igual a:
A) R$ 675,00.
B) R$ 1.125,00.
C) R$ 2.025,00.
D) R$ 1.575,00.
E) R$ 1.350,00.
04. Dois operários contratam um serviço por R$180,00.
Como devem repartir essa quantia, se um trabalhou 7
horas e o outro 8 horas, sendo a divisão diretamente
proporcional ao tempo de trabalho?
09.Ao dividir o número 120 em partes diretamente
proporcionais a 2 e 3, obtemos:
a) ( ) 60 e 60.
b) ( ) 52 e 68.
c) ( ) 48 e 72.
d) ( ) 30 e 90.
10.(CEFET-MG) Uma herança de R$60.000,00 foi
dividida entre três filhos A, B e C, de maneira
inversamente proporcional às respectivas idades 10, 15
e 18 anos. A quantia, em reais, que o filho B recebeu
foi:
a) ( ) 12.000,00
b) ( ) 14.000,00
c) ( ) 18.000,00
d) ( ) 27.000,00
11. Os três jogadores mais disciplinados de um
campeonato de futebol amador irão receber um prêmio
de R$3340,00 rateados em partes inversamente
proporcionais ao número de faltas cometidas em todo o
campeonato. Os jogadores cometeram 5, 7 e 11 faltas.
Qual a premiação, em reais, referente a cada um deles
respectivamente?
a) ( ) 1530, 1000, 810.
b) ( ) 1540, 1100, 700.
c) ( ) 700, 1100, 1540.
d) ( ) 810, 1000, 1530.
45
12. ( UFT – TO ) Em uma fazenda produtora de soja duas
colheitadeiras A e B são utilizadas para a colheita da
produção. Quando trabalham juntas conseguem fazer toda
a colheita em 72 horas. Porém, utilizando apenas a
colheitadeira A, em 120 horas. Se o produtor utilizar
apenas a colheitadeira B, toda a colheita será feita em:
a) 180 horas
b) 165 horas
c) 157 horas
d) 192 horas
13. Uma verba de R$ 2.700.000,00 deve ser dividida
entre os municípios A, B e C em partes proporcionais ao
número de matrículas no Ensino Fundamental de cada um
deles. O número de alunos matriculados de A é o dobro
do número de alunos matriculados de B que, por sua
vez, tem o triplo do número de matrículas de C. Com base
nessas informações, pode-se afirmar que o município A
deverá receber, em milhares de reais, uma quantia igual a:
a) 270
b) 810
c) 1270
d) 1620
14. Uma mina d'água localiza-se na divisa de dois sítios.
Os dois proprietários, Sr. Edson e Sr. José, resolveram
construir, na saída da mina, uma caixa de água coberta e
vão dividir as despesas entre si, em partes inversamente
proporcionais às distâncias de suas casas em relação à
mina. Se as despesas totalizarem R$ 5.600,00 e se as
casas do Sr. Edson e do Sr. José distam,
respectivamente, 5 km e 3 km da mina, então a parte
da despesa que caberá ao Sr. Edson é
a) R$ 1.900,00
b) R$ 2.100,00
c) R$ 2.200,00
d) R$ 3.100,00
e) R$ 3.500,00
de reais.
06. 120, 80 e 60.
07. 40 pulseiras, 30 colares e 24 anéis
08. ***
09. c
10. c
11. b
12. A
13. D
14. B
15. 03
REGRA DE TRÊS SIMPLES E REGRA DE TRÊS
COMPOSTA
Consta na história da matemática que os gregos e
os romanos conhecessem as proporções, porem não
chegaram a aplicá-las na resolução de problemas.
Na idade média, os árabes revelaram ao mundo a
regra de três. Nos século XIII, o italiano Leonardo de
Pisa difundiu os princípios dessa regra em seu livro
Líber Abaci, com o nome de Regra de Três Números
Conhecidos.
15. ( FASA - 2015 ) O tempo médio de espera de um
pronto-socorro é diretamente proporcional ao número de
pacientes atendidos, mas inversamente proporcional ao
número de médicos atendentes. Em um dia no qual havia
12 médicos e foram atendidos 75 pacientes, esse tempo
foi de 1h15min. Em outro dia, no qual 15 médicos atendam
100 pacientes, calcula-se que esse tempo seja de
01) 1h40min
02) 1h30min
03) 1h20min
04) 1h10min
05) 1h
GABARITO
01. D
02. C
03. D
04. R$84,00 e R$96,00.
05. 1 milhão de reais; 2 milhões de reais e 3 milhões
46
REGRA DE TRÊS SIMPLES
Exercício resolvido
Regra de três simples é um processo prático para
resolver problemas que envolvam quatro valores dos quais
conhecemos três deles. Devemos, portanto, determinar
um valor a partir dos três já conhecidos. Passos utilizados
numa regra de três simples:
a) Em 8 horas, 20 caminhões descarregam 160m 3 de
areia. Em 5 horas, quantos caminhões serão
necessários para descarregar 125m 3?
Para iniciar a resolução desse tipo de regra de três,
devemos organizar as informações.
 Construir uma tabela, agrupando as grandezas da
mesma espécie em colunas e mantendo na
mesma linha as grandezas de espécies diferentes
em correspondência.
 Identificar se as grandezas são diretamente ou
inversamente proporcionais.
 Montar a proporção e resolver a equação.
Exercícios resolvidos
Agora iremos analisar as situações para definir o
sentido das setas.
Aumentando o número de horas de trabalho,
podemos diminuir o número de caminhões.Portanto a
relação é inversamente proporcional (seta para cima na
1ª coluna).
a)
Se 8m de tecido custam 156 reais, qual o preço de
12 m do mesmo tecido?
Observe que as grandezas são diretamente
proporcionais,
aumentando o metro do tecido aumenta na mesma
proporção o preço a ser pago, então teremos:
8 156
156.12

 8 x  156.12  x 
12
x
8
 x  234
A quantia a ser paga é de R$234,00.
b) Um carro, à velocidade de 60km/h, faz certo percurso
em 4 horas. Se a velocidade do carro fosse de 80km/h, em
quantas horas seria feito o mesmo percurso?
Aumentando o volume de areia, devemos aumentar
o número de caminhões. Portanto a relação é
diretamente proporcional (seta para baixo na 3ª
coluna).
Devemos agora igualar a razão que contém o termo
x com o produto das outras razões de acordo com o
sentido das setas, ficando:
20 5 160
20 20
 .


 20 x  25.20
x 8 125
x 25
25.20
x
 x  25
20
Será preciso de 25 caminhões.
QUESTÕES
Observe que as grandezas são inversamente
proporcionais, aumentando a velocidade o tempo diminui
na razão inversa, então teremos:
80 4
60.4
  80 x  60.4  x 
60 x
80
 x3
O carro gastará 3 horas para fazer o mesmo percurso.
REGRA DE TRÊS COMPOSTA
A regra de três composta é utilizada em problemas com
mais de duas grandezas, direta ou inversamente
proporcionais.
01. (ENEM) Segundo as regras da Fórmula 1, o peso
mínimo do carro, de tanque vazio, com o piloto, é de
605 kg, e a gasolina deve ter densidade entre 725 e
780 gramas por litro. Entre os circuitos nos quais
ocorrem competições dessa categoria, o mais longo é
Spa-Francorchamps, na Bélgica, cujo traçado tem 7 km
de extensão. O consumo médio de um carro da
Fórmula 1 é de 75 litros para cada 100 km.
Suponha que um piloto de uma equipe específica,
que utiliza um tipo de gasolina com densidade de 750
g/L, esteja no circuito de Spa-Francorchamps, parado
no Box para reabastecimento. Caso ele pretenda dar
mais 16 voltas, ao ser liberado para retornar à pista,
seu carro deverá pesar, no mínimo,
A) 617 kg.
B)668 kg.
C)680 kg.
47
D) 689 kg.
E) 717 kg
02. (UFMG) Um menino percorre, de bicicleta, 7 km em 35
minutos, com velocidade constante. Aumentando essa
velocidade de 1/5 de seu valor, o tempo que leva, em
minutos, para percorrer 12 km, é:
A) 30
B) 40
C) 50
D) 60
E) 72
03. (USP) Uma família composta de 6 pessoas consome
em 2 dias 3 kg de pão. Quantos quilos serão necessários
para alimentá-la durante 5 dias estando ausentes 2
pessoas?
A) 3
B) 2
C) 4
D) 6
E) 5
04. (UFMG) Dez máquinas, funcionando 6 horas por dia,
durante 60 dias, produzem 90.000 peças. O número de
dias para que 12 dessas máquinas, funcionando 8 horas
por dia, produzam 192.000 peças é:
A) 40
B) 50
C) 70
D) 80
E) 90
05.(IBGE-UFRJ)Em uma fábrica, quatro máquinas
idênticas são capazes de produzir vinte peças em dez
horas. Se apenas duas dessas máquinas forem utilizadas,
dez peças serão produzidas na seguinte quantidade de
horas:
A) 4
B) 8
C) 10
D) 16
E) 20.
06.(BNDES-CESGRANRIO) O estoque de pó de café em
um escritório é suficiente para seus 16 funcionários
durante 62 dias. Depois de 12 dias, passam a trabalhar no
escritório mais 4 funcionários. Passados mais 15 dias, 10
funcionários são transferidos para outro escritório.
Quantos dias mais durará o estoque de pó de café?
A) 23
B) 25
C) 30
D) 35
E) 50
07.(ENEM) Uma escola lançou uma campanha para seus
alunos arrecadarem, durante 30 dias, alimentos não
perecíveis para doar a uma comunidade carente da
região. Vinte alunos aceitaram a tarefa e nos primeiros
10 dias trabalharam 3 horas diárias, arrecadando 12 kg
de alimentos por dia. Animados com os resultados, 30
novos alunos somaram-se ao grupo, e passaram a
trabalhar 4 horas por dia nos dias seguintes até o
término da campanha. Admitindo-se que o ritmo de
coleta tenha se mantido constante, a quantidade de
alimentos arrecadados ao final do prazo estipulado
seria de
A) 920 kg.
B) 800 kg.
C) 720 kg.
D) 600 kg.
E) 570 kg
08.(UNIFOR-CE) Se 6 impressoras iguais produzem
1000 panfletos em 40 minutos, em quanto tempo 3
dessas impressoras produziriam 2000 desses
panfletos?
a) ( ) 1 hora e 50 minutos
b) ( ) 2 horas
c) ( ) 2 horas e 30 minutos
d) ( ) 2 horas e 40 minutos
e) ( ) 3 horas
09.(UFRGS-RS) Se foram empregados 4 Kg de fios
para tecer 14 m de fazenda com 80 cm de largura,
quantos quilogramas serão necessários para produzir
350 m de fazenda com 120 cm de largura?
a) ( ) 130
b) ( ) 150
c) ( ) 160
d) ( ) 180
e) ( ) 250
10.Andando a pé, 8 horas por dia, um rapaz conseguiu,
em 10 dias, percorrer a distância de 320 Km. Quantos
quilômetros esse rapaz poderia percorrer, em 8 dias,
na mesma velocidade, se andasse 12 horas por dia?
a) ( ) 170
b) ( ) 266
c) ( ) 384
d) ( ) 400
11. Em 4 horas, 9 rapazes colhem uma quantidade de
laranja que enche 360 caixas. Quantos rapazes colhem
a quantidade necessária para encher 510 caixas em 3
horas?
12. ( UFSC ) Observe as proposições abaixo
I ) Se 2 impressoras trabalhando 10 horas por dia
levam 5 dias para fazer determinado trabalho, então
3
impressoras (com a mesma eficiência das
anteriores) trabalhando 8 horas por dia levarão 6 dias
para fazer o mesmo trabalho.
II ) Um investidor tem seu dinheiro aplicado a 2% ao
mês. Deseja comprar um bem no valor de
R$
100.000,00, que pode ser pago a vista ou em três
parcelas de R$ 34.000,00, sendo a primeira de entrada
48
e as outras em 30 e 60 dias. Ele sairá lucrando se fizer
a compra parcelada.
III ) Duplicando-se o lado de um triângulo eqüilátero, sua
área fica também duplicada.
IV ) Obter 7 acertos numa prova de 12 questões é um
desempenho inferior a obter 6 acertos numa prova de 10
questões, porém superior a obter 5 acertos numa prova
de 9 questões.
Assinale a alternativa que contém todas as afirmativas
INCORRETAS.
a) I e II.
b) II e III.
c) III e IV.
d) I, II e IV.
e) I, II e III.
GABARITO
1) B
2) C
3) E
8) D
10) C
13) D
9) B
14) E
4) D
5) C
6) E
11) 17 rapazes
7) A
12) E
15) C
13. ( UNICAMP – SP ) Uma obra será executada por 13
operários (de mesma capacidade de trabalho) trabalhando
durante 11 dias com jornada de trabalho de 6 horas por
dia. Decorridos 8 dias do início da obra 3 operários
adoeceram e a obra deverá ser concluída pelos operários
restantes no prazo estabelecido anteriormente. Qual
deverá ser a jornada diária de trabalho dos operários
restantes nos dias que faltam para a conclusão da obra no
prazo previsto?
a) 7h 42
b) 7h 44
c) 7h 46
d) 7h 48
e) 7h 50
14. Um engenheiro, para calcular a área de uma cidade,
copiou sua planta numa folha de papel de boa qualidade,
recortou e pesou numa balança de precisão, obtendo 40
g. Em seguida, recortou do mesmo desenho, uma praça
de dimensões reais 100 m x 100m, pesou o recorte na
mesma balança e obteve 0,08g. Com esses dados foi
possível dizer que a área da cidade, em metros
quadrados, é de, aproximadamente,
A) 800
B) 10000
C) 320000
D) 400000
E) 5000000
( PM – MG ) Um fazendeiro tem milho para alimentar 15
galinhas durante 20 dias. No fim de 2 dias, compra mais 3
galinhas; 4 dias depois desta compra, uma raposa come
algumas galinhas. o fazendeiro pôde alimentar as galinhas
que restaram durante 18 dias. Quantas galinhas a raposa
comeu?
A) 5
B) 6
C) 7
D) 8
49
02. (ENEM - 2010)
PORCENTAGEM
Suponhamos o seguinte problema: Um curso prévestibular aprovou 300 de seus 2.500 alunos. Em cada
100 alunos, quantos foram aprovados?
Observe a regra de três:
2.500 alunos 
100 alunos

300 2500

x
100
300 aprovados
x
 2500x = 30000
 x = 12
Portanto, em cada 100 alunos, 12 foram aprovados.
Dizemos que 12% (doze por cento) dos aluno: foram
aprovados ou que tal curso teve uma porcentagem de
12% de aprovação ou ainda que a taxa percentual de
aprovação foi de 12%.
Uma porcentagem equivale, na prática, a uma razão de
denominador 100.
Exemplos:



5
= 1 = 0,05
100
20
0,2
0,2% =
= 2 = 0,002
100
1000
200
200% =
=2
100
5% =
Exemplo:
Vamos calcular 3,5% de 3800.
3,5% de 3800 = 3,5 x 3800 =133
100
QUESTÕES
01. (UEMG) “O ministro da Saúde, José Gomes
Temporão, afirmou nesta sexta-feira que mais 19 casos de
gripe suína - a gripe A (H1N1) - foram confirmados no
Brasil. Com isso, o número de pessoas infectadas sobe
para 756.
Os novos casos foram confirmados em São Paulo (7),
Minas Gerais (6), Rio de Janeiro (2), Rio Grande do Sul
(2), Paraná (1) e Mato Grosso do Sul (1). De acordo com o
governo, a maioria dos infectados no país, desde 8 de
maio, já recebeu alta ou está em processo de
recuperação”.
Folha OnLine 03/07/2009
Com base nestas informações, em relação aos novos
casos da gripe suína, o número de infectados, na região
sudeste, corresponde, APROXIMADAMENTE:
A) 79% dos casos.
B) 65% dos casos.
C) 70% dos casos.
D) 90% dos casos.
03.(UNIMONTES) Um aluno acertou 60% das 40
questões já feitas do teste de matemática. Para
conseguir 80% de acertos, o número de questões a
mais que ele precisa resolver e acertar é
A) 64.
B) 40.
C) 80.
D) 30.
04.(UFOP) A concentração do álcool na gasolina
brasileira, segundo o CNP – Conselho Nacional de
Petróleo –, é de 25%. Certo posto de gasolina foi
interditado após a fiscalização determinar que a
gasolina possuía concentração de 30% de álcool.
Havia nesse posto um estoque de 80.000 litros dessa
gasolina adulterada. O número de litros de gasolina
pura que deve ser adicionado a esse estoque de modo
a se obter uma mistura com 25% de álcool é:
A) 16.000
B) 20.000
C) 24.000
D) 30.000
05. (FIP) Em uma sala onde estão 100 pessoas, sabese que 99% são homens. Quantos homens devem sair
para que a porcentagem de homens passe a ser de
98%?
A) 2
B) 1
50
QUESTÕES DO ENEM
C) 50
D) 98
06.Um carro bicombustível percorre 8 km com um litro de
álcool e 11 km com um litro do combustível constituído de
75% de gasolina e de 25% de álcool, composição
adotada, atualmente, no Brasil. Recentemente, o Governo
brasileiro acenou para uma possível redução, nessa
mistura, da porcentagem de álcool, que passaria a ser de
20%. Suponha que o número de quilômetros que esse
carro percorre com um litro dessa mistura varia
linearmente de acordo com a proporção de álcool
utilizada. Então, é CORRETO afirmar que, se for utilizado
um litro da nova mistura proposta pelo Governo, esse
carro percorrerá um total de
A) 11,20 km .
B) 11,35 km .
C) 11,50 km .
D) 11,60 km .
07. (CTSP) O valor de
A-( ) 30%
B-( ) 30
C-( ) 3
D-( ) 3%
é:
08. ( MACK – 2001 ) Numa festa, a razão entre o número
de moças e o de rapazes
rapazes na festa é :
a) 44%
b) 45%
d) 48%
e) 46%
é
13
. A porcentagem de
12
c) 40%
09. ( Fuvest – SP ) O quadrado de 6%, a raiz quadrada
positiva de 49% e 4% de 180 valem, respectivamente :
a) 36% ; 7% ; 7,2
b) 0,36% ; 70% ; 7,2
c) 0,36% ; 7% ; 72
d) 36% ; 70% ; 72
e) 3,6% ; 7% ; 7,2
GABARITO
01.
02.
03.
04.
05.
06.
07.
08.
09.
A
C
B
A
C
A
A
D
B
01. (ENEM-2009) Os calendários usados pelos
diferentes povos da terra são muito variados. O
calendário islâmico, por exemplo, é lunar, e nele cada
mês tem sincronia com a fase da lua. O calendário
maia segue o ciclo de Vênus, com cerca de 584 dias, e
cada 5 ciclos de Vênus corresponde a 8 anos de 365
dias da terra.
MATSSURA, Oscar. Calendário e o fluxo do tempo. Scientific American Brasil.
Disponível em: http://www.uol.com.br Acesso em: 14 out. 2008 (adaptado)
Quantos ciclos teria, em Vênus, um período terrestre
de 48 anos?
A) 30 ciclos.
B) 40 ciclos.
C) 73 ciclos.
D) 240 ciclos.
E) 384 ciclos.
02.(ENEM-2009) Pneus usados geralmente são
descartados de forma inadequada, favorecendo a
proliferação de insetos e roedores e provocando sérios
problemas de saúde pública. Estima-se que, no Brasil,
a cada ano, sejam descartados 20 milhões de pneus
usados. Como alternativa para dar uma destinação final
a esses pneus, a Petrobras, em sua unidade de São
Mateus do Sul, no Paraná, desenvolveu um processo
de obtenção de combustível a partir da mistura dos
pneus com xisto. Esse procedimento permite, a partir
de uma tonelada de pneu, um rendimento de cerca de
530 kg de óleo.
Disponível
em:
http://www.ambientebrasil.com.br.
Acesso em 3 out. 2008 (adaptado)
Considerando que uma tonelada corresponde, em
média, a cerca de 200 pneus, se todos os pneus
descartados anualmente fossem utilizados no processo
de obtenção de combustível pela mistura com xisto,
seriam então produzidas
(A) 5,3 mil toneladas de óleo.
(B) 53 mil toneladas de óleo.
(C) 530 mil toneladas de óleo.
(D) 5,3 milhões de toneladas de óleo.
(E) 530 milhões de toneladas de óleo.
03.(ENEM-2009) As abelhas domesticadas da América
do Norte e da Europa estão desaparecendo, sem
qualquer motivo aparente. As abelhas desempenham
papel fundamental na agricultura, pois são
responsáveis pela polinização (a fecundação das
plantas). Anualmente, apicultores americanos alugam 2
milhões de colméias para polinização de lavouras. O
sumiço das abelhas já inflacionou o preço de locação
das colméias. No ano passado, o aluguel de cada caixa
(colméia) com 50.000 abelhas estava na faixa de 75
dólares. Depois do ocorrido, aumentou para 150
dólares. A previsão é que faltem abelhas para
polinização neste ano nos EUA. Somente as lavouras
de amêndoa da Califórnia necessitam de 1,4 milhões
de colméias. Disponível em: http://veja.abril.com.br.
Acesso em: 23 fev. 2009 (adaptado)
De acordo com essas informações, o valor a ser gasto
51
pelos agricultores das lavouras de amêndoa da Califórnia
com o aluguel das colméias será de
A) 4,2 mil dólares.
B)105 milhões de dólares.
C)150 milhões de dólares. D) 210 milhões de dólares.
E) 300 milhões de dólares.
04.(ENEM-2009) Segundo a Associação Brasileira de
Alumínio (ABAL), o Brasil foi o campeão mundial, pelo
sétimo ano seguido, na reciclagem de latas de alumínio.
Foi reciclagem 96,5% do que foi utilizado no mercado
interno em 2007, o equivalente a 11,9 bilhões de latinhas.
Este número significa, em média, um movimento de 1,8
bilhão de reais anuais em função da reutilização de latas
no Brasil, sendo 523 milhões referentes à etapa da coleta,
gerando, assim, “emprego” e renda para cerca de 180 mil
trabalhadores, Essa renda, em muitos casos, serve como
complementação do orçamento familiar e, em outros
casos, como única renda da família.
Revista Conhecimento Prático Geografia,
nº.22.
(adaptado)
Com base nas informações apresentadas, a renda média
mensal dos trabalhadores envolvidos nesse tipo de coleta
gira em torno de
A) R$173,00.
B) R$242,00.
D) R$504,00.
E) R$841,00.
C) R$343,00.
05.(ENEM-2009) Uma fotografia tirada em uma câmera
digital é formada por um grande número de pontos,
denominados pixels. Comercialmente, a resolução de
uma câmera digital é especificada indicando os milhões de
pixels, ou seja, os megapixels de que são constituídas as
suas fotos.
Ao se imprimir uma foto digital em papel fotográfico, esses
pontos devem ser pequenos para que não sejam
distinguíveis a olho nu. A resolução de uma impressora é
indicada pelo termo dpi (dot per inch), que é a
quantidade de pontos que serão impressos em uma linha
com uma polegada de comprimento. Uma foto impressa
com 300 dpi, que corresponde a cerca de 120 pontos por
centímetro, terá boa qualidade visual já que os pontos
serão tão pequenos, que o olho não será capaz de vê-los
separados e passará a ver um padrão contínuo.
Para se imprimir uma foto retangular de 15 cm por 20 cm,
com resolução de pelo menos 300 dpi, qual é o valor
aproximado de megapixels que a foto terá?
A) 1,00 megapixel.
C) 2,70 megapixels
E) 4,32 megapixels.
B) 2,52 megapixels.
D) 3,15megapixels.
06.(ENEM-2009) No depósito de uma biblioteca há caixas
contendo folhas de papel de 0,1 mm de espessura, e em
cada uma delas estão anotadas 10 títulos de livros
diferentes. Essas folhas foram empilhadas formando uma
torre vertical de 1 m de altura.
Qual a representação, em potência de 10, correspondente
à quantidade de títulos de livros registrados nesse
empilhamento?
2
4
A) 10
B) 10
5
6
C) 10
D) 10
7
E) 10
07.(ENEM-2009) Um comerciante contratou um novo
funcionário para cuidar das vendas. Combinou pagar a
essa pessoa R$120,00 por semana, desde que as
vendas se mantivessem em torno dos R$600,00
semanais e, como um estímulo, também propôs que na
semana na qual ele vendesse R$1.200,00, ele
receberia R$200,00, em vez de R$120,00.
Ao término da primeira semana, esse novo
funcionário conseguiu aumentar as vendas para
R$990,00e foi pedir ao seu patrão um aumento
proporcional ao que consegui aumentar as vendas. O
patrão concordou e, após fazer alguns cálculos, pagou
ao funcionário a quantia de
A) R$160,00.
D) R$180,00.
B) R$165,00.
E) R$198,00.
C) R$172,00.
08.(ENEM-2009) A taxa anual de desmatamento na
Amazônia é calculada com dados de satélite, pelo
Instituto Nacional de Pesquisas Espaciais (INPE), de 1º
de agosto de um ano a 31 de julho do ano seguinte. O
mês de julho de 2008 foi registrado que o
desmatamento acumulado nos últimos 1 meses havia
sido 64% maior do que no ano anterior, quando o INPE
registrou 4.974 km 2 de floresta desmatada. Nesses
mesmos 12 meses acumulados, somente o estado de
Mato Grosso foi responsável por, aproximadamente,
56%da área total desmatada na Amazônia.
Jornal O Estado de São Paulo. Disponível em:
<http://www.estadao.com.br>. Acesso em 30 ago.2008
(adaptado).
De acordo com os dados, a área desmatada sob a
responsabilidade do estado do Mato Grosso,em julho
de 2008, foi
(A) inferior a 2.500 km 2.
2
2
(B) superior a 2.500 km e inferior a 3.000 km .
2
2
(C) superior a 3.000 km e inferior a 3.900 km .
2
(D) superior a 3.900 km e inferior a 4.700 km 2.
(E) superior a 4.700 km2.
09.(ENEM-2009) No mundial de 2007, o americano
Bernard Lagat, usando pela primeira vez uma sapatilha
34% mais levedo que a média, conquistou o ouro na
corrida de 1.500 metros com um tempo de 3,58
minutos. No ano anterior, em 2006, ele havia ganhado
medalha de ouro com um tempo de 3,65 minutos nos
mesmos 1.500 metros.
Revista Veja, São Paulo, ago. 2008 (adaptado)
Sendo assim, a velocidade média do atleta aumentou
em aproximadamente
A) 1,05
B) 2,00%
C) 4,11%
D) 4,19%
E) 7,00%
52
10.(ENEM-2009)Uma pesquisa foi realizada para tentar
descobrir, do ponto de vista das mulheres, qual é o perfil
da parceira ideal procurada pelo homem do séc XXI.
Alguns resultados estão apresentados no quadro abaixo.
pelo correio. O diretor da escola pesquisou que tipos
de selos deveriam ser utilizados. Concluiu que, para o
primeiro tipo de folheto, bastava um selo de R$ 0,65
enquanto para folhetos do segundo tipo seriam
necessários três selos, um de R$ 0,65, um de R$ 0,60
e um de R$ 0,20. O diretor solicitou que se
comprassem selos de modo que fossem postados
exatamente 500 folhetos do segundo tipo e uma
quantidade restante de selos que permitisse o envio do
máximo possível de folhetos do primeiro tipo.
Quantos selos de R$ 0,65 foram comprados?
A) 476
B) 675
C) 923
D) 965
E) 1 538
Se a pesquisa foi realizada com 300 mulheres,
então a quantidade delas que acredita que os homens
odeiam ir ao shoping e pensam que eles preferem que
elas façam todas as tarefas da casa é
A) inferior a 80.
B) superior a 80 e inferior a 220.
C) superior a 100 e inferior a 120.
D) superior a 120 e inferior a 140.
E) superior a 140.
14.(ENEM-2010) Em 2006, a produção mundial de
etanol foi de 40 bilhões de litros e a de biodiesel, de 6,5
bilhões. Neste mesmo ano, a produção brasileira de
etanol correspondeu a 43 % da produção mundial, ao
passo que a produção dos Estados Unidos da América,
usando milho, foi de 45 %.
11.(ENEM-2010) No monte do Cerro Amazones, no
deserto do Atacama, no Chile, ficará o maior telescópio da
superfície terrestre, o Telescópio Europeu Extremamente
Grande (E – ELT). O E–
ELT terá um espelho primário de 42m de diâmetro, “O
maior olho do mundo voltado para o céu”.
Ao ler o texto em sala de aula, a professora fez uma
suposição de que o diâmetro do olho humano mede
aproximadamente 2,1cm.
Qual a razão entre o diâmetro do olho humano, e o
diâmetro do espelho primário do telescópio citado?
A) 1:20;
B) 1:100;
C) 1:200;
D) 1:1000;
E) 1:2000.
12.(ENEM-2010) Uma empresa possui um sistema de
controle de qualidade que classifica o seu desempenho
financeiro anual, tendo como base o do ano anterior. Os
conceitos são: insuficiente, quando o crescimento é menor
que 1%; regular, quando o crescimento é maior ou igual a
1% e menor que 5%; bom, quando o crescimento é maior
ou igual a 5% e menor que 10%; ótimo, quando é maior ou
igual a 10% e menor que 20%; e excelente, quando é
maior ou igual a 20%. Essa empresa apresentou lucro de
R$ 132 000,00 em 2008 e de R$ 145 000,00 em 2009.
De acordo com esse sistema de controle de qualidade, o
desempenho financeiro dessa empresa no ano de 2009
deve ser considerado
A) insuficiente.
B) regular.
C) bom.
D) ótimo.
E) excelente.
13.(ENEM-2010) Uma escola recebeu do governo uma
verba de R$ 1000,00 para enviar dois tipos de folhetos
Disponível em: planetasustentavel.abril.com.br. Acesso em: 02 maio 2009.
Considerando que, em 2009, a produção mundial de
etanol seja a mesma de 2006 e que os Estados Unidos
produzirão somente a metade de sua produção de
2006, para que o total produzido pelo Brasil e pelos
Estados Unidos continue correspondendo a 88% da
produção mundial, o Brasil deve aumentar sua
produção em, aproximadamente,
A) 22,5%.
B) 50,0%.
C) 52,3%.
D) 65,5%
E) 77,5%.
15.(ENEM-2010) A disparidade de volume entre os
planetas é tão grande que seria possível colocá-los uns
dentro dos outros. O planeta Mercúrio é o menor de
todos. Marte é o segundo menor: dentro dele cabem
três Mercúrios. Terra é o único com vida: dentro dela
cabem sete Martes. Netuno é o quarto maior: dentro
dele cabem 58 Terras. Júpiter é o maior dos planetas:
dentro dele cabem 23 Netunos.
Revista Veja. Ano 41, nº 25, 25 jun. 2008 (adaptado).
Seguindo o raciocínio proposto, quantas Terras cabem
dentro de Júpiter?
A) 406
B) 1 334
C) 4 002
D) 9 338
E) 28 014
16.(ENEM-2010) Um dos grandes problemas da
poluição dos mananciais (rios, córregos e outros)
ocorre pelo hábito de jogar óleo utilizado em frituras
nos encanamentos que estão interligados com o
sistema de esgoto. Se isso ocorrer, cada 10 litros de
óleo poderão contaminar 10 milhões de litros de água
potável.
Manual de etiqueta. Parte integrante das revistas Veja (ed. 2055), Cláudia
(ed. 555),
National Geographic (ed. 93) e Nova Escola (ed. 208)
(adaptado).
Suponha que todas as famílias de uma cidade
descartem os óleos de frituras através dos
53
encanamentos e consomem 1 000 litros de óleo em
frituras por semana. Qual seria, em litros, a quantidade de
água potável contaminada por semana nessa cidade?
–2
3
A) 10
B) 10
4
C) 10
C) 10 6
9
E) 10
17.(ENEM-2013)Muitos
processos
fisiológicos
e
bioquímicos, tais como batimentos cardíacos e taxa de
respiração, apresentam escalas construídas a partir da
relação entre superfície e massa (ou volume) do animal.
Uma dessas escalas, por exemplo, considera que “o cubo
da área S da superfície de um mamífero é proporcional ao
quadrado de sua massa M”.
HUGHES-HALLETT, D. et al. Cálculo e aplicações. São Paulo: Edgard Blücher, 1999
(adaptado).
Isso é equivalente a dizer que, para uma constante k > 0,
a área S pode ser escrita em função de M por meio da
expressão:
A) S = k . M
B) S  k. M
1
3
C) S  k
1
1
3.M 3
D) S  k
1
2
3.M 3
1
E) S  k 3 . M2
18.(ENEM-2013) Uma indústria tem um reservatório de
água com capacidade para 900 m 3. Quando há
necessidade de limpeza do reservatório, toda a água
precisa ser escoada. O escoamento da água é feito por
seis ralos, e dura 6 horas quando o reservatório está
cheio.
Esta indústria construirá um novo reservatório, com
capacidade de 500 m3, cujo escoamento da água deverá
ser realizado em 4 horas, quando o reservatório estiver
cheio. Os ralos utilizados no novo reservatório deverão ser
idênticos aos do já existente.
A quantidade de ralos do novo reservatório deverá ser
igual a
A) 2.
B) 4.
C) 5.
D) 8.
E) 9.
nas rodovias brasileiras é o excesso de carga
transportada pelos caminhões. Dimensionado para o
tráfego dentro dos limites legais de carga, o piso das
estradas se deteriora com o peso excessivo dos
caminhões. Além disso, o excesso de carga interfere
na capacidade de frenagem e no funcionamento da
suspensão do veículo, causas frequentes de acidentes.
Ciente dessa responsabilidade e com base na
experiência adquirida com pesagens, um caminhoneiro
sabe que seu caminhão pode carregar, no máximo, 1
500telhas ou 1 200 tijolos.
Considerando esse caminhão carregado com 900
telhas, quantos tijolos, no máximo, podem ser
acrescentados à carga de modo a não ultrapassar a
carga máxima do caminhão?
A)300 tijolos
B)360 tijolos
C) 400 tijolos
D)480 tijolos
E)600 tijolos
21.(ENEM-2013) Uma torneira não foi fechada
corretamente e ficou pingando, da meia-noite às seis
horas da manhã, com a frequência de uma gota a cada
três segundos. Sabe-seque cada gota d’agua tem
volume de 0,2 mL.Qual foi o valor mais aproximado do
total de água desperdiçada nesse período, em litros?
A) 0,2
B) 1,2
C) 1,4
D) 12,9
E) 64,8
22.(ENEM-2013) Nos Estados Unidos a unidade de
medida de volume mais utilizada em latas de
refrigerante é a onça fluida (fl oz), que equivale a
aproximadamente 2,95 centilitros (cL).
Sabe-se que o centilitro é a centésima parte do litro e
que a lata de refrigerante usualmente comercializada
no Brasil tem capacidade de 355 mL.
Assim, a medida do volume da lata de refrigerante de
355 mL, em onça fluida (fl oz), é mais próxima de
A) 0,83.
B) 1,20.
C) 12,03.
D) 104,73.
E) 120,34.
23.(ENEM-2013)A figura apresenta dois mapas, em
que o estado do Rio de Janeiro é visto em diferentes
escalas.
19.(ENEM-2013) Para se construir um contrapiso, é
comum, na constituição do concreto, se utilizar cimento,
areia e brita, na seguinte proporção: 1 parte de cimento, 4
partes de areia e 2 partes de brita. Para construir o
contrapiso de uma garagem, uma construtora
encomendou um caminhão betoneira com 14 m3 de
concreto.
Qual é o volume de cimento, em m3, na carga de concreto
trazido pela betoneira?
A) 1,75
B) 2,00
C) 2,33
D) 4,00
E) 8,00
20.(ENEM-2013) Um dos grandes problemas enfrentados
54
de R$ 10,00 por trabalhador por dia de trabalho, e R$
1.000,00 pelo aluguel diário de cada máquina. O
fazendeiro argumentou que fecharia contrato se a
cooperativa colhesse 180 hectares de milho em 6 dias,
com gasto inferior a R$ 25.000,00.
Para atender às exigências do fazendeiro e supondo
que o ritmo dos trabalhadores e das máquinas seja
constante, a cooperativa deveria
A) manter sua proposta.
B) oferecer 4 máquinas a mais.
C) oferecer 6 trabalhadores a mais.
D) aumentar a jornada de trabalho para 9 horas diárias.
E) reduzir em R$ 400,00 o valor do aluguel diário de
uma máquina.
Há interesse em estimar o número de vezes que foi
ampliada a área correspondente a esse estado no mapa
do Brasil.
Esse número é
A) menor que 10.
B) maior que 10 e menor que 20.
C) maior que 20 e menor que 30.
D) maior que 30 e menor que 40.
E) maior que 40.
24.(ENEM-2013) A Secretaria de Saúde de um município
avalia um programa que disponibiliza, para cada aluno de
uma escola municipal, uma bicicleta, que deve ser usada
no trajeto de ida e volta, entre sua casa e a escola. Na
fase de implantação do programa, o aluno que morava
mais distante da escola realizou sempre o mesmo trajeto,
representado na figura, na escala 1 : 25 000, por um
período de cinco dias.
26. (ENEM/2009) O mapa ao lado representa um bairro
de determinada cidade, no qual as flechas indicam o
sentido das mãos do tráfego. Sabe-se que esse bairro
foi planejado e que cada quadra representada na figura
é um terreno quadrado, de lado igual a 200 metros.
Desconsiderando-se a largura das ruas, qual seria o
tempo, em minutos, que um ônibus, em velocidade
constante e igual a 40km/h, partindo do ponto X,
demoraria para chegar até o ponto Y?
A) 25 min
B) 15 min
C) 2,5 min D)1,5 min
E) 0,15 min
27.(ENEM/2009) Uma resolução do Conselho Nacional
de Política Energética (CNPE) estabeleceu a
obrigatoriedade de adição de biodísel ao óleo dísel
comercializado nos postos. A exigência é que, a partir
de 1.º de julho de 2009, 4% do volume da mistura final
seja formada por biodísel. Até junho de 2009, esse
percentual era de 3%. Essa medida estimula a
demanda de biodísel, bem como possibilita a redução
da importação de dísel de petróleo.
Disponível em: http://www1.folha.uol.com.br.
Acesso em: 12 jul. 2009 (adaptado).
Quantos quilômetros esse aluno percorreu na fase de
implantação do programa?
A) 4
B) 8
C) 16
D) 20
E) 40
25.(ENEM/2009) Uma cooperativa de colheita propôs a
um fazendeiro um contrato de trabalho nos seguintes
termos: a cooperativa forneceria 12 trabalhadores e 4
máquinas, em um regime de trabalho de 6 horas diárias,
capazes de colher 20 hectares de milho por dia, ao custo
Estimativas indicam que, com a adição de 4% de
biodísel ao dísel, serão consumidos 925 milhões de
litros de biodísel no segundo semestre de 2009.
Considerando-se essa estimativa, para o mesmo
volume da mistura final dísel/biodísel consumida no
segundo semestre de 2009, qual seria o consumo de
biodísel com a adição de 3%?
A)27,75 milhões de litros.
B)37,00 milhões de litros.
C)231,25 milhões de litros.
D)693,75 milhões de litros.
E)888,00 milhões de litros
55
28.(ENEM/2009) Técnicos concluem mapeamento do
aquífero Guarani
O aquífero Guarani localiza-se no subterrâneo dos
territórios da Argentina, Brasil, Paraguai e Uruguai, com
extensão total de 1.200.000 quilômetros quadrados, dos
quais 840.000 quilômetros quadrados estão no Brasil. O
aquífero armazena cerca de 30 mil quilômetros cúbicos de
água e é considerado um dos maiores do mundo.
Na maioria das vezes em que são feitas referências à
água, são usadas as unidades metro cúbico e litro, e não
as unidades já descritas. A Companhia de Saneamento
Básico do Estado de São Paulo (SABESP) divulgou, por
exemplo, um novo reservatório cuja capacidade de
armazenagem é de 20 milhões de litros.
Disponível em: http://noticias.terra.com.br.
Acesso em: 10 jul. 2009 (adaptado).
Comparando as capacidades do aquífero Guarani e desse
novo reservatório da SABESP, a capacidade do aquífero
Guarani é
2
A)1,5  10 vezes a capacidade do reservatório novo.
B)1,5  103 vezes a capacidade do reservatório novo.
C)1,5  106 vezes a capacidade do reservatório novo.
D)1,5  108 vezes a capacidade do reservatório novo.
E)1,5  109 vezes a capacidade do reservatório novo.
29.(ENEM/2009) A figura a seguir mostra as medidas reais
de uma aeronave que será fabricada para utilização por
companhias de transporte aéreo. Um engenheiro precisa
fazer o desenho desse avião em escala de 1:150.
constante, a quantidade de alimentos arrecadados ao
final do prazo estipulado seria de
A) 920 kg.
B)800 kg.
C)720 kg.
D)600 kg.
E)570 kg.
31.(ENEM/2009) Segundo as regras da Fórmula 1, o
peso mínimo do carro, de tanque vazio, com o piloto, é
de 605 kg, e a gasolina deve ter densidade entre 725 e
780 gramas por litro. Entre os circuitos nos quais
ocorrem competições dessa categoria, o mais longo é
Spa-Francorchamps, na Bélgica, cujo traçado tem 7 km
de extensão. O consumo médio de um carro da
Fórmula 1 é de 75 litros para cada 100 km.
Suponha que um piloto de uma equipe específica, que
utiliza um tipo de gasolina com densidade de 750 g/L,
esteja no circuito de Spa-Francorchamps, parado no
box para reabastecimento. Caso ele pretenda dar mais
16 voltas, ao ser liberado para retornar à pista, seu
carro deverá pesar, no mínimo,
A) 617 kg.
B) 668 kg.
C) 680 kg.
D) 689 kg.
E) 717 kg.
32.(ENEM/2009) A vazão do rio Tietê, em São Paulo,
constitui preocupação constante nos períodos
chuvosos. Em alguns trechos, são construídas
canaletas para controlar o fluxo de água. Uma dessas
canaletas, cujo corte vertical determina a forma de um
trapézio isósceles, tem as medidas especificadas na
figura I. Neste caso, a vazão da água é de 1.050 m 3/s.
3
O cálculo da vazão, Q em m /s, envolve o produto da
área A do setor transversal (por onde passa a água),
em m2, pela velocidade da água no local, v, em m/s, ou
seja, Q = Av.
Planeja-se uma reforma na canaleta, com as
dimensões especificadas na figura II, para evitar a
ocorrência de enchentes.
Para o engenheiro fazer esse desenho em uma folha de
papel, deixando uma margem de 1 cm em relação às
bordas da folha, quais as dimensões mínimas, em
centímetros, que essa folha deverá ter?
A) 2,9 cm  3,4 cm.
B)3,9 cm  4,4 cm.
C) 20 cm  25 cm.
D) 21 cm  26 cm.
E)192 cm  242 cm.
30.(ENEM/2009) Uma escola lançou uma campanha para
seus alunos arrecadarem, durante 30 dias, alimentos não
perecíveis para doar a uma comunidade carente da
região.
Vinte alunos aceitaram a tarefa e nos primeiros 10 dias
trabalharam 3 horas diárias, arrecadando 12 kg de
alimentos por dia. Animados com os resultados, 30 novos
alunos somaram-se ao grupo, e passaram a trabalhar 4
horas por dia nos dias seguintes até o término da
campanha.
Admitindo-se que o ritmo de coleta tenha se mantido
Na suposição de que a velocidade da água não se
alterará, qual a vazão esperada para depois da reforma
na canaleta?
56
A) 90 m3/s.
3
C) 1.050 m /s.
3
E)2.009 m /s.
B) 750 m3/s.
3
D) 1.512 m /s.
33.(ENEM/2009) A resolução das câmeras digitais
modernas é dada em megapixels, unidade de medida que
representa um milhão de pontos. As informações sobre
cada um desses pontos são armazenadas, em geral, em
3bytes.Porém, para evitar que as imagens ocupem muito
espaço, elas são submetidas a algoritmos de compressão,
que reduzem em até 95% a quantidade de bytes
necessários para armazená-las. Considere 1 KB = 1.000
bytes, 1 MB = 1.000 KB, 1 GB = 1.000 MB.
Utilizando uma câmera de 2.0 megapixels cujo algoritmo
de compressão é de 95%, João fotografou 150 imagens
para seu trabalho escolar. Se ele deseja armazená-las de
modo que o espaço restante no dispositivo seja o menor
espaço possível, ele deve utilizar
A)um CD de 700 MB.
B)um pendrivede 1 GB.
C)um HD externo de 16 GB.
D)um memorystickde 16 MB.
E)um cartão de memória de 64 MB.
34.(ENEM/2010) A resistência elétrica e as dimensões
do condutor
A relação da resistência elétrica com as dimensões do
condutor foi estudada por um grupo de cientistas por meio
de vários experimentos de eletricidade. Eles verificaram
que existe proporcionalidade entre:
 resistência (R) e comprimento (), dada a mesma secção
transversal (A);
 resistência (R) e área da secção transversal (A). dado o
mesmo comprimento () e
 comprimento () e área da secção transversal (A), dada
a mesma resistência (R).
Considerando os resistores como fios, pode-se
exemplificar o estudo das grandezas que influem na
resistência elétrica utilizando as figuras seguintes.
d)inversa, direta e direta.
e)inversa, direta e inversa.
GABARITO
01. A
02. B
03. D
04. B
05. E
06. C
07. C
08. D
09. B
10. C
11. E
12. C
13. C
14. C
15. B
16. E
17. D
18. C
19. B
20. D
21. C
22. C
23. D
24. E
25. D
26. D
27. D
28. E
29. D
30. A
31. B
32. D
33. E
34. C
Disponível em: http://www.efeitojoule.com.
Acesso em: abr. 2010 (adaptado)
As figuras mostram que as proporcionalidades existentes
entre resistência (R) e comprimento (), resistência (R) e
área da secção transversal (A), e entre comprimento () e
área da secção transversal (A) são, respectivamente,
a)direta, direta e direta.
b)direta, direta e inversa.
c)direta, inversa e direta.
57
CÁLCULO ALGÉBRICO
EXPRESSÃO ALGÉBRICA
Chama-se expressão algébrica todo conjunto de
números e variáveis ligados entre si pelas operações
numéricas usuais.
Chama-se variável qualquer símbolo que representa
um elemento genérico de um conjunto, que é denominado
então domínio da variável.
Exemplos
a.
3x  y
2x 
x 2
b.
5a 3 
x3 y

6
2
MONÔMIOS OU TERMOS ALGÉBRICOS
Chama-se monômio ou termo algébrico toda
expressão algébrica em que as constantes e as variáveis
estão ligadas apenas pela operação multiplicação.
Exemplo:
6x = 6 . x
semelhantes.
Exemplos:

5x – 3x + 6x + x = (5 – 3 + 6 +1)x = 9x

2ab2 –
1 
1
ab2
1 2

ab – ab2 =  2   1ab2  ab2 
2
2
2
2


A adição
e a subtração de monômios não
semelhantes não resulta em um monômio.
Exemplos
 5x + 3y2 – 6x – x + 4y2 + xy2 =
= (5x – 6x – x) + (3y + 4y2) + xy2 = – 2x + 7y2 + xy2
A multiplicação, a divisão e a potenciação de expoente
natural se efetuam, no conjunto dos monômios,
utilizando-se as propriedades dessas operações em IR.
A divisão de monômios pode resultar ou não em
monômio.
Exemplos:

(–2x3y).(5xyz).(–xz4)
= (–2). 5 (–1).(x3.x.x).(y.y).(z.z4)
Num monômio, distinguimos duas partes: o coeficiente
(ou parte constante) e a parte variável.
Exemplo:
2
2
No monômio M(a, b)   a3 b5 , o coeficiente é 
e
3
3
a parte variável é a3 b5.
O grau de um monômio o expoente de sua variável
(se ela é única) ou a soma dos expoentes de suas
variáveis.
Exemplo:
A (x) = 3x5 é um monômio de 5° grau
MONÔMIOS SEMELHANTES
Dois termos ou monômios que apresentam a parte
variável igual são chamados termos ou monômios
semelhantes.
Exemplos:
 São semelhantes os termos 2xy4, –2xy4 e xy4
 Não são semelhantes os monômios 5a3b2 e 5a2b3.
OPERAÇÕES COM MONÔMIOS
A adição e a subtração de monômios semelhantes
resulta sempre em um monômio. Basta aplicar a
propriedade distributiva da multiplicação em relação a
adição. Tal procedimento é chamado redução de termos
= 10 x5 y2 z5.

 6ax 3 8x 4 y  6x 2 8 3


 x y
3x
5a
3
5a 2 x
MDC E MMC DE MONÔMIOS
O máximo divisor comum e o mínimo múltiplo
comum de monômios são calculados de maneira
semelhante ao MDC e MMC de números naturais.
–MDC: fatores comuns com os menores expoentes;
–MMC:fatores comuns e não comuns com os maiores
expoentes.
Exemplo:

Seja os monômios
A  6x 3 y 2 z e B  8x 5 y .
MDC (A, B)  2x 3 y e MMC (A, B)  24x 5 y 2 z
IDENTIDADES ALGÉBRICAS NOTÁVEIS
Uma igualdade algébrica envolvendo dois polinômios
pode ser de dois tipos:
a) identidade: verifica-se quaisquer que sejam os
valores reais atribuídos às variáveis.
b) equação: verifica-se apenas para
58
determinados valores atribuídos às variáveis.
Algumas identidades algébricas aparecem com muita
freqüência e possuem importantes aplicações. São as
chamadas identidades notáveis. Apresentamos as mais
importantes no quadro a seguir.
2
= a + 2ab + b
2
= a2 – 2ab + b2
(a + b)
(a – b)
2
(a + b)3
= a3 + 3a2b + 3ab2 + b3
(a – b)3
= a3 – 3a2b + 3ab2 – b3
a3 + b3
= (a + b)(a2 – ab + b2)
a3 – b3
= (a – b)(a2 + ab + b2)
(a+b+c)
2
2, obtemos: x 
2
= a + b + c +2ab +2ac +2bc
Exemplos:
2
2
 Calcule (5x – 3) (5x + 3).
Observe que se trata do produto da soma de dois
termos pela diferença dos mesmos termos. Considerando
2
a = 5x e b = 3; Então,
2
2
2 2
2
4
(5x - 3) (5x + 3) = (5x ) – 3 = 25x – 9.

Calcule (2x – y)3.
Trata-se do cubo de uma diferença, sendo a = 2x e b =
y.
3
3
8 x  6 x  10  7
 2 x  17
Dividindo ambos os membros dessa igualdade por
= (a + b)(a – b)
2
2
8x  7  6 x  10
Subtraindo 6 x de cada membro da equação e
adicionando 7 a cada membro, obtemos:
2
a2 – b2
2
Exemplo
Determinar o número real x tal que
Resolução
2
(2x – y) = (2x) – 3.(2x) . y + 3.(2x) . y – y
3
Então (2x – y)3 = 8x3 – 12x2y + 6xy2 – y3
17
.
2
Conjunto Universo E Conjunto Solução De Uma
Equação
Ao estabelecemos um conjunto universo U para uma
equação, estamos exigindo que sejam aceitas como
soluções apenas as raízes da equação que pertençam
a U. O conjunto formado por essas soluções é
chamado de
conjunto solução(S) ou conjunto
verdade(V) da equação.
Exercício resolvido
1. (UNIUBE) A fim de arrecadar fundos para obras
sociais, um grupo de amigos promoveu um almoço
beneficente em que adultos pagaram R$ 6,00 e
crianças R$ 3,00. Entre adultos e crianças,
compareceram 100 pessoas e o total arrecadado foi
R$ 555,00. Compareceram ao almoço um total de:
a) 20 crianças
b) 15 crianças
c) 25 crianças
d) 30 crianças
EQUAÇÕES DO 1° GRAU
As equações do 1° grau são aquelas que podem ser
representadas sob a forma:
ax  b  0
em que a e b são constantes reais, com a  0 , e x é a
incógnita.
A resolução desse tipo de equação é fundamentada
nas propriedades da igualdade, descritas a seguir.
 Adicionando um mesmo número a ambos os
membros de uma igualdade, ou subtraindo um
mesmo número de ambos os membros, a
igualdade se mantém.
 Dividindo ou multiplicando ambos os membros de
uma igualdade por um mesmo número não-nulo, a
igualdade se mantém.
59
EXERCÍCIOS
01. Um carpinteiro cortou um caibro de 11m de
comprimentos em dois pedaços. Um dos pedaços tem 1m
a menos que o dobro do outro. Qual é a medida do maior
pedaço?
02.( VUNESP) Um clube promoveu um show de música
popular brasileira ao qual compareceram 200 pessoas
entre sócios e não-sócios. No total o valor arrecadado foi
R$1400,00 e todas as pessoas pagaram ingressos.
Sabendo-se que o preço do ingresso foi R$ 10,00 e cada
sócio pagou a metade desse valor, o número de sócios
presentes no show é:
a) 80
b) 100
c) 120
d) 140
e)160
03.( PUC) A soma das idades de um pai e de seu filho é
65 anos. Daqui a 2 anos o pai terá exatamente o dobro da
idade do filho. Determinar a diferença de idade entre pai e
filho.
04. A soma de três números ímpares consecutivos excede
o maior deles em 32 unidades. O menor desses números
é:
a) múltiplo de 6
b) múltiplo de 10
c) divisor de 16
d) divisor de 30
05.( PUC-MG) Todos os alunos de uma turma vão ao
laboratório de informática. Se em cada computador
ficarem 2 alunos, 8 ficarão sem computador. Porém, se
em cada computador ficarem 3 alunos, haverá 4
computadores sobrando. O número de alunos dessa turma
é:
a) 42
b) 48
c) 54
d) 60
06. (UFMG) Um estudante planejou fazer uma viagem de
férias e reservou uma certa quantia em dinheiro para o
pagamento de diárias. Ele tem duas opções de
hospedagem: a Pousada A, com diária R$ 25,00 , e a
Pousada B, com diárias de R$ 30,00 . Se escolher a
Pousada A, em vez da Pousada B, ele poderá ficar três
dias a mais de férias. Neste caso, é correto afirmar que,
para o pagamento de diárias, esse estudante reservou:
a) R$ 300,00
b) R$ 600,00
c) R$ 350,00
d) R$ 450,00
07.(PAES) Um granjeiro ia vender ovos a R$ 1,60 a
dúzia. Quando os estava colocando na prateleira,
quebraram-se cincos dúzias. Não pretendendo ter
prejuízos, o granjeiro resolveu vender os ovos
restantes a R$ 1,80 a dúzia. Quantas dúzias possuía
no início?
a) 20
b) 15
c) 30
d) 45
08.(CESPE/UNB) Suponha que, em 2006, em um
estado brasileiro, o número de candidatos à Câmara
Federal foi igual a doze vezes o número de candidatos
ao Senado Federal, e o número de candidatos à
Câmara Estadual foi igual ao triplo do número de
candidatos à Câmara Federal. Sabendo-se que, nesse
estado, o número de candidatos à Câmara Federal
adicionado ao número de candidatos ao Senado
Federal era igual a 65, é correto concluir que, nesse
estado, o número de candidatos à Câmara Estadual em
2006 foi
A) inferior a 150.
B) superior a 150 e inferior a 160.
C) superior a 160 e inferior a 170.
D) superior a 170.
09. Paulo é 6 anos mais novo que Marcos. Sabendo-se
que há 4 anos a soma das idades de Paulo Marcos era
46 anos qual será a idade de Marcos daqui a 5 anos?
a) 32
b) 33
c) 34
d) 35
GABARITO
01. 7 cm
05. B
02. C
06. D
03. 23 anos
07. D 08. D
04. D
09. D
QUESTÕES DO ENEM
01. (ENEM-2009) Diante de um sanduíche e de uma
porção de batatas fritas, um garoto, muito interessado
na quantidade de calorias que pode ingerir em cada
refeição, analisa os dados de que dispõe. Ele sabe que
a porção de batatas tem 200g, o que equivale a 560
calorias, e que o sanduíche tem 250 g e 500 calorias.
Como ele deseja comer um pouco do sanduíche e um
pouco das batatas, ele se vê diante da
questão:”Quantos gramas de sanduíche e quantos
gramas de batata eu posso comer para ingerir apenas
as 462 calorias permitidas para esta refeição?”
Considerando que x e y representam, respectivamente,
60
em gramas, as quantidades do sanduíche e das batatas
que o garoto pode ingerir, assinale a alternativa
correspondente à expressão algébrica que relaciona
corretamente essas quantidades.
A) 2x + 2,8y = 462
C) 1,8x + 2,3y = 1.060
E) 0,4x + 1/2y = 462
B) 2,8x + 2y = 462
D) 1/2x + 0,4y = 462
02. (ENEM-2010) O Salto Triplo é uma modalidade do
atletismo em que o atleta dá um salto em um só pé, uma
passada e um salto, nessa ordem. Sendo que o salto com
impulsão em um só pé será feito de modo que o atleta
caia primeiro sobre o mesmo pé que deu a impulsão; na
passada ele cairá com o outro pé, do qual o salto é
realizado.Disponível em: www.cbat.org.br (adaptado).
Um atleta da modalidade Salto Triplo, depois de estudar
seus movimentos, percebeu que, do segundo para o
primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro
para o segundo salto, o alcance diminuía 1,5 m. Querendo
atingir a meta de 17,4 m nessa prova e considerando os
seus estudos, a distância alcançada no primeiro salto teria
de estar entre
A) 4,0 m e 5,0 m.
C) 6,0 m e 7,0 m.
E) 8,0 m e 9,0 m.
B) 5,0 m e 6,0 m.
D) 7,0 m e 8,0 m.
03. (ENEM-2010) Um grupo de pacientes com Hepatite C
foi submetido a um tratamento tradicional em que 40%
desses pacientes foram completamente curados. Os
pacientes que não obtiveram cura foram distribuídos em
dois grupos de mesma quantidade e submetidos a dois
tratamentos inovadores. No primeiro tratamento inovador,
35% dos pacientes foram curados e, no segundo, 45%.
Em relação aos pacientes submetidos inicialmente, os
tratamentos inovadores proporcionaram cura de
A) 16%.
D) 48%.
B) 24%.
E) 64%.
C) 32%.
04. (ENEM-2009) Um grupo de 50 pessoas fez um
orçamento inicial para organizar uma festa, que seria
dividido entre elas em cotas iguais. Verificou-se ao final
que, para arcar com todas as despesas, faltavam R$
510,00, e que 5 novas pessoas haviam ingressado no
grupo. No acerto foi decidido que a despesa total seria
dividida em partes iguais pelas 55 pessoas. Quem não
havia ainda contribuído pagaria a sua parte, e cada uma
das 50 pessoas do grupo inicial deveria contribuir com
mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota
calculada no acerto final para cada uma das 55 pessoas?
A) R$ 14,00.
D) R$ 32,00.
B) R$ 17,00.
E) R$ 57,00.
C) R$ 22,00.
05. (ENEM-2013) Uma fábrica de fórmicas produz placas
quadradas de lados de medida igual a y centímetros.
Essas placas são vendidas em caixas com N unidades e,
na caixa, é especificada a área máxima S que pode ser
coberta pelas N placas.
Devido a uma demanda do mercado por placas
maiores, a fábrica triplicou a medida dos lados de suas
placas e conseguiu reuni-las em uma nova caixa, de tal
forma que a área coberta S não fosse alterada.
A quantidade X, de placas do novo modelo, em cada
nova caixa será igual a:
A) N/9
B) N/6
C) N/3
D) 3N
E) 9N
06. (ENEM-2013) Na aferição de um novo semáforo, os
tempos são ajustados de modo que, em cada ciclo
completo (verde-amarelo-vermelho), a luz amarela
permaneça acesa por 5 segundos, e o tempo em que a
luz verde permaneça acesa seja igual a 2/3 do tempo
em que a luz vermelha fique acesa. A luz verde fica
acesa, em cada ciclo, durante X segundos e cada ciclo
dura Y segundos. Qual é a expressão que representa a
relação entre X e Y?
A) 5X − 3Y + 15 = 0
B) 5X − 2Y + 10 = 0
C) 3X − 3Y + 15 = 0
D) 3X − 2Y + 15 = 0
E) 3X − 2Y + 10 = 0
07.(ENEM/2009)
O
Indicador
do
CadÚnico
(ICadÚnico), que compõe o cálculo do Índice de
Gestão Descentralizada do Programa Bolsa Família
(IGD), é obtido por meio da média aritmética entre a
taxa de cobertura qualificada de cadastros (TC) e a
taxa de atualização de cadastros (TA), em que ,
TC 
NV
,
NF
TA 
NA
, NVé o número de cadastros
NV
domiciliares válidos no perfil do CadÚnico, NF é o
número de famílias estimadas como público alvo do
CadÚnico e NA é o número de cadastros domiciliares
atualizados no perfil do CadÚnico.
Portaria n° 148 de 27 de abril de 2006 (adaptado).
Suponha que o IcadÚnico de um município específico é
0,6. Porém, dobrando NF o IcadÚnico cairá para 0,5.
Se NA +NV = 3.600, então NF é igual a
A) 10.000. B)7.500.
C)5.000.
D)4.500.
E)3.000.
GABARITO
01.
02.
03.
04.
05.
06.
07.
A
D
B
D
A
B
C
61
EQUAÇÕES DO 2° GRAU
As equações do 2° grau são aquelas que podem ser
representadas sob a forma:
ax 2  bx  c  0
em que a, b e c são constantes reais, com
incógnita.
Exemplos:
 x2 – 5x + 6 = 0
2
 -3x + 27 = 0
a  0, e x é a
Qualquer equação do 2°grau pode ser resolvida pela
fórmula a seguir, conhecida como fórmula de Bhaskara.
x
b  
2.a
 2
S  1, 
 5
EXERCÍCIOS
01. O valor de R$ 450,00 deveria ser distribuído entre
um certo número de pessoas, mas, na hora da
distribuição, 3 pessoas não compareceram, fazendo
com que os presentes recebessem R$ 5,00 a mais do
que receberiam. Quantas pessoas haviam
inicialmente?
2
em que:   b  4ac .
A expressão  (delta), chamada de discriminante da
equação, informa-nos se a equação tem raízes reais e, no
caso de existirem, se não são iguais ou diferentes.
 Quando   0 , a equação possui duas raízes
reais distintas.
02.(UNICAMP – SP) Um fio de 48 cm de comprimento
é cortado em duas partes, para formar dois quadrados,
de modo que a área de um deles seja quatro vezes a
área do outro.
a) Qual deve ser o comprimento de cada uma das
partes do fio?
 Quando   0 , a equação possui duas raízes
reais iguais.
 Quando
reais.
  0 , a equação não possui raízes
b) Qual será a área de cada um dos quadrados
formados?
Se x1 e x2 são as raízes da equação do 2° grau
ax 2  bx  c  0 , então a soma S e o produto P dessas
raízes são:
S
b
a
e
P
c
a
Exercício resolvido
1. Resolver, no universo dos números reais, a equação do
2° grau: 5 x  3x  2  0 .
Resolução
Identificam-se os coeficientes a,b e c.
2
a  5 ; b  3
e
c  2
Calcula-se o discriminante
  b 2  4ac :
  (3) 2  4.5.(2)  49
03.(UFMG) Se a equação x2 + px + q = 0 admite duas
raízes e simétricas, então:
a) p = 1 e q > 0
b) p = 1 e q < 0
c) p = 0 e q < 0
d) p < 0 e q < 0
4
04.A soma dos quadrados das raízes da equação x +
2
4x – 5 = 0, vale:
a) 25
b) 5
c) 4
d) 2
e) 0
Aplica-se a fórmula resolutiva:
b 
x
2.a
 (3)  49 3  7
x 

2.5
10

05.(UNIMONTES) As raízes da equação 2 x + 2 x
5 podem ser encontradas resolvendo-se a equação
1
2
=
2
5
Conclui-se que o conjunto solução S da equação é
Logo: x  1 ou x  
62
06. ( PUC – SP ) O valor de k, para que a equação
quadrática 2x2 + 4x + k = 0 possua duas soluções reais e
iguais é:
a)
2
b)
3
c)
4
d)
5
e)
6
07. ( UERGS ) Sendo S a soma e P o produto das
2
soluções da equação 2x − 5x − 7 = 0 , pode-se afirmar
que
A) S − P = 6 .
B) S + P = 2 .
C) S ⋅ P = 4 .
D) S/P= 1
E) S < P .
08.(UCS-RS) Se uma das raízes da equação 2x² – 3px +
40 = 0 é 8, pode-se afirmar que o valor de p é:
A) 3
B) 4
C) 5
D) 6
E) 7
09. ( UFRS ) Os possíveis valores reais de m, para que a
equação quadrática 2x2 + 4x + m = 0 possua duas
soluções reais e diferentes é:
a) m < 2
b) m > 2
c) m < – 2
d) m > – 2
e) m < 3
10 .(FIP-2010) Doze amigos brasileiros viajaram animados
para assistir à Copa do Mundo. Ao chegar à África do Sul,
conheceram um restaurante brasileiro, onde agendaram
um jantar para um dia antes de seu retorno ao Brasil. No
dia do jantar, quatro deles não puderam comparecer. Por
isso, para que o pagamento do jantar fosse efetuado, cada
um dos participantes precisou desembolsar R$20,00 a
mais. Qual era, em reais, o valor total desse jantar?
A) 480,00
B) 520,00
C) 640,00
D) 720,00
11. (FIP-2012) Duas velas de mesma altura são acesas ao
mesmo tempo. A primeira é consumida em 4 horas e a
segunda em 3 horas. Suponha que as velas queimem em
velocidade constante. Nas condições dadas, após quanto
tempo, depois de terem sido acesas que a altura da
primeira vela, será o dobro da altura da segunda?
A) 1h 32min
B) 2h 24min
C) 2h 40min
D) 1h 56min
12. ( UECE ) Sejam x1 e x2 as soluções da equação
2
2
2x - 6 x + p – 2 = 0 . Se ( x1 + x2 ) = x1 . x2, então
p é igual a:
a) 1
b) 3
c) 5
d) 7
13. (Unimontes / PAES) Um granjeiro ia vender ovos a
R$ 1,60 a dúzia. Quando os estava colocando na
prateleira,
quebraram-se
cincos
dúzias.
Não
pretendendo ter prejuízos, o granjeiro resolveu vender
os ovos restantes a R$ 1,80 a dúzia. Quantas dúzias
possuía no início?
A) 20
B) 15
C) 30
D) 45
14. ( PUC – SP ) Sabendo que x’ e x’’ são as raízes
da equação quadrática x2 – 8x + m = 0, o valor de m
para que se tenha 3x’ – 4x’’ = 3 é:
a) m = 15
b) m = 12
c) m = 7
d) m = 16
GABARITO
01. 18 pessoas
02. a) 16 cm e 32 cm
03. C
04. D
05. D
06. A
07. A
08. E
09. A
10. A
11. B
12. C
13. D
14. A
b) 16 cm2 e 64 cm2
63
EQUAÇÕES IRRACIONAIS
Equação irracional é uma equação em que há incógnita
em um ou mais radicais. São equações irracionais:
2. (PUC -MG) O número de soluções reais da equação
a) 0
d) 3
b) 1
e) 4
c) 2
As raízes podem ter qualquer índice, mas no nosso
estudo trataremos apenas das equações irracionais que
apresentarem raízes quadradas. Não existe fórmula para
resolver essas equações, mas temos um processo de
resolução prático e seguro que nos conduz a equações
cuja resolução já conhecemos.
Exercícios Resolvidos
1. (FUVEST) Seja V o conjunto dos números reais que são
soluções da equação irracional
A equação só admite uma raiz S = { 16}
Resposta: alternativa B
EXERCÍCIOS
01. Resolva as equações em IR :
02.(FEI – SP) Resolva, em IR, a equação:
03. (FGV – SP) Resolva, no campo real, a equação:
GABARITO
01. A) X=3
02. S={15}
03. S={ }
B) X=5 C) X=-2 D) X=1
64
FATORAÇÃO DE POLINÔMIOS
Fatorar um polinômio significa transformá-lo em um
produto de fatores de grau menor, podemos dizer, a
grosso modo, que fatorar é o "caminho inverso" de
multiplicar.
1º caso: colocar fator comum em evidência
Este caso se baseia na propriedade distributiva da
multiplicação em relação à adição e subtração:
ab + ac – ad = a.(b + c – d)
Dizemos que o fator a, comum a todos os termos do 1º
membro, foi colocado em evidência.
De maneira geral, ao fatorar um polinômio, colocamos
em evidência o máximo divisor comum (MDC) de seus
termos e, em seguida, dividimos cada termo por esse
MDC.
Exemplos:
 3x3y2 – 6x4y3 + 12x6y4 = 3x3y2 (1 – 2xy + 4x3y2)
 a3x2y + a2xy3 = a2xy(ax + y2)
2
2
2
x – 6x + 9 = x – 2.x.3 + 3 = (x – 3)
2
Então, B = 4x. (x – 3)
2
3º caso: Trinômio de 2ºgrau
Prova-se que um trinômio de 2º grau ax2 + bx + c
(a  0), pode ser fatorado em IR caso admita raízes
reais (   0). Sendo x1 e x2 suas raízes, sua fatoração
é o produto do coeficiente a por dois fatores do 1º grau:
ax2 + bx + c = a(x – x1) (x – x2)
Exemplo:
2
 Fatore x – 5x + 6
Raízes: x1 = 2 e x2 = 3
x2 – 5x + 6 = 1.(x - 2)(x - 3) = (x – 2) (x – 3)
Exercícios Resolvidos
1. Desenvolva os produtos:
Em alguns casos, não há fator comum a todos os
termos para se colocar em evidência. Agrupando-se
convenientemente os termos, é possível às vezes efetuar
mesmo assim a fatoração.
Exemplos:
 ax + ay + bx + by = a(x + y) + b(x + y)
Observe que agora (x + y) é fator comum. Colocando-o em
evidência, temos finalmente
(x + y) (a + b)
 x4 – 2x3 – 3x + 6 = x3(x – 2) – 3(x – 2) = (x – 2) (x3 – 3)
2º caso:aplicar as identidades notáveis
As identidades notáveis que acabamos de estudar são
muito úteis na fatoração de certos polinômios.
É importante observar que, em todas elas, o 1º membro
nada mais é que a fatoração do 2º membro. Desta forma,
basta estabelecer uma analogia entre o polinômio a ser
fatorado e uma qualquer das identidades notáveis.
Exemplos:
4
2
 Fatore A = x – 9y
2 2
Observe que A = (x ) – (3y)2. Trata-se do uma diferença
de quadrados do tipo a2 – b2 com a = x2 e b = 3y. Então;
x4 – 9y2 = (x2)2 –(3y)2 = (x2 + 3y) (x2 –3y)

Fatore B = 4x3 – 24x2 + 36x
Colocando 4x em evidência, B = 4x (x 2 – 6x + 9)
A expressão x2 – 6x + 9 é do tipo a2 – 2ab + b2 , sendo a =
x e b = 3. Assim,
65
03. ( U. São Francisco ) O valor numérico da expressão
x 2  y 2 x 2  2xy  y 2

x  y 
x  y 2
igual a:
A) 23,25
B) 25,75
C) 26,25
D) 28,00
E) 32,25
2. Fatore as seguintes expressões :
para x = 17,25 e y = 10,75, é
04. (CTSP) O resultado da operação :
x6  y6
x 2  xy  y 2
para
x = 5 e y = 3 é igual a:
A) 304
B) 268
C) 125
D) 149
1
, então a
a
expressão ( a + b )³ + ( a – b )³ é igual a :
A) 1
B) 2
C) 2a²
D) a
05. (CTSP) Sabendo que a 2  3b 2 
EXERCÍCIOS
01.( UC – MG ) A expressão
a 3  a 2b
3a 5  6a 4 b  3a 3 b 2
x 2  y 2  z 2  2xy
equivale a :
a
a)
3a  b
b)
c)
d)
e)
x 2  y 2  z 2  2xy  2xz  2yz
obtemos:
2x  y  2z
A)
2
a
3a  b 
1
3a  b
1
3aa  b
1
3aa  b
2y  2z  x
yz
C) 2x – z + y
xyz
D)
xyz
B)
02. ( Mack – SP ) Uma expressão equivalente a
x y  2x y  xy
3
2 2
x 2 y  xy 2
a) x + y
b) x – y
c) x.y
d)
e)
x
y
xy
x.y
06. (CTSP) Simplificando a expressão
3
é:
07. Se m  IN, o valor do quociente
A)
B)
C)
D)
E)
2m  3  2m  1
5  2m  1
1
2
4
8
um valor que depende de m
08. ( UFMG ) ( a–1 + b–1)–2 é igual a
ab
A)
a  b2
ab
B)
2
2
a  b2
C) a2 + b2


66
a 2b 2
D)
a  b2
09.(UFOP) Simplificando a expressão
ax 2  ay 2
x  4xy  3y 2
2
para x ≠ y, obtém-se
A) a( x  y)
x  3y
xy
B)
x  3y
a( x  y)
C)
x  3y
( x  y)
D)
x  3y
10. (UFMG) Sejam x e y números reais não-nulos tais
que
A)
B)
C)
D)
x
2

y2
 2 . Então é correto afirmar que:
x
y
x2 – y = 0
x + y2 = 0
2
x +y=0
x – y2 = 0
GABARITO
01. E
02. A
03. D
04. A
05. B
06. D
07. C
08. D
09. C
10. B
67
A LINGUAGEM DAS FUNÇÕES
CAIU NO ENEM !!!
01.(ENEM)
PLANO CARTESIANO
O plano cartesiano ortogonal é constituído por dois
eixos x e y perpendiculares entre si que se cruzam na
origem.
O eixo horizontal é o eixo das abscissas (eixo OX) e
o eixo vertical é o eixo das ordenadas (eixo OY).
Associando a cada um dos eixos o conjunto de todos os
números reais, obtém-se o plano cartesiano ortogonal.
y(eixo das ordenadas)
x(eixo das abscissas)
Cada ponto P=(a,b) do plano cartesiano é formado
por um par ordenado de números, indicados entre
parênteses, a abscissa e a ordenada respectivamente.
Este par ordenado representa as coordenadas de um
ponto.
O primeiro número indica a medida do deslocamento
a partir da origem para a direita (se positivo) ou para a
esquerda (se negativo).
O segundo número indica o deslocamento a partir da
origem para cima (se positivo) ou para baixo (se
negativo).Observe no desenho que: (a, b) ≠ (b, a) se a ≠ b.
y
b
(a, b)
(b, a)
a
a
b
GABARITO
x
01. A
Os dois eixos dividem o plano em quatro regiões
denominadas quadrantes sendo que tais eixos são retas
concorrentes na origem do sistema formando um ângulo
reto. Os nomes dos quadrantes são indicados no sentido
anti-horário.
y
2º Quadrante
1º Quadrante
x
3º Quadrante
4º Quadrante
68
INTRODUÇÃO
Exemplos:
Ao lermos um jornal ou uma revista, diariamente,
deparamo-nos com gráficos, tabelas e ilustrações –
instrumentos muito utilizados nos meios de comunicação.
Um texto com ilustrações é muito mais interessante,
chamativo, agradável e de fácil compreensão. Não é só
nos jornais ou nas revistas que encontramos gráficos. Os
gráficos estão presentes nos exames laboratoriais, nos
rótulos de produtos alimentícios, nas informações de
composição química de cosméticos, nas bulas de
remédios, enfim, em todos os lugares. Ao interpretarmos
esses gráficos, verificamos a necessidade dos conceitos
de plano cartesiano.
O Sistema ABO dos grupos sangüíneos é explicado
pela recombinação genética dos alelos (a,b,o), e este é
um bom exemplo de uma aplicação do conceito de
produto cartesiano, já que existe uma correspondência
biunívoca desse sistema com os fatores Rh+ Rh−.
Uma aplicação prática do conceito de relação é a
discussão sobre a interação de neurônios (células
nervosas do cérebro), ligada ao bom funcionamento do
corpo humano.
Ao relacionarmos espaço em função do tempo,
número do sapato em função do tamanho dos pés,
intensidade da fotossíntese realizada por uma planta em
função da intensidade de luz a que ela é exposta ou
pessoa em função da impressão digital, percebemos quão
importantes são os conceitos de funções para
compreendermos as relações entre os fenômenos físicos,
biológicos, sociais.
Observamos, então, que as aplicações de plano
cartesiano, produto cartesiano, relações e funções estão
presentes no nosso cotidiano.
1. Dados os conjuntos A = {1, 2, 3} e B = {4, 5}, dê
os elementos dos seguintes produtos cartesianos:
a) A x A
Solução:
A x A = {(1, 1); (1, 2); (1, 3); (2, 1); (2, 2); (2, 3);(3, 1);
(3, 2); (3, 3)}
b) A x B
Solução:
A x B = {(1, 4); (1, 5); (2,4); (2,5); (3,4); (3,5)}
c) BxA
Solução:
B x A = {(4,1); (4,2); (4,3); (5,1); (5,2); (5,3)}
2. Dados os conjuntos abaixo, represente graficamente
o produto cartesiano BxA:
RELAÇÃO BINÁRIA
Sejam A e B conjuntos não-vazios. Uma relação em
AxB é qualquer subconjunto R de AxB.
PRODUTO CARTESIANO
Dados dois conjuntos, podemos formar pares
ordenados por meio de uma relação entre eles; o conjunto
formado por estes pares ordenados é denominado produto
cartesiano definido por:
A x B = {(x,y) | x
Aey
B}.
Quando A ou B são vazios, temos que A x B é vazio.
A relação mostrada na figura acima é:
R = {(a, 3), (b, 3), (c, 2), (c, 3), (d, 2), (d, 3)}
Uma relação R de A em B pode ser denotada por
R: A → B
69
Exemplos:
a) Se A={1,2} e B={3,4}, o produto cartesiano é
AxB={(1,3),(1,4),(2,3),(2,4)}
e, neste caso, temos algumas relações em AxB:
R1 ={(1, 3),(1, 4)}
R2 ={(1, 3)}
R3 ={(2, 3),(2, 4)}
b) Dados os conjuntos A = {1, 2, 3, 4} e B = {2, 3, 4, 5,
6}.
Determine R = {(x, y) AxB / y = x + 1}.
b) Determine o domínio, imagem e contradomínio da
relação R.
R = {(1,2), (2,4), (3,6)}
D(R) = {1, 2, 3}
Im(R) = {2, 4, 6}
CD(R) = B
EXERCÍCIOS
DOMÍNIO, IMAGEM E CONTRADOMÍNIO DE
UMA RELAÇÃO
a) Domínio
Chamamos de domínio de uma relação o conjunto dos
elementos do primeiro conjunto que apresentam pelo
menos um correspondente no segundo conjunto.
b) Contradomínio
Chamamos de contradomínio o conjunto formado pelos
elementos que ficam à disposição para serem ou não
correspondentes de um ou mais elementos do primeiro
conjunto. O contradomínio é sempre o segundo conjunto
da relação.
C) Conjunto imagem
Chamamos de imagem cada um dos elementos do
segundo conjunto que é correspondente de algum
elemento do primeiro conjunto da relação binária. O
conjunto formado por todas as imagens da relação é
chamado conjunto imagem.
01. (MACK - SP) Sejam A = { 0, 1, 2, 3 }, B = { 1, 2, 4,
5 } e a relação R ={( x, y ) A x B | y = 2x + 1}. O
domínio e a imagem dessa relação são
respectivamente:
a) { 1, 3} e { 1, 5}
b) { 0, 1, 2} e { 2, 4}
c) { 0, 1, 2, 3} e { 1}
d) A e B
e) n.d.a
02. (PUC - SP) O domínio da relação R = {( x, y)
N | y = x - 5} é:
a) N
b) N*
c) R
d) { x N | x 6}
e) { x N | x 5}
Nx
03. (UFPE) Assinale a única alternativa abaixo que
representa o gráfico do conjunto B x A onde A = { y
/ 1 x 3} e B = { x R / 1 x 2}
R
Exemplo:
Dados os conjuntos A = {1, 2, 3, 4} e B = {2, 3, 4, 5,
6}.
a) Determine R = {(x, y) AxB / y = 2x}
70
08. ( UFPA ) Dados os conjuntos A ={ a, b, c } e B
={ a, b }, qual dos conjuntos abaixo é uma relação de
A em B ?
a) { ( a, a ) ; ( b, b ) ; ( c, c ) }
b) { ( a, a ) ; ( b, b ) ; ( b, c ) }
c) { ( a, a ) ; ( b, b ) ; ( a, c ) }
d) { ( a, a ) ; ( b, b ) ; ( a, b ) }
e) { ( c, b ) ; ( b, c ) }
04. (UFPA) Dados os conjuntos A = { a, b, c} e B = { a, b},
qual dos conjuntos abaixo é uma relação de A em B?
a) { ( a, a); ( b, b); ( c, c) }
b) { ( a, a); ( b, b); ( b, c) }
c) { ( a, a); ( b, b); ( a, c) }
d) { ( a, a); ( b, b); ( a, b) }
e) { ( c, b); ( b, c) }
GABARITO
01. E
02. E
03. E
04. D
05. E
06. E
07. A
08. D
05. (FCC - BA) Dados os conjuntos A = { 0 , 1}, B = { 1, 2}
e C = { 0, 2}, então ( A x B) - (B x C) é o conjunto:
a) { }
b) { ( 1, 1) ; ( 1, 2) }
c) { ( 0, 1) ; ( 2, 0) ; ( 2, 2) }
d) { ( 1, 1) ; ( 0, 2) ; ( 2, 2) }
e) { ( 0, 1) ; ( 0, 2) ; ( 1, 1) }
06. ( FCC – BA ) Dados os conjuntos A = { 0, 1 }, B = { 1,
2 } e C = { 0, 2 }, então ( A x B ) – ( B x C ) é o
conjunto:
a) 
b) { ( 1, 1 ) , ( 1, 2 ) }
c) { ( 0, 1 ) , ( 2, 0 ) , ( 2 , 2 )}
d) { ( 1, 1 ) , ( 0, 2 ) , ( 2 , 2 )}
e) { ( 0, 1 ) , ( 0, 2 ) , ( 1 , 1 )}
07. ( PUCC ) Dados os conjuntos A = { x  R / 1 ≤ x ≤
3 } e B = { x  R / – 1 ≤ x ≤ 1 }, o gráfico que melhor
representa o produto cartesiano B x A é :
71
FUNÇÃO
O conceito de função é um dos mais importantes em
toda a matemática. O conceito básico de função é o
seguinte: toda vez que temos dois conjuntos e algum tipo
de associação entre eles, que faça corresponder a todo
elemento do primeiro conjunto um único elemento do
segundo, ocorre uma função.
Observe, por exemplo, o diagrama das relações
abaixo:
Considere:
x → variável independente → DOMÍNIO
y → variável dependente → IMAGEM
A relação acima não é uma função, pois existe o
elemento 1 no conjunto A, que não está associado a
nenhum elemento do conjunto B.
A relação acima é uma função, pois todo elemento do
conjunto A, está associado a somente um elemento do
conjunto B.
De um modo geral, dados dois conjuntos A e B, e uma
relação entre eles, dizemos que essa relação é uma
função de A em B se e somente se, para todo x  A
existe um único y  B de modo que x se relacione com
y, ou seja, cada elemento de A deve relacionar com
um único elemento de B.
Empregando a linguagem das funções:
O conjunto A é o domínio da função.
O conjunto B é o contradomínio da função.
O elemento y de B, associado ao elemento x de
A, é denominado imagem de x.
O subconjunto de B formado pelos elementos que
são imagens dos elementos de A é denominado
conjunto imagem ou apenas imagem da função.
Exemplos:
a) O valor pago em função da quantidade de combustível
que um carro consome.
RECONHECIMENTO DE UMA FUNÇÃO
Por meio do diagrama de flechas
As condições que uma relação representada por
meio do seu diagrama de flechas deve satisfazer para
ser uma função são:
1°.Todo elemento de A deve servir como ponto de
partida de uma flecha.
2°. Essa flecha deve ser única.
b) A taxa de natalidade infantil em função do tempo.
Exemplos:
1. Diga em quais itens temos funções:
72
a)
Por meio de seu gráfico cartesiano
Dizemos que uma relação binária R: A → B é
função ou aplicação no gráfico, quando toda reta
vertical tocar em um e único ponto em R, ∀ x A.
Não, pois existem elementos de A que não possuem
correspondentes em B.
b)
Exemplos:
a)
Sim, pois todos os elementos de A possuem um único
representante em B.
Representa o gráfico de uma função ou aplicação.
c)
b)
Sim, pois todos os elementos de A possuem um único
representante em B.
Exercício resolvido
01.(UFPE) Dados os conjuntos A ={a, b, c, d} e
B={1, 2, 3, 4, 5}, assinale a única alternativa que define
uma função de A em B .
a) {(a, 1), (b , 3), (c, 2)}
b) {(a, 3), (b, 1), (c, 5), (a, 1)}
c) {(a, 1), (b, 1), (c, 1), (d, 1)}
d) {(a, 1), (a, 2), (a, 3), (a, 4), (a, 5 )}
e) {(1, a), (2, b), (3, c), (4, d), (5, a )}
Solução:
Para que f: A em B seja uma função, devemos ter para
cada um elemento de A um único correspondente em B,
logo a solução é {(a, 1),(b, 1), (c, 1), (d, 1)}, ou seja:
Não é uma função, já que existem retas que tocam o
gráfico em mais de um ponto.
c)
Representa o gráfico de uma função ou aplicação.
EXERCÍCIOS
1) Os diagramas abaixo representam algumas
relações binárias. Verifique qual dessas relações
pode ser considerada uma função f: A  B.
73
RAIZ OU ZERO DE UMA FUNÇÃO
2) Nos gráficos abaixo, quais podem representar uma
função ?
Dada uma função y = f(x), os valores, os valores de
x para os quais f(x) = 0 são chamados raízes de uma
função. No gráfico cartesiano da função, as raízes são
abscissas dos pontos onde o gráfico corta o eixo
horizontal. Observe o gráfico abaixo:
No gráfico acima temos:f(x1) = 0, f(x2) = 0 e f(x3) = 0.
Portanto x1, x2 e x3 são raízes da função.
**Para obter a raiz de uma função de forma rápida,
basta igualar à função a zero, obtendo uma equação,
o conjunto solução da equação será o conjunto que
representa a raiz ou raízes da função.
VARIAÇÃO DE UMA FUNÇÃO
3) Dos gráficos abaixo, qual pode ser definido como uma
função f: R –  R – ?
Função constante :Uma função y = f(x) = b é
constante se em sua lei de formação observamos a
presença de um termo independente de x (b).
O gráfico de uma função constante f(x) = b é uma
reta horizontal que intercepta o eixo y no valor b.
Exemplo:
Função crescente :Uma função f real de variável real,
é crescente em A , A  D(f), se e somente se , para
quaisquer números x1 e x2do conjunto A, ocorre x2
> x1 → f(x2) > f(x1).
y
f
f(x2)
f(x1)
x1
x2
x
x2> x1→f(x2)>f(x1)
74
Função decrescente: Uma função f real de variável real,
é decrescente em A , A  D(f), se e somente se , para
quaisquer números x1 e x2 do conjunto A , ocorre x2 > x1
→ f(x2) < f(x1).
Condição: o radicando de um radical de índice par
deve ser um número maior ou igual a zero (positivo ou
nulo).
y
f(x1)
f(x2)
x1
x
x2
f
x2> x1→ f(x2)<f(x1)
Exemplo: Seja a função f , cujo o gráfico é:



f é crescente no intervalo [-6, -2];
f é constante no intervalo [-2, 3];
f é decrescente no intervalo [3, 5];
DOMÍNIO DE UMA FUNÇÃO REAL DE VARIÁVEL
REAL
3° caso: Quando a variável aparece no radicando e um
radical de índice par e esse radical está no
denominador de uma fração.
Condição: este caso é a reunião dos dois primeiros
casos; logo, o radicando deve ser maior que zero.
EXERCÍCIOS
01.(UFSJ) Considere os seguintes gráficos , que
representam relações entre o conjunto A={1,2,3,4} e o
conjunto B={a,b,c,d)
O domínio consiste em determinar os valores reais de
x, para os quais as operações indicadas na lei de
associação sejam possíveis em IR. Para isso, teremos que
determinar a condição de existência (C.E.) da função
dada. Exemplos de determinação da condição de
existência nas diferentes situações:
1° caso: Quando a variável aparece no denominador de
uma fração.
Condição: o denominador de uma fração deve ser
diferente de zero.
2° caso: Quando a variável aparece no radicando de um
radical de índice par.
O(s) gráficos(s) que NÃO representa(m) função(ões) é
(são)
a) os gráficos I e III
b) apenas o gráfico III
c) apenas I
d) os gráficos III e IV
75
02. ( FEI – SP ) Qual das seguintes curvas não
representa função ?
08.(UFOP) Seja uma função f: R  R tal que:
I) f ( x + y ) = f (x) . f (y)
II) f (1) = 2
 
III) f 2  4


Então o valor de f 3  2 é dado por:

a) 3  2
d) 24

2
b) 9  2
e) 32
09.(UFOP) Sejam
satisfazendo:
03. ( PAES – 2005 ) Seja f: R  R uma função. O
conjunto dos pontos de intersecção do gráfico de f com
uma reta vertical
a) possui um só elemento
b) possui exatamente dois elementos
c) é vazio
d) possui, pelo menos, dois elementos
04. ( PAES – 2005 ) É dado o esboço do gráfico de uma
função f , de R em
R. Em relação a essa função, é
y
correto afirmar que :
f:IR  IR
c) 16
e
g:N  N,
 g(0)  1
g(x)  
g(n) .
g(n  1)  2
Então, f(3) – g(3) é igual a:
a) 11
b) 16
c) 93
d) 109
e) 125
f x  2  x3
e
3
10.( UE – Londrina ) Seja a função f( x ) = ax + b. Se
f( – 1 ) = 2 e f( 1 ) = 4, então “a” e “b” valem,
respectivamente:
a) – 1 e – 3
b) 3 e – 1
c) – 1 e 3
d) 3 e 1
e) 1 e 3
11.( UFP – RS ) Qual é o domínio de y =
0
1

x
3
funções

x4
?
x2
a)R – { 4 } b) 4,   c) [ 4, + ∞ )
d) ( 2, 5 )e) x ≠ 2
a) é uma função crescente para todo x > 0.
b) é uma função decrescente para todo x < 0
c) é uma função quadrática
d) É uma função linear
2
05.( Mack – SP ) Se f( x – 1 ) = x , então o valor de f( 2 )
é:
a) 1
b) 4
c) 6
d) 9
e) 16
06.( MACK – SP ) A função f de R em R é tal que,
para todo xR, f( 3x ) = 3.f( x ) . Se f( 9 ) = 45, então :
a) f( 1 ) = 5
b) f( 1 ) = 6
c) f( 1 ) = 9
d) f( 1 ) não pode ser calculado
07.( Fuvest – SP ) Uma função f de variável real satisfaz
a condição f( x + 1 ) = f( x ) + f( 1 ), qualquer que seja o
valor da variável x. Sabendo que f( 2 ) = 1, podemos
concluir que f( 5 ) é igual a :
a)
1
2
d) 5
b) 1
c)
12.( UFP – RS ) Qual é o domínio de y =
x2  7x  10
2x  7
?
 7
 7

 7

a)R –   b)   ,    c)  ,  
 2
 2

 2

d) ( 2, 5 ) e) 
13.O domínio da função f(x) =
2x  4
x5
em qual dos intervalos reais abaixo?
a) { x  R / 2 ≤ x < 5 }
b) { x  R / 2 < x < 5 }
c) { x  R / 2 ≤ x ≤ 5 }
d) { x  R / 2 ≤ x <– 5 }
e) { x  R / – 2 ≤ x < 5 }
está definido
14. Dê o domínio de cada função abaixo
a) f(x) = x3 + 7x – 5
5
2
e) 10
76
b) f(x) =
c) f(x) =
3
x 7  5x 4  3
x 3
 x 1
representada pelo gráfico
 x 1
15.( Unimontes / PAES) Os alunos da primeira série do
ensino médio, ao concluírem o estudo do sinal de uma
função g, obtiveram o seguinte resultado:
g(x) = 0  x = – 3 ou x = – 1 ou x = 3
g(x) > 0  – 3 < x < – 1
g(x) < 0  x < – 3 ou x > – 1 e x ≠ 3
Das figuras abaixo, a que representa o esboço do
gráfico da função acima é :
18.(Unimontes) Em relação ao esboço de gráfico
apresentado na figura abaixo, podemos afirmar que:
a) representa uma função cujo domínio é [1, 5].
b) representa uma função cujo conjunto imagem é [3, 5]
{2}.
c) não pode representar uma função.
d) representa uma função crescente.
16.( PUC – SP ) Se D = { 1, 2, 3, 4, 5 } é o domínio da
função f(x) = (x – 2).(x – 4), então seu conjunto imagem
tem :
a) 1 elemento
b) 2 elementos
c) 3 elementos
d) 4 elementos
e) 5 elementos
19. Observando o gráfico da função real f, pode-se
afirmar que, das alternativas, a única falsa é :
a) A função admite 6 raízes reais
b) O domínio de f é |R.
c) A imagem de f é ( – ∞, 5 ]
d) f(1) + f(7) + f(0) + f(6) = 3
e) Para x > 6, f(x) é crescente
17.(ENEM) Muitas vezes o objetivo de um remédio é
aumentar a quantidade de uma ou mais substâncias já
existentes no corpo do indivíduo para melhorar as defesas
do organismo. Depois de alcançar o objetivo, essa
quantidade deve voltar ao normal.
Se uma determinada pessoa ingere um medicamento
para aumentar a concentração da substância A em seu
organismo, a quantidade dessa substância no organismo
da pessoa, em relação ao tempo, pode ser melhor
77
20. Observando o gráfico da função f, podemos concluir
que :
a) Se f(x) < 0, então x > 1
b) Se x > 1, então f(x) é decrescente
c) Se x < 1 , então f(x) é decrescente
d) Se f(x) < 0, então x < 1
e) Se x > 0, então f(x) > 0
GABARITO
1) B
2) D
3) A
4) B
8) E
9) D
10) E
11) E
14)
15) D
16) C
17) D
5) D
6) A
12) B
18) B
7) C
PROPRIEDADES DE UMA FUNÇÃO
Essas são algumas propriedades que caracterizam
uma função f : A  B :
 Função injetora : Uma função f:A→B é
injetora se, e somente se, elementos quaisquer
do domínio de f, distintos entre si , tiverem
imagens também distintas entre si , através de
f.
A
B
Reconhecemos graficamente, uma função injetora
quando, uma reta horizontal, qualquer que seja,
interceptar o gráfico da função, uma única vez.
13) A
19) E
20) D
 Função sobrejetora: Uma função f: A→B é
sobrejetora se, e somente se, Im(f) = CD(f) =
B.
A
B
Todos elementos
do conjunto B são
utilizados.
Im(f) = CD(f)
78
Reconhecemos, graficamente, uma função sobrejetora
quando, a imagem dessa função for igual ao seu
contradomínio.
Verificaremos se as funções abaixo f:[a, b]→[c, d] são ou
não sobrejetoras.
Observe que o contra domínio [c, d] é dado mas, a
imagem tem que ser encontrada em cada gráfico.
y
Reconhecemos graficamente, uma função bijetora
quando, toda reta horizontal, interceptar o gráfico da
função, uma única vez e ela for sobrejetora.
Observe que a função f:[a, b]→[c, d] abaixo é
injetora (retas horizontais cortam f em um único ponto)
e sobrejetora ( Im(f) = CD(f) ), logo f é BIJETORA.
y
A imagem e o
contradomínio são
DIFERENTES.
d
d
Im(f) ≠ CD(f)
c
a
x
b
y
c
A função não é
sobrejetora
A imagem e o
contradomínio são
DIFERENTES.
d
a
b
x
*****Existem funções que não se encaixam nem como
injetora, nem como sobrejetora. São chamadas funções
sem classificação.
Im(f) ≠ CD(f)
c
A função não é
sobrejetora
FUNÇÃO INVERSA
d
A imagem e o
contradomínio são
IGUAIS.
Considere a função f: A→B, bijetora. Chama-se função
inversa de f a função g: B→A quando e somente
quando f(m) = n equivaler a g(n) = m, quaisquer que
sejam mA e nB. Indicaremos a função inversa de f
por f –1 .
c
Im(f) = CD(f)
a
x
b
y
a
x
b
A
função
sobrejetora
é
y
d
A imagem e o
contradomínio são
IGUAIS.
c
Im(f) = CD(f)
a
x
b
A
função
sobrejetora
Observe que os diagramas abaixo representam
funções bijetoras e que, sendo assim, admitem
inversa( existe f: A→B e f: B→A )
A
B
A
B
é
Exemplos
 Função bijetora: Uma função f: A→B é bijetora
se, e somente se , todo elemento y , y B , for
imagem , através de f, de um único x, x  A.
A
B
Uma função é
bijetora quando
ela é injetora e
sobrejetora
ao
mesmo tempo.
1) Determinar a função inversa de f(x)=2x – 4
Y= 2x –4 ,trocando x por y , temos :
X = 2y –4 , isolando y, vem :
2y  x  4  y 
logo, y 
x 4
x
  y  2,
2 2
2
x
 2 é função inversa procurada .
2
2) O gráfico de f-1 .
O Gráfico da função e sua inversa são simétricos
em relação a bissetriz do 1º e 3º quadrantes.
79
EXERCÍCIOS
1) (Uberaba-MG) Os diagramas abaixo definem as
funções f, g e h de E em E, sendo E = {1, 2, 3,
4}
Então:
a) f e g são injetoras
b) g e h são sobrejetoras
c) todas são funções bijetoras
d) g admite função inversa
e) nenhuma delas é sobrejetoras
Exercícios Resolvidos
2) ( UNIMONTES ) Considera a função f: N  2N
definida por f ( n ) = 2n sendo N = { 0, 1, 2, 3, ...}
e 2N = { 0, 2, 4, 6, ...}.
Com relação a f todas as afirmativas abaixo são
verdadeiras, EXCETO:
a) f é uma função bijetiva e, portanto, admite
função inversa;
b) o gráfico de f é o conjunto Gf = { ( n, y )  N 
2N  y = 2n };
c) a representação gráfica de
f
no plano
cartesiano é uma reta;
d) por f pode-se concluir que existem tantos
números pares quantos números naturais.
3)
( UFF ) Considere as funções f, g e h, todas
definidas em [m, n] com imagens em [p, q]
representadas através dos gráficos a seguir :
Pode-se afirmar que:
a) f é bijetiva, g é sobrejetiva e h não é injetiva.
b) f é sobrejetiva, g é injetiva e h não é
sobrejetiva.
c) f não é injetiva, g é bijetiva e h é injetiva.
d) f é injetiva, g não é sobrejetiva e h é bijetiva.
e) f é sobrejetiva, g não é injetiva e h é
sobrejetiva.
4) ( UFPE ) Dentre as curvas a seguir, qual pode
ser o gráfico de uma função injetora y = f(x) ?
80
) é:
5) (UFMT) A figura abaixo apresenta o gráfico de uma
função y = f(x) .
8) ( Santa Casa – SP ) Se f – 1 é a função inversa da
função f , de R em R, definida por f(x) = 3x – 2,
–1
então f ( – 1 ) é igual a :
a) – 1
b)
c)
d)
A partir das informações contidas no gráfico, marque V
para as afirmativas verdadeiras e F para as falsas.
( ) f(x) é uma função injetora.
( ) O domínio de f(x) é o intervalo ] –2, 3]
( ) f(x) = 2, para todo 2 ≤ x ≤ 4
 5 
( ) f(x) ≥ 0,  x   , 0  [1, 5]
 2 
Assinale a seqüência correta.
A) F, F, F, V
B) F, V, V, F
C) V, F, V, V
D) V, V, V, F
E) F, V, F, F
6) ( Unifor – CE ) A lei que define a inversa da função
bijetora f(x) = 2 .x  1 é :
e)
1
3
1

5
1
5
1
3

9) ( FCC ) A função inversa da função f( x ) =
é:
a) f – 1( x ) =
b) f – 1( x ) =
c) f – 1( x ) =
d) f
e) f
–1
(x)=
–1
(x)=
3
2x  1
x3
x3
2x  1
2x  1
x 3
1  2x
3x
3x  1
x2
3x  1
2x
–1
3
3
.x 
2
2
3
–1
b) f (x) = .x  1
2
3
–1
c) f (x) = .x  1
2
3
3
–1
d) f (x) = .x 
2
2
a) f –1(x) =
10) Uma função real f(x) é bijetora onde f (x) é sua
–1
–1
–1
inversa. Se f (1) = 3, f (2) = 7 e f (5) = 11, podef (3)  f (11)
se afirmar que valor de
é:
f (7 )
A) 3
B) 4
C) 5
D) 6
E) 7
7) Observe o gráfico da função bijetora f( x ) abaixo.
GABARITO
y
f( x )
1) D
2) C
3) A
4) E
5) A
6) A
7) C
8) E
9) E
10) A
x
O gráfico que melhor representa a função inversa de f( x
81
FUNÇÃO PAR
FUNÇÃO COMPOSTA
Chama-se função composta (ou função de função ) à
função obtida substituindo-se a variável independente x ,
por uma função.
Dizemos que uma função f : A → B é par se, e
somente se: ∀ x A ⇒ f(x) = f(–x). Isto é, domínios
opostos quaisquer de A têm imagens iguais.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Os gráficos da função par são simétricos em
relação ao eixo y.
Veja o esquema a seguir:
y
y
x
x
y
Obs : atente para o fato de que fog
x
gof.
Exercícios Resolvidos
01. Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se
determinar gof(x) e fog(x).
y
x
Exemplo:
Seja a função f : IR → IR definida por f(x) = x 2.
Resolução
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
FUNÇÃO IMPAR
Dizemos que uma função f : A → B é ímpar se, e
somente:∀ x Α ⇒ f(x) = – f(–x). Isto é, domínios
opostos quaisquer de A têm imagens opostas.
Os gráficos da função ímpar são simétricos em
relação a origem do plano cartesiano.
y
y
x
x
Exemplos:
Seja a função f : IR definida por f(x) = 2x
.
82
EXERCÍCIOS
1) ( Cescem – SP ) Se f( x ) = a + 1 e g( z ) = 2z + 1,
então g( f(x) ) vale:
a) 2a + 2
b) a + 4
c) 2a – 3
d) 2a + 3
e) a + 3
2) (MACK) Dadas as funções f, g e h, de IR em IR,
definidas por f(x) = 3x, g(x) = x2 – 2x + 1 e h(x) = x
+ 2, então h[f(g(2))] é igual a:
a) 1
d) 4
b) 2
c) 3
e) 5
3) ( Fuvest – SP ) Sendo f uma função tal que f(x + 3) =
x2 + 1, para todo x real, então f(x) é igual a :
a) x2 – 2
b) 10 – 3x
c) – 3 x2 + 16x – 20
d) x2 – 6x + 10
e) x2 + 6x – 10
4) (UFMG) Observe a figura.
7) ( Mack – SP ) Dada a função f e g de R em R,
sendo f(x) = 4x – 5 e f( g( x ) ) = 11 – 8x, então
g(x) é :
a) g(x) = 4 – 2x
b) g(x) = 2 – 2x
c) g(x) = 2 + 3x
d) g(x) = 2x + 3
e) g(x) = 2 – 4x
8) ( Mack – SP ) Sejam f dada por f(x) = 2x – 1 e
g dada por g(x) = x + 1. Então, g(f( 2 )) é igual a:
a) 1
b) 2
c) 3
d) 4
e) 5
9) ( UFMG ) considere a função definida por:
 3 x se  1  x  1

f ( x )   5 se 1  x  4
 x  4 se x  4

Pode-se afirmar que o valor de f( f( f(2) ) ) é :
a)
Nessa figura, estão representados os gráficos das funções
f e g.
Se, h(x ) 
f (2x )  g(2x  a)
então o valor de h(a) é:
f (g( x ))
a) 1 + a
b) 1 + 3a
d) 2
e)
c)
4
3
5
2
5) (UEFS) A função real inversível f tal que
–1
f(2x – 1) = 6x + 2 tem inversa f (x) definida por:
3x  5
a)
d) 3x + 5
2
x 5
b)
e) 3x – 15
3
e) 5x – 3
6) (UESB) Considerando-se as funções f(x) = 3x + 2 e
g(x) = –2x + 1, pode-se afirmar que (fog –1)(x) é
definida por
b)
c)
d)
e)
1
3
1
3
5
9
10) (UFOP) Sendo f(x) = 1 – 8x e g(x) = k – 2x, o valor
de k para que (fog) (x) = (gof) (x) deve ser:
a) 1/7
b) 7
c) 1/3
d) 3
11) (UNIMONTES) Considere apenas funções de IR
em IR. Uma função f é par se f (−x) = f (x), para
todo elemento x de seu domínio. Uma função f é
ímpar se f (−x) = − f (x), para todo elemento x de
seu domínio. Com base nessa definição, todas as
afirmações abaixo são verdadeiras, EXCETO
A) A função f, dada por f (x) = x, é uma função
ímpar.
2
B) A função f, dada por f(x)=x - 3, é uma função
par.
C) A função f, dada por f (x) = 2x +1, não é uma
função par nem ímpar.
D) A função f, dada por f (x) = 2x, é uma função par
83
12) (FIP-2009) Seja uma função f(x) = 3 + 2 x – 1 e f –1 (x)
a sua inversa. Nessas condições, o valor de fof – 1
3
  , é:
2
13) (FIP-2013) A função afim abaixo definida mostra a
concentração de álcool no sangue para um indivíduo
do sexo masculino com 75 quilogramas de massa
corporal, que ingere 1 lata de cerveja (350 ml) por
hora, durante 5 horas:
Onde a é a quantidade de álcool retido e t é o tempo em
horas.
Pela “Nova Lei Seca”, que entrou em vigor no Brasil em
janeiro de 2013, a tolerância à presença de álcool retido
no sangue é zero.
Após ter cessado a ingestão de cerveja, o indivíduo
apresentado na questão está apto a dirigir com segurança
e não infringir a Lei de tolerância zero, aproximadamente
em:
A) 3 horas e 20 minutos.
B) 3 horas e 30 minutos.
C) 3 horas e 45 minutos.
D) 3 horas e 7 minutos.
GABARITO
1) D
2) E
3) D
8) D
9) C
10) C
4) D
11) D
5) B
6) 01
12) B
7) A
13) D
84
FUNÇÃO AFIM (1° GRAU)
Situação-problema:
O gráfico da função afim é uma reta não paralela a
qualquer dos eixos coordenados.
Como exemplos, veja os gráficos das funções y = 2x
– 1 e y = – 2x + 3
Numa loja, o salário fixo mensal de um vendedor é 500
reais. Além disso, ele recebe de comissão 50 reais por
produto vendido.
a) Escreva uma equação que expresse o ganho mensal y
desse vendedor, em função do número x de produto
vendido.
Solução:
y = 2x – 1
y = – 2x
y = salário fixo + comissão por produto vendido
y = 500 + 50x
(a > 0)
b) Quanto ele ganhará no fim do mês se vendeu 4
produtos?
Observe que destacamos, nos dois gráficos, os
pontos onde as retas cortam os eixos coordenados.
Solução:
Na primeira função y = 2x – 1, temos:
y = 500 + 50x, onde x = 4
y = 500 + 50.4 = 500 + 200 = 700
x = 0  y = 2.0 – 1  y = – 1  (0, – 1)
c) Quantos produtos ele vendeu se no fim do mês recebeu
1000 reais?
(a < 0)
y = 0  0 = 2x – 1  x = 1/2  (1/2, 0)
Na segunda função y = – 2x + 3, encontramos:
x = 0  y = – 2.0 + 3 = 3  (0, 3)
Solução:
y = 500 + 50x, onde y = 1000
1000 = 500+50x ⇒ 50x = 1000 − 500 ⇒
50x = 500 ⇒ x = 10
A relação assim definida por uma equação do 1.º grau é
denominada função do 1.º grau, sendo dada por:
DEFINIÇÃO
Toda função do tipo f(x)= ax + b com {a, b}
e a
é denominada função do 1° grau ou função afim.
f(x) = ax + b
y = 0  0 = –2x + 3  x = 3/2  (3/2 ,0)
Observe que a raiz da primeira função é 1/2 e a raiz
da segunda função é 3/2. A raiz é exatamente a
abscissa do ponto onde a reta corta o eixo x.
O valor de y para x = 0 nada mais é que o
coeficiente linear da função.
Analisando ainda os dois gráficos anteriores,
observamos que a primeira função (a > 0) é crescente
ao passo que a segunda função (a < 0) é decrescente.
Sintetizando, dada a função afim y = ax + b de IR
em IR, seu gráfico é uma reta não paralela aos eixos,
podendo ser de dois tipos:
Na função afim y = ax + b, chamamos:
a: coeficiente angular ou inclinação da reta
b: coeficiente linear ( onde a reta intercepta o eixo y )
Exemplos

y = 3x – 1 é uma função afim de coeficiente angular 3
e coeficiente linear – 1.

y =  5 x , é uma função afim de coeficiente angular
3
5
 e coeficiente linear0. Logo, a função é também
3
linear. ( Função linear é toda função do tipo y = ax + b
onde b = 0,ou seja, é toda reta que passa pela
origem)
a > 0  função
crescente
a < 0  função
decrescente
A reta corta o eixo y num ponto cuja ordenada é o
coeficiente linear b.
85
A reta, corta o eixo x num ponto cuja abscissa é a raiz da
b
função, dada por ax + b = 0 x  
a
Exercícios resolvidos
ESTUDO DO SINAL DE UMA FUNÇÃO AFIM
1. Resolver em IR as inequações.
Ao estudar o sinal de uma função qualquer é
simplesmente determinar os valores que podem ser
adotados a x para os quais y seja positivo ou negativo.
Consideremos uma função afim y = f(x) = ax + b vamos
estudar seu sinal.
b
Sendo a raiz de uma função afim x   , sabemos
a
que poderá ocorrer apenas duas situações:
a) (2x + 4) (6 – 3x) ≥ 0.
1º- A função é crescente quando a > 0.
2º- A função é decrescente quando a < 0.

Então teremos graficamente as seguintes situações:
INEQUAÇÃO DO 1° GRAU
Resolução:
Estudando a variação do sinal de cada uma das
funções f(x)= 2x + 4 e g(x)= 6 – 3x, temos :
1. Sendo f(x) = 2x + 4:
Raiz de f : 2x  4  0  x  - 2
 Variação do sinal de f : a > 0 , f é crescente .
Graficamente temos:
2. Sendo g(x) = 6 – 3x, tem-se:
CAIU NO ENEM !!
01.(ENEM)

Raiz de g : 6 - 3x  0  3x  6  x  2
 Variação do sinal de g: a < 0 , g é decrescente.
Graficamente temos:
Representando no eixo real a variação de f, g e f.g,
temos
GABARITO
S  x  IR /  2  x  2
01. B
b)
3x  2
1
x 3
3x  2  (x  3)
3x  2
1  0 
0
x 3
x 3
86
3x  2  x  3
0
x 3

2x  1
0
x 3
RESOLUÇÃO GRÁFICA DE INEQUAÇÕES
Considere a inequação 2x + 3y ≤ 6 .
Vamos mostrar alguns pares ordenados que
verificam essa inequação:

(-1, 2), pois 2. (-1) + 3.(2) = -2 + 6 = 4 e 4

(-3, 1), pois 2. (-3) + 3. (1) = -6 + 3 = -3 e -3

(3, -2), pois 2. (3) + 3. (-2) = 6 - 6 = 0 e 0
6
6
6
É evidente que não podemos enumerar todos os
pares ordenados de números reais que satisfazem
essa inequação, pois são infinitos, mas podemos
representá-los graficamente, isto é, representar
graficamente a solução da inequação.
Para isso, procederemos assim:
1. Traçamos a reta correspondente à função que se
obtém quando isolamos y após substituirmos o sinal
de desigualdade pelo de igualdade. No nosso exemplo,
temos:
2. Escolhemos um ponto qualquer (ponto auxiliar), não
pertencente à reta.
3. Verificamos se as coordenadas do ponto auxiliar
tornam a inequação verdadeira ou falsa:

se verdadeira, a solução da inequação é o
semiplano ao qual pertence o ponto auxiliar;

se falsa, a solução da inequação é o semiplano
oposto àquele ao qual pertence o ponto auxiliar.
Observe a solução gráfica das inequações
87
Exemplo
Vamos resolver cada sistema de inequações a seguir.
a)
A solução gráfica é o semiplano no qual está o ponto
auxiliar testado, incluindo a reta.
Observe o gráfico da inequação .
A reta está tracejada porque os pontos pertencentes a
ela não pertencem ao gráfico da inequação.
Veja, por exemplo, que o ponto (-3, 4) pertence à reta,
mas não pertence à inequação
pois:
EXERCÍCIOS
01.(UFJF) Para promover um baile, um clube fez o
seguinte levantamento de gastos:
Banda - R$ 3.000,00
Decoração - R$ 2.400,00
Iluminação - R$ 400,00
Também podemos resolver graficamente um sistema
de inequações desse tipo. Para isso, devemos construir,
num mesmo plano cartesiano, a solução gráfica
correspondente a cada inequação e tomar a região de
intersecção dessas soluções que será a solução gráfica
correspondente a cada inequação e tomar a região de
intersecção dessas soluções que será a solução do
sistema.
Além dos gastos, o buffet cobrará R$ 35,00 por
pessoa. O preço do convite individual é R$ 70,00.
O número mínimo de convites que o clube deve vender
para que o baile não dê prejuízo é:
A) 165.
B) 166.
C) 168.
D) 170.
E) 175.
02.(FGV-SP) O gráfico da função f(x) = mx + n passa
pelos pontos A(1, – 2) e B(4, 2). Podemos então
afirmar que:
a) m + n = – 2
b) m – n = –2
88
3
4
5
d) n =
2
c) m =
09. (UNIMONTES – PAES) A inequação que descreve
o semiplano da figura ao lado é
e) m.n = –1
03.( UFAL ) Seja f , de R em R, uma função definida por
f(x) = mx + p. Se os pontos (– 2, 7) e (2, – 1) pertencem
ao gráfico de f , então m – p é igual a:
a) – 6
b) – 5
c) – 3
d) 1
e) 6
04.( FGV – SP ) Uma função polinomial f do 1º grau é tal
que f(3) = 6 e f(4) = 8. Portanto, o valor de f(10) é:
a) 16
b) 17
c) 18
d) 19
e) 20
05.( UFSM ) Seja f: IR  IR uma função definida por f(x)
= mx + p. Se f passa pelos pontos A(0,4) e B(3,0),
então f –1 passa pelo ponto
a) (8, –2)
b) (8, 3)
c) (8, –3)
d) (8, 2)
e) (8, 1)
06.( PUC – MG ) A função f(x) = (8 – 2m)x + m – 5 é
estritamente crescente. É correto afirmar que m:
a) Está entre 4 e 5
b) É menor do que 4
c) É maior que 5
d) É qualquer número real
e) É qualquer número real positivo
07.( UEL – PR ) Seja f a função de R em R dada por f(X)
= (k2 - 4)x + 3k, na qual k é uma constante real. Se f é
decrescente e seu gráfico intercepta o eixo das abscissas
no ponto (1; 0), então um outro ponto do gráfico de f é
a) (–3; 6)
b) (–2; 9)
c) (–1; 1)
d) (2; 3)
e) (0; 6)
08.( USF – SP ) Sobre a função real de variável real dada
por f(x) = – 3x + 5, é verdade afirmar que:
a) A imagem de f é
b)
c)
d)
e)
 ,  5 2
A única raiz de f é 5/3
f é crescente
f é positiva se f > 5/3
f é negativa se f < – 5/3
a) y − 2x > 1.
b) 2y − x > 2 .
c) 2y + x > 2 .
d) y + 2x > −1.
10.(Uneb-BA) Para uma função f: R → R , que satisfaz
as condições
I. f(x + y) = f(x) + f(y)
II. f(1) = 3,
O valor de f(3) é igual a:
a) 1
b) 3
c) 6
d) 9
e) 27
11. ( UFPE ) Um provedor de acesso à Internet oferece
dois planos para seus assinantes:
Plano A - Assinatura mensal de R$ 8,00 mais R$
0,03 por cada minuto de conexão durante o mês.
Plano B - Assinatura mensal de R$ 10,00 mais R$
0,02 por cada minuto de conexão durante o mês.
Acima de quantos minutos de conexão por mês é mais
econômico optar pelo plano B?
a) 160
b) 180
c) 200
d) 220
e) 240
12. ( UFES ) Uma produtora pretende lançar um filme
em fita de vídeo e prevê uma venda de 20.000 cópias.
O custo fixo de produção do filme foi R$ 150.000,00 e o
custo por unidade foi de R$ 20,00 (fita virgem,
processo de copiar e embalagem).
Qual o preço mínimo que deverá ser cobrado por fita,
para não haver prejuízo?
a) R$ 20,00
b) R$ 22,50
c) R$ 25,00
d) R$ 27,50
e) R$ 35,00
13. ( UFRN ) A academia "Fique em Forma" cobra uma
taxa de inscrição de R$ 90,00 e uma mensalidade de
R$ 50,00. A academia "Corpo e Saúde" cobra uma taxa
de inscrição de R$ 60,00 e uma mensalidade de R$
55,00.
a) Determine as expressões algébricas das funções
que representam os gastos acumulados em relação
89
aos meses de aulas, em cada academia.
b) Após quantos meses a academia “Fique em forma” será
vantajosa se comparada coma academia “Corpo e saúde”
? Justifique, explicitando seu raciocínio.
14.( UFRN ) Na figura a seguir, tem-se o gráfico de uma
reta que representa a quantidade, medida em mL, de um
medicamento que uma pessoa deve tomar em função de
seu peso, dado em kgf, para tratamento de determinada
infecção.
O medicamento deverá ser aplicado em seis doses.
Assim, uma pessoa que pesa 85kgf receberá em cada
dose:
a) 7 mL
b) 9 ML
c) 8 mL
d) 10 mL
a) Só dois deles são positivos.
b) A soma de todos eles é dez.
c) O maior deles é múltiplo de 3.
d) O produto de todos eles é zero.
e) O produto de todos é um número negativo.
19.( UFMG ) O conjunto solução da inequação – 3x +
a > 7 é {x  IR | x < 2}. Então, o valor de a é
a) 1
b) 2
c) 7
d) 10
e) 13
20.( UFRS ) Se –1 < 2x + 3 < 1, então 2 – x está
entre
a) 1 e 3
b) –1 e 0
c) 0 e 1
d) 1 e 2
e) 3 e 4
21.( Cesgranrio ) A solução real da inequação ( 3x – 2
)3 ( x – 5 ) 2 ( 2 – x ) x > 0 é :
a) { x  R / x < 0 ou 2 < x < 2 }
b) { x  R / x > 0
15.( PAES ) O esboço que melhor representa a região do
plano cartesiano delimitada pelas retas de equações y – 2
= 0, x – 3 = 0, x – 7 = 0 e 3x – 4y + 11 = 0 é:
a)
y
c)
c) { x  R / x < 0
d) { x  R / x < 0
y
e) { x  R / x < 0
x
b)
y
x
d)
22.( MACK – SP ) O conjunto solução da inequação ( x
+3)(x–2)0 é :
a) { x  R / x  3 }
b) { x  R / 2  x  3 }
c) { x  R / x  2 ou x  3 }
d) { x  R / – 3  x  2 }
e) { x  R / – 2  x  3 }
y
x
x
16.(UNIMONTES) Todos os valores reais de x que
satisfazem a inequação
intervalo:
a) [0, +[
c) ]- , -2[  ]0, + [
3
ou 2 > x > 2 }
3
ou – 2 < x < 2 }
3
2
ou
<x<5}
3
ou 2 < x < – 2 }
3
x2
 1 , pertencem ao
x2
23.( FEI – SP ) No gráfico seguinte, a região em
destaque representa as condições de temperatura ( x )
e umidade ( y ) favoráveis ao desenvolvimento de um
tipo de fungo.
y
b) ]0, + [
d) ]- , -2[  [0, + [
17.(UFMG) O número real x satisfaz
15
4x  3
 2 . Assinale
x1
a alternativa em que estão incluídas
possibilidades para x.
a) –1 < x < 5/2
b) x > 5/2
c) x < -1
d) x < -1 ou x > 5/2
todas
as
18.( CFTCE ) Considere a inequação (x – 1)(x – 4)  0.
Considerando os números inteiros que a satisfazem. É
correto concluir que:
30
x
Assinale a alternativa cujo conjunto de desigualdades
descreve a região indicada :
a) x  0 , y  0 , x + 2y  30
b) x  0 , y  0 , x + 2y  30
c) x < 0 , y  0 , x + 2y  30
d) x  0 , y  0 , x  2y
e) x  0 , y  0 , x  2y
90
24.( UFMG ) Na figura estão esboçados os gráficos de
duas funções f e g.
y
f
g
–1
0
2
x
A) 8.000 assinaturas.
B) 4.000 assinaturas.
C) 2.000 assinaturas.
D) 6.000 assinaturas.
28.(FIP-2013) Pensando em otimizar seu lucro, a
empresa “Nexxus” fabrica um único tipo de produto, e
todas as unidades são vendidas. O custo total (C) da
produção e a receita (R),considerando a quantidade de
produtos vendidos, estão representados abaixo:
O conjunto { x  R : f(x) . g(x) < 0 } é dado por :
a) x > 0 ou x < – 1
b) – 1 < x < 0
c) 0 < x < 2
d) – 1 < x < 2
e) x < – 1 ou x > 2
25.(FIP-2009) Um táxi cobra R$ 20,00 pelo primeiro quarto
de quilômetro rodado e R$ 5,00 por cada quarto de
quilômetro adicional. Quanto custará, em reais, uma
viagem de x quilômetros?
A) P(x) = 20 + 5.(4x – 1)
B) P(x) = 20 + 4.(x – 1)
C) P(x) = 20 + 20.(x – 1)
D) P(x) = 20 + 5x
26.(FIP-2012) Os preços cobrados por duas empresas
que administram planos de saúde estão dispostos na
tabela abaixo:
Pode-se afirmar que o plano mais econômico é oferecido
pela empresa:
A) A, quando o número de consultas não exceder o total
de 20 por mês.
B) B, quando o número de consultas for superior a 3 por
mês.
C) B, quando o número de consultas não exceder o total
de 10 por mês.
D) A, quando o número de consultas for superior a 6 por
mês.
27.(FIP-2012)A Gráfica Universitária das Fipmoc pretende
comercializar a Revista Multidisciplinar no mercado nortemineiro. Os responsáveis pela empresa que irá
confeccionar a revista estimam gastos variáveis de R$
1,50 por revista processada e gastos fixos na ordem de R$
10.000,00 por mês. Por outro lado, também esperam obter
R$ 1,00 por revista comercializada, além de R$ 13.000,00
mensais relativos à receita de publicidade. Permanecendo
as demais condições constantes, para se alcançar um
lucro de R$ 1.000,00 por mês, será necessário
comercializar:
Com base nos dados apresentados, pode-se inferir
corretamente que a expressão que fornece o lucro (L),
considerando a quantidade de produtos vendidos (q)
pela referida empresa, é:
A) L(q) = 25q – 1000
B) L(q) = 50q – 1000
C) L(q) = 50q + 2000
D) L(q) = – 25q + 2000
29.(FIP-2013) Os estacionamentos em Montes Claros
estão cobrando entre R$3,00 e R$5,00 por hora. Um
estacionamento no centro da cidade cobra R$5,00 por
hora, mas possui uma promoção em que o cliente pode
comprar um selo no valor de R$20,00, com o qual
passa a pagar apenas R$ 1,00 por hora.
A partir de quanto tempo passa a ser vantajoso
comprar o selo promocional?
A) 3 horas
B) 4h 20 min
C) 5h
D) 5h 40 min
30. A expressão C = 0,012t + 65 fornece o
comprimento C, em centímetros, de uma barra de
metal em função de sua temperatura t, em graus
Celsius (°C). Andréa mediu o comprimento dessa barra
à noite onde a temperatura era de 10º e voltou a medilo no dia seguinte cuja temperatura era de 30º. Qual a
variação encontrada no comprimento da barra?
a) 0,12 cm
b) 0,24 cm
c) 0,36 cm
d) 0,48 cm
GABARITO
1) B
2) A
3) B
91
4) E
5) C
6) B
FUNÇAO QUADRÁTICA (2° GRAU)
7) B
8) B
9) C
INTRODUÇÃO
10) D
11) C
12) D
14) B
15) B
16) D
A função do 2.º grau está sempre presente em
nosso cotidiano. Pode-se observá-la na Física quando
se vê um fruto caindo de uma árvore; um carro
passando pela rua, etc.
Dentro do movimento uniformemente variado, em
trajetória vertical, temos as seguintes características:
17) D
18) B
19) E
1. a aceleração é igual a da gravidade (g);
20) E
21) A
22) D
23) A
24) E
25) A
2. quando há a queda de um corpo, sua velocidade
aumenta (movimento acelerado);
26) D
27) B
28) A
29) C
30) B
13) a) f(x) = 90 + 50x e g(x) = 60 + 55x
b) Após o 6º mês
3. na subida de um corpo a velocidade dele diminui
(movimento retardado) gradualmente até anular-se no
ponto mais alto, ou seja, nesse ponto a velocidade
passa a ser igual a zero.
DEFINIÇÃO
Imagine um retângulo em que a medida da base
seja duas unidades a mais do que a medida da altura.
Para calcular a área desse retângulo, precisamos
multiplicar a medida da altura pela medida da base. Se
chamarmos a área desse retângulo de y, e a medida da
altura de x, vamos ter:
y = x.(x + 2)
y = x2 + 2x
Essa expressão mostra que a área (y) desse tipo de
retângulo está relacionada à medida (x) da altura por
uma equação que é também de uma função de 2.o
grau. Se o valor x da altura for, por exemplo, 3cm, o
retângulo terá a
seguinte área:
2
y = 3 + 2.3
y=9+6
y = 15cm2
Chama-se função polinomial do 2º grau, ou função
quadrática, a toda função f : IR → IR definida por
f(x) = ax2 + bx + c, onde a, b, c
IR e a ≠ 0.
92
GRÁFICO
4° Vértice da parábola
O gráfico da função quadrática é uma curva
denominada parábola.
Será feito agora, uma série de observações sobre os
fatores que influem no aspecto da parábola.
Observe as parábolas abaixo:
1° - Sinal de a
a > 0 concavidade voltada para cima
a < 0 concavidade voltada para baixo
2°- Sinal de 
É claro que os pontos onde eventualmente a parábola
corta o eixo x são os pontos em que y = 0. Portanto, as
abscissas de tais pontos representam as raízes reais da
função. Como conseqüência, temos que:
O ponto V de ambos os gráficos é chamado vértice
da parábola.
9
Note que, no 1 caso ( a < 0), o ponto V é o ponto
"mais alto" do gráfico, ou seja, o ponto de ordenada
máxima enquanto que, no 2º caso (a > 0), o ponto V é
o ponto "mais baixo" do gráfico, isto é, o ponto de
ordenada mínima.
Chamando xv a abscissa e yv, a ordenada do
vértice, prova-se que
b

e yV  
xV  
2a
4a
O valor de yv limita o conjunto imagem de uma
função quadrática. Veja os dois casos:
Podemos escrever, então:
3°- Valor do coeficiente c
Na função quadrática y = ax2 + bx + c, fazendo x = 0
encontramos y = c. Portanto, toda parábola passa pelo
ponto (0, c), do eixo das ordenadas. Assim:
O coeficiente c é a ordenada do ponto onde a parábola
intercepta o eixo y.
a < 0 f(x) admite um máximo

b
quando x V  
yV  
4a
2a
a > 0 f(x) admite um mínimo

b
quando x V  
yV  
4a
2a
É importante observar, ainda, que
93
ESTUDO
DO
QUADRÁTICA
SINAL
DE
UMA
FUNÇÃO
Genericamente, a discussão da variação dos sinais
de uma função do segundo grau, f(x) = ax2 + bx + c,
recairá sempre em um dos seguintes casos:
Observações
Para ∆ > 0
a) O gráfico de f é sempre uma parábola com eixo de
simetria paralelo ao eixo Oy.
b) Se a > 0, então a parábola tem a “concavidade voltada
para cima”.
c) Se a < 0, então a parábola tem a “concavidade voltada
para baixo”.
d) A parábola sempre intercepta o eixo Oy no ponto (0;
c).
e) Se Δ = b2 – 4ac < 0, então f não admite raízes reais.
A parábola não intercepta o eixo Ox.
f) Se Δ = b2 – 4ac = 0, então f admite uma única raiz. A
parábola tangencia o eixo Ox.
Para ∆ = 0:
g) Se Δ = b2 – 4ac > 0, então f admite duas raízes reais
distintas. A parábola intercepta o eixo Ox em dois pontos.
A parábola que representa uma função polinomial do
2.º grau pode ser seis tipos possíveis, conforme os valores
de a e de Δ. A saber:
Para ∆ < 0:
94
INEQUAÇÕES DO 2° GRAU
Chama-se “inequação do 2° grau” toda inequação
apresentada em cada uma das seguintes formas :
ax2 + bx + c ≠ 0
ax2 + bx + c > 0
2
ax + bx + c < 0
2
ax + bx + c ≥ 0
2. Determinar os valores de k R, tais que:
2
f(x) = kx + 2(k + 1) x – (k + 1) seja estritamente
negativo para todo valor real de x.
1.º caso:
Se k = 0, temos f(x) = 2x – 1, que não é negativo para
qualquer x.
2.º caso:
Se k ≠ 0, o trinômio tem que ter um gráfico do tipo:
ax2 + bx + c ≤ 0
com {a, b, c}  IR e a ≠ 0.
A resolução desse tipo de equação é fundamentada no
estudo da variação de sinal da função do 2° grau,
conforme mostram os exercícios resolvidos a seguir.
Exercícios resolvidos
1. Resolver, em IR, a inequação x 2  2x  3  0 .
Resolução
Uma boa maneira de resolver uma inequação do 2°
grau é construindo seu gráfico.
Raízes da função f (x)  x 2  2x  3
x 2  2x  3  0
  b 2  4.a.c    (2) 2  4.1.(3)  16
b  
 (2)  16
x
2a
2.1
24
x
2
Logo: x 1  1 e x 2  3
Portanto,a parábola intercepta o eixo Ox nos pontos de
abscissas x 1  1 e x 2  3
x
Gráfico de f
Como o coeficiente de x2 é positivo (a > 0), a parábola
possui a concavidade voltada para cima, conforme a
seguir.
3. Vamos resolver a inequação-produto
A inequação pede os valores de x para os quais f(x)>0,
ou seja, x 2  2x  3  0 . Essa desigualdade ocorre se, e
somente se, x  1 ou x  3 . Logo, o conjunto solução é:
S  x  IR / x  1 ou x  3
95
03.(CTSP) Qual o conjunto solução da inequação, em
4  x2
>0
3x  x 2
A) – 3 < x < 2
B) – 2 < x < 3
C) 0 < x < 3
D) 0 < x < 2
04. Um projétil é lançado do solo, verticalmente para
2
cima, obedecendo a função H = 50t – 2t onde H é a
altura em metros e t é o tempo em segundos.
Determine:
a) A altura máxima atingida pelo projétil;
Quadro de sinais:
b) O tempo gasto para o projétil voltar ao solo, após o
disparo.
EXERCÍCIOS
01. ( Unimontes ) Considere a equação ax2 + bx + a = 0,
onde a>0, a, b Z. Se essa equação possui duas raízes
reais iguais, então
a) b<a
b) b é um número ímpar
c) b é um número par
d) b = a
02.(UNIMONTES) O gráfico da função f : IR  IR, definida
2
por f(x) = ax + bx + c onde b e c são números reais,
 2
passa pelos pontos (0, 0) e (1, 2). Então,f    vale
 3
05. (Enem 2ª aplicação 2010) Um laticínio possui dois
reservatórios de leite. Cada reservatório é abastecido
por uma torneira acoplada a um tanque resfriado. O
volume, em litros, desses reservatórios depende da
quantidade inicial de leite no reservatório e do tempo t,
em horas, em que as duas torneiras ficam abertas. Os
volumes são dados pelas funções
3
3
V1(t) = 250t – 100t + 3000 e V2(t) = 150t + 69t +
3000
Depois de aberta cada torneira, o volume de leite de
um reservatório é igual ao do outro no instante t = 0 e,
também, no tempo t igual a
A) 1,3 h.
B) 1,69 h.
C) 10,0 h.
D) 13,0 h.
E) 16,9 h.
06.( Unimontes / PAES) Um agricultor deseja cercar
um campo retangular no qual um dos lados mede o
triplo do outro. O material da cerca custa R$4,00 por
metro, para os lados menores, e R$5,00 por metro,
para os outros lados. Se esse agricultor tem apenas
R$380,00 para gastar com essa cerca, então a maior
área possível que pode ser cercada é, em metros
quadrados, igual a :
a) 1200
b) 300
c) 200
d) 1100
07.(UFMG) Um terreno retangular, com área de 800 m
e frente maior que a lateral, foi cercado com um muro.
2
96
O custo da obra era de R$ 12,00 por metro linear
construído na frente, e de R$ 8,00 por metro linear
construído nas laterais e no fundo. Se foram gastos R$
1040,00 para cercar o terreno, o comprimento total do
muro construído, em metros é:
a) 114
b) 120
c) 132
d) 180
08.( Vunesp – SP ) O gráfico da função quadrática
2
definida por y = x – mx + ( m – 1 ), em que m  R, tem
um único ponto em comum com o eixo das abscissas.
Então, o valor de y que essa função associa a x = 2 é :
a) – 2
b) – 1
c) 0
d) 1
e) 2
09.( UNICAMP ) Os valores de m de modo que o gráfico
da função y = x2 + mx + 8 – m seja tangente ao eixo
dos x são :
a) – 6 e 4
b) – 8 e 4
c) – 4 e 6
d) – 8 e 6
e) – 4 e 8
10.(UNIMONTES) O lucro semanal de uma siderúrgica
(em milhares de reais) é dado em função da quantidade q
de toneladas de minério processadas pela fórmula L(q) =
100(10 − q)(q − 2). A diretoria da siderúrgica espera um
lucro semanal mínimo de R$1.200.000,00. Para que isso
ocorra,
a
quantidade
de
minério
processada,
semanalmente,
A) não poderá ser inferior a 5 toneladas.
B) não poderá superar 6 toneladas.
C) não poderá superar 8 toneladas.
D) deverá ser superior a 6 toneladas.
11.(UFJF) Um ônibus de 54 lugares foi fretado para uma
excursão. A empresa cobrou de cada passageiro a quantia
de R$ 55,00 e mais R$ 2,50 por lugar vago. O número de
passageiros que dá à empresa rentabilidade máxima é:
A) 16.
B) 24.
C) 38.
D) 49.
E) 54.
12.( PAES ) A reta r representa a função f : R  R ,
definida pela regra f(x) = x – 2. O conjunto interseção
dessa reta com a parábola que representa a função f(x)=
x2 – x – 2 é o conjunto:
A) 
B) {(0, – 2); (2, 0) }
C) { x R/ –2  x  2 }
D) {2, –2}
13.(UNIMONTES) Seja f a função f: IR  IR definida
2
por f(x) = x – 10x + . Podemos afirmar que
a) a soma das raízes de f é um número irracional
b) f possui duas raízes reais diferentes
c) o produto das raízes de f é um número racional
d) f possui duas raízes reais e iguais
14.( FCC – BA ) Sabe-se que – 2 e 3 são raízes
de uma função quadrática. Se o ponto ( – 1, 8 )
pertence ao gráfico da função, então :
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor mínimo é 12,5
d) o seu valor máximo é 12,5
e) o seu valor mínimo é 0,25
15.( PAES ) Numa pequena empresa de roupas, o
custo médio da produção de x camisas é dado por
C(x) = – x2 + 30x – 20 reais. O custo máximo da
produção diária é, em reais, igual a :
a) 380
b) 150
c) 205
d) 45
16.( FCC – BA ) Se a função f(x) = x2 – ( k + 2 )x – k +
1 é estritamente positiva para qualquer x real, então :
a) – 8 < k < 0
b) – 8  k  0
c) k  – 8 e k  8
d) k < – 8 ou k > 8
e) K = – 8 ou k = 0
17. (UFMG) Observe a figura que representa o gráfico:
y
y = ax2 + bx + c
x
Assinale a única afirmativa falsa em relação a esse
gráfico:
a) b é positivo
b) c é negativo
2
c) ac é negativo
d) b – 4ac é positivo
18. ( Vunesp – SP ) O gráfico da função quadrática
2
definida por y = x – mx + ( m – 1 ), em que m  R,
tem um único ponto em comum com o eixo das
abscissas. Então, o valor de y que essa função
associa a x = 2 é :
a) – 2
b) – 1
c) 0
d) 1
e) 2
97
19. ( PUC – SP ) Sabendo que x’ e x’’ são as raízes da
função quadrática f(x) = x2 – 8x + m, o valor de m para
que se tenha 3x’ – 4x’’ = 3 é:
a) m = 15
b) m = 12
c) m = 7
d) m = 16
e) m = 24
20.( PAES ) Maria e Joana são revendedoras de um certo
produto de beleza. Em um determinado mês, a renda
mensal ( em reais ) de Maria foi dada pela função R(x) =
17x – 30 e a de Joana foi R(x) = x2 + 5x – 3, onde R é a
renda mensal e x é o número de unidades que cada uma
vendeu. Maria terá um rendimento mensal maior que o de
Joana se vender:
a) mais que nove unidades
b) entre 3 e 9 unidades
c) exatamente 10 unidades
d) 9 unidades
21.( Unimontes / PAES ) Um menino está à distância de
6m de um muro de 3m de altura e chuta uma bola que vai
bater exatamente sobre o muro. Se a função da trajetória
da bola em relação ao sistema de coordenadas indicado
pela figura é y = ax2 + ( 1 – 4a ) x, então a altura máxima
atingida pela bola é igual a:
a) 4m
y
b) 4,5m
c) 3m
d) 3,5m
25.(FIP-2010) Num dos jogos da Copa do Mundo, a
bola chutada por um jogador, em determinado lance,
descreve uma trajetória parabólica, conforme a figura
abaixo:
x
22.( Cesgranrio – RJ )
4x  1
x 2  2x  1
Os valores de
x, tais que
 0, são aqueles que satisfazem :
Supondo que a trajetória da bola seja descrita pela
equação y = –x² + 6x, em que y é a altura atingida
pela bola (em metros), e x é o tempo decorrido (em
segundos), qual a altura máxima atingida por ela, e
após quanto tempo isso ocorre, respectivamente?
A) 6 metros e 9 segundos
B) 9 metros e 6 segundos
C) 6 metros e 3 segundos
D) 9 metros e 3 segundos
a) x  4
b) x  4
1
c)x 
4
d) x  1
1
e)x 
4
23.( UFPA ) O domínio da função y = x .
4  x2
x2  3x  4
éo
conjunto :
a) ] -1 ; 4 ]
b) ] -  ; - 2 ]  ] 4 ; +  [
c) [ - 2 ; 1 [  [ 2 ; 4 [  { 0 }
d) ] -  ; - 1 [  ] 4 ; +  [  { 0 }
e) ] -  ; - 1 [  ] 4 ; +  [
24.( PAES ) Considere a função f: ]1, 3[  ]–1, 3 [ , definida por
f(x) = x2 – 2x. O esboço da função inversa de f, f – 1 é
26.(FIP-2013) O dono de um restaurante vende, em
média, 300 refeições por dia a R$5, 00 cada uma, que
tem um preço de custo de R$3, 00. Ele observou que, a
cada R$0, 20 que oferece de desconto no preço da
refeição, há um aumento de 40 refeições em sua
venda.
A que preço ele deve oferecer a refeição para que seu
lucro seja máximo?
A) R$7,40
B) R$6,50
C) R$5,25
D) R$4,75
98
27.(FIP-2013) Pensando em aproveitar o seu terreno, o Sr.
Paulo observou que poderia construir um cercado para
cultivar suas plantas. Ele possui um muro, com 6 metros
de comprimento, que irá aproveitar como parte dos lados
desse cercado retangular. Para completar o contorno
desse cercado,ele irá usar 34 metros de cerca.
Veja na figura abaixo.
b) R$ 8,00
c) R$ 7,00
d) R$ 6,00
e) R$ 5,00
31. Uma criança arremessa uma bola de basquete cujo
centro segue uma trajetória plana de equação
1 2 8
y
x  x  2 , na qual os valores de x e y
7
7
são dados em metros.
Essa criança acerta o arremesso, e o centro da bola
passa pelo centro da cesta, que está a 3 metros de
altura. A distância do centro da cesta ao eixo y é:
a) 6 metros
b) 7 metros
y
c) 8 metros
d) 9 metros
e) 10 metros
x
A maior área que o Sr. Paulo poderá cercar é:
A) 34 m2
B) 13 m2
C) 91 m2
D) 45,5 m2
28. ( Fuvest – SP ) Sejam x’ e x’’ as raízes da função
f(x) = 10x2 + 33x – 7. O número inteiro mais próximo do
número N = 5.( x’. x’’ ) + 2.( x’ + x’’ ) é:
a) 9
b) – 9
c)
10
d) – 10
e) – 13
29. ( UFMG ) Observe a figura.
Nessa figura, está representada a parábola de vértice V,
gráfico da função de segundo grau cuja expressão é
a) y = (x2 / 5) – 2x
y
b) y = x2 – 10x
2
c) y = x + 10x
2
d) y = (x / 5) – 10x
2
e) y = (x / 5) + 10x
5
–5
x
v
30. ( Cesgranrio ) O diretor de uma orquestra percebeu
que, com o ingresso a R$ 9,00 em média 300 pessoas
assistem aos concertos e que, para cada redução de R$
1,00 no preço dos ingressos, o público aumenta de 100
espectadores. Qual deve ser o preço para que a receita
seja máxima?
a) R$ 9,00
32. ( PUC – SP ) O lucro de uma empresa é definido
pela função L(q) = – q2 +10q – 16, onde q representa
a quantidade de produtos vendidos pela empresa num
determinado mês. Podemos concluir que esta
empresa terá lucro positivo, se o número q de
produtos vendidos estiver compreendido em:
(A) 2 ≤ q ≤ 8.
(B) 2 < q < 8.
(C) q < 2 ou q > 8 .
(D) q ≤ 2 ou q ≥ 8.
(E) q < 10 ou q > 16.
33. ( FIPMoc – 2015 ) No Mercado Municipal de
Montes Claros, é comum, no período de safra,
encontrar diversos produtores vendendo pequi, fruto
típico da região. Ao longo de um desses períodos,
constatou-se que a quantidade diária de dúzia de pequi
vendida (x) variava de acordo com o preço de venda da
dúzia (p), e a relação quantitativa entre essas variáveis
era dada pela lei:
1
9
P(x)  
x
20
2
Para que esse produtor tenha uma receita máxima,
deve-se vender a dúzia de pequi por:
A) R$2,25.
B) R$1,25.
C) R$3,25.
D) R$4,25.
E) R$5,25.
99
GABARITO
01. C
02. D
04. a) 312,5 metros
03. D
b) 25 segundos
05. A
06. B
07. A
08. D
09. B
10. C
11. C
12. B
13. B
14. D
15. C
16. A
17. A
18. D
19. A
20. B
21. A
22. C
23. E
24. A
25. D
26. D
27. sem resposta ( 100 m )
28. D
29. A
30. D
2
31. B
32. B
33. A
100
EQUAÇÕES EXPONENCIAIS
Ou y 
Chamamos de equações exponenciais toda equação
na qual a incógnita aparece em expoente.
Exemplos
1) 3x = 81 (a solução é x = 4)
2) 2x-5 = 16 (a solução é x = 9)
1
8
2 x  8 (falso, já que
2x  0 )
1
 2x 23  x  3
8
S={-3}
2x 
05. Determine o conjunto solução da equação
Para resolver equações exponenciais,
realizar dois passos importantes:
devemos
x
x
4 − 20.2 + 64 = 0
1º) redução dos dois membros da equação a potências
de mesma base;
2º) aplicação da propriedade:
Exercícios resolvidos
01. Resolva a equação exponencial: 2 3x+1 = 128
Resolução:
23x 1  128  23x 1  27
 3x  1  7  3x  6
x 2
S={2}
7X = 1
03. Resolva a equação exponencial:
3x = 2x
3 x 2x

2x 2x
3x = 2x
x
x=2 e x=4
06. Determine o conjunto solução da equação
02. Resolva a equação exponencial:
7x = 1
7x = 70
x=0  S={0}
x
Substituindo y1 e y2 na equação acima, temos que:
4x + 2 . 14x = 3 . 49x
0
3
3
3
   1     
2
2
 
 
2

x=0
S={0}
04. Resolva a equação exponencial:
2 x  3  63 
8
2x
Resolução:
2x 3  63 
8
2x
Faça 2 x  y
8
8y  63  
y
 2x.23  63 
8y 2  63y  8  0
8
2x
 y  8
101
FUNÇÃO EXPONENCIAL
Chama-se de função exponencial elementar toda
função
tal que f(x) = ax, com
.
Exemplos:
x
GRÁFICO DA FUNÇÃO EXPONENCIAL
x
A função exponencial f:IR → IR+ definida por f(x) = a ,
com a
e a ≠ 1 tem como representação gráfica as
seguintes curvas:
 1
1
2) y    (nesse caso, a  , logo 0 < a < 1)
2
2
 
Atribuindo alguns valores a x e calculando os
correspondentes valores de y, obtemos a tabela e o
gráfico abaixo:
Exponencial crescente: base a > 1
Exponencial decrescente: base 0 < a < 1
Nos dois exemplos, podemos observar que:
a) O gráfico nunca intercepta o eixo horizontal; a
função não tem raízes;
b) O gráfico corta o eixo vertical no ponto (0, 1);
Exemplos:
1) y  2 x (nesse caso, a = 2, logo a > 1)
Atribuindo alguns valores a x e calculando os
correspondentes valores de y, obtemos a tabela e o
gráfico abaixo:
c) Os valores de y são sempre positivos (potência
de base positiva é positiva), portanto o conjunto
imagem é Im =
.
INEQUAÇÃO EXPONENCIAL
Chamamos de inequações exponenciais todas
inequações na qual a incógnita aparece em expoente.
Para resolver inequações exponenciais, devemos
realizar dois passos importantes:
1°. Redução dos dois membros da inequação para
potências de mesma base;
2°. Aplicação da propriedade:
102
Exercícios resolvidos
01. Resolva a inequação exponencial: (0,1) 5x-1  (0,1) 2x 8
Resolução:
(0,1)5x-1  (0,1)2x 8  5x 1  2x  8 , já que
0  0,1  1  5x  2x  8  1
 3x  9
x3
Na reta real, teremos que:
02.(UFSJ) A soma das coordenadas dos pontos de
interseção do gráfico da função f(x) = (3x+2)3 + 8 , no
sistema cartesiano retangular XY, com os eixos
coordenados, é igual a
A) 44/3
B) 46/3
C) –10
D) 10
03.(Unimontes) O valor de a, para que a função dada
x
por f (x) = 0,1·(a – 1) seja decrescente, é
A) a = 1.
B) a = 0,1.
C) 1 < a < 2 .
D) a ≥2.
3
04. .(UFV) Considere a expressão f(x) 
Por propriedade, teríamos:
S  {x  IR/ x  3}
Por intervalo, teríamos:
S = [3;+∞[
02. Resolva a seguinte inequação: 2x> 23
03. Determine o domínio da função:
1
1 3 x
.A
soma f(x) + f (−x) corresponde a:
a) 3
b) 2
c) 1
d) 0
05. (UFV) Para resolver a equação exponencial
4 2x -2  24 . 4 x 2  8  0 , Aline tomou o cuidado de
inicialmente multiplicar ambos os membros da equação
por 16. Tendo resolvido corretamente, Aline encontrou
dois números reais cujo produto vale:
a) 5
b) 4
c) 3
d) 2
06.( PUC – SP ) Resolvendo a equação 4x + 4 = 5. 2x,
obtemos :
a) x' = 0 e x’’ = 1
b) x' = 1 e x’’ = 4
c) x' = 0 e x’’ = 2
d) x' = - 1 e x’’ = - 2
EXERCÍCIOS
01.( Unimontes / PAES ) Um almoço causou mal-estar
nos frequentadores de um certo restaurante. Uma
investigação revelou a presença da bactéria salmonela na
maionese. Essa bactéria multiplica-se, segundo a lei n(t )
= 200. 2at, em que n(t) é o número de bactérias
encontradas na amostra de maionese t horas após o
início do almoço, e a é uma constante real. Se, após 3
horas do início do almoço, o número de bactérias era de
800, após 6 horas esse número será de:
A) 1400
B) 1200
C) 3200
D) 2800
07. ( UFBA ) O conjunto verdade da equação 2x – 2 – x
= 5 ( 1 – 2 –x ) é :
a) { 1, 4 }
b) { 1, 2 }
c) { 0, 1 }
d) { 0, 2 }
e) 
x+1
08.( PUC – RS ) A solução da equação 2
– 6 = 0 Pertence ao intervalo :
a) – 1  x < 2
b) – 2 < x ≤ 2
c) 2 < x < 4
d) 2 < x  4
e) 3  x < 4
3–x
– 2
103
09.( Fatec – SP ) Seja m o menor número real que é
solução da equação 5x
2
2
 1 
: 25  

 125 
x
. Então,
m é
um número:
a) Par
b) primo
c) não real
d) irracional
e) divisível por 3
10.( Fatec – SP ) Se x é um número real tal que
2  x .4 x  8 x 1 , então :
a)
b)
c)
d)
e)
–2<x<2
x=1
x=0
x < 3/2
x > –3/2
11.( UFPA ) O conjunto solução da desigualdade
x 2 2
 1
 
2
a) { x
b) { x
c) { x
d) { x
e) { x
1
é:
4
R/–2<x<2}
 R / x < – 2 ou x > 2 }
 R / x < 0 ou x > 2 }
R/0<x<2}
 R / x < – 2 ou x > 0 }

12.( FGV – SP ) Encontre a solução da inequação
 1
 
2
x 2  5 x 1
D) 810 e 860 milhões.
E) 870 e 910 milhões.
1

2
13.( PUC – RS ) Encontre o domínio da função definida
15.(SEE-SP) Dez pessoas fundaram, no início do ano,
um clube. Um dos regulamentos de seu regimento
interno prevê que cada sócio pode apresentar, no
máximo, 2 novos sócios ao final de cada ano. A
expressão que permite calcular o número máximo de
sócios após decorrerem x anos é
A) 3. 10X + 10
B) 2. 10X
X
C) 10 + 2
X
D) 10. 2
E) 10. 3X
16. ( FIPMOC ) Um jantar causou mal-estar nos
clientes de um restaurante. Após análise, foi
comprovada a presença da bactéria Salmonella na
maionese. Essa bactéria multiplica-se, segundo a
função B(t) = 200 . 2at, em que B(t) é o número de
bactérias encontradas na amostra de maionese, t
horas após o início do jantar, e a é uma constante real.
Se, após 3 horas do início do jantar, o número de
bactérias era 800, podemos concluir que o número de
bactérias será maior ou igual que 3.200 bactérias
depois de
(A) 5 horas.
(B) 6 horas.
(C) 7 horas.
(D) 8 horas.
(E) 9 horas.
17. A produção mensal, em toneladas de certa
indústria é dada pela expressão y = 200.4–0,05x, na
qual x é o número de meses contados a partir de 1º
de janeiro. A produção mensal ultrapassará 100
toneladas a partir de:
A) 1º de setembro do mesmo ano.
B) 1º de outubro do mesmo ano.
C) 1º de novembro do mesmo ano.
D) 1º de dezembro do mesmo ano.
por f(x) = 2 x 1  2  x
GABARITO
14.(ENEM) Suponha que o modelo exponencial y =
363.e0,03x, em que x = 0 corresponde ao ano 2000, x = 1
corresponde ao ano 2001, e assim sucessivamente, e que
y é a população em milhões de habitantes no ano x, seja
usado para estimar essa população com 60 anos ou mais
de idade nos países em desenvolvimento entre 2010 e
2050 Desse modo, considerando e0,3 = 1,35, estima-se
que a população com 60 anos ou mais estará, em 2030,
entre
A) 490 e 510 milhões.
B) 550 e 620 milhões.
C) 780 e 800 milhões.
01. C
02. A
03. C
04. C
05. C
06. C
07. D
08. B
09. C
10. E
11. B
12. S = { x  R / – 5 ≤ x ≤ 0 }
13. Df = { x  R / x  
16. B
1
}
2
14. E
15. E
17. C
104
CONSEQUÊNCIAS DA DEFINIÇÃO
LOGARITIMOS
A) Sempre que o logaritmando for igual a “1”, o logaritmo
será igual a zero.
O CONCEITO DE LOGARITMO
O logaritmo do número a na base b é o expoente c, de forma
logb 1  0
c
tal que a = b. A simbolgia é:
logb a  c

b  a , com:
c
a>0
b>0 e b1
Onde: a é o logaritmando
B) Sempre que o logaritmando for igual a base, o logaritmo
será igual a um.
loga a  1
c) Sempre que o logaritmando for uma potência cuja base
for igual a base do logaritmo, o logarítmo será igual ao
expoente do logaritmando.
b é a base
c é o logaritmo
logb bw  w Ex.: log3 37  7
Exemplos:
D) Se dois logaritmos de mesma base forem iguais, os
logaritmandos desses logaritmos seram iguais.
log2 16  4 , pois24 = 16
Se loga b  loga k b = k
log3 243  5 , pois3 = 243
5
E) Se o expoente de uma potência, for um logaritmo cuja
base for igual à base dessa potência, o valor dessa potência
será igual ao logaritmando do expoente.
log 1000  3 , pois103 = 1000
k logk w  w EX.: 3log3 5  5
EXERCÍCIOS
1) Encontre o valor de log3 81
LOGARITMOS DECIMAIS
È todo logaritmo cuja base for igual a 10.
EX.: log10 7  log 7 (quando a base for igual a 10, não
é necessário colocar o valor da base)
2) Qual é o valor de log 0,01 ?
LOGARITMOS NEPERIANOS
É todo logaritmo na base e ( e = 2,718..., denominado de
número de Euler)
EX.: loge 5 = ln5 (quando a for igual a ”e”, o logaritmo
pode ser representado como ln)
3) Encontre o valor de log 5 0,6
3
4) Qual é o valor do logaritmo de
3
PROPRIEDADES OPERATÓRIAS
 Logaritmo de um produto: O logaritmo de um produto
de dois ou mais fatores reais e positivos, de base real,
positiva e diferente de 1, é à soma dos logaritmos
desses fatores, na menma base.
16 na base8 ?
logb (m.n )  logb m  logb n
CONDIÇÕES DE EXISTENCIA
x
log b a  3
a) Não existe log – 3 27, pois não existe a igualdade (-3) = 27
Ex.: Se
b) Não existe log 0 7, pois não existe a igualdade 0x = 7
log2 y é:
x
c) Não existe log 1 3, pois não existe a igualdade 1 = 3
x
d) Não existe log 2 (-8), pois não existe a igualdade 2 = -8
e) Não existe log 5 0, pois não existe a igualdade 5x = 0
e
logb (a.b)  y ,o valor de
a) 2**
b) 3
c) 1/2
d) 1/3
e) 4
105
 Logaritmo de um quociente: O logaritmo de um quociente
de dois números reais e positivos de base real, positiva e
diferente de 1, é à diferença entre o logaritmo do dividendo
e o logaritmo do divisor, na menma base.
logb (m / n )  logb m  logb n
Ex.: Se log2 b  log2 a  5 então o valor de b é:
Ex2.: Considerando que log2 = 0,30 e que
0,48, pode-se afirmar que log6 4 é:
a) 5/7
b) 10/13***
c) 11/15
d) 13/17
e) 17/19
log3 =
a
a) 5/2
b) 10
c) 3
d) 32**
e) 5
 Logaritmo de uma potência: O logaritmo de uma potência
de expoente reail é igual ao produto desse expoente pelo
logaritmo da base dessa potência.
logb nk  k . logb n
Ex1.:( Fuvest – SP ) Resolvendo-se a igualdade
3. log7 x  2. log7 8 , podemos afirmar que o valor de x
é:
a) 2
b) 3
c) 4**
d) 5
e) 6
COLOGARITMO
É o oposto do logaritmo de a na base b.
colog b a  logb a
Ex.: O cologaritmo de 1/9 na base 3 é:
a) 3
b) 2**
c) – 2
d) – 3
e) – 4
EQUAÇÕES LOGARÍTMICAS
São aquelas que apresentam a incógnita no logaritmando
ou na base do logaritmo.
Ex2.:Sabendo que loga 2  0,69 e que loga 3  1,1 , pode-se
Obs.: Não esquecer de verificar as condições de existência
para saber se a solução convém ou não.
afirmar que o valor de loga 4 12 é:
a) 0,34
b) 0,47
c) 0,53
d) 0,62**
e) 0,79
As equações logarítmicas podem se apresentar em três
tipos principais:
MUDANÇA DE BASE
1º TIPO: Aquelas em que aplicaremos apenas
DEFINIÇÃO DE LOGARITMO para sua resolução.
Exemplo
a
1) determinar o conjunto solução das equações logarítmicas
abaixo:
A) log5 (log2 x) = 0
S = {2}
Nos casos em que o logaritmo apresentar uma base que não
convém, esta poderá ser substituída por outra.
Para mudarmos a base de um logba para a base c, por
exemplo, efetuamos a divisão entre o logc a pelo logcb.
logb a 
logc a
logc b
Ex1.: Passe para a base 2 o logaritmo de 5 na base 8.
B) logx( x + 6 )= 2
S = {3}
106
2º TIPO: Aquelas em que aplicaremos as PROPRIEDADES DE
LOGARITMO para sua resolução.
Exemplo
FUNÇÃO LOGARÍTMICA
1) Qual é o conjunto verdade da equação logarítmica
logx(3x+4) = logx(4x+2)
V = {2}
loga x.
x
Seja a função exponencial y = a , com a > 1 . A sua
inversa chama-se função logaritmica e é indicada por y =
GRÁFICOS ( f(x) = loga x )
1º CASO: ( a > 1 ) f será crescente.
2) determinar o conjunto solução da equação logarítmica
log3(x+7) + log3(x–1) = 2
S ={2}
x
f(x)
½
-1
2
1
4
2
y
f(x) = log2 x
2
1
½
1 2
3
x
4
-1
*
Domínio: Df = R 
3) (UFSC) Qual o valor de x compatível para a equação log2(2x
– 1) – log2(x + 2) = log2(4x + 1) – log2(x + 10) ?
S = {2; 3}
2º CASO: (0 < a < 1 )
Imagem: Imf = R
f será decrescente.
y
1 2
1
3 4
-1
Exemplos
1) A solução da equação logaritmica log4 x + log2 x = 6 é:
a) 4
b) 8
c) 12
d) 16**
e) 20
f(x)
½
1
2
-1
4
-2
x
½
3º TIPO: Aquelas em que aplicaremos a MUDANÇA DE BASE
para sua resolução.
x
-2
f(x) = log1/2 x
*
Domínio: Df = R 
COMPARANDO
LOGARÍTMICA
AS
Imagem: Imf = R
FUNÇÕES
EXPONENCIAL
E
Função exponencial
y
(crescente )
Função logarítmica
2) ( UNIMONTES ) Os possíveis valores de x para os
quais
1
(crescente )
log 9 x + log x 9 = 5/2, são:
a) divisores de 243**
b) múltiplos de 27
c) primos entre si
d) múltiplos de 9
1
x
1
x
y
Função exponencial
(decrescente )
1
Função logarítmica
(decrescente )
107
EXEMPLOS
1)
( Fuvest – SP ) A figura a seguir mostra o gráfico da
função logaritmo na base b.
O valor de b é:
a) 1/4.
b) 2.
c) 3.
d) 4.**
e) 10.
EXERCÍCIOS
01.(UFV) Os números reais log2(x−1), log2(2x) e
log2(6x)
formam, nesta ordem, uma progressão
aritmética. O valor de x é:
a) 3
b) 9
c) 2
d) 4
02. (UFOP) Se

inequação log n
2)

2

eS é o conjunto solução da

 3 log n  2  0 , então, é correto
( PAES – 2009 ) O esboço de gráfico abaixo
representa a função real dada por f(x) = log x, x >0.
A área colorida vale:
y
a) log15
b) log7
c) log12**
d) 2 log4
x
1 2 3 4 5
afirmar que:
a)S contém 4 múltiplos de 20.
b)S contém 90 elementos.
c)S contém 46 números ímpares.
d)S contém 46 números pares.
INEQUAÇÕES LOGARÍTMICAS
Se a é raiz dessa equação, então calcule
03. (UFOP) Considere que as funções logarítmicas
envolvidas na equação a seguir são reais e de variável
real.
As inequações logarítmicas caracterizam-se por
possuírem desigualdades ( <, >, ≤, ≥ ) entre as expressões
logarítmicas.
Para se resolver inequações logarítmicas, deve-se observar os
valores das bases.
Considerando o logaritmo como loga x,temos dois casos.
1º CASO: Quando a base for um número real maior que 1. (a >
1)
Nesse caso a função é crescente e o sentido da desigualdade é
mantido.
Exemplo
1) Encontre a solução real da inequação logaritmica log2(x+2)<
3.
S = {xR / – 2 < x < 6 }
2º CASO: Quando a base for um número real entre 0 e 1. (a >
0 e a < 1)
Nesse caso a função é decrescente e o sentido da
desigualdade é invertido.
Exemplo
1) Encontre a solução real da inequação logaritmica log0,2 (2x–
3) ≤ log0,2 4.
04. ( FGV – SP ) Na equação y = 2
igual a 8 quando x for igual a :
a) 13
b) –3
c) –1
d) 5
e) 23
log3 ( x  4 )
, y será
05.(UNIMONTES-2009) As soluções da equação
x+1
4-x
4 + 4 - 80 = 0 são a e b, sendo a < b. O valor de
b
log 4 (ab)  log 4   é
a
a) 2.
b) 4.
c) 3.
d) 1.
06.(Unimontes-2007) Resolvendo a equação 3x = 7
em uma calculadora que tem a tecla log x, obtêm-se
os seguintes números:
A) log3, log 7 e log 7 − log3.
B) log3, log 7 e log73.
C) log3, log 7 e log7 : log3.
7
7
D)
e log
3
3
07.(PASES) A intensidade M de um terremoto, na
Escala Richter, pode ser calculada pela fórmula 3M =
2.log10 (kE), onde k é uma constante positiva e E, em
108
quilowatt/hora, é a energia liberada no terremoto. Se um
terremoto de intensidade 8 libera uma energia E1 e outro
terremoto de intensidade 6 libera uma energia E2 , então
a razão E1/E2 é a seguinte potência:
a) 105
3
b) 10
2
c) 10
d) 106
e) 104
08.(PASES) A intensidade I de uma onda sonora, medida
em Watt por metro quadrado, possui uma faixa de valores
muito grande. Por essa razão é conveniente o uso de
logaritmos em seu cálculo. O nível sonoro N , medido em
 I 
decibéis ( dB ), é definido por N(I) = 10. log10   , onde
 I0 
I0 é uma intensidade de referência padrão. O nível sonoro
de uma sala de aula típica é N1(I1) = 50 dB , enquanto
que o nível sonoro mais intenso que um ser humano pode
suportar antes de sentir dor é N2(I2) = 120 dB. A razão
entre as intensidades sonoras I2 e I1 é:
a) 104
b) 105
c) 106
7
d) 10
e) 108
09.(PASES) Gastão resolveu fazer uma aplicação junto ao
banco onde possui conta. O gerente o informou de que
estão disponíveis as seguintes opções de investimento a
juros compostos:
I. taxa de rendimento de 20% ao ano, para aplicação
mínima de R$ 500,00;
II. taxa de rendimento de 30% ao ano, para aplicação
maior ou igual a R$ 4.500,00.
Sabendo que Gastão vai iniciar seu investimento com
R$3.125,00, o tempo MÍNIMO, em anos, necessário para
que seu capital alcance o valor de R$ 58.500,00 é:
(Considere: log1,3 = 0,1.)
a) 15
b) 11
c) 13
d) 09
10.(UNIMONTES) Acrescentando-se 16 unidades a um
número, seu logaritmo na base 3 aumenta de 2
unidades. Esse número é
a) 5
b) 8
c) 2
d) 4
log x  log y  log y
11. (FAAP) Resolver o sistema 
 3 x  2y  33
12.( UFU – 2007 ) Se x e y são números reais
positivos, tais que logx3 = 4 e logy5 = 6, então, (xy)12
é igual a
a) 625.
b) 640.
c) 648.
d) 675.
13.(UNIMONTES-2010) Sendo a e b números reais,
uma solução da equação log a + log b = log(a + b)
existe se, e somente se,
b
b 1
2
B) a  b
1 b
b
C) a 
b 1
1
D) a 
b 1
A) a 
14.(UNIMONTES) A raiz da equação exponencial
8x − 5x = 0 é
A) log85
B) 5/8
C) 0
D) 8/5
15. (Paes )A igualdade log2 = 0,30 significa que
A) 0,3010 = 2
B) 20,30 = 1
1
C) 2 10  0,30
D) 100,30 = 2
16. ( FEI – SP ) Se a.b = 1, então logb a é igual a:
a) 2
b) – 1/2
c) 1/2
d) 1/a2
17.( UNIMONTES ) Os possíveis valores de x para os
quais log 9 x + log x 9 = 5/2, são:
a)
b)
c)
d)
divisores de 243
múltiplos de 27
primos entre si
múltiplos de 9
18.( Fuvest – SP ) O número real x que satisfaz a
equação log2 (12 – 2x) = 2x é:
a) log2 5
b) log2 3
c) 2
d) log2 5
e) log2 3
109
19.(PUC-SP) A energia nuclear, derivada de isótopos
radiativos, pode ser usada em veículos espaciais para
fornecer potência. Fontes de energia nuclear perdem
potência gradualmente, no decorrer do tempo. Isso pode

t
ser descrito pela função exponencial P  P0 .e 250 , na
qual P é a potência instantânea, em watts, de
radioisótopos de um veículo espacial; P0 é a potência
inicial do veículo; t é o intervalo de tempo, em dias, a
partir de t0 = 0; e é a base do sistema de logaritmos
neperianos. Nessas condições, quantos dias são
necessários, aproximadamente, para que a potência de
um veículo espacial se reduza à quarta parte da potência
inicial? (Dado: In2=0,693)
a) 336
b) 338
c) 340
d) 342
e) 346
20.(FIP-2009) Sem uma fonte de energia, a capacidade de
funcionamento celular cessaria, provocando a morte. Essa
energia é satisfeita pelo consumo de alimentos que
contém calorias. Um hambúrguer de dois andares, por
exemplo, contém 512 cal. Qual das afirmativas abaixo
expressa esse valor?
21.(FIP-2012) Alpargatas anuncia fábrica em Montes
Claros
Maior empresa de calçados da América Latina, a
Alpargatas S.A. anunciou a construção de uma nova
fábrica, em Montes Claros, no norte de Minas. A empresa
pretende investir R$ 177 milhões nos próximos quatro
anos na unidade mineira, e espera gerar cerca de 2,3 mil
empregos diretos e mais de 3 mil indiretos.
O principal item das novas linhas de produção serão as
sandálias Havaianas, tradicional marca da companhia
controlada pelo grupo Camargo Corrêa. A nova planta,
que começa a ser construída em agosto deste ano e deve
entrar em operação no segundo semestre de 2012, vai
fabricar cerca de 100 milhões de pares de calçados por
ano, o que representa um aumento de 35% na produção
atual.
A empresa fabricou e vendeu no ano passado 244 milhões
de unidades de calçados, vestuário e acessórios.
"Optamos por gerar empregos no Brasil. Temos condições
competitivas de fabricar nosso produto localmente", diz
Márcio Utsch, presidente da Alpargatas S.A.
Fonte: ADENORMG | Agência de Desenvolvimento da
Região Norte de Minas Gerais.
Suponha que um estudo estatístico tenha permitido a
conclusão de que, após t anos (t ³ 0), a empresa terá
sua produção dada pela expressão P(t) = 100. (1,35)t ,
em milhões de pares de calçados.
Segundo esse estudo, a fábrica atingirá uma produção
de 246 milhões de unidades de calçados em:
(Dados: log 2,46 = 0,39 e log 1,35 = 0,13)
A) 2015
B) 2013
C) 2017
D) 2020
22.(FIP-2012) O pH de uma solução varia de 0 a 14,
conforme a tabela:
O aparelho mostrado na figura a seguir é o phmetro.
Para medir o pH de uma solução, ele utiliza a relação
 1 
pH=log    , onde H+ é a concentração de hidrogênio
H 
em íons-grama por litro de solução.
Um estudante ao realizar uma pesquisa, encontrou a
concentração de hidrogênio de uma solução igual a
H+ = 12.10– 4.
Considerando: log2= 0,3 e log3=0,48, conclui-se que se
trata de uma solução:
A) ácida, uma vez que seu pH é maior que 0 e menor
que 3.
B) básica, uma vez que seu pH é maior que 11 e menor
que 13.
C) básica, uma vez que seu pH é maior que 7 e menor
que 9.
D) ácida, uma vez que seu pH é maior que 4 e menor
que 6.
23.(FIP-2012) Terremoto com mortos na Itália
aumenta a apreensão por ser 2 pontos superior ao
ocorrido em Montes Claros
O terremoto de 6 graus ocorrido no Norte da Itália, na
manhã de domingo, que provocou sete mortes e deixou
50 feridos, causou mais apreensão nos moradores de
Montes Claros por ser apenas dois pontos superior ao
ocorrido no município mineiro. Contudo, o professor
George Sands de França, do
Observatório Sismológico da UnB, não vê motivo para
alarme. “A população não deve se preocupar,
pois trata-se de uma medição de ordem de grandeza.
Se um tremor alcança 4 graus na escala Richter e outro
passa de 5 graus, esse ponto de diferença significa
uma intensidade 32 vezes maior”, explica França. O
Observatório Sismológico confirmou que o tremor de
sábado de manhã foi o de maior intensidade ocorrido
em Montes Claros até hoje: 4,2 graus.
O professor George Sands França, se referiu, a relação
110
E1
 101,5(M1 M 2 ) onde é possível perceber quantas
,
E2
vezes um terremoto é mais intenso que outro, sendo que
nesta relação:
E1 = energia liberada pelo terremoto 1
E2 = energia liberada pelo terremoto 2
M2 = grau do terremoto 1 na escala Richter
M2 = grau do terremoto 2 na escala Richter
Considerando que 100, 7 = 5 , quantas vezes a intensidade
do terremoto da Itália, foi maior do que o de Montes
Claros?
A) 500
B) 150
C) 800
D) 1.000
24.(FIP-2013) Devido a uma grande campanha de
esclarecimento, realizada neste ano pelo Instituto
Nacional do Câncer - INCA, sobre a prevenção das
infecções causadas pelo HPV, é projetada uma
importante redução do número de mulheres que
desenvolverão câncer no colo do útero.
Considerando MO como o número atual de mulheres com
essa doença, daqui a t anos esse número será:
Desse modo, sabendo-se que log2 = 0,3, pode-se
considerar que o número de mulheres com a doença
será igual a 1 do atual daqui a:
16
A)12 anos.
C)6 anos.
B)9 anos.
D)3 anos.
25. (FIP-2013) O tremor de terra ocorrido na cidade de
Montes Claros, no dia 18 de abril de 2013 teve amplitude
de 1000 micrômetros.
O sismógrafo mede a amplitude e a frequência dessas
vibrações. A magnitude (Ms) do terremoto pode ser
calculada pela equação logarítmica:
h(t) = 1,5 + log3(t + 1),
com h(t) em metros e t em anos. Se uma dessas
árvores foi cortada quando seu tronco atingiu 3,5m de
altura, o tempo (em anos) transcorrido do
momento da plantação até o do corte foi de:
a) 9.
b) 8.
c) 5.
d) 4.
27. A intensidade M de um terremoto, na Escala Richter,
pode ser calculada pela fórmula 3M = 2log10 (kE) , onde k é
uma constante positiva e E , em quilowatt/hora, é a energia
liberada no terremoto. Se um terremoto de intensidade 8
libera uma energia E1 e outro terremoto de intensidade 6
libera uma energia E2 , então a razão E1 / E2 é a seguinte
potência:
a) 105
b) 103
c) 102
d) 106
28. Um químico deseja produzir uma solução com pH =
2, a partir de duas soluções: uma com pH = 1 e uma
com pH = 3.
Para tanto, ele mistura x litros da solução de pH = 1
com y litros da solução de pH = 3. Sabe-se que pH = –
log10[H+] em que [H+] é a concentração de íons, dada
em mol por litro. Considerando-se essas informações, é
x
CORRETO afirmar que é:
y
1
A)
100
1
B)
10
C) 10
D) 100
29. A lei de resfriamento de Newton estabelece para
dois corpos, A e B, com temperatura inicial de 80ºC e
160ºC, respectivamente, imersos num meio com
temperatura constante de 30ºC, que as temperaturas
dos corpos, após um tempo t, serão dadas pelas
funções
T A = 30 + 50 x 10-kt e TB= 30 + 130 x 10-2kt
Onde A é a amplitude, dada em micrômetros e f é a
frequência, dada em Hertz (Hz).
O referido tremor teve uma frequência de:
26. A altura média do tronco de certa espécie de árvore,
que se destina à produção de madeira, evolui, desde
que é plantada, segundo o seguinte modelo matemático:
onde k é uma constante. Qual será o tempo decorrido
até que os corpos tenham temperaturas iguais?
1
A) log 5
k
2
18
B) log
k
5
1
13
C) log
k
5
5
2
D) log
k
2
111
30. O pH de uma solução é dado em função da
+
concentração de hidrogênio H em mols por litro de
 1 
solução, pela seguinte expressão pH  log 10    ou
H 

.
Sendo
assim,
determine
o
pH
de
uma
pH  log H
+
-8
solução que tem H = 1,0.10 .
a) 2
b) 4
c) 6
d) 8
 
FUNÇÃO DEFINIDA POR MAIS DE UMA
SENTENÇA
Dependendo dos valores de x uma função f(x) pode
ser definida por duas ou mais sentenças.
Exemplos
Seja a função f(x) de IR em IR definida por:
1, se x  0

f(x) =  x  1, se; 0  x  2
3, se x  2

GABARITO
1. A
2. D
3. 1
4. E
5. D
6. C
7. B
8. D
9. C
10. C
11. (9,3)
13. C
14. C
15. D
16. B
17. A
18. E
19. E
20. D
21. A
22. A
23. A
24. C
25. C
26. B
27. B
28. B
29. C
30. D
12. D
 x 2 , se x  0
f(x) = 
 3, se x  0
CAIU NO ENEM !!!
01.(ENEM)
112
a)
0t2
5t  10, se

2t6
v( t ) = 20, se
10t  40, se
6t8

0t2
2t  10, se

2t6
b)v( t ) = 20, se
10t  40, se
6t8

0t2
5t  10, se

2t6
c)v( t ) = 20, se
10t  20, se
6t8

0t2
5t  10, se

2t6
d) v( t ) = 20, se
5t  40, se
6t8

GABARITO
01. A
02. A
TRANSLAÇÃO E ROTAÇÃO DE EIXOS
Sendo a função f(x) : RR e k ≥ 0, temos as
seguintes situações :
Exemplos:
2.( UCB – DF ) O gráfico a seguir mostra a variação da
velocidade, em metros por segundo, de um móvel em
função do tempo. A lei que expressa v em função de t é
:
V
40
20
10
2
6
8
t
113
y
y
y = f(–x)
y = f(x)
y = f(x)
02.( PAES – 2007 ) O esboço do gráfico da função f: R
3
 R, definida por f(x) = – x , é
y
x
x
y = – f(–x)
y = – f(x)
EXERCÍCIOS
01.(UNIMONTES) Na figura abaixo, está representado o
gráfico da função f.
x
O esboço do gráfico da função f: R  R, definida por
f(x) = x3 – 2, é
O esboço do gráfico da função g, tal que g(x) = f(x + 1) +
1é
03.( UFMG ) Nesta figura, está representado o gráfico
da função y = f (x):
Com base nas informações desse gráfico, assinale a
alternativa cuja figura melhor representa o gráfico da
função g(x) = f(1–x).
114
A) W e L.
C) K e L.
E) K e K.
B) W e K.
D) K e W.
03.(ENEM-2009) Muitas vezes o objetivo de um
remédio é aumentar a quantidade de uma ou mais
substâncias já existentes no corpo do indivíduo para
melhorar as defesas do organismo. Depois de alcançar
o objetivo, essa quantidade deve voltar ao normal.
Se uma determinada pessoa ingere um
medicamento para aumentar a concentração da
substância A em seu organismo, a quantidade dessa
substância no organismo da pessoa, em relação ao
tempo, pode ser melhor representada pelo gráfico
GABARITO
01. B
02. A
03. B
QUESTÕES DO ENEM
01. (ENEM-2009) Na cidade de João e Maria, haverá
shows em uma boate. Pensando em todos, a boate propôs
pacotes para que os fregueses escolhessem o que seria
melhor para si.
Pacote 1: taxa de 40 reais por show.
Pacote 2: taxa de 80 reais mais 10 reais por show.
Pacote 3: taxa de 60 reais para 4 shows, e 15 reais por
cada show a mais.
João assistirá a 7 shows e Maria, a 4. As melhores
opções para João e Maria são, respectivamente,os
pacotes
A) 1 e 2.
C) 3 e 1.
E) 3 e 3.
B) 2 e 2.
D) 2 e 1.
02. (ENEM-2009) Três empresas de Táxi W, K e L estão
fazendo promoções: a empresa W cobra R$2,40 a cada
quilômetro rodado e com custo inicial de R$3,00; a
empresa K cobra R$2,25 a cada quilômetro rodado e uma
taxa inicial de R$3,80 e, por fim, a empresa L, que cobra
R$2,50 a cada quilômetro rodado e com taxa inicial de
R$2,80. Um executivo está saindo de casa a vai de táxi
para uma reunião que é a 5 km do ponto de táxi, e sua
esposa sairá do hotel e irá para o aeroporto, que fica a 15
km do ponto de táxi.
Assim, os táxis que o executivo e sua esposa deverão
pegar, respectivamente, para terem a maior economia são
das empresas
04.(ENEM-2009) A empresa WQTU Cosméticos vende
um determinado produto x, cujo custo de fabricação de
cada unidade é dado por 3x2 + 232, e o seu valor de
venda é expresso pela função 180x – 116. A empresa
vendeu 10 unidades do produto x, contudo a mesma
deseja saber quantas unidades precisa vender para
obter um lucro máximo.
A quantidade máxima de unidades a serem vendidas
pela empresa WQTU para a obtenção do maior lucro é
A) 10
C) 58
E) 232
B) 30
D) 116
05.(ENEM-2009) A empresa SWK produz um
determinado produto x, cujo custo de fabricação é dado
pela equação de uma reta crescente, com inclinação 2
e de variável x. Se não tivermos nenhum produto
produzido, a despesa fixa é de R$7,00 e a função
venda de cada unidade x é dada por –2x2+ 229,76x –
441,84.
Tendo em vista uma crise financeira, a empresa fez
algumas demissões. Com isso, caiu em 12% o custo da
115
produção de cada unidade produzida. Nessas condições,
a função lucro da empresa pode ser expressa como
(A) L(x)= –2x2 + 228x – 448,00
2
(B) L(x)= –2x + 227,76x – 448,84
2
(C)L(x)= –2x + 228x – 441,84
(D) L(x)= –2x2 + 229,76x – 441,84
(E)L(x)= –2x2 + 227,76x – 448,96
06.(ENEM-2010) Acompanhando o crescimento do filho,
um casal constatou que, de 0 a 10 anos, a variação da sua
altura se dava de forma mais rápida do que dos 10 aos 17
anos e, a partir de 17 anos, essa variação passava a ser
cada vez menor, até se tornar imperceptível. Para ilustrar
essa situação, esse casal fez um gráfico relacionando as
alturas do filho nas idades consideradas.
Que gráfico melhor representa a altura do filho desse
casal em função da idade?
07.(ENEM-2010) A figura a seguir é a representação de
uma região por meio de curvas de nível, que são
curvas fechadas representando a altitude da região,
com relação ao nível do mar. As coordenadas estão
expressas em graus de acordo com a longitude, no
eixo horizontal, e a latitude, no eixo vertical. A escala
em tons de cinza desenhada à direita está associada à
altitude da região.
Um pequeno helicóptero usado para reconhecimento
sobrevoa a região a partir do ponto X = (20; 60). O
helicóptero segue o percurso:
Ao final, desce verticalmente até pousar no solo.
De acordo com as orientações, o helicóptero pousou
em um local cuja altitude é
A. menor ou igual a 200 m.
B. maior que 200 m e menor ou igual a 400 m.
C. maior que 400 m e menor ou igual a 600 m.
D. maior que 600 m e menor ou igual a 800 m.
E. maior que 800 m.
08.(ENEM-2010) Embora o Índice de Massa Corporal
(IMC) seja amplamente utilizado, existem ainda
inúmeras restrições teóricas ao uso e às faixas de
116
normalidade preconizadas.
O Recíproco do Índice Ponderal (RIP), de acordo com o
modelo alométrico, possui uma melhor fundamentação
matemática, já que a massa é uma variável de dimensões
cúbicas e a altura, uma variável de dimensões lineares.
As fórmulas que determinam esses índices são:
11.(ENEM-2013) A parte interior de uma taça foi
gerada pela rotação de uma parábola em torno de um
eixo z, conforme mostra a figura.
Se uma menina, com 64 kg de massa, apresenta IMC
igual a 25 kg/m², então ela possui RIP igual a
09.(ENEM-2010) Nos processos industriais, como na
indústria de cerâmica, é necessário o uso de fornos
capazes de produzir elevadas temperaturas e, em muitas
situações, o tempo de elevação dessa temperatura deve
ser controlado, para garantir a qualidade do produto final e
a economia no processo.
Em uma indústria de cerâmica, o forno é programado para
elevar a temperatura ao longo do tempo de acordo com a
função
em que T é o valor da temperatura atingida pelo forno, em
graus Celsius, e t é o tempo, em minutos, decorrido desde
o instante em que o forno é ligado.
Uma peça deve ser colocada nesse forno quando a
temperatura for 48 °C e retirada quando a temperatura for
200 °C.
O tempo de permanência dessa peça no forno é, em
minutos, igual a
A) 100.
C) 128.
E) 150.
B) 108.
D) 130.
10.(ENEM-2009) Um posto de combustível vende 10.000
litros de álcool por dia a R$ 1,50 cada litro. Seu
proprietário percebeu que, para cada centavo de desconto
que concedia por litro, eram vendidos 100 litros a mais por
dia. Por exemplo, no dia em que o preço do álcool foi R$
1,48, foram vendidos 10.200 litros. Considerando x o valor,
em centavos, do desconto dado no preço de cada litro, e V
o valor, em R$, arrecadado por dia com a venda do álcool,
então a expressão que relaciona V e x é
A função real que expressa a parábola, no plano
cartesiano da figura, é dada pela lei
onde C é a medida da altura do líquido contido na taça,
em centímetros. Sabe-se que o ponto V, na figura,
representa o vértice da parábola, localizado sobre o
eixo x.
Nessas condições, a altura do líquido contido na taça,
em centímetros, é
A) 1.
B) 2.
C) 4.
D) 5.
E) 6.
12.(ENEM-2013) A Lei da Gravitação Universal, de
Isaac Newton, estabelece a intensidade da força de
atração entre duas massas. Ela é representada pela
expressão:
ondem1 e m2 correspondem às massas dos corpos, d à
distância entre eles, G à constante universal da
gravitação e F à força que um corpo exerce sobre o
outro.
O esquema representa as trajetórias circulares de
cinco satélites, de mesma massa, orbitando a Terra.
117
radioativo, após t anos, é calculada pela expressão
M(t) = A · (2,7)kt, onde A é a massa inicial e k é
uma constante negativa.
Considere 0,3 como aproximação para log2.
Qual o tempo necessário, em anos, para que uma
quantidade de massa do césio-137 se reduza a 10% da
quantidade inicial?
A)27
C)50
E)100
Qual gráfico expressa as intensidades das forças que a
Terra exerce sobre cada satélite em função do tempo?
B)36
D)54
14.(ENEM-2013)A temperatura T de um forno (em
graus centígrados) é reduzida por um sistema a partir
do instante de seu desligamento (t = 0) e varia de
acordo com a expressão
Com t em minutos. Por motivos de segurança, a trava
do forno só é liberada para abertura quando o forno
atinge a temperatura de 39 ºC.
Qual o tempo mínimo de espera, em minutos, após se
desligar o forno, para que a porta possa ser aberta?
A) 19,0
B) 19,8
C) 20,0
D) 38,0
E) 39,0
15.(ENEM/2009) Suponha que o modelo exponencial
y = 363.e0,03x, em que x = 0 corresponde ao ano 2000,
x = 1 corresponde ao ano 2001, e assim
sucessivamente, e que y é a população em milhões de
habitantes no ano x, seja usado para estimar essa
população com 60 anos ou mais de idade nos países
em desenvolvimento entre 2010 e 2050. Desse modo,
considerando e0,3 = 1,35, estima-se que a população
com 60 anos ou mais estará, em 2030, entre
A) 490 e 510 milhões.
B) 550 e 620 milhões.
C) 780 e 800 milhões.
D) 810 e 860 milhões.
E) 870 e 910 milhões.
13.(ENEM-2013)Em setembro de 1987, Goiânia foi palco
do maior acidente radioativo ocorrido no Brasil, quando
uma amostra de césio-137, removida de um aparelho de
radioterapia abandonado, foi manipulada inadvertidamente
por parte da população. A meia-vida de um material
radioativo é o tempo necessário para que a massa desse
material se reduza à metade. A meia-vida do césio-137 é
30 anos e a quantidade restante de massa de um material
16.(ENEM/2009) Uma pousada oferece pacotes
promocionais para atrair casais a se hospedarem por
até oito dias. A hospedagem seria em apartamento de
luxo e, nos três primeiros dias, a diária custaria R$
150,00, preço da diária fora da promoção. Nos três dias
seguintes, seria aplicada uma redução no valor da
diária, cuja taxa média de variação, a cada dia, seria de
R$ 20,00. Nos dois dias restantes, seria mantido o
preço do sexto dia. Nessas condições, um modelo para
a promoção idealizada é apresentado no gráfico a
seguir, no qual o valor da diária é função do tempo
medido em número de dias.
118
Que expressão fornece a quantidade de canudos em
função da quantidade de quadrados de cada figura?
A) C = 4Q
B) C = 3Q + 1
C) C = 4Q – 1
D) C = Q + 3
E) C = 4Q – 2
De acordo com os dados e com o modelo, comparando o
preço que um casal pagaria pela hospedagem por sete
dias fora da promoção, um casal que adquirir o pacote
promocional por oito dias fará uma economia de
A) R$ 90,00.
B) R$ 110,00.
C) R$ 130,00. D)R$ 150,00.
E)R$ 170,00.
17. (ENEM/2009) Um experimento consiste em colocar
certa quantidade de bolas de vidro idênticas em um copo
com água até certo nível e medir o nível da água,
conforme ilustrado na figura a seguir. Como resultado do
experimento, concluiu-se que o nível da água é função do
número de bolas de vidro que são colocadas dentro do
copo.
O quadro a seguir mostra alguns
experimento realizado.
número de bolas (x)
nível da água (y)
5
6,35 cm
10
6,70 cm
15
7,05 cm
resultados
GABARITO
01. E
02. B
03. D
04. B
05. A
06. A
07. A
08. E
09. D
10. D
11. E
12. B
13. E
14. D
15. E
16. A
17. E
18. B
do
Disponível em: www.penta.ufrgs.br.
Acesso em: 13 jan. 2009 (adaptado).
Qual a expressão algébrica que permite calcular o nível da
água (y) em função do número de bolas (x)?
A) y = 30x.
B) y = 25x + 20,2.
C) y = 1,27x.
D) y = 0,7x.
E) y = 0,07x + 6.
18.(ENEM/2010) Uma professora realizou uma atividade
com seus alunos utilizando canudos de refrigerante para
montar figuras, onde cada lado foi representado por um
canudo. A quantidade de canudos (C) de cada figura
depende da quantidade de quadrados (Q) que formam
cada figura. A estrutura de formação das figuras está
representada a seguir.
119
EQUAÇÕES MODULARES
Toda equação que contiver a incógnita em um módulo
num dos membros será chamada equação modular.
Exemplos:
a) |x2 − 5x| = 1
b) |x + 8| = |x2 − 3|
Observe que:
Se |f(x)| = r com r ≥ 0, teremos f(x) = r ou f(x) = −r
Se |f(x)| = |g(x)|, teremos f(x) = g(x) ou f(x) =− g(x)
Exercícios resolvidos
1. Resolver a equação |3x − 1| = 2.
Resolução:
Temos que analisar dois casos:
Caso 1: 3x − 1 = 2
Caso 2: 3x − 1 = −2
S = {−1, 2, 3, 6}
3. Resolver a equação |x − 6| = |3 − 2x|.
Resolução:
Temos que analisar dois casos:
Caso 1: x − 6 = 3 − 2x
Caso 2: x − 6 = −(3 − 2x)
2
2. Resolver a equação |x − 5x| = 6.
Resolução:
Temos que analisar dois casos:
2
Caso 1: x − 5x = 6
S = {−3, 3}
Caso 2: x2 − 5x = −6
120
INEQUAÇÕES MODULARES
Chamamos de inequações modulares as inequações em
que aparecem módulos de expressões que contém a
incógnita.
Representando geometricamente, o módulo de um
número real x é igual à distância do ponto que representa,
na reta real, o número x ao ponto de origem, como
sabemos. Assim:
 Se |x| < a (com a > 0), significa que a distância entre x e
a origem é menor que a, isto é, x deve estar entre −a e a,
ou seja
 Se |x| > a (com a > 0), significa que a distância entre x e
a origem é maior que a, isto é, deve estar à direita de a
ou à esquerda de −a na reta real, ou seja:
Exercício resolvido
Resolver a inequação |2x − 6| < 2.
Para resolver essa equação, apresentamos dois
métodos diferentes:
FUNÇÃO MODULAR
Seja g: A→IR, com A IR, uma função.
Chamamos de função modular a função f: A → IR, com
A IR, definida por f(x) = |g(x)|, ou seja:
Observe, então, que a função modular é uma função
definida por duas sentenças.
Exemplos:
CONSTRUINDO GRÁFICOS
1. Vamos construir, no plano cartesiano, o gráfico da
função f(x) = |x|. Não devemos esquecer que D(f) = IR.
Vamos elaborar uma pequena tabela onde vamos
achar, pela função, a imagem de alguns números:
121
EXERCÍCIOS
01. (UESB) O gráfico que melhor representa a função
.
2. Vamos construir, no plano cartesiano, o gráfico da
função f(x) = |x2 − 1|. Não devemos esquecer que D(f) =
IR. Vamos elaborar uma pequena tabela e nela achar,
pela função, a imagem de alguns números:
02.(UFMG) Considere a função f(x) = x.| 1 – x | .
Assinale a alternativa em que o gráfico dessa função
está CORRETO.
03. Resolva, no universo R, as equações abaixo:
a) | x – 3 | = 4
122
b) | 3x – 8 | = 2x – 1
c) | x | . | x – 5 | = 6
07.( Cesgranrio ) O conjunto Imagem da função f(x) =
|x2 – 4x + 8| + 1 é o intervalo:
a) [ 5, +  [
b) [ 4, +  [
c) [ 3, +  [
d) [ 1, +  [
e) [ 0, +  [
08. ( UFLA – MG ) O gráfico da expressão |x| + |y| = 4
é dado por:
04. A Resolva, no universo R, as inequações abaixo:
a) | 3x – 1| ≤ 8
b) | x2 – 5x | > 6
09. ( UFRN ) Um posto de gasolina encontra-se
localizado no km 100 de uma estrada retilínea. Um
automóvel parte do km 0, no sentido indicado na figura
abaixo, dirigindo-se a uma cidade a 250km do ponto de
partida. Num dado instante, x denota a distância (em
quilômetros) do automóvel ao km 0. Nesse instante, a
distância (em quilômetros) do veículo ao posto de
gasolina é:
05.Esboce o gráfico de cada função abaixo:
a) f(x) = | 3x – 6 |
2
b) f(x) = | x – 6x + 8 |
a) |100 + x |
b) x – 100
c) 100 – x
d) |x – 100|
10. ( UFES ) O gráfico abaixo representa a função
06. ( Unitau – SP ) Se x é uma solução de |2x - 1| < 5 –
x, então:
a) 5 < x < 7.
b) 2 < x < 7.
c) – 5 < x < 7.
d) – 4 < x < 7.
e) – 4 < x < 2.
a) f(x) = | | x | - 1|
123
b) f(x) = |x - 1| + |x + 1| - 2
c) f(x) = | | x | + 2| - 3
d) f(x) = |x - 1|
e) f(x) = | | x | + 1| - 2
GABARITO
1. 05
2. B
6. E
7. A
8. A
9. D
10. A
124
PROGRESSÕES
PROGRESSÃO ARITMÉTICA ( P.A.)
Definição
Consideremos a sequência ( 2, 4, 6, 8, 10, 12,14, 16).
Observamos que, a partir do segundo termo, a
diferença entre qualquer termo e seu antecessor é sempre
a mesma:
4 – 2 = 6 – 4 = 10 – 8 = 14 – 12 = 16 – 14 = 2
Exemplo
Consideremos a PA (3, 6, 9, 12, 15, 18, 21) e o
termo médio é 12. Observemos que o termo médio é
sempre a média aritmética do primeiro e do último, ou
seja:
3  21
 12 (termo central )
2
• A soma de dois termos equidistantes dos extremos de
uma PA finita é igual à soma dos extremos.
Exemplo
Consideremos a PA (3, 7, 11, 15, 19, 23, 27, 31).
Sequências como esta são denominadas progressões
aritméticas (PA). A diferença constante é chamada de
razão da progressão e costuma ser representada por r.
Na PA dada temos r = 2.
Podemos, então, dizer que:
Progressão aritmética é toda seqüência numérica em
que cada termo,a partir do segundo é igual à soma do
termo precedente(anterior) com uma constante r. O
número é chamado de razão da progressão aritmética.
.
Notação
Considere a P.A.( a1, a2, a3, a4, ...., an)
Onde:
a1= primeiro termo
an= último termo, termo geral ou n-ésimo termo
TERMO GERAL
Uma PA de razão r pode ser escrita assim:
PA (a1, a2, a3, a4, ...., an–1, an)
Portanto, o termo geral será:
an = a1 + ( n – 1 ).r , para n  N *
n= número de termos (se for uma PA finita)
r = razão
INTERPOLAÇÃO ARITMÉTICA
A razão influencia na PA da seguinte maneira:

r > 0, dizemos que a P.A é crescente

r < 0, dizemos que a P.A é decrescente

r = 0, todos os termos da P.A são iguais, ou seja, a
P.A é constante.
Interpolar ou inserir é determinar os n meios
aritméticos, entre dois números dados, de tal forma que
todos passem a constituir uma progressão aritmética.
Exemplo: Inserir sete meios aritméticos entre 2 e 26
Propriedades:
• Numa PA, qualquer termo, a partir do segundo,
é a média aritmética do seu antecessor e do seu sucessor.
a2 
a1  a3
2
• Numa PA qualquer de número ímpar de termos, o termo
do meio (médio) é a média aritmética do primeiro termo e
do último termo.
125
SOMA DOS N PRIMEIROS TERMOS DE UMA PA
EXERCÍCIOS
Consideremos a seqüência (2, 4, 6, 8, 10, 12,14, 16,
18, 20). Trata-se de uma PA de razão 2.
Suponhamos que se queira calcular a soma dos termos
dessa seqüência, isto é, a soma dos 10 termos da PA (2,
4, 6, 8, ..., 18, 20).
Poderíamos obter esta soma manualmente, ou seja,
01.( UNESP – SP ) Num laboratório, foi feito um estudo
sobre a evolução de uma população de vírus. Ao final
de um minuto do início das observações, existia 1
elemento na população; ao final de dois minutos,
existiam 5, e assim por diante. A seguinte seqüência
de figuras apresenta as populações do vírus
(representado por um círculo) ao final de cada um dos
quatro primeiros minutos.
Supondo que se manteve constante o ritmo de
desenvolvimento da população, o número de vírus no
final de 1 hora era de:
a) 241
b) 239
c) 237
d) 235
e) 232
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 = 110.
Mas se tivéssemos de somar 100, 200, 500 ou 1000
termos? Manualmente seria muito demorado. Por isso,
precisamos de um modo mais prático para somarmos os
termos de uma PA. Na PA( 2, 4, 6, 8, 10, 12, 14, 16, 18,
20) observe:
a1+a10 = 2 + 20 = 22
a2+a9 = 4 + 18 = 22
a3+a8 = 6 + 16 = 22
a4+a7 =8 + 14 = 22
a5+a6 = 10 + 12 = 22
Note que a soma dos termos eqüidistantes é constante
(sempre 22) e apareceu exatamente 5 vezes (metade do
número de termos da PA, porque somamos os termos dois
a dois).
Logo, devemos, em vez de somarmos termo a termo,
fazermos apenas 5 x 22 = 110, e assim, determinamos
S10 = 110 (soma dos 10 termos).
E agora, se fosse uma progressão de 100 termos,
como a PA(1, 2, 3, 4,...,100), como faríamos?
Procederemos do mesmo modo. A soma do a1
com a100 vale 101 e esta soma vai-se repetir 50 vezes
(metade de 100), portanto
S100 = 101x50 = 5050.
Então, para calcular a soma dos n termos de uma PA,
somamos o primeiro com o último termo e esta soma irá
n
se repetir
vezes.
2
Assim, podemos escrever:
Exemplo
Considerando a P.A. abaixo determine a soma dos seus
termos:
02. (Enem 2ª aplicação 2010) Nos últimos anos, a
corrida de rua cresce no Brasil. Nunca se falou tanto no
assunto como hoje, e a quantidade de adeptos
aumenta progressivamente, afinal, correr traz inúmeros
benefícios para a saúde física e mental, além de ser
um esporte que não exige um alto investimento
financeiro.
Disponível em:http://www.webrun.com.br. Acesso em: 28 abr.
2010.
Um corredor estipulou um plano de treinamento diário,
correndo 3 quilômetros no primeiro dia e aumentando
500 metros por dia, a partir do segundo. Contudo, seu
médico cardiologista autorizou essa atividade até que o
corredor atingisse, no máximo, 10 km de corrida em um
mesmo dia de treino. Se o atleta cumprir a
recomendação médica e praticar o treinamento
estipulado corretamente em dias consecutivos, podese
afirmar que esse planejamento de treino só poderá ser
executado em, exatamente,
A) 12 dias.
B) 13 dias.
C) 14 dias.
D) 15 dias.
E) 16 dias.
03.( MACK – SP ) Determine a razão da P.A.(a1 , a2
, a3 , ... , an ), sabendo que an = 3n+2.
a) 2
b) 3
c) 4
d) 5
e) 6
04.( FATEC – SP ) Inserindo-se 5 números entre 18 e
96, de modo que a seqüência (18, a2, a3, a4, a5, a6, 96)
seja uma progressão aritmética, tem-se a3 igual a:
a) 43
b) 44
c) 45
d) 46
e) 47
126
05.( FGV – SP ) Para todo n natural não nulo, sejam as
seqüências
(3, 5, 7, 9, ..., an, ...)
(3, 6, 9, 12, ..., bn, ...)
(C1, C2, C3, ..., Cn, ...)
Com Cn = an + bn.
Nessas condições, C25 é igual a
a) 25
b) 37
c) 101
d) 119
e) 126
06. (Enem 2ª aplicação 2010) O trabalho em empresas
exige dos profissionais conhecimentos de diferentes
áreas. Na semana passada, todos os funcionários de uma
dessas empresas estavam envolvidos na tarefa de
determinar a quantidade de estrelas que seriam utilizadas
na confecção de um painel de Natal.
Um dos funcionários apresentou um esboço das primeiras
cinco linhas do painel, que terá, no total, 150 linhas.
Após avaliar o esboço, cada um dos funcionários esboçou
sua resposta:
Funcionário I: aproximadamente 200 estrelas.
Funcionário II: aproximadamente 6 000 estrelas.
Funcionário III: aproximadamente 12 000 estrelas.
Funcionário IV: aproximadamente 22 500 estrelas.
Funcionário V: aproximadamente 22 800 estrelas.
Qual funcionário apresentou um resultado mais próximo
da quantidade de estrelas necessária?
a) I
b) II
c) III
d) IV
e) V
07.( CFTMG ) A seqüência (x, 2x + 1, x2 + 2) com x  0
formam, nessa ordem, uma progressão aritmética;
portanto o valor de x é
a) 1
b) 2
c) 3
d) 4
08.( PUC – RIO ) Os números 4, 7, 10, 13... formam uma
progressão aritmética. O número de termos desta
progressão aritmética para que a soma 4 + 7 + 10 +...
seja 144 é:
a) 12
b) 10
c) 9
d) 19
e) 13
09. (UFV-MG) Usando-se um conta-gotas, um produto
químico é misturado a uma quantidade de água da
seguinte forma: a mistura é feita em intervalos
regulares, sendo que no primeiro intervalo são
colocadas 4 gotas e nos intervalos seguintes são
colocadas 4 gotas mais a quantidade misturada no
intervalo anterior. Sabendo-se que no último intervalo o
número de gotas é 100, o total de gotas do produto
misturadas à água é:
a)1300
b)1100
c)1600
d)900
e)1200
10. (Unimontes / PAES ) Num teatro ao ar livre, cada
fileira, a partir da primeira, tem 4 cadeiras a mais que
a anterior. Se há 15 fileiras, sendo que a quinta tem
44 cadeiras, o número de espectadores necessários
para lotar esse teatro é:
a) 840
b) Superior a 1000
c) 990
d) Inferior a 720
11.( PUCCAMP – SP ) Um veículo parte de uma cidade
A em direção a uma cidade B, distante 500 km. Na
1ª hora do trajeto ele percorre 20 km, na 2ª hora 22,5
km, na 3ª hora 25 km e assim sucessivamente. Ao
completar a 12ª hora do percurso, a que distância esse
veículo estará de B?
a) 95 km
b) 115 km
c) 125 km
d) 135 km
e) 155 km
12.( PUC – MG ) Uma atleta amadora começa a treinar
diariamente e, a cada dia, anda 200 metros a mais que
no dia anterior. Se, ao final de 10 dias, essa atleta tiver
percorrido um total de 15.000 metros, a distância
percorrida por ela, durante o treino do segundo dia, em
metros, foi igual a:
a) 800
b) 1.000
c) 1.200
d) 1.500
13.( Mackenzie – SP ) Se f(n), nN, é uma seqüência
f (0)  1
definida por 
, o valor de f(200) é :
f (n  1)  f (n)  3
a)
b)
c)
d)
e)
601
611
621
631
641
127
14.( PAES ) A soma dos algarismos do número
52 53 5 4
5 2008 5 2009
 2  3  ...  2007  2008
5
5
5
5
5
é:
A) 10
B) 9
c) 6
d) 5
15.( PAES ) Dois atletas estão treinado juntos para uma
competição. O primeiro corre uniformemente 12km por
dia. Outro corre 10km no primeiro dia e, do segundo dia
em diante, corre 0,5km à mais que no dia anterior. Após
quantos dias de treinamento os dois terão percorrido a
mesma distância ?
A) 5 dias
B) 7 dias
C) 6 dias
D) 9 dias
21.(UNIMONTES) Se (3  x , x , 9  x , ...) é uma
progressão aritmética, seu 6.° termo é
A) 5.
B) − 5.
C) 0.
D) 3.
22.(UNIMONTES) Em uma progressão aritmética, a
soma do primeiro termo com o quarto é 16, e a soma
do terceiro com o quinto é 22. O primeiro termo dessa
progressão é
A) 4.
B) 3.
C) 5.
D) 2.
23.(UNIRIO) Considere a sequência não decrescente
(1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,...). Observe que ela
contém exatamente m vezes o inteiro m. Determine em
que posição desta sequência encontra-se o primeiro
número 100.
16.( FGV – SP ) Qual a soma dos 500 primeiros termos
da seguinte progressão ( 1, 3, 5, 7, 9, ... ) ?
17.( Mack – SP ) A soma dos n primeiros termos de
uma P.A é dada por Sn = 3n( n – 2 ) , para todo n.
Determinar o 5º termo dessa P.A .
24.(UNIMONTES – PAES) As medidas dos lados do
triângulo da figura abaixo formam uma progressão
aritmética em que 2a é o termo central. O perímetro do
triângulo é
2a
A) 9.
a+1
B) 14.
C) 18.
a+5
D) 30.
18.( UECE ) Seja ( a1, a2, a3, a4, a5, a6, a7, a8 ) uma
progressão aritmética. Se a2 + a5 = 8 e a8 = 7, então a3
+ a7é igual a:
a) 8
b) 28/3
c) 10
d) 32/3
e) 31/3
25.(Uel) Numa progressão aritmética de primeiro termo
1/3 e razão 1/2, a soma dos n primeiros termos é
20/3. O valor de n é
a) 5
b) 6
c) 7
d) 8
e) 9
19.(UECE) Os termos da sucessão ( a1, a2, ..., an ) estão
relacionados pela fórmula an+1 = 1 + 2.an, onde n = 1, 2, 3,
... . Se a1 = 0, então a6 é:
a) 25
b) 27
c) 29
d) 31
26. (Cesgranrio) A média aritmética dos 20 números
pares consecutivos, começando em 6 e terminando em
44, vale:
a) 50.
b) 40.
c) 35.
d) 25.
e) 20.
20.(UNIFESP) A soma dos termos que são números
primos da seqüência cujo termo geral é dado por an = 3n
+ 2, para n natural, variando de 1 a 5, é
a) 10.
b) 16.
c) 28.
d) 33.
e) 36.
27. (PUCMG) Na seqüência (1/2, 5/6, 7/6, 3/2,...), o
termo de ordem 30 é:
a) 29/2
b) 61/6
c) 21/2
d) 65/6
e) 67/6
128
28. (CFO/) Um professor de Educação Física, utilizando
1540 alunos, quer alinhá-los de modo que a figura
formada seja um triângulo. Se na primeira fila for colocado
1 aluno, na segunda 2, na terceira 3 e assim por diante,
quantas filas serão formadas?
A) 45 filas.
B) 35 filas.
C) 60 filas.
D) 55 filas.
29. ( Fuvest – SP ) Os números 1, 3, 6, 10, 15, ... são
chamados de números triangulares, nomenclatura esta
justificada pela seqüência de triângulos abaixo.
Observando a figura acima pode se verificar que o
primeiro triângulo é formado por um ponto, que o segundo
triângulo é formado por três pontos, que o terceiro
triângulo é formado por seis pontos e assim
sucessivamente. Quantos pontos terá o trigésimo triângulo
?
a) 465
b) 470
c) 475
d) 480
e) 485
30. ( OBMEP ) A sequência 0, 3, 7, 10, 14, 17, 21, ... é
formada a partir do número 0 somando-se alternadamente
3 ou 4 ao termo anterior, isto é: o primeiro termo é 0, o
segundo é 3 a mais que o primeiro, o terceiro é 4 a mais
que o segundo, o quarto é 3 a mais que o terceiro, o
quinto é 4 a mais que o quarto e assim sucessivamente.
A) Escreva os 20 primeiros termos desta sequência.
B) Qual é o 1000º termo desta sequência?
C) Algum termo desta sequência é igual a 2 000? Por
quê?
31. (Fuvest) Os números inteiros positivos são
dispostos em "quadrados" da seguinte maneira:
O número 500 se encontra em um desses "quadrados". A
"linha" e a "coluna" em que o número 500 se encontra são,
respectivamente:
a) 2 e 2.
b) 3 e 3.
c) 2 e 3.
d) 3 e 2.
e) 3 e 1.
32. (Unirio) Passando em uma sala de aula, um aluno
verificou que, no quadro-negro, o professor havia
escrito os números naturais ímpares da seguinte
maneira:
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
O aluno achou interessante e continuou a escrever, até
a décima linha.
Somando os números dessa linha, ele encontrou
a) 800
b) 900
c) 1000
d) 1100
e) 1200
33. (Ufsm) Tisiu ficou sem parceiro para jogar bolita
(bola de gude); então pegou sua coleção de bolitas e
formou uma seqüência de "T" (a inicial de seu nome),
conforme a figura
Supondo que o guri conseguiu formar 10 "T"
completos, pode-se, seguindo o mesmo padrão,
afirmar que ele possuía
a) mais de 300 bolitas.
b) pelo menos 230 bolitas.
c) menos de 220 bolitas.
d) exatamente 300 bolitas.
e) exatamente 41 bolitas.
34. (Ufrj) Num Ka Kay, o oriental famoso por sua
inabalável paciência, deseja bater o recorde mundial de
construção de castelo de cartas.
Ele vai montar um castelo na forma de um prisma
triangular no qual cada par de cartas inclinadas que se
tocam deve estar apoiado em uma carta horizontal,
excetuando-se as cartas da base, que estão apoiadas
em uma mesa. A figura a seguir apresenta um castelo
com três níveis.
Num Ka Kay quer construir um castelo com 40 níveis.
Determine o número de cartas que ele vai utilizar.
129
GABARITO
01. C
02. D
03. B
04. B
06. C
07. C
09. C
09. A
10. A
11. A
12. A
13. A
05. E
14. D ( SOMA = 1 + 0 + 0 + 4 + 0 )
15. D
16. 250.000
19. D
17. 21
18. C
20. D
21. A
22. C
23. 4951
24. C
25. A
26. D
27. B
28. D
33) B
34) 2420 cartas
29. A
30. a)
b) 3496
c) Não
31. A
32. C
130
PROGRESSÃO GEOMÉTRICA( PG)
2. Numa PG, o produto dos termos eqüidistantes dos
extremos é igual ao produto dos extremos.
Definição
Progressão geométrica (P.G) é uma seqüência
numérica em que cada termo, a partir do segundo, é igual
ao anterior, multiplicado por uma constante chamada
razão da progressão geométrica.
FÓRMULA DO TERMO GERAL
Eis alguns exemplos de progressões geométricas:
Seja a PG genérica: (a1, a2, a3, a4, ... , an, ... ),
onde a1 é o primeiro termo, e an é o n-ésimo termo,
ou seja, o termo de ordem n. Sendo q a razão da
PG, da definição podemos escrever:
a2 = a1 . q
a3 = a2 . q = (a1 . q).q = a1 . q
2
2
a4 = a3 . q = (a1 . q ).q = a1 . q
3
Infere-se (deduz-se) que:
que é denominada fórmula do termo geral da PG.
Exemplos
01.Dada a PG (2, 4, 8, ... ), pede-se calcular o
décimo termo.
Temos: a1 = 2, q = 2.
Para calcular o décimo termo, ou seja, a10, vem
pela fórmula:
a10 = a1 . q
Propriedades
1. Numa PG, cada termo (a partir do segundo) é a
média geométrica dos termos vizinhos deste.
9
9
a10= 2 . 2
a10= 2. 512
a10= 1024
02. Sabe-se que o quarto termo de uma PG crescente
é igual a 20, e o oitavo termo é igual a 320. Qual a
razão desta PG?
Temos:a4 = 20 e a8 = 320.
Logo, podemos escrever:
a8 = a4 . q8–4 .
Daí, vem:
320 = 20.q
4
Então
q4 =16
e portanto: q = 2.
131
INTERPOLAÇÃO GEOMÉTRICA
Interpolar ou inserir n meios geométricos entre dois
números, é determinar os n meios, de tal forma que todos
passem a constituir uma progressão geométrica.
Exemplo: Inserir cinco meios geométricos entre 3 e 192.
MÓDULO DO PRODUTO DOS TERMOS DE UMA
P.G. FINITA
Dada uma P.G.(a1, a2, a3 , ..., an ), o produto dos n
primeiros termos desta P.G. é dado por:
SOMA DOS N PRIMEIROS TERMOS DE UMA PG
Exemplo
Calcule o produto dos vinte primeiros termos da
P.G.(1, 2, 4, 8, ...).
Assim como as Progressões Aritméticas, existem
também exercícios que pedem para calcular a soma dos
termos de uma PG. Este também pode ser calculado
manualmente, mas quando for pedido um número muito
alto de termos usamos uma fórmula.
Esta fórmula é um pouco menos "intuitiva" do que a
fórmula da PA. Por conta disso vamos ver então como se
comporta o uso da fórmula.
Para o cálculo da soma dos n primeiros termos Sn,
vamos considerar o que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
SOMA DOS TERMOS DE UMA PG INFINITA
Para realizar a soma dos n primeiros termos de uma
PG utilizamos a seguinte forma:
a1.(1  qn )
OU
sn 
1 q
a1.(qn  1)
sn 
q1
Onde:
 Sn = é a soma dos “n” termos da P.G.

a1 é o primeiro termo

q é a razão
Exemplo
Calcular a soma dos sete primeiros termos da P.G.(1;
3; 9; ... )
a1 = 1 ; q = 3 ; n = 7
Uma Progressão Geométrica infinita de razão q,
com −1<q <1 é chamada de série geométrica
convergente, pois a soma de seus termos converge
(tende) para um valor constante.
A soma dos termos de uma P.G. infinita de razão q,
com −1<q <1 é dada por:
a
S  1
1 q
Onde:
• a1 é o primeiro termo;
• q é a razão (−1<q <1) .
Exemplo
Qual a soma dos infinitos termos da progressão
1 1 1

, , ...  ?
Geométrica  ,
2 4 8

132
03.( UN. BAURU – SP ) São inseridos 5 meios
geométricos entre 4 e 2.916, nessa ordem, de modo
a formar uma P.G. crescente. Assinale a alternativa
que indica o seu 4º termo:
a) 324
b) 729
c) 1428
d) 108
04.( MACK – SP ) Determine o 1º termo de uma P.G.
Como a razão q =1/2 caracteriza uma série geométrica
convergente, aplicamos a fórmula da soma
cujo 8º termo é 1 e cuja razão também é 1 .
2
2
a) 8
b) 16
c) 32
d) 64
Portanto a soma dos infinitos termos é igual a 1.
A figura a seguir ilustra a soma dos infinitos termos:
1
4
1
2
1
8
1
16
1
32
EXERCÍCIOS
01. ( Unimontes / PAES ) O tempo necessário para a
desintegração da metade dos átomos radioativos,
inicialmente presentes em uma substância química, é
chamado de meia-vida. Após quantas meias vidas, 160
gramas de uma substância química terá 1,25 gramas ?
a) 6 meias-vidas
b) 5 meias-vidas
c) 7 meias-vidas
d) 8 meias-vidas
02. ( PUC – SP ) O 7º termo de uma PG é 8 e a razão
é –2. O primeiro termo dessa PG é :
1
1
a)
b)
4
2
1
1
c)
d)
6
8
1
e)
3
05.( PUC – MG ) O número de assinantes de uma
revista de circulação na grande BH aumentou, nos
quatro primeiros meses de 2005, em progressão
geométrica, conforme assinalado na tabela abaixo.
Com base nessas informações, pode-se afirmar que,
de fevereiro para abril, o número de assinantes dessa
revista teve um aumento igual a:
a) 1.050
b) 1.155
c) 1.510
d) 1.600
06.( UEL ) Para testar o efeito da ingestão de uma
fruta rica em determinada vitamina, foram dados
pedaços desta fruta a macacos. As doses da fruta são
arranjadas em uma seqüência geométrica, sendo 2g e
5g as duas primeiras doses. Qual a alternativa correta
para continuar essa seqüência?
a) 7,5 g;
10,0 g;
12,5 g ...
b) 125 g;
312 g;
619 g ...
c) 8 g;
11 g;
14 g ...
d) 6,5 g;
8,0 g;
9,5 g ...
e) 12,5 g;
31,25 g; 78,125 g ...
07.( FAFEOD ) Sobre uma progressão geométrica ( a1,
a2, a3, ... ), sabe-se que a21 = 40 e a24 = 2560. É
CORRETO afirmar, então, que a soma dos algarismos
do termo a26 é igual a :
a) 24
b) 20
c) 19
d) 18
e) 16
08.( UFRRJ ) A seqüência (x, 6, y, z, 162) é uma
Progressão Geométrica. É correto afirmar que o
produto de x por z vale
a) 36.
b) 72.
c) 108.
d) 144.
133
e) 180.
09.( PUC – SP ) O valor de x para que a seqüência ( 4x,
2x + 1, x – 1, ... ) seja uma PG é :
1
1
a)
b) 
2
2
1
c)
8
1
e)
3
d)  1
8
10.( FESP ) A razão da P.G. ( a, a + 3, 5a – 3, 8a ) é:
a) 1
b) 2
c) 3
d) 4
e) 5
11.(UESB) Somando-se um valor constante k a cada um
dos termos da seqüência (2, 1, 3), obtém-se, nessa
mesma ordem, uma nova seqüência, que é uma
progressão geométrica.
A soma dos termos dessa progressão é igual a
01) 9
02) 6
03) 5
04) 3
05) 1
12.(UEFS) A quantidade de cafeína presente no
organismo
de uma pessoa decresce a cada hora,
segundo uma progressão geométrica de razão 1/8. Sendo
assim, o tempo t para que a cafeína presente no
organismo caia de 128mg para 1mg é tal que:
a) 0 < t < 1
b) 1 < t < 2
c) 2 < t < 4
d) 4 < t < 6
e) 6 < t < 8
13.(CFO/PM) Um vazamento em um tanque de gasolina
provocou a perda de 2 litros no 1º dia. Como o orifício
responsável pelas perdas foi aumentado, no dia seguinte o
vazamento foi o dobro do dia anterior. Se essa perda foi
dobrada a cada dia, quantos litros de gasolina foram
desperdiçados no total, em 10 dias ?
A) 1048 litros.
B) 1256 litros.
C) 2046 litros.
D) 2056 litros.
14.( PAES ) Em um determinado jogo, o prêmio dado a
cada acertador é 20 vezes o valor de sua aposta. Certo
jogador aposta R$ 5,00 na primeira jogada, mas não
acerta. Ele continua tentando, apostando nas jogadas
seguintes o dobro da aposta da jogada anterior. Se, na
oitava jogada, ele acertar, o lucro obtido por esse
apostador, nesse jogo, será de:
A)
B)
C)
D)
R$ 12800,00
R$ 1275,00
R$ 11525,00
R$ 640,00
15.( PUC / MG )S = 2 + 3 + 9 + 27 + . . .
2
8
soma dos infinitos termos de
geométrica. O valor de 3 S é :
a) 2
b) 4
c) 6
d) 8
e) 10
32
uma
16.(UNIMONTES )A solução da equação
éa
progressão
2x
+
3
4x
+
9
8x
+ ... = 2 é :
27
a) 4
b) 3
c) 2
d) 1
17.( FGV – SP ) Quando n cresce, a fração
1 1 1
1
1    ...  n  ...
2 4 8
2
tende a:
1 1 1
1
1  
 ...  n  ...
3 9 27
3
a) 3
b) 4/3
c) 
d) 0
e) 1
18.( PAES ) Acima de uma reta r foi desenhado um
quadrado de lado 4 cm. Outros quadrados foram
desenhados, de modo que o lado de cada quadrado, a
partir do segundo, é metade do lado do quadrado
anterior, conforme o desenho abaixo.
Desenhando-se
4 cm mais quadrados, seguindo a regra
acima indefinidamente, podemos concluir que
A) a soma das áreas dos quadrados não chegará a
22cm2.
B) a soma das áreas dos quadrados não chegará a
2
20cm .
C)
a soma das áreas dos quadrados aumenta,
tendendo ao infinito.
D)
a soma das áreas dos quadrados aumenta,
2
tendendo a 32cm .
19. Uma progressão aritmética e uma geométrica têm o
número 2 como primeiro termo. Seus quintos termos
134
também coincidem e a razão da PG é 2. Sendo assim, a
razão da PA é:
a) 8
b) 6
c) 32/5
d) 4
e) 15/2
20.(FIP-MOC) Abaixo estão representados alguns
números figurados. Esses números são chamados de
números oblongos, pois contam a quantidade de pontos
sobre um plano, de maneira a formar um retângulo em que
o número de linhas é uma unidade maior que o número de
colunas, do seguinte modo:
A1 A2
A3
Nessas condições, quantas bolinhas terá o número A65?
A) 65
B) 256
C) 3788
D) 4.290
E) 6.320
21.(FIP-2010) Em 2010, está sendo realizada, na África do
Sul, a 19ª Copa do Mundo de Futebol, competição criada
pelo francês Jules Rimet, em 1928, após ter assumido o
comando da instituição mais importante do futebol
mundial: a FIFA (Federation International Football
Association). A Copa do Mundo é realizada de 4 em 4
anos, se nenhuma guerra e/ou desastre mundial
acontecer. Desse modo, considerando-se que nenhum
empecilho ocorrerá, quantas copas serão realizadas entre
2010 e 2998, incluindo esses anos?
A) 250
B) 246
C) 248
D) 252
22.(FIP-2012) São mais de 53 mil carros, mais de 47 mil
motos, cerca de quatro mil caminhões, oito mil
caminhonetes e quase mil ônibus, de acordo o IBGE. Sem
contar com os micro-ônibus, tratores, caminhões-trator,
motonetas, carroças e bicicletas que também utilizam as
ruas e avenidas de Montes Claros.
Fonte: www.revistatempo.com.br jul. 2011
O aumento considerável na frota de veículos fez com que
se ampliassem os estacionamentos na área central de
Montes Claros. Com isso, os preços variam de um para
outro, de acordo com a estratégia do proprietário.
Suponha que o preço de um estacionamento é
estabelecido por um valor fixo para as duas primeiras
horas e um adicional por cada hora subsequente. Se o
estacionamento por 3 horas custa R$ 5,00, e por 5 horas
custa R$ 6,00, quanto custa o estacionamento por 8
horas?
A) R$ 13,33
B) R$ 7,50
C) R$ 7,00
D) R$ 9,60
23. (FIP-2012) O laboratório de química das Fipmoc
precisou contratar um funcionário para catalogar os
seus equipamentos. Estimou que o serviço fosse
realizado entre 30 e 60 dias e ofereceu um pagamento
no valor de R$ 20,00 por dia, para o pretendente.
Um acadêmico de Medicina fez a seguinte proposta:
Se o serviço for realizado em 40 dias, ele aceitaria a
proposta da faculdade, contudo se o serviço
ultrapassasse os 40 dias ele receberia R$1,00 pelo 1º
dia de serviço, R$2,00 pelo 2º dia de serviço,
R$3,00 pelo 3º dia, e assim sucessivamente até o
último dia do serviço.
O departamento financeiro aceitou a proposta do
acadêmico.
O serviço foi completado em 45 dias.
Nessas condições, pode-se afirmar que o acadêmico:
A) obteve vantagem de R$ 315,00 em relação à oferta
da faculdade.
B) não obteve nem lucro nem prejuízo, em relação à
sua proposta;
C) ficou no prejuízo de R$ 35,00 em relação à oferta da
faculdade;
D) obteve vantagem de R$ 135,00 na sua negociação;
24. ( UEL – PR ) Na figura abaixo, a aresta do cubo
maior mede a, e os outros cubos foram construídos de
modo que a medida da respectiva aresta seja a metade
da aresta do cubo anterior. Imaginando que a
construção continue indefinidamente, a soma dos
volumes de todos os cubos será:
a3
7a 3
a) 0
b)
c)
2
8
d)
8a 3
7
e) 2a3
25. ( Unimontes ) Se y =
então y é igual a :
a
3
3
x . x .3 x ... , com x ≥ 0,
1
a) x 27
1
b) x 3
c)
x
d)
13
x 27
26. (Cesgranrio) Desde 1992, certo instituto de
Pesquisa vem monitorando, no início de cada ano, o
crescimento populacional de uma pequena cidade do
interior do estado. Os itens a seguir mostram o
resultado dos três primeiros anos, em milhares de
habitantes.
I- Ano de 1992, População(em milhares) = 25,6.
II- Ano de 1993, População(em milhares) = 38,4.
III- Ano de 1994, População(em milhares) = 57,6.
135
Mantendo-se esta mesma progressão de crescimento, o
número de habitantes dessa cidade, no início do ano
2000, em milhares, será, aproximadamente, de:
a) 204
b) 384
c) 576
d) 656
e) 728
A cada nova etapa consideram-se os quadrados de
menor lado ( l ) acrescentados na etapa anterior e
acrescentam-se, para cada um destes, três novos
quadrados de lado l /3. As três primeiras etapas de
construção de F são
apresentadas a seguir.
27. (Ufrs) Na seqüência de figuras, cada quadrado tem
1cm2 de área.
Supondo que as figuras continuem evoluindo no mesmo
padrão aqui encontrado, a área da figura 20 terá valor
a) entre 0 e 1000
b) entre 1000 e 10.000
c) entre 10.000 e 50.000
d) entre 50.000 e 100.000
e) maior que 100.000
28. (Fuvest) Um país contraiu em 1829 um empréstimo de
1 milhão de dólares, para pagar em cem anos, à taxa de
juros de 9% ao ano. Por problemas de balança comercial,
nada foi pago até hoje, e a dívida foi sendo "rolada", com
capitalização anual dos juros. Qual dos valores a seguir
está mais próximo do valor da dívida em 1989?
Para os cálculos adote (1,09)8  2.
a) 14 milhões de dólares.
b) 500 milhões de dólares.
c) 1 bilhão de dólares.
d) 80 bilhões de dólares.
e) 1 trilhão de dólares.
29. (UEL) Numa aplicação financeira, chama-se
MONTANTE em certa data à soma da quantia aplicada
com os juros acumulados até aquela data.
Suponha uma aplicação de R$50.000,00 a juros
compostos, à taxa de 3% ao mês. Nesse caso, os
montantes em reais, no início de cada período de um mês,
formam um progressão geométrica em que o primeiro
termo é 50000 e a razão é 1,03.
Os juros acumulados ao completar 10 meses de aplicação
são
Dado: 1,0310 = 1,3439
a) R$ 10300,00
b) R$ 15000,00
c) R$ 17195,00
d) R$ 21847,00
e) R$ 134390,00
A área de F será igual a:
A) 2/3
B) 3/2
C) 4/3
D) 3/4
E) 5/3
31. A figura abaixo é formada por infinitos círculos,
tangentes dois a dois, de tal forma que o diâmetro do
círculo C2 é igual ao raio R do círculo C1, o diâmetro
do círculo C3 é igual ao raio do círculo C2 e assim
sucessivamente. A soma das infinitas áreas desses
círculos, em função de R, é:
A)
3R 2
2
B)
4R 2
3
C) 3R 2
D) 4R 2
GABARITO
1) C
2) D
3) D
8) C
9) D
10) B
4) D
5) B
11) 05
6) E
12) C
7) C
13) C
14) C
15) A
16) D
17) B
18) A
19) E
20) D
21) C
22) B
23) D
24) D
25) C
26) D
27) E
28) E
29) C
30) B
31) B
30. (Ufrj) A região fractal F, construída a partir de um
quadrado de lado 1 cm, é constituída por uma infinidade
de quadrados e construída em uma infinidade de etapas.
136
MATEMÁTICA FINANCEIRA
determinar o segundo desconto. Observe:
AUMENTOS E DESCONTOS SUCESSIVOS
Uma loja determinou a venda de todo o estoque de
eletrodomésticos, com descontos que atingiram o
percentual de 25%. Uma pessoa, ao comprar uma
televisão no pagamento à vista, foi premiada com um
desconto de 12% sobre a dedução promocional. Se o
aparelho sem os descontos era anunciado por R$
1.200,00, qual o valor final com os descontos
recebidos?
AUMENTOS
O
conhecimento
de
operações
matemáticas
financeiras, presentes no nosso cotidiano, facilita a
realização de cálculos envolvendo aumentos e descontos
sucessivos. Em certas situações envolvendo a crescente
alta da inflação, os aumentos de mercadorias e serviços
acontecem de forma intensa. A inflação é um índice
econômico responsável pela elevação dos preços de
produtos, bens de consumo e serviços prestacionais,
como seguros e planos de saúde.
Vamos entender como funciona um aumento sucessivo
de preços:
25
100
25% x 1200 =
x 1200
12
100
12% x 900 =
Em virtude da elevação da taxa de inflação semanal,
um comerciante atentou-se para a importância de
aumentar os preços das mercadorias em 8%, visando à
contenção de prejuízos. Na semana seguinte, em
decorrência de outra crescente no índice inflacionário, se
viu obrigado a aumentar novamente o preço das
mercadorias na faixa de 12%. Determine o preço de uma
mercadoria que antes do primeiro aumento custava R$
55,00.
900 – 108 = R$792,00
8% x 55 =
8
100
x 55
=
440
100
= 4,4
12
100
x 59,40
=
= 300
x 900
=
10800
100
= 108
O preço final do aparelho com os descontos sucessivos
é de R$ 792,00.
JUROS SIMPLES E JUROS COMPOSTOS
Uma operação financeira muito comum é aquela em
que uma pessoa ou instituição empresta dinheiro a
outra mediante a cobrança de uma comissão.
Nesse tipo de operação, comparecem em geral as
seguintes grandezas:
Capital (c) 
Tempo (t) 
valor emprestado
tempo de empréstimo
Taxa (i)

percentual a ser cobra do pelo
empréstimo na unidade de tempo.
Juros (j)  valor da comissão
Montante (M)  soma do capital com os juros
55 + 4,4 = R$59,40
12% x 59,40 =
30000
100
1200 – 300 = R$900,00
Exemplo
Nesse tipo de problema é comum que as pessoas
somem os aumentos percentuais. Nesse caso, muitos
realizariam o cálculo somando 8% e 12%, relatando um
único aumento de 20% sobre o valor de R$ 55,00, o que
tornaria o cálculo totalmente errado. O segmento
matemático correto seria determinar o aumento de 8% em
relação ao valor de R$ 55,00 e sobre o resultado, realizar
um novo aumento de 12%. Observe:
=
712,8
100
= 7,13
Suponha que você empreste a alguém R$ 1000,00.
Ao fazer essa transação, você combina com essa
pessoa:
a) o prazo após o qual esse valor deverá ser devolvido
a você.
59,40 + 7,13 = R$66,53
O preço da mercadoria, após os dois aumentos
sucessivos de 8% e 12%, é de R$ 66,53.
DESCONTOS
Nos descontos sucessivos, devemos calcular o primeiro
desconto sobre o valor inicial e sobre o resultado,
b) um valor, que você acha justo, essa pessoa deverá
pagar-lhe findo o prazo do empréstimo, como uma
“remuneração” pelo seu dinheiro que ficou disponível
nas mãos dessa pessoa.
Esse acréscimo ao capital emprestado é que
chamamos de juro. O juro é calculado sempre após um
determinado período e combinado no ato da transação.
Para simplificar o cálculo, é comum expressá-lo através
137
de uma taxa, a taxa de juros. Assim, por exemplo, numa
certa transação podemos combinar uma taxa de 5% ao
mês.
Isso significa que para cada R$ 100,00, o tomador deve
pagar, após o período de um mês, R$ 5,00.
O juro é simples se tiver taxa fixa e for calculado
sempre sobre a quantia inicial. Por exemplo, se você
emprestar R$ 100,00, a 5% ao mês, receberá ao fim do 1º
mês R$ 5,00 de juro. Ao fim do 2º mês, mais R$ 5,00 de
juro e assim por diante.
Normalmente, o que ocorre é o juro ser acrescido ao
capital, após o 2º mês a taxa de juro incide sobre esse
montante e assim por diante. Nesse caso, temos o juro
composto.
triplique?
Dados
i= 3% ao mês = 0,03 ao mês
M = 3.c pois o capital deve triplica
M = 3c  c + j = 3c  j = 2c
Logo
cit = 2c  it = 2  0,03t = 2  t = 200/3
Observe que o tempo encontrado está em meses,
já que a taxa utilizada é mensal.
200 meses 2
t = 200/3 meses = 5 anos, 6 meses, 20 dias
CALCULANDO JUROS SIMPLES
CALCULANDO JUROS COMPOSTOS
Em operação com juros simples, os juros são
diretamente proporcionais ao capital, à taxa e ao tempo.
Estando a taxa i e o tempo t expressos na mesma
unidade de tempo, os juros simples j produzidos por um
capital c são dados pela fórmula
j = c.i.t
Caso i e t não sejam dados na mesma unidade de
tempo, é necessário efetuar as transformações
adequadas
Suponhamos que um capital c seja aplicado a juros
compostos, segundo uma taxa mensal i.
Tratando-se de juros compostos, é como se o
capital c sofresse reajustes mensais acumulados,
sendo o fator mensal de reajuste igual a (1+ i),
conforme vimos no tópico anterior.
Chamando de M1, M2, M3, ... os montantes
acumulados no final do 1º mês, do 2° mês, do 3º mês,
... temos portanto:
M1 = c(1 + i)
M2 = M1.(1 + i) = c(1 + i) .(1 + i) = c(1 + i)2
M3 = M2.(1 + i) = c(1 + i)2.(1 + i) = c(1 + i)3
e assim sucessivamente.
Exemplos

Um indivíduo toma R$ 1.500,00 emprestado em um
banco a juros simples com uma ta mensal de 4%.
Vamos calcular os juros pagos ao final de 1 ano e 4
meses.
Os dados do problema são:
C = R$1.500,00
i = 4% ao mês = 0,04 ao mês
t = 1 ano e 4 meses = 16 meses
j=?
j = cit = R$1.500,00 . 0,04 . 16 = R$ 960,00

Um capital aplicado a juros simples de 15% ano
durante 8 meses produziu um montante de R$
7.634,00. Determinemos esse capital.
Observe os dados do problema:
i = 15% ao ano = 0,15 ao ano
t = 8 meses = 8/12 do ano = 2/3 do ano
M = R$ 7.634,00
j = cit = c . 0,15 . 2/3 = 0,1 c
M = c + j  R$ 7.634,00 = c + 0, 1 c 
1,1c = R$ 7.634,00  c = R$ 6.940,00

Durante quanto tempo deve ser aplicado um capital a
juros simples de 3% ao mês para que seu valor
Chamando de M o montante acumulado no final de
t meses, temos a fórmula geral:
M = c(1 + i)t
Se tivéssemos considerado, por exemplo, a taxa
anual e o tempo t em anos, é claro que chegaríamos
ao mesmo resultado. Portanto, a fórmula acima é válida
desde que se utilize a mesma unidade de tempo para i
e t.
Exemplos

Aplicando-se R$ 3.500,00 à taxa de 4% ao mês
durante 2 meses, com juros capitalizados
mensalmente, quanto se apurou de juros?
Dados
c = R$ 3.500,00
i = 4% ao mês = 0,04 ao mês
t = 2 meses
M = c (1 + i)t = R$ 3.500,00(1 + 0,04)2 =
2
= R$ 3.500,00 . (1,04) = R$ 3.500,00 . 1,0816 =
= R$ 3.785,60
138
j = M – c = R$ 3.785,60 – R$ 3.500,00 = R$ 285,60

Um terreno sofre uma valorização anual de 100%.
Sabendo que daqui a 5 anos ele valerá R$ 49.920,00,
qual é seu valor atual?
Dados:
M = R$ 49.920,00
i = 100% ao ano  i = 1
t = 5 anos
c ? (valor atual)
M = c(1 + i)  R$ 49.920,00 = c(1 + 1)
t
5
 R$ 49.920,00 = c . 25= 32c  c  R$49920,00 =
proporcionou 20% de lucro em relação ao custo e, a
outra, 20% de prejuízo em relação ao custo. Na venda
de ambas, ele
A) perdeu 1 real.
B) não ganhou nem perdeu.
C) ganhou 1 real.
D) perdeu 50 centavos.
04.(ENEM) Paulo emprestou R$ 5.000,00 a um amigo,
a uma taxa de juros simples de 3% ao mês. Considere
x o número de meses do empréstimo e M(x) o
montante a ser devolvido para Paulo no final de x
meses. Nessas condições, a representação gráfica
correta para M(x) é
32
= R$ 1.560,00

Um capital de R$ 6.500,00, aplicado a juros
compostos capitalizados anualmente, produziu ao finai
de 2 anos R$ 2 860,00 de juros. Qual foi a taxa anual
de aplicação
Dados:
c = R$ 6.500,00
t = 2 anos
j = R$ 2.860,00
M = c + j = R$ 6.500,00 + R$ 2.860,00 =R$ 9.360,00
M = c (1 + i)t
R$ 9.360,00 = R$ 6.500,00 (1 + i)2
R $9360,00
 1,44  1  i  1,44
 (1  i)2 
R $6500,00
 1 + i = 1,2  i = 0,2 = 20%
Como utilizamos o tempo em anos, a taxa é de 20% ao
ano.
EXERCÍCIOS
01.(UNIMONTES) João aplicou R$520,00 a juros simples
de 3% ao mês. Seu irmão aplicou R$450,00 a uma outra
taxa. Ao final do 6.° mês, ambos atingiram o mesmo
montante. A taxa mensal de juros (simples) aplicada ao
dinheiro do irmão de João foi de, aproximadamente,
A) 6% ao mês.
B) 5% ao mês.
C) 4% ao mês.
D) 3,5% ao mês.
02.(UNIMONTES) Uma televisão, cujo preço de venda era
R$2500,00, sofreu dois descontos sucessivos, um de 20%
e outro de 15%. O novo preço da televisão ficou reduzido
a
A) 32% do preço inicial.
B) 68% do preço inicial.
C) 35% do preço inicial.
D) 65% do preço inicial.
03.(UNIMONTES) Um comerciante vendeu
mercadorias a R$12,00 cada uma. Uma
duas
delas
05.(UFOP) Em 2007, o salário mínimo sofreu 8,6% de
reajuste sobre seu valor de 2006. Em 2008, foi
reajustado em 9,2% e, em janeiro de 2009, sofreu mais
um reajuste, de 12%, sempre sobre seu valor no ano
anterior. Assim, em relação ao valor de 2006, o salário
mínimo de 2009 reflete um reajuste acumulado de:
A) 29,8%.
B) aproximadamente 32,8%.
C) mais do que a metade.
D) menos do que a quinta parte.
06.(CESGRANRIO) Uma empresa oferece aos seus
clientes desconto de 10% para pagamento no ato da
compra ou desconto de 5% para pagamento um mês
após a compra. Para que as opções sejam indiferentes,
a taxa de juros mensal praticada deve ser,
aproximadamente,
A) 5,6%.
B) 5,0%.
C) 4,6%.
D) 3,8%.
E) 0,5%.
139
07.(UFMG) Por um empréstimo de R$ 80000,00, à taxa de
i% ao mês, paga-se, de uma única vez, após 2 meses, o
montante de R$ 115200,00. Por terem sido aplicados juros
compostos, a taxa mensal foi de:
A) 15%
B) 20%
C) 22%
D) 24%
E) 26%
08.(UESB) Para fazer uma viagem ao exterior, uma
pessoa foi a uma instituição financeira comprar dólares.
Nesse dia, um dólar estava sendo cotado a 0,85 euros e
um real estava sendo cotado a 0,25 euros. Com base
nesses dados, pode-se afirmar que, para comprar 500
dólares, essa pessoa gastou, em reais,
01) 1700,00
02) 1640,00
03) 1520,00
04) 1450,00
05) 1360,00
09.(UFMG) O preço de venda de determinado produto tem
a seguinte composição: 60% referentes ao custo, 10%
referentes ao lucro e 30% referentes a impostos. Em
decorrência da crise econômica, houve um aumento de
10% no custo desse produto, porém, ao mesmo tempo,
ocorreu uma redução de 20% no valor dos impostos. Para
aumentar as vendas do produto, o fabricante decidiu,
então, reduzir seu lucro à metade.
É CORRETO afirmar, portanto, que, depois de todas
essas alterações, o preço do produto sofreu redução de
A) 5%.
B) 10%.
C) 11%.
D) 19%.
10.(Unimontes) Uma loja de brinquedos resolveu fazer a
seguinte promoção “Presenteie com bonecas”: a pessoa
paga o preço de 3 bonecas e leva 5. Quanto uma pessoa
economizará comprando 5 bonecas nessa promoção?
A) 60%.
B) 40%.
C) 33,3%.
D) 66,66%.
11.(Unimontes) Uma mercadoria, que custa R$50,00 à
vista, é adquirida a prazo, com uma entrada de R$30,00
mais uma parcela de R$25,00 com 30 dias de prazo. A
taxa de juros mensal, cobrada nessa operação, é de
A) 20%.
B) 15%.
C) 25%.
D) 10%.
12.(Unimontes) Um comerciante aplicou um capital a 24%
ao ano e o triplo desse capital a 26% ao ano. Depois de
um ano, ele recebeu R$1530,00. Qual o capital total
aplicado?
A) R$9000,00
B) R$4500,00
C) R$5000,00
D)R$6000,00
13. (UFMG) Um capital de R$ 30 000,00 foi dividido em
duas aplicações: a primeira pagou uma taxa de 8% de
juros anuais; a outra aplicação, de risco, pagou uma
taxa de 12% de juros anuais. Ao término de um ano,
observou-se que os lucros obtidos em ambas as
aplicações foram iguais. Assim sendo, a diferença dos
capitais aplicados foi de
A) R$ 8 000,00.
B) R$ 4 000,00.
C) R$ 6 000,00.
D) R$ 10 000,00.
14. O preço de uma geladeira era igual a 60% do preço
de uma TV.No último mês, esses produtos tiveram
aumentos de 30% e 20% respectivamente. A razão
entre os novos preços da geladeira e da TV passou a
ser de:
A) 62% B) 63%
C) 64% D) 65%
E) 66%
15. (Uesc) Um automóvel foi comprado e revendido,
sucessivamente, por três pessoas. Cada uma das duas
primeiras pessoas obteve, por ocasião da revenda, um
lucro de 10%, e a terceira teve um prejuízo de 10%
sobre o respectivo preço de compra. Se a terceira
pessoa vendeu o automóvel por 13068,00, então a
primeira o adquiriu por
a) R$12000,00
b) R$12124,00
c) R$12260,00
d) R$12389,00
e) R$12500,00
16. ( Viçosa – MG ) Dois descontos sucessivos, um de
10% e outro de 20%, correspondem a um desconto
único de:
a) 30%
b) 29%
c) 28%
d) 27%
e) 26%
17. ( PUC – SP ) Uma cooperativa compra a produção
de pequenos horticultores, revendendo-a para
atacadistas com um lucro de 50% em média. Estes
repassam o produto para os feirantes, com um lucro de
50% em média. Os feirantes vendem o produto para o
consumidor e lucram, também, 50% em média. O preço
pago pelo consumidor tem um acréscimo médio, em
relação ao preço dos horticultores, de:
a) 150%
b) 187%
c) 237,5%
d) 285,5%
e) 350%
140
18. ( UFRS ) Um capital, aplicado a juros simples,
triplicará em 5 anos se a taxa anual for de :
a) 30%
b) 40%
c) 50%
d) 75%
e) 100%
19. ( Vassouras ) Um artigo custa, à vista R$ 200,00 ,
mas também é vendido a prazo com uma entrada de R$
120,00 e outra parcela de R$ 100,00 um mês depois.
Quem opta pela compra a prazo paga juros mensais na
taxa de :
a) 25%
b) 20%
c) 15%
d) 10%
e) 5%
20. ( UFMG ) Uma compra de R$ 100 000,00 deverá ser
paga em duas parcelas iguais, sendo uma à vista e a outra
a vencer em 30 dias. Se a loja cobra juros de 20% sobre o
saldo devedor, então o valor de cada parcela,
desprezando-se os centavos, será de :
a) R$ 54 545,00
b) R$ 56 438,00
c) R$ 55 000,00
d) R$ 58 176,00
e) R$ 60 000,00
21. (FIP-2010) Durante a Copa do Mundo de 2006, na
Alemanha, o slogan no ônibus que transportava a seleção
brasileira era: "Veículo monitorado por 180 milhões de
corações brasileiros". Essa frase dizia respeito à
população total brasileira daquele ano. Segundo as
estimativas do Instituto Brasileiro de
Geografia e Estatística – IBGE, no ano de 2025 a
população brasileira deverá atingir 228 milhões de
habitantes. Considerando os dados apresentados, qual é o
aumento, aproximado, estimado pelo IBGE da população
brasileira de 2006 até 2025?
A) 32,4%
B) 26,7%
C) 18,6%
D) 41,2%
22. (FIP-2011) Pequenos consumos podem parecer
bobagem, mas, quando somados, tornam-se grandes
gastos. Para ajudarmos nosso planeta e também
economizarmos nosso salário, devemos desligar os
aparelhos e não os deixar no modo de espera, conhecido
por stand by. Diante disso, considere a situação:
· Um determinado DVD consome 20W, em stand by;
· Admita que esse DVD permaneça, em média, 23 horas
por dia em stand by;
· 1 kwh de energia equivale ao consumo de um aparelho
de 1.000 w de potência durante uma hora de uso;
· O preço de 1kwh é R$ 0,40.
Considerando 1 ano de 365 dias, qual será,
aproximadamente, a média anual, de consumo desse
aparelho em stand by?
A) R$ 19,00
B) R$ 95,00
C) R$ 67,00
D) R$ 65,00
23. (FIP-2011) Na compra a prazo de uma TV, o total
pago por uma pessoa foi de R$ 672,00. A entrada teve
valor correspondente a um sexto do total, e o restante
foi pago em quatro parcelas, cujos valores formam uma
progressão aritmética crescente de razão R$ 40,00.
Qual foi o valor da última prestação?
A) R$ 205,00
B) R$ 210,00
C) R$215,00
D) R$ 200,00
24. (FIP-2012) O preço do tomate teve alta de mais de
100% para o consumidor em 2008, informação que foi
divulgada no início do mês de março, pelo IBGE –
Instituto Brasileiro de Geografia e Estatística – e pela
FGV – Fundação Getúlio Vargas. Mas, para os
produtores, comerciantes e consumidores da Ceanorte
– Central de abastecimento de Montes Claros –, o
tomate iniciou esta semana com o preço médio quase
45% mais barato em relação à passada. A caixa com
22 quilos do fruto foi comercializada, na segunda-feira,
a R$25,00.
Fonte: O NORTE DE MINAS. 29 Mar 2011
O Sr. Horta Liço, pequeno produtor de Nova
Esperança, distrito de Montes Claros, entrega caixas
de 22kg de tomate, na Ceanorte, ao preço estipulado
de R$ 25,00 a caixa. Porém, na feira de fim de semana,
para facilitar seu trabalho, ele distribui os tomates em
sacolas de 2 kg. Quantas sacolas, nas condições
especificadas, ele precisará vender para arrecadar R$
300,00?
A) 132
B) 335
C) 123
D) 220
25. (FIP-2012) A campanha de matrícula de uma
escola para o ano de 2012 apresenta, em seu site, a
seguinte regra de desconto:
No mês de novembro, comparativamente a outubro,
houve, em relação aos preços:
A) redução de 10%
B) aumento de 10%
C) aumento de 12,5%
141
D) redução de 12,5%
26. (FIP-2012) Sem fazer tanto alarde o Hyundai HR, vem
conseguindo conquistar um grande público no Brasil, o
modelo figura entre os 10 utilitários mais vendidos. A
receita é simples, um preço atrativo, (em média é achado
por R$ 55.900 mil), uma mecânica robusta com motor
turbodiesel, somada a uma ótima capacidade de carga,
faz do HR uma boa opção para quem busca transportar
cargas nas grandes cidades no dia-a-dia.
HR HYUNDAI MODELO : 2011
VALOR R$ 58.000,00
PLANOS DE 80 MESES :R$ 867,66
CAPACIDADE DE CARGA: 1.800 kg
O Sr. Juvenal gostou da propaganda do Hyundai HR e
adquiriu um. Algum tempo depois, precisou fazer um
transporte de material de construção (cimento e tijolo) para
uma obra de sua propriedade. Ele verificou que seria
possível transportar 36 sacos de cimento ou 720 tijolos em
seu caminhão.
De acordo com as informações, a ÚNICA alternativa
INCORRETA é:
A) Se já foi colocado 15 sacos de cimento sobre o
caminhão, então é possível colocar mais 500 tijolos.
B) 17 sacos de cimento totalizam 850 kg
C) 460 tijolos totalizam 1.150 kg
D) 12 sacos de cimento e 480 tijolos completam a carga
máxima do caminhão
27.(FIP-2012) Medida provisória que altera regras da
poupança é publicada
Foi publicada nesta sexta-feira (4) no "Diário Oficial da
União" a medida provisória editada pelo governo federal
que altera as regras da poupança. Segundo a nova
resolução, quando a taxa básica de juros for de 8,5% ao
ano ou menor, o rendimento da caderneta será fixado em
70% da taxa Selic. A mudança só vale para os depósitos
que forem feitos a partir desta sexta.
Suponha que um pequeno investidor, tenha feito uma
aplicação de R$ 1.000,00 após essa mudança.
Caso os juros caiam para 8,5% e se mantenham nesse
patamar, qual será, de acordo com as informações
acima, o rendimento anual desse investidor?
A) R$58,00 B) R$61,70 C) R$61,50 D) R$63,70
28.(FIP-2013)
O IPVA (Imposto sobre a Propriedade de Veículos
Automotores) é um imposto estadual, cobrado
anualmente, cuja alíquota varia em cada Estado, de
acordo com o valor do veículo.
Em Minas Gerais, desde 2004, calcula-se o IPVA
aplicando-se sobre a base de cálculo (preço de
mercado) a alíquota de 4% para automóveis, veículos
de uso misto e utilitários. Esse valor pode ser dividido
em 3 parcelas mensais e iguais ou ser pago a vista
com desconto de 3,6%.
De acordo com as taxas apresentadas, é correto
afirmar que:
A)O valor do IPVA de um veículo de uso misto,
cujo preço de mercado é R$25.000,00 é
R$1.200,00.
142
B)O valor do IPVA de um veículo de uso misto, cujo preço
de mercado é R$25.000,00 é R$980,00, se for pago a
vista.
C)O valor de mercado de um veículo de uso misto
cujo IPVA sem desconto foi de R$800,00 é
R$15.000,00.
D)O valor de mercado de um veículo de uso misto
cujo IPVA, pago a vista, foi de R$771,20 é
R$20.000,00.
29. (FIP-2013) O Número de Ouro é um número irracional
que surge numa infinidade de elementos da natureza na
forma de uma razão. Esse número é representado pela
letra grega Φ (Phi maiúscula) (lê-se “fi”) e é o número
1,618033989, sendo considerado por muitos como uma
oferta de Deus ao mundo. Esse número não é mais do
que um valor numérico e é reconhecido como o símbolo
da harmonia.
Algumas curiosidades sobre o número de ouro:
1) Se você pegar uma concha em formato de espiral e
calcular a razão de cada diâmetro de uma espiral para a
seguinte, chegará sempre a um valor aproximado de
1,618.
2) Se você pegar sua altura e dividir pela distância entre
seu umbigo e o chão, encontrará um valor de
aproximadamente 1,618.
3) Se você dividir o número de fêmeas pelo número de
machos em uma colmeia de abelhas, sempre chegará ao
mesmo número aproximado: 1,618.
Calcule, aproximadamente, o percentual de fêmeas em
uma colmeia.
A) 38,2%
B) 65,7%
C) 61,8%
D) 54,5%
30. (FIP-2013) A Lei 12.433/2011, que entrou em vigor no
dia 29 de junho de 2011, alterou sensivelmente o
panorama da remição de penas no Brasil. Ao modificar a
redação dos artigos 126, 127 e 128 da Lei de Execução
Penal, passou a permitir que, além do trabalho, o estudo
seja causa de diminuição de pena.
Essa lei determina que a contagem do tempo será feita à
razão de 1 (um) dia de pena por 3 (três) de trabalho ou
estudo, o que significa que, a cada três dias trabalhados
ou estudados, o condenado terá direito a redução de 1 dia
em sua pena.
Fonte:
http://jus.com.br/revista/texto/21100/a-novaremicao-de-penas acesso em 20/11/2012
Um réu que foi condenado a 12 anos de prisão fez a prova
do ENEM e foi aprovado; e fará o curso em 4 anos. Se ele
completar o curso nesse período, quanto tempo deverá
permanecer na prisão?
A) 10 anos e 3 meses
B) 10 anos e 8 meses
C) 10 anos e 4 meses
D) 11 anos e 3 meses
31. (FIP-2013) A Rede Globo apresentou a novela
Avenida Brasil, que foi um frenesi na vida dos
brasileiros. Uma das situações da novela apresentou o
sequestro de Tufão, cujo resgate foi de R$ 20 milhões.
Na novela, foi mostrado que esse resgate foi colocado
em duas sacolas de lixo. Considerando que os R$ 20
milhões tenham sido pagos em notas de R$100,00 e
que cada nota pesa 1 grama, e, ainda, que, em média,
sacos de lixo de fabricação no Rio de Janeiro suportam
40 quilos, então a cena da novela:
A) não está correta, pois seriam necessários no mínimo
3 sacos de lixo;
B) não está correta, pois bastaria 1 saco de lixo;
C) está correta, pois seriam necessários exatos 2
sacos de lixo.
D) não está correta, pois seriam necessários no mínimo
4 sacos de lixo;
32. Um comerciante aumenta o preço de seu produto
em 10% e, após dias, diminui seu preço em 10%.
Podemos AFIRMAR CORRETAMENTE que:
a) O produto ficou com o mesmo preço inicial.
b) O produto ficou 1% mais baixo que seu preço inicial.
c) O produto ficou 1% mais caro que seu preço inicial.
d) O produto ficou 0,1% mais baixo que seu preço
inicial.
GABARITO
1. A
2. B
8. 01 9. A
15. A 16. C
22. C 23. D
29. C 30. B
3. A
10. B
17. C
24. A
31. A
4. A
11. C
18. B
25. C
32. B
5. B
12. D
19. A
26. A
6. A
13. C
20. A
27. C
7. B
14. D
21. B
28. D
QUESTÕES DO ENEM
(ENEM-2009) Paulo emprestou R$5.000,00 a um
amigo, a uma taxa de 3% ao mês. Considere x o
número de meses do empréstimo e M(x) o montante a
ser devolvido para Paulo no final de x meses.
Nessas condições, a representação gráfica correta
para M(x) é:
143
02.(ENEM-2009) Uma empresa produz jogos pedagógicos
para computadores, com custos fixos de R$1.000,00 e
custos variáveis de R$100,00 por unidade de jogo
produzida. Desse modo, o custo total para x jogos
produzidos é dado por C(x) = 1 + 0,1x (em R$1.000,00).
A gerência da empresa determina que o preço de
venda do produto seja de R$700,00. Com isso a receita
bruta para x jogos produzidos é dada por R(x)=0,7x (em
R$1.000,00). O lucro líquido, obtido pela venda de x
unidades de jogos, é calculado pela diferença entre a
receita bruta e os custos totais.
O gráfico que modela corretamente o lucro líquido dessa
empresa, quando são produzidos x jogos, é
03. (ENEM-2013) O contribuinte que vende mais de R$
20 mil de ações em Bolsa de Valores em um mês
deverá pagar Imposto de Renda. O pagamento para a
Receita Federal consistirá em 15% do lucro obtido com
a venda das ações.
Disponível em: www1.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).
Um contribuinte que vende por R$ 34 mil um lote de
ações que custou R$ 26 mil terá de pagar de Imposto
de Renda à Receita Federal o valor de
A) R$ 900,00.
B) R$ 1 200,00.
C) R$ 2 100,00. D) R$ 3 900,00.
E) R$ 5 100,00.
04.(ENEM-2013) Para aumentar as vendas no início do
ano, uma loja de departamentos remarcou os preços
de seus produtos 20% abaixo do preço original.
Quando chegam ao caixa, os clientes que possuem o
cartão fidelidade da loja têm direito a um desconto
adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava
R$ 50,00 antes da remarcação de preços. Ele não
possui o cartão fidelidade da loja.
Caso esse cliente possuísse o cartão fidelidade da loja,
a economia adicional que obteria ao efetuar a compra,
em reais, seria de
A) 15,00.
B) 14,00.
C) 10,00.
D) 5,00.
E) 4,00.
05.(ENEM-2013) Um comerciante visita um centro de
vendas para fazer cotação de preços dos produtos que
deseja comprar. Verifica que se aproveita 100% da
quantidade adquirida de produtos do tipo A, mas
apenas 90% de produtos do tipo B. Esse comerciante
deseja comprar uma quantidade de produtos, obtendo
o menor custo/benefício em cada um deles. O quadro
mostra o preço por quilograma, em reais, de cada
produto comercializado.
Os tipos de arroz, feijão, soja e milho que devem ser
escolhidos pelo comerciante são, respectivamente,
A) A, A, A, A.
B) A, B, A, B.
C) A, B, B, A.
D) B, A, A, B.
144
E) B, B, B, B.
06.(ENEM/2009) João deve 12 parcelas de R$ 150,00
referentes ao cheque especial de seu banco e cinco
parcelas de R$ 80,00 referentes ao cartão de crédito. O
gerente do banco lhe ofereceu duas parcelas de desconto
no cheque especial, caso João quitasse esta dívida
imediatamente ou, na mesma condição, isto é, quitação
imediata, com 25% de desconto na dívida do cartão. João
também poderia renegociar suas dívidas em 18 parcelas
mensais de R$ 125,00. Sabendo desses termos, José,
amigo de João, ofereceu-lhe emprestar o dinheiro que
julgasse necessário pelo tempo de 18 meses, com juros
de 25% sobre o total emprestado.
A opção que dá a João o menor gasto seria
A) Renegociar suas dívidas com o banco.
B) Pegar emprestado de José o dinheiro referente à
quitação das duas dívidas.
C) Recusar o empréstimo de José e pagar todas as
parcelas pendentes nos devidos prazos.
D) Pegar emprestado de José o dinheiro referente à
quitação do cheque especial e pagar as parcelas do cartão
de crédito.
E) Pegar emprestado de José o dinheiro referente à
quitação do cartão de crédito e pagar as parcelas do
cheque especial.
GABARITO
01. A
02. B
03. B
04. E
05. D
06. E
145
MATRIZES, DETERMINANTES E SISTEMAS
LINEARES
MATRIZES
MATRIZ GENÉRICA
Vamos representar uma matriz AmXn de duas formas
genéricas:
a)
 a 11 a 12
a
 21 a 22
 ...
...

a
a
m2
 m1
REPRESENTAÇÃO
As matrizes são representadas de três formas:
parênteses, colchetes ou barras duplas.
Exemplos
... a 1n 
... a 2n 
... ... 

... a mn 
b) A  (a ij )m x n sendo aij o elemento localizado na
i-ésima linha e j-ésima coluna, com 1  i  m e
1 j  n
Exemplos
a) Representar explicitamente a matriz A  (a ij ) 2 x 3 ,
Identificando linhas e colunas e os elementos.
Considerando a matriz
tal que aij = i + j.
A matriz é do tipo 2 x 3
 a11
A 
 a21
a12
a22
a13 

a23 
2x3
Vamos encontrar os elementos da matriz obedecendo
a lei de formação aij = i + j
temos que:
Elementos:
12 é o elemento da
1ª linha 1ª coluna
3 é o elemento da
1ª linha 2ª coluna
8 é o elemento da
1ª linha 3ª coluna
5 é o elemento da
2ª linha 1ª coluna
6 é o elemento da
2ª linha 2ª coluna
7 é o elemento da
2ª linha 3ª coluna
9 é o elemento da
3ª linha 1ª coluna
10 é o elemento da
3ª linha 2ª coluna
17 é o elemento da
3ª linha 3ª coluna
Representação
Geral dos elementos
a11
a12
a13
a21
b) Representar explicitamente a matriz B  (bij )2 x 2 ,
a22
1, se i  j
tal que 
0, se i  j
a23
a31
a32
a33
A matriz é do tipo 2 x 2
b11 b12 

B = b
 21 b 22 
Vamos encontrar os elementos da matriz obedecendo
a lei de formação.
Observando a tabela acima percebe-se que o primeiro
número representa a linha e o segundo a coluna, então
podemos representá-los genericamente da seguinte
forma:
aij ( i = linha e o j = coluna ).
146
MATRIZES ESPECIAIS
Matriz nula
Algumas matrizes, por suas características, recebem
denominações especiais.
Toda matriz em que todos os elementos são nulos;
é representada por 0m x n. Por exemplo:
Matriz linha
Toda matriz do tipo 1 x n, ou seja, com uma única
linha. Por exemplo, a matriz
A =[4 7 −3 1].
Matriz coluna
Matriz diagonal
Toda matriz quadrada em que todos os elementos
que não estão na diagonal principal são nulos. Por
exemplo:
Toda matriz do tipo m x 1, ou seja, com uma única
coluna. Por exemplo:
 1
 
B   2 .
  1
 
.
Matriz quadrada
Toda matriz do tipo n x n, ou seja, com o mesmo
número de linhas e colunas; dizemos que a matriz é de
ordem n. Por exemplo:
2 7
C
 é do tipo 2 x 2, isto é quadrada de ordem 2.
4 1
Numa matriz quadrada, definimos a diagonal principal e
a diagonal secundária. A principal é formada pelos
elementos aijtais que i = j. Na secundária, temos i + j = n
+ 1.
Veja:
Matriz identidade ou Unidade
Toda matriz quadrada em que todos os elementos
da diagonal principal são iguais a 1 e os demais são
nulos; é representada por In, sendo n a ordem da
matriz. Por exemplo:
Assim, para uma matriz identidade:

An x In = An
Matriz transposta
É matriz At obtida a partir da matriz A trocando-se
ordenadamente as linhas por colunas ou as colunas
por linhas. Por exemplo:
Observe a matriz a seguir:
Desse modo, se a matriz A é do tipo m x n, Até do
tipo n x m.
a
a
Note que a 1 linha de A corresponde à 1 coluna
t
a
a
de A e a 2 linha de A corresponde à 2 coluna de At.
a11 = −1 é elemento da diagonal principal, pois i = j = 1
a31= 5 é elemento da diagonal secundária, pois i + j = n +
1
(3 + 1 = 3 + 1)
IGUALDADE DE MATRIZES
Duas matrizes, A e B, do mesmo tipo m x n, são
iguais se, e somente se, todos os elementos que
ocupam a mesma posição são iguais:
147
A  B  aij  bij para todo 1 ≤ i ≤ m e todo 1 ≤ j≤ n.
07
12  5   5 7 17 
  1 6
S  T   3  0
4  (2)  20  (2)   3 2  22
1 3
 4  10   5 4
6 
0  (5)
07
12  5   7  7
7 
  1 6



ST 30
4  (2)  20  (2)   3
6  18
0  (5)
1 3
 4  10   5  2  14
Matriz simétrica
È uma matriz quadrada de ordem n, tal que A = At. Por
exemplo:
é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4,
ou seja, temos sempre aij = aji.
Matriz oposta
ALGUMAS PROPRIEDADES DA ADIÇÃO.
 Associativa: A+(B+C) = (A+B)+C
 Comutativa: A+B = B+A
 Elemento Neutro: A+0 = A, sendo 0 uma
matriz nula de mesma ordem de A.
 Elemento Oposto: A+(–A) = 0, sendo 0 uma
matriz nula de mesma ordem de A.
MULTIPLICAÇÃO POR UM NÚMERO REAL
A matriz obtida a partir de A trocando-se o sinal de
todos os elementos de A. Por exemplo:
Dado um número real K e uma matriz A mn .
Multiplicar K pela matriz A significa multiplicarmos
todos os elementos dessa matriz A pelo número K.
Exemplo
  1 9
Calcule 3.A, sabendo que A  

 5 0
Matriz anti-simétrica
Uma matriz anti-simétrica é aquela com a qual
sua matriz transposta coincide com sua matriz oposta:
  1 3 9  3   3 27
3A  


 5  3 0  3  15 0 
At = − A
MULTIPLICAÇÃO DE MATRIZES
Exemplo:
OPERAÇÕES COM MATRIZES
SOMA E SUBTRAÇÃO DE MATRIZES
Para que possamos somar ou subtrair duas mais
matrizes, elas devem ser do mesmo tipo (mesma ordem).
Em seguida é só somar (subtrair) seus elementos
correspondentes em cada matriz.
O produto de uma matriz por outra não é
determinado por meio do produto dos seus respectivos
elementos.
Assim, o produto das matrizes A = (aij)mXp e
B = (bij)pxn é a matriz C = (cij)mxn em que cada elemento
cijé obtido por meio da soma dos produtos dos
elementos correspondentes da i-ésima linha de A pelos
elementos da j-ésima coluna B.
Exemplo
Vamos multiplicar a matriz A pela matriz
entender como se obtém cada Cij :
B para
Exemplo
5 
7 12 
 1 0
6



S   3 4  20 T   0  2  2
 0 1  4 
 5 3 10 
148
Da definição, temos que a matriz produto AxB só existe
se o número de colunas de A for igual ao número de
linhas de B:
Amxn .Bnxp = (A.B)mxp
A matriz produto terá o número de linhas de A(m) e o
número de colunas de B(n):
Se A3 x 2 e B2 x 5 , então (A . B)3 x 5
Se A3 x 2 e B3 x 2, então não existe o produto
Se A4 x 2 e B2 x 1, então (A . B)4 x 1
PROPRIEDADES
Verificadas as condições de existência para a
multiplicação de matrizes, valem as seguintes
propriedades:
a) associativa: (A . B). C = A .(B . C)
b) distributiva em relação à adição:
A .(B + C)=A . B + A . C ou (A + B). C = A . C + B . C
Portanto, A . B ≠ B . A, ou seja, para a multiplicação de
matrizes não vale a propriedade comutativa.
Vejamos outro exemplo com as matrizes:
c) elemento neutro: A x In = In x A = A, sendo Ina
matriz identidade de ordem n.
Vimos que a propriedade comutativa, geralmente,
não vale para a multiplicação de matrizes. Não
vale também a anulação do produto, ou seja:
sendo 0m x n uma matriz nula, A x B = 0mxn não
implica, necessariamente, que
A = 0 m x n ou B = 0 m x n.
EQUAÇÃO MATRICIAL
Uma equação matricial é forma da por uma ou mais
operações entre matrizes
Exemplos
Considerando as matrizes
 1 3 4 
 5 0 2
A
eB

 , determine a matriz
 2 0 1
  3 4 3
X, tal que A + X = B
149
Da igualdade A + X = B temos que:
X = B – A, substituindo as matrizes, vem:
 5 0 2   1 3 4   6  3  2 
X

 
2
 3 4 3  2 0 1    5 4
Obs.: em qualquer equação matricial, é só aplicar os
conceitos já aprendidos e resolver a equação
normalmente sem qualquer mistério.
MATRIZ INVERSA
Seja a matriz A quadrada de ordem n chama-se
inversa de A e representa-se por A-1, a matriz que
obedece a propriedade:
onde In é a matriz identidade .
1 2
06 .(UNIFEI MG) Dadas as matrizes A  
,
2 3
0 3
 1 0 
B
e C

 , considere as seguintes
 1 4
 2  1
afirmativas:
2 5 
I. X=A+B–C= 

1 8
 0 1
II . Y = B – A – C = 

 3 2
3 4
III . Z = 2A – C = 

2 7
Pode-se afirmar que:
A) apenas as afirmativas I e II são verdadeiras.
B) todas as afirmativas são verdadeiras.
C) apenas as afirmativas II e III são verdadeiras.
D) todas as afirmativas são falsas.
E) apenas II é verdadeira
07. (UFBA) A matriz 2 x 3, com
EXECÍCIOS
01. Determine os valores de a, b, x e y, nas matrizes
abaixo sabendo que:
 x  y 2a  b   3  1

  

 2x  y a  b   0 7 
02. Qual a soma de todos os elementos bij da matriz B =
[ bij ]3 x 3 tal que bij = ( i – j )2 ?
03. Dadas as matrizes A e B abaixo,
de x, y e z para que B = At.
0
0  6
2 4



A   6 3 y e B  x 3
5
4 8
1 2


determine o valor
5
1
z 
04. Ache x, y, z e w, nas matrizes abaixo de modo que:
x y   2 3   1 0 

  
  

 z w   4  1  8  5 
05. Nas matrizes abaixo, ache m, n, p e q, de modo que:
m 2m n  n  7 8
 p p   q  3q  1 5

 
 

 aij  2i  j, se i  j

 aij  i  j, se i  j é:

2 0


a) - 3 4 
-1 1 


2
0
1


d)
3 4 1 
2 3


b) 0 4 
 1 1


2
0 - 1


e)
- 3 4 1 
2 3


c) 0 4 
 1 2


08. ( ABC – SP ) Seja A = ( a ij ) uma matriz quadrada
de ordem 3, tal que
 0, se i  j

a ij   i  j, se i  j
 i - j, se i  j

Então o valor da soma de todos os elementos da matriz
A é:
a) 16
b) 14
c) 12
d) 10
e) 8
09. (Unesp – SP) Considere três lojas, L1, L2 e L3, e
três tipos de produtos, P1, P2 e P3. A matriz a seguir
descreve a quantidade de cada produto vendido por
cada loja na primeira semana de dezembro. Cada
elemento aij da matriz indica a quantidade do produto
vendido pela loja , com i e j = 1, 2, 3.
150
se A = – At. Nessas condições, se a
x y z 
matriz A =  2 0  3 é uma matriz anti-simétrica,
 1 3 0 
então x + y + z é igual a:
a) 3
b) 1
c) 0
d) –1
e) – 3
SIMÉTRICA
Analisando a matriz, podemos afirmar que
A) a quantidade de produtos do tipo P2 vendidos pela loja
L2 é 11.
B) a quantidade de produtos do tipo P1 vendidos pela loja
L3 é 30.
C) a soma das quantidades de produtos do tipo P3
vendidos pelas três lojas é 40.
D) a soma das quantidades de produtos do tipo Pi
vendidos pelas lojas Li, i = 1, 2, 3, é 52.
E) a soma das quantidades dos produtos dos tipos P1 e P2
vendidos pela loja L1 é 45.
10. (FGV – RJ) A organização econômica Merco é
formada pelos países 1, 2 e 3. O volume anual de
negócios realizados entre os três parceiros é representado
em uma matriz A, com 3 linhas e 3 colunas, na qual o
elemento da linha i e coluna j informa quanto o país i
exportou para o país j, em bilhões de dólares.
Então o país que mais exportou e o que mais importou no
Merco foram, respectivamente:
a) 1 e 1
b) 2 e 2
c) 2 e 3
d) 3 e 1
e) 3 e 2
 a2  2
11. ( Fatec – SP ) Sejam X = 
 4a
 2a 
 2  a2 
e Y=
16. ( VUNESP – SP ) Considere as matrizes A =
 2 1 

 e I =
 1  1
 1 0

 . A Matriz B, tal que A.B = I é
 0 1
dada por :
 1 1

  1 2
 1 1 

d) 
  1  2
 1 1

  2 1
 2 1

  1 1
 1 1 

e) 
1  2
c) 
b) 
 2
a =3
a = -3
a = 1/3
a = - 1/3
 0 3 x 
12. ( ICÉS – MG ) Para que a matriz  3 0 5  seja
  2  5 0 
anti-simétrica, o valor de x deve ser :
a) 0
b) 2
c) 3
d) 5
e) 10
13. (UEL) Uma matriz quadrada
15. (UEL) Sobre as sentenças:
I. O produto de matrizes A3x2 . B2x1 é uma matriz 3x1.
II. O produto de matrizes A5x4 . B5x2 é uma matriz 5x2.
III. O produto de matrizes A2x3 . B3x2 é uma matriz
quadrada 2x2.
é verdade que
a) somente I é falsa.
b) somente II é falsa.
c) somente III é falsa.
d) somente I e III são falsas.
e) I, II e III são falsas.
a) 
6
 7

 , onde a  R . Se X = Y, então:

12
7 

a)
b)
c)
d)
14. (UEL) Sejam as matrizes A 3x 4 e Bpxq . Se a
matriz A.B é 3 x 5, então é verdade que
a) p = 5 e q = 5
b) p = 4 e q = 5
c) p = 3 e q = 5
d) p = 3 e q = 4
e) p = 3 e q = 3
2 
 1 0
17. ( FATEC – SP ) Se A = 
 e B= 

0 1
 3 3 
são duas matrizes quadradas de ordem 2, então A2 –
5A + 3B é igual a :
3 0 
1 0 
a) 9B
b) 
c) 


3
0


0 3 
 3
6 
d) 

24  3
 0
0
e) 

  18 16
18. ( UFV – MG ) Considere as matrizes:
I) A = ( aij ), 3 x 4, definida por aij = i – j
i–j
II) B = ( bij ), 4 x 3, definida por bij = 2
III) C = ( cij ), C = A x B
A se diz
ANTI-
151
O elemento C32 é :
a) – 7
b) – 4
c) – 2
d) 0
e) 2
24. (UNIMONTES) Considere as seguintes matrizes
 1 2
2 y 
19. ( PUC – MG ) Se A = 
, B= 
 e A.B =
0 3 
0 5 
B.A, o valor de y é :
a) 1
b) 2
c) 3
d) 4
e) 5
a 0 
2
20. (UEL) Considere as matrizes M = 
e M =

b  a
8 0 
0 8  . Conclui-se que o número real “a” pode ser:


a) 2 3
Podemos afirmar que:
A) A. B = B . A = I.
B) não existe a matriz inversa da matriz A.
C) A e B são inversas, pois A.B = I.
D) B.I = I.B = B.
25. (MACK) Se A é uma matriz 3 x 4 e B uma
matriz n x m, então:
a) existe AB se, e somente se, n = 4 e m = 3
b) existem AB e BA se, e somente se, n = 4 e m = 3
c) existem, iguais, AB e BA se, e somente se, A = B
d) existe A + B se, e somente se, n = 4 e m = 3
e) existem, iguais, A + B e B + A se, e somente se,
A=B
26. (Unimontes) Sejam x e y números reais
positivos. Considere as matrizes
b) 2 2
c) 2
d) – 2
e) – 3
 1 0
21. ( FEI – SP ) Dadas as matrizes: A  
,
  1 2
 2 7 
0 0
B
 e 0  0 0 , determine a matriz X de
0
4




ordem 2 tal que : 2X – AB = 0 .
x y 
 e L =
z w
22. ( ICÉS – MG ) Sendo K = 
 11 9 

 ,
  8  2
 11 9 
 é necessário que os
  2 12 
para que se tenha K x L = 
valores de x, y, z e w sejam, nessa ordem, iguais a:
a) 0, 0, 4, 6
b) 1, 0, 2, 3
c) 1, 1, 4, – 6
d) 1, 2, 0, 3
e) 1, 1, 1/4, – 6
2 3 
23. ( CEFET - MG ) Se a matriz inversa de A = 
 é
3 x 
 5 3 

 o valor de x é :
 3 2 
a)
b)
c)
d)
e)
5
6
7
9
10
Com base nessas informações, é CORRETO afirmar
que os valores de x e y, de modo que se tenha A.B =
B.A, são, respectivamente,
27. (UNIMONTES) Uma fábrica produz 3 tipos
diferentes de artigos . Numa semana são vendidos 100
unidades do artigo A , 150 unidades do artigo B e 200
unidades do artigo C . Os preços de venda , por
unidade de cada artigo , são respectivamente .
R$20,00 , R$30,00 , R$10,00 . A quantidade total de
artigos , na ordem A, B e C , vendidos em uma
semana, podem ser representada pela matriz
 20 
 
X  100 150 200  . A matriz Y   30  representa o
 10 
 
preço de venda por unidade de artigo , tomado na
ordem dada . Com base nos dados apresentados , é
correto afirmar que o produto X.Y representa .
a)Uma matriz de ordem 1 , que fornece o total apurado
diariamente pela venda dos artigos A, B e C .
b) Uma matriz de ordem 1 , que fornece o total apurado
semanalmente pela venda dos artigos A, B e C .
c) Uma matriz de ordem 3 .
d) Uma matriz de 3 linhas e 1 coluna .
152
28. (UFMG) Milho, soja e feijão foram plantados nas
regiões P e Q, com ajuda dos fertilizantes X, Y e Z.
A matriz A indica a área plantada de cada cultura, em
hectares, por região:
02.(FIP-2012) O Brasileirão 2011 contou com 20
clubes que disputaram entre si, ponto a ponto, qual o
melhor time brasileiro da atualidade. A forma de
pontuação manteve igual a do ano passado, em que
cada vitória valia 3 pontos e os empates, apenas 1
ponto, conforme tabela 1. E para se tornar campeão,
todos os times disputaram, entre si, em jogos de turno
e returno; ao final, o time com mais pontos sagrou-se o
campeão brasileiro.
A matriz B indica a massa usada de cada fertilizante, em
kg, por hectare, em cada cultura:
a) CALCULE a matriz C = AB.
b) EXPLIQUE o significado de C23, o elemento da segunda
linha e terceira coluna da matriz C.
 4 6
29. ( UFV – MG ) Sejam as matrizes A  
e

 1 2
y
 x
 . Onde x e y são números reais e M é a
M 1
2

 2

matriz inversa de A. Então o produto x. y é:
A) 0
B) – 3
C) 4
D) – 2
E) 3
Na 33ª rodada do Campeonato Brasileiro 2011, o
resultado dos 4 últimos times era o que se lê na
tabela2:
Sabendo que cada tabela pode ser transformada em
uma matriz, temos a seguinte situação:
Tabela 1, que corresponde à seguinte matriz
Tabela 2, que corresponde à seguinte matriz
30. (FIP) Considere a matriz de segunda ordem
A
2
1
3
e seja A–1 sua inversa. Se a matriz B,
2
também de segunda ordem é dada por B 

então a expressão A 5 . A 1

32
2
5
Nessa rodada do campeonato, qual matriz abaixo
corresponde ao resultado dos pontos para cada
equipe?
3
7
. B é igual a:
153
GABARITO
1) x = 1, y = 2, a = 2 e b = – 5
3) y = 8
x=
2
4) x = –3; y = 3; z = 12; w = –6
5) m = 5; n = 2; q = –1; p = 2
9) E
15) B
10) C
16) E
7 

 1 2 
21) X  

1
1
2 

25) B
26) B
2) 12
6) B
7) D
8) A
11) B
12) B
13) D
14) B
17) C
18) C
19) C
20) B
22) B
23) A
24) B
27) B
28)
a)
b) A massa de fertilizante Z usada na área Q.
29) E
30) C
31) B
154
DETERMINANTES
DETERMINANTE DE 3ª ORDEM
CONCEITO DE DETERMINANTE
REGRA DE SARRUS
Toda matriz quadrada tem, associado a ela, um
número chamado de determinante da matriz, obtido a
partir de operações que envolvem todos os elementos da
matriz.
Essa regra só é valida para determinantes de ordem
2 e 3.
Consideremos a matriz:
1º Passo:Escrevemos a matriz e repetimos a 1ª e a 2ª
colunas à direita da 3ª.
.
O Determinante de uma Matriz A pode ser denotado
por detA.
CÁLCULO DOS DETERMINANTES
DETERMINANTE DE 1ª ORDEM
A = (a11)
⇒
det(A) = a11
2º Passo: Efetuamos a adição algébrica dos produtos
dos elementos indicados pelas setas conforme o
esquema:
DETERMINANTE DE 2ª ORDEM
REGRA DE SARRUS
O determinante de uma matriz quadrada de ordem 2 é
dado pela diferença entre o produto dos elementos da
diagonal principal e o produto dos elementos da diagonal
secundária.
Exemplo
Considerando a matriz A, calcule o valor de Det(A).
1 2 1
A  2 1 3
2 1 2
Exemplo
***Mas adiante após outros conceitos, iremos ver outro
processo para cálculo do determinante de uma matriz
de ordem
.
155
MENOR COMPLEMENTAR
Chama-se menor complementar de uma matriz A de
ordem
de um elemento aij, ao valor ,
correspondente ao determinante da Matriz que se obtém
eliminando a linha i e a coluna j onde se encontra o
elemento aij.
CÁLCULO DO DETERMINANTE DE ORDEM
REGRA DE LAPLACE
Seja uma matriz A de ordem
, o determinante
da matriz A é dado pela soma do produto de uma de
suas filas pelo seus respectivos cofatores.
Exemplo
Exemplo
Calcule o determinante da matriz abaixo:
COFATOR OU COMPLEMENTAR ALGÉBRICO
Chama-se cofator do elemento aij de uma matriz A de
ordem
, ao elemento Aij que se obtém multiplicando o
fator (-1)i + j pelo menor complementar .
PROPRIEDADES DE DETERMINANTES
P1 - Se uma fila de uma matriz (linha ou coluna) for
nula, então seu determinante é igual a zero.
156
P2 - Se duas fileiras, horizontais ou verticais, de uma
matriz forem iguais ou proporcionais, então seu
determinante é nulo.
P8- O determinante de uma matriz transposta é igual
ao determinante dessa matriz
detAt = detA
P3 - Permutando-se duas linhas ou duas colunas de uma
matriz, o seu determinante muda de sinal.
Permuta 1ª linha com a 2ª linha
P9- O determinante do produto de duas matrizes é
igual ao produto dos determinantes dessas matrizes.
det(A.B) = detA . detB
P 10 – O determinante de uma matriz inversa é igual ao
inverso do determinante dessa matriz
–1
–1
Se DetA = K, logo Det(A )= 1 ou Det(A )=
k
P4 - Se os elementos que estão acima e/ou abaixo da
diagonal principal forem nulos, então o determinante é
dado pelo produto dos elementos da diagonal principal.
1
DetA
MATRIZ INVERSA
Seja a matriz A quadrada de ordem n chama-se
inversa de A e representa-se por A-1, a matriz que
obedece a propriedade:
onde In é a matriz identidade .
Propriedades
P5 - Fazendo a combinação linear de duas linhas ou duas
colunas de uma matriz, seu determinante não altera.
1. Uma matriz só admite inversa, quando seu
determinante for diferente de zero.
2.
1ª linha menos a 2ª linha
-
ou
de ordem n.
-
⇒
-
, onde In é a matriz identidade
3. Quando uma matriz não admite inversa é chamada
matriz singular.
P6 - Multiplicando-se uma fila de uma matriz por uma
constante, então o determinante dessa matriz fica
multiplicado por essa constante.
Exemplo
Determinar a inversa da matriz:
P7- Multiplicando-se uma Matriz quadrada por uma
constante k, seu determinante obedece a seguinte
relação:
157
d) 3bc
2 2
e) b c
03. ( UFES ) A solução real da equação
é:
a)
b)
c)
d)
Uma matriz é chamada de inversível ou não singular se, e
somente se, seu determinante for diferente de zero, por
isso uma matriz só pode ser inversível se for uma matriz
quadrada com determinante diferente de zero. Um método
para determinar a matriz inversa é chamado de método
de inversão por matriz adjunta. A utilização desse método
depende do teorema M 1 
1
.M , onde:
Det(M)

M-1 é a matriz inversa de M.

Det(M) é o determinante da matriz M

M é a matriz adjunta de M.
A matriz adjunta é o nome que se dá a matriz quadrada
que se obtém fazendo transposta da matriz dos
cofatores de uma matriz original.
M1 
a)
b)
c)
d)
e)
EXERCÍCIOS
01. ( Faap – SP ) Resolva a equação
x
4
3x
 14
2x
05. ( PUC-RS) A equação
2 1
3
4  1 x  1  12 , tem
x 0
x
como conjunto verdade:
a) {-6, 2}
b) {-2, 6}
c) {2, 6}
d) {-6, 6}
e) {-2, 2}
06. ( FGV – SP ) A solução da equação
a)
b)
c)
d)
e)
( “x” real ) é:
não tem solução real
x= 3
x=1
x=1
x = -1
8 7 4
07.( UFBA ) Se X  10 1 5
0 20 1
02. ( FGV – SP )
determinante
a) 0
b) bc
c) 2bc
a b
c d
Se
a b 0
0 d 1
c 0 2
é:
= 0, então o valor do
1 1 2
1 2 x = 0 é:
3 0 1
–3
–1
0
1
3
x 0 1
1 x 0 0
0 1 x
1
.M
Det(M)
=0
x=1 e x=2
x=2 e x=3
x = -1 e x = 2
x=1 e x=3
04. ( UFRS ) A solução da equação
MATRIZ INVERSA: INVERSÃO POR MATRIZ
ADJUNTA
x 2 0
1 3 3
0 x 3
então :
a)
b)
c)
d)
e)
e Y
8 7 4
0 20 1 ,
10 1 5
X=Y0
X=Y=0
X = 2Y
2X = Y
X+Y=0
08. ( Unicap – PE ) Calcule o valor de x, a fim de que o
determinante da matriz A seja nulo.
158
A) – 4
B) 1/4
C) 1
D) 2
E) 4
 1 0 1 
09. ( UNIFORM ) Sejam as matrizes A  
 e
 0 2  2
2  1
B   1 2  . O determinante da matriz A.B é:
0 1 
a) 64
b) 8
c) 0
d) – 8
e) – 64
p 2 2 
10. ( UESP ) Se o determinante da matriz p 4 4 é
p 4 1
p  1 2
igual a –18, então o determinante da matriz p  2 4 é
p  2 1
igual a:
a) – 9
b) – 6
c) 3
d) 6
e) 9
 2  1
11. (MACK) Se A3 = 
 , o triplo do determinante da
 4 6 
matriz A é igual a
a) 3
b) 6
c) 9
d) 12
e) 15
12. (UFRGS) Se A é uma matriz 2x2 e det A = 5, então o
valor de det 2A é:
a) 5
b) 10
c) 20
d) 25
e) 40
13. ( FATEC – SP ) Se x é um número real positivo tal
 1  1
 x 1 
que A = 
, B =

 e det (A.B) = 2, então
x 0 
 1  1
x  x é igual a:
14. (Ufes) Se A é uma matriz quadrada de ordem 3
com det(A) = 3 e se k é um número real tal que
det(kA) = 192, então o valor de k é:
a) 4
b) 8
c) 32
d) 64
e) 96
2 1 0 
15. ( UESP ) Se o determinante da matriz k k k 
 1 2  2
é igual a
10, então o determinante da matriz
1
0 
 2
k  4 k  3 k  1 é igual a:


 1
2
 2 
a) 7
b) 8
c) 9
d) 10
e) 11
16. ( PUC
2 1
A  1 2
0 1
a) 2
b) 1
c) – 1
d) – 2
e) 3
– SP ) O cofator do elemento a23 da matriz
3
1 é:
2
17. (ESAF) Considere as matrizes
onde os elementos a, b e c são números naturais
diferentes de zero. Então, o determinante do produto
das matrizes X e Y é igual a
a) 0.
b) a.
c) a + b + c.
d) a + b.
e) a + c.
18. (Unimontes) Indicaremos por det(X) o
determinante de uma matriz X. Seja A uma matriz 2×2.
Nessas condições, é CORRETO afirmar:
A) det(2A) é igual a 2.det(A).
159
B) se det(A) = 1, então A é a matriz identidade.
C) se multiplicarmos a segunda linha de A por 2, o
determinante da nova matriz será igual a 2.det(A).
D) se det(A) = 0, então A é a matriz nula.
19. (UNIMONTES) As afirmações abaixo são falsas,
EXCETO
a) Se det A = det B, então A = B.
b) det(A⋅ A) = det A.
c) Se det A ≠ 0 , então a matriz A possui matriz inversa.
d) Se a matriz B possui inversa, então det B = 1.
20.
(
1
0
0
0
a)
b)
c)
d)
e)
–
FMJ
0 0
2 0
0 3
0 1
0
0
1
4
SP
)
O
valor
do
determinante
é:
– 26
– 24
– 13
24
26
21. ( ABC – SP ) Seja A = (aij) uma matriz quadrada de
 0, se i  j

ordem 3, tal que ( aij )   i  j, se i  j . Então o valor do

i  j, se i  j


determinante da matriz A é:
a) 0
b) 12
c) 24
d) 48
e) 60
 1 0  1
22.(CEFET) Para que a matriz A = k 1 3  não seja
 1 k 3 
inversível, os valores de k são:
a) k = – 4
b) k = – 3
c) k = – 5
d) k = 3
e
e
e
e
k=1
k=2
k = -2
k=2
GABARITO
1) S = {-1, 7 }
7) E
8) x = 13
13) B
14) A
19) C
20) A
2) D
9) D
15) C
21) D
C) A
4) A
10) E
16) D
5) B
11) B
17) A
6) E
12) C
18) C
22) A
160
SISTEMAS LINEARES
EQUAÇÃO LINEAR
É toda equação da forma
onde
.
,
Exemplo
x + 2y + z – 4w = 9
SISTEMA LINEAR
É todo sistema formado por duas ou mais equações
lineares.
Indicando por A a matriz dos coeficientes de um
sistema linear com número de equações igual ao
número de incógnitas, têm-se:
⇔
⇔
Exemplo
Determine o valor de k, de modo que o sistema seja
possível e determinado.
** Chama-se solução de um sistema linear qualquer
solução comum a todas as equações do sistema. (Essa
solução pode não existir)
EQUAÇÃO MATRICIAL NA FORMA A.X = B
Qualquer sistema linear pode ser representado em
forma de uma equação matricial na forma A.X = B
Sendo:
A - matriz dos coeficientes
X - matriz das variáveis
B - matriz dos termos independentes
CLASSIFICAÇÃO E DISCUSSÃO DE UM SISTEMA
LINEAR
TIPOS ESPECIAIS DE SISTEMAS LINEARES
SISTEMA LINEAR QUADRADO:É quando o número
de equações é igual ao número de variáveis.
SISTEMA HOMOGÊNEO: É todo sistema onde os
termos independentes são nulos. O sistema
homogêneo é sempre possível, pois apresenta no
mínimo a solução trivial.
Os sistemas lineares são classificados quanto ao
número de soluções da seguinte forma:
x1 = x2 = ... = xn = 0
Solução trivial: S = {(0, 0, 0, ..., 0)}
161
RESOLUÇÃO DE UM SISTEMA LINEAR
Exemplo
Determine o valor de m, de modo que o sistema
apresente apenas a solução trivial.
Resolver um sistema linear significa obter o conjunto
S, denominado conjunto solução do sistema, cujos
elementos são todas as soluções do sistema.
Dentre os vários métodos existentes para a
resolução
de
um
sistema,
optamos
pelo
escalonamento e regra de Cramer.
ESCALONAMENTO DE UM SISTEMA LINEAR
(MÉTODO DE GAUSS)
Dado o sistema:
SISTEMAS LINEARES NÃO QUADRADOS
1º) Se o número de equações maior que o número de
variáveis:
 O sistema é possível e determinado ( três retas
concorrentes em um único ponto )

O sistema é possível e indeterminado (três retas
paralelas distintas)

O sistema é impossível ( não tem solução ) .
ou
Identifica-se as equações e trabalha-se duas a duas.
ou
Exemplo
È importante trabalharmos para eliminar a mesma
incógnita z.
Juntando as equações IV e V, teremos:
Três retas concorrentes em um único ponto.
2º) Se o número de equações for menor que o número de
variáveis:
 O sistema nunca é determinado ( Pois dois planos
nunca tem um único ponto comum )

Agora basta substituir nas outras equações,
vejamos:
O sistema é possível e indeterminado ( planos
secantes ) ou o sistema é impossível ( planos
paralelos distintos ).
Exemplo
162
REGRA DE CRAMER
Dado um sistema
EXERCÍCIOS
01. (UNITAU – SP) A solução do sistema de equações
algébricas lineares é dada por:
xy  2

2x  y  1
1º. Calcula-se o detA.
2º. Calcula-se o determinante das variáveis,
substituindo-se os seus coeficientes pelos termos
independentes.
a) x = 1 e y = 1
b) x = -1 e y = 1
c) x = y = 0
d) x = 1 e y = -1
e) x = -1 e y = -1
3º. Cada variável é a razão entre seu determinante e o
determinante dos coeficientes.
(UESP) Se o terno (x1, y1, z1) é a solução do sistema
abaixo, então 3.x1 + 5.y1 + 4.z1 é igual a:
Exemplo
Utilizando a regra de Cramer, determine a solução
do sistema abaixo:
a) -8
b) -7
c) -6
d) -5
e) -4
03. (UFRN) Três amigos, denominados X, Y e Z, utilizam o
computador todas as noites. Em relação ao tempo em
horas em que cada um usa o computador, por noite, sabese que:
• o tempo de X mais o tempo de Z excede o tempo de Y
em 2;
• o tempo de X mais o quádruplo do tempo de Z é igual a 3
mais o dobro do tempo de Y;
• o tempo de X mais 9 vezes o tempo de Z excede em 10
o tempo de Y.
A soma do número de horas de utilização do computador,
pelos três amigos, em cada noite, é igual a:
a) 4 h
b) 7 h
c) 5 h
d) 6 h
GABARITO
01. D
02. B
03. D
S = {(x,y,z)} = {(1,1,3)}
163
DISCUSSÃO DE UM SISTEMA LINEAR ATRAVÉS DE
RETAS E PLANOS
INTERPRETAÇÃO GEOMÉTRICA DE SISTEMAS
LINEARES 3 X 3
Interpretação geométrica de sistemas lineares 2 x 2
Em sistemas lineares 3 x 3 da forma
Considere o sistema com duas variáveis
 ax  by  c

a 1x  b1y  c 1
Se considerarmos ax + by = c
as equações (I), (II) e (III) representam planos π1, π2
e π3 no espaço tridimensional.
As possibilidades para as posições dos três planos
são oito e correspondem a:

SISTEMA IMPOSSÍVEL ( NENHUMA SOLUÇÃO
π1 π2 π3 =  )
a)1//2//3
1
2
3

Na situação I as retas são coincidentes logo a
interseção entre elas é um conjunto infinito de pontos,
portanto podemos afirmar que o sistema formado por
elas é possível e indeterminado.

Na situação II as retas são paralelas não havendo
interseção entre elas logo o sistema formado por elas
é impossível pois não tem pontos (soluções) em
comum.

Na situação III as retas são concorrentes e possuem
apenas um ponto em comum logo apenas uma
solução daí dizer que o sistema formado por elas é
possível e determinado.
b)1// (2 = 3)
1
2 = 3
c)(1// 2)  3
e
r//s
3
r = 13
Resumidamente teríamos:
1
 ax  by  c

a 1x  b1y  c 1
s = 23
2
Se:
a
b
c


a1 b1 c1
(retas coincidentes ( S.P.I )

a
b
c


a1 b1 c1
(retas paralelas distintas ( S.I )

a
b

a1 b1
(retas concorrentes ( S.P.D )

3
d) r // s // t
r
2
s
t
1
164

SISTEMA POSSÍVEL E INDETERMINADO
(INFINITAS SOLUÇÕES; π1 π2 π3 = π
ou π1 π2 π3 = r )
1 = 2 = 3
2º) Possibilidade
 2x  3y  2z  2 (I)

O sistema  3x  2y  4z  2 (II)
4x  y  6z  3 (III)

não tem solução.
3
r = 13
1 = 2
Um maneira simples de verificarmos esse fato é, por
exemplo, somar as equações ( I ) e ( III ) e comparar o
resultado com a equação ( II ). Veja:
 3x  2y  4z  2
(I)

6x  4 y  8z  5 (II)  (III)
3
Dobramos os coeficientes das incógnitas, mas o
termo independente não dobrou.
2
r = 123
1
Consideremos agora os sistemas formados por ( I )
e ( II ) e ( III ). Podemos concluir que:
π1 ∩ π2 é uma reta r
π1 ∩ π3 é uma reta s
π2 ∩ π3 é uma reta t
Vamos verificar que r, s e t são paralelas.

SISTEMA POSSÍVEL E DETERMINADO
( SOLUÇÃO ÚNICA; π1 π2 π3 = {P} )
2
3
P
1
Vamos examinar alguns exemplos:
1º) Possibilidade
O sistema
tem infinitas soluções, pois, se suas equações forem
simplificadas, todas representarão o mesmo plano.
Geometricamente, (I), (II), (III) representam três planos
coincidentes.
Os pontos de r satisfazem ( I ) e ( II ), logo não
satisfazem ( III ), pois o sistema é impossível. Portanto,
temos r paralela π3
Como s está contida em π3 , então r e s não se
cortam.
Uma vez que ambas estão em π1 elas são
paralelas.
Analogamente, vemos que s é paralela a t.
Portanto, a interpretação geométrica do sistema em
questão é: o sistema é impossível porque os planos
representados por suas equações se intersectam dois
a dois segundo três retas paralelas.
QUANTIDADE DE SOLUÇÕES INTEIRAS E NÃO
NEGATIVAS DE UMA EQUAÇÃO LINEAR
Existem alguns tipos de questões (comuns em
concursos militares e não em vestibulares) que
desejam determinar o número de soluções inteiras e
não negativas de uma equação linear, muitos pensam
que a sua resolução será através dê sistemas lineares.
A resolução de questões desse tipo será através da
análise combinatória como veremos a seguir:
Considerando uma equação linear com n variáveis
do tipo x1 + x2 + x3 + ... + xn = k, o número de solução
inteiras e positivas dessa equação, é dado por:
165
02. Um bar vende três tipos de refrigerantes: Guaraná,
Soda e Tônica. De quantas formas diferentes uma
pessoa pode comprar 5 garrafas de refrigerante?
RESOLUÇÃO COM A FÓRMULA
Ou de uma maneira mais prática:
Exemplos
01. Na equação linear x + y + z = 7, encontre o número de
soluções inteiras, não negativas, possíveis.
Trata-se então chegar ao número de soluções inteiras
não negativas da equação x + y + z = 5 que é então:
Resolução Prática
Um raciocínio alternativo, seria o seguinte:
Temos que dividir 7 unidades em 3 partes ordenadas,
de modo que fique em cada parte um número maior ou
igual a zero.
Indiquemos cada unidade por um ponto então, elas
serão representadas por.
{  }
Como queremos dividir as 7 unidades em 3 partes,
vamos usar duas barras para fazer a separação.
Cada modo de dispormos os pontos e as barras dará
origem a uma solução.
EXERCÍCIOS
01.Uma pastelaria vende pastéis de carne, queijo e
palmito. De quantas formas diferentes uma pessoa
pode comer 5 pastéis?
Por exemplo:

p p b
{
1ª Parte
}
p
p
p
b
p
2ª Parte
02.Quantas soluções inteiras e não negativas tem as
equações:
p
3ª Parte
3 Partes
a) x + y + z = 6
ou
{
 }
p p p p b
1ª Parte
p
b
p
2ª Parte
p
3ª Parte
b) x + y + z + t = 10
3 Partes
ou
{
 0  }
p p p p p b b
1ª Parte
c) x + y + z + t + w = 10
p
2ª Parte
p
3ª Parte
3 Partes
Ora, como temos 9 símbolos ( 7 bolinhas e 2 barras).
O número de permutações, com repetição, destes
símbolos será:
GABARITO
01.21
que é o número de soluções inteiras não negativas da
equação.
Tal raciocínio pode ser utilizado no lugar da fórmula,
que é um pouco mais complicada de trabalhar.
02. a) 28
b) 286
c) 1001
166
EXERCÍCIOS
x  y  z  6

01.(UFRN) A solução do sistema 4x  2y  z  5 é:
x  3y  2z  13

a) (-2, 7, 1)
b) (4, -3, 5)
d) (2, 3, 1)
e) (1, 2, 3)
c) (0, 1, 5)
08. (FGV-SP) É dado o sistema
02.( PAES ) Um par de tênis, duas bermudas e três camisetas
custam, juntos, R$100,00. Dois pares de tênis, cinco bermudas e
oito camisetas custam, juntos, R$235,00. Um par de tênis, duas
bermudas e duas camisetas custam, juntos, R$95,00. Quanto
custam, juntos, um par de tênis, uma bermuda e uma camiseta?
A) R$50,00
B) R$70,00
C) R$60,00
D) R$65,00
03.( PAES ) Em uma loja de brinquedos, uma bola, duas petecas
e três quebra-cabeças custam R$10,00. Duas bolas, cinco
petecas e oito quebra-cabeças custam R$23,50. Na compra de
uma bola, uma peteca e um quebra-cabeça, pagarei
A) R$7,00.
B) R$6,00.
C) R$7,50.
D) R$8,50.
04. (FUVEST-SP) Carlos e sua irmã Andréia foram com
seu cachorro Bidú à farmácia de seu avó. Lá encontraram
uma velha balança com defeito, que só indicava
corretamente pesos superiores a 60 kg. Assim, eles se
pesaram dois a dois e obtiveram as seguintes marcas:
• Carlos e o cão pesam juntos 87 kg;
• Carlos e Andréia pesam 126 kg; e
• Andréia e Bidú pesam 66 kg.
Podemos afirmar que:
A) Cada um deles pesa menos que 60 kg.
B) Dois deles pesam mais que 60 kg.
C) Andréia é mais pesada dos três.
D) Carlos é mais pesado que Andréia e Bidú juntos.
05. (UEL – PR ) Se os sistemas abaixo são equivalentes,
encontre o valor de a2 + b2
 xy 1
 ax  by  5


x  2y  5
 bx  ay  1
06. (Unimontes) Se um número de dois dígitos é 9 vezes
a soma de seus dígitos, então o número formado pela
troca dos dígitos é a soma dos dígitos multiplicada por
A) 2.
B) 3.
C) 4.
D) 1.
07.(Unimontes) O conjunto solução do sistema de
equações lineares
, pode-se
dizer que x + y é igual a:
a) 18
b) -21
c) 27
d) 3
e) -9
09. (BNB-ACEP) Uma agência bancária vende dois
tipos de ações. O primeiro tipo é vendido a R$1,20 por
cada ação e o segundo a R$1,00. Se um investidor
pagou
R$1.050,00
por
mil
ações,
então
necessariamente ele comprou:
a)
b)
c)
d)
e)
300 ações do primeiro tipo
300 ações do segundo tipo
250 ações do primeiro tipo
250 ações do segundo tipo
200 ações do primeiro tipo
10. (Bnb/2007) Dentre os serviços que um BANCO
presta à comunidade, há três pelos quais cobra as
taxas X, Y e Z em reais. Ao final do expediente de um
dia de trabalho, os caixas A, B e C anotaram os valores
recebidos referentes às taxas supracitadas:
Logo, a soma das taxas X + Y + Z é, em real, igual
a:
a) 35,40
b) 46,20
c) 44,70
d) 33,80
e) 36,70
11. (CTSP) Um mesmo conjunto de farda é vendido em
duas lojas A e B, sendo R$ 40,00 mais caro na loja
B. Se a loja B oferecer 10% de desconto no preço do
produto, este ainda assim será 5 % mais caro do que
custa na loja A. O preço do conjunto na loja A é:
A) R$ 300,00
B) R$ 280,00
C) R$ 260,00
D) R$ 240,00
12. (CTSP) Os 180 alunos de uma escola estão
dispostos de forma retangular,em filas, de tal modo que
o número de alunos de cada fila supera em 8 o número
de filas.Quantos alunos há em cada fila?
A) 20
167
18. (Fuvest-SP) Para quais valores de k o sistema
B) 15
C) 18
D) 22
linear
13. (Esaf-MPU).Ana e Júlia, ambas filhas de Márcia,
fazem aniversário no mesmo dia. Ana, a mais velha, tem
olhos azuis; Júlia, a mais nova, tem olhos castanhos.
Tanto o produto como a soma das idades de Ana e Júlia,
consideradas as idades em número de anos completados,
são iguais a números primos. Segue-se que a idade de
Ana – a filha de olhos azuis –, em número de anos
completados, é igual
A) à idade de Júlia mais 7 anos.
B) ao triplo da idade de Júlia.
C) à idade de Júlia mais 5 anos.
D)ao dobro da idade de Júlia.
E) à idade de Júlia mais 11 anos.
14. ( UFVJM ) Considere o sistema indeterminado
 2x  y  a
. Nele o valor de a + b vale:

4x  by  2
a) 1/2
b) 3/2
c) 2
d) 3
15. (UEL) O sistema abaixo, de incógnitas x e y, é:
6x  ky  9

2x  7y  1
a) impossível, para todo k real diferente de - 21;
b) possível e indeterminado, para todo k real diferente de
- 63;
c) possível e determinado, para todo k real diferente de 21;
 x  y  Z  1

 3x  y  2Z  3

y  kZ   2

 x  2y  z  3
 3x  y  2z  2

,podemos afirmar que ele é:
A) possível e determinado
B) possível e indeterminado
C) impossível
D) homogêneo
E) impossível e homogêneo
2x  3y  z  0

20. (FGV – SP) O sistema x  2y  4z  0 é:
x  14z  0

a) determinado.
b) Impossível
c) Determinado e admite como solução (1, 1, 1).
d) Indeterminado.
e) N.D.A.
21. (UFSC) Para qual valor de m o sistema
mx  2y  z  0

x  my  2z  0 admite infinitas soluções?
3x  2y  0

a) m = 0
d) m = 10
b) m  0
c) m = 2
e) m = 1
k 2 x  y  0
nas incógnitas x e
x  ky  0
e) possível e determinado, para todo k real diferente de 1 e - 63.
y:
infinitas soluções. Logo pode-se afirmar que:
a) k = 3
b) k = ± 3
c) k = – 3
d) k = 0
e) não existe K real
17. (FMU – SP) O valor de a para que o sistema
x  2y  18
seja possível e indeterminado é:

3x  ay  54
a) -6
d) -2
b) 6
e) 3/2
c) 2
e
19. (CEFET) A respeito do sistema  2x  y  z  1
22. (FCC – BA) O sistema 
 3x  y  1
possui
2
k x  3 y  k  6
compatível
determinado?
d) possível e indeterminado, para todo k real diferente de
- 3;
16. (UFV – MG) O sistema linear 
é
a)
b)
c)
d)
e)
é impossível se k  1
admite apenas a solução trivial se k = 1
é possível e indeterminado se k = -1
é impossível para todo k real
admite apenas a solução trivial para todo k real.
ax  y  z  0

23. (Cesgranrio) O sistema x  ay  z  1 tem uma
x  y  b

infinidade de soluções. Então, sobre os valores dos
parâmetros a e b, podemos concluir que:
a) a = 1 e b arbitrário.
b)
c)
d)
e)
a=1
a=1
a=0
a=0
e b0
e b=1
e b=1
e b=0
168
 x   y  2z  0

24. (Fuvest – SP) O sistema linear: x  y  z  1
x  y  z  3

admite solução se  for igual a:
a) 0
b) 1
d) 2
c) -1
e) -2
25. O sistema linear abaixo
 2x  y  3z  7

4x  2y  6z  14
6x  3y  9z  17

Pode ser representado geometricamente como:
a) Três planos paralelos e distintos
b) Três planos coincidentes
c) Dois planos paralelos distintos e outro secante aos dois
d) Três planos secantes dois a dois
e) Dois planos coincidentes e outro paralelo aos dois
26. O sistema linear abaixo
 x  y  2z  9

2 y  2 x  4 z  12
 x  3 y  4 z  17

Pode ser representado geometricamente como:
a) Dois planos coincidentes e outro paralelo aos dois
b) Dois planos paralelos distintos e outro secante aos dois
c) Três planos paralelos e distintos
d) Três planos coincidentes
e) Três planos secantes dois a dois
27. ( PAES – 2006 )
1
1
2
 1
 5x5y5z 5

 1
1
1
2
x y z

3
3
3
3

2
2
4
 2
 7x 7y 7z 7

Quanto ao número de soluções do sistema de equações
lineares apresentado acima, é CORRETO afirmar que
A) esse sistema tem infinitas soluções.
B) esse sistema não tem solução.
C) esse sistema tem uma única solução.
D) esse sistema tem apenas duas soluções.
28.( PAES – 2011 ) Para o sistema linear
2x  3y  9
, a

6y  4x  9
solução geométrica é:
A)
0x  y  0z  0

0x  0y  z  0
 0x  y  z  0

pode ser interpretado, geometricamente, como sendo:
A) Um ponto
B) Um plano
C) Uma reta
D) Uma reta e um plano paralelos
30. O sistema linear abaixo
2x  3y  2z  2

3x  2y  4z  2
 4x  y  6z  3

Pode ser representado geometricamente como:
a) Três planos paralelos e distintos
b) Três planos coincidentes
c) Dois planos paralelos distintos e outro secante aos
dois
d) Três planos secantes dois a dois
e) Três planos que se interceptam em um único ponto
31.( PAES ) Ao escalonar o sistema linear
chegou-se a
.
Então, È CORRETO afirmar que os três planos dados pelas
equações do sistema inicial
A) têm apenas uma reta em comum.
B) têm apenas um ponto em comum.
C) são paralelos.
D) têm interseção vazia, porque dois deles são paralelos.
 x yz 1
32.( PAES ) O sistema linear 
2x  2y  2z  4

yz 0

pode ser representado, geometricamente, por
A)
B)
C)
D)
B)
C)
D)
29.( PAES ) O conjunto-solução do sistema de equações lineares
33. (UFJF) Um nutricionista está preparando uma
refeição com 2 alimentos A e B. Cada grama do
alimento A contém 2 unidades de proteína, 3 unidades
de carboidrato e 2 unidades de gordura. Cada grama
do alimento B contém 4 unidades de proteína, 4
unidades de carboidrato e 3 unidades de gordura. Essa
refeição deverá fornecer exatamente 400 unidades de
proteína e 500 unidades de carboidrato. A quantidade
de gordura que essa refeição irá fornecer é:
169
A) 300 unidades.
B) 350 unidades.
C) 400 unidades.
D) 450 unidades.
E) 500 unidades.
34. (UFJF) Uma lanchonete vende cada copo de suco de
laranja por R$ 1,50, obtendo um lucro de 50% sobre o
custo do suco. Devido a uma queda na safra, o preço da
laranja subiu, o que acarretou um aumento de 20% no
custo do suco. O dono da lanchonete, para não diminuir as
vendas de suco de laranja, decidiu manter o preço de
cada copo de suco em R$ 1,50 e reduzir o tamanho do
copo de modo a conservar a margem de lucro de 50%
sobre o custo do suco. Originalmente, a capacidade do
copo era 300 ml. O novo copo deve ter capacidade de:
A) 150 ml.
B) 200 ml.
C) 250 ml.
D) 275 ml.
E) 280 ml.
35. (FIP-2012) Durante os três primeiros dias de exibição
do filme “Os Vingadores”, em determinada cidade, foram
vendidos 8000 bilhetes, e a arrecadação foi de R$
76.800,00. O preço do bilhete para adulto era de R$ 12,00
e, para criança, era de R$ 8,00.
A razão entre o número de crianças e o de adultos que
assistiram ao filme nesse período foi de:
A) 1/2
B) 3/4
C) 3/2
D) 1/4
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
D
10
A
A
C
C
A
D
C
D
D
C
C
A
{k  IR/ k ≠ 1/4}
C
A
C
C
D
E
E
B
B
C
C
D
A
D
B
C
A
E
36. (FIPMOC - 2015 ) Ao chegarem de um intercâmbio na
Espanha, três alunos brasileiros foram até uma casa de
câmbio e trocaram por reais as quantias que possuíam em
dólares, libras e euros. Os valores envolvidos na
transação de cada um estão expressos na tabela a seguir:
Com a troca, o aluno A arrecadou R$335,00; o aluno B,
R$715,00; e o aluno C, R$960,00.
No dia em que os alunos efetuaram a transação, o valor
de 1 dólar era:
A) R$3,00.
B) R$2,00.
C) R$3,50.
D) R$2,80.
E) R$2,50.
GABARITO
01. E
02. B
03. NULA ( 6,50 )
170
ANÁLISE COMBINATÓRIA
INTRODUÇÃO
número representa o número de possibilidades para
cada posição.
Desta forma, temos:
Acompanhe os seguintes problemas:
• De quantas maneiras distintas cinco pessoas podem ser
colocadas em fila indiana?
• De quantos modos diferentes pode ocorrer o resultado
do sorteio dos números da mega sena?
• De quantas formas distintas dez amigos podem ocupar 5
lugares de um automóvel se apenas três deles sabem
dirigir?
Problemas como esses são tratados pela Análise
Combinatória - parte da Matemática que consiste em
estudar técnicas de contagem.
PRINCÍPIO FUNDAMENTAL DA CONTAGEM.
Considere a seguinte situação.
Quatro pessoas participam de uma corrida. Quantos
resultados diferentes podem ter para 1º, 2º e 3º lugares?
Vamos considerar que os corredores são A, B, C e D.
Nessa corrida podemos ter qualquer um dos corredores
com chance de chegar em 1º lugar, após a chegada do
primeiro, qualquer um dos três restantes pode ser o
segundo e assim sucessivamente.
Podemos então esquematizar a situação utilizando um
gráfico conhecido como diagrama da árvore ou árvore
de possibilidades.
Esse processo é conhecido como princípio
multiplicativo ou princípio fundamental da
contagem.
Definição
Se um evento Eé composto pelas etapas E1, E2,
E3, ..., En. E cada etapa pode ocorrer de n1, n2, n3, ...,
nn modos, respectivamente, então esse evento pode
ocorrer de n1 . n2 . n3 . ... . nn maneiras distintas.
Exercícios resolvidos
1. Quantos números naturais de três algarismos
podem ser formados com os algarismos 1, 2, 3, 5 e 7.
Resolução:
5 . 5. 5 = 125 números.
2. De quantas maneiras diferentes oito pessoas podem
sentar-se em um carro de cinco lugares, se apenas
duas delas estão aptas para dirigir?
Resolução:
Sejam a, b, c, d e e os lugares do carro conforme
a figura a seguir:
Considere as etapas sucessivas:
Do diagrama podemos concluir que nessa corrida
podemos ter 24 resultados diferentes.
O mesmo problema poderia ter sido resolvido utilizando
a seguinte idéia:
Como são três posições no pódio a serem ocupadas,
podemos realizar o produto de três números, onde cada
1ª etapa: escolha da pessoa que senta no lugar a.
2ª etapa: escolha da pessoa que senta no lugar b.
3ª etapa: escolha da pessoa que senta no lugar c.
4ª etapa: escolha da pessoa que senta no lugar d.
5ª etapa: escolha da pessoa que senta no lugar e.
171
EXERCÍCIOS
Logo o total de possibilidades é:
2p . 7p . 6p . 5p . 4p = 1680 maneiras
As pessoas podem sentar-se de 1680 maneiras diferentes.
3. A diretoria de uma empresa deve ser formada a partir
dos dez membros de seu conselho. A diretória da empresa
deve ter um presidente, um vice-presidente, um secretário
e um tesoureiro, sendo que o presidente do conselho não
pode ser o presidente da empresa.
De quantos modos diferentes essa diretoria pode ser
formada?
Resolução:
Como a presidência apresenta uma restrição, devemos
começar o estudo dos números de possibilidades
justamente por esta etapa:
9p . 9p . 8p . 7p = 4536
4. Quantos números pares de quatro algarismos distintos,
existem no nosso sistema de numeração?
Resolução:
1º : números que terminam em zero
9p . 8p . 7p . 1p = 504 nºs pares terminados em zero
2º : números que terminam em 2, 4, 6 e 8.
8p . 8p . 7p . 4p = 1792
Assim o total de números que podem ser formados é:
504 + 1792 = 2296
01. ( UFES ) Um "Shopping Center" possui 4 portas de
entrada para o andar térreo, 5 escadas rolantes ligando
o térreo ao primeiro pavimento e 3 elevadores que
conduzem do primeiro para o segundo pavimento.
De quantas maneiras diferentes uma pessoa, partindo
de fora do "Shopping Center" pode atingir o segundo
pavimento usando os acessos mencionados?
A) 12
B) 17
C) 19
D) 23
E) 60
02. ( U.F. FLUMINENSES – RJ ) Uma moça vai desfilar
vestindo saia, blusa, bolsa e chapéu. O organizador
afirma que três modelos de saia, três de blusa, cinco
tipos de bolsa e um certo número de chapéus permitem
mais de duzentas possibilidades de diferentes escolhas
de traje. Assinale a alternativa que apresenta o número
mínimo de chapéus que torna verdadeira a afirmação
do organizador.
a) 189
b) 30
c) 11
d) 5
e) 4
03. ( Fatec – SP ) Para mostrar aos seus clientes
alguns dos produtos que vende, um comerciante
reservou um espaço em uma vitrine, para colocar
exatamente 3 latas de refrigerante, lado a lado. Se ele
vende 6 tipos diferentes de refrigerante, de quantas
maneiras distintas pode expô-los na vitrine?
a) 144
b) 132
c) 120
d) 72
e) 20
04. (ENEM) No Nordeste brasileiro, é comum
encontrarmos peças de artesanato constituídas por
garrafas preenchidas com areia de diferentes cores,
formando desenhos. Um artesão deseja fazer peças
com areia de cores cinza, azul, verde e amarela,
mantendo o mesmo desenho, mas variando as cores
da paisagem (casa, palmeira e fundo), conforme a
figura.
O fundo pode ser representado nas cores azul ou
cinza; a casa, nas cores azul, verde ou amarela; e a
palmeira, nas cores cinza ou verde. Se o fundo não
pode ter a mesma cor nem da casa nem da palmeira,
por uma questão de contraste, então o número de
variações que podem ser obtidas para a paisagem é
A) 6.
B) 7.
C) 8.
D) 9.
E) 10
172
05. (FUVEST) Quantos são os números inteiros positivos
de 5 algarismos que não têm algarismos adjacentes
iguais?
9
A) 5
B) 9 × 84
4
C) 9 × 8
5
D) 8
E) 95
06. (ENEM, 2007) Estima-se que haja no Acre 209
espécies de mamíferos, distribuídas conforme a tabela a
seguir:
a) 180
b) 200
c) 800
d) 1600
e) 1800
09. ( UFRJ ) Um construtor dispõe de quatro cores
(verde, amarelo, cinza e bege) para pintar cinco casas
dispostas lado a lado. Ele deseja que cada casa seja
pintada com apenas uma cor e que duas casas
consecutivas não possuam a mesma cor. Determine o
número de possibilidades diferentes de pintura.
10. ( Mack – SP ) Os números pares com 4 algarismos
distintos, que podemos obter com os elementos do
conjunto {0; 3; 4; 5; 6; 7; 8}, são em número de:
a) 63
b) 420
c) 5.62
d) 5.43
e) 380
Deseja-se realizar um estudo comparativo entre três
dessas espécies de mamíferos – uma do grupo cetáceos,
outra do grupo primatas e a terceira do grupo roedores.
O número de conjuntos distintos que podem ser formados
com essas espécies para esse estudo é igual a:
a) 1.320
b) 2.090
c) 5.845
d) 6.600
e) 7.245
07. (UNIMONTES) Numa reunião estão 10 pessoas, entre
elas José e Marta. Quantas diretorias com presidente,
vice-presidente, secretário e tesoureiro podem ser
escolhidas entre as 10 pessoas, sem que nem José e
Marta ocupem algum cargo:
a) 210
b) 1680
c) 70
d) 5040
08. (UNEB 2003) Um empresário, visando proteger o
sistema de segurança de sua firma, deseja criar senhas
constituídas de seqüências de quatro dígitos distintos,
sendo os dois primeiros vogais e os dois últimos
algarismos.
O número de senhas distintas, do tipo descrito, que podem
ser formadas é igual a
11. ( FGV ) Uma pessoa vai retirar dinheiro de um caixa
eletrônico de um banco mas, na hora de digitar a
senha, esquece o número. Lembra que o número tem 5
algarismos, começa com 6, não tem algarismos
repetidos e tem o algarismo 7 em alguma posição. O
número máximo de tentativas para acertar a senha é:
a) 1680
b) 1344
c) 720
d) 224
e) 136
12. (UNIMONTES-PAES) “Um número natural é
divisível por 2, quando a ordem das unidades for par”.
Usando-se este critério de divisibilidade e os
algarismos 1, 2, 3, 4, 5 e 6, quantos números naturais
de 4 algarismos distintos e divisíveis por 2 podem ser
formados?
a) 18
b) 180
c) 648
d) 375
13. (UNIMONTES) O número de inteiros positivos,
pares, que se escrevem com três algarismos distintos
é:
a) 320
b) 360
c) 328
d) 405
14. (UnB) Uma pessoa joga simultaneamente 3 dados
de cores diferentes. As cores dos dados são amarela,
vermelha e branca. Calcule o número de casos
173
possíveis em que o dado vermelho apresenta o mesmo
resultado que o branco.
15. (Diamantina 2003) Considere a seguinte situação:
Cinco meninos e cinco meninas terão aula de
computação em um mesmo laboratório de informática,
onde existem apenas cinco computadores.
Em frente de cada computador, há um banco de dois
lugares.
O professor exige que, em cada banco, haja um menino
e uma menina.
Considerando os dados acima, é CORRETO afirmar que a
quantidade total de modos diferentes de atender à
exigência do professor é igual a
a) 480.600
b) 350.400
c) 460.800
d) 340.500
16. (UFMG) Observe o diagrama.
R
X
Y
Z
S
O número de ligações distintas entre X e Z é :
a) 39
b) 35
c) 45
d) 41
17. (UNIMONTES) Considere E = {1, 2, 3} e F = {1, 2, 3,
4, 5}.
O número de funções injetoras de E em F é:
a) 15
b) 60
c) 20
d) 125
18. ( FUVEST – SP ) A escrita Braille para cegos é um
sistema de símbolos onde cada caractere é formado por
uma matriz de 6 pontos dos quais pelo menos um se
destaca em relação aos outros. Como no exemplo abaixo.
Qual o número máximo de caracteres distintos que podem
ser representados neste sistema de escrita?
a) 63
b) 89
c) 26
d) 720
e) 36
19. (UEL) Um número capicua é um número que se pode
ler indistintamente em ambos os sentidos, da esquerda
para a direita ou da direita para a esquerda (exemplo:
5335). Em um hotel de uma cidade, onde os jogadores
de um time se hospedaram, o número de quartos era
igual ao número de capicuas pares de 3 algarismos.
Quantos eram os quartos do hotel?
20. (UNIMONTES) Em um teste de 10 questões de
múltipla escolha, cada questão apresenta 5
alternativas. Sendo assim, é correto afirmar que a
quantidade total de possíveis gabaritos e a quantidade
de gabaritos nos quais a alternativa A aparece
exatamente uma vez são, respectivamente,
21. (UFSJ) O código Morse, inventado por Samuel
Morse em 1834, usa dois símbolos, ponto e traço, para
representar letras e sinais de pontuação da linguagem
escrita, combinando, para tal efeito, de um a quarto
desses símbolos. Considerando-se essa informação, é
CORRETO afirmar que o número total de letras e sinais
de pontuação possíveis representados dessa forma
pelo código Morse é igual a
A) 30
B) 24
C) 28
D) 36
22. (PUC-MG) Em certo município, um pedestre foi
atropelado por um carro cujo motorista fugiu sem
prestar socorro à vítima. Uma testemunha anotou e
forneceu à polícia a placa do veículo (que era desse
município),
, faltando a segunda letra
e o penúltimo algarismo. Nesse município, as placas
dos automóveis são identificadas por três letras
distintas do conjunto M = {A, B, C, D, E, F, G, H} e
quatro algarismos distintos. O número de possíveis
veículos envolvidos nesse atropelamento é:
A) 28
B) 36
C) 42
D) 54
23. (UFOP) Um trem de passageiros é constituído por
uma locomotiva e cinco vagões distintos, sendo um
deles, utilizado como restaurante. Sabe-se que a
locomotiva deve ir à frente e o vagão restaurante não
pode ser colocado imediatamente após a locomotiva. O
número de modos diferentes de montar-se o trem é:
a) 5
b) 24
c) 96
d) 120
174
24. ( PUC – MG ) Considerando todos os elementos do
conjunto A = { 0, 1, 2, 4, 5, 6, 7, 9 }, Quantos números
inteiros de cinco algarismos distintos, maiores que 64000,
podem ser formados ?
a) 1980
b) 2100
c) 2160
d) 2200
e) 2240
25. ( UNIRIO ) Nos anos de 1987 e 1988, discutiu-se na
Assembléia Nacional Constituinte a criação de um novo
estado na Região Sudeste. Resultante da divisão do
Estado de Minas Gerais, este receberia o nome de Estado
do Triângulo e o novo mapa da região Sudeste seria como
na figura a seguir:
FATORIAL DE UM NÚMERO
Chamamos de n! (lê-se: “fatorial de n ou n fatorial”),
com
, ao produto dos n primeiros
números naturais positivos.
Exemplo
2! = 2.1 = 2;
3! = 3.2.1 = 6;
4! = 4.3.2.1 = 24;
5! = 5.4.3.2.1 = 120.
......................
Generalizando, temos:
n! = n.(n – 1).(n – 2) . . . 3. 2. 1
Como conseqüência da definição de fatorial de um
número, temos que:

1! = 1

0! = 1
Exercícios Resolvidos
Suponha que um cartógrafo pretenda colorir o novo mapa
da região Sudeste, de acordo com as seguintes regras:
(i) Cada Estado será colorido com uma cor.
(ii) Estados com fronteira comum não podem ter a mesma
cor.
De quantos modos distintos este mapa pode ser colorido,
usando, no máximo, 5 cores ?
GABARITO
1) E
2) D
3) C
4) B
5) E
6) A
7) B
8) E
9) 324
10) B
11) B
12) B
13) C
14) 36
15) C
16) D
17) B
18) A
19) 40
20) A
21) A
22) C
23) C
24) C
25) 642
3. Em quantos zeros termina o número 20!
Veja que destacamos os múltiplos de 5, pois são
eles que produzem os zeros finais de um número.
Portanto 20! termina em quatro zeros.
175
EXERCÍCIOS
01. ( UNIMONTES )
VERDADEIRA.
1
1
1


a)
3
3 ! 3 !
b) 4! . 5! = 20!
05)
Assinale a única alternativa
16 !
 16.15.14.13
13 !
d) ( 7! ) + ( 3! ) = 10!
c)
02. ( PUC – SP ) Se ( n - 6 )! = 720, então n é igual a:
a) 12
b) 576
c) 16
d) 4
e) 30
(n  1)!  n!
(n  1)!  n!
07.(CESPE/UNB) Para aumentar a segurança no
interior do prédio do TSE, foram distribuídas senhas
secretas para todos os funcionários, que deverão ser
digitadas na portaria para se obter acesso ao prédio.
As senhas são compostas por uma seqüência de três
letras (retiradas do alfabeto com 26 letras), seguida de
uma seqüência de três algarismos (escolhidos entre 0 e
9). O número de senhas distintas que podem ser
formadas sem que seja admitida a repetição de letras,
mas admitindo-se a repetição de algarismos, é igual a
GABARITO
01.
02.
03.
04.
05.
06.
07.
03. ( UFRN ) Se ( x + 1 )! = 3( x )!, então x é igual a:
a) 1
b) 2
c) 3
d) 4
e) 5
04. ( UFRS ) A expressão
3
A
A
B
E
D
05
D
, com n inteiro
estritamente positivo, vale:
2
a) n  n
1 n
b)
c)
n2  n
1 n
n
1 n
2
d) n  n  1
2
n
e)
n2
05. (UFRJ) O produto 20.18.16.14.......6.4.2 é equivalente
a:
A) 20! / 2
B) 2.10!
C) 20! / 2¹º
D) 2¹º.10!
E) 20! / 10!
06. (UESC-07) O valor
x  2!. 2x  2!  40 , é:
2x  1!. x  1 x !
01)
6
02)
5
03)
4
04)
2
de
x

N,
tal
que
176
TIPOS DE AGRUPAMENTOS
Quando formamos grupos com elementos de um
conjunto, chamamos esses grupos de agrupamentos.
Podemos dividir os agrupamentos em ordenados e
não ordenados.
ARRANJO SIMPLES
Chamamos de arranjo de n elementos tomados p a
p, a qualquer agrupamento ordenado dos p elementos
distintos escolhidos dos n elementos existentes.
Para calcularmos o arranjo de n tomados p a p,
temos:
Ordenados: eles diferem pela ordem em que os
elementos são tomados.
Exemplo: Com os elementos 1, 2, 3, 5 e 7 forma-se
números de 3 algarismos.
237 ≠ 273
Não ordenados: eles não diferem pela ordem em que são
tomados e sim pela quantidade de elementos.
Exemplo: Com as pessoas A, B, C e D, forma comissões
de 3 pessoas.
ABC=BAC
Atenção!!!
Com os mesmos elementos podemos formam
agrupamentos ordenados e não ordenados.
Exercício resolvido
1. Ao se cadastrar em um portal eletrônico de compras,
o usuário deve criar uma senha formada por duas
letras distintas (entre as 26 do alfabeto) seguidas por
dois algarismos distintos. Quantas senhas podem ser
criadas nessas condições?
Resolução:
A senha BG 18 é diferente da senha GB 81, isto é,
importa a ordem em que as letras e os algarismos são
escolhidos.
Trata-se, portanto, de um arranjo.
Exemplos
1. Com os números 1, 2, 3, 5 e 7 podemos:


Formar produto de 3 fatores 1.2.3 = 3.1.2(não
ordenado)
Formar número de 3 algarismos 123 ≠
213(ordenado)
AGRUPAMENTOS SIMPLES
São agrupamentos em que um mesmo elemento não
pode repetir.
Exemplo: Com os algarismos 1, 2, 3, 5, 7 e 8 formam-se
números de 4 algarismos distintos.
1358 → sem repetição
1835 → sem repetição
AGRUPAMENTOS COMPLETOS
São agrupamentos em que um mesmo elemento pode
ou não ser repetido.
Exemplo: Com os algarismos 1, 2, 5, 6 e 7 formam-se
números de 3 algarismos.
125 → sem repetição
Logo, pelo PFC, há ao todo 650 x 90 = 58.500 senhas.
Considere agora outro problema:
De quantos modos distintos Bráulio pode escolher
quatro entre as nove camisetas regata que possui para
levar em uma viagem para Muquén.
Suponha que Bráulio escolha as camisas a, b,c e d.
Veja que
{a, b, c e d} = {a, c, d, b},
pois não importa em que ordem Bráulio escolhe as
camisas que vai levar, o que importa é que as camisas
escolhidas são as mesmas na primeira e na segunda
situação.
Problemas como esse são resolvidos com a idéia de
Combinação e não podem ser resolvidos usando
arranjo.
155 → com repetição
177
EXERCÍCIOS
01. (OSEC-SP) Uma faculdade mantém 8 cursos
diferentes. No vestibular, os candidatos podem fazer
opção por 3 cursos, determinando-os por ordem de
preferência. Então, o número de possível de formas de
optar é:
a) 6.720
b) 336
c) 520
d) 120
e) 56
02. (UNIMONTES) Numa reunião estão 10 pessoas, entre
elas José e Marta. Quantas diretorias com presidente,
vice-presidente, secretário e tesoureiro podem ser
escolhidas entre as 10 pessoas, sem que nem José e
Marta ocupem algum cargo:
a) 210
b) 1680
c) 70
d) 5040
03. ( UNESP /Adaptada ) O conselho administrativo de
um sindicato é constituído por dez pessoas, das quais
uma é o presidente deste conselho. A diretoria do
sindicato tem quatro cargos a serem preenchidos por
membros do conselho, sendo que o presidente do
conselho não deve assumir nenhum desses cargos. Se os
cargos são de DIRETOR, VICE-DIRETOR, SECRETÁRIO
e TESOUREIRO de quantas maneiras diferentes esta
diretoria poderá ser formada?
a) 5040
b) 3024
c) 2780.
d) 2560
e) 2330
04. ( UNIOESTE ) Quatro amigos vão ao cinema e
escolhem, para sentar-se, uma fila em que há seis lugares
disponíveis. Sendo n o número de maneiras como
poderão sentar-se, encontre o valor de n/5 .
a) 144
b) 132
c) 120
d) 72
e) 20
07. ( PUC – MG ) Em um campeonato de dois turnos,
do qual participam dez equipes, que jogam entre si
uma vez a cada turno, o número total de jogos
previstos é igual a:
a) 45
b) 90
c) 105
d) 115
08. ( UFRN ) Em virtude de uma crise financeira, uma
fábrica dispõe de apenas quatro vigilantes para
ocuparem sete postos de vigilância.
Considerando que, em cada posto, fica, no máximo, um
vigilante e que o posto da entrada principal não pode
ficar desguarnecido, indique a opção correspondente
ao número de maneiras distintas de que o chefe de
segurança pode dispor para distribuir os vigilantes.
Obs.: Duas maneiras são ditas idênticas se, em ambas,
os vigilantes ocupam os mesmos postos e cada posto é
ocupado pelo mesmo vigilante; caso contrário, são
ditas distintas.
a) 35
b) 80
c) 480
d) 840
09. (CFTMG ) Em um campeonato de tênis de mesa,
com dez participantes, em que todos jogam contra
todos, sabe-se que um dos participantes vence todas
as partidas. As classificações possíveis para os três
primeiros colocados é
a) 72
b) 78
c) 82
d) 90
05. ( UFMG ) Duas das cinqüenta cadeiras de uma sala
serão ocupadas por dois alunos. O número de maneiras
distintas possíveis que esses alunos terão para escolher
duas das cinqüenta cadeiras, para ocupá-las, é
a) 1225
b) 2450
50
c) 2
d) 49!
e) 50!
10. ( MACK – SP ) Uma prova de atletismo é disputada
por 9 atletas, dos quais apenas 4 são brasileiros. Os
resultados possíveis para a prova, de modo que pelo
menos um brasileiro fique numa das três primeiras
colocações, são em número de:
a) 426
b) 444
c) 468
d) 480
e) 504
06. ( FATEC – SP ) Para mostrar aos seus clientes alguns
dos produtos que vende, um comerciante reservou um
espaço em uma vitrine, para colocar exatamente 3 latas
de refrigerante, lado a lado. Se ele vende 6 tipos
diferentes de refrigerante, de quantas maneiras distintas
pode expô-los na vitrine?
11. ( UERJ ) Ana dispunha de papéis com cores
diferentes. Para enfeitar sua loja, cortou fitas desses
papéis e embalou 30 caixinhas de modo a não usar a
mesma cor no papel e na fita, em nenhuma das 30
embalagens.
A menor quantidade de cores diferentes que ela
178
necessitou utilizar para a confecção de todas as
embalagens foi igual a:
a) 30
b) 18
c) 6
d) 3
12. ( PUC - MG ) O número inteiro positivo que verifica a
equação An,3 = 3.( n - 1 ) é
A) 1
B) 2
C) 3
D) 4
E) 5
ARRANJOS COMPLETOS
São agrupamentos ordenados contendo p
elementos distintos ou não de um conjunto A.
Exercício resolvido
Formar números de 2 algarismos com os números
1, 2, 3, 5 e 7.
2
A5, 2 = 5 = 25 OU
pelo PFC 5p . 5p = 25
GABARITO
1) B
2) B
3) B
4) 72
5) B
7) B
8) C
9) A
10) B
11) C
6) C
12) C
COMBINAÇÃO
Chamamos de combinação de
n elementos
tomados p a p, a qualquer agrupamento nãoordenado dos p elementos distintos escolhidos dos n
elementos existentes.
Para calcularmos a combinação de n tomados p a
p, temos:
EXEMPLOS
01. ( ENEM – 2009 ) Doze times se inscreveram em um
torneio de futebol amador. O jogo de abertura do
torneio foi escolhido da seguinte forma: primeiro foram
sorteados 4 times para compor o Grupo A. Em seguida,
entre os times do Grupo A, foram sorteados 2 times
para realizar o jogo de abertura do torneio, sendo que o
primeiro deles jogaria em seu próprio campo, e o
segundo seria o time visitante.
A quantidade total de escolhas possíveis para o Grupo
A e a quantidade total de escolhas dos times do jogo
de abertura podem ser calculadas através de:
a) Uma combinação e um arranjo, respectivamente.
b) Um arranjo e uma combinação, respectivamente.
c) Um arranjo e uma permutação, respectivamente.
d) Duas combinações.
e) Dois arranjos.
02. De quantos modos distintos Bráulio pode escolher
quatro entre as nove camisetas regata que possui para
levar em uma viagem para Muquén.
Suponha que Bráulio escolha as camisas a, b, c e
d.
Veja que: {a, b, c e d} = {a, c, d, b},
pois não importa em que ordem Bráulio escolhe as
camisas que vai levar, o que importa é que as camisas
179
escolhidas são as mesmas na primeira e na segunda
situação.
Resolvendo o problema, temos:
Existem 126 maneiras diferentes para Bráulio escolher
4 camisetas das 9 que possui.
03. Num acampamento, o monitor deve montar uma
equipe com quatro jovens para improvisar uma ponte que
possibilite a travessia do riacho. Se há 8 rapazes e 6
moças, quantas equipes de dois rapazes e duas moças
podem ser formadas?
Resolução
b) 30 dias
c) 90 dias
d) 105 dias
e) 110 dias
02. ( UFF ) Niterói é uma excelente opção para quem
gosta de fazer turismo ecológico. Segundo dados da
prefeitura, a cidade possui oito pontos turísticos dessa
natureza. Um certo hotel da região oferece de brinde a
cada hóspede a possibilidade de escolher três dos oito
pontos turísticos ecológicos para visitar durante sua
estada. O número de modos diferentes com que um
hóspede pode escolher, aleatoriamente, três destes
locais, independentemente da ordem escolhida, é:
A) 8
B) 24
C) 56
D) 112
E) 336
03. ( Unimontes ) Se sobre uma circunferência se
marcam
8 pontos distintos, então o número de
quadriláteros convexos que podem ser formados com
vértices nesses pontos é :
a) 80
b) 70
c) 35
d) 45
Pelo PFC, a equipe poderá ser formada de 28 x 15 = 420
maneiras distintas.
ENEM – 2009) Doze times se inscreveram em um torneio
de futebol amador. O jogo de abertura do torneio foi
escolhido da seguinte forma: primeiro foram sorteados 4
times para compor o Grupo A. Em seguida, entre os times
do Grupo A, foram sorteados 2 times para realizar o jogo
de abertura do torneio, sendo que o primeiro deles jogaria
em seu próprio campo, e o segundo seria o time visitante.
A quantidade total de escolhas possíveis para o Grupo A e
a quantidade total de escolhas dos times do jogo de
abertura
podem
ser
calculadas
através
de
A) uma combinação e um arranjo, respectivamente. **
B) um arranjo e uma combinação, respectivamente.
C) um arranjo e uma permutação, respectivamente.
D) duas combinações.
E) dois arranjos.
EXERCÍCIOS
01. (UFRRJ) Caroline vai todos os dias à sorveteria para
saborear um “sorvetão” (um sorvete formado por duas
bolas de sabores diferentes). Sabe-se que há um total de
15 tipos de sabores diferentes de sorvetes na sorveteria.
Se Caroline saborear apenas 1 “sorvetão” por dia, e se
considerarmos que a ordem das bolas não importa, ela
terá experimentado todos os possíveis “sorvetões” em :
a) 15 dias
04 .( PUC – MG ) Um técnico de futebol de salão tem à
disposição 8 jogadores de linha e 2 goleiros. Um time
deve ter quatro jogadores de linha e um goleiro. O
número de times distintos que o técnico pode
escalar é :
a) 60
b) 70
c) 80
d) 140
05. (UnB) Cada pedra de “um jogo de dominó” é
constituída por dois números.
É o mesmo que
Quantas peças diferentes podem ser formadas usando
os números 0, 1, 2, 3, 4, 5, 6, 7 e 8?
06. ( Mack – SP ) Num grupo de 10 pessoas temos
somente 2 homens. O número de comissões de 5
pessoas que podemos formar com 1 homem e 4
mulheres é:
a) 70.
b) 84.
c) 140
d) 210.
e) 252.
180
07. ( ENEM – 2010 ) Considere que um professor de
arqueologia tenha obtido recursos para visitar 5 museus,
sendo 3 deles no Brasil e 2 fora do país. Ele decidiu
restringir sua escolha aos museus nacionais e
internacionais relacionados na tabela a seguir.
B) 30.
C) 24.
D) 120.
E) 360.
12. (FIP-MOC) Considere a figura abaixo
De acordo com os recursos obtidos, de quantas maneiras
diferentes esse professor pode escolher os 5 museus para
visitar?
a) 6
b) 8
c) 20
d) 24
e) 36
08. ( Fesp ) Um vendedor de livros tem oito livros de
assuntos distintos para distribuir a três professores A, B
e C. De quantos modos ele poderá fazer a distribuição,
dando três livros ao professor A, quatro livros ao
professor B e um livro ao professor C ?
09. ( UNESP ) Nove times de futebol vão ser divididos em
3 chaves, todas com o mesmo número de times, para a
disputa da primeira fase de um torneio. Cada uma das
chaves já tem um cabeça de chave definido. Nessas
condições, o número de maneiras possíveis e diferentes
de se completarem as chaves é:
a) 21.
b) 30.
c) 60.
d) 90.
e) 120.
10. (UFV) Um farmacêutico dispõe de 4 tipos de
vitaminas e 3 tipos de sais minerais e deseja combinar 3
desses nutrientes para obter um composto químico. O
número de compostos que poderão ser preparados
usando-se, no máximo, 2 tipos de sais minerais é:
A) 32
B) 28
C) 34
D) 26
E) 30
11. (Esaf-MPU) Paulo possui três quadros de Gotuzo e
três de Portinari e quer expô-los em uma mesma parede,
lado a lado. Todos os seis quadros são assinados e
datados. Para Paulo, os quadros podem ser dispostos em
qualquer ordem, desde que os de Gotuzo apareçam
ordenados entre si em ordem cronológica, da esquerda
para a direita. O número de diferentes maneiras que os
seis quadros podem ser expostos é igual a
A) 20.
A sequência de pontos forma a letra A de nosso
alfabeto. Existem n triângulos distintos com vértices
nos pontos dessa figura. Qual é o valor de n?
A) 286
B) 5
C) 242
D) 728
13. ( UFMG ) Observe a figura abaixo. Nessa figura, o
número de triângulos que se obtém com vértices nos
pontos D, E, F, G, H, I, J é
a) 20
b) 21
c) 25
d) 31
e) 35
14 .( UEL ) São dados 12 pontos num plano, 3 a 3 não
colineares. O número de retas distintas determinadas
por esses pontos é
a) 66
b) 78
c) 83
d) 95
e) 131
15. (ILHÉUS / Adaptada) Sobre duas retas paralelas e
não coincidentes, r e s, são considerados cinco
pontos distintos em r e três pontos distintos em s.
Com base nessas informações, encontre:
a) O número de triângulos que podem ser formados,
tendo como vértices três desses 8 pontos.
b) O número de quadriláteros convexos que podem ser
formados, tendo como vértices quatro desses
8
pontos.
16. Um químico possui 10 tipos de substâncias. De
quantos modos possíveis poderá associar 6 dessas
substâncias se, entre as dez, duas somente não podem
ser misturadas porque produzem mistura explosiva?
181
17. ( UNESP ) O conselho administrativo de um sindicato
é constituído por doze pessoas, das quais uma é o
presidente deste conselho. A diretoria do sindicato tem
quatro cargos a serem preenchidos por membros do
conselho, sendo que o presidente da diretoria e do
conselho não devem ser a mesma pessoa. De quantas
maneiras diferentes esta diretoria poderá ser formada?
a) 40.
b) 7920.
c) 10890.
d) 11!.
e) 12!.
‘
18. (FIP) Os professores de Educação Física de uma
escola, animados com o sucesso da Copa do Mundo,
organizaram um torneio de futebol. Segundo o
regulamento do torneio, todas as equipes deveriam
enfrentar-se apenas uma vez, e a equipe com maior
número de vitórias seria a campeã. Se durante toda a
competição foram realizados 190 jogos, quantas equipes
participaram do torneio?
A) 40
B) 10
C) 20
D) 30
19. (UFV) Na primeira fase de um campeonato de futebol,
os times participantes são divididos em 8 grupos de n
times. Se, em cada grupo, todos os times se enfrentam
uma única vez, então o número de jogos realizados nesta
fase é:
A)n.(n – 1)
B) 8n.(n – 1)
C) 8n
D) 4n.(n – 1)
E) 4n
20. ( ITA – SP ) Dentre 4 moças e 5 rapazes deve-se
formar uma comissão de 5 pessoas com, pelo menos, 1
moça e 1 rapaz. De quantas formas distintas tal comissão
poderá ser formada?
21. ( UFSM ) A reforma agrária ainda é um ponto crucial
para se estabelecer uma melhor distribuição de renda no
Brasil. Uma comunidade de sem-terra, após se alojar
numa fazenda comprovadamente improdutiva, recebe
informação de que o INCRA irá receber uma comissão
para negociações. Em assembléia democrática, os semterra decidem que tal comissão será composta por um
presidente geral, um porta-voz que repassará as notícias à
comunidade e aos representantes e um agente que
cuidará da parte burocrática das negociações. Além
desses com cargos específicos, participarão dessa
comissão mais
6 conselheiros que auxiliarão
indistintamente em todas as fases da negociação.
Se, dentre toda a comunidade, apenas 15 pessoas forem
consideradas aptas aos cargos, o número de comissões
distintas que poderão ser formadas com essas
pessoas é obtido pelo produto
2
2
4
a) 13. 11. 7. 5 . 3 . 2
b) 13. 11. 7. 5. 3. 2
c) 13. 11. 72. 52. 33. 26
2
2
3
6
d) 13. 7 . 5 . 3 . 2
2
2
3
e) 13. 11. 7 . 5. 3 . 2
15
22. (UFMG) Um teste é composto por 15 afirmações.
Para cada uma delas, deve-se assinalar, na folha de
respostas, uma das letras V ou F, caso a afirmação
seja, respectivamente, verdadeira ou falsa. A fim de se
obter, pelo menos, 80% de acertos, o número de
maneiras diferentes de se marcar a folha de respostas
é
a) 455
b) 576
c) 560
d) 620
23. ( Fuvest ) O jogo da sena consiste no sorteio de 6
números distintos, escolhidos ao acaso, entre os
números 1, 2, 3, ..., até 50. Uma aposta consiste na
escolha (pelo apostador) de 6 números distintos entre
os 50 possíveis, sendo premiadas aquelas que
acertarem 4(quadra), 5(quina) ou todos os 6(sena)
números sorteados.
Um apostador, que dispõe de muito dinheiro para jogar,
escolhe 20 números e faz todos os 38760 jogos
possíveis de serem realizados com esses 20 números.
Realizado o sorteio, ele verifica que TODOS os 6
números sorteados estão entre os 20 que ele escolheu.
Além de uma aposta premiada com a sena.
a) Quantas apostas premiadas com a quina este
apostador conseguiu?
b) Quantas apostas premiadas com a quadra ele
conseguiu?
24. (UFPA) No cartão da mega-sena existe a opção de
aposta em que o apostador marca oito números inteiros
de 1 a 60. Suponha que o apostador conheça um
pouco de Análise Combinatória e que ele percebeu que
é mais vantajoso marcar um determinado número de
cartões, usando apenas os oito números, de modo que,
se os seis números sorteados estiverem entre os oito
números escolhidos, ele ganha, além da sena, algumas
quinas e algumas quadras. Supondo que cada aposta
seja feita usando apenas seis números, a quantidade
de cartões que o apostador deve apostar é
(A) 8
(B) 25
(C) 28
(D) 19
(E) 17
182
25. Para montar um time de basquete, um técnico tem à
sua disposição 12 atletas, sendo que, dentre eles, João e
Carlos são os mais habilidosos. Sabendo que um time de
basquete é formado por cinco atletas, de quantos modos
diferentes esse treinador poderá montar essa equipe
sendo que João e Carlos sempre deverão fazer parte do
time?
A) 196 modos
B) 168 modos
C) 144 modos
D) 120 modos
2) Uma fila indiana é formada por 7 pessoas. De
quantos modos diferentes essas 7 pessoas podem ser
organizadas nessa fila?
Queremos formar agrupamentos de 7 pessoas
utilizando apenas 7 pessoas, isto é, mudando essas 7
pessoas de lugar (permutando essas pessoas).
P7 = 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1
3) Com as letras da palavra ESTUDAR, encontre o
número de anagramas que podem ser formados, onde:
A) Comecem com a letra T e terminem com a letra D.
T ESUAR D
1p
1p
5!
GABARITO
1) D
2) C
3) B
7) D
8) 280
9) D
13) D
14) A
15) a) 45
b) 30
16) 140
18) C
19) D
20) 125
21) E
22) B
23) a) 84 b) 1365
4) D
5) 45 peças
10) C
24) C
11) D
6) C
12) C
 1 . 120 . 1 = 120
B) Comecem e terminem com vogais.
17) C
25) D
= 5040
V1 5 LETRAS V2
3p
2p
5!
 3 . 120 . 2 = 720
C) Tenham as letras TUD juntas e nessa ordem.
TUD E S A R
Permutações simples de n elementos distintos são os
agrupamentos formados com todos os n elementos e que
diferem uns dos outros pela ordem de seus elementos.
Com os elementos A, B, C são possíveis as seguintes
permutações: ABC, ACB, BAC, BCA, CAB e CBA.
O número total de permutações simples de n
elementos distintos é dado por n!, isto é:
 5! = 120
5!
PERMUTAÇÃO
D) Tenham as letras TUD juntas.
TUD E S A R
 3! . 5! = 720
3!
5!
E) Tenham as vogais em ordem alfabética.
AEU S T D R
.
Exercícios resolvidos
1) Quantos números de 5 algarismos distintos podem ser
formados, usando-se os algarismos 1, 3, 5, 7 e 8?
Queremos formar números (agrupamentos) de 5
algarismos com os 5 algarismos dados (1, 3, 5, 7 e 8).
Podem ser formados 120 números.
Para isso fazemos:
(total de letras)!
(letras em ordem)!
As vogais podem ficar juntas ou
separadas, no começo ou no fim. Mas
devem ficar em ordem alfabética.

(7)! 7 . 6 . 5 . 4 . 3!

 840
(3)!
3!
03.(UNIMONTES ) Uma professora pediu para seus
alunos permutarem, de todas as formas possíveis, os
algarismos 1, 2, 4, 6 e 7. A seguir, pediu que os
números assim formados fossem dispostos em uma
lista, em ordem crescente. Nessa lista, o número 46721
deverá figurar em
A) 67.° lugar.
B) 63.° lugar.
C) 66.° lugar. *****
D) 65.° lugar.
183
PERMUTAÇÕES CIRCULARES
Vamos analisar o número de modos em que podemos
dispor n elementos distintos em torno de um círculo.
Cada uma dessas disposições possíveis é uma
permutação circular dos n elementos, e indicamos o total
desses agrupamentos por Pn.
Para melhor entendermos o cálculo, vamos imaginar,
como exemplo, que quatro pessoas A, B, C e D vão
sentar-se em volta de uma mesa redonda, e, neste caso, o
número de modos de dispor essas pessoas é indicado por
P4. Inicialmente vamos analisar o que diferencia as
possíveis
disposições.
Assim,
consideramos
as
disposições:
Esta observação nos leva a concluir que:
De modo análogo, concluímos que, a cada
permutação circular de n elementos, correspondem n
permutações simples. Então:
EXERCÍCIO RESOLVIDO
Podemos perceber que as disposições são diferentes,
embora A e C estejam frente a frente, nas duas
disposições, o mesmo acontece com B e D. No entanto,
em uma disposição D, está à esquerda de A e, na outra, à
direita. O que diferencia uma permutação circular de outra
é a mudança na posição relativa dos elementos.
Então, quando partimos de uma disposição possível e
fazemos os elementos girarem em conjunto ao redor do
círculo, sem alterar a posição relativa de qualquer dos
elementos, todas as disposições obtidas representarão a
mesma permutação circular.
01. Uma família é composta por seis pessoas: o pai, a
mãe e quatro filhos. Em um restaurante, essa família
ocupa uma mesa redonda. Encontre:
a) O número de modos diferentes que essa família
poderá sentar-se em torno dessa mesa
P6'  ( 6 – 1 )!
P6'  5!
P6'  5 x 4 x 3 x 2 x 1 = 120 modos
b) O número de modos diferentes que essa família
poderá sentar-se em torno dessa mesa, de modo que o
pai e a mãe fiquem juntos.
M
F4
Como o pai e a mãe devem ficar
juntos, eles serão considerados
como uma única pessoa.
P
F1
MESA
F3
F2
P5'  ( 5 – 1 )! =4! =24
Mas, como o pai e a mãe podem
permutar-se entre si, teremos 2!.
Logo a solução será:
24 x 2!
24 x 2 = 48 modos
Assim 4 permutações simples constituem uma única
permutação circular:
PERMUTAÇÃO COM ELEMENTOS REPETIDOS
Se entre os n elementos de um conjunto, existem a
elementos repetidos, b elementos repetidos, c
elementos repetidos e assim sucessivamente, o
184
número total de permutações que podemos formar é dado
por:
a!.b!.c!....!
Pn

n!
a!.b!.c!. ... !
Exercícios resolvidos
1) Quantos anagramas tem a palavra NATÁLIA?
A palavra NATÁLIA tem 7 letras, sendo que 3 são
iguais a A, portanto,
840 anagramas
2) Determine o número de anagramas da palavra
MATEMÁTICA.
Temos 10 elementos, com repetição. Observe que a
letra M está repetida duas vezes, a letra A três, a letra T,
duas vezes.
Na fórmula anterior, teremos: n=10, A=3, T=2 e M=2
.
151200 anagramas.
3. O diagrama seguinte representa caminhos em um
labirinto. Quantos percursos diferentes pode fazer o
ratinho para chegar ao queijo andando só para cima ou
para a direita?
Nos percursos apresentados, e em qualquer outro, o
rato sobe (s) 6 vezes e anda 4 vezes para a direita (d).
Reciprocamente, qualquer seqüência de 6 s e 4d
representa um percurso.
Assim, o número de percursos é o número de
permutações de s s s s s s d d d d, ou seja:
Podemos, também, raciocinar da seguinte forma: o
ratinho deve dar 10 “passos”, sendo 6 para cima (s) e 4
para a direita (d).
Vamos escolher, de todas as formas possíveis, os
“passos” que ele dará para cima; consequentemente,
os 4 restantes serão para a direita:
Escolha dos passos para cima: C10, 6 = 210
Escolha dos passos para a direita: C4, 4 = 1
C10, 6 x C10, 6 = 210 x 1 = 210
Observação:
Existem alguns tipos de questões (comuns em
concursos militares e não em vestibulares) que
desejam determinar o número de soluções inteiras e
não negativas de uma equação linear, muitos pensam
que a sua resolução será através dê sistemas lineares.
A resolução de questões desse tipo será através da
análise combinatória como veremos no final de
sistemas lineares desta apostila.
EXERCÍCIOS
01. (FUVEST SP) O número de anagramas da palavra
FUVEST que começam e terminam por vogal é:
a) 24
b) 96
c) 144
d) 120
e) 48
Resolução
Considere alguns percursos possíveis para chegarmos
ao total deles:
02. (Unimontes) O número de anagramas da palavra
UNIMONTES, nos quais as letras I, M e O aparecem
sempre juntas, nessa ordem, é:
a) 5040
b) 5400
c) 2520
d) 25200
03. ( CEFET – MG ) Seis pessoas, entre elas Paulo e
Matheus, vão ao teatro. Existem seis lugares vagos,
alinhados e consecutivos. Encontre o número de
maneiras distintas de como as seis pessoas podem se
sentar, onde:
a) Paulo e Matheus fiquem juntos
b) Paulo e Matheus fiquem separados
185
04. (UFMG) Para montar a programação de uma emissora
de rádio, o programador musical conta com 10 músicas
distintas, de diferentes estilos, assim agrupadas: 4 de
MPB, 3 de Rock e 3 de Pop. Sem tempo para fazer essa
programação, ele decide que, em cada um dos programas
da emissora, serão tocadas, de forma aleatória, todas as
10 músicas. Assim sendo, é CORRETO afirmar que o
número de programas distintos em que as músicas vão
ser tocadas agrupadas por estilo é dado por
a) 4! . 3! . 3! . 3!
b) 10! / 7!
c) 4! . 3! . 3!
d) 10! / (7! . 3! )
05. (Milton Campos) O número de anagramas que
podemos formar, permutando-se as letras da palavra
MILTON iniciados por M e terminados por O é igual a :
a) P6- 2
b) P4
c) P6 – P2
d) P22, 6
06. ( UNA ) O número de anagramas da palavra MACACA
é igual ao dobro da idade de BRUNO. Podemos afirmar
então que Bruno tem:
a) 20 anos
b) 30 anos
c) 35 anos
d) 40 anos
07. (UNIMONTES) Considerando M1 o número de
anagramas da palavra COTEC que terminam com T e M2
o número de anagramas da palavra PAES, é possível
afirmar que M1 x M2 vale ?
08. ( Unb – DF ) Em um tabuleiro quadrado, de 5 x 5,
mostrado na figura I, deseja-se ir do quadrado esquerdo
superior (ES) ao quadrado direito inferior (DI). Somente
são permitidos os movimentos horizontal (H), vertical (V) e
diagonal (D), conforme ilustrado na figura II.
Com base nessa situação e com o auxílio dos princípios
de análise combinatória, julgue os itens que se seguem.
( ) Se forem utilizados somente movimentos horizontais e
verticais, então o número de percursos possíveis será
igual a 70.
( ) Se forem utilizados movimentos horizontais e verticais
e apenas um movimento diagonal, o número de percursos
possíveis será igual a 140.
( ) Utilizando movimentos horizontais, verticais e três
movimentos diagonais, o número de percursos possíveis é
igual a 10.
09. ( Ufrs ) No desenho a seguir, as linhas horizontais
e verticais representam ruas, e os quadrados
representam quarteirões. A quantidade de trajetos de
comprimento mínimo ligando A e B que passam por C
é
a) 12
b) 13
c) 15
d) 24
e) 30
10. ( Uff ) Três ingleses, quatro americanos e cinco
franceses serão dispostos em fila (dispostos em linha
reta) de modo que as pessoas de mesma
nacionalidade estejam sempre juntas. De quantas
maneiras distintas a fila poderá ser formada de modo
que o primeiro da fila seja um francês?
a) 34.560 maneiras
b) 30.240 maneiras
c) 28.720 maneiras
d) 26.430 maneiras
e) 24.210 maneiras
11. ( FGV – SP ) O número de permutações da palavra
ECONOMIA que não começam nem terminam com a
letra O é
a) 9.400.
b) 9.600.
c) 9.800.
d) 10.200.
e) 10.800
12. ( UFES ) De quantas maneiras 10 clientes de um
banco podem se posicionar na fila única dos caixas de
modo que as 4 mulheres do grupo fiquem juntas?
a) 4! × 7!
b) 5! × 6!
c) 6 × 6!
d) 10 × 6!
e) 4! + 10!
13. ( UFMG ) Num grupo constituído de 15 pessoas,
cinco vestem camisas amarelas, cinco vestem camisas
vermelhas e cinco vestem camisas verdes.
Deseja-se formar uma fila com essas pessoas de forma
que as três primeiras vistam camisas de cores
diferentes e que as seguintes mantenham a seqüência
de cores dada pelas três primeiras.
Nessa situação, de quantas maneiras distintas se pode
fazer tal fila?
a) 3.(5!)3
b) (5!)3
c) (5!)3 .(3!)
d) 15! /(3!.5!)
186
14. ( ITA – SP ) O número de anagramas da palavra
VESTIBULANDO, que não apresentam as cinco vogais
juntas, é:
a) 12!
b) (8!) (5!)
c) 12! – (8!) (5!)
d) 12! – 8!
e) 12! – (7!) (5!)
15. (ENEM - 2011) O setor de Recursos Humanos de uma
empresa vai realizar uma entrevista com 120 candidatos a
uma vaga de contador. Por sorteio, eles pretendem atribuir
a cada candidato um número, colocar a lista de números
em ordem numérica crescente e usá-la para convocar os
interessados. Acontece que, por um defeito do
computador, foram gerados números com 5 algarismos
distintos e em nenhum deles apareceram dígitos pares.
Em razão disso, a ordem de chamada do candidato que
tiver recebido o número 75.913 é
a) 24
b) 31
c) 32
d) 88
e) 89
16. (Esaf-MPU) Ana guarda suas blusas em uma única
gaveta em seu quarto. Nela encontram-se sete blusas
azuis, nove amarelas, uma preta, três verdes e três
vermelhas. Uma noite, no escuro, Ana abre a gaveta e
pega algumas blusas. O número mínimo de blusas que
Ana deve pegar para ter certeza de ter pegado ao menos
duas blusas da mesma cor é
A) 6.
B) 4.
C) 2.
D) 8.
E) 10.
17.(Fuvest) A partir de 64 cubos brancos, todos iguais,
forma-se um novo cubo. A seguir, este novo cubo tem
cinco de suas seis faces pintadas de vermelho. O número
de cubos menores que tiveram pelo menos duas de suas
faces pintadas de vermelho é
a) 24
b) 26
c) 28
d) 30
e) 32
18.(FIP-2010) Os professores de Educação Física de uma
escola, animados com o sucesso da Copa do Mundo,
organizaram um torneio de futebol. Segundo o
regulamento do torneio, todas as equipes deveriam
enfrentar-se apenas uma vez, e a equipe com maior
número de vitórias seria a campeã. Se durante toda a
competição foram realizados 190 jogos, quantas
equipes participaram do torneio?
A) 40
B) 10
C) 20
D) 30
19.(FIP-2011) A dengue é considerada, na atualidade,
um dos principais problemas de saúde pública de todo
o mundo. Ela é uma doença infecciosa febril aguda,
causada por um vírus da família Flaviridaee é
transmitida através do mosquito Aedes aegypti,
também infectado pelo vírus.
Pensando nesse grave problema, um professor das
FIP-Moc deseja realizar um trabalho sobre o combate à
dengue. A turma que fará a pesquisa é constituída por
20 alunos, sendo 15 homens e 5 mulheres. Antes de
iniciar as atividades, o professor solicitou a formação
de duplas, de modo que as mulheres não ficassem
juntas.
O número de maneiras diferentes de formar as duplas
na sala, atendendo à regra do professor, é igual a
A) 180.
B) 190.
C) 200.
D) 240.
20. (FIP-2012) Os anéis olímpicos são o emblema
dos Jogos Olímpicos. Eles são compostos de cinco
anéis entrelaçados, nas cores azul, amarelo, preto,
verde e vermelho.
Um artista plástico deseja construir um conjunto de
anéis olímpicos e pintá-los, seguindo as seguintes
regras:
• O anel central, e somente ele, deverá ser pintado de
preto;
• Os demais anéis poderão ser pintados com as
quatro cores restantes, podendo-se repetir a mesma
cor, desde que dois anéis que se entrelacem não sejam
pintados da mesma cor.
Assim, pode-se afirmar que o artista plástico poderá
pintar os anéis olímpicos de k maneiras distintas,
sendo k igual a:
A) 288
B) 72
C) 144
D) 256
21.(FIP-2013) 20 horas e 02 minutos de 20 de fevereiro
de 2002 foi um momento que entrou para a história.
Durante um minuto, houve uma formação numérica que
somente
ocorre
duas
vezes
por
milênio:
20h0220/02/2002
Esta é uma simetria que na matemática recebe o nome
de capicua(números inteiros que lidos da esquerda
para a direita ou da direita para a esquerda não se
alteram).
A próxima vez que ocorrerá outra capicua será às
21horas e 12 minutos de 21 de dezembro de 2112:
187
21h12 21/12/2112
Depois,nunca mais haverá outra capicua, pois em 30
de março de 3003 não ocorrerá essa coincidência
matemática, uma vez que não existe a hora 30.
Quantas capicuas é possível formar com cinco
algarismos?
A) 720
B) 900
C) 1200
D) 360
GABARITO
1) E
2) C
6) B
7) 288
3) a) 48
b) 480
8) V V F
4) A
5) B
9) E
10) A
11) E
16) A
17) A
12) A
13) C
14) C
15) E
18) C
19) A
20) C
21) B
QUESTÕES DO ENEM
01. (ENEM-2009) O xadrez é jogado por duas pessoas.
Um jogador joga com as peças brancas, o outro, com as
peças pretas. Neste jogo, vamos utilizar somente a Torre,
uma das peças do xadrez. Ela pode mover-se para
qualquer caso ao longo da coluna ou linha que ocupa,
para frente ou ara trás, conforme indicado na figura a
seguir.
movimentação no jogo, qual é o menor número de
movimentos possíveis e necessários para que a Torre
chegue à casa C1?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 7
02. (ENEM-2009) Uma pessoa decidiu depositar
moedas de 1, 5, 10, 25 e 50 centavos em um cifre
durante certo tempo. Todo dia da semana ela
depositava uma única moeda, sempre nesta ordem: 1,
5, 10, 25, 50, e, novamente, 1, 5, 10, 25, 50, assim
sucessivamente.
Se a primeira moeda foi depositada em uma segundafeira, então essa pessoa conseguiu a quantia exata de
R$95,05 após depositar a moeda de
(A) 1 centavo no 679º dia, que caiu numa segunda
feira.
(B) 5 centavos no 186º dia, que caiu numa quinta feira.
(C) 10 centavos no 188º dia, que caiu numa quinta
feira.
(D) 25 centavos no 524º dia, que caiu num sábado.
(E) 50 centavos no 535º dia, que caiu numa quinta
feira.
03. (ENEM-2010) João mora na cidade A e precisa
visitar cinco clientes, localizados em cidades diferentes
da sua. Cada trajeto possível pode ser representado
por uma sequência de 7 letras. Por exemplo, o trajeto
ABCDEFA, informa que ele sairá da cidade A, visitando
as cidades B, C, D, E e F nesta ordem, voltando para a
cidade A. Além disso, o número indicado entre as letras
informa o custo do deslocamento entre as cidades. a
figura mostra o custo de deslocamento entre cada uma
das cidades.
O jogo consiste em chegar a um determinado ponto sem
passar por cima dos pontos pretos já indicados.
Respeitando-se o movimento da peça Torre e as regras de
Como João quer economizar, ele precisa determinar
qual o trajeto de menor custo para visitar os cinco
clientes. Examinando a figura, percebe que precisa
considerar somente parte das sequências, pois os
trajetos ABCDEFA e AFEDCBA têm o mesmo custo.
188
Ele gasta 1min30s para examinar uma sequência e
descartar sua simétrica, conforme apresentado.
O tempo mínimo necessário para João verificar todas as
sequências possíveis no problema é de
A) 60 min.
B) 90 min.
C) 120 min.
D) 180 min.
E) 360 min.
04. (ENEM-2009) Doze times se inscreveram em um
torneio de futebol amador. O jogo de abertura do torneio
foi escolhido da seguinte forma: primeiro foram sorteados
4 times para compor o Grupo A. Em seguida, entre os
times do Grupo A, foram sorteados 2 times para realizar o
jogo de abertura do torneio, sendo que o primeiro deles
jogaria em seu próprio campo, e o segundo seria o time
visitante. A quantidade total de escolhas possíveis para o
Grupo A e a quantidade total de escolhas dos times do
jogo de abertura podem ser calculadas através de
A) uma combinação e um arranjo, respectivamente.
B) um arranjo e uma combinação, respectivamente.
C) um arranjo e uma permutação, respectivamente.
D) duas combinações.
E) dois arranjos.
05. (ENEM-2013) Um banco solicitou aos seus clientes a
criação de uma senha pessoal de seis dígitos, formada
somente por algarismos de 0 a 9, para acesso à conta
corrente pela internet.
Entretanto, um especialista em sistemas de segurança
eletrônica recomendou à direção do banco recadastrar
seus usuários, solicitando, para cada um deles, a criação
de uma nova senha com seis dígitos, permitindo agora o
uso das 26 letras do alfabeto, além dos algarismos de 0 a
9. Nesse novo sistema, cada letra maiúscula era
considerada distinta de sua versão minúscula. Além disso,
era proibido o uso de outros tipos de caracteres.
Uma forma de avaliar uma alteração no sistema de senhas
é a verificação do coeficiente de melhora, que é a razão
do novo número de possibilidades de senhas em relação
ao antigo.
O coeficiente de melhora da alteração recomendada é
diferentes, nesse formato, o artesão poderá obter?
A) 6
B) 12
C) 18
D) 24
E) 36
07. (ENEM – 2014) Um cliente de uma videolocadora
tem o hábito de sempre alugar dois filmes por vez.
Quando os devolve, sempre pega outros dois filmes e
assim sucessivamente. Ele soube que a videolocadora
recebeu alguns lançamentos, sendo 8 filmes de ação, 5
de comédia e 3 de drama e, por isso, estabeleceu uma
estratégia para ver todos esses 16 lançamentos.
Inicialmente alugará, em cada vez, um filme de ação e
um de comédia. Quando se esgotarem as
possibilidades de comédia, o cliente alugará um filme
de ação e um de drama, até que todos os lançamentos
sejam visto e sem que nenhum filme seja repetido.
A) 20 x 8! + (3!)2
B) 8! x 5! x 3!
C)
D)
E)
8! x5! x3!
28
8! x5! x3!
22
16!
28
08. (ENEM – 2009 ) A população brasileira sabe, pelo
menos intuitivamente, que a probabilidade de acertar
as seis dezenas da mega sena não é zero, mas é
quase. Mesmo assim, milhões de pessoas são atraídas
por essa loteria, especialmente quando o prêmio se
acumula em valores altos. Até junho de 2009, cada
aposta de seis dezenas, pertencentes ao conjunto {01,
02, 03, ..., 59, 60}, custava R$ 1,50.
Disponível em: www.caixa.gov.br. Acesso em: 7 jul. 2009.
06. (ENEM-2013) Um artesão de joias tem à sua
disposição pedras brasileiras de três cores: vermelhas,
azuis e verdes. Ele pretende produzir joias constituídas
por uma liga metálica, a partir de um molde no formato de
um losango não quadrado com pedras nos seus vértices,
de modo que dois vértices consecutivos tenham sempre
pedras de cores diferentes.
A figura ilustra uma joia, produzida por esse artesão, cujos
vértices A, B, C e D correspondem às posições ocupadas
pelas pedras.
Com base nas informações fornecidas, quantas joias
Considere que uma pessoa decida apostar exatamente
R$ 126,00 e que esteja mais interessada em acertar
apenas cinco das seis dezenas da mega sena,
justamente pela dificuldade desta última. Nesse caso, é
melhor que essa pessoa faça 84 apostas de seis
dezenas diferentes, que não tenham cinco números em
comum, do que uma única aposta com nove dezenas,
porque a probabilidade de acertar a quina no segundo
caso em relação ao primeiro é, aproximadamente:
1
A) 1 vezes menor
2
1
B) 2 vezes menor
2
C) 4 vezes menor
D) 9 vezes menor
E) 14 vezes menor
189
09. (ENEM – 2011) O setor de recursos humanos de uma
empresa vai realizar uma entrevista com 120 candidatos a
uma vaga de contador. Por sorteio, eles pretendem atribuir
a cada candidato um número, colocar a lista de números
em ordem numérica crescente e usá-la para convocar os
interessados. Acontece que, por um defeito do
computador, foram gerados números com 5 algarismos
distintos e, em nenhum deles, apareceram dígitos pares.
Em razão disso, a ordem de chamada do candidato que
tiver recebido o número 75.913 é:
A) 24.
B) 31.
C) 32.
D) 88.
E) 89.
GABARITO
01. C
02. D
03. B
04. A
05. A
06. B
07. B
08. C
09. E
10. A
11. C
10. (ENEM – 2012) O diretor de uma escola convidou os
280 alunos de terceiro ano a participarem de uma
brincadeira. Suponha que existem 5 objetos e 6
personagens numa casa de 9 cômodos; um dos
personagens esconde um dos objetos em um dos
cômodos da casa. O objetivo da brincadeira é adivinhar
qual objeto foi escondido por qual personagem e em qual
cômodo da casa o objeto foi escondido. Todos os alunos
decidiram participar. A cada vez um aluno e sorteado e da
a sua resposta. As respostas devem ser sempre distintas
das anteriores, e um mesmo aluno não pode ser sorteado
mais de uma vez. Se a resposta do aluno estiver correta,
ele e declarado vencedor e a brincadeira e encerrada.
O diretor sabe que algum aluno acertara a resposta
porque há:
a) 10 alunos a mais do que possíveis respostas distintas.
b) 20 alunos a mais do que possíveis respostas distintas.
c) 119 alunos a mais do que possíveis respostas distintas.
d) 260 alunos a mais do que possíveis respostas distintas.
e) 270 alunos a mais do que possíveis respostas distintas.
11. (ENEM-2012) O designer português Miguel Neiva criou
um sistema de símbolos que permite que pessoas
daltônicas identifiquem cores. O sistema consiste na
utilização de símbolos que identificam as cores primarias
(azul, amarelo e vermelho), Além disso, a justaposição de
dois desses símbolos permite identificar cores secundarias
(como o verde, que é o amarelo combinado com o azul). O
preto e o branco são identificados por pequenos
quadrados: o que simboliza o preto é cheio, enquanto o
que simboliza o branco é vazio. Os símbolos que
representam preto e branco também podem ser
associados aos símbolos que identificam cores,
significando se estas são claras ou escuras.
Folha de São Paulo. Disponível em: www1.folha.uol.com.br.
Acesso em: 18 fev. 2012 (adaptado)
De acordo com o texto, quantas cores podem ser
representadas pelo sistema proposto?
a) 14
b) 18
c) 20
d) 21
e) 23
190
BINÔMIO DE NEWTON
NÚMERO BINOMIAL
O número de combinações de n elementos tomados p
a p, indicado antes por C(n, p) é chamado Coeficiente
Binomial ou número binomial, denotado na literatura
n
científica como   , onde n e p são números naturais e
p 
p  n.
n
n!
   C(n, p) 
p! (n  p)!
p 
Exercício resolvido:
1. Resolver a equação:
7
d)   =
4
Podemos observar que nos exemplos anteriores, os
5
5
números binomiais   e   são complementares,
2
3
e por isso possuem o mesmo valor.
7
O mesmo acontece com os números binomiais   e
3
7
  , pois3 + 4 = 7.
4
Os números binomiais abaixo não são complementares
7 7
   ≠   , pois 4 + 5 não é igual a 7
 4 5
9 9
   ≠   , pois 3 + 7 não é igual a 9
3 7
Temos alguns casos de números binomiais especiais:
n
   = 1, logo:
0
n
   = 1, logo:
n
NÚMEROS BINOMIAIS COMPLEMENTARES
7
  = 1;
0
7
  = 1;
7
 n 
 = n, logo:
 
 n  1
5
  = 1;
0
5
  = 1;
5
7
  = 7;
6
 13 
  = 1
0
 13 
  = 1
 13 
5
  = 5;
4
 13 
  = 13
 12 
IGUALDADE ENTRE NÚMEROS BINOMIAIS
Neste, caso, k e n – k são chamados termos
complementares.
Exemplos
1) Encontre os valores dos números binomiais abaixo:
5
a)   =
2
5
b)   =
3
7
c)   =
3
Dois números binomiais são ditos iguais se, e
somente si, eles são idênticos ou eles são
complementares.
Exemplo
1) Encontre os possíveis valores de x na igualdade de
7  7 
 .
números binomiais   = 
 2 x   x  1
Resolução:
1º caso: os números binomiais são idênticos, logo:
2x = x + 1 logo, x = 1
2º caso: os números binomiais são complementares,
logo:
2x + (x + 1) = 7 logo, 3x = 6  x = 2
Solução: x = 1 e x = 2
191
n
  = 1
n
RELAÇÃO DE STIFEL
A relação de Stifel diz o seguinte: “ Um número
binomial pode ser representado através da soma de dois
números binomiais.
De forma geral, podemos escrever a relação da
seguinte maneira:
 n   n   n  1
 n   n  1  n  1
   
  
 ou    
  

 p   p  1  p  1
 p   p  1  p 
3ª) Cada elemento do triângulo que não seja da coluna
0 nem o último de cada linha é igual à soma daquele
que está na mesma coluna e linha anterior com o
elemento que se situa à esquerda deste último (relação
de Stifel).
O Triângulo de Pascal pode ser escrito da seguinte
maneira:
Observe que:
iguais
aumenta 1
 n   n   n  1
   
  

 p   p  1  p  1
aumenta 1
iguais
Exemplos
Calculando o valor de cada número binomial,
obtemos o seguinte triângulo:
TRIÂNGULO DE PASCAL
O Triângulo de Pascal, é um triângulo numérico infinito
formado por números binomiais  n  onde n representa o
p 
 
número da linha (posição vertical) e p representa o
número da coluna (posição horizontal).
O triângulo foi descoberto, segundo alguns autores,
pelo matemático chinês Yang Hui, e alguns séculos depois
várias de suas propriedades foram estudadas pelo francês
Blaise Pascal.
Construção do triângulo de Pascal
PROPRIEDADES DO TRIÂNGULO DE PASCAL
Para construir o triângulo do Pascal, basta lembrar as
seguintes propriedades dos números binomiais, não sendo
necessário calculá-los:
1) Em Qualquer linha, dois números binomiais
eqüidistantes dos extremos são iguais.
1ª) Todos os elementos da coluna 0 são iguais a 1, pois:
n
  = 1,
0
2ª) o último elemento de cada linha é igual a 1, pois:
192
2) Teorema das linhas: A soma de todos os elementos
n
de uma linha n qualquer é 2 .
TEOREMA
DE
NEWTON
PARA
DESENVOLVIMENTO DA POTÊNCIA ( a + b )
O
n
n
O binômio da forma (a + b) , com n N, é
denominado binômio de Newton.
Substituindo alguns valores de n no binômio e
desenvolvendo, teremos:
De modo geral temos:
n
n
n n n
 n  n
  i    0    1   2   ...  n  1  n  2
n
i0
3) Teorema das colunas: A soma dos elementos de
qualquer coluna, do 1º elemento até um qualquer, é igual
ao elemento situado na coluna à direita da considerada e
na linha imediatamente abaixo.
Observações:
1. Os expoentes de a decrescem de n até zero,
enquanto os expoentes de b aumentam de zero até
n.
2. Os coeficientes dos desenvolvimentos do binômio
(a + b)n são os termos da linha n do triângulo de
Pascal.
A fórmula geral para o binômio de Newton, usando
os números binomiais, é:
4) Teorema das diagonais: A soma dos elementos
situados na mesma diagonal desde o elemento da 1ª
coluna até o de uma qualquer é igual ao elemento
imediatamente abaixo deste.
Note que, em qualquer termo do desenvolvimento, a
soma dos expoentes de a e b é sempre n.
A fórmula geral do binômio de Newton também pode
ser escrita na forma de somatório.
1. TERMO GERAL DO BINÔMIO DE NEWTON
Todo termo do desenvolvimento do binômio de
Newton do tipo (a + b)n pode ser representado pela
expressão:
193
n
TP1   . anp . bp
p 
Denominada termo geral do binômio, na qual:
p + 1: é a posição do termo;
n: é o expoente do binômio.
Observe que o número de termos do desenvolvimento do
binômio é dado por n + 1.
n
02. Se   representa um número binomial, encontre o
p 
valor das operações abaixo.
8 8 8 8  8  8 8 8
a)                        =
 0   1  2   3   4   6   7   8 
7 7 7 7
7 7
b)             ...       =
 0   1  2   3 
6 7
6 6 6  6 
c)            =
2 3 3  4
Exercício resolvido
Obter o termo independente de x no desenvolvimento
10
1 

de  x 6  4 
x 

Resolução:
n
TP1   . anp . bp
p 
2 3  4 5 6
 28   29   30 
d)                ...         
2 2  2  2 2
2 2 2
=
8
e)
9
 p  
p 1
⇒
20
⇒
⇒
f)
n
  4  
n 4
⇒
Termo independente de x:
60 – 10P = 0
60 = 10P
P = 6 ( logo é o 7º termo )
⇒
⇒
⇒
⇒
EXERCÍCIOS
01. Encontre o(s) valor(es) de
abaixo.
 11   11 
  

a) 
 x  1  2x  3 
b)
c)
x
8  8   9 
       
3  4  x 
x x x
 x 
         ...  
  2046
 1  2   3 
 x  1
em cada equação
7
03. ( UFRN ) A expressão   +
3
a:
a) 30
b) 35
c) 40
d) 45
e) 50
7 
  – 35 é igual
4
 n  n
04. ( UFPR ) O valor de n de modo que   +   +
 0   1
n
n
  + . . . +   = 1024é :
2
n
a) 5
b) 8
c) 10
d) 11
e) 12
05. ( PUC – RS ) A soma dos valores que m pode
 17   17 
=
 é:
 m  1  2m  6 

 

assumir na igualdade 
a) 1
b) 8
c) 13
d) 15
e) 17
194
n
06. ( FGV – SP ) O símbolo   , { n, p }  N e p  n
p 
representa um número binomial. Os valores de p de
8 8 9
modo que   +   =   são:
 3   4  p 
a) P = 4
b) P = 4 ou p = 6
c) P = 4 ou p = 5
d) P = 3 ou p = 5
e) P = 5
07.
(
PUC
–
RJ
)
A
 10   10   10   10 
 10 
            ...   
0  1 2 3
 10 
binomiais vale:
a) 210
b) 20.
c) 10.
d) 10!.
e) 0.
08.
(
UFSM
)
As
6  6  7  8 
           são:
3  4 5  x 
a) x = 2 e x = 6
b) x = 3 e x = 5
c) x = 1 e x = 7
d) x = 0 e x = 8
e) x = 4 e x = 4
soma
soluções
de
alternada
coeficientes
da
equação
09. ( UFPR ) Os números reais x e y são tais que:
5
5
5
5
x – y = 1 e x 5 +   x4y +   x3y2 +   x2y3 +   xy4
 1
2
3
4
x
+ y5 = 243. O quociente
vale :
y
a) 1
b) 1/2
c) 3
d) 2
e) 1/3
 m  1
 m 
  10 e 
  55 , então o
10. ( PUC – SP ) Se 
 p  1
m  p
 m  1
 é igual a:
valor de 
 p 
a) 40
b) 45
c) 50
d) 55
e) 60
11. (PUC) Um colecionador possui determinado
número de selos raros e diferentes entre si. Agrupandoos 4 a 4, obteve o mesmo número de grupos que se os
juntasse 6 a 6. Quantos, pois são os selos raros que o
colecionador possuía?
A) 10.
B) 16.
C) 36.
D) 20.
E) 45.
12. ( UEL – PR ) Para qualquer valor natural de
n, o número de termos do desenvolvimento do
binômio ( x + a )n é:
A) n + 1.
B) n.
C) n – 1.
D) par.
E) ímpar.
13. (CEFET) O 4º termo do desenvolvimento de ( x
+2)6 é:
A) 80x3
B) 80x4
C) 40x5
D) 320x3
E) 160x3
14.( FEI – SP ) A soma de todos os coeficientes do
desenvolvimento de (14x – 13y)237 é:
a) 0
b) 1
c) – 1
d) 331.237
e) 1.973.747
15. (UFV) A soma dos coeficientes do desenvolvimento
de (2x + 3y)m é 625. O valor de m é:
A) 5.
B) 6.
C)10.
D) 3.
E) 4.
16. Sabendo-se que a soma dos coeficientes no
desenvolvimento do binômio (a + b)m é igual a 256,
calcule (m/2).
17. ( UFPI ) Se a e b são números reais tais que (a +
10
b) = 1024 e se o 6º termo do desenvolvimento
binomial é igual a 252, então:
a) a = 1/2 e b = 3/2
b) a = 3 e b = -1
c) a = 2/3 e b = 4/3
d) a = 1/3 e b = 5/3
e) a = 1 e b = 1
195
18. ( UEL – PR ) Se um dos termos do desenvolvimento
5
2
do binômio (x + a) , com a  IR, é 80x , então o valor de
a é
a) 6
b) 5
c) 4
d) 3
e) 2
19. O coeficiente do termo em x–3 no desenvolvimento de
6
1

 x  x  é:


A) 1.
B) 6.
C) 10.
D) 15
E) inexistente.
21. (MACK) No desenvolvimento de ( 2x – y )5 . ( 2x + y )5,
a soma dos coeficientes numéricos vale:
a) 3
b) 9
c) 27
d) 81
e) 243
22. (FGV-SP) Sabendo-se que a soma dos coeficientes do
p
desenvolvimento de ( x + a ) é igual a 512, p vale:
a) 8
b) 6
c) 9
d) 12
e) 15
23. (UFCE) O coeficiente de x15 no desenvolvimento de
2
-3 15
( x + x ) é:
a) 455
b) 500
c) 555
d) 643
e) 545
(UNESP)
25. (FGV) O sexto termo do desenvolvimento de
10
1

 2x   é:
x


a) 8064
2
b) 13440x
-2
c) 3360x
d) 13440x-2
e) 8064x2
26. ( UFES ) Qual é o termo central de ( x – 3 )6 ?
3
a) – 540x
b) – 3240x3
c) 3240x3
d) 540x3
4
e) 540x
20. ( EMF – PR ) Se o desenvolvimento de ( 2x + y )6 é
( 2x + y )6 = 64x6 + 192x5y + ax4y2 + ...+ bxy5 + y6, então
a razão a/b vale:
a) 5
b) 20
c) 2
d) 1
e) 10
24.
d) 0
e) 1
O
termo
independente
de
x
6
27. (MACK) No desenvolvimento de ( x + 3 ) , o
número de termos com coeficiente par é:
a) 3
b) 4
c) 5
d) 6
e) 2
28. (PUC-SP) O desenvolvimento de ( y – 2 )7 possui :
a) 7 termos
b) 560 por coeficiente de y3
c) coeficiente negativo se o expoente de y for ímpar
6
d) coeficiente de y igual ao coeficiente de y
e) 6 termos
29. ( MACK ) O 4º termo do desenvolvimento de
( a + b )6 é 540. Se ( a + b )5 = 210 então | a - b |
vale:
a) -3
b) 3
c) 4
d) 2
e) 7
30.(UNIMONTES-PAES)
1

binômio  x  
x

A) não existe.
B) é 1.
C) é 5.
D) é 1/5
No
desenvolvimento
do
15
, o termo independente de x
no
6
1

desenvolvimento de  x 2   é igual a:
x

a) 30
b) 15
c) 4
196
GABARITO
1) a) x = 2 ou x = 5
2) a) 200
3) B
10) B
16) 24
b) 0
4) C
11) A
17) E
b) x = 4 ou x = 5
c) 70
5) C
d) 4495
6) C
12) A
7) E
13) E
e) 510
8) B
14) B
c) x = 11
f) 20349
9) D
15) E
18) E
19) D
20) B
21) E
25) A
26) A
27) A
22) C
23) A
24) B
28) B
29) D
30) A
197
ESPAÇO AMOSTRAL EQUIPROVÁVEL
PROBABILIDADE
O CONCEITO DE PROBABILIDADE
A história da teoria das probabilidades teve início com
os jogos de cartas, dados e de roleta. Esse é o motivo da
grande existência de exemplos de jogos de azar no estudo
da probabilidade.
A teoria da probabilidade permite que se calcule a
chance de ocorrência de um evento em um experimento
aleatório.
Dizemos que um espaço amostral é equiprovável
quando seus eventos elementares têm probabilidades
iguais de ocorrência.
Exemplo

No lançamento de um dado não viciado.

No lançamento de uma moeda não viciada.
DEFINIÇÃO DE PROBABILIDADE
EXPERIMENTO ALEATÓRIO
É aquele experimento que quando repetido em iguais
condições, podem fornecer resultados diferentes, ou seja,
são resultados explicados ao acaso.
Quando se fala de tempo e possibilidades de ganho na
loteria, a abordagem envolve cálculo de experimento
aleatório.
Exemplos
 O lançamento de uma moeda
 O lançamento de um dado.
 O sorteio de um cupom de uma promoção.
Sejam E um espaço amostral equiprovável, finito e
não-vazio, e A um evento de E. A probabilidade de
ocorrer algum elemento de A é indicada por P(A) e
definida por:
P( A) 
n( A)
n(E)
em que n(A) e n(E) indicam, respectivamente, o
numero de elementos de A e E.
Exercício resolvido
ESPAÇO
AMOSTRAL
ALEATÓRIO
DE
UM
EXPERIMENTO
Conjunto de todos os resultados possíveis de ocorrer num
experimento aleatório é chamado de espaço amostral
desse experimento.
A letra que representa o espaço amostral, é E.
Exemplos

No lançamento de uma moeda o espaço amostral é o
conjunto E={cara,coroa}

No lançamento de um dado, o espaço amostral é E{1,
2, 3, 4, 5, 6}
EVENTO DE UM ESPAÇO AMOSTRAL
Qual a probabilidade de, jogando um dado de 6
faces, obtermos um número maior que 4?
n(E) = 6, pois temos 6 faces no dado
n(A) = 2, pois os números possíveis serão o 5 ou 6.
Assim :
PROPRIEDADES IMPORTANTES:
1. Evento Certo
É o próprio espaço amostral S
Qualquer subconjunto de um espaço amostral é
chamado de evento desse espaço.
Exemplo: ocorrência de um divisor de 60 no conjunto
B={1,2,3,4,5,6}
Exemplo
Seja o lançamento de um dado. O espaço amostral é
dado por E={1, 2, 3, 4, 5, 6}.
Podemos considerar como evento desse espaço
amostral um subconjunto qualquer de E, sendo, por
exemplo, uma face de valor par o evento será A = {2, 4, 6}
2. Evento Impossível
É o conjunto vazio
Exemplo: ocorrência de um número maior que 7 ao
se laçar um dado.
198
3. Evento complementar
Evento A: (ser número Par)
Se A e A’ são eventos complementares, então:
P( A ) + P( A' ) = 1
Exemplo
A = {2,4,6,8,10}
n(A) = 5
Evento B: (ser maior que 4)
B = {5,6,7,8,9,10}
n(B) = 6
Evento (A  B) : (ser número par e maior que 4)
Qual a probabilidade de não ocorrer o número 4 no
lançamento de um dado?
Sabemos que para ocorrer o número 4 temos:
(A  B) = {6,8,10}
n(A  B) = 3
A probabilidade P(A  B) será dada por:
logo para não ocorrer :
EVENTOS MUTUAMENTE EXCLUSIVOS
Os eventos A e B são chamados de mutuamente
exclusivos se, e somente se , A  B = { }. E nesse caso
teremos:
P( A  B)  P( A)  P(B)
Intervalo de existência
A probabilidade de um evento é sempre um número
entre 0 (probabilidade de evento impossível) e 1
(probabilidade do evento certo).
0% ≤ P ≤ 100%
ou
0≤P≤1
ADIÇÃO DE PROBABILIDADES (UNIÃO DE DOIS
EVENTOS)
Seja E um espaço amostral equiprovável finito e nãovazio. Para quaisquer eventos A ou B de E , tem-se
que :
P( A  B)  P( A)  P(B)  P( A  B)
Essa identidade é conhecida como teorema da adição
de probabilidades.
O teorema da adição de probabilidades é aplicado na
resolução de problemas que pedem a probabilidade de
ocorrer um evento A ou um evento B, pois o conectivo
ou indica a união dos eventos.
PROBABILIDADE CONDICIONAL
Considerando os eventos A e B de um espaço
amostral E, a probabilidade condicional de ocorrer o
evento A, tendo ocorrido o evento B é indicada por:
PA / B 
n( A  B)
n(B)
Exercício resolvido
Numa urna temos 100 bolas numeradas de 1 a 100.
Sabe-se que a bola sorteada é par. Vamos calcular a
probabilidade de ser um múltiplo de 10.
n(A) = 50 (pois de 1 a 100 temos 50 números pares)
n(B) = 10 (pois de 1 a 100 temos 10 números múltiplos
de 10)
n(A  B) = 10 (pois temos 10 números pares e
múltiplos de 10)
Assim a probabilidade de ser um múltiplo de 10,
sabendo-se que a bola sorteada é par será:
Exercício resolvido
Numa urna, existem 10 bolas numeradas de 1 a 10.
Uma bola é tirada ao acaso. Qual a probabilidade de se
retirar um número par ou maior que 4.
Espaço Amostral:
E = {1,2,3,4,5,6,7,8,9,10}
n(E) = 10
199
EVENTOS INDEPENDENTES
Dois eventos A e B de um espaço amostral S são
independentes quando PA / B  P( A ) ou PB / A   P(B)
.
MULTIPLICAÇÃO DE PROBABILIDADES
Seja E um espaço amostral equiprovável, finito e nãovazio. Sejam A e B eventos de E; temos que:
P(A  B)  P(A) . P(B / A)
Essa identidade é conhecida como teorema da
multiplicação de probabilidades. O teorema da
multiplicação de probabilidades é aplicado em problemas
que pedem a probabilidade de ocorrer um evento A e
um evento B, pois o conectivo e indica a intersecção dos
eventos.
Nota
Se A e B forem independentes, então:
P(A  B)  P(A) . P(B)
Exercício resolvido
01. Uma urna tem 30 bolas, sendo 10 vermelhas e 20
azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez
e sem reposição, qual será a probabilidade de a primeira
ser vermelha e a segunda ser azul?
Seja o espaço amostral S = 30 bolas, e considerarmos
os seguintes eventos:
A: vermelha na primeira retirada e P(A) = 10/30
B: azul na segunda retirada e P(B) = 20/29
Assim:
P( A  B ) = P(A).(B/A) =
10 20 20
.

30 29 87
EXERCÍCIOS
01. (ENEM – 2012) José, Paulo e Antônio estão
jogando dados não viciados, nos quais, em cada uma
das seis faces, há um número de 1 a 6. Cada um deles
jogará dois dados simultaneamente. José acredita que,
após jogar seus dados, os números das faces voltadas
para cima lhe darão uma soma igual a 7. Já Paulo
acredita que sua soma será igual a 4 e Antônio acredita
que sua soma será igual a 8.
Com essa escolha, quem tem a maior probabilidade de
acertar sua respectiva soma é
A) Antônio, já que sua soma é a maior de todas as
escolhidas.
B) José e Antônio, já que há 6 possibilidades tanto para
escolha de José quanto para a escolha de Antônio, e
há apenas 4 possibilidades para a escolha de Paulo.
C) José e Antônio, já que há 3 possibilidades tanto para
a escolha de José quanto para a escolha de Antônio, e
há apenas 2 possibilidades para a escolha de Paulo.
D) José, já que há 6 possibilidades para formar sua
soma, 5 possibilidades para formar a soma de Antônio
e apenas 3 possibilidades para formar a soma de
Paulo.
E) Paulo, já que sua soma é a menor de todas.
02. ( Osec – SP ) O número da chapa de um carro é
par. A probabilidade de o algarismo das unidades ser
zero é :
a) 1/10
c) 4/9
e) 1/5
b) 1/2
d) 5/9
03. (ENEM – 2012) Em um blog de variedades,
músicas, mantras e informações diversas, foram
postados ”Contos de Halloween“. Após a leitura, os
visitantes poderiam opinar, assinalando suas relações
em: ”Divertido“, ”Assustador“ ou ”Chato“. Ao final de
uma semana, o blog registrou que 500 visitantes
distintos acessaram esta postagem.
O gráfico a seguir apresenta o resultado da enquete.
02. Uma urna tem 30 bolas, sendo 10 vermelhas e 20
azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a
sorteada na urna, qual será a probabilidade de a primeira
ser vermelha e a segunda ser azul?
Como os eventos são independentes, a probabilidade de sair
vermelha na primeira retirada e azul na segunda retirada é
igual ao produto das probabilidades de cada condição, ou
seja, P( A  B ) = P(A).P(B). Ora, a probabilidade de sair
vermelha na primeira retirada é 10/30 e a de sair azul na
segunda retirada 20/30. Daí, usando a regra do produto,
temos:
10 20
2
Observe que na segunda retirada foram
.

30 30
9
consideradas todas as bolas, pois houve reposição. Assim,
P(B/A) = P(B), porque o fato de sair bola vermelha na
primeira retirada não influenciou a segunda retirada, já que
ela foi reposta na urna.
O administrador do blog irá sortear um livro entre os
visitantes que opinaram na postagem ”Contos de Halloween“.
Sabendo que nenhum visitante votou mais de uma vez, a
probabilidade de uma pessoa escolhida ao acaso entre as
que opinaram ter assinalado que o conto ”Contos de
Halloween“ é ”Chato“ é mais aproximada por
A) 0,09.
B) 0,12.
C) 0,14.
D) 0,15.
200
E) 0,18.
04. ( UFSCar – SP ) Uma urna tem 10 bolas idênticas,
numeradas de 1 a 10. Se retirarmos uma bola da urna, a
probabilidade de não obtermos a bola de número 7 é
igual a :
a) 2/9 b) 1/10
c) 1/5 d) 9/10
e) 9/11
05. (UFJF) Um soldado de esquadrão anti-bombas tenta
desativar um certo artefato explosivo que possui 5 fios
expostos. Para desativá-lo, o soldado precisa cortar 2 fios
específicos, um de cada vez, em uma determinada ordem.
Se o soldado escolher aleatoriamente 2 fios para cortar,
numa determinada ordem, a probabilidade do artefato não
explodir ao cortá-lo é igual a:
a) 2
25
2
c)
5
b) 1
20
d) 1
10
06. ( FEI – SP ) Numa urna existem 20 bolas numeradas
de 1 a 20, todas indistinguíveis ao tato. Retirando uma
bola ao acaso, qual a probabilidade de ocorrer múltiplos
de 2 ou múltiplos de 3 ?
a) 11/20
b) 13/20
c) 3/5
d) 4/5
e) 7/10
07. ( MACK – SP ) Uma urna contém 30 bolas numeradas
de 1 a 30. Retirando-se ao acaso uma bola da urna, qual
a probabilidade de essa bola ter um número múltiplo de 4
ou de 3 ?
08 .(UFU) De uma urna que contém bolas numeradas de 1
a 100 será retirada uma bola. Sabendo-se que qualquer
uma das bolas tem a mesma chance de ser retirada, qual
é a probabilidade de se retirar uma bola, cujo número é
um quadrado perfeito ou um cubo perfeito?
A) 0,14
B) 0,1
C) 0,12
D) 0,16
09. (UNIMONTES) Na tabela abaixo, estão dispostos
números de votos válidos para a categoria prefeito,
obtidos pelos partidos A,B e C, nas cidades M, N e P, no
processo eleitoral de setembro/2000.
NÚMEROS DE VOTOS NAS CIDADES
PARTIDOS
M
N
P
A
B
C
TOTAL
300
360
440
1100
320
200
200
720
720
500
700
1920
TOTAL
1340
1060
1340
3740
Selecionando-se o acaso uma pessoa que votou nessa
categoria, qual a possibilidade de ela ser eleitora do
partido A ou C?
a) 134
187
53
c)
187
b) 120
187
d) 67
187
10. ( UE Maringá – PR ) Um número é escolhido ao
acaso entre os 20 inteiros de 1 a 20. A probabilidade
de o número escolhido ser primo ou quadrado perfeito
é:
a) 1/5
b) 2/25
c) 4/25
d) 2/5
e) 3/5
11. ( UNESP ) Dois dados perfeitos e distinguíveis são
lançados ao acaso. A probabilidade de que a soma dos
resultados obtidos seja 3 ou 6 é:
a) 7/18
b) 1/18
c) 7/36
d) 7/12
e) 4/9
12. ( Mauá – SP ) Uma urna contém 40 bolas
brancas, 25 bolas pretas e 15 vermelhas, todas de
mesmo formato e indistinguíveis pelo tato. Retirando
uma bola ao acaso, determine a probabilidade de que
ela seja preta ou vermelha.
1
12
1
c)
6
1
e)
2
a)
1
8
1
d)
4
b)
13. ( UBC – Mogi ) Jogamos dois dados. A
probabilidade de obtermos números iguais de pontos
nos dois é :
a) 1/3
b) 1/36
c) 1/6
d) 5/36
e) 7/36
14. ( PUCC ) Considere um lançamento de dois dados
iguais. A probabilidade de a soma das faces obtidas ser
um valor x tal que 6  x  8 é:
a) 4/9
b) 1/2
c) 1/6
d) 5/6
e) 6/13
15.( Unesp ) Numa gaiola estão nove camundongos
rotulados
1, 2, 3, . . ., 9. Selecionando-se
conjuntamente dois camundongos ao acaso, a
probabilidade de que na seleção ambos os
camundongos tenham rótulo ímpar é :
a) 0,3777...
b) 0,47
c) 0,17
d) 0,2777...
e) 0,1333...
201
16. ( UFMG ) Dois jovens partiram do acampamento em
que estavam em direção à Cachoeira Grande e à
Cachoeira Pequena, localizadas na região, seguindo a
trilha indicada nesse esquema:
Em cada bifurcação encontrada na trilha, eles escolhiam,
com igual probabilidade, qualquer um dos caminhos e
seguiam adiante. Então, é CORRETO afirmar que a
probabilidade de eles chegarem a Cachoeira Pequena é:
a) 1/2
Cachoeira Grande
b)2/3
c) 3/4
d) 5/6
Cachoeira Pequena
Acampamento
17. Pedro e João se encontram diante de uma urna com
duas bolas azuis e uma bola verde. Eles, confiando na
sorte, apostam em quem consegue tirar a bola verde
primeiro, sendo que, os apostadores irão repor as bolas
tiradas até a bola verde sair. Se Pedro começar o jogo,
qual a probabilidade dele vencer ?
a) 1/3
b) 2/3
c) 2/5
d) 3/5
e) 4/5
18. (IFAC – 2012 ) Paulo e Ana resolvem fazer um jogo
usando uma moeda honesta. Paulo inicia o jogo lançando
a moeda e, se obtiver cara ele ganha, caso contrario, Ana
joga a moeda e se der cara ela vence. Portanto, o jogo
será vencido pelo primeiro que obtiver cara num
arremesso. Qual a probabilidade de Paulo vencer?
A) 50%
B) 55%
C) 57,75%
D) 60%
E) 66,67%
19. ( Unirio ) Em uma fábrica de parafusos, a
probabilidade de um parafuso ser perfeito é de 96%. Se
retirarmos da produção, aleatoriamente, três parafusos, a
probabilidade de todos eles serem defeituosos é igual a:
a) 5 –2
b) 5 –3
c) 5 –4
–5
d) 5
–6
e) 5
20. ( FGV ) Uma urna contém 6 bolas vermelhas e 4
brancas. Três bolas são sucessivamente sorteadas, sem
reposição. A probabilidade de observarmos 3 bolas
brancas é:
a) 1/15
b) 1/20
c) 1/25
d) 1/30
e) 1/35
21. ( FEI – SP ) Uma caixa contém 3 bolas verdes, 4
bolas amarelas e 2 bolas pretas. Duas bolas são
retiradas ao acaso e sem reposição. A probabilidade de
ambas serem da mesma cor é:
a) 13/72
b) 1/18
c) 5/18
d) 1/9
e) 1/4
22. ( PUC – RJ ) As cartas de um baralho são
amontoadas aleatoriamente. Qual é a probabilidade de
a carta de cima ser de copas e a de baixo também ? O
baralho é formado por 52 cartas de 4 naipes
diferentes, sendo 13 cartas de cada naipe.
a) 1/17
b) 1/25
c) 1/27
d) 1/36
e) 1/45
23. ( UNAERP ) Em um campeonato de tiro ao alvo,
dois finalistas atiram num alvo com probabilidade de
60% e 70%, respectivamente, de acertar. Nessas
condições, a probabilidade de ambos errarem o alvo é:
a) 30 %
b) 42 %
c) 50 %
d) 12 %
e) 25 %
24. ( Mack – SP ) A probabilidade de um casal ter um
filho do sexo masculino é 0,25. Então a probabilidade
do casal ter dois filhos de sexos diferentes é:
a) 1/16
b) 3/8
c) 9/16
d) 3/16
e) 3/4
25. A probabilidade de que um atirador acerte o alvo
em cada tiro é 2 . Em três tiros, qual é a probabilidade
5
de que esse atirador :
a) Acerte os dois primeiros tiros e erre o terceiro tiro ?
b) Acerte apenas dois tiros ?
26. ( Cesgranrio ) Três moedas não viciadas são
lançadas simultaneamente. A probabilidade de se obter
duas caras e uma coroa é:
a) 1/8
b) 1/4
c) 5/16
202
d) 3/8
e) 1/2
27. ( UEL – PR ) Um juiz de futebol tem três cartões no
bolso. Um é todo amarelo, outro é todo vermelho e o
terceiro é amarelo de um lado e vermelho do outro. Num
determinado lance, o juiz retira, ao acaso, um cartão do
bolso e mostra ao jogador. A probabilidade de a face que
o juiz vê ser vermelha e de a outra face, mostrada ao
jogador ser amarela é:
a) 1/2
b) 2/5
c) 1/5
d) 2/3
e) 1/6
28. ( FMTM ) Uma urna contém 2 bolas azuis e 4
vermelhas, dela é retirada uma bola escolhida ao acaso.
Essa bola é colocada em uma 2ª urna que já continha 1
bola azul e 3 vermelhas. Depois, retira-se uma bola dessa
2ª urna. A probabilidade de essa bola ser azul é:
a) 4/15
b) 11/15
c) 7/12
d) 5/12
e) 17/30
29. ( Unesp – SP ) João lança um dado sem que Antônio
veja. João diz que o número mostrado pelo dado é par. A
probabilidade de Antônio descobrir esse número é :
a) 1/2
b) 1/6
c) 4/6
d) 1/3
e) 3/36
30. ( Unimontes ) Considere a seguinte distribuição da
dieta diária de um grupo de 360 pessoas.
Carnes
Vermelhas
Carnes
Brancas
Verduras
e
Legumes
Homens
92
35
47
Mulheres
101
33
52
Total
Escolhe-se uma pessoa ao acaso. Sabendo-se que essa
pessoa come verduras e legumes, qual é a probabilidade
de que ela seja homem?
47
360
99
c)
360
a)
47
99
52
d)
99
b)
31. (ENEM – 2013) Numa escola com 1 200 alunos foi
realizada uma pesquisa sobre o conhecimento desses em
duas línguas estrangeiras, inglês e espanhol.
Nessa pesquisa constatou-se que 600 alunos falam inglês,
500 falam espanhol e 300 não falam qualquer um desses
idiomas.
Escolhendo-se um aluno dessa escola ao acaso e
sabendo-se que ele não fala inglês qual a probabilidade
de que esse aluno fale espanhol?
A) 1/2
B) 5/8
C) 1/4
D) 5/6
E) 5/14
32. ( UMC ) A tabela a seguir fornece, por sexo e área
escolhida, o número de inscritos em um Vestibular para
ingresso no curso superior:
Escolhido, ao acaso, um dos inscritos e representando
por p1 a probabilidade de o escolhido ser do sexo
masculino e ter optado por Exatas e
p2, a
probabilidade de o escolhido ser do sexo feminino
sabendo que optou por Biomédicas, pode-se concluir
que:
a) p1 = 0,6 e p2= 0,375
b) p1 = 0, 6 e p2= 0,15
c) p1 = 0,15 e p2= 0,15
d) p1 = 0,15 e p2= 0,375
e) p1= 0,375 e p2= 0,15
33. ( Vunesp – SP ) Um baralho de 12 cartas tem 4
ases. Retiram-se 2 cartas, uma após a outra.
Determine a probabilidade de a segunda ser um ás,
sabendo que a primeira foi um ás.
34. ( Mauá – SP ) Uma caixa contém 11 bolas
numeradas de 1 a 11. Retirando-se uma delas ao
acaso, observa-se que ela tem um número ímpar.
Determine a probabilidade de esse número ser menor
que 5.
35. ( UFES ) Um dado é lançado duas vezes e todos os
resultados possíveis para cada lançamento são
equiprováveis. Sabendo que pelo menos um dos
resultados destes dois lançamentos foi um número par,
a probabilidade de que ambos os resultados sejam
pares é:
a) 1/2
b) 2/3
c) 3/4
d) 4/9
e) 1/3
36. ( UFSCar – SP ) Dois dados usuais e não viciados
são lançados. Sabe-se que os números observados
são ímpares. Então a probabilidade de que a soma
deles seja 8 é :
203
a)
b)
c)
d)
e)
2/36
1/6
2/9
1/4
2/18
37. ( Fatec – SP ) Considere todos os números de cinco
algarismos distintos obtidos pela permutação dos
algarismos 4, 5, 6, 7 e 8. Escolhendo-se um desses
números, ao acaso, a probabilidade dele ser um número
ímpar é
a) 1
b) 1/2
c) 2/5
d) 1/4
38. (VUNESP) Dois jogadores, A e B, vão lançar um par
de dados. Eles combinam que, se a soma dos números
dos dados for 5, A ganha, e se essa soma for 8, B é
quem ganha. Os dados são lançados. Sabe-se que A não
ganhou. Qual a probabilidade de B ter ganhado?
10
36
5
c)
36
a)
5
32
5
d)
35
b)
e) Não se pode calcular sem saber os números sorteados.
39. ( PUC – RJ ) Uma doença congênita afeta 1 em
cada 700 homens. Numa população de um milhão de
homens, a probabilidade de que um homem, tomado ao
acaso, não seja afetado é:
a) superior a 0,99
b) igual a 0,99
c) menor que 0,98
d) igual a
e)
1
700
1
ou 50%
2
40. ( Fuvest – SP ) A probabilidade de que a população
atual de um país seja de 110 milhões ou mais é de 95%.
A probabilidade de ser 110 milhões ou menos é de 8%.
Calcule a probabilidade de ser 110 milhões .
41. ( PUCCAMP – SP ) Num grupo, 50 pessoas
pertencem a um clube A, 70 pertencem a um clube B,
30 a um clube C, 20 pertencem aos clubes A e B, 22
aos clubes A e C, 18 aos clubes B e C e 10
pertencem aos 3 clubes. Escolhida ao acaso uma das
pessoas presentes, a probabilidade de ela :
a) pertencer aos três clubes é 3/5.
b) pertencer somente ao clube C é zero.
c) Pertencer a pelo menos a dois clubes é de 60%.
d) Não pertencer ao clube B é 40%.
42. ( Unesp ) Num grupo de 100 pessoas da zona
rural, 25 estão afetadas por uma parasitose intestinal A
e 11 por outra parasitose intestinal B, não se
verificando nenhum caso de incidência conjunta de A
e B. Duas pessoas desse grupo são escolhidas,
aleatoriamente, uma após a outra. Determine a
probabilidade de que, dessa dupla, a primeira pessoa
esteja afetada por A e a segunda por B.
43. ( FEI – SP ) Em uma pesquisa realizada em uma
Faculdade foram feitas duas perguntas aos alunos.
Cento e vinte responderam "sim" a ambas; 300
responderam "sim" à primeira; 250 responderam "sim"
à segunda e 200 responderam "não" a ambas. Se um
aluno for escolhido ao acaso, qual é a probabilidade de
ele ter respondido "não" à primeira pergunta?
a) 1/7
b) 1/2
c) 3/8
d) 11/21
e) 4/25
44. ( PAES ) No concurso do “Banco Moc”,
compareceram 360 candidatos, sendo que 120 foram
reprovados na prova escrita; 90, na entrevista, e 48, na
prova escrita e na entrevista. Qual a probabilidade de
um dos participantes, escolhido ao acaso, ter sido
reprovado na prova escrita e aprovado na entrevista ?
A) 1/5
B) 4/9
C) 4/11
D) 4/5
45. ( UEL – PR ) Considere todos os anagramas da
palavra LONDRINA que começam e terminam pela
letra N. A probabilidade de escolher-se ao acaso um
desses anagramas e ele ter as vogais juntas é:
a) 1/5
b) 1/4
c) 2/5
d) 1/2
e) 3/5
46. ( Mack – SP ) Num grupo de 12 professores,
somente 5 são de matemática. Escolhidos ao acaso 3
professores do grupo, a probabilidade de no máximo
um deles ser de matemática é:
a) 3/11.
b) 5/11.
c) 7/11.
d) 8/11.
e) 9/11.
47. ( Fuvest – SP ) Ao lançar um dado muitas vezes,
uma pessoa percebeu que a face 6 saía com o dobro
de freqüência da face 1, e que as outras faces saíam
com a freqüência esperada em um dado não viciado.
Qual a freqüência da face 1?
a) 1/3.
b) 2/3.
c) 1/9.
d) 2/9.
e) 1/12.
204
48. ( PUC – SP ) Uma urna contém bolas numeradas de 1
a 5. Sorteia-se uma bola, verifica-se o seu número e ela é
reposta na urna.
Num segundo sorteio, procede-se da mesma forma que no
primeiro sorteio. A probabilidade de que o número da
segunda bola seja estritamente maior que o da primeira é
a) 4/5
b) 2/5
c) 1/5
d) 1/25
e) 15/25
49. ( Fatec – SP ) Considere todos os números de cinco
algarismos distintos obtidos pela permutação dos
algarismos 4, 5, 6, 7 e 8. Escolhendo-se um desses
números, ao acaso, a probabilidade dele ser um número
ímpar é
a) 1
b) 1/2
c) 2/5
d) 1/4
50. ( UFMG ) Considere uma prova de Matemática
constituída de quatro questões de múltipla escolha, com
quatro alternativas cada uma, das quais apenas uma é
correta.
Um candidato decide fazer essa prova escolhendo,
aleatoriamente, uma alternativa em cada questão.
Então, é correto afirmar que a probabilidade de esse
candidato acertar, nessa prova, exatamente uma questão
é:
a) 27/64
b) 27/256
c) 9/64
d) 9/256
51. (Enem) Em um determinado semáforo, as luzes
completam um ciclo de verde, amarelo e vermelho em 1
minuto e 40 segundos. Desse tempo, 25 segundos são
para a luz verde, 5 segundos para a amarela e 70
segundos para a vermelha. Ao se aproximar do semáforo,
um veículo tem uma determinada probabilidade de
encontrá-lo na luz verde, amarela ou vermelha. Se essa
aproximação for de forma aleatória, pode-se admitir que a
probabilidade de encontrá-lo com uma dessas cores é
diretamente proporcional ao tempo em que cada uma
delas fica acesa.
Suponha que um motorista passa por um semáforo duas
vezes ao dia, de maneira aleatória e independente uma da
outra. Qual é a probabilidade de o motorista encontrar
esse semáforo com a luz verde acesa nas duas vezes em
que passar?
A) 1/25
B) 1/16
C) 1/9
D) 1/3
E) 1/2
52. (FIP-2013) Sobre o lançamento de um dado com 20
lados, com as faces numeradas de 1 a 20, os alunos de
um colégio fizeram as seguintes afirmativas:
Aluno X: A probabilidade de sair um número par no
lançamento desse dado é menor que a probabilidade de
sair um número maior ou igual a 10.
Aluno Y: A probabilidade de sair um número quadrado
perfeito no lançamento desse dado é de 10%.
Aluno Z: A probabilidade de sair um número primo no
lançamento desse dado excede a probabilidade de sair
um número ímpar maior que 11 em 20%.
Fizeram afirmativas corretas:
A) Somente os alunos X e Y.
B) Somente os alunos X e Z.
C) Os alunos X, Y e Z.
D) Somente os alunos Y e Z.
53. (ENEM – 2012) Em um jogo há duas urnas com 10
bolas de mesmo tamanho em cada urna. A tabela a
seguir indica as quantidades de bolas de cada cor em
cada urna.
Uma jogada consiste em:
1º) o jogador apresenta um palpite sobre a cor da bola
que será retirada por ele da urna 2;
2º) ele retira, aleatoriamente, uma bola da urna 1 e a
coloca na urna 2, misturando-a com as que lá estão;
3º) em seguida ele retira, também aleatoriamente, uma
bola da urna 2;
4º) se a cor da última bola retirada for a mesma do
palpite inicial, ele ganha o jogo.
Qual cor deve ser escolhida pelo jogador para que ele
tenha a maior probabilidade de ganhar?
A) Azul.
B) Amarela.
C) Branca.
D) Verde.
E) Vermelha
54. (ENEM – 2013) Uma loja acompanhou o número
de compradores de dois produtos, A e B, durante os
meses de janeiro, fevereiro e março de 2012. Com
isso, obteve este gráfico:
A loja sorteará um brinde entre os compradores do
produto A e outro brinde entre os compradores do
produto B. Qual a probabilidade de que os dois
sorteados tenham feito suas compras em fevereiro de
2012?
A) 1/20
B) 3/242
C) 5/22
D) 6/25
E) 7/15
205
55. A probabilidade de um casal ter um filho homem com
certa doença congênita é de 10% e se for mulher, a
probabilidade aumenta para 20%. Se esse casal tiver
quatro filhos, sendo dois homens e duas mulheres, qual a
probabilidade de que todos sejam saudáveis?
A) 16,44%
B) 19,44%
C) 23,57%
D) 44,32%
56. Um cubo maciço, confeccionado em plástico branco,
foi totalmente coberto por uma tinta cinza e após secar,
teve todas as suas arestas cortadas em três partes
idênticas, dando origem a cubos com arestas menores
(figura). Se uma pessoa desmontar esse cubo e escolher
um cubo menor ao acaso, qual a probabilidade de esse
cubo ter exatamente quatro faces brancas?
A) 8/27
B) 4/9
C) 2/9
D) 16/27
GABARITO
1) D
2) E
9) A
10) E
3) D
16) C
17) D
23) D
24) B
27) E
33) 3/11
4) D
11) C
29) D
45) A
46) C
51) B
52) B
35) E
41) B
47) D
53) E
6) B
13) C
19) E
25) a)12/125
34) 1/3
40) 3%
12) E
18) E
28) A
39) A
5) B
7) 1/2
14) A
20) D
b)36/125
30) B
31) A
36) C
37) C
42) 1/36
43) D
8) C
15) D
21) C
22) A
26) D
32) D
38) B
44) A
48) B
49) C
50) A
54)A
55) B
56) B
QUESTÕES DO ENEM
01. (ENEM-2009) Dados do Instituto de Pesquisas
Econômicas Aplicadas (IPEA) revelaram que no biênio
2004/2005, nas rodovias federais, os atropelamentos com
morte ocuparam o segundo lugar no ranking de
mortalidade por acidente. A cada 34 atropelamentos,
ocorreram 10 mortes. Cerca de 4 mil atropelamentos/ano,
um a cada duas horas, aproximadamente.
Disponível em: http://www.ipea.gov.br. Acesso em: 6 jan.
2009.
De acordo com os dados, se for escolhido
aleatoriamente para investigação mais detalhada um dos
atropelamentos ocorridos no biênio 2004/2005, a
probabilidade de ter sido um atropelamento sem morte é
A) 2/17
B) 5/17
C) 2/5
D) 3/5
E) 12/17
02. (ENEM-2009) Em um concurso realizado em uma
lanchonete, apresentavam-se ao consumidor quatro
cartas voltadas para baixo, em ordem aleatória,
diferenciadas pelos algarismos 0, 1, 2 e 5. O
consumidor selecionava uma nova ordem ainda com as
cartas voltadas para baixo. Ao desvirá-las, verificava-se
quais delas continham o algarismo na posição correta
dos algarismos do número 12,50 que era o valor, em
reais, do trio-promoção. Para cada algarismo na
posição acertada, ganhava-se R$1,00 de desconto. Por
exemplo, se a segunda carta da sequência escolhida
pelo consumidor fosse 2 e a terceira fosse 5, ele
ganharia R$2,00 de desconto.
Qual é a probabilidade de um consumidor não ganhar
qualquer desconto?
A) 1/24
B) 3/24
C) 1/3
D) 1/4
E) 1/2
03. (ENEM-2009) Um casal decidiu que vai ter 3 filhos.
Contudo, que exatamente 2 filhos homens e decide
que, se a probabilidade fosse inferior a 50%, iria
procurar uma clínica para fazer um tratamento
específico para garantir que teria os dois filhos homens.
Após os cálculos, o casal conclui que a probabilidade
de ter exatamente 2 filhos homens é
A) 66,7%, assim ele não precisará fazer um tratamento.
B) 50%, assim ele não precisará fazer um tratamento.
C) 7,5%, assim ele não precisará fazer um tratamento.
D) 25%, assim ele precisará procurar uma clínica para
fazer um tratamento.
E) 37,5%, assim ele precisará procurar uma clínica
para fazer um tratamento.
04. (ENEM-2010) A figura I abaixo mostra um esquema
das principais vias que interligam a cidade A com a
cidade B. Cada número indicado na figura II representa
a probabilidade de pegar um engarrafamento quando
se passa na via indicada. Assim, há uma probabilidade
de 30% de se pegar engarrafamento no deslocamento
do ponto C ao ponto B, passando pela estrada E4, e de
50%, quando se passa por E3. Essas probabilidades
são independentes umas das outras.
Paula deseja se deslocar da cidade A para a cidade B
usando exatamente duas das vias indicadas,
percorrendo um trajeto com a menor probabilidade de
engarrafamento possível. O melhor trajeto para Paula é
A) E1 E3
B) E1 E4
C) E2 E4
D) E2 E5.
E) E2 E6.
206
E) péssimo.
05. (ENEM-2010) O diretor de um colégio leu numa revista
que os pés das mulheres estavam aumentando. Há alguns
anos, a média do tamanho dos calçados das mulheres era
de 35,5 e, hoje, é de 37,0. Embora não fosse uma
informação científica, ele ficou curioso e fez uma pesquisa
com as funcionárias do seu colégio, obtendo o quadro a
seguir:
Escolhendo uma funcionária ao acaso e sabendo que ela
tem calçado maior que 36,0, a probabilidade de ela calçar
38,0 é
A) 1/3
B) 1/5
C) 2/5
D) 5/7
E) 5/14
06. (ENEM-2013) Numa escola com 1200 alunos foi
realizada uma pesquisa sobre o conhecimento desses em
duas línguas estrangeiras, inglês e espanhol. Nessa
pesquisa constatou-se que 600 alunos falam inglês, 500
falam espanhol e 300 não falam qualquer um desses
idiomas.
Escolhendo-se um aluno dessa escola ao acaso e
sabendo-se que ele não fala inglês, qual a probabilidade
de que esse aluno fale espanhol?
08. (ENEM-2013) Considere o seguinte jogo de
apostas:
Numa cartela com 60 números disponíveis, um
apostador escolhe de 6 a 10 números. Dentre os
números disponíveis, serão sorteados apenas 6. O
apostador será premiado caso os 6 números sorteados
estejam entre os números escolhidos por ele numa
mesma cartela.
O quadro apresenta o preço de cada cartela, de acordo
com a quantidade de números escolhidos.
Cinco apostadores, cada um com R$ 500,00 para
apostar, fizeram as seguintes opções:
Arthur: 250 cartelas com 6 números escolhidos;
Bruno: 41 cartelas com 7 números escolhidos e 4
cartelas com 6 números escolhidos;
Caio: 12 cartelas com 8 números escolhidos e
10 cartelas com 6 números escolhidos;
Douglas:4 cartelas com 9 números escolhidos;
Eduardo:2 cartelas com 10 números escolhidos.
Os dois apostadores com maiores probabilidades de
serem premiados são
A) Caio e Eduardo.
B) Arthur e Eduardo.
C) Bruno e Caio.
D) Arthur e Bruno.
E) Douglas e Eduardo.
07. (ENEM-2013) Uma fábrica de parafusos possui duas
máquinas, I e II, para a produção de certo tipo de
parafuso. Em setembro, a máquina I produziu 54/100 do
total de parafusos produzidos pela fábrica. Dos parafusos
produzidos por essa máquina, 25/1000 eram defeituosos.
Por sua vez, 38/1000 dos parafusos produzidos no mesmo
mês pela máquina II eram defeituosos.
O desempenho conjunto das duas máquinas é classificado
conforme o quadro, em que P indica a probabilidade de
um parafuso escolhido ao acaso ser defeituoso.
09. (ENEM/2009) A população mundial está ficando
mais velha, os índices de natalidade diminuíram e a
expectativa de vida aumentou. No gráfico seguinte, são
apresentados dados obtidos por pesquisa realizada
pela Organização das Nações Unidas (ONU), a
respeito da quantidade de pessoas com 60 anos ou
mais em todo o mundo. Os números da coluna da
direita representam as faixas percentuais. Por exemplo,
em 1950 havia 95 milhões de pessoas com 60 anos ou
mais nos países desenvolvidos, número entre 10% e
15% da população total nos países desenvolvidos.
O desempenho conjunto dessas máquinas, em setembro,
pode ser classificado como
A) excelente. B) bom.
C) regular.
D) ruim.
Fonte: “Perspectivas da População Mundial”, ONU, 2009
207
Disponível em: www.economist.com.
Acesso em: 9 jul. 2009 (adaptado).
Em 2050, a probabilidade de se escolher, aleatoriamente,
uma pessoa com 60 anos ou mais de idade, na população
dos países desenvolvidos, será um número mais próximo
de
1
.
2
1
D)
.
5
A)
7
.
20
3
E)
.
25
B)
C)
8
.
25
10. (ENEM/2009) O controle de qualidade de uma
empresa fabricante de telefones celulares aponta que a
probabilidade de um aparelho de determinado modelo
apresentar defeito de fabricação é de 0,2%. Se uma loja
acaba de vender 4 aparelhos desse modelo para um
cliente, qual é a probabilidade de esse cliente sair da loja
com exatamente dois aparelhos defeituosos?
4
2
A) 2  (0,2%) .
B) 4  (0,2%) .
2
2
C) 6  (0,2%)  (99,8%) .
D) 4  (0,2%).
E) 6  (0,2%)  (99,8%).
11. (ENEM/2009) A população brasileira sabe, pelo menos
intuitivamente, que a probabilidade de acertar as seis
dezenas da mega sena não é zero, mas é quase. Mesmo
assim, milhões de pessoas são atraídas por essa loteria,
especialmente quando o prêmio se acumula em valores
altos. Até junho de 2009, cada aposta de seis dezenas,
pertencentes ao conjunto {01, 02, 03, ..., 59, 60}, custava
R$ 1,50.
Disponível em: www.caixa.gov.br. Acesso em: 7 jul. 2009 .
Considere que uma pessoa decida apostar exatamente R$
126,00 e que esteja mais interessada em acertar apenas
cinco das seis dezenas da mega sena, justamente pela
dificuldade desta última. Nesse caso, é melhor que essa
pessoa faça 84 apostas de seis dezenas diferentes, que
não tenham cinco números em comum, do que uma única
aposta com nove dezenas, porque a probabilidade de
acertar a quina no segundo caso em relação ao primeiro é,
aproximadamente,
1
2
a) 3 doses.
c) 6 doses.
e) 10 doses.
b) 4 doses.
d) 8 doses.
13. (ENEM – 2012) José, Paulo e Antônio estão
jogando dados não viciados, nos quais, em cada uma
das seis faces, há um número de 1 a 6. Cada um deles
jogará dois dados simultaneamente. José acredita que,
após jogar seus dados, os números das faces voltadas
para cima lhe darão uma soma igual a 7. Já Paulo
acredita que sua soma será igual a 4 e Antônio acredita
que sua soma será igual a 8.
Com essa escolha, quem tem a maior probabilidade de
acertar sua respectiva soma é:
a) Antônio, já que sua soma e a maior de todas as
escolhidas.
b) José e Antônio, já que há 6 possibilidades tanto para
a escolha de José quanto para a escolha de Antônio, e
há apenas 4 possibilidades para a escolha de Paulo.
c) José e Antônio, já que há 3 possibilidades tanto para
a escolha de José quanto para a escolha de Antônio, e
há apenas 2 possibilidades para a escolha de Paulo.
d) José, já que há 6 possibilidades para formar sua
soma, 5 possibilidades para formar a soma de Antônio
e apenas 3 possibilidades para formar a soma de
Paulo.
e) Paulo, já que sua soma é a menor de todas.
GABARITO
1. E
2. D
3. E
4. D
5. D
6. A
8. A
9. C
10. C
11. C
12. B
13. D
7. B
1
vezes menor .
2
A) 1 vezes menor .
B) 2
C) 4 vezes menor.
E) 14 vezes menor.
D) 9 vezes menor.
12. (ENEM – 2009) Um médico está estudando um novo
medicamento que combate um tipo de câncer em estágios
avançados. Porém, devido ao forte efeito dos seus
componentes, a cada dose administrada há uma chance
de 10% de que o paciente sofra algum dos efeitos
colaterais observados no estudo, tais como dores de
cabeça, vômitos ou mesmo agravamento dos sintomas da
doença. O médico oferece tratamentos compostos por 3,
4, 6, 8 ou 10 doses do medicamento, de acordo com o
risco que o paciente pretende assumir. Se um paciente
considera aceitável um risco de até 35% de chances de
que ocorra algum dos efeitos colaterais durante o
tratamento, qual é o maior número admissível de doses
para esse paciente?
208
ESTATÍSTICA
INTRODUÇÃO
A coleta de dados, o processamento, a interpretação e
a apresentação de dados numéricos pertencem todos ao
domínio da estatística.
A palavra “estatística” é usada em vários sentidos.
Pode referir-se não só à simples tabulação de informações
numéricas, como a relatórios de transações na bolsa de
valores, como as técnicas utilizadas para processar ou
analisar dados.
Amostra: 400 pessoas que visitaram o museu nos
primeiros seis meses.
FREQÜÊNCIA
Chama-se freqüência de um valor da variável o
número de vezes em que este valor é observado na
amostra.
Freqüência Relativa
Chama-se freqüência relativa a razão da freqüência
absoluta para o número total (freqüência total) de
observações realizadas.
ONDE SE APLICA A ESTATÍSTICA?
Ela é utilizada em todas as ciências, na administração
e em outras atividade que afetam diretamente nossas
vidas como, por exemplo:
Obs. Usualmente se expressa esta razão como um
percentual.
• O uso de técnicas matemáticas na avaliação de controles
de poluição.
• Na analise de problemas de tráfego.
• No estudo de dietas e outros.
Distribuição de Freqüência
UNIVERSO ESTATÍSTICO
É a coleta de dados sobre determinado assunto.
Exemplo
O governo encomenda ao IBGE uma pesquisa para
conhecer o salário médio, do brasileiro. O universo
estatístico ou população estatística é, nesse caso, o
conjunto de todos os assalariados brasileiros.
Os valores observados, suas respectivas freqüências
e
as
correspondentes
freqüências
relativas,
conjuntamente, constituem a distribuição de freqüência
da variável em estudo. Para representar uma
distribuição de freqüências usa-se uma tabela e diz-se
que a tabela é a distribuição de freqüência.
Exemplos
O universo estatístico pode ser:
a) Finito: Quando apresenta um número finito de
elementos.
Em uma prova realiza com 40 alunos da 5ª série de
uma determinada escola, obteve-se o seguinte
resultado em número de pontos por alunos.
Exemplo
• O número de funcionários de um colégio.
• A torcida do GALO em um jogo no Mineirão.
b) Infinito: Quando apresenta um número infinito de
elementos.
Exemplo
• A produção futura de alimento no mundo.
AMOSTRA
Quando o universo estatístico é muito vasto ou quando
não é possível coletar dados de todos os seus elementos,
retira-se desse universo um subconjunto, chamado de
amostra e os dados são coletados nessa amostra.
Exemplo
• Foi feito um estudo com 1500 pessoas que visitaram o
museu do Louvre nos últimos doze meses.
Represente a distribuição de freqüência dos dados.
Pontos(x)
Frequência(F)
0
1
2
3
4
5
6
7
8
9
1
5
3
2
2
6
8
2
6
5
40
Frequência
Relativa(Fr).
2,5%
12,5%
7,5%
5%
5%
15%
20%
5%
15%
12,5%
100%
209
A distribuição de freqüências pode ser completada com
mais uma coluna, chamada freqüências acumuladas ( F.
acum.), cujos valores são obtidos adicionando a cada
freqüência os valores das freqüências anteriores.
Pontos(x)
Freq.
(Fr)
Freq.
Acum.
(Fr.Acum.)
0
1
2
3
4
5
6
7
8
9
1
5
3
2
2
6
8
2
6
5
40
1
6
9
11
13
19
27
29
35
40
Freq.
Relati
va
(Fr).
2,5%
12,5%
7,5%
5%
5%
15%
20%
5%
15%
12,5%
100%
Vamos separar os elementos da amostra em cinco
classes de mesma amplitude:
Observações:
Classe
È o intervalos que contém uma sequência de dados
numéricos
Exemplo
A distribuição de freqüências pode ser completada com
mais uma coluna, chamada freqüências relativas
acumuladas ( F. rel. acum.), cujos valores são obtidos
adicionando a cada freqüência relativa os valores das
freqüências relativas anteriores.
Pontos(
x)
Freq.
(F)
0
1
2
3
4
5
6
7
8
9
1
5
3
2
2
6
8
2
6
5
40
Freq.
Acum.
(Fr.
Acum.
)
1
6
9
11
13
19
27
29
35
40
Freq.
Relativa
(Fr).
2,5%
12,5%
7,5%
5%
5%
15%
20%
5%
15%
12,5%
100%
Freq.
relativa
Acumulad
a
(Fr. acum.)
2,5%
15%
22,5%
27,5%
32,5%
47.5%
67,5%
72,5%
87,5%
100%
Existem muitas maneiras de se construir uma tabela de
distribuição de freqüências, uma delas é agrupando os
diversos valores em intervalos.
Exemplo
Os alunos de uma amostra apresentaram as seguintes
massas corpóreas, em quilograma.
[64,5 ; 68,5[
Amplitude
É a diferença entre o maior e o menor elemento de
uma classe, nessa ordem.
Exemplo
[72,5 ; 76,5[
A=4
Atenção:
Os extremos das classes não precisam ser,
necessariamente, elementos da amostra. Começamos
da medida 60,5 kg, mas poderíamos ter começado de
outra medida qualquer, por exemplo, 62 kg, que é o
menor elemento da amostra.
REPRESENTAÇÃO GRÁFICA
Introdução
A confecção de gráficos permite uma melhor
visualização dos dados, mostrando mais claramente as
diferenças existentes. Os gráficos mais comuns são o
gráfico de setores, de barras horizontais ou de barras
verticais e o gráfico de linha.
O tipo de gráfico a ser utilizado depende do que se
deseja enfatizar. Assim, o gráfico de setor, também
conhecido como "gráfico de pizza", é utilizado quando
se deseja ressaltar diferenças entre proporções. O
gráfico de barras horizontais ou barras verticais mostra
diferenças entre os valores absolutos e o gráfico de
linha é utilizado quando se deseja mostrar variações ao
longo do tempo.
210
Exemplo
Para uma pré-avaliação do desempenho dos
candidatos em um exame vestibular, foi retirada uma
amostra de80 provas.
Depois de corrigidas essas provas, as notas foram
organizadas em uma tabela, obedecendo as seguintes
convenções:
• A amostra foi separada em classes,determinadas pelas
notas das provas;
• O número de notas que pertencem a uma mesma classe
é chamada de freqüência (F) dessa classe;
GRÁFICO DE BARRAS HORIZONTAIS.
As freqüências são colocadas em um eixo horizontal.
• A soma das freqüências de todas as classes é a
freqüência total (F t ) da amostra;
• Dividindo a freqüência F de uma classe pela freqüência
total F t , obtém-se um número chamado de freqüência
relativa (F%) da classe.
Com esse dados, construiu-se a tabela de distribuição de
freqüência:
GRÁFICO DE SETORES.
Divide-se um círculo em setores, com ângulos de
medidas proporcionais às freqüências das classes.
Os dados apresentados nessa tabela podem também
ser descritos por gráficos, como, por exemplo:
GRÁFICO DE LINHA
A medida α , em graus, do ângulo central que
corresponde a uma classe de freqüência F é dada por:
Por exemplo, a medida do ângulo central
correspondente à nota 6 é dada por:
.
Obs. Nesse tipo de gráfico, apenas os extremos dos
segmentos de reta oferecem informações sobre o
comportamento da amostra.
GRÁFICO DE BARRAS VERTICAIS
As freqüências são colocadas em um eixo vertical.
MEDIDAS DE POSIÇÃO
As medidas de posição mostram o posicionamento
dos elementos de uma amostra de números quando
esta é disposta em rol. Algumas dessas medidas são: a
média aritmética, a mediana e a moda.
211
MÉDIA ARITMÉTICA
Chama-se média aritmética de n números reais a1, a2,
a3, ... , an o número real MA dado por
MA 
n
a1  a 2  a 3  ...  a n
n
Xh 
Exemplo
A média aritmética de 6, 17, 7 e – 4 é:
MA 




n


X
h

1
.
Xh 
1
1 
 1
1
1
1

 ... 

 ... 


Xn 
 X1 X2
X1 X 2
Xn
1
6  17  7  ( 4) 26

 6,5
4
4
n
1
1
1

 ... 
X1 X2
Xn
Exemplo - Calcular a média harmônica dos seguintes
conjuntos de números:
a) { 10, 60, 360 }. Resp:.. 3/(1/10+1/60+1/360) = 25,12
MÉDIA ARITMÉTICA PONDERADA
MODA
Chama–se média aritmética ponderada de n números
reais a1, a2, a3, ..., an, com pesos respectivos p1,p2, p3, ...,
pn, o número real MP assim definido:
MP 
a1p1  a 2 p 2  a 3 p 3  ...  a np n
p1  p 2  p 3  ...  p n
Observe que cada número deve ser multiplicado pelo
respectivo peso. Em seguida, a soma dos valores obtidos
é dividida pela soma dos pesos.
A moda de uma amostra, cujas freqüências dos
elementos não são todas iguais, é todo elemento maior
FREQUÊNCIA.
Exemplo
a) As idades de oito alunos, em anos, são
16,15, 16, 17, 18, 19 e 14.
Essa amostra tem duas modas; Mo = 16 anos e M’o =
18 anos.
Exemplo

Se um candidato a um concurso obtém, em 3 provas
realizadas, notas 6, 9 e 8 com pesos respectivos 3, 5,
e 2, sua média será:
MP 
6.3  9.5  8.2 18  45  16 79


 7,9
352
10
10
b) As quantidades, em milímetros, constatadas em seis
latas de óleo foram:
900, 908, 895, 890,905 e 910.
Essa amostra não tem moda.
MEDIANA
a) Para obter a mediana da amostra dos salários de
cinco pessoas:
MÉDIA GEOMÉTRICA
É a raiz n-ésima do produto das n variáveis.
R$ 850,00; R$ 980,00; R$ 720,00; R$ 640,00 e R$
1.200,00,
Xg  X1 . X2 . ... . Xn
escrevemos os valores em rol (do menor para o maior
ou do maior para o menor);
Exemplo: Calcular a média geométrica dos seguintes
conjuntos de números:
R$ 640,00; R$ 720,00; R$ 850,00; R$ 980,00; R$
1.200,00.
n
O termo médio desse rol é a mediana, isto é
Md = R$ 850,00.
a) { 1, 4, 16 }....
Xg  3 1.4.16 .. Xg 
3
64 .
Xg  4
b) Para obter a medida da amostra das massas, e
quilogramas, seis pessoas:
MÉDIA HARMÔNICA
A média harmônica de dois números reais positivos é o
inverso da média aritmética dos inversos desses números.
58, 62, 56, 72, 70, 69,58, 56.
A mediana é a media aritmética entre o 3º e o 4º
termos desse rol, isto é,
Md = (62 + 58)/2 Kg =60 Kg.
212
Emprego da Mediana



Quando desejamos obter o ponto que divide a
distribuição em duas partes iguais.
Quando há valores extremos que afetam de
maneira acentuada a média aritmética.
Quando a variável em estudo é salário.
CAIU NO ENEM !!
01.(ENEM)
GABARITO
01. C
02. D
DISTRIBUIÇÃO
DE
FREQÜÊNCIA
COM
INTERVALOS DE CLASSE
02.(ENEM)
Quando o tamanho da amostra for elevado é mais
racional efetuar o agrupamento dos valores em vários
intervalos de
classe.
Veja o exemplo abaixo, que relaciona as idades dos
moradores de um edifício de apartamentos com a
freqüência dessas idades.
213
ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA (com intervalos de classe):
CLASSE: são os intervalos de variação da variável e é
simbolizada por i e o número total de classes simbolizada
por k.
Ex: na tabela anterior k = 5 e 12 |------ 18 é a 3ª classe,
logo i = 3.
LIMITES DE CLASSE: são os extremos de cada classe.
O menor número é o limite inferior de classe ( li ) e o
maior número, limite superior de classe ( Li ). Ex: em
12 |------- 18, li = 12 e Li = 18.
O símbolo |------- representa um intervalo fechado à
esquerda e aberto à direita. O dado 24 do ROL não
pertence a classe 4 e sim a classe 5 representada por 24
|------- 30.
Observe que na tabela acima não há nenhuma pessoa
com 30 anos.
AMPLITUDE DO INTERVALO DE CLASSE: é obtida
através da diferença entre o limite superior e inferior da
classe e é simbolizada por hi = Li – li. Ex: na tabela
anterior hi = 24 – 18 = 6.
Obs: Na distribuição de freqüência com classes, o hi será
igual em todas as classes.
Freqüências simples ou absolutas: são os valores
que realmente representam o número de dados de
cada classe. A soma das freqüências simples é igual
ao número total dos dados da distribuição.
Freqüências relativas: são os valores das razões
entre as freqüências absolutas de cada classe e a
freqüência total da distribuição. A soma das
freqüências relativas é igual a 1 (100 %).
Polígono de freqüência: é um gráfico em linha, sendo
as freqüências marcadas sobre perpendiculares ao
eixo horizontal, levantadas pelos pontos médios dos
intervalos de classe.
Para realmente obtermos um polígono (linha
fechada), devemos completar a figura, ligando os
extremos da linha obtida aos pontos médios da classe
anterior à primeira e da posterior à última, da
distribuição. Observe que o polígono de freqüências
tem como referencial o histograma.
AMPLITUDE TOTAL DA DISTRIBUIÇÃO: é a diferença
entre o limite superior da última classe e o limite inferior da
primeira classe. AT = L(max) – l(min). Ex: na tabela
anterior AT = 30 – 0 = 30.
AMPLITUDE TOTAL DA AMOSTRA (ROL): é a diferença
entre o valor máximo e o valor mínimo da amostra (ROL).
PONTO MÉDIO DE CLASSE: é o ponto que divide o
intervalo de classe em duas partes iguais. ....... Ex: em
12 |------- 18 o ponto médio é ( 12 + 18 ) / 2 = 15.
REPRESENTAÇÃO GRÁFICA DE UMA DISTRIBUIÇÃO
Histograma, Polígono de freqüência e Polígono de
freqüência acumulada
.
Freqüência simples acumulada de uma classe: é o
total das freqüências de todos os valores inferiores ao
limite superior do intervalo de uma determinada classe.
Freqüência relativa acumulada de uma classe: é a
freqüência acumulada da classe, dividida pela
freqüência total da distribuição.
Em todos os gráficos acima utilizamos o primeiro
quadrante do sistema de eixos coordenados cartesianos
ortogonais. Na linha horizontal (eixo das abscissas)
colocamos os valores da variável e na linha vertical (eixo
das ordenadas), as freqüências.
Histograma: é formado por um conjunto de retângulos
justapostos, cujas bases se localizam sobre o eixo
horizontal, de tal modo que seus pontos médios coincidam
com os pontos médios dos intervalos de classe. A área de
um histograma é proporcional à soma das freqüências
simples ou absolutas.
214
Sendo fa = freq. simples; xi = ponto médio de classe; Fr
(D) = freqüência relativa em decimal; Fr (F) = freqüência
relativa em fração; Fr (%) = freqüência relativa em
porcentagem
Obs: uma distribuição de freqüência sem intervalos de
classe é representada graficamente por um diagrama
onde cada valor da variável é representado por um
segmento de reta vertical e de comprimento proporcional à
respectiva freqüência ( gráfico de colunas por exemplo ).
MÉDIA E MODA COM INTERVALOS DE CLASSE
Neste caso, convencionamos que todos os valores
incluídos em um determinado intervalo de classe
coincidem com o seu ponto médio, e determinamos a
média aritmética ponderada por meio da fórmula:
X
 Xi.fi /  fi ..onde
Xi será o ponto médio da
Resp: a classe modal é 58 |---- 62, pois é a de maior
freqüência.
A moda Mo = (58+62) / 2, logo Mo = 60 cm ( este
valor é estimado, pois não conhecemos o valor real da
moda).
Obs: A moda é utilizada quando desejamos obter uma
medida rápida e aproximada de posição ou quando a
medida de posição deva ser o valor mais típico da
distribuição. Já a média aritmética é a medida de
posição que possui a maior estabilidade.
classe.
Exemplo: Calcular a estatura média de bebês conforme a
tabela abaixo.
MEDIDAS DE DISPERSÃO
DESVIO ABSOLUTO MÉDIO
O desvio absoluto médio de uma amostra de
números x1, x2, x3, ...¸ xn de media aritmética , é o
número dado por:
VARIÂNCIA
A variância de uma amostra de números x 1, x2, x3,
...¸ xn ,de media aritmética , é o número dado por:
Aplicando a fórmula acima temos: X = 2.440 / 40
X = 61 cm
A classe que apresenta a maior freqüência é
denominada classe modal. Pela definição, podemos
afirmar que a moda, neste caso, é o valor dominante que
está compreendido entre os limites da classe modal. O
método mais simples para o cálculo da moda consiste em
tomar o ponto médio da classe modal. Damos a esse valor
a denominação de moda bruta.
Exemplo: Calcule a estatura modal conforme a tabela
abaixo.
DESVIO PADRÃO
O desvio padrão é o número representado pela letra
σ e definido como a raiz quadrada da variância.
Exemplo
Dois torneios, Pedro e Antonio, concorrendo a uma
vaga em uma metalúrgica, submeteram-se ao seguinte
teste de precisão; cada um deles construiu quatro
rodas de ferro, que deveriam ter 5 cm de diâmetro. A
tabela abaixo descreve o desempenho de cada um.
Como os diâmetros médios foram iguais, o critério
de desempate pode ser a regularidade, isto é, quem
teve o desempenho mais regular merece a vaga. Para
215
comparar os desempenhos, pode-se usar qualquer um
dos três desvios: Dam, Var ou DP.
Adotando um deles, o conjunto de diâmetros que tiver o
menor desvio correspondo ao desempenho mais regular.
Observe a comparação feita pelo Dam:
Há exatamente 10 alunos com mais de 16
anos.
c) O número de meninos é igual ao número de
meninas
d) O número de meninos com idade maior que 15
anos é maior que o número de meninas nesse
mesmo intervalo de idades.
02. (UNIMONTES) No ano de 2005, foram
disponibilizados pelo Banco Moc mais de 6 milhões de
reais em financiamentos de curto e longo prazos,
conforme os valores indicados na figura a seguir.
Como Dam (Pedro) <Dam (Antonio), concluímos que
Pedro teve um desempenho mais regular, portanto merece
a vaga.
Chega-se a mesma conclusão por meio da variância:
Como Var (Pedro) < Var (Antonio), concluímos que
Pedro teve um desempenho mais regular e, portanto,
merece a vaga.
Analogicamente, pode-se chegar à mesma conclusão
por meio do desvio padrão, que é a raiz quadrada da
variância:
Com base nas informações acima, é CORRETO
afirmar que o crescimento dos financiamentos em
2005, com relação ao ano de 2004, foi
A) igual a 34%.
B) superior a 33%.
C) inferior a 33%.
D) igual a 32%.
03. (COTEC) No gráfico abaixo, observamos o número
de alunos em cada turma de 5ª série da Escola Banzé.
Como DP(P) < DP (A), concluímos que Pedro teve um
desempenho mais regular e, portanto, merece a vaga.
EXERCÍCIOS
01. (UFSCar – SP ) Num curso de iniciação à informática,
a distribuição das idades dos alunos, segundo o sexo, é
dado pelo gráfico seguinte:
Número de Alunos
Legenda
4
Meninos
Meninas
3
2
1
14
15
16
17
18
Idade ( Anos )
Com base nos dados do gráfico, pode-se afirmar que :
a) o número de meninas com, no máximo, 16 anos é
maior que o número de meninos nesse mesmo
intervalo de idades.
b) O número total de alunos é 19
Analisando esse gráfico, percebemos que o total de
alunos de todas as 5as séries e a turma menos
numerosa são, respectivamente:
A) total de alunos: 150; 5ª série C.
B) total de alunos: 140; 5ª série C.
C) total de alunos: 150; 5ª série A.
D) total de alunos: 160; 5ª série D.
04. ( UFRS ) As questões de Matemática do Concurso
Vestibular da UFRGS de 2004 foram classificadas em
categorias quanto ao índice de facilidade, como mostra
o gráfico de barras a seguir.
Se esta classificação fosse apresentada em um gráfico
de setores circulares, a cada categoria corresponderia
um setor circular. O ângulo do maior desses setores
mediria
a) 80°.
b) 120°.
c) 157°.
d) 168°.
216
e) 172°.
05. (UNIMONTES – PAES) O gráfico de setor, abaixo, foi
construído após uma pesquisa feita junto a 450 alunos do
ensino médio do Colégio Alfa que responderam à seguinte
pergunta: Qual a disciplina de que você mais gosta?
O ângulo do setor que indica o número de alunos que
gostam da disciplina Física mede
a) 86º 24’.
b) 86º 40’.
c) 86º 4’.
d) 88º 4’.
Analise as afirmações a seguir, de acordo com os
dados acima.
( ) As intenções de voto no candidato J sempre
foram superiores às do candidato C.
( ) As intenções de voto no candidato C sempre
decresceram, a partir da segunda pesquisa.
( ) O crescimento percentual das intenções de voto
no candidato J, entre a primeira e a quinta pesquisa,
foi igual ao decrescimento percentual do candidato C
no mesmo período.
( ) A média de intenções de voto no candidato J, nas
cinco pesquisas, foi superior a 38%.
( ) Da segunda à quinta pesquisa, as intenções de
voto no candidato J cresceram linearmente.
08. (Ufmg 2006) Este gráfico representa o resultado de
uma pesquisa realizada com 1 000 famílias com filhos
em idade escolar:
06. ( ENEM -2012 ) O dono de uma farmácia resolveu colocar à
vista do público o gráfico mostrado a seguir, que apresenta a
evolução do total de vendas (em Reais) de certo medicamento
ao longo do ano de 2011.
De acordo com o gráfico, os meses em que ocorreram,
respectivamente, a maior e a menor venda absolutas em
2011 foram
A) março e abril.
B) março e agosto.
C) agosto e setembro. D) junho e setembro.
E) junho e agosto.
07. (Ufpe 2005) Em cinco pesquisas sobre as intenções
de voto para as próximas eleições, os candidatos J e C
obtiveram os resultados percentuais ilustrados no gráfico a
seguir.
Considere estas afirmativas referentes às famílias
pesquisadas:
I) O pai participa da renda familiar em menos de 850
dessas famílias.
II) O pai e a mãe participam, juntos, da renda familiar
em mais de 500 dessas famílias.
Então, é CORRETO afirmar que
a) nenhuma das afirmativas é verdadeira.
b) apenas a afirmativa I é verdadeira.
c) apenas a afirmativa II é verdadeira.
d) ambas as afirmativas são verdadeiras.
09. (Ufg 2008) O gráfico a seguir mostra a prevalência
de obesidade da população dos EUA, na faixa etária de
20 a 74 anos, para mulheres e homens, e de 12 a 19
anos, para meninas e meninos.
217
e) tanto em 2001, como em 2003, o que indica não
haver relação significativa entre lucro, produtividade e
número de operários.
11. (Bnb) Um servidor federal recebeu o seu salário
referente ao mês de janeiro de 2007 e planejou seus
gastos de acordo com a planilha a seguir:
De acordo com os dados apresentados neste gráfico,
A) de 1960 a 2002, em média, 30% dos homens estavam
obesos.
B) a porcentagem de meninas obesas, no período 19992002, era o dobro da porcentagem de meninas obesas no
período 1988-1994.
C) no período 1999-2002, mais de 20% dos meninos
estavam obesos.
D) no período 1999-2002, mais de 50% da população
pesquisada estava obesa.
E) a porcentagem de mulheres obesas no período19881994 era superior à porcentagem de mulheres obesas no
período 1976-1980
10. ( ENEM ) As empresas querem a metade das pessoas
trabalhando o dobro para produzir o triplo.
(Revista "Você S/A", 2004)
Preocupado em otimizar seus ganhos, um empresário
encomendou um estudo sobre a produtividade de seus
funcionários nos últimos quatro anos, entendida por ele,
de forma simplificada, como a relação direta entre seu
lucro anual (L) e o número de operários envolvidos na
produção (n). Do estudo, resultou o gráfico a seguir.
Sendo R$ 1.800,00 o salário líquido recebido por esse
servidor, a quantia gasta por ele no carnaval foi:
a) R$ 441,00
b) R$ 270,00
c) R$ 288,00
d) R$ 108,00
e) R$ 252,00
12. (UNIMONTES – PAES) A primeira etapa da prova
da 3ª Olimpíada Brasileira de Matemática das Escolas
Públicas foi aplicada na Escola Delta. A freqüência
registrada dos alunos foi a seguinte:
O número de alunos do Nível 1 que compareceram à
realização da prova foi de
a) 375.
b) 450.
c) 350.
d) 1250.
13. (BNDES) A tabela a seguir mostra o número de
gols marcados pela equipe X nas partidas do último
torneio que disputou.
Ao procurar, no gráfico, uma relação entre seu lucro,
produtividade e número de operários, o empresário
concluiu que a maior produtividade ocorreu em 2002, e o
maior lucro
a) em 2000, indicando que, quanto maior o número de
operários trabalhando, maior é o seu lucro.
b) em 2001, indicando que a redução do número de
operários não significa necessariamente o aumento dos
lucros.
c) também em 2002, indicando que lucro e produtividade
mantêm uma relação direta que independe do número de
operários.
d) em 2003, devido à significativa redução de despesas
com salários e encargos trabalhistas de seus operários.
Qual foi o número médio de gols, por partida, marcados
por essa equipe?
A) 1
B) 1,25
C) 1,5
D) 1,75
E) 2
14. (UNIMONTES – PAES) Os funcionários da
empresa ZETA são classificados em quatro níveis, e os
salários são de acordo com os mesmos. Abaixo temos
descrita a tabela dos salários.
218
e) 138 cm
17. ( ENEM – 2012 ) A tabela a seguir mostra a evolução da
receita bruta anual nos três últimos anos de cinco
microempresas (ME) que se encontram à venda.
O salário médio mensal dos funcionários dessa empresa
é, aproximadamente,
a) 585.
b) 595.
c) 580.
d) 590.
15. (Enem) Brasil e França têm relações comerciais há
mais de 200 anos. Enquanto a França é a 5.ª nação mais
rica do planeta, o Brasil é a 10.ª, e ambas se destacam na
economia mundial. No entanto, devido a uma série de
restrições, o comércio entre esses dois países ainda não é
adequadamente explorado, como mostra a tabela
seguinte, referente ao período 2003-2007.
Os dados da tabela mostram que, no período considerado,
os valores médios dos investimentos da França no Brasil
foram maiores que os investimentos do Brasil na França
em um valor
A) inferior a 300 milhões de dólares.
B) superior a 300 milhões de dólares, mas inferior a 400
milhões de dólares.
C) superior a 400 milhões de dólares, mas inferior a 500
milhões de dólares.
D) superior a 500 milhões de dólares, mas inferior a 600
milhões de dólares.
E) superior a 600 milhões de dólares.
16. (Bnb) A tabela a seguir indica a distribuição de
freqüência das estaturas das crianças de um
acampamento infantil.
a)
b)
c)
d)
A altura média das crianças desse acampamento é
145 cm
143 cm
147 cm
153 cm
Um investidor deseja comprar duas das empresas listadas na
tabela. Para tal, ele calcula a média da receita bruta anual
dos últimos três anos (de 2009 até 2011) e escolhe as duas
empresas de maior média anual. As empresas que este
investidor escolhe comprar são
A) Balas W e Pizzaria Y.
B) Chocolates X e Tecelagem Z.
C) Pizzaria Y e Alfinetes V.
D) Pizzaria Y e Chocolates X.
E) Tecelagem Z e Alfinetes V.
18. (UNIMONTES-2010) Em um conjunto de 10
números, se cada um deles for aumentado de 20
unidades, a média aritmética dos dez números originais
A) é aumentada de 200 unidades.
B) permanece a mesma.
C) é aumentada de 2 unidades.
D) é aumentada de 20 unidades.
19. ( FGV – SP ) A tabela abaixo representa a
distribuição de freqüências dos salários de um grupo de
50 empregados de uma empresa, em certo mês.
Nº da classe
salário do mês
nº de empregados
1
1000
2000
20
2
2000
3000
18
3
3000
4000
9
4
4000
5000
3
O salário médio desses empregados, nesse mês, foi de
A) R$ 2637,00
B) R$ 2520,00
C) R$ 2500,00
D) R$ 2420,00
E) R$ 2400,00
20. ( PUC – SP ) O histograma abaixo apresenta a
distribuição de freqüência das faixas salariais numa
pequena empresa. Com os dados disponíveis, pode-se
concluir que a média desses salários é,
aproximadamente:
Nº de funcionários
a) R$ 420,00
14
b) R$ 536,00
c) R$ 562,00
d) R$ 640,00
e) R$ 708,00
4
2
0
500
1000 1500 2000 2500
salários
219
21. ( Fuvest – SP ) A distribuição das idades dos alunos
de uma sala de aula é dada pelo seguinte gráfico:
Nº de alunos
23
20
10
5
2
24. ( Unimontes – 2006 ) Em uma escola de ensino
médio, para ser aprovado, é necessário ter média 5.
Os alunos fazem 4 provas durante o ano. A primeira
tem peso 1; a segunda e a terceira, peso 2; a quarta,
peso 3. Na tabela abaixo, temos as notas obtidas por
quatro colegas
PROVAS
ALUNOS
16 17 18 19 20
Idade ( anos )
Qual das alternativas representa melhor a média das
idades dos alunos ?
a) 16 anos e 10 meses
b) 17 anos e 1 mês
c) 17 anos e 5 meses
d) 18 anos e 6 meses
e) 19 anos e 2 meses
22. ( FGV – SP ) Numa pesquisa em determinada cidade
foram obtidos os seguintes dados, relativos ao número de
crianças por família :
Nº de crianças
por família
Porcentagem de
famílias na cidade
0
5
1
25
2
30
3
20
4
5 ou mais
BENTO
JORGE
MARIA
PEDRO
1ª
4
8
5
7
2ª
3ª
4ª
5
7
6
6
5
5
7
6
6
3
8
5
As médias finais de Bento,
foram, respectivamente :
a) 5,25 ; 6,125 ; 6,875 ;
b) 5,25 ; 5,125 ; 6,875 ;
c) 5,25 ; 5,125 ; 6,125 ;
d) 5,25 ; 5,125 ; 6,875 ;
Jorge, Maria e Pedro
5,75
5,75
5,75
6,75
25. (ENEM) Depois de jogar um dado em forma de
cubo e de faces numeradas de 1 a 6, por 10 vezes
consecutivas, e anotar o número obtido em cada
jogada, construiu-se a seguinte tabela de distribuição
de frequências.
10
10
O número médio de crianças nas famílias com 5 ou mais
filhos é 5,8. O número médio de crianças por família nesta
cidade é, então, igual a :
a) 2,00
b) 2,30
c) 2,43
d) 2,55
e) 3,00
23. ( PUCCAMP ) A tabela abaixo mostra os resultados de
uma pesquisa sobre a faixa salarial dos funcionários de
uma empresa que usam bicicleta para ir ao trabalho.
O salário médio desses trabalhadores é
A) R$ 425,00
B) R$ 480,00
C) R$ 521,00
D) R$ 565,00
A média, mediana e moda dessa distribuição de
frequências são, respectivamente
A) 3, 2 e 1
B) 3, 3 e 1
C) 3, 4 e 2
D) 5, 4 e 2
E) 6, 2 e 4
26. (ENEM) Na tabela, são apresentados dados da cotação
mensal do ovo extra branco vendido no atacado, em Brasília,
em reais, por caixa de 30 dúzias de ovos, em alguns meses
dos anos 2007 e 2008.
De acordo com esses dados, o valor da mediana das
cotações mensais do ovo extra branco nesse período era
igual a
a) R$ 73,10.
b) R$ 81,50.
c) R$ 82,00.
d) R$ 83,00
e) R$ 85,30
220
27. (ENEM/2009) Suponha que a etapa final de uma
gincana
escolar
consista
em
um desafio
de
conhecimentos. Cada equipe escolheria 10 alunos
para realizar uma prova objetiva, e a pontuação da
equipe seria dada pela mediana das notas obtidas
pelos alunos. As provas valiam, no máximo, 10 pontos
cada. Ao final, a vencedora foi a equipe Ômega, com
7,8 pontos, seguida pela equipe Delta, com 7,6
pontos. Um dos alunos da equipe Gama, a qual ficou
na terceira e última colocação, não pôde comparecer,
tendo recebido nota zero na prova. As notas obtidas
pelos 10 alunos da equipe Gama foram 10; 6,5; 8;
10; 7; 6,5; 7; 8; 6; 0.
Se o aluno da equipe Gama que faltou tivesse
comparecido, essa equipe
A) teria a pontuação igual a 6,5 se ele obtivesse nota 0.
B) seria a vencedora se ele obtivesse nota 10.
C) seria a segunda colocada se ele obtivesse nota 8.
D) permaneceria na terceira posição, independentemente
da nota obtida pelo aluno.
E) empataria com a equipe Ômega na primeira colocação
se o aluno obtivesse nota 9.
28. (COTEC) A distribuição dada pela tabela abaixo
apresenta os pares de calçados numa loja, em
determinado dia, de acordo com o numero usado de certa
marca.
Número
Frequência
usado
36
2
37
2
38
3
39
3
40
2
41
4
42
1
43
2
A mediana para essa distribuição é igual a
A) 40
B) 41
C) 38
D) 39
29. (FGV-SP) Quatro amigos calcularam a média e a
mediana de suas alturas, tendo encontrado como
resultados 1,72 m e 1,70 m , respectivamente. A média
entre as alturas do mais alto e do mais baixo, em metros,
é igual a:
A)1,71
B)1,72
C)1,73
D)1,74
30. (FGV-SP) Sejam os números 7, 8, 3, 5, 9 e 5 seis
números de uma lista de nove números inteiros. O
maior valor possível para a mediana dos nove números da
lista é:
a) 5
b) 6
c) 7
d) 8
e) 9
31. (UFU-MG) As 10 medidas colhidas por um cientista
num determinado experimento, todas na mesma
unidade, foram os seguintes: 1,2; 1,2; 1,4; 1,5; 1,5;
2,0; 2,0; 2,0; 2,0; 2,2
Ao trabalhar na análise estatística dos dados, o
cientista esqueceu-se, por descuido, de considerar
uma dessas medidas. Dessa forma, comparando os
resultados obtidos pelo cientista em sua análise
estatística com os resultados corretos para
amostra, podemos afirmar que:
a) a moda e a média foram afetadas.
b) a moda não foi afetada, mas a média foi.
c) a moda foi afetada, mas a média não foi.
d) a moda e a média não foram afetadas.
32. (ENEM) A classificação de um país no quadro de
medalhas nos Jogos Olímpicos depende do número de
medalhas de ouro que obteve na competição, tendo
como critérios de desempate o número de medalhas de
prata seguido do número de medalhas de bronze
conquistados. Nas Olimpíadas de 2004, o Brasil foi o
décimo sexto colocado no quadro de medalhas, tendo
obtido 5 medalhas de ouro, 2 de prata e 3 de bronze.
Parte desse quadro de medalhas é reproduzida a
seguir
Se o Brasil tivesse obtido mais 4 medalhas de ouro, 4
de prata e 10 de bronze, sem alteração no número de
medalhas dos demais países mostrados no quadro,
qual teria sido a classificação brasileira no quadro de
medalhas das Olimpíadas de 2004?
A) 13º
B) 12º
C) 11º
D) 10º
E) 9º
33. (ENEM) Os dados do gráfico seguinte foram
gerados a partir de dados colhidos no conjunto de seis
regiões metropolitanas pelo Departamento Intersindical
de Estatística e Estudos Socioeconômicos (Dieese).
221
35. ( UERJ ) O gráfico a seguir representa, em reais,
as vendas anuais de uma empresa no período de 1996
a 2001.
Determine :
a) A média anual das vendas dessa empresa
Supondo que o total de pessoas pesquisadas na região
metropolitana de Porto Alegre equivale a 250000, o
número de desempregados em março de 2010, nessa
região, foi de
A) 24500.
B) 25000.
C) 220500.
D) 223000.
E) 227500.
b) O desvio
empresa
médio
da
arrecadação
dessa
c) A variância da arrecadação dessa empresa
36. (UfPR 2008) Considere as seguintes medidas
descritivas das notas finais dos alunos de três turmas:
34. (UNIMONTES – PAES) A tabela abaixo indica a
quantidade de salários mínimos (SM) mensais pagos a
200 empregados da Empresa Delta.
O gráfico que indica a porcentagem de funcionários de
cada faixa salarial em relação ao total dos funcionários é
Com base nesses dados, considere as seguintes
afirmativas:
1. Apesar de as médias serem iguais nas três turmas,
as notas dos alunos da turma B foram as que se
apresentaram mais heterogêneas.
2. As três turmas tiveram a mesma média, mas com
variação diferente.
3. As notas da turma A se apresentaram mais
dispersas em torno da média.
Assinale a alternativa correta.
A) Somente a afirmativa 2 é verdadeira.
B) Somente as afirmativas 2 e 3 são verdadeiras.
C) Somente as afirmativas 1 e 2 são verdadeiras.
D) Somente as afirmativas 1 e 3 são verdadeiras.
37. (Fgv 2003) Um conjunto de dados numéricos tem
variância igual a zero. Podemos concluir que:
a) a média também vale zero.
b) a mediana também vale zero.
c) a moda também vale zero.
d) o desvio padrão também vale zero.
e) todos os valores desse conjunto são iguais a zero.
38. ( ENEM – 2012 ) Um produtor de café irrigado em
Minas Gerais recebeu um relatório de consultoria
estatística, constando, entre outras informações, o
desvio padrão das produções de uma safra dos talhões
de sua propriedade. Os talhões têm a mesma área de
30 000 m2 e o valor obtido para o desvio padrão foi de
90 kg/talhão. O produtor deve apresentar as
222
informações sobre a produção e a variância dessas
2
produções em sacas de 60 kg por hectare (10 000 m ).
A variância das produções dos talhões expressa em
2
(sacas/hectare) é
A) 20,25.
B) 4,50.
C) 0,71.
D) 0,50.
E) 0,25.
notas conforme os histogramas abaixo.
Nº de questões acertadas
GRUPO A
90
70
50
30
10
39. ( FGV – SP ) Dois atiradores, A e B, numa série de
20 tiros num alvo com a forma indicada na figura seguinte
obtiveram os resultados que estão anotados no quadro ao
lado da figura.
0
10
20
30
50
ATIRADORES
PONTOS
50
30
20 10
0
A
4
6
5
4
1
B
6
3
5
3
3
Observando o quadro acima pode-se afirmar que :
a) Em relação ao atirador
A, a “Moda” em sua
seqüência de tiros foi de 50 pontos.
b) Em relação ao atirador
B, a “Moda”
em sua
seqüência de tiros foi de 30 pontos.
c) O atirador A teve, em média, a melhor pontuação;
d) O atirador B teve, em média, a melhor pontuação;
e) Os dois atiradores tiveram a mesma pontuação média;
40. ( Unimontes / PAES – 2002 ) Em um relatório acerca
do resultado final do balanço de uma empresa que havia
obtido prejuízo, o contador apresentou cálculo, mostrando
que o lucro tinha média “ – 1000 ” ( em reais ) e desvio
padrão “ – 150 ” ( em reais ). O diretor da empresa
devolveu o mesmo, alegando incorreções.
Com respeito à situação descrita, podemos afirmar que :
a) tanto a média quanto o desvio padrão estavam
errados;
b) o contador está certo;
c) o diretor de empresa tinha razão e havia erro na
média;
d) o diretor de empresa tinha razão e havia erro no
desvio padrão;
41. ( Unimontes – 2006 ) Os números abaixo
correspondem às alturas ( em cm ) dos jogadores da
seleção de futebol de um certo país.
169 159 166 168 169 166 164 159 161 166 162
A moda desse conjunto de dados é
A) 165
B) 159
C) 166
D) 169
42. ( PAES / UNIMONTES – 2003 ) Considere a seguinte
definição:
Desvio médio é a média aritmética das diferenças, em
módulo, entre os valores de uma seqüência de dados e a
média aritmética dessa seqüência.
Dois grupos de cinco alunos, grupo A e grupo B, foram
submetidos a um teste com 100 questões, obtendo as
Aluno 1 Aluno 2 Aluno 3 Aluno 4 Aluno 5
Nº de questões acertadas
GRUPO B
70
60
50
40
30
Aluno 1 Aluno 2 Aluno 3 Aluno 4 Aluno 5
O desvio médio das notas de cada grupo é,
respectivamente :
a) 50 e 30
b) 24 e 10
c) 5 e 10
d) 24 e 12
43. Em um supermercado, a reposição de pacotes de
arroz por dia, permitiu a construção da seguinte tabela
de dados :
Marca do Arroz
Nº de Pacotes
A
B
C
D
80
20
60
40
Pode-se afirmar que o desvio médio existente nas
quantidades de pacotes de arroz das marcas A,
B, C e D é :
a) 16
b) 17
c) 18
d) 19
e) 20
44. (Unicamp – SP ) A média aritmética de um grupo
de 120 pessoas é de 40 anos. Se a média aritmética
das idades das mulheres é de 35 anos e a dos
homens é de 50 anos, qual o número de pessoas de
cada sexo no grupo ?
45. ( Fuvest – SP ) Sabe-se que a média aritmética de
cinco números inteiros distintos, estritamente positivos,
é 16. O maior valor que um desses inteiros pode
assumir é de :
a) 16
223
b)
c)
d)
e)
20
50
70
100
46. (FIP-2012) ENEM: uma evolução do número de
participantes
Em 1998, apenas 157.200 inscritos participaram da
primeira edição. Em 2001, com a concessão de isenção
da taxa de inscrição aos alunos da rede pública de todo
país pelo MEC, Ministério da Educação, o número de
inscritos saltou para um valor expressivo de 1.600.000
participantes. O ano de 2004 foi marcado pela criação do
Programa Universidade para Todos (ProUni), com
concessões de bolsas em IES privadas agregadas às
notas obtidas no Exame. No ano seguinte ao lançamento
do ProUni, o Enem alcançou a histórica marca de 3
milhões de inscritos. No ano de 2008, o Exame teve mais
de 4 milhões de inscritos. A evolução do número de
inscritos é apresentada no gráfico abaixo.
Com base nas informações e no gráfico, observa-se que a
ÚNICA alternativa INCORRETA é:
A) O número de participantes dobrou no período de 2004
para 2005.
B) O ano de 2008 teve mais de 4 milhões de inscritos, um
valor entre 25 e 30 vezes mais do que a primeira edição.
C) Nos anos de 2001 e 2005, aconteceram aumentos
expressivos no número de participantes.
D) Todos os segmentos de reta apresentados no gráfico
têm inclinação positiva, indicando, portanto, um
crescimento constante a cada nova edição do Enem.
47. (FIP-2012) Muito mais motos, ainda muito mais
mortos.
Analise o quadro abaixo sobre a Evolução da frota de
veículos, das vítimas e das taxas de vítimas (por 100 mil
veículos) em acidentes de trânsito.
De acordo com os dados acima, é correto inferir que:
A) A frota de motocicletas cresceu 369% nessa
década, enquanto as mortes de motociclistas
cresceram 417%.
B) A frota de automóveis aumentou 24%, e as vítimas
de acidentes com automóvel, 57%.
C) Nessa década, o número de vítimas de automóvel
oscilou de um mínimo de 32,5 até um máximo de 41,5,
com média decenal de 38 mortes por grupo de cada
100 mil automóveis registrados. Isto é, a mortalidade
envolvendo motocicletas por veículo foi quase 2,5
vezes maior que a dos automóveis.
D) Em 1998, havia 2,8 milhões de motos,
representando 11,5% da frota total do país. Em 2008, o
número salta para 13,1 milhões, representando 32% do
total nacional de veículos.
GABARITO
01. C
02. B
03. A
04. D
224
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
A
E
FFFVF
C
E
B
E
B
B
C
D
B
D
D
E
E
C
C
D
B
B
D
D
D
D
D
B
B
A
A
a) 3 milhões b) 1.333.333,33
C
D
E
E
D
C
D
E
40 homens e 80 mulheres
D
D
C
Com base no gráfico, qual item foi determinante para a
inflação de maio de 2008?
A) Alimentação e bebidas. B) Artigos de residência.
C) Habitação.
D) Vestuário.
E) Transportes.
c) 2,67
QUESTÕES DO ENEM
01. (ENEM-2009) Para o cálculo da inflação, utiliza-se,
entre outros, o Índice Nacional de Preços ao Consumidor
Amplo (IPCA), que toma como base os gastos das
famílias residentes nas áreas urbanas, com rendimentos
mensais compreendidos entre um e quarenta salários
mínimos. O gráfico a seguir mostra as variações do IPCA
de quatro capitais brasileiras no mês de maio de 2008.
02.(ENEM-2009) A importância do desenvolvimento da
atividade turística no Brasil relaciona-se especialmente
com os possíveis efeitos na redução da pobreza e das
desigualdades por meio da geração de novos postos
de trabalho e da contribuição para o desenvolvimento
sustentável regional.
No gráfico são mostrados três cenários – pessimista,
previsível, otimista – a respeito da geração de
empregos pelo desenvolvimento de atividades
turísticas.
De acordo com o gráfico, em 2009, o número de
empregos gerados pelo turismo será superior a
A) 602.900 no cenário previsível.
B) 660.000 no cenário otimista.
C) 316.000 e inferior a 416.000 no cenário previsível.
D) 235.700 e inferior a 353.800 no cenário pessimista.
E) 516.000 e inferior a 616.000 no cenário otimista.
03. (ENEM-2009) Nos últimos anos, o aumento da
população, aliado ao crescente consumo de água, tem
gerado inúmeras preocupações, incluindo o uso desta
na produção de alimentos. O gráfico mostra a
quantidade de litros de água necessária para a
produção de 1 kg de alguns alimentos.
225
Na região Norte, a frequência relativa de eleição dos
prefeitos no 2º turno foi, aproximadamente,
A) 42,86%
B) 44,44%
C) 50,00%
D) 57,14%
E) 57,69%
Com base no gráfico, para a produção de 100 kg de milho,
100 kg de trigo, 100 kg de arroz,100 kg de carne de porco
e 600 kg de carne de boi,a quantidade média necessária
de água, por quilograma de alimento produzido, é
aproximadamente igual a
A) 415 litros por quilograma.
B) 11.200 litros por quilograma.
C) 27.000 litros por quilograma.
D) 2.240.000 litros por quilograma.
E) 2.700.000 litros por quilograma.
04. (ENEM-2009) No quadro seguinte, são informados os
turnos em que foram eleitos os prefeitos das capitais de
todos os estados brasileiros em 2004.
05. (ENEM-2009) Cinco equipes A, B, C, D e E
disputaram uma prova de gincana na qual as
pontuações recebidas podiam ser 0, 1, 2 ou 3. A
mediadas cinco equipes foi de 2 pontos.
As notas das equipes foram colocadas no gráfico a
seguir, entretanto, esqueceram de representar as notas
da equipe D e da equipe E.
Mesmo sem aparecer as notas das equipes D e E,
pode-se concluir que os valores da moda e da mediana
são, respectivamente,
A) 1,5 e 2,0.
B) 2,0 e 1,5.
C) 2,0 e 2,0.
D) 2,0 e 3,0.
E) 3,0 e 2,0.
06. (ENEM-2009) Considere que as médias finais dos
alunos de um curso foram representadas no gráfico a
seguir.
Sabendo que a média para aprovação nesse curso
era maior ou igual a 6,0, qual foi a porcentagem de
alunos aprovados?
A) 18%
B) 21%
C) 36%
D) 50%
226
E) 72%
07. (ENEM-2009) Depois de jogar um dado em forma de
cubo e de faces numeradas de 1 a 6, por 10 vezes
consecutivas,e anotar o número obtido em cada jogada,
construí-se a seguinte tabela de distribuição de
freqüências.
A média, mediana e moda dessa distribuição de
frequências são respectivamente:
A) 3, 2 e 1
B) 3, 3 e 1
C) 3, 4 e 2
D) 5, 4 e 2
E) 6, 2 e 4
08. (ENEM-2010) Em sete de abril de 2004, um jornal
publicou o ranking de desmatamento, conforme o gráfico,
da chamada Amazônia Legal, integrada por nove estados.
Considerando-se que até 2009 o desmatamento cresceu
10,5% em relação aos dados de 2004, o desmatamento
médio por estado em 2009 está entre
A.100 km² e 900 km².
B. 1 000 km² e 2 700 km².
C. 2 800 km² e 3 200 km².
D. 3 300 km² e 4 000 km².
E. 4 100 km² e 5 800 km².
09. (ENEM-2010)Os dados do gráfico foram coletados por
meio da Pesquisa Nacional por Amostra de Domicílios.
Supondo-se que, no Sudeste, 14 900 estudantes foram
entrevistados nessa pesquisa, quantos deles possuíam
telefone móvel celular?
A) 5 513
B) 6 556
C) 7 450
D) 8 344
E) 9 536
10. (ENEM-2010) O gráfico a seguir representa o gasto
militar dos Estados Unidos, no período de 1988 a 2006.
Com base no gráfico, o gasto militar no início da guerra
no Iraque foi de
A. U$ 4.174.000,00.
B. U$ 41.740.000,00.
C. U$ 417.400.000,00.
D. U$ 41.740.000.000,00.
E. U$ 417.400.000.000,00.
11. (ENEM-2010) A classificação de um país no
quadro de medalhas nos Jogos Olímpicos depende do
número de medalhas de ouro que obteve na
competição, tendo como critérios de desempate o
número de medalhas de prata seguido do número de
medalhas de bronze conquistados. Nas Olimpíadas de
2004, o Brasil foi o décimo sexto colocado no quadro
de medalhas, tendo obtido 5 medalhas de ouro, 2 de
prata e 3 de bronze. Parte desse quadro de medalhas é
reproduzida a seguir.
227
Se o padrão na variação do período 2004/2010 se
mantiver nos próximos 6 anos, e sabendo que o
número de favelas em 2010 é 968, então o número de
favelas em 2016 será
A. menor que 1 150.
B. 218 unidades maior que em 2004.
C. maior que 1 150 e menor que 1 200.
D. 177 unidades maior que em 2010.
E. maior que 1 200.
Se o Brasil tivesse obtido mais 4 medalhas de ouro, 4 de
prata e 10 de bronze, sem alteração no número de
medalhas dos demais países mostrados no quadro, qual
teria sido a classificação brasileira no quadro de medalhas
das Olimpíadas de 2004?
A)13º
B) 12º
C) 11º
D) 10º
E) 9º
14. (ENEM-2010) O gráfico apresenta a quantidade de
gols marcados pelos artilheiros das Copas do Mundo
desde a Copa de 1930 até a de 2006.
12. (ENEM-2010) Os dados do gráfico seguinte foram
gerados a partir de dados colhidos no conjunto de seis
regiões metropolitanas pelo Departamento Intersindical de
Estatística e Estudos Socioeconômicos (DIEESE).
A partir dos dados apresentados, qual a mediana das
quantidades de gols marcados pelos artilheiros das
Copas do Mundo?
A) 6 gols
B) 6,5 gols
C) 7 gols
D) 7,3 gols
E) 8,5 gols
Supondo que o total de pessoas pesquisadas na região
metropolitana de Porto Alegre equivale a 250000, o
número de desempregados em março de 2010, nessa
região, foi de
A) 24 500.
B) 25 000.
C) 220 500.
D) 223 000.
E) 227 500.
15. (ENEM-2010) Marco e Paulo foram classificados
em um concurso. Para classificação no concurso o
candidato deveria obter média aritmética na pontuação
igual ou superior a 14. Em caso de empate na média, o
desempate seria em favor da pontuação mais regular.
No quadro a seguir são apresentados os pontos
obtidos nas provas de Matemática, Português e
Conhecimentos Gerais, a média, a mediana e o desvio
padrão dos dois candidatos.
Dados dos candidatos no concurso
13. (ENEM-2010) O gráfico mostra o número de favelas no
município do Rio de Janeiro entre 1980 e 2004,
considerando que a variação nesse número entre os anos
considerados é linear.
O candidato com pontuação mais regular, portanto
mais bem classificado no concurso, é
A. Marco, pois a média e a mediana são iguais.
B. Marco, pois obteve menor desvio padrão.
C. Paulo, pois obteve a maior pontuação da tabela, 19
em Português.
D. Paulo, pois obteve maior mediana.
E. Paulo, pois obteve maior desvio padrão.
228
15. (ENEM-2010) O quadro seguinte mostra o
desempenho de um time de futebol no último campeonato.
A coluna da esquerda mostra o número de gols marcados
e a coluna da direita informa em quantos jogos o time
marcou aquele número de gols.
Se X, Y e Z são, respectivamente, a média, a mediana e a
moda desta distribuição, então
A. X = Y < Z.
B. Z < X = Y.
C. Y < Z < X.
D. Z < X < Y.
E. Z < Y < X.
16. (ENEM-2010) Para conseguir chegar a um número
recorde de produção de ovos de Páscoa, as empresas
brasileiras começam a se planejar para esse período com
um ano de antecedência. O gráfico a seguir mostra o
número de ovos de Páscoa produzidos no Brasil no
período de 2005 a 2009.
Analisando os dados percentuais do gráfico, qual a
diferença entre o maior e o menor centro em
crescimento no pólo das indústrias?
A) 75,28
B) 64,09
C) 56,95
D) 45,76
E) 30,07
18. (ENEM-2013) Cinco empresas de gêneros
alimentícios encontram-se à venda. Um empresário,
almejando ampliar os seus investimentos, deseja
comprar uma dessas empresas. Para escolher qual
delas irá comprar, analisa o lucro (em milhões de reais)
de cada uma delas, em função de seus tempos (em
anos) de existência, decidindo comprar a empresa que
apresente o maior lucro médio anual.
O quadro apresenta o lucro (em milhões de reais)
acumulado ao longo do tempo (em anos) de existência
de cada empresa.
De acordo com o gráfico, o biênio que apresentou maior
produção acumulada foi
A. 2004-2005.
B. 2005-2006.
C. 2006-2007.
D. 2007-2008.
E. 2008-2009.
O empresário decidiu comprar a empresa
A) F.
B) G.
C) H.
D) M.
E) P.
17. (ENEM-2013) A cidade de Guarulhos (SP) tem o 8º
PIB municipal do Brasil, além do maior aeroporto da
América do Sul. Em proporção, possui a economia que
mais cresce em indústrias, conforme mostra o gráfico.
19. (ENEM-2013) Deseja-se postar cartas não
comerciais, sendo duas de 100 g, três de 200 g e uma
de 350 g. O gráfico mostra o custo para enviar uma
carta não comercial pelos Correios:
229
A quantidade total de arroz, em toneladas, que deverá
ser produzida no período de 2012 a 2021 será de
A) 497,25.
B) 500,85.
C) 502,87.
D) 558,75.
E)563,25.
O valor total gasto, em reais, para postar essas cartas é
de
A) 8,35.
B) 12,50.
C) 14,40.
D) 15,35.
E) 18,05.
20. (ENEM-2013) Foi realizado um levantamento nos 200
hotéis de uma cidade, no qual foram anotados os valores,
em reais, das diárias para um quarto padrão de casal e a
quantidade de hotéis para cada valor da diária. Os valores
das diárias foram: A = R$ 200,00; B = R$ 300,00; C = R$
400,00 e D = R$ 600,00. No gráfico, as áreas representam
as quantidades de hotéis pesquisados, em porcentagem,
para cada valor da diária.
O valor mediano da diária, em reais, para o quarto padrão
de casal nessa cidade, é
A) 300,00.
B) 345,00.
C) 350,00.
D) 375,00.
E)400,00.
21. (ENEM-2013)As projeções para a produção de arroz
no período de 2012 - 2021, em uma determinada região
produtora, apontam para uma perspectiva de crescimento
constante da produção anual. O quadro apresenta a
quantidade de arroz, em toneladas, que será produzida
nos primeiros anos desse período, de acordo com essa
projeção.
22. (ENEM-2013) As notas de um professor que
participou de um processo seletivo, em que a banca
avaliadora era composta por cinco membros, são
apresentadas no gráfico. Sabe-se que cada membro da
banca atribuiu duas notas ao professor, uma relativa
aos conhecimentos específicos da área de atuação e
outra, aos conhecimentos pedagógicos, e que a média
final do professor foi dada pela média aritmética de
todas as notas atribuídas pela banca avaliadora.
Utilizando um novo critério, essa banca avaliadora
resolveu descartar a maior e a menor notas atribuídas
ao professor.
A nova média, em relação à média anterior, é
A) 0,25 ponto maior.
B) 1,00 ponto maior.
C) 1,00 ponto menor.
D) 1,25 ponto maior.
E) 2,00 pontos menor.
23. (ENEM-2013)Uma falsa relação
O cruzamento da quantidade de horas estudadas como
desempenho no Programa Internacional de Avaliação
de Estudantes (Pisa) mostra que mais tempo na escola
não é garantia de nota acima da média.
230
2001. Nesse período, o tamanho da frota de veículos
mudou pouco, tendo no final de 2008 praticamente o
mesmo tamanho que tinha em 2001.
O gráfico a seguir mostra um índice de produtividade
utilizado pelas empresas do setor, que é a razão entre
o total de passageiros transportados por dia e o
tamanho da frota de veículos.
Dos países com notas abaixo da média nesse exame,
aquele que apresenta maior quantidade de horas de
estudo é
A) Finlândia.B) Holanda.C) Israel.
D) México.E) Rússia.
24. (ENEM-2013) O índice de eficiência utilizado por um
produtor de leite para qualificar suas vacas é dado pelo
produto do tempo de lactação (em dias) pela produção
média diária de leite(em kg), dividido pelo intervalo entre
partos (em meses).
Para esse produtor, a vaca é qualificada como eficiente
quando esse índice é, no mínimo, 281 quilogramas por
mês, mantendo sempre as mesmas condições de
manejo(alimentação, vacinação e outros). Na comparação
de duas ou mais vacas, a mais eficiente é a que tem maior
índice.
A tabela apresenta os dados coletados de cinco vacas:
Após a análise dos dados, o produtor avaliou que a vaca
mais eficiente é a
A) Malhada.
B) Mamona.
C) Maravilha.
D) Mateira.
E) Mimosa.
25. (ENEM-2009)Dados da Associação Nacional de
Empresas de Transportes Urbanos (ANTU) mostram que o
número de passageiros transportados mensalmente nas
principais regiões metropolitanas do país vem caindo
sistematicamente. Eram 476,7 milhões de passageiros em
1995, e esse número caiu para 321,9 milhões em abril de
Disponível em: http://www.ntu.org.br.
Acesso em 16 jul. 2009 (adaptado).
Supondo que as frotas totais de veículos naquelas
regiões metropolitanas em abril de 2001 e em outubro
de 2008 eram do mesmo tamanho, os dados do gráfico
permitem inferir que o total de passageiros
transportados no mês de outubro de 2008 foi
aproximadamente igual a
A) 355 milhões.
B) 400 milhões.
C) 426 milhões.
D) 441 milhões.
E) 477 milhões.
26.(ENEM-2009) A suspeita de que haveria uma
relação causal entre tabagismo e câncer de pulmão foi
levantada pela primeira vez a partir de observações
clínicas. Para testar essa possível associação, foram
conduzidos inúmeros estudos epidemiológicos. Dentre
esses, houve o estudo do número de casos de câncer
em relação ao número de cigarros consumidos por dia,
cujos resultados são mostrados no gráfico a seguir.
Centers for Disease Control and Prevention CDC-EIS
Summer Course – 1992 (adaptado).
De acordo com as informações do gráfico,
A) o consumo diário de cigarros e o número de casos
de câncer de pulmão são grandezas inversamente
proporcionais.
B) o consumo diário de cigarros e o número de casos
de câncer de pulmão são grandezas que não se
relacionam.
C) o consumo diário de cigarros e o número de casos
de câncer de pulmão são grandezas diretamente
proporcionais.
231
D) uma pessoa não fumante certamente nunca será
diagnosticada com câncer de pulmão.
E) o consumo diário de cigarros e o número de casos de
câncer de pulmão são grandezas que estão relacionadas,
mas sem proporcionalidade.
27.(ENEM-2009) Brasil e França têm relações comerciais
há mais de 200 anos. Enquanto a França é a 5ª nação
mais rica do planeta, o Brasil é a 10ª, e ambas se
destacam na economia mundial. No entanto, devido a uma
série de restrições, o comércio entre esses dois países
ainda não é adequadamente explorado, como mostra a
tabela seguinte, referente ao período 2003-2007.
Investimen tos Bilaterais
(em milhões de dólares)
Ano Brasil na França França no Brasil
2003
367
825
2004
357
485
2005
354
1.458
2006
539
744
2007
280
1.214
Disponível em: www.cartacapital.com.br.
Acesso em: 7 jul. 2009.
Os dados da tabela mostram que, no período considerado,
os valores médios dos investimentos da França no Brasil
foram maiores que os investimentos do Brasil na França
em um valor
A) inferior a 300 milhões de dólares.
B) superior a 300 milhões de dólares, mas inferior a 400
milhões de dólares.
C) superior a 400 milhões de dólares, mas inferior a 500
milhões de dólares.
D) superior a 500 milhões de dólares, mas inferior a 600
milhões de dólares.
E) superior a 600 milhões de dólares.
28.(ENEM/2009) A tabela mostra alguns dados da
emissão de dióxido de carbono de uma fábrica, em função
do número de toneladas produzidas.
Produção
Emissão de dióxido de carbono
(em toneladas)
(em partes por milhão - ppm)
1,1
2,14
1,2
2,30
1,3
2,46
1,4
2,64
1,5
2,83
1,6
3,03
1,7
3,25
1,8
3,48
1,9
3,73
2,0
4,00
Cadernos do Gestar II, Matemática TP3.
Disponível em: www.mec.gov.br. Acesso em: 14 jul. 2009.
Os dados na tabela indicam que a taxa média de variação
entre a emissão de dióxido de carbono (em ppm) e a
produção (em toneladas) é
A) inferior a 0,18.
B) superior a 0,18 e inferior a 0,50.
C) superior a 0,50 e inferior a 1,50.
D) superior a 1,50 e inferior a 2,80.
E)superior a 2,80.
29.(ENEM/2009) Suponha que a etapa final de uma
gincana escolar consista em um desafio de
conhecimentos. Cada equipe escolheria 10 alunos para
realizar uma prova objetiva, e a pontuação da equipe
seria dada pela mediana das notas obtidas pelos
alunos. As provas valiam, no máximo, 10 pontos cada.
Ao final, a vencedora foi a equipe Ômega, com 7,8
pontos, seguida pela equipe Delta, com 7,6 pontos. Um
dos alunos da equipe Gama, a qual ficou na terceira e
última colocação, não pôde comparecer, tendo
recebido nota zero na prova. As notas obtidas pelos 10
alunos da equipe Gama foram 10; 6,5; 8; 10; 7; 6,5; 7;
8; 6; 0.
Se o aluno da equipe Gama que faltou tivesse
comparecido, essa equipe
A) teria a pontuação igual a 6,5 se ele obtivesse nota 0.
B) seria a vencedora se ele obtivesse nota 10.
C) seria a segunda colocada se ele obtivesse nota 8.
D)
permaneceria
na
terceira
posição,
independentemente da nota obtida pelo aluno.
E) empataria com a equipe Ômega na primeira
colocação se o aluno obtivesse nota 9.
30.(ENEM/2009) Na tabela, são apresentados dados
da cotação mensal do ovo extra branco vendido no
atacado, em Brasília, em reais, por caixa de 30 dúzias
de ovos, em alguns meses dos anos 2007 e 2008.
Mês
Outubro
Novembro
Dezembro
Janeiro
Fevereiro
Março
Abril
Cotação
R$ 83,00
R$ 73,10
R$ 81,60
R$ 82,00
R$ 85,30
R$ 84,00
R$ 84,60
Ano
2007
2007
2007
2008
2008
2008
2008
De acordo com esses dados, o valor da mediana das
cotações mensais do ovo extra branco nesse período
era igual a
A) R$ 73,10.
B) R$ 81,50.
C) R$ 82,00.
D) R$ 83,00.
E) R$ 85,30.
GABARITO
01. A
02. E
03. B
04. A
05. C
06. E
07. B
08. C
09. D
10. E
232
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
B
A
C
B
B
E
C
B
D
C
D
B
C
D
A
E
D
D
D
D
233
CURSO DE MATEMÁTICA
HAMILTON E ALEX
 Semi-reta: Seja r uma reta dada e um ponto
O qualquer pertencente a ela. A região da reta r que
tem o ponto O como origem e que passa por um ponto
B, por exemplo, denomina-se semi-reta OB .
GEOMETRIA PLANA
CUIDADOS IMPORTANTES
r
1º - NUNCA PARTICULARIZE UMA FIGURA
Quando esboçar uma figura seja o mais genérico
possível.
Ex.: Ao desenhar um quadrilátero, não tente classificálo em uma categoria específica ( quadrado, retângulo,
paralelogramo ) desenhe um quadrilátero qualquer, com
lados e ângulos diferentes, como o da figura abaixo.
O
 Segmento de reta:
É a parte da reta
compreendida por dois pontos distintos especificados.
Os pontos A e B são os extremos do segmento.
A
B
B
A
D
B
r
Reta suporte do
segmento AB
C
ÂNGULOS
2º - NUNCA CLASSIFIQUE UMA FIGURA POR SUA
APARÊNCIA

Não conclua, por exemplo, que um triângulo é
equilátero só porque seus lados “parecem” iguais.
No triângulo ao lado,
os lados podem ou não
ter o mesmo tamanho.
RIGIÃO CONVEXA
Uma região é convexa se, e somente se, quaisquer dois
pontos distintos
A
e
B
dessa região
são
extremidades de um segmento de reta AB totalmente
contido nessa região.
Ex.:
____
AB  
A

B
Não considere que um triângulo é retângulo só
porque um de seus ângulos “parece” medir 90º .
A
B

Nota : Observe que a reta é um conjunto de pontos
convexos pois, para todo ponto A e para todo
ponto B pertencentes à reta, o segmento AB está
totalmente contido nessa reta.
O triângulo ao lado pode
ser ou não retângulo.
C
A
B
s
____
 A,  B e  r ( A  B, A  r, B  r )  AB  r
PONTO, RETA E PLANO
Os mais simples entes geométricos imaginados
são: Ponto, reta e plano. Eles são o ponto de partida
para a construção das figuras geométricas.
A

( Ponto )

r
( reta )
REGIÃO CÔNCAVA
Nem todos os segmentos
contidos nessa região.
Ex.:
( plano )
Por definição, reta e plano são entes geométricos
ilimitados.
AB
estão totalmente
B
A
234
CURSO DE MATEMÁTICA
SEMI-PLANO
HAMILTON E ALEX
RESOLVA AS OPERAÇÕES ABAIXO
Uma reta r contida num plano qualquer divide esse
plano em dois semi-planos opostos em relação à essa
reta r.
r
Ex.:
135º 57’ 49”
+ 81º 34’ 36”
40º 31’ 25”
x
152º 1’ 40”
5
3
’’
’
’ e ’’ são semi-planos opostos em relação à reta
r.

Ângulos
A
região
côncava
O

O RADIANO: É a medida angular, formada pelos
raios de uma circunferência, quando o arco
compreendido por esses raios tiver o mesmo
comprimento do raio.
região
convexa
1 rad  57,32º
r
r
B
1 rad
r
 rad = 180º
Ângulo AÔB = 
Não esqueça que   3,14 e que  rad = 180°
UNIDADES DE MEDIDA DE UM
ÂNGULO
ÂNGULOS ESPECIAIS


1
O GRAU : É
da circunferência. Por definição,
360
uma circunferência mede 360º.

SUBMÚLTIPLOS DO GRAU
Dois submúltiplos do grau merecem destaque: o
minuto e o segundo.
1
 Minuto: Um minuto ( 1’ ) é igual a
do
60
1º
grau; 1’ =
, logo:
60
1º = 60’
Ângulo Reto
É todo ângulo que medir 90º.

Ângulo agudo
É todo ângulo maior que 0º e menor que 90º.
A
O
C


1
Segundo: Um segundo ( 1’’ ) é igual a
do
60
1'
minuto; 1’’ =
, logo:
60
Ângulo Obtuso
É todo ângulo maior que 90º e menor que 180º.
A
B
O
1’ = 60’’
Observe que:
90º = 89º 59’ 60’’
180º = 179º 59’ 60’’

Ângulo Nulo
É aquele cujos lados coincidem. Sua medida é 0º.
O
B
A
235
CURSO DE MATEMÁTICA


Ângulo Raso
É aquele cujos lados são semi-retas opostas. Sua
medida é 180º.
AÔB = 180º
HAMILTON E ALEX
Ângulos Suplementares
São dois ângulos onde a soma de suas
medidas é igual a 180º.
180º
A
B
O


O ângulo raso também é chamado de “dois retos”.
 +  = 180º
Suplemento de um Ângulo x

Ângulos Opostos Pelo Vértice
Dois ângulos são opostos pelo vértice se, e
somente se, os lados de um deles são as respectivas
semi-retas do outro.
A
C
O
B
Sx = 180º – x
Observe que:

A medida de um ângulo é “x”

A metade da media de um ângulo é

D
Cx
2
Ângulos opostos pelo vértice são congruentes.
AÔB  CÔD

 Bissetriz de um ângulo
É uma semi-reta que tem origem no vértice e que
divide esse ângulo ao meio( em duas partes
congruentes ).
A
( Bissetriz de AÔB )
x
x
O

x
2
A metade do complemento de um ângulo é:
90º x
2
O complemento da metade de um ângulo é:
90º –

ou
x
2
Replemento de um Ângulo x
Rx = 360º – x
B
Ângulos Complementares

São dois ângulos onde a soma de suas
medidas é igual a 90º.
Ex = 270º – x
Esplemento de um Ângulo x


 +  = 90º
RETAS PERPENDICULARES
Complemento de um Ângulo x
Cx = 90º – x
Duas retas são perpendiculares ( símbolo  ) se, e
somente se, são concorrentes (único ponto em comum)
e formarem ângulos de 90º entre si.
Demonstração:
A
Cx
x
O
AÔB = 90º;
Se BÔC = x , então
Cx + x = 90º ; Logo :
C
B
Cx = 90º – x
236
CURSO DE MATEMÁTICA
Distância de um Ponto P a uma Reta r
HAMILTON E ALEX

É a distância do ponto P à sua projeção ortogonal
P’ sobre a reta r.
P
Quando os ângulos entre duas retas paralelas
apresentam-se na forma da figura abaixo, temos
que:
a+c+e = b+d
a
b
r
P’
c
d
e
Retas Paralelas Interceptadas Por Uma
Transversal
a
c
e
g
b
Região
Externa
d
Região
Interna
f
Região
Externa
h
Quando duas retas paralelas são interceptadas por uma
transversal, oito ângulos são determinados. Dois a dois
estes ângulos podem ser :

e
e
e
e
e
f
g
h
Ângulos de mesma medida
( Congruentes )
Ângulos Colaterais Externos
a e g
b e h

Ângulos de mesma medida
( Congruentes )
Ângulos Alternos Internos
c e f
d e e

2) Sejam AB = 12 cm e BC = 20 cm segmentos
adjacentes e sejam M e N os pontos médios de
AB e AC , respectivamente. Podemos afirmar que
a medida do segmento MN é :
a) 10 cm
b) 12 cm
c) 16 cm
d) 18 cm
e) 20 cm
Ângulos de mesma medida
( Congruentes )
Ângulos Alternos Externos
a e h
b e g

1) As bissetrizes internas de dois ângulos adjacentes
AÔB e BÔC formam um ângulo de 54º. Qual a
medida, em graus, do ângulo AÔC ?
A) 104º
B) 108º
C) 144º
D) 156º
E) 168º
Ângulos Correspondentes
a
b
c
d

EXERCÍCIOS
São Suplementares
a + g = 180º
b + h = 180º
Ângulos Colaterais Internos
c e e
d e f
São Suplementares
c + e = 180º
d + f = 180º
3) ( UFMG ) Os pontos A, B, C e D são colineares
e tais que AB = 6 cm, BC = 2 cm, AC = 8 cm e
BD = 1 cm. Nessas condições, uma possível
disposição desses pontos é :
a) ADBC
b) ABCD
c) ACBD
d) BCDA
4)
( PUC – MG ) Uma circunferência é dividida em
sete arcos de medidas iguais. Dente as alternativas,
o valor que mais se aproxima da medida de cada
um desses arcos é:
a) 51º 43’
b) 52º
c) 51º 25’ 42”
d) 51º 25’ 10”
e) 53º
237
CURSO DE MATEMÁTICA
5)
( Mackenzie – SP ) A figura abaixo mostra dois
ângulos adjacentes suplementares.
B
C
O
A
Podemos afirmar que:
a) As bissetrizes dos ângulos AÔB e BÔC são
perpendiculares.
b) A medida do ângulo AÔB é a metade da
medida do ângulo BÔC.
c) O ângulo BÔC mede o triplo de AÔB.
d) O ângulo formado pelas bissetrizes dos ângulos
AÔB e BÔC tem medida menor que 90º.
e) N.d.a.
6) ( Cescem – SP ) A medida de um ângulo está para
a medida do seu complemento assim como 1 está
para 5. Esse ângulo mede:
a) 75º
b) 20º
c) 10º
d) 15º
e) 25º
7) ( UFPA ) Na figura abaixo, as retas r e s são
perpendiculares e as retas m e n são paralelas.
Então, a medida do ângulo , em graus, é igual a:
s
A) 70
r
B) 60
C) 45
m

D) 40
E) 30
20º
n
8) ( UFPI ) O complemento de um ângulo é igual à
terça parte do suplemento desse ângulo. A medida
desse ângulo é:
a) 35º
b) 40º
c) 45º
d) 50º
e) 55º
9)
( UFMG ) Se a medida de um ângulo é 26º 40’
51”, sua terça parte mede:
a) 8º 13’ 17”
b) 8º 13’ 37”
c) 8º 33’ 37”
d) 8º 53’ 17”
e) 8º 53’ 37”
10) ( UECE ) O ângulo igual a
5
do seu suplemento
4
HAMILTON E ALEX
a)
b)
c)
d)
100º
144º
36º
80º
11) ( UFES ) O triplo do complemento de um ângulo é
igual à terça parte do suplemento desse ângulo.
Esse ângulo mede:
7
a)
rad
8
5
b)
rad
16
7
rad
c)
4
7
d)
rad
16
12) ( Itaúna ) A soma de um ângulo com a quarta parte
de seu suplemento vale 108º. A metade desse
ângulo vale :
a) 42º
b) 60º
c) 72º
d) 80º
e) 84º
13) ( U.F.Uberlândia ) Dois ângulos consecutivos são
complementares. Então, o ângulo formado pelas
bissetrizes desses ângulos é :
a) 20º
b) 30º
c) 35º
d) 40º
e) 45º
14) ( UFMG ) As bissetrizes de dois ângulos adjacentes
formam um ângulo de 46º. Se um ângulo mede
32º, a medida do outro é :
a) 23º
b) 39º
c) 55º
d) 60º
e) 62º
15) ( UFMG ) Na figura BE  ED , AE  EC e AEˆ D =
B
144º . O ângulo BEˆ C mede :
A
a) 30º
C
b) 32º
c) 34º
d) 36º
D
E
e) 54º
mede :
238
CURSO DE MATEMÁTICA
16) ( UFMG ) Na figura, OC é a bissetriz do ângulo
AÔB, BÔD = 50º e AÔD = 22º . A medida do
ângulo DÔC é :
B
a) 36º
b) 28º
c) 22º
C
O
d) 16º
D
e) 14º
A
17) ( FCM Santos – SP ) Às 9h 10min, o ângulo
formado pelos ponteiros de um relógio é:
a) 150º
b) 147º 30’
c) 145º
d) 160º
e) n.d.a
18) ( Cesgranrio ) As retas r e s da figura são
paralelas cortadas pela transversal t . Se o ângulo
B̂
a)
b)
c)
d)
é o triplo de  , então B̂ –  é :
90º
85º
80º
75º
B
HAMILTON E ALEX
21) ( FEI – SP ) Na figura, as retas r e s são
paralelas. A medida do ângulo indicado com x é:
a) 70
x
b) 50
2x + 20º
c) 60
r
d) 85
e) 65
70º
s
22) Numa gincana, a equipe "Já Ganhou" recebeu o
seguinte desafio:
Na cidade de Curitiba, fotografar a construção
localizada na rua Marechal Hermes no número igual
à nove vezes o valor do ângulo  da figura a
seguir:
Se a Equipe resolver corretamente o problema irá
fotografar a construção localizada no número:
r
a) 990.
b) 261.
r//s
c) 999.
29º
d) 1026.
75º
e) 1053
Â
65º
t
A
s
r
s
19) ( UniUb – 2000 ) Considere a figura abaixo em que
as retas p e q são paralelas e as retas r e s
são perpendiculares. Sendo  = 36º, qual é a
medida, em graus, do ângulo  ?
23) ( F. C. Chagas – SP ) Na figura seguinte tem-se r
// s ; t e u são transversais ; o valor de  + 
é?
a) 140º
70º
s
20º
b) 130º
c) 120º
d) 100º

e) 90º
r

u
t
r

24) ( PUC ) Na figura, r // s, então x vale ?
p
r
10º
q

s
x
20) ( Fuvest – SP ) Na figura, as retas r e s são
paralelas, o ângulo 1 mede 45º e o ângulo 2
mede 55º. A medida em graus do ângulo 3 é:
a) 50º
r
1
b) 55º
c) 60º
d) 80º
3
e) 100º
2
s
s
25) Na figura a seguir temos r//s e t//u//v. Com base
nos estudos dos ângulos formados por retas
paralelas cortadas por uma transversal pode-se
afirmar que:
I – O ângulo X mede 127° 30'.
II – O ângulo Y mede 117°.
III – O ângulo Z mede 64° 30'.
Analise as proposições acima e assinale a
alternativa correta.
a) Somente as afirmações I e II estão corretas.
b) Somente as afirmações I e III estão corretas.
239
CURSO DE MATEMÁTICA
c) Somente a afirmação I está correta.
d) As afirmações I, II e III estão corretas.
e) Somente as afirmações II e III estão corretas.
26) ( UFSC ) Na figura a seguir sabe-se que r// s// t. A
diferença x – y é:
a) 20º
20º
b) 22º
r
c) 24º
d) 26º
s
y
e) 28º
HAMILTON E ALEX
GABARITO
1) B
2) A
3) A
8) C
9) E
10) A
4) C
15) D
16) E
17) C
21) B
22) C
23) B
27) B
28) A
5) A
11) D
18) A
6) D
12) A
7) A
13)E 14) D
19) 126º
24) 100º
20) E
25) A
26) C
TRIÂNGULOS
É toda figura plana formada por segmentos de
retas que têm três lados e três ângulos.
A
t
x
112º
27) ( PUC – PR ) Na figura, as retas r
paralelas. O valor de x é:
a) 38º 30’
b) 39º 30’
c) 40º 30’
d) 39º
e) 40º
C
B
x
e s são

r
PERÍMETRO
É a soma das medidas dos lados do triângulo e é
indicada por 2P.
2P = AB + BC + AC
3x
79º
s
28) (FIP-2013) Sobre um relógio de forma circular,
graduado de 1 a 12, sendo os dígitos igualmente
espaçados entre si, pode-se afirmar corretamente que:
A) O menor ângulo formado por seus ponteiros das
horas e minutos quando estiver marcando 3h 25min
mede 47º30’.
B) O maior ângulo formado por seus ponteiros das
horas e minutos quando estiver marcando 14h 20min
mede 210º.
C) O maior ângulo formado por seus ponteiros das
horas e minutos quando estiver marcando 3h 25min
mede 254º45’.
D) O menor ângulo formado por seus ponteiros das
horas e minutos quando estiver marcando 14h 20min
mede 52º.

LEI DE FORMAÇÃO DE UM TRIÂNGULO
( DESIGUALDADE TRIANGULAR )
Qualquer um dos lados de um triângulo tem que ser
menor que a soma e maior que a diferença em
módulo dos outros dois lados.
x
y
|x–y|  z  x+y
|z–y|  x  z+y
z
|x–z|  y  x+z
Classificação:
 Quanto aos ângulos:
Retângulo: Triângulo que possui um ângulo reto
(ângulo de 90º)
c
a
2
2
2
a = b +c
b
240
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Apenas em “triângulos retângulos” podemos
usar o teorema de PITÁGORAS :
2
2
Obs.: Oposto ao maior ângulo de um triângulo temse o maior lado; e vice versa.
A
2
a = b + c
80º
c
60º
B
Acutângulo: Triângulo que possui 3 ângulos
a > b > c
b
40º
C
a
agudos (menor que 90º)
c
Soma dos ângulos Internos de um Triângulo
a
2
2
2
a < b +c
a
a + b + c = 180º
b
b
c
Obtusângulo: Triângulo que possui um ângulo
obtuso (maior que 90º)
Medida de um ângulo externo
a
2
2
2
a > b +c
b
a
c
Ex.: Verifique se o triângulo de lados medindo 4 cm, 5
cm e 6 cm, caso existir, é retângulo, obtusângulo ou
acutângulo.
ê = â + b̂
e
b
A medida de um ângulo externo é igual à soma dos
ângulos internos não adjacentes a ele.
EXEMPLO:
1) Encontre a medida de cada ângulo interno no
triângulo ABC abaixo.
4x
 Quanto aos lados:
Escaleno: Triângulo que possui 3 lados diferentes.
x +10º
7x – 30º
Isósceles: Triângulo que possui pelo menos dois
lados congruentes.
base
A base é o lado com
medida diferente.
Os ângulos da base são congruentes.
Equilátero: Triângulo que possui os três lados
congruentes
 Os 3 ângulos medem 60º

Todo triângulo
isósceles.
equilátero
também
é
SEGMENTOS NOTÁVEIS NO TRIÂNGULO
Nos triângulos temos três segmentos que se
destacam, esses segmentos são chamados de
cevianas .
As cevianas são: medianas, bissetrizes e as alturas
do triângulo.

Mediana: Segmento do triângulo que tem um
extremo no vértice e o outro extremo no ponto
médio do lado oposto.
Mediana
241
CURSO DE MATEMÁTICA

Bissetriz interna: Semi reta que divide um ângulo
interno em dois ângulos congruentes.
 
HAMILTON E ALEX
CIRCUNCENTRO – Definição
O ponto de encontro das mediatrizes dos lados de um
triângulo é o circuncentro do triângulo.
Bissetriz

m3
Altura: Segmento de reta que tem um extremo no
vértice e o outro extremo no lado oposto ou
prolongamento desse. A altura, por definição, é
perpendicular ao lado ou ao prolongamento
desse.
H
H
PONTOS NOTÁVEIS NO TRIÂNGULO
BARICENTRO - Definição
O ponto de encontro das três medianas de um triângulo
é o baricentro do triângulo.
B
M2
G
C
m1  m2  m3 = { O }
 circuncentro é o ponto do plano do triângulo que
fica à igual distância de seus VÉRTICES .
ORTOCENTRO – Definição
O ponto de encontro das alturas de um triângulo é o
ortocentro do triângulo.
A
AH1BH2CH3 = {H}
As alturas são perpendiculares aos lados por ela
interceptados.
H2
H3
H
B
C
H1
C

Nota : Os únicos pontos notáveis que podem
ser externos ao triângulo são o CIRCUNCENTRO
e o ORTOCENTRO.

No triângulo ISÓSCELES, os três pontos
notáveis são COLINEARES.

No triângulo EQUILÁTERO, os três pontos
notáveis são COINCIDENTES.
{ G } = AM 1  BM2  CM3

O
 circuncentro é o centro da circunferência que
circunscreve o triângulo.
AG = 2 . GM1
M1
B
m2
m1
A
M3
A
Baricentro divide cada mediana em duas
partes tais que, a parte que contém o vértice
é o DOBRO da outra.
INCENTRO – Definição
O ponto de encontro das três bissetrizes internas de
um triângulo é o incentro do triângulo.
A
S3
I
B
S1
S2
AS1  BS2  CS3 = { I }
{ I } = {G} = {O} = {H}
C

Incentro é o centro da circunferência inscrita
no triângulo.

Incentro é o ponto do plano do triângulo que
fica à igual distância de seus LADOS .
242
CURSO DE MATEMÁTICA
Exercício
1) ( UFMG ) Num triângulo, dois lados medem 3 e 7.
Se a medida do terceiro lado pertence ao conjunto
x = { 2, 3, 4, 5, 10 }, então o terceiro lado mende :
a) 10
b) 5
c) 4
d) 3
e) 2
2) ( UNEB ) Os lados AB , BC , CD e DA de
um
quadrilátero
convexo
ABCD
medem
respectivamente 2, 4, 2 e 6. Se a medida de uma
das diagonais desse quadrilátero é um número
inteiro, essa diagonal mede :
a) 2
b) 4
c) 5
d) 6
e) 7
3) ( Fuvest – SP ) No quadrado ABCD de 12 de lado,
temos AE = 13 e CF = 3. O ângulo AÊF é agudo,
reto ou obtuso ?
Justifique.
A
6) ( PUC – SP ) Na figura BC = CA = AD = DE, o
ângulo CÂD mede:
A
a) 10º
b) 30º
c) 60º
d) 20º
40º
40º
e) 40º
B
D
C
E
E
7) ( PUC – SP ) Na figura abaixo, a = 100º e b =
110º. Quanto mede o ângulo x ?
x
a
b
8) (Fuvest - SP) Na figura, AB = AC, BX = BY e CZ =
CY. Se o ângulo  mede 40º, então o ângulo XYZ
mede:
C
Z
a)40º
b)55º
Y
c)60º
A
d)70º
e)65º
X
B
B
F
D
HAMILTON E ALEX
C
4) ( UFMG ) Os ângulos  e  da figura medem:
D
a)  = 20º;  = 30º
b)  = 30º;  = 20º
 
c)  = 60º;  = 20º
d)  = 20º;  = 20º
e)  = 10º;  = 20º
80º 80º
60º
A
B
C
5) (UFMG) Na figura abaixo, AB=AC, BD é bissetriz
de ABˆ C , CE é bissetriz de BCˆ D , a medida do
ˆ F é 140º. A medida do ângulo DÊC é:
ângulo AC
9) ( UFPA ) Na figura abaixo, os comprimentos dos
lados AB e BC do triângulo ABC são congruentes.
Qual a medida, em graus, de  ?
A) 18º
B) 20º
C) 25º
D) 22º
E) 17º
10) ( UNIMONTES – 2000 )
Dado um triângulo
isósceles ABC ( AB  AC ), com um caminho de três
segmentos congruentes AD  DB  BC, então a
medida, em graus, do ângulo CBˆ D , é :
a) 45º
A
b) 72º
c) 60º
d) 36º
D
A
a)
b)
c)
d)
e)
20º
30º
40º
50º
60º
B
E
C
D
140º
B
C
F
243
CURSO DE MATEMÁTICA
11) ( FAFEOD – 2000 ) Na figura abaixo, o triângulo
ABC é isósceles, com AB = AC, e nele está
inscrito o triângulo equilátero DEF. Se as medidas,
em graus, dos ângulos BD̂F
e DÊA são,
respectivamente, 50º e 80º, então é correto afirmar
que a medida, em graus, do ângulo CFE é igual a :
a) 45º
B
F
C
b) 65º
c) 55º
d) 75º
D
E
A
12) ( STA CASA – SP ) O triângulo ABC, representado
na figura abaixo, é isósceles de base BC. A medida
A
do ângulo x indicado é :
a) 90
20º
b) 100
c) 105
d) 110
e) 120


C
H
G
C
ˆ C é:
e 70º, pode-se afirmar que o valor de BO
A
105º
110º
115º
O
120º
125º
B
B
17) ( UFMG )
BM = CM
m
BÂD = CÂD
C
14) ( UFLA ) Na figura abaixo, o ponto O é o centro da
circunferência inscrita no triângulo ABC. Se os
ângulos ABˆ C e BÂC medem respectivamente
F
16) ( Cesgranrio ) Na figura, ABCD é um quadrado,
ADE e ABF são triângulo equiláteros. Se os
pontos C, A e M são colineares, então o ângulo
FÂM mede :
E
a) 75º
M
b) 80º
c) 82º 30’
A
D
d) 85º
e) 87º 30’
F
A
13) ( UFMG ) Observe a figura. Nessa figura, AB = BD
= DE e BD é bissetriz de EBˆ C . A medida de
AÊB, em graus, é :
D
a) 96º
b) 100º
E
c) 104º
d) 108º
e) 110º A
B
C
B
DG e EG, respectivamente, podemos afirmar que
a medida x do ângulo DÂE é igual a :
a) 108º
A
b) 115º
D
E
c) 120º
d) 130º
e) 135º
x
B
60º
A)
B)
C)
D)
E)
HAMILTON E ALEX
B
H
M
D
C
No triângulo ABC, as seguintes atribuições são feitas:
I - AH = altura, AM = mediana, m = bissetriz
II - AD = altura, AM = mediana, m = mediatriz
III - m = mediatriz, AM = mediana, AH = altura
IV - AD = bissetriz, AH = altura, m = mediatriz
Pode-se afirmar que:
a) I e II são verdadeiras
b) II e III são verdadeiras
c) II e IV são verdadeiras d) I e IV são verdadeiras
e) III e IV são verdadeiras
18) ( E. E. MAUÁ ) Na figura, BF e CE são
respectivamente, bissetrizes dos ângulos B e C
do triângulo ABC; calcule a medida do ângulo Â.
A
F
C
E
50º
15) ( Conc. Público – GDF ) Na figura abaixo, o
triângulo ABC representa a vista frontal da
sustentação de um telhado. Por questão de
economia, os segmentos CH, HD, DG, GE, EF, e
FB têm comprimentos iguais. Sabendo que os
triângulos CGD e BGE são isósceles de bases
B
C
244
CURSO DE MATEMÁTICA
19) Na figura sabe-se que os triângulos ABC e DEF
são equiláteros. Encontre a medida “x” do ângulo
E
F
H
POLÍGONOS
Polígono é uma figura plana, fechada, formada por
segmentos de reta consecutivos não-colineares, mais a
sua região interna.
CHˆ G indicado.
B
HAMILTON E ALEX
x

Polígono Convexo
Todos os ângulos internos são convexos( menores que
180º).
C
G
75º
65º
A
D

Polígono Côncavo
Possui pelo menos um ângulo interno maior que 180º.
20) ( CESESP ) Dentre os quatro centros principais de
um triângulo qualquer, há dois deles que podem se
situar no seu exterior, conforme o tipo do triângulo.
Assinale a alternativa em que os mesmos são
citados.
a) o baricentro e o ortocentro
b) o baricentro e o incentro
c) o circuncentro e o incentro
d) o circuncentro e o ortocentro
e) o incentro e o ortocentro
Elementos de um Polígono
Ângulo interno
A
B
E
Diagonal
Lado
Ângulo Externo
D
GABARITO
C
Vértice
1) B
2) C
3) Agudo
8) D
9) B 10) D
4) D
11) B
5) C
12) B
6) D
13) D
7) 30º
Lado: Segmento de reta que une dois vértices
consecutivos. ( BC ).
14) E
Vértice: Ponto de interseção de dois lados.
15) A
16) A
17) E
18) 80º
19) 40º
20) D
Diagonal: Segmento que une dois vértices não
consecutivos. ( EC ).
QUESTÃO EXTRA
Ângulo interno: Ângulo de “dentro” do polígono,
formado por dois lados consecutivos.
1) Na figura abaixo, ABC é um triângulo equilátero
e ABMN é um quadrado. Qual a medida do ângulo
?
Ângulo externo: Ângulo de “fora” do polígono, formado
por um lado e pelo prolongamento de outro lado
consecutivo.
N

M
C

Polígono Regular
Um polígono é regular, se e somente se, possui seus
lados e ângulos congruentes.
Octógono
regular
A
Hexágono
regular
Pentágono
regular
B
245
CURSO DE MATEMÁTICA
 Soma dos Ângulos Internos de um Polígono
Convexo Qualquer
Sn = ( n – 2 ) . 180º
para n ≥ 3 e n  |N.
 Soma dos Ângulos Externos de um Polígono
Convexo Qualquer
Se = 360º
Se o polígono for REGULAR, ainda temos:
A soma dos Ângulos
Internos será:
Sn = n . i
Logo:
A soma dos Ângulos
Externos será:
Se = n . e
Como, Se = 360º, temos:
i = Sn / n
360º = n . e , Logo:
e = 360º/n
ou
n = 360º / e
Onde “i” é o valor de um ângulo interno e “e” é o valor de
um ângulo externo.

Diagonais de um Polígono Convexo
HAMILTON E ALEX
EXERCÍCIO
1) Em um polígono convexo a quantidade de diagonais
é o triplo do número de lados, mais 5 unidades.
Esse polígono é :
a) Eneágono
b) Decágono
c) Undecágono d) Dodecágono
e) Pentadecágono
2) ( PUC – SP ) Qual é o polígono regular em que o
nº de diagonais é o dobro do nº de lados ?
a) dodecágono;
b) pentágono;
c) octógono;
d) heptágono;
e) hexágono.
3) ( PUC – PR ) O polígono convexo em que o
número de lados é igual ao número de diagonais é :
a) Pentágono
b) Heptágono
c) Eneágono
d) Dodecágono
4) ( ACAFE – SC ) Num polígono regular convexo, o
ângulo interno vale 3/2 do ângulo externo. O
polígono é:
a)
pentágono
b)
hexágono
c)
heptágono
d)
eneágono
5) ( UnB ) Num polígono convexo, o número de lados
é o dobro do número de diagonais. Calcule o
número de lados desse polígono.
Diagonais que Partem de um único Vértice:
Dv = n – 3
onde:
Dv é o n.º de diagonais por vértice.
n é o n.º de vértices ou lados.
Número Total de Diagonais de um Polígono:
D
( n 3 ) .n
2
Observação: Apenas em polígonos regulares ,
com número par de lados , algumas diagonais
passam pelo seu centro.
O número de diagonais que
passam pelo centro do
polígono será:
6) ( Fuvest – SP ) Dois ângulos internos de um
polígono convexo medem 130º cada um e os
demais ângulos internos medem 128º cada um. O
número de lados do polígono é :
a) 6
b) 7
c) 13
d) 16
e) 17
7) (UFMG) – Determine o ângulo formado pelas retas
suportes dos lados AB e CD de um pentágono
regular ABCDE.
A
a) 108º
E
b) 32º
B
c) 72º
d) 36º
D
C
e) 100º
Dc = n / 2
246
CURSO DE MATEMÁTICA
8) ( UERJ ) O decágono da figura abaixo foi dividido
em 9 partes: 1 quadrado no centro, 2 hexágonos
regulares e 2 triângulos equiláteros, todos com os
lados congruentes ao do quadrado, e mais 4 outros
triângulos.
Sendo T a área de cada triângulo equilátero e Q
a área do quadrado, pode-se concluir que a área do
decágono é equivalente a:
A) 14 T + 3 Q
B) 14 T + 2 Q
C) 18 T + 3 Q
D) 18 T + 2 Q
E) 16 T + Q
9) ( PUCCAMP ) A figura descreve o movimento de
um robô:
2m
HAMILTON E ALEX
c) Apenas a III
d) I e III
e) Apenas a II
12) (ENEM – 2011) O polígono que dá forma a essa
calçada é invariante por rotações, em torno de seu
centro, de
A) 45°.
B) 60°.
C) 90°
D) 120°.
E) 180°.
13) Na figura abaixo, determine a medida do ângulo 
em função de .
45º
3
2m
45º
A

Partindo de A, ele sistematicamente avança 2m e
gira 45º para a esquerda. Quando esse robô
retornar ao ponto A a trajetória percorrida terá
sido:
a)
Uma circunferência
b)
Um hexágono regular
c)
Um octógono regular
d)
Um decágono regular
2

2m
14) Calcule o valor de x na figura:
4x
x
4x
2x
2x
5x
10) (UFPA) A figura abaixo mostra um quadrado, um
pentágono regular e um hexágono regular que
foram unidos por alguns de seus lados.
A medida do ângulo  é:
A) 40º
B) 42º
C) 48º

D) 46º
E) 44º
11) (UNIMONTES) – Considere as afirmações:
I – Um polígono convexo é regular se, e somente
se, tem todos os lados congruentes.
II – A expressão Si = (n – 2).180º, é verdadeira para
todo polígono convexo de n lados (n 3).
III– O dodecágono possui, a partir de um de seus
vértices, tantas diagonais quantas são as diagonais
de hexágono.
Podemos concluir que a alternativa que apresenta
a(s) afirmativa(s) correta(s) é:
a) Apenas a I
b) II e III
15) ( MACK ) Os lados de um polígono regular de n
lados ( n > 4 ) são prolongados para formar uma
estrela. O número de graus em cada vértice da
estrela é:
360º
a)
n
(n  4).180º
n
(n  2).180º
c)
n
b)
d) 180º –
90º
n
16) ( Fuvest – SP ) A, B, C e D são vértices
consecutivos de um hexágono regular. A medida,
em graus, de um dos ângulos formados pelas
diagonais AC e BD é :
a) 90º
b) 100º
c) 110º
d) 120º
e) 150º
247
CURSO DE MATEMÁTICA
17 .(FIP-2013)
HAMILTON E ALEX
Qual das alternativas abaixo seria utilizada para a
criação de um mosaico de Escher?
A) Pentágono regular, quadrado e triângulo.
B) Hexágono regular, pentágono regular e triângulo
equilátero
C) Pentágono regular, quadrado e triângulo equilátero
D) Hexágono regular, quadrado e triângulo equilátero
GABARITO
1) B
Veja, nos passos a seguir, como Escher cria os seus
répteis:
2) D
3) A
4) A
5) n = 4
8) A
9) C 10) B
11) B
12) D
15) B
16) D
6) B
13) 6θ
7) D
14) 20º
17) D
Escher opta por utilizar hexágonos regulares como
ponto de partida, para criar um mosaico feito
exclusivamente com polígonos regulares. Ele teria
somente três opções, pois somente esses três permitem
ladrilhamento ou pavimentação. Isso ocorre, porque a
pavimentação só é possível, quando os ângulos
internos completam 360º ao se juntarem.
248
CURSO DE MATEMÁTICA
HAMILTON E ALEX
SEMELHANÇA DE TRIÂNGULOS
TEOREMA DE TALES
Se um feixe de retas paralelas é interceptado por
duas ou mais transversais, os segmentos determinados
nessas transversais são diretamente proporcionais.
Dois triângulos são semelhantes, se e somente se,
possuem pelo menos dois ângulos congruentes.
y
a
A
E
c
r//s//t//u
r
x
b
B
F
z
s
C
G
t
H
D
Se dois triângulos são semelhantes seus lados
correspondentes são proporcionais.
u
a b c
 
z x y
AB BC CD AC AD




EF FG GH EG EH
a b c 2p
  
z x y 2P
ou
E ainda temos:
Exemplo 1 : Qual o valor de
sabendo que r // s // t ?
x
2
2
2
 Área menor 
c
a
b

         

z
x
y
 Área Maior 
na figura abaixo
r
x + 12
TEOREMA FUNDAMENTAL DE SEMELHANÇA
x+9
s
x+2
x+4
t
x  12 x  9

x4
x 2
Se uma reta DE for paralela a qualquer lado de
um triângulo ABC, o triângulo BDE determinado será
semelhante ao triângulo ABC.
D
A
x  2 x  12 x  24  x  9 x  4 x  36
2
2
D
A
x  12
E
B
B
Exemplo 2 : Determine o valor de x, y, e z na figura
abaixo sabendo que r//s//t//u.
E
C
B
C
Observando a semelhança, temos:
r
x
3
BD DE BE


AB AC BC
s
y
14
6
t
z
12
Casos de semelhança
u
14 21

x
3
x 2
14 21

y
6
y 4
14 21

z
12
z8

Caso ( AA-- ) : Se dois triângulos possuem dois
ângulos congruentes, esses triângulos são
semelhantes.

Caso ( LAL ) : Se dois triângulos possuem dois
lados correspondentes proporcionais e o ângulo
249
CURSO DE MATEMÁTICA
compreendido por eles
triângulos são semelhantes.
bk
ak

congruentes,
esses
b
a
bk
EXEMPLO 4 (ÂNGULOS INTERNOS CONGRUENTES)
ˆ D . Determine a
No triângulo ABC abaixo, BÂC = CB
medida do segmento CD sabendo que BC = 6cm e AC
= 10cm.
B
Caso ( LLL ) : Se dois triângulos possuem lados
correspondentes proporcionais, esses triângulos
são semelhantes.
ak
HAMILTON E ALEX
A
C
D
b
a
c
ck
Exemplo 1: ( LADOS PARALELOS )
No triângulo ABC temos que BC//DE. Determine a
medida do segmento CE sabendo que BC = 8cm, DE =
6cm e AC = 10cm.
TEOREMA DA BISSETRIZ INTERNA
 
a
y
x
B
b
a b

x y
D
Exercícios
A
C
E
1)
Exemplo 2:( LADOS PARALELOS )
Na figura abaixo temos que os lados AB = 6 e CD = 4
são paralelos. Encontre a medida do lado CE, sabendo
que BE = 9.
( UnB ) Considere a figura abaixo, sabendo-se
que os segmentos AB, BC e
A’B’ tem
comprimentos
4 cm,
2 cm
e
8 cm,
respectivamente, determine o comprimento do
segmento B’C’.
A
Obs.: AA’ // BB’ // CC’
A’
C
A
a)
b)
c)
d)
E
2 cm
3 cm
4 cm
6 cm
B’
B
C’
C
D
B
Exemplo 3
( UNESP ) Na figura, B é um ponto do segmento de reta
AC e os ângulos DAB, DBE e BCE são retos. Se o
segmento AD = 6 dm, o segmento AC = 11 dm e o
segmento EC = 3 dm, as medidas possíveis de AB,
em dm, são:
a) 4,5 e 6,5
b) 7,5 e 3,5
c) 8 e 3
d) 7 e 4
e) 9 e 2
2) ( UNIRIO ) No desenho abaixo apresentado, as
frentes para a rua A dos quarteirões I e II
medem, respectivamente, 250 m e 200 m, e a
frente do quarteirão I para a rua B mede 40 m a
mais do que a frente do quarteirão II para a
mesma rua. Sendo assim, pode-se afirmar que a
medida em metros, da frente do menor dos dois
quarteirões para a rua B é:
a) 160
b) 180
c) 200
d) 220
e) 240
Rua A
I
II
Rua B
Ruas Paralelas
250
CURSO DE MATEMÁTICA
HAMILTON E ALEX
3) Na figura abaixo, as retas a, b e c são paralelas.
O valor de x é:
a) 1/2
2x + 1
3
b) 5/2
c) 7/2
d) 9/2
4
7) ( UFSE ) Na figura abaixo, são dados AC = 8 cm e
CD = 4 cm. A medida de BD é em cm :
a) 9
b) 10
A
c) 12
d) 15

e) 16

x+1
D
B
8)
4) ( Unicamp - SP ) A figura mostra um segmento AD
dividido em três partes:
AB = 2 cm, BC = 3 cm e
CD = 5 cm. O segmento AD’ mede 13 cm e as retas
BB’ e CC’ são paralelas a DD’. O comprimento dos
segmentos AB’, B’C’ e C’D’, em cm, é:
D
a) 2,3; 4,7; 6,0
C
b) 2,6; 4,4; 6,0
B
c) 2,6; 3,9; 6,5
d) 2,6; 4,0; 6,4 A
B’
D’
5) ( MAPOFEI ) Três terrenos tem frentes para a rua
“A” e para a rua “B” conforme a figura. As divisas
laterais são perpendiculares à rua “A”. Qual a
medida, em metros, da frente para a rua “B” de
cada lote, sabendo- se que a frente total para essa
rua é de 120 metros ?
a)
b)
c)
d)
160/3; 40; 80/3
180/3; 40; 70/3
60; 40; 20
140/3; 50; 30
Rua A
40
30
20
Rua B
6) ( UnB ) Determine o valor de x, na figura abaixo,
onde r, s e t são retas paralelas.
a)
b)
c)
d)
e)
21
22
23
24
25
( MACK – SP ) Na figura, DE é paralela a BC e
AM é bissetriz interna do triângulo ABC. Então
x + y é igual a:
A
a) 35
b) 30
x
6
c) 25
D
E
d) 20
5
e) 15
2
B
C’
C
6
M
y
C
9) ( UFPA ) Uma pessoa com 1,5 metro de altura
percebe que em determinado momento do dia
projeta uma sombra de 6 metros e que no mesmo
momento um prédio projeta uma sombra de 40
metros. Com base nestas informações pode-se
afirmar que a altura do prédio é:
A) 10 metros
B) 25 metros
C) 30 metros
D) 35 metros
E) 38 metros
10) ( ENEM 2009 ) A rampa de um hospital tem na sua
parte mais elevada uma altura de 2,2 metros. Um
paciente ao caminhar sobre a rampa percebe que
se deslocou 3,2 metros e alcançou uma altura de
0,8 metro. A distância em metros que o paciente
ainda deve caminhar para atingir o ponto mais alto
da rampa é
A) 1,16 metros.
B) 3,0 metros.
C) 5,4 metros.
D) 5,6 metros.
E) 7,04 metros.
11) (UFMG) Dois círculos de raios 6m e 4m têm centro
na altura relativa à base do triângulo isósceles da
figura e são tangentes exteriormente. A altura do
triângulo relativa à base, em metros, é:
a) 25
b) 26
c) 30
d) 32
e) 36
251
CURSO DE MATEMÁTICA
12) ( CESGRANRIO ) O losango ADEF está inscrito no
triângulo ABC, como mostra a figura. Se AB = 12m
e AC = 6m, o lado a do losango mede :
a) 5m
A
b) 3m
D
c) 2m
d) 4m
F
e) 8m
B
E
C
13) ( FUVEST ) Na figura, o triângulo ABC é retângulo
em A, ADEF é um quadrado, AB = 1 e AC = 3.
Quando mede o lado do quadrado ?
a) 0,70
B
b) 0,75
E
c) 0,80
D
d) 0,85
e) 0,90
A
F
C
14) No trapézio ABCD abaixo, temos AB = 4 cm e PE =
2.PA. Se E é ponto médio de CD, a medida da
base maior é:
A
B
a) 8
b) 12
P
c) 16
d) 20
C
E
D
15) ( UFMG ) Os lados de um triângulo ABC são AB =
15cm, BC = 10cm e AC = 20cm. Se AM = 3cm, o
perímetro, em cm, do paralelogramo MNCP é:
C
a) 26
b) 30
c) 32
P
N
d) 36
e) 54
A
M
HAMILTON E ALEX
- colocou-se no ponto P, em uma das margens do
rio, em frente a uma árvore A que havia crescido
bem rente à outra margem do rio.
- a partir do ponto P, em uma trajetória
perpendicular ao segmento PA, deu seis passos e
colocou uma estaca E no solo. Ainda na mesma
trajetória e no mesmo sentido, deu mais quatro
passos, marcando o ponto Q.
- a partir do ponto Q, deslocou-se na perpendicular
ao segmento PQ para o ponto F, de modo que o
ponto F, a estaca E e a árvore A ficassem
perfeitamente alinhados. A distância entre os pontos
Q e F corresponde a seis passos.
Como cada passo de Pedro mede 80 cm, a largura do
rio, em metros, é de aproximadamente
a) 5.
b) 6.
c) 7.
d) 8.
e) 9.
18) ( UFPA ) Uma fonte luminosa a 25 cm do centro de
uma esfera projeta sobre uma parede uma sombra
circular de 28 cm de diâmetro, conforme figura
abaixo. Se o raio da esfera mede 7 cm, a distância
(d) do centro da esfera até a parede, em cm, é:
A) 23
B) 24
C) 25
D) 27
E) 32
B
16) ( UFMG ) Na figura abaixo, consideremos os
quadrados de lados x, 6 cm e 9 cm. A área do
quadrado de lado x mede :
a) 9 cm
b) 12 cm
c) 15 cm
d) 16 cm
e) 19 cm
9
6
x
17) ( UFJF – MG ) Pedro precisa medir a largura do rio
que passa próximo ao seu sítio. Como não dispõe
dos equipamentos adequados para esse fim, e
lembrando-se de suas aulas de Matemática,
estabeleceu o seguinte procedimento:
19) ( UFMG ) No paralelogramo ABCD da figura, AB = 4
3 m, AD = 3 m e BM = 2 m. O segmento CN
mede :
A
B
3
a)
2
M
b)
3
D
C
N
c) 2 3
d)
5 3
2
e) 3 3
252
CURSO DE MATEMÁTICA
20) ( CESESP ) Considere a figura abaixo, onde G é o
baricentro do triângulo ABC.
Assinale a única alternativa que corresponde à
razão entre as áreas dos triângulos ABG e EGD.
a) 1
B
b) 2
c) 3
D
d) 4
G
e)12
A
E
C
21) ( MACK – 2001 ) O triângulo ABC da figura foi
dividido em duas partes de mesma área pelo
BC
segmento DE, que é paralelo a BC. A razão
DE
vale :
A
a) 2
3
b)
2
5
E
D
c)
2
d)
2
e)
3 2
2
B
C
22) .(FIP-2012) A figura a seguir mostra a planta de três
lotes, disponíveis para venda. Todos eles têm frente
tanto para a rua “Bela Vista” quanto para a rua
“Recanto”. As divisas laterais são perpendiculares
à rua “Bela Vista”.
Sabendo que a frente total para a rua “Recanto”
tem 180m, assinale a alternativa que indica as
medidas CORRETAS da frente dos lotes A, B e C
respectivamente:
HAMILTON E ALEX
Considere que a rampa que dá acesso ao Palácio do
Planalto tenha 4 metros de altura em sua parte mais
alta. Uma pessoa começou a subi-la e, após um tempo,
percebe que já caminhou 12,3 metros sobre a rampa.
Nesse instante, ela se encontra a 1,5 metro de altura
em relação ao solo.
De acordo com a situação apresentada, pode-se
concluir corretamente que, para atingir o ponto mais alto
da rampa, a pessoa ainda deve caminhar:
A) 32,8 metros.
B) 52,8 metros.
C) 20,5 metros.
D) 12,8 metros
24) (CESGRANRIO) Na figura dada, as circunferências
de centro P e S são ambas tangentes à reta l no
mesmo ponto Q e a reta que passa por P e R tangencia
a circunferência menor no ponto T. Sendo os raios das
circunferências respectivamente 8m e 3m, a medida do
segmento QR é:
l
a) 4 m
b) 6 m
R
T
c) 8 m
Q
d) 2 m
P
S
e) n.r.a
DESAFIOS
1) Em um triângulo ABC, os lados AB = 9 e AC =
12. Sabendo que o incentro e o baricentro desse
triângulo estão em uma reta paralela ao lado BC,
pode-se afirmar que a medida de BC é:
A
a) 10
b) 10,5
c) 11
d) 11,5
e) 12
B
A) 100 m, 55 m e 25m.
B) 70 m, 60 m e 50 m.
C) 80 m, 70 m e 50 m.
D) 80 m, 60 m e 40 m.
C
2) ( ITA – SP ) O comprimento da diagonal de um
pentágono regular de lado medindo 1 unidade é
igual à raiz positiva de:
a) x2 + x – 2 = 0
b) x2 – x – 1 = 0
2
c) x – 2x + 1 = 0
d) x2 + x – 1 = 0
2
e) x – x – 1 = 0
23. (FIP-2013)
3) ( ITA – SP ) Considere uma circunferência inscrita
num triângulo isósceles com base de 6 cm e altura
de 4 cm. Seja t uma reta tangente a esta
253
CURSO DE MATEMÁTICA
circunferência e paralela à base do triângulo.
Determine a medida do segmento de
t
compreendido entre os lados do triângulo.
HAMILTON E ALEX
QUADRILÁTEROS NOTÁVEIS

O quadrilátero é um polígono simples de 4 lados.
Os quadriláteros notáveis são os trapézios e os
paralelogramos.
4) ( UFMG ) Uma folha de papel quadrada, ABCD ,que
mede 12 cm de lado,é dobrada na reta r ,como
TRAPÉZIO
mostrado nesta figura:
É todo quadrilátero plano convexo que possui dois
lados paralelos.
A
D
Os lados paralelos são as bases
do trapézio.
N
E
F
Em relação aos lados não paralelos , temos:
 Trapézio isósceles, se esses lados
congruentes.
r
B
M
são
C
Isósceles
Feita essa dobra, o ponto D sobrepõe-se ao ponto N,
e o ponto A , ao ponto médio M , do lado BC .

Nessas condições, encontre:
Trapézio escaleno, se esses lados não são
congruentes.
a) A medida, em cm, do segmento FB
Escaleno

b)
Trapézio retângulo possui dois ângulos retos.
A medida, em cm, do segmento CE
retângulo
CONSEQÜÊNCIAS ( Trapézios )

GABARITO
1) C
2) A
3) A
8) B
9) A
10) D
4) C
5) A
11) E
6) E
12) D
Os ângulos consecutivos dos lados não paralelos
são suplementares.
7) C
13) B
14) C
15) D
16) D
17) C
18) A
20) D
21) D
22) D
23) C
24) B
a k
b
â + b = 180º
t
k̂ + t̂ = 180º
19) C
PARALELOGRAMO
É todo quadrilátero plano convexo que possui os lados
opostos paralelos.
Paralelogramo
Retângulo
Quadrado
Losango
254
CURSO DE MATEMÁTICA

HAMILTON E ALEX
QUADRADO
Os paralelogramos podem ser:

RETÂNGULO
É todo quadrilátero plano convexo que possui 4
ângulos retos.
A
B
Â, B̂ , Ĉ e D̂ são retos.
D
Diagonais congruentes e
perpendiculares.
 Todo quadrado é retângulo e também é
losango.
C
LOSANGO
DIAGRAMA:
É todo quadrilátero plano convexo que possui os 4
lados congruentes.
U
P
T
Q
R
QUADRADO
É todo quadrilátero plano convexo que possui os 4
ângulos retos e os 4 lados congruentes.
PROPRIEDADES DOS PARALELOGRAMOS
 Ângulos opostos congruentes.
 Lados opostos congruentes.
 Diagonais dividem-se ao meio.
L
Onde:
U é o conjunto dos quadriláteros convexos; T é o
conj. dos trapézios; P é o conjunto dos
paralelogramos; R é o conj. dos retângulos; L é o
conj. dos losangos e Q é o conj. dos quadrados.
Base Média do Triângulo
A
M
B
N
x
C
2x
Se M e N são pontos médios, temos:
PROPRIEDADES DO RETÂNGULO, DO
LOSANGO E DO QUADRADO
 O segmento MN é a base média do triângulo
ABC.
 O segmento MN é paralelo à base BC do
triângulo.
 A base média é igual à metade da base do
triângulo.
RETÂNGULO

MN 
Diagonais congruentes.
BC
2
C
D
A
B
Observe que:
 todo retângulo pode ser decomposto em um triângulo
retângulo onde a hipotenusa é o dobro da medida da
mediana relativa a essa hipotenusa.
 Os triângulos ADB e BCD são isósceles.
Base Média do Trapézio
A
M
C
B
N
D
Se M e N são pontos médios, temos:
LOSANGO

Diagonais perpendiculares
 O segmento MN é a base média do trapézio.
 O segmento MN é paralelo às bases do
trapézio.
255
CURSO DE MATEMÁTICA
 A base média é igual à média aritmética das bases
do trapézio.
MN 
AB  CD
2
Exercícios
1)
(PUC – CAMP) Considere as afirmações:
I – Todo retângulo é um paralelogramo;
II – Todo quadrado é um retângulo;
III – Todo losango é um quadrado.
Associe a cada uma delas a letra V, se for
verdadeira, ou
F caso seja falsa. Na ordem
apresentada temos:
a) F, F, F
b) F, F, V
c) V, F, F
d) V, V, F
e) N.d.a
2) ( VUNESP ) Considere as seguintes proposições :
- Todo quadrado é um losango ;
- Todo quadrado é um retângulo ;
- Todo retângulo é um paralelogramo ;
- Todo triângulo equilátero é isósceles ;
Pode-se afirmar que :
a) Só uma é verdadeira;
b) Todas são verdadeiras ;
c) Só uma é falsa ;
d) Duas são verdadeiras ;
e) Todas são falsas ;
3) ( CESGRANRIO ) Assinale a alternativa que contém
a propriedade diferenciadora do quadrado em
relação aos demais quadriláteros.
a) Todos os ângulos são retos
b) Os lados são todos iguais
c) As diagonais são iguais e perpendiculares entre
si.
d) As diagonais se cortam ao meio.
e) Os lados opostos são paralelos e iguais.
4) ( UFMG ) Sobre figuras planas, é correto afirmar
que:
a) Um quadrilátero convexo é um retângulo se os
lados opostos têm comprimentos iguais.
b) Um quadrilátero que tem suas diagonais
perpendiculares é um quadrado.
c) Um trapézio que tem dois ângulos consecutivos
congruentes é isósceles.
d) Um triângulo equilátero também é isósceles.
e) Um triângulo retângulo é aquele cujos ângulos
são retos.
HAMILTON E ALEX
5) ( CESGRANRIO ) Seja ABC um triângulo retângulo,
onde D é o ponto médio da hipotenusa BC. Se AD
= AB, então o ângulo ABC mede:
a) 67º 30’
b) 60º
c) 55º
d) 52º 30’
e) 45º
6) ( UFF – 2001 ) Um pedaço de papel tem a forma do
triângulo equilátero PQR, com 7cm de lado, sendo
M o ponto médio do lado PR. Dobra-se o papel de
modo que os pontos Q e M coincidam, conforme
o ilustrado a seguir.
O perímetro do trapézio PSTR, em cm, é:
a) 9
Q
b) 17,5
c) 24,5
S
T
d) 28
e) 49
P
M
R
P
M=Q
R
7) ( ITA – SP ) Considere um quadrilátero ABCD cujas
diagonais AC e BD medem, respectivamente, 5
cm e 6 cm. Se R, S, T e U são os pontos médios
dos lados do quadrilátero dado, então o perímetro
do quadrilátero RSTU vale:
a) 22 cm
b) 13 cm
c) 11 cm
d) 8,5 cm
e) 5,5 cm
8)
( UFPA ) O triângulo retângulo ABC, da figura,
representa um terreno com área igual a 760 m2. A
região sombreada foi demarcada para construção
de uma casa e o restante do terreno ficou reservado
para lazer. Sabendo-se que M e N são pontos
médios dos catetos do triângulo ABC, pode-se
afirmar que a área do triângulo ONC é igual a, em
m2, a:
A) 180
B) 190
C) 200
D) 210
E) 220
9) ( Fuvest – SP ) O retângulo abaixo de dimensões a
e b está decomposto em quadrados. Qual o valor
da razão a/b ?
a) 5/3
b) 2/3
b
c) 2
d) 3/2
e) 1/2
a
256
CURSO DE MATEMÁTICA
10) ( VUNESP ) A afirmação falsa é:
a) Todo quadrado é um retângulo
b) Um losango pode não ser um paralelogramo
c)Todo Paralelogramo é um quadrilátero
d) Existem retângulos que não são losangos
11) (ENEM-2010) Em canteiros de obras de construção
civil é comum perceber trabalhadores realizando
medidas de comprimento e de ângulos e fazendo
demarcações por onde a obra deve começar ou se
erguer. Em um desses canteiros foram feitas
algumas marcas no chão plano. Foi possível
perceber que, das seis estacas colocadas, três
eram vértices de um triângulo retângulo e as outras
três eram os pontos médios dos lados desse
triângulo, conforme pode ser visto na figura, em que
as estacas foram indicadas por letras.
A região demarcada pelas estacas A, B, M e N
deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
A) À mesma área do triângulo AMC
B) À mesma área do triângulo BNC
C) À metade da área formada pelo triângulo ABC
D) Ao dobro da área do triângulo MNC
E) Ao triplo da área do triângulo MNC
12) ( ITA – SP ) Dadas as afirmações:
I – Quaisquer dos ângulos opostos de um
quadrilátero são suplementares.
II – Quaisquer dos ângulos consecutivos de um
paralelogramo são suplementares.
III – Se as diagonais de um paralelogramo são
perpendiculares entre si, então esse paralelogramo
é o losango.
Podemos garantir que:
a) Todas são verdadeiras;
b) Apenas I e II são verdadeiras;
c) Apenas II e III são verdadeiras;
d) Apenas II é verdadeira;
e) Apenas III é verdadeira.
13) ( UFPI ) Em um paralelogramo a diferença de dois
ângulos consecutivos  e  é de 64º. A medida
desse ângulos, em gruas, é :
a) 58º e 122º
b) 60º e 120º

c) 56º e 124º

d) 54º e 126º
HAMILTON E ALEX
14) ( UFMG ) Num triângulo equilátero ABC, de 8 cm
de lado, traça-se MN // BC, de modo que ele se
decomponha num trapézio e num novo triângulo.
O valor de MN para o qual o perímetro do trapézio é
igual ao do triângulo AMN é:
a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm
e) 6 cm
15) ( PUC – MG / 2001 ) No trapézio retângulo da
figura, a medida do ângulo obtuso é cinco vezes a
medida do ângulo agudo. A medida do ângulo
agudo, em graus, é :
a) 15º
b) 20º
c) 30º
d) 45º
16) (UNIMONTES) – Com relação ao trapézio isósceles
ABCD, sabendo-se que:
I – M e N são os pontos médios dos lados AB e CD,
respectivamente;
II – O ângulo B tem medida igual a 120º ;
III – Os lados BM e PC são paralelos.
Pode-se afirmar que x + 2y é igual a:
a) 180º
B
C
b) 60º
x
c) 90º
P y N
M
d) 120º
e) 110º
A
17) ( Fuvest – SP )
D
No Quadrilátero ABCD abaixo,
ABˆ C = 150º, AD = AB = 4cm, BC = 10cm,
MN =
2cm, sendo M e N os pontos médios de CD e BC. A
medida em centímetros quadrados, da área do
triângulo BCD é:
D
M
a) 10
C
b) 15
A
c) 20
N
d) 30
B
18) No trapézio isósceles da figura,
DB é bissetriz de
AD̂C e é perpendicular a BC. O ângulo
mede :
A
B
a) 30º
b) 35º
c) 40º
d) 45º
D
C
e) 50º
BD̂C
257
CURSO DE MATEMÁTICA
19) ( UFMG ) Num losango, a soma dos ângulos
obtusos é o dobro da soma dos ângulos agudos e a
diagonal menor mede 9 cm. O perímetro o losango
é:
a) 36 cm
b) 40 cm
HAMILTON E ALEX
GABARITO
1) D
2) B
3) C
8) B
9) A
c) 30 2 cm
14) E
15) C
d) 30 3 cm
e) N. R. A
20) B
21) B
4) D
10) B
16) A
5) B
11) E
17) C
6) B
7) C
12) C
13) A
18) A
19) A
22) E
20) ( U.C. SALVADOR ) Sejam :
P: o conjunto dos retângulos
Q: o conjunto dos quadrados
L: o conjunto dos losangos
A figura que melhor representa as relações
existentes entre eles é :
a)
P
b) L
Q
P
c) L
Q
Q
L
d)
L
P
P
e)
L
P
Q
Q
21) Na figura, ABCD é um paralelogramo. AE é
bissetriz de DÂB e EB = EC. A medida do ângulo
DCˆ B é :
a)
b)
c)
d)
e)
50º
52º
56º
60º
65º
D
E
C
78º
A
B
22) ( CESGRANRIO ) As bases MQ e NP de um
trapézio medem 42 cm e 112 cm respectivamente.
Se o ângulo MQP é o dobro do ângulo PNM, então
o lado PQ mede:
a) 154 cm
Q
M
b) 133 cm
c) 91 cm
d) 77 cm
e) 70 cm
N
P
258
CURSO DE MATEMÁTICA
 TRIÂNGULO RETÂNGULO
HAMILTON E ALEX
Relações Métricas no Triângulo Retângulo
É todo triângulo que possui um ângulo reto.
b
a
b
c
a
Apenas em triângulos retângulos temos:
O quadrado da hipotenusa é igual a soma
dos quadrados dos catetos.
2
2
a =b +c
m
Hipotenusa
Cateto
Cateto
Teorema de Pitágoras
2
9
c
h
Onde:
c
b
n
a
A altura relativa à hipotenusa divide essa hipotenusa
em dois segmentos “m” e “n” que são as projeções
dos catetos “b” e “c” sobre a hipotenusa “a”.
Por semelhança de triângulos podemos obter as
seguintes fórmulas:





a2 = b2 + c2
b2 = m . a
c2 = n . a
h2 = m . n
b.c=h.a
Ex.: Determine as medidas indicadas na figura abaixo.
3
3
5
4
25
16
4
h
x
y
52 = 42 + 32
25 = 16 + 9
25 = 25

Diagonal do quadrado
D
l
D2 = l2 + l2
D2 = 2 l2
2l2
D=
l
D=l 2

raio de uma circunferência sempre é
perpendicular à reta tangente no ponto de
tangência.
r
r s
s
259
CURSO DE MATEMÁTICA
EXERCÍCIOS
01. ( UFSE ) No triângulo retângulo, representado na
figura abaixo, BC = 10 e AD = 4. A medida de CD ,
em cm, pode ser :
a) 7
A
b) 5
c) 4
d) 2
e) 1
C
D
B
HAMILTON E ALEX
06. ( Enem – 2006 ) Na figura abaixo, que representa o
projeto de uma escada com 5 degraus de mesma
altura, o comprimento total do corrimão é igual a
A) 1,8 m.
B) 1,9 m.
C) 2,0 m.
D) 2,1 m.
E) 2,2 m.
02. ( UFRS ) Na figura, ABC é um triângulo retângulo
em A, AP  CB , CP mede 1,8 e PB mede 3,2. O
perímetro de ABC é :
a) 6
A
b) 8
c) 9
d) 10
e) 12
P
C
B
03. ( U.C. Salvador ) Na situação do mapa abaixo,
deseja-se construir uma estrada que ligue a cidade A à
estrada BC , com o menor comprimento possível. Essa
estrada medirá em Km :
a) 24
A
b) 28
40 km
c) 30
d) 32
e) 40
C
B
50 km
04. ( PUC – SP ) A soma dos quadrados dos três lados
de um triângulo retângulo é igual a 32. Quanto mede a
hipotenusa do triângulo ?
a) 3
b) 4
c) 5
d) 6
e) 8
05. ( UFPA ) Uma corda de 3,9 m de comprimento
conecta um ponto na base de um bloco de madeira a
uma polia localizada no alto de uma elevação, conforme
o esquema abaixo. Observe que o ponto mais alto
dessa polia está 1,5 m acima do plano em que esse
bloco desliza. Caso a corda seja puxada 1,4 m, na
direção indicada abaixo, a distância x que o bloco
deslizará será de:
A) 1,0 m
B) 1,3 m
C) 1,6 m
D) 1,9 m
E) 2,1 m.
07. ( UFMG – 2001 ) Observe a figura:
T
O
Q
P
Nessa figura o circulo tem centro O e raio 6 e OP =
16. A reta PT é tangente ao círculo em T e o
segmento TQ é perpendicular à reta OP . Assim
sendo, o comprimento do segmento QP é :
a) 13,75
b) 13,85
c) 14,25
d) 14,5
08. ( UnB ) De um círculo, conhece-se apenas a parte
que é representada na figura abaixo. Então, a medida
de seu raio é :
1m
a) 3m
3m
3m
b) 4m
c) 5m
d) 6m
e) 7m
09. ( FATEC ) O valor do raio da circunferência de
centro O da figura é :
a) 7,5
b) 14,4
O
c) 12,5
d) 9,5
10
10
5
10. ( UFRJ ) Duas circunferências são tangentes
exteriores. A distância entre seus centros é de 13 cm e
a diferença entre seus raios é de 5 cm. A medida do
raio menor, do raio maior e do segmento AB da reta
tangente comum às circunferências, nessa ordem, é :
260
CURSO DE MATEMÁTICA
a)
b)
c)
d)
e)
3; 8; 11
4; 9; 12
3; 8; 12
4; 9; 11
5; 10; 13
HAMILTON E ALEX
A)
B)
C)
D)
E)
B
6m
A
11. ( FESP – SP ) Na figura abaixo, ABC e BDE são
triângulos equiláteros de lados
2a
e
a,
respectivamente. Podemos afirmar, então, que o
segmento CD mede:
C
a) a 2
D
b) a 6
c) 2a
A
d) 2a 5
A
9 metros
10 metros
11 metros
12 metros
13 metros
B
E
e) a 3
12. ( ENEM - 2012 ) Em exposições de artes plásticas,
é usual que estátuas sejam expostas sobre plataformas
giratórias. Uma medida de segurança é que a base da
escultura esteja integralmente apoiada sobre a
plataforma. Para que se providencie o equipamento
adequado, no caso de uma base quadrada que será
fixada sobre uma plataforma circular, o auxiliar técnico
do evento deve estimar a medida R do raio adequado
para a plataforma em termos da medida L do lado da
base da estátua.
Qual relação entre R e L o auxiliar técnico deverá
apresentar de modo que a exigência de segurança seja
cumprida?
A) R ≥ L / 2
B) R ≥ 2L / π
C) R ≥ L / 
D) R ≥ L / 2
E) R ≥ L / (2 2 )
13. ( PUC – Campinas ) Um quadrado tem dois vértices
numa circunferência e um lado tangente a ela no ponto
T, como mostra a figura. Se a área do quadrado é 64
cm2, o raio da circunferência é:
a) 4 2
2m
B
3m
15. ( ENEM – 2010 ) Uma fábrica de tubos acondiciona
tubos cilíndricos menores dentro de outros tubos
cilíndricos. A figura mostra uma situação em que quatro
tubos cilíndricos estão acondicionados perfeitamente
em um tubo com raio maior.
Suponha que você seja o operador da máquina que
produzirá os tubos maiores em que serão colocados,
sem ajustes ou folgas, quatro tubos cilíndricos internos.
Se o raio da base de cada um dos cilindros menores for
igual a 6 cm, a máquina por você operada deverá ser
ajustada para produzir tubos maiores, com raio da base
igual a
A) 12 cm
B) 12 2 cm
C) 24 2 cm
D) 6(1 +
E) 12(1 +
2 )cm
2 )cm
16. ( ENEM – 2010 ) Devido aos fortes ventos, uma
empresa exploradora de petróleo resolveu reforçar a
segurança de suas plataformas marítimas, colocando
cabos de aço para melhor afixar a torre central.
Considere que os cabos ficaram perfeitamente
esticados e terão uma extremidade no ponto médio das
arestas laterais da torre central (pirâmide quadrangular
regular) e a outra no vértice da base da plataforma (que
é um quadrado de lados paralelos aos lados da base da
torre central e centro coincidente com o centro da base
da pirâmide), como sugere a ilustração.
Se a altura e a aresta da base da torre central medem,
respectivamente, 24 m e 6 2 m e o lado da base da
plataforma mede 19 2 m, então a medida, em metros,
de cada cabo será igual a
b) 3 2

c) 5 2
d) 5

14. Uma corda foi amarrada do ponto A ao ponto B
contornando um bloco retangular maciço cujas
dimensões são: 3m, 2m e 6m como indicado na
figura abaixo. A medida dessa corda é:
A)
288
B)
313
C)
328
D)
400
E)
505
261
CURSO DE MATEMÁTICA
17. (ENEM-2013) Um restaurante utiliza, para servir
bebidas, bandejas com bases quadradas. Todos os
copos desse restaurante têm o formato representado na
figura.
7
Considere que AC  BD e que L é a medida de um
5
dos lados da base da bandeja. Qual deve ser o menor
valor da razão
B
HAMILTON E ALEX
CIRCUNFERÊNCIA
Chama-se circunferência de centro O e raio r ( r > 0 )
o lugar geométrico dos pontos do plano que estão a
uma distância r do ponto O.

( O, r ) é a circunferência 
r
para que uma bandeja tenha
O
capacidade de portar exatamente quatro copos de uma
só vez?

de centro em O e raio r.
Raio
O raio r de uma circunferência é o segmento que
tem como extremos o centro O e um ponto
qualquer da circunferência.

Os raios de uma
circunferência são
congruentes.
r
O
r
r
18. A logomarca de uma empresa é composta de
círculos tangentes, como indicados na figura abaixo.
Essa empresa resolveu fazer chaveiros com o mesmo
formato dessa logomarca, para presentear seus
clientes. Se o raio do circulo menor deve medir 1cm,
qual medida, aproximada, do raio dos outros dois
círculos? ( considere 2 = 1,4 )
A) 2,5 cm e 6 cm
B) 2,1 cm e 5,6 cm
C) 2,8 cm e 6,2 cm
D) 2,2 cm e 5,8 cm

Corda
É todo segmento que tem como extremos dois
pontos distintos da circunferência.
A
C
E
D
Toda corda que passar pelo
centro O de uma circunferência
chama-se diâmetro.
O
EF = 2R
F
B

Círculos Concêntricos
Se dois círculos possuem o mesmo centro eles são
chamados de círculos concêntricos.
R
r
GABARITO
1) D
8) C
14) B
2) E
9) C
15) D
3) A
10) B
4) B
5) C
6) D
11) E
12) A
13) D
16) D
17) D
18) A
7) A
PROPRIEDADES
1ª - O raio de uma circunferência sempre é
perpendicular a uma reta tangente no ponto de
tangência.
r
rs
s
262
CURSO DE MATEMÁTICA
2ª - Se um raio passar pelo ponto médio de qualquer
corda ele será perpendicular a essa corda.
A
HAMILTON E ALEX
 Conseqüências
1ª ) Todo ângulo inscrito é igual à metade do arco que
A
ele contém.

/2
r AB
B
B
ÂNGULOS NA CIRCUNFERÊNCIA
2ª ) Todos os ângulos Inscritos que contêm o mesmo
arco são congruentes.
A
 Ângulo Central
É todo ângulo que tem o vértice no centro da
circunferência.
A
O
/2
E
/2


/2

B
B
 O ângulo AÔB =  é o ângulo central.
 Por definição, o ângulo central tem a mesma
medida do arco que ele compreende.
3ª ) Todo triângulo inscrito em uma semicircunferência e
que tem o diâmetro como lado é um triângulo
retângulo.
A
AB = AÔB = 
180º
 Ângulo Inscrito
É todo ângulo que possui seu vértice contido na
circunferência.
B
A
 Ângulo de Segmento
É todo ângulo formado por uma corda e uma reta
que tangencia a circunferência em um dos extremos
dessa corda.

E
B
AÊB =  é o ângulo inscrito.
A

C

 Relação entre o Ângulo Central e o Ângulo
Inscrito
B
A
E
/2
O


Todo ângulo
Inscrito é a metade
do ângulo Central
que ele contém.
 O ângulo A B̂ C =  é o ângulo de segmento.
 O ângulo de segmento é igual a metade do arco
que ele contém.
 = /2
B
263
CURSO DE MATEMÁTICA
HAMILTON E ALEX
 Ângulo de Vértice Interior
Exercício
É todo ângulo que possui seu vértice no interior da
circunferência.

x 

x

2
 Ângulo de Vértice Exterior
É todo ângulo que possui seu vértice no exterior da
circunferência.

x


x
x 

 
2
1) ( PUC - SP )
Na figura, AB é diâmetro da
circunferência. O menor dos arcos AC mede:
C
a) 100º
b) 120º
c) 140º
40º
A
B
d) 150º
e) 160º
2) ( U. C. SALVADOR ) Sabendo que O1 e O2 são os
centros das circunferências, calcule o valor de “x”.
a) 10º
b) 15º
c) 20º
80º
x
d) 25º
O1
O2
e) 30º
3) ( MACK - SP ) Na figura, sabe-se que m(CÂD) =
20º e m(CÊD) = 70º. Então AMB é igual a:
a) 50º
B
A
b) 45º
c) 60º
d) 22º 30’
E
e) 30º
D

x
C

M
QUADRILÁTEROS INSCRITOS
Um quadrilátero é inscrito se possui todos os
seus vértices pertencentes à circunferência.
4) (UNIMONTES) – Sendo O o centro do círculo,
calcule o valor de x que aparece nos ângulos
assinalados na figura abaixo.
a) 12º
V
b) 9º
5x
c) 18º
d) 6º
O
e) n.d.a A
6x + 48º
A
B
x
5) ( UFMG – 99 ) Observe a figura:
Nessa figura, BD é um diâmetro da circunferência
circunscrita ao triângulo ABC, e os ângulos ABD e
AÊD medem, respectivamente, 20º e 85º.
B
D
y
X̂ + Ŷ =180º
C
 Em todo quadrilátero inscrito, a soma das
medidas dos ângulos opostos é igual a 180º.
Assim sendo, o ângulo CB̂D mede:
a) 40º
A
b) 25º
c) 35º
B
d) 30º
E
D
C
264
CURSO DE MATEMÁTICA
6) ( UFGO ) Se a corda AB da figura é um lado de um
triângulo equilátero inscrito na circunferência de
centro em O, a medida do ângulo , em radianos é:
a) 2/3
A
b) 3/2
c) 3/4
O 
d) /3
e) /6
B
7) ( FEI – SP ) Na figura, ABCD é um quadrilátero
inscrito num círculo; x e y são as medidas, em
graus, de ACˆ D e ADˆ C , respectivamente. O valor
de
a)
b)
c)
d)
e)
y– xé:
55º
35º
50º
42º 30’
45º
B
45º
C
40º
12) ( UC - Salvador ) Na figura abaixo, o triângulo ABC
é isósceles de base BC e BD é a bissetriz do
ângulo de vértice B. A medida  do ângulo
A
assinalado é:
a) 55º
 35º
D
b) 50º
c) 45º
d) 40º
e) 35º
M
P
N
O
Suponha que as medidas dos ângulos PŜQ , QŜR
e SP̂R , assinalados na figura, sejam 45º, 18º e
38º, respectivamente. A medida do ângulo PQ̂S ,
S
em graus, é:
a) 38º
45º 18º
b) 63º
R
c) 79º
d) 87º
38º
Q
Q
P
9) (UFMG) – Na figura A, B e D são pontos da
circunferência de centro O e diâmetro AC, M é
ˆ M mede
ponto médio da corda AB e o ângulo AD
35º. A medida x do ângulo BÂC em graus, é :
B
a) 20
b) 25
c) 30
d) 35
e) 37,5
C
13) ( UFMG ) Observe a figura abaixo.
D
8) ( UECE – 2000 ) Na figura, a reta MN é tangente
à circunferência em P, a secante MQ passa pelo
centro O da circunferência e a medida do ângulo
QMP é 40º. A medida do ângulo NPˆ Q é igual a :
65º
60º
55º
50º
11) ( UFES ) Na figura, a medida de em graus é :
a) 50º
b) 52º
c) 54º

d) 56º
32º
e) 58º
B
A
a)
b)
c)
d)
HAMILTON E ALEX
M
O
A
C
D
10) ( PUC – SP ) Na figura abaixo, AP é tangente e AB
é secante à circunferência. Se o arco b = 100º e Â
= 50º, a medida do arco a, em graus, é igual a:
a) 50
b) 60
P
A
c) 65
d) 75
a
e) 80
14) ( CESGRANRIO ) As semi-retas PM e PN são
tangentes ao círculo da figura e o comprimento do


arco MGN é 4 vezes o do arco MFN . O ângulo
MP̂N vale:
a)
b)
c)
d)
e)
76º
80º
90º
108º
120º
M
G
F
P
N
15) ( CESGRANRIO ) Em um círculo de centro O, está

inscrito o ângulo . Se o arco AMB mede 130º, o
ângulo mede :
a) 25º
b) 30º
O
c) 40º

B
A
d) 45º
e) 50º
M
B
b
265
CURSO DE MATEMÁTICA
16) ( PUC – SP ) O pentágono ABCDE abaixo está
inscrito em um círculo de centro O. O ângulo
central CÔD mede 60º. Então x + y é igual a:
A
a) 180º
b) 185º
c) 190º
B x
y E
O
d) 210º
e) 250º
C
B
18) ( MACK ) Na figura, temos um trapézio inscrito. Se o
menor dos arcos AB = 60º, então o menor dos
arcos MN mede:
A
B
a) 90º
b) 110º
c) 120º
d) 140º
75º
e) 150º
M
N
19) ( VUNESP ) Os pontos A, B, C, D, E, e F
pertencem à circunferência. O valor de  é ?
A
120º
21) ( Fuvest - SP ) Numa circunferência está inscrito
um triângulo ABC; seu lado BC é igual ao raio da
circunferência. O ângulo BÂC mede:
a) 15º
b) 30º
c) 36º
d) 45º
e) 60º
22) ( MACK ) Na figura abaixo, tem-se m(BÂD) = 108º
D
17) ( UFMG ) De um ponto M, exterior a um círculo de
centro O, traçam-se as tangentes MA e MB. Se a
corda AB é um lado do pentágono regular inscrito
ˆ B é:
nesse círculo, a medida do ângulo AM
a) 144º
b) 120º
A
c) 108º
O
M
d) 96º
e) 72º
B
HAMILTON E ALEX
F

e
a)
b)
c)
d)
e)
m( AD̂C ) = 112º. A medida de EB̂C é:
E
68º
B
72º
108º
A
112º
n.d.a
D
C
23) ( CESGRANRIO ) Um quadrilátero convexo está
inscrito em um círculo. A soma em radianos, dos
ângulos e  mostrados na figura é:
a) /4
b) /2
c) 

d) 3/2

e) 2
GABARITO
1) A
8) A
9) A
14) D
15) A
18) C
E
22) D
110º
C
2) C
3) E
4) A
10) E
19) 50º
5) B
11) E
16) D
20) C
6) A
7) A
12)D 13) C
17) C
21) B
23) C
D
20) ( Cesgranrio ) Se, na figura, AB = 20º, BC = 124º,
CD = 36º e DE = 90º, então o ângulo x mede:
a) 34º
E
b) 35º 30’
c) 37º
D
d) 38º 30’
A
e) 40º
x
B
C
266
CURSO DE MATEMÁTICA
HAMILTON E ALEX
SEGMENTOS TANGENTES
Se de um ponto P, fora de uma circunferência ,
conduzirmos os segmentos PA e PB ambos
Exercícios
1) ( CESCEM ) Seja P o ponto de tangência da
circunferência inscrita no triângulo ABC, com o lado
AB. Se AB = 7, BC = 6 e AC = 8, quanto vale AP ?
tangentes a essa circunferência em A e B, PA e PB
são chamados de segmentos tangentes.
A
P
B

2) Na figura, determine a medida do segmento BD
sabendo que a circunferência de centro O está
inscrita no triângulo ABC, e que os lados AB, BC e
AC medem respectivamente 6cm, 8cm e 10cm.
A
Se PA e PB são segmentos tangentes, eles são
congruentes.
PA  PB
B
QUADRILÁTERO CIRCUNSCRITO
Um quadrilátero convexo é circunscrito a uma
circunferência  se, e somente se, seus quatro lados
são tangentes à circunferência.
A
B


D
ABCD está circunscrito
à .
 está inscrita em
ABCD.
D
C
3) ( UFMG ) Na figura, o círculo está inscrito no
triângulo ABC cujos lados medem AB = 9 cm, BC
= 8 cm e AC = 5 cm e M é o ponto de tangência.
A medida de MB é : C
a) 5 cm
b) 5,5 cm
c) 6 cm
d) 6,5 cm
A
M
B
4) Na figura, PA = 10 cm. Calcule o perímetro do
triângulo PRS sabendo-se que RS é tangente à .
C
R A
P
PROPRIEDADE
Se um quadrilátero convexo é circunscrito a uma
circunferência, a soma de dois lados opostos é igual à
soma dos outros dois.
A
B
AB + DC = AD + BC
D
C
S B
5) Na figura, o círculo está inscrito no triângulo ABC,
retângulo em A. Se BM = 6 m e MC = 4 m, o raio
do círculo é :
A
a) 1,8
b) 2,0
c) 2,2
d) 2,4
C
M
B
e) 2,5
6) Calcule o valor do raio r do círculo inscrito no
trapézio retângulo abaixo.
A
10
D
13
B
15
C
267
CURSO DE MATEMÁTICA
7) ( F.C.M.S.C ) Na figura abaixo, o valor de d é :
a)
ba
b)
2ab
c)
2 ab
d)
2a a  b
e)
2 ab  2a
a
d
b
8) ( MACK – SP ) A hipotenusa de um triângulo
retângulo é 8 e o raio do círculo inscrito é 2. O
perímetro do triângulo é igual a:
a) 28
b) 26
c) 24
d) 22
e) 20
9) ( EPUSP ) As bases de um trapézio isósceles
circunscrito a uma circunferência medem 9m e
6m. Cada um dos outros dois lados do trapézio
mede:
a) 4,5 m
b) 6 m
c) 7,5 m
d) 8 m
e) n.d.a
HAMILTON E ALEX
12) (ENEM – 2010) Uma metalúrgica recebeu uma
encomenda para fabricar, em grande quantidade,
uma peça com o formato de um prisma reto com
base triangular, cujas dimensões da base são 6 cm,
8 cm e 10 cm e cuja altura é 10 cm. Tal peça deve
ser vazada de tal maneira que a perfuração na
forma de um cilindro circular reto seja tangente às
suas faces laterais, conforme mostra a figura.
O raio da perfuração da peça é igual a
A) 1
B) 2
C) 3
D) 4
E) 5
GABARITO
1) 4,5
10) ( UFMS )
Na figura abaixo, tem-se uma
circunferência inscrita num triângulo
ABC,
retângulo em A e isósceles. Se a hipotenusa do
8) E
2) 2
9) C
3) C
10) C
4) 20
11) C
5) B
6) 6
7) C
12) B
triângulo mede 8 2 cm, o raio da circunferência,
em cm, é :
a)
4 2 8
b)
48 2
c)
84 2
d)
63 2
C
A
B
11) A figura abaixo representa uma praça triangular.
Nela deseja-se fazer um heliporto circular com a
maior área possível. O raio desse círculo será?
A) 3 metros
B) 3,5 metros
C) 4 metros
10 m
D) 4,5 metros
E) 5 metros
24 m
268
CURSO DE MATEMÁTICA
COMPRIMENTO DE UMA CIRCUNFERÊNCIA

A
Em uma circunferência de raio r temos :
r
HAMILTON E ALEX
Apótema do Hexágono Regular ( a6 )
l
 a6 = Apótema do hexágono regular, ele é
igual à altura de um triângulo equilátero.
 3,14
C
a6

360º
l 
2 rad.
l
 rad.
.r.
180º
1) O comprimento de uma circunferência inscrita em
um quadrado é 6 cm. Determine:
a) A medida do lado do quadrado
l = .r
b) A medida da diagonal do quadrado.
Apótemas de Polígonos Regulares
O apótema de um polígono regular é igual a medida do
raio de uma circunferência inscrita nesse polígono.

l 3
Exercício
l
2..r

l
AC =
Em Radianos
l
2..r
 AC = diagonal menor do hexágono
 AC é igual a altura de dois triângulos
equiláteros
Comprimento de um Arco de Circunferência

l 3
2
l
Comprimento da circunferência: C = 2..r
Em Graus
a6 =
b) A medida do lado do quadrado;
Apótema do Quadrado ( a4 )
R
R =
l 2
2
a4 =
l
2
2) O apótema de um quadrado mede 4 cm. Determine:
a) O comprimento da circunferência inscrita;
c) A medida da diagonal do quadrado
a4
d) O comprimento da circunferência circunscrita.
l

3) Um triângulo equilátero está inscrito em uma
circunferência de raio igual a 6 cm. Determine :
a) A altura do triângulo equilátero;
Apótema do Triângulo Equilátero ( a3 )
R
H=
l 3
2
l3 = R 3
b) O lado do triângulo;
r a3
a3 =
l
R=
R = 2r
R+r=H
1
.H
3
2
.H
3
a3 =
R=
H = 3r
l 3
3
l 3
6
c) O raio da circunferência inscrita nesse triângulo.
4) O comprimento da circunferência que circunscreve
um triângulo equilátero é de 8 cm. Determine:
a) A altura desse triângulo.
269
CURSO DE MATEMÁTICA
b) A medida do lado desse triângulo
c) A medida do apótema do triângulo
d) O comprimento da circunferência inscrita nesse
triângulo.
HAMILTON E ALEX
9) ( UFPA ) Uma pista de atletismo está representada
na figura abaixo, sendo que os arcos são
semicircunferências. Nesse contexto, assinale a
única alternativa correta.
A) O contorno interno da pista é maior que 290 m.
B) A área da região englobada pela pista é maior
que 4500 m2
2
C) A área da pista é maior que 3200 m
D) O contorno externo da pista é menor que 350 m
5) O lado de um hexágono regular mede 2 3 cm .
Determine:
a) O apótema desse hexágono;
b) O comprimento da circunferência inscrita;
c) O comprimento da circunferência circunscrita.
10) (PUC – SP) A figura mostra um hexágono regular
de lado a a diagonal AB mede ?
a) 2a
A
b) a 2
6) O apótema de um hexágono regular inscrito em
uma circunferência é 2 3 . Determine a medida do
lado de um quadrado inscrito nessa mesma
circunferência.
7) ( UFRJ – 99 ) Na figura, o triângulo AEC é
equilátero e ABCD é um quadrado de lado 2cm.
Calcule a distância do vértice B ao vértice E .
E
A
B
D
C
8) ( PUC/RIO – 2001 ) Qual a razão entre os raios dos
círculos circunscrito e inscrito de um triângulo
equilátero de lado a ?
a) 2
b)
3
c)
d)
2
3a
e)
3.a 2
c)
a 3
2
d) a 3
B
11. (FIP-2013) A quadratura do círculo
Quando uma pessoa está fazendo um cálculo errado,
absurdo, é comum dizer que ela quer “quadrar o
círculo”.
Essa expressão significa, simplesmente, que, dado
um círculo, deve-se construir um quadrado que
tenha exatamente a mesma área do círculo, usando
somente uma régua não graduada e um compasso.
É muito fácil construir um quadrado de área
aproximadamente igual à de um círculo dado.
Sobre a situação apresentada, três estudantes
formularam as seguintes hipóteses:
I – Abel: Para que um quadrado tenha área igual à de
um círculo de raio 1, seu lado deve medir
.
II – Bianca: Se um círculo possui área igual a 4, a
diagonal do quadrado de mesma área mede 2 2 .
III – Camila: Um quadrado de lado igual a 5 possui
mesma área de um círculo de raio igual a 5  .
É correto o que é afirmado em:
270
CURSO DE MATEMÁTICA
A)somente III.
B) I e III somente
C) I e II somente
D) I, II e III.
HAMILTON E ALEX
ÁREAS DE FIGURAS PLANAS

12. (ENEM-2013) Em um sistema de dutos, três canos
iguais, de raio externo 30 cm, são soldados entre si e
colocados dentro de um cano de raio maior, de medida
R. Para posteriormente ter fácil manutenção, é
necessário haver uma distância de 10 cm entre os
canos soldados e o cano de raio maior.
Essa distância é garantida por um espaçador de metal,
conforme a figura:
Utilize 1,7 como aproximação para .
O valor de R, em centímetros, é igual a
A) 64,0.
B) 65,5.
C) 74,0.
D) 81,0.
E) 91,0.
Quadrado
l
A = l2
l

Retângulo
A=B.h
h
B

Paralelogramo
h
A = B. h
B

Losango
l
l
A
d
l
l
D
GABARITO
1) a) 6cm
2) a) 8 cm
b) 6 2 cm
b) 8cm

c) 8 2 cm
Trapézio
d) 8 2 cm
5) a) 3 cm
6) 4 2 cm
10) D
b) 4 3 cm
7)
11) D
c) 2 cm
6 2
8) A
A=
( B b ).h
2
B
d) 4 cm

c) 4 3 cm
b) 6 cm
b
h
3) a) 9cm b) 6 3 cm c) 3 cm
4) a) 6 cm
D. d
2
Triângulo Retângulo
h
A=
B. h
2
B
9) D
12) C

Triângulos Quaisquer

(Ângulo compreendido entre dois lados)
b
A=

a
1
. a. b. sen
2

271
CURSO DE MATEMÁTICA

HAMILTON E ALEX

( Em função dos três lados )
Área do segmento circular
c
b
r
a
A = (A do setor) – (A do )

r

A = p . (p - a) . (p - b) . (p - c)
onde, A =
r 2 . sen 
2
Onde, p é o semi-perímetro.

Área do Triângulo circunscrito
A=p.r
r

Área da coroa circular
A = AC – Ac
r
A =  ( R2 – r2 )
p é semi perímetro.

a
c
r

R
Área do Triângulo inscrito
A=
a. b. c
4. r
b
Triângulo Equilátero
l
l
A=
l2 3
4
Exercícios
1) ( MACK-SP) A área da parte sombreada vale ? (A
figura contém Semicircunferências de raios a e
centro nos vértices do quadrado menor).
a) a2(4 –  )
a
b) a2(2 –  )
c) 2a2
2
d) a
l


Hexágono Regular
l
l
l
l
A = áreas de 6
A=
3.l 2 3
2
Área do Círculo
A = . r2
( Área )
2) ( UEG ) O jardim da casa de Terêncio tem o formato
e as dimensões descritas na figura acima, em que
uma parte é um semicírculo e a outra é um triângulo
retângulo. Se cada planta que João tem no jardim
ocupa 0,25m2 e utilizando a aproximação  = 3,14,
a quantidade máxima de plantas que Terêncio
poderá plantar é
a) 222.
b) 253.
c) 287.
d) 410.
6m
r
C = 2 . . r

(Comprimento)
Área do setor circular
r

r
A=
.r 2 .
360º
8m
3) ( UTFPR ) A área de uma sala com a forma da
figura a seguir é de:
a) 30 m2
2
b) 26,5 m
2
c) 28 m
d) 24,5 m2
e) 22,5 m2
272
CURSO DE MATEMÁTICA
4) ( UFRS ) Seis octógonos regulares de lado 2 são
justapostos em um retângulo, como representado
na figura adiante. A soma das áreas das regiões
sombreadas na figura é
a) 16.
b) 16 2
c) 20.
d) 20 2
e) 24.
HAMILTON E ALEX
8) ( PUC – SP ) Seja o octógono EFGHIJKL, inscrito
num quadrado de 12 cm de lado, conforme mostra
a figura abaixo. Se cada lado do quadrado está
dividido pelos pontos assinalados em segmentos
congruentes entre si, então a área do octógono, em
centímetros quadrados, é :
E
L
a) 98
b) 102
F
K
c) 108
d) 112
G
J
e) 120
H
5) ( CEFET/RJ – 2001 ) As retas  e  são paralelas.
No triângulo retângulo ABC, o cateto AC mede 8
cm e a hipotenusa AB mede 17 cm. A área do
triângulo escaleno ACD, cujo lado CD mede 20
cm, é :
B
D

a) 60
b) 80
c) 120
d) 186

C
e) 340
A
6) ( CEFET/RJ – 2001 ) Cada lado de um quadrado
ABCD mede 1 dm. Desenha-se um quadrante de
círculo de raio 1 dm, apoiado sobre o lado AD,
centrado em A. A seguir, desenha-se um quadrante
de círculo de raio 2 dm, centrado em B, depois um
centrado em C e, finalmente, um centrado em D,
como mostrado na figura.
A soma das áreas dos 4 quadrantes de círculo
vale:
a) 5 dm2
b) 7,5 dm2
c) 10 dm2
C
D
d) 12,5 dm2
2
e) 30 dm
A
I
9) ( UFSC ) A área da figura sombreada é:
a) 4 - 
b) 2 ( 2 –  )
2
c) 4 ( 1 –  )
d) 4
2
e) 
10) ( UnB ) A área da região hachurada, onde os
semicírculos têm diâmetros de medida igual ao lado
do quadrado, é :
a 2 (4   )
a)
4
a
2
a (2   )
b)
4
2
a (4   )
c)
2
2a 2 (4   )
d)
3
B
7) ( FUVEST – SP ) Aumentamos a altura de um
triângulo em 10% e diminuímos a sua base em
10%. Então a área do triângulo:
a) aumenta 1%
b) aumenta 0,5%
c) decresce 0,5%
d) decresce 1%
e) não se altera
11) ( UFRS ) Um triângulo equilátero foi inscrito em um
hexágono regular, como representado na figura a
seguir. Se a área do triângulo equilátero é 2, então
a área do hexágono é
a) 2 2
b) 3.
c) 2 3
d) 2 +
e) 4.
3
273
CURSO DE MATEMÁTICA
12) ( UFPR) Um cavalo está preso por uma corda do
lado de fora de um galpão retangular fechado de 6
metros de comprimento por 4 metros de largura. A
corda tem 10 metros de comprimento e está fixada
num dos vértices do galpão, conforme ilustra a
figura abaixo. Nessas condições pode-se afirmar
que a área total da região que o animal pode se
deslocar é:
A) 88 m2
2
B) 92 m
C) 96 m2
D) 100 m2
E) 104 m2
HAMILTON E ALEX
15) ( PUC /MG – 2001 ) Na figura, o lado do quadrado
ABCD mede uma unidade. O arco BED pertence à
circunferência de centro em A e raio unitário; o
arco BFD pertence à circunferência de centro em
C e raio unitário. A medida da área da região
sombreada é :
D
a)
b)
c)
d)
13) (UFG – 2000 ) Um quadrado de 4 cm de lado é
dividido em dois retângulos. Em um dos retângulos,
coloca-se um círculo tangenciando dois de seus
lados opostos, conforme figura abaixo.
Determine o raio que o círculo deve ter, para que a
soma das áreas do círculo e do retângulo, que não
o contém, seja a menor possível.
14) ( UFPA ) Considere a região mais escura, no
interior do semicírculo de centro O, limitada por
semicircunferências, conforme mostra a figura a
seguir.
Se a área dessa região é 24π cm2 e AM = MN =
NB, então a medida AB, em centímetros, é:
A) 9
B) 12
C) 16
D) 18
E) 24
C
2
2
2
2
3
2
4
E
F
A
B
16) ( Viçosa – 2000 ) Une-se um dos vértices de um
quadrado aos pontos médios dos lados que não
contêm esse vértice, obtendo-se um triângulo
isósceles (veja figura). A área deste triângulo, em
relação à área do quadrado, representa a
percentagem de :
a) 38,5 %
b) 37,5 %
c) 36,5 %
d) 35,5 %
e) 39,5 %
17) ( Viçosa – 2000 ) Na figura abaixo, A, B, C e D
são pontos do círculo de centro O. Sabe-se que
AB = CD = 4 e que a área do triângulo AOB é 6.
Então a área da região sombreada é igual a :
a) 6 – 12
C
D
b) 13 – 12
c) 13 – 4
O
d) 11 – 12
e) 6 – 6
A
B
18) ( ENEM – 2012 ) Para decorar a fachada de um
edifício, um arquiteto projetou a colocação de vitrais
compostos de quadrados de lado medindo 1 m,
conforme a figura a seguir.
Nesta figura, os pontos A, B, C e D são pontos
médios dos lados do quadrado e os segmentos AP e
QC medem 1/4 da medida do lado do quadrado. Para
confeccionar um vitral, são usados dois tipos de
materiais: um para a parte sombreada da figura, que
custa R$ 30,00 o m2, e outro para a parte mais clara
(regiões ABPDA e BCDQB), que custa R$ 50,00 o m2.
274
CURSO DE MATEMÁTICA
De acordo com esses dados, qual é o custo dos
materiais usados na fabricação de um vitral?
A) R$ 22,50
B) R$ 35,00
C) R$ 40,00
D) R$ 42,50
E) R$ 45,00
19) ( UFRJ ) O Tangram é um antigo quebra-cabeça
chinês formado por um quadrado decomposto em
sete peças: cinco triângulos, um paralelogramo e
um quadrado, como mostra a figura A. A figura B é
obtida a partir da figura A por meio de translações e
rotações de seis dessas peças. A razão da área da
figura A para a área da figura B é:
a) 8/7 ****
b) 8/6
c) 7/6
d) 1
e) 8/9
HAMILTON E ALEX
Se A(12, 0) e o ângulo AÔP mede 60º, podemos
afirmar que:
y
A
B
x
a) A área do círculo menor é a quarta parte da
área do círculo maior.
b) A área do círculo menor é igual a 8 unidades
de área.
c) O comprimento da circunferência menor é 8
unidades de comprimento.
d) O raio do círculo menor é 3 unidades de
comprimento.
e) A distância do centro do círculo menor à semireta OP é 3 unidades de comprimento.
22) ( CPFO ) Na figura abaixo, as três circunferência de
raio igual a 2 cm são tangentes. Logo a área das
regiões hachuradas, em cm 2, é igual a :
a)

3
c) 
e) 3
20) ( FATEC – 2001 ) Na figura abaixo, os catetos do
triângulo ABC medem 8 cm, sendo N e M
pontos médios dos lados
AC
e
AB,
respectivamente. A circunferência tangencia os
segmentos MB, BC e NM.
Considerando  = 3,1 , tem-se que a área da
2
região hachurada, em cm , é igual a :
a) 11,6
A
b) 11,8
c) 12,4
N
M
d) 24,2
e) 37,6
P
b)

2
d) 2
23) ( CICE ) Três círculos de mesmo raio r são
tangentes exteriormente dois a dois. Então a área
hachurada é:
r
C
21) ( UPE – 2001 ) A circunferência menor da figura
abaixo é tangente à circunferência maior e às semiretas OA e OP, onde O é o centro da
circunferência maior.
24) (ENEM-2009) Dois holofotes iguais, situados em H1
e H2, respectivamente, iluminam regiões circulares,
ambas de raio R. Essas regiões se sobrepõem e
determinam uma região S de maior intensidade
luminosa, conforme a figura.
2
Área do setor circular: Asc=  R /2,  em radianos.
275
CURSO DE MATEMÁTICA
A área da região S, em unidades de área, é igual a
A) 2  R /3 –
2
2
3 R /2
B) (2  – 3 3 )R /12
2
2
C)  R /12 – R /8
2
D)  R /2
E)  R2/3
2
HAMILTON E ALEX
28) ( IME – RJ ) Calcule a área assinalada, em função
de r, sabendo que AB e AC são tangentes ao
círculo menor.
a) r2
A
B
2
b) r /2
2
c) 2r /3
r
r
2
d) 2r
C
25) ( ITA – SP ) Se os lados de um triângulo ABC
medem, respectivamente, 30cm, 40cm e 50cm,
então a área do círculo inscrito nesse triângulo
mede:
a) 10 cm2
b) 52  cm2
c) 5 cm2
d) 100 cm2
e) 25 cm2
26) ( ITA – SP ) Considere as circunferências inscrita e
circunscrita a um triângulo equilátero de lado l . A
área da coroa circular formada por estas
circunferências é dada por:
 2
6
2
l
a)
b)
l
4
2
c)
3 2
l
3
e)
 2
l
2
d)
3 l
2
27) ( UFMG ) Observe a figura.
Nessa figura, a região hachurada está delimitada pelos
arcos BC, AC e AB das circunferências de centros A, B
e C, respectivamente, e a medida do segmento BC é
2. A área dessa região é:
a)  -
3 3
8
c)  – 3
e)  + 3
b)  d)  +
3
4
29) ( MACK ) Na figura, ABCD é um quadrado de 6 cm
de lado. M é o ponto médio do lado DC e A é o
ponto médio de PC. A área do triângulo MDN, em
2
cm , é:
D
a) 4
b) 5
M
N
c) 6
P
C
d) 7
A
e) 8
B
GABRITO
1) C
2) B
3) B
4) E
8) D
9) A
10) A
11) E
14) E
15) B
18) B
19) A
22) D
2
23) r .(2 3  )
26) A
16) B
20) A
2
27) C
28) A
5) A
6) B
12) A
13)
7) D
4

17) B
21) C
24) A
25) D
39) C
A
3
4
B
C
276
CURSO DE MATEMÁTICA
HAMILTON E ALEX
QUESTÕES DO ENEM
01. (ENEM-2013) O dono de um sítio pretende colocar
uma haste de sustentação para melhor firmar dois
postes de comprimentos iguais a 6 m e 4 m. A figura
representa a situação real na qual os postes são
descritos pelos segmentos AC e BD e a haste é
representada pelo segmento EF, todos perpendiculares
ao solo, que é indicado pelo segmento de reta AB. Os
segmentos AD e BC representam cabos de aço que
serão instalados.
Qual deve ser o valor do comprimento da haste EF?
A) 1 m
B) 2 m
C) 2,4 m
D) 3 m
E) 2
m
02. (ENEM-2009) A fotografia mostra uma turista
aparentemente beijando a esfinge de Gizé, no Egito.. A
figura a seguir mostra como, na verdade, foram
posicionadas a câmera fotográfica, a turista e a esfinge
Medindo-se com uma régua diretamente na fotografia,
verifica-seque a medida do queixo até o alto da
cabeçada turista é iguala 2/3 da medida do queixo da
esfinge até o alto da sua cabeça. Considere que essas
medidas na realidade são representadas por d e d’,
respectivamente, que a distância da esfinge à lente da
câmera fotográfica, localizada no plano horizontal do
queixo da turista e da esfinge, é representada por b, e
que a distância da turista à mesma lente, por a
A razão entre b e a será dada por
A) b/a = d’/c
B) b/a = 2d/3c
C) b/a =3d’/2c
D) b/a = 2d’/3c
E) b/a = 2d’/c
03. (ENEM-2009) Um chefe de cozinha utiliza um
instrumento cilíndrico afiado para retirar parte do miolo
de uma laranja. Em seguida, ele fatia toda a laranja em
secções perpendiculares ao corte feito pelo cilindro.
Considere que o raio do cilindro e da laranja sejam
iguais a 1 cm e 3 cm, respectivamente.
A área da maior fatia possível é
(A) duas vezes a área da secção transversal do cilindro.
(B) três vezes a área da secção transversal do cilindro.
(C) quatro vezes a área da secção transversal do
cilindro.
(D) seis vezes a área da secção transversal do cilindro.
(E) oito vezes a área da secção transversal do cilindro.
04. (ENEM-2013) Para o reflorestamento de uma área,
deve-se cercar totalmente, com tela, os lados de um
terreno, exceto o lado margeado pelo rio, conforme a
figura. Cada rolo de tela que será comprado para
confecção da cerca contém 48 metros de comprimento.
277
CURSO DE MATEMÁTICA
HAMILTON E ALEX
C) triplicasse a área do quadrado.
D) ampliasse a medida do lado do quadrado em 4%.
E) ampliasse a área do quadrado em 4%.
A quantidade mínima de rolos que deve ser comprada
para cercar esse terreno é
A) 6.
B) 7.
C) 8.
D) 11.
E) 12.
05. (ENEM-2013) A cerâmica constitui-se em um
artefato bastante presente na história da humanidade.
Uma de suas várias propriedades é a retração
(contração), que consiste na evaporação da água
existente em um conjunto ou bloco cerâmico quando
submetido a uma determinada temperatura elevada.
Essa elevação de temperatura, que ocorre durante o
processo de cozimento, causa uma redução de até 20%
nas dimensões lineares de uma peça.
Disponível em: www.arq.ufsc.br. Acesso em: 3 mar. 2012.
Suponha que uma peça, quando moldada em argila,
possuía uma base retangular cujos lados mediam 30 cm
e 15 cm. Após o cozimento, esses lados foram
reduzidos em 20%.
Em relação à área original, a área da base dessa peça,
após o cozimento, ficou reduzida em
A) 4%.
B) 20%.
C) 36%.
D) 64%.
E) 96%.
06. (ENEM/2009) O governo cedeu terrenos para que
famílias construíssem suas residências com a condição
de que no mínimo 94% da área do terreno fosse
mantida como área de preservação ambiental. Ao
BC
receber o terreno retangular ABCD, em que AB 
,
2
Antônio demarcou uma área quadrada no vértice A,
para a construção de sua residência, de acordo com o
AB
desenho, no qual AE 
é lado do quadrado.
5
Nesse caso, a área definida por Antônio atingiria
exatamente o limite determinado pela condição se ele
A) duplicasse a medida do lado do quadrado.
B) triplicasse a medida do lado do quadrado.
07. (ENEM/2011) Em uma certa cidade, os moradores
de um bairro carente de espaços de lazer reivindicam à
prefeitura municipal a construção de uma praça. A
prefeitura concorda com a solicitação e afirma que irá
construí-la em formato retangular devido às
características técnicas do terreno. Restrições de
natureza orçamentária impõem que sejam gastos, no
máximo, 180 m de tela para cercar a praça. A prefeitura
apresenta aos moradores desse bairro as medidas dos
terrenos disponíveis para a construção da praça:
Terreno 1: 55 m por 45 m
Terreno 2: 55 m por 55 m
Terreno 3: 60 m por 30 m
Terreno 4: 70 m por 20 m
Terreno 5: 95 m por 85 m
Para optar pelo terreno de maior área, que atenda às
restrições impostas pela prefeitura, os moradores
deverão escolher o terreno
A) 1.
B) 2.
C) 3.
D) 4.
E) 5.
08. (ENEM-2009) Um fazendeiro doa, como incentivo,
uma área retangular de sua fazenda para seu filho, que
está indicada na figura como 100% cultivada. De acordo
com as leis, deve-se ter uma reserva legal de 20% de
sua área total. Assim, o pai resolve doar mais uma parte
para compor a reserva para o filho, conforme a figura.
De acordo com a figura acima, o novo terreno do filho
cumpre a lei, após acrescentar uma faixa de largura x
metros contornando o terreno cultivado, que se
destinará à reserva legal (filho). O dobro da largura x da
faixa é
(A) 10% (a+b)2
2
(B) 10% (a.b)
(C)
a  b – (a+b)
(D)
(a  b) 2  ab – (a+b)
(E)
(a  b) 2  ab + (a+b)
09. (ENEM/2009) Ao morrer, o pai de João, Pedro e
José deixou como herança um terreno retangular de
278
CURSO DE MATEMÁTICA
HAMILTON E ALEX
3km  2km que contém uma área de extração de ouro
delimitada por um quarto de círculo de raio 1 km a partir
do canto inferior esquerdo da propriedade. Dado o
maior valor da área de extração de ouro, os irmãos
acordaram em repartir a propriedade de modo que cada
um ficasse com a terça parte da área de extração,
conforme mostra a figura.
Em relação à partilha proposta, constata-se que a
porcentagem da área do terreno que coube a João
corresponde, aproximadamente, a (considere
3
 0,58 )
3
A) 50%.
B) 43%.
C) 37%.
D) 33%.
E)19%.
GABARITO
01.
02.
03.
04.
05.
06.
07.
08.
09.
C
D
E
C
C
C
C
D
E
279
NOMENCLATURA DOS CATETOS
TRIGONOMETRIA
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
A trigonometria possui uma infinidade de aplicações
práticas. Desde a antiguidade, já se usava da
trigonometria para obter distâncias impossíveis de serem
calculadas por métodos comuns.
Algumas
aplicações
da
trigonometria
são:
Determinação da altura de um certo prédio.
Os catetos recebem nomes especiais de acordo
com a sua posição em relação ao ângulo sob análise.
Se estivermos operando com o ângulo C, então o lado
oposto, indicado por c, é o cateto oposto ao ângulo C
e o lado adjacente ao ângulo C, indicado por b, é o
cateto adjacente ao ângulo C.
Um dos objetivos da trigonometria é mostrar a
utilidade do conceitos matemáticos no nosso cotidiano.
Iniciaremos estudando as propriedades geométricas e
trigonométricas no triângulo retângulo. O estudo da
trigonometria é extenso e minucioso.
Os gregos determinaram a medida do raio da Terra,
por um processo muito simples. Seria impossível se medir
a distância da Terra à Lua, porém com a trigonometria
isso torna simples.
Um engenheiro precisa saber a largura de um rio para
construir uma ponte, o trabalho dele é mais fácil quando
ele usa dos recursos trigonométricos.
Um cartógrafo (desenhista de mapas) precisa saber a
altura de uma montanha, o comprimento de um rio, etc.
Sem a trigonometria ele demoraria anos para desenhar
um mapa.
Tudo isto é possível calcular com o uso da
trigonometria do triângulo retângulo.
Os lados de um triângulo retângulo recebem nomes
especiais. Estes nomes são dados de acordo com a
posição em relação ao ângulo reto. O lado oposto ao
ângulo reto é a hipotenusa. Os lados que formam o ângulo
reto (adjacentes a ele) são os catetos.
C
a
b
A
c
B
Termo
Origem da palavra
Cateto
Cathetós
(Perpendicular)
Hipotenusa
Propriedades do triângulo retângulo
Ângulos: Um triângulo retângulo possui um ângulo
reto e dois ângulos agudos complementares.
Lados: Um triângulo retângulo é formado por três
lados, uma hipotenusa (lado maior) e outros dois lados
que são os catetos.
Altura: A altura de um triângulo é um segmento que
tem uma extremidade num vértice e a outra
extremidade no lado oposto ao vértice, sendo que este
segmento é perpendicular ao lado oposto ao vértice.
Existem 3 alturas no triângulo retângulo, sendo que
duas delas são os catetos.
RELAÇÕES TRIGONOMÉTRICAS
Considerando o triângulo retângulo abaixo temos:
B
Hypoteinusa
Hypó (por baixo) +
Teino (eu estendo)
a
C
Para padronizar o estudo da Trigonometria,adotaremos
as seguintes notações:
C

c

b
A
Em relação ao triângulo acima e pela propriedades
das razões do seno, cosseno e tangente tem-se:
a
b
A
c
B
280
ÂNGULOS NOTÁVEIS
Para estudar os próximos conceitos, convém
conhecermos o seno, cosseno e tangente de alguns
ângulos. Escolhemos, pela facilidade das demonstrações,
os ângulos de medidas 30°, 45° e 60°, que chamamos de
ângulos notáveis.
O RADIANO, UNIDADE DE MEDIDA DE ARCO
E DE ÂNGULO
Um radiano (1rad) é um arco cujo comprimento é
igual ao do raio da circunferência que o contém.
As medidas de um arco em graus e radianos são
proporcionais. Por isso podemos transformar uma
unidade em outra por uma regra de três.
r
r
1 rad
r
1 rad  57,32º
 rad = 180º
Não esqueça que   3,14 e que  rad = 180°
Exemplos
ÂNGULOS COMPLEMENTARES
Se
é a medida de um ângulo agudo, então:
Se dois ângulos agudos são complementares, então o
seno de um deles é igual ao cosseno do outro.
Aplicações
1. Uma escada de 12m de comprimento está apoiada em
um muro fazendo com este um ângulo de 60º. A altura do
muro é:
CICLO TRIGONOMÉTRICO
2. No triângulo retângulo abaixo o valor do ângulo α é
igual a:
Define-se como ciclo trigonométrico a toda
circunferência orientada, de raio unitário e centro no
sistema de coordenadas cartesianas. Por convenção, o
ponto P(1,0) é a origem da orientação, o sentido
positivo é o sentido anti-horário e negativo no sentido
horário.
Observe a representação.
Sentido Anti-horário
Positivo ( + )
P(0, 1)
Sentido Horário
Negativo ( – )
281
As definições acima podem ser ilustradas na figura
tg
a seguir.
Cos
ELEMENTOS
90º

T
Origem 0º
P
P’
180º
360º

O
270º
A
P”
Sen
Considere o ciclo trigonométrico acima.
Os eixos cartesianos limitam a circunferência
trigonométrica () em quatro partes denominadas
quadrantes e numeradas de 1 a 4, no sentido anti-horário.
 1º quadrante: arcos entre 0º e 90º, medidos a
partir da origem.
 2º quadrante: arcos entre 90º e 180º, medidos a
partir da origem.
 3º Quadrante: arcos entre 180º e 270º, medidos
a partir da origem.
 4º Quadrante: arcos entre 270º e 360º, medidos
a partir da origem.
DEFINIÇÃO DE SENO, COSSENO E TANGENTE
DE UM ARCO
Considere no ciclo trigonométrico um arco AP de
medida α e uma reta t paralela ao eixo das ordenadas,
que passa pelo ponto A, origem do ciclo. Observe a figura.
Cos α = Valor do segmento OP’’.
Tg α = Valor do segmento AT.
ARCOS CÔNGRUOS
Como os arcos no ciclo trigonométrico possuem a
mesma origem, então dois arcos no ciclo são côngruos
quando a diferença entre suas medidas possui a forma
2k (com kZ) , ou seja, podemos expressar todos os
arcos côngruos a , no ciclo, na forma  + 2k (com
kZ). De modo análogo, representamos os arcos
côngruos ao ângulo , em graus,na forma  + k.360º
(com kZ).
Exemplos:
t
E1 ) Os arcos – 330º, 390º e – 690º são congruentes
ao arco de 30º, pois as diferenças 30º – (– 330º ),
30º – 390º e – 690º – 30º são múltiplas de 360º.
A
E2 ) Os arcos – 10º e 710º são côngruos ao arco
350º, pois – 10º = 350º – (1 x 360º) e 710º = 350º +
(1 x 360º).
P

Sen α = Valor do segmento OP’.
O
PRIMEIRA DETERMINAÇÃO POSITIVA
Define-se como seno do arco AP (indicado por senα ) a
medida algébrica do segmento OP’, em que P’ é a
projeção ortogonal do ponto P no eixo vertical. O eixo
vertical será chamado de eixo dos senos.
Um arco  é chamado de primeira determinação
positiva ao arco , se satisfaz as condições abaixo:
 Define-se como cosseno do arco AP (indicado por cos
α) a medida algébrica do segmento OP’’, em que P’’ é a
projeção ortogonal do P no eixo horizontal. O eixo
horizontal será chamado de eixo dos cossenos.
II) 0 rad ≤ β < 2 rad.
 Define-se como tangente do arco AP (indicado por tgα)
a medida algébrica do segmento AT, em que T é o ponto
de intersecção da reta suporte do raio OP com a reta t.
O eixo t será chamado de eixo das tangentes.
E.1)30º é a primeira determinação positiva dos
arcos 390º, pois, 390º = 30º + (1x360º) .
I) β é côngruo a .
Exemplos:
282
E.2) Determine a primeira determinação positiva
do ângulo 1910º.
1910º 360º
110º 5
Número de voltas
 Quanto passa de 180º?
 Verifique o sinal da função.
 O arco AM é do 3ºQ e o arco AM’ é a redução
desse arco para o 1ºQ.
1ª determinação positiva ( resto )
E.3) Encontre a primeira determinação positiva
do ângulo 1720º.
1720º 360º
280º 4
Arco no 4º quadrante
90º
Número de voltas
M’
1ª determinação positiva ( resto )
A 0º
360º
180º
O
REDUÇÃO AO 1º QUADRANTE (ARCOS SIMÉTRICOS)
Reduzir um arco do 2ºQ, 3ºQ ou 4ºQ. ao 1ºQ é obter
um novo arco, entre 0º e 90º (1ºQ), que possui os
mesmos valores para as funções trigonométricas que o
arco dado ao mesmo sinal.
M
270º
 Quanto falta para 360º?
 Verifique o sinal da função.
Arco no 2º quadrante
 O arco AM é do 3ºQ e o arco AM’ é a redução
desse arco para o 1ºQ.
90º
M’
M
Variação do sinal do seno e do cosseno
A 0º
360º
180º
O
O seno de um arco é a ordenada da extremidade
desse arco e o cosseno de uma arco é a abscissa da
extremidade desse arco. Como as coordenadas podem
ser positivas e negativas em relação ao ângulo
trabalhado, temos o seguinte quadro de sinais:
270º
 Quanto falta para 180º?
 Verifique o sinal da função.
 O arco AM é do 2ºQ e o arco AM’ é a redução
desse arco para o 1ºQ.
Arco no 3º quadrante
*** Dica
90º M’
Lembre-se da seguinte dica:
180º
O
A 0º
360º
.
RELAÇÕES FUNDAMENTAIS E AUXILIARES
M
270º
Se x é um ângulo agudo num triângulo retângulo e
de
acordo com as definições das funções
trigonométricas, podemos verificar que:
283
Fórmulas auxiliares
Para deduzir duas outras fórmulas muito importantes
da trigonometria, vamos partir da relação fundamental
da trigonometria, inicialmente dividindo ambos os
membros por cos2x ≠ 0. Teremos:
sen2 x
2
cos x

cos2 x
cos2 x

1
cos2 x
Das fórmulas anteriores, concluiremos inevitavelmente
a seguinte fórmula que relaciona a tangente e a secante
de um arco trigonométrico x:
tg 2 x  1  sec2 x
Se em vez de dividirmos por cos2x, dividíssemos
ambos os membros por sen2x, chegaríamos a:
cot g 2 x  1  cos sec2 x
As duas fórmulas anteriores são muito importantes
para a solução de exercícios que comparecem nos
vestibulares; merecem, por isto, uma atenção maior.
Exemplo
SOMA E DIFERENÇA DE ARCOS
Conhecendo os valores de senos, cossenos e
tangentes dos ângulos notáveis, podemos calcular
essas razões para alguns ângulos não notáveis.
Veremos, então, algumas expressões que nos
permitem encontrar o seno, o cosseno e a tangente de
um arco, transformando-o em uma soma ou uma
diferença de arcos. Dados dois arcos α e β, temos:
284
EQUAÇÕES E INEQUAÇÕES
Exemplos
Resolva as equações abaixo:
c) Tgx= 3 /3, perceba que o resultado da tangente de
x é 3 /3 (valor positivo), então você deverá analisar
os quadrantes em que a tangente é positiva. Como já
estudamos em aulas atrás, a tangente é positiva no 1°
e 3° quadrantes e o único valor de x para que a
tangente seja
logo:
3 /3 no 1° quadrante é 30° ou π/6,
a)Senx = 1/2, perceba que o resultado de seno de x é
1/2 (valor positivo), então você deverá analisar os
quadrantes em que o seno é positivo.
Como já estudamos em aulas atrás, o seno é positivo
no 1°e 2° quadrantes e o único valor de x para que o seno
seja 1/2no 1° quadrante é 30° ou π/6, logo:
d) Resolva a inequação abaixo:
b) Cosx=
2 /2, perceba que o resultado de cosseno de
xé 2 /2 (valor positivo), então você deverá analisar os
quadrantes em que o cosseno é positivo. Como já
estudamos em aulas atrás, o cosseno é positivo no 1°e 4°
quadrantes e o único valor de x para que o seno seja 2
/2 no 1° quadrante é 45° ou π/4, logo:
Para o seno ser maior que
intervalo fechado entre
1
,devemos tomar o
2

5
e
, então temos:
6
6
285
FUNÇÕES SENO E COSENO
Considere as seguintes funções:
f(x) = A . sen( B . x )
f(x) = A . cos( B . x )
Altera o período da
função
Altera a imagem da
função
Exemplo
Determine o domínio, imagem, período da função
f(x) = 3.sen2x.
Domínio:D = IR
Imagem: O número 3 está multiplicando a função,
então
[-1,1] será multiplicado por 3, logo,
f : A B
Imagem: Im = [-3, 3]
Contra-Domínio
Domínio
As funções seno e cosseno são definidas assim:
f:R→R
Período: Pela fórmula do período temos
P
2
B
=
2
= , logo: P = 
2
A FUNÇÃO TANGENTE
Temos:
Domínio d(f) = IR
Contra-domínio cd(f)= IR
Imagem Im = [-1, 1]
Período = 2π
***A imagem e o período podem ser alterados
286
EXERCÍCIOS
01. (UFOP) Uma ponte levadiça está construída sobre um
rio cujo leito tem largura igual a 80 m, conforme ilustra a
figura. A largura L do vão entre as rampas dessa ponte,
quando o ângulo de elevação das rampas é de 30°, é:
L
40 m
40 m
30º
A) 50 –
30º
80 m
3
B) 4(20 – 10 3 )
6 - 2 ) metros mais alto que o ponto de partida, a
distância, em metros, percorrida pelo veiculo é:
a)600
b)500 2
c)500 3
d)500
06.(UNIMONTES) Considere as funções reais de
variáveis reais e seus gráficos abaixo, representados
pelas letras M, N, P e Q.
I. f(x) = sen (x/2)
II. g(x) = sen 2x
III. h(x) = 2 + sen x
IV. l(x) = cos x
C) 4(10 – 20 3 )
D) 20(4 –
3)
02.(Vunesp) Uma pessoa, no nível do solo, observa o
ponto mais alto de uma torre vertical, à sua frente, sob o
ângulo de 30º. Aproximando-se 40 metros da torre, ela
passa a ver esse ponto sob o ângulo de 45º. A altura
aproximada da torre, em metros, é
a) 44,7.
b) 48,8.
c) 54,6.
d) 60,0.
e) 65,3.
03.(UFRN) Um observador, no ponto O da figura, vê um
prédio segundo um ângulo de 75°. Se esse observador
está situado a uma distância de 12m do prédio e a 12mde
altura do plano horizontal que passa pelo pé do
prédio,então a altura do prédio, em metros, é:
A seqüência correta que associa gráfico-função é:
a) I-P, II-M, III-N, IV-Q
b) I-M, II-N, III-Q, IV-P
c) I-M, II-Q, III-N, IV-P
d) I-N, II-M, III-P, IV-Q
07. (UNIMONTES – PAES) Em uma biblioteca pública,
deve ser construída uma rampa para acesso a
portadores de deficiência.
Sabendo-se que a altura da rampa é de 1,5me que a
inclinação deve ser de 30°, o comprimento da rampa
será de
A) 3m.
B) 4,5 m.
04.(UNIFOR-CE) Em certa hora do dia, os raios do Sol
incidem sobre um local plano com uma inclinação de 60º
em relação à horizontal. Nesse momento, o comprimento
da sombra de uma construção de 6m de altura será,
aproximadamente:
a) 10,2m
b) 8,5m
c) 5,9m
d) 4,2m
e) 3,4m
05.(UFSJ) Um veículo percorre uma estrada reta com
inclinação de 15°. Se o ponto de chegada situa-se 150(
C) 3 m.
D)
3
m.
2
08.(UNIMONTES) Se senx =
3


e x   ,   , então
5
2

o valor de tgx é igual a
3
a) 
4
3
b)
4
287
c)
3
d)  3
09. (UNIMONTES) Se
podemos afirmar que a
interseção dos gráficos das funções
sen x e cos x
5
a) contém o ponto de abscissa
.
4
b) depende da escala usada.
c) é vazia.
d) contém mais de dois pontos.
10. (UFOP – Aberta) Nos triângulos a seguir, o ângulo Â
é reto. A medida do segmento CB é 20 cm, a do
segmento BD é 11cm e a do segmento DA é 5cm.
13. (Cefet-PR) Se f(x) =

f   é igual a :
6
3
a)
2
b) 0
c) 1
5
d)
2
e) 2
3 .cossec(2x) + cos(8x),
14.(UFMG) Determine todos os valores de x
pertencentes ao intervalo ] 0,  [ que satisfazem a
equação : 3.tgx  2 cos x  3. sec x .
15.(UESC) A expressão mais simples para
1
1
 sec2 x é :
2
cos x .cossec2 x
Determine o valor de tg .
a) 1
b) -1
c) 0
d) tgx
e) sec 2 x
16.(FGV-SP) A expressão
11. (UFV) O valor de tg 10º.(sec 5º + cossec 5º).(cos 5º
– sen 5º) é igual a:
A) 2
1
B)
2
C) 1
D)
2
12. (UFMG) Observe a figura:
senx  0 , é idêntica a:
2
a)
cos x
1
b)
senx
c) sec x
senx
1  cos x
, para

1  cos x
senx
d) 2.cossec x
cos x
e)
1  senx
cossecx  senx
, com
sec x  cos x
cos x  0 e senx  0 , identicamente igual a :
17.(PUC – SP) A expressão
a) cotg3 x
Nessa figura o ponto M é o ponto médio do lado DC,
do quadrado ABCD. A tangente do ângulo α é:
1
A)
2
B) 1
C) 2
D)
3
2
b) sec 2 x
c) sen 2 x  cos x
d) tg2 x  sec x
e) cossec 3 x
18.
(UFPR)
Se
cos x  0 ,
a
expressão
sec x  tg x  1 é idêntica a:
4
4
a) tg2 x
b)  tg2 x
288
c) 2.tgx
2
d) 2.tg x
e) 1
19. (Fatec-SP) Se x é um número real tal que
sen 2  3senx  2 , então x é igual a:

a)  k, com k  
2
3
b)
 k, com k  
2
3
c)
 k 2, com k  
2

d)  k 2 , com k  
2

e)  k, com k  
4
20.(U.F.Ouro Preto-MG)
senx  cos x são:
As soluções da
equação

, com k  
4

b) x  ( 2k  1) , com k  
4
c) x  2.k, com k  
23. (UNIMONTES) Uma escada de 25m
está
encostada na parede vertical de um edifício, de forma
que o pé da escada está a 7m da base do prédio. Se
o topo da escada escorrega 4m, o pé da escada
escorregará
A) 14m.
B) 8m.
C) 15m.
D) 9m.
24.(UNICAMP – SP) A água utilizada na casa de um
sitio é captada e bombeada do rio para uma caixa
d’água a 50m de distância. A casa está a 80m de
distancia da caixa d’água e o ângulo formado pelas
direções: caixa d’agua-bomba e caixa d’agua - casa é
de 60º. Se a idéia é bombear água do mesmo ponto de
captação até a casa, quantos metros de encanamento
são necessários?
a) 80m
b) 70m
c) 50m
d) 90m
e) 60m
a) x  ( 4k  1)
25.(UNIMONTES) Se
então o valor de
x para o qual senx = y, no intervalo [0,2[, é
a) 

b)
2
3
c)
2
d) 0
d) x  k, com k  

e) x  ( 3k  1) , com k  
2
21.(UEL -PR) A função dada por f(x) = (tgx).(cotgx) está
definida se, e somente se
A) x é um número real qualquer
B) x  2k, com k  
C) x  k, com k  
k
D) x 
, com k  
2
k
E) x 
, com k  
4
22. (UFJF) Sejam x e y tais que senx. cos x 
= senx + cosx. Pode-se afirmar que:
5
a) y =
2
5
5
b) y  
ou y 
2
2
5
c) y 
2
5
5
d) y  
ou y 
2
2
5
5
e) y 
ou y 
2
2
26.(FIP-2013) Num dia chuvoso, uma descarga elétrica
queimou uma das lâmpadas da casa de Bernardo.
Após a chuva,ele resolveu trocar a lâmpada
queimada. Para isso, encostou uma escada na
parede, de modo que o topo da escada ficou a uma
altura de 4 metros, conforme mostra a figura a seguir:
1
e y
8
Após subir alguns degraus, Bernardo tomou um
susto, pois a base da escada escorregou por 1
metro, e só parou ao tocar um muro paralelo à parede,
formando, assim, um ângulo de 45º com o piso
horizontal. A nova situação pode ser observada na
figura a seguir:
289
AB̂I ( 60º ). Qual é, aproximadamente, a distância IP ,
da ilha até a praia ?
a) 30m
I Ilha
b) 220m
c) 660m
d) 940m
Mar
e) 1275m
P
A distância entre a parede da casa e o muro é de:
27.(UNIMONTES) Considere x um arco com extremidade
no segundo quadrante, tal que sec x = – 5/3 . Assim, o
2
valor da expressão A = 5(sen x) – 3 tg x vale
36
5
32
b) 
15
4
c)
5
36
d)
5
a) 
28. ( PUC – MG ) No triângulo da figura, B̂ > Ĉ e tg B̂ =
4
. O valor do seno do ângulo Ĉ é:
3
C
1
1
a)
b)
4
2
2
2
c)
d)
3
5
B
A
3
e)
5
29.( Cefet – PR ) A rua Tenório Quadros e a avenida
Teófilo Silva, ambas retilíneas, se cruzam segundo um
ângulo de 30º. O posto de gasolina Estrela do Sul se
encontra na avenida Teófilo Silva a 4000 metros do citado
cruzamento. Portanto, a distância entre o posto de
gasolina Estrela do Sul e a rua Tenório Quadros, em km,
é igual a :
a) 4
b) 12
c) 2
d) 5
4000 m
e) 8
B
A
Praia
31. ( FEI – SP ) Na figura abaixo, BD mede 9 cm,
CD tem 5 cm e AD mede 13 cm. O valor de tg 
é:
13
A
a)
5
13
b)
9
13

c)
B
D
C
14
5
d)
6
6
e)
7
32.( UFRS ) Considere as seguintes afirmações para
arcos medidos em radianos:
I) sen 1 < sen 3
II) cos 1 < cos 3
III) cos 1 < sen 1
Quais são verdadeiras?
a) Apenas I é verdadeira.
b) Apenas II é verdadeira.
c) Apenas III é verdadeira.
d) São verdadeiras apenas I e II.
e) São verdadeiras I, II e III.
33.( Vunesp – SP ) A figura representa o perfil de uma
escada cujos degraus têm todos a mesma extensão,
além de mesma altura. Se AB = 2 m e BĈA mede
30º, então a medida da extensão de cada degrau é :
a)
2 3
3
b)
2
3
6
c)
3
A
B
C
3
2
3
e)
3
d)
30. ( PUCC – SP ) Na praia, mediu-se a distância de A
até B ( 750 m ) e de A até P ( 620 m ), além do ângulo
290
34.( FMJ – SP ) Na figura abaixo são dados: O triângulo
ABC retângulo em B̂ ; o triângulo CDB, retângulo em D̂
e CB̂D de 30º. Se BC = 4 3 cm, a área do triângulo
ADB, em centímetros quadrados, é :
C
a) 6 3
b) 9
D
c) 9 3
d) 18
30º
e) 18 3
A
Um cliente solicitou a produção de telhas que fossem
duas vezes mais sanfonadas e que tivessem o triplo
da altura da telha-padrão, como na figura abaixo.
B
35.( Unimontes – PAES / 2004 ) Se sen x =
3
e x
5


 2 ,   , então o valor de tg x é igual a :


3
a) 
4
3
b)
4
c)
3
d)
 3
Marque a opção que representa a curva geratriz dessa
nova telha.
A)
36.( Unimontes – PAES / 2005 ) O valor de x  R, para o
qual a igualdade cos = 2x – 5 seja possível, está no
intervalo real :
a) [2, 3]
b) ]2, 3[
c) [4, 6]
d) ]4, 6[
B)
C)
D)
E)
37.( Unimontes – PAES / 2006“anulada” ) Os pontos x
do ciclo trigonométrico, correspondentes às soluções do
 sen 2x  0
, 2x  [ 0, 2 ], pertencem ao :
 cot g x  0
sistema 
a)
b)
c)
d)
e)
1° quadrante, somente
3º quadrante, somente
4º quadrante, somente
1º ou 2º quadrante, somente
N.d.a
38. (FIP/2014) Uma empresa produz telhas senoidais,
como a da figura abaixo.
39. (FIP/2014) Num hemocentro, o número de doações
de sangue varia periodicamente. No ano de 2013, esse
número, de janeiro a dezembro, foi calculado mediante
a função

em que D(t) é dado em milhares e t em meses, com
0 ≤ t ≤ 11.
O número de doações de sangue nos meses de agosto
e outubro foi de:
A) 4
B) 7,5
C) 3,5
D) 3,86
E) 7
Para a criação do molde da telha a ser fabricada, é
necessário fornecer a função cujo gráfico será a curva
geratriz da telha. A telha padrão produzida pelo fabricante
possui por curva geratriz o gráfico da função y = sen (x).
GABARITO
01. B
02. C
03. A
291
04. E
05. A
06. A
07. A
08. A
09. A
10. 33/56
11. A
12. A
13. A
TRIÂNGULOS QUAISQUER
Lei dos cossenos
Em qualquer triângulo, o quadrado de um dos lados é
igual à soma dos quadrados dos outros dois lados,
menos o dobro do produto desses dois lados pelo
cosseno do ângulo formado entre eles.
c
14.
15. C
16. D
17. A
18. D
19. D
20. B
21. D
22. B
23. B
24. B
25. C
26. A
27. D
28. E
29. C
30. C
31. E
32. C
33. E
34. E
35. A
36. B
37. E
38. B
39. B
b

a
b2 = a2 + c2 – 2. a. c . cos 
Exemplos
1) Encontre a medida do lado AB no triângulo ABC
abaixo.
A
4
C
60º
6
B
2) No triângulo ABC abaixo, encontre o valor do
cosseno do ângulo .
B
6
4
A

8
C
292
Lei dos senos
EXERCÍCIOS
O seno de um ângulo de um triângulo qualquer é
proporcional à medida do lado oposto a esse ângulo.
1) ( Fuvest – SP ) Um triângulo tem os lados com
medidas iguais a 4, 5 e 6. O co-seno do maior
ângulo interno desse triângulo é :
4
5
a)
b)
6
5
3
2
c)
d)
4
3
1
e)
8
C
A
R
c
b
a
OU
b
B
C
B
a
c
A
a
ˆ
senA

b
ˆ
senB

c
ˆ
senC
= 2R
2) ( PUC – SP ) Na figura abaixo, qual o valor de
cos ?
2
1
Exemplos

1) Encontre a medida do lado AC no triângulo ABC
abaixo.
2
B
4 2
A
105º
45º
C
2) O triângulo ABC abaixo, está inscrito em uma
circunferência, conforme a figura. Encontre a medida
do raio dessa circunferência.
3) ( Cesgranrio ) Os lados de um triângulo são 3, 4
e 6. O co-seno do maior ângulo interno desse
triângulo vale:
a) 11/24
b) – 11/24
c) 3/8
d) – 3/8
e) – 3/10
4) ( UFMG ) Na figura, o ângulo BÂC mede 60º e
o segmento BC mede 4 cm. Qual a medida do
raio da circunferência que contém os pontos A, B
e C ?
A
C
B
A 60º
6 3
B
C
5) ( UFPR ) Em um triângulo ABC têm-se que BC
= 6 cm e CÂB = 30º. A medida do raio da
circunferência circunscrita a esse triângulo é :
a) 6
b) 12
C
c) 8
d) 9
A
e) 10
B
293
6) (ESPM ) Num triângulo isósceles, a base tem 8 cm
e o ângulo oposto à base mede 120°. Cada um dos
outros dois lados do triângulo mede: DADOS : Cos
1
3
120º =  ; sen 120º =
2
2
a)
3 cm
b) 2 5 cm
x
120º
x
c) 4 5 cm
d) (4 3 )/3 cm
8 cm
e) (8 3 )/3 cm
7) ( CFTMG ) Um dos ângulos internos de um
paralelogramo de lados 4 m e 6 m mede 120°. A
maior diagonal desse paralelogramo mede, em metros
a) 2 17
b) 2 19
c) 2 21
d) 2 23
8) ( UFPE )Uma ponte deve ser construída sobre um rio,
unindo os pontos A e B, como ilustrado na figura
abaixo. Para calcular o comprimento AB, escolhe-se
um ponto C, na mesma margem em que B está, e
medem-se os ângulos CBA = 57° e ACB = 59°.
Sabendo que BC mede 30m, indique, em metros, a
distância AB. ( Dado: use as aproximações sen(59°)
= 0,87 e sen(64°) = 0,90 )
a) 28
b) 29
c) 30
d) 31
e) 32
a) 3 +
5
b) 5 +
3
c) 3 +
3
d) 3 +
7
e) 5 +
7
11) Na figura abaixo o triângulo ABC está inscrito na
circunferência de raio R. Se a medida do lado AB
R
é
, pode-se afirmar que o valor do seno do
2
ângulo  é
A
a) 1/2
b) 1/4
B
c) 1/3

d) 1/5
C
e) 2/3
12) ( CFTCE ) Na figura a seguir o valor de x pode
ser :
a) 1/2
b) 3/2
c) 2/3
d) 4/3
e) 1/5
13) ( Cesgranrio ) No triângulo ABC, os lados AC e
BC medem 8 cm e 6 cm, respectivamente, e o
ângulo A vale 30°.
B
O seno do ângulo B vale:
a) 1/2
b) 2/3
c) 3/4
d) 4/5
A
e) 5/6
C
9) ( Fuvest – SP ) No quadrilátero a seguir, BC = CD = 3
cm, AB = 2 cm, ADC = 60° e ABC = 90°. A medida,
em cm, do perímetro do quadrilátero é:
a) 11.
b) 12.
c) 13.
d) 14.
e) 15.
10) ( UFPI ) Em um triângulo, um dos ângulos mede 60° e
os lados adjacentes a este ângulo medem 1cm e
2cm. O valor do perímetro deste triângulo, em
centímetros, é:
14) ( CESCEM ) Se, em um triângulo, o quadrado de
um lado é igual à soma dos quadrados dos outros
dois lados menos o produto desses dois lados,
calcule o ângulo interno que os mesmos dois lados
formam.
GABARITO
3
1) E
2)
4
7) B
8) B
13) B
14) 60º
3) B
9) B
4)
4 3
3
10) C
5) A
11) B
6) E
12) B
294
QUESTÕES DO ENEM
figura, e suponha que o ponto P percorra, no sentido
anti-horário, uma distância d  r sobre a circunferência.
01. (ENEM-2013) As torres Puerta de Europa são duas
torres inclinadas uma contra a outra, construídas numa
avenida de Madri, na Espanha. A inclinação das torres é
de 15° com a vertical e elas têm, cada uma, uma altura de
114 m (a altura é indicada na figura como o segmento
AB). Estas torres são um bom exemplo de um prisma
oblíquo de base quadrada e uma delas pode ser
observada na imagem.
Disponível em: www.flickr.com. Acesso em: 27 mar. 2012.
Utilizando 0,26 como valor aproximado para a tangente de
15° e duas casas decimais nas operações, descobre-se
que a área da base desse prédio ocupa na avenida um
espaço
A) menor que 100 m2.
B) entre 100 m2 e 300 m2.
C) entre 300 m2 e 500 m2.
D) entre 500 m2 e 700 m2.
E) maior que 700 m2.
02.(ENEM-2009) Uma empresa precisa comprar uma
tampa para o seu reservatório, que tem a forma de um
tronco de cone circular reto, conforme mostrado na figura.
Considere que a base do reservatório tenha raio r = 2 3
m e que sua lateral faça um ângulo de 60º com o solo.
Então, o ponto Q percorrerá, no eixo x, uma distância
dada por
d
d


A) r  1  sen 
B) r  1 cos 
r
r


d

r
C) r  1 tg 
D) r.sen 
r
 d

r
E) r. cos 
 d
04. (ENEM-2011) Para determinar a distância de um
barco até a praia, um navegante utilizou o seguinte
procedimento: a partir um ponto A, mediu o ângulo visual
α fazendo mira em um ponto fixo P da praia. Mantendo
o barco no mesmo sentido, ele seguiu até um ponto B de
modo que fosse possível ver o mesmo ponto P da praia,
no entanto sob um ângulo visual 2α. A figura ilustra essa
situação.
Trajetória do
barco
Suponha que o navegante tenha medido o ângulo
α = 30° e, ao chegar ao ponto B, verificou que o barco
havia percorrido a distância AB = 2 000 m. Com
base nesses dados e mantendo a mesma trajetória, a
menor distância do barco até o ponto fixo P será
A) 1000m
B) 1000 3 m
C) 2000 3 3 m
D) 2000m
E) 2000 3
GABARITO
01. E
02. B
03. B
04. B
Se a altura do reservatório é 12m, a tampa a ser
comprada deverá cobrir uma área de
A) 12 m2.
B) 108 m2.
2
2
C) (12 + 2 3 )  m .
D) 300  m .
2
2
2
E) (24 + 2 3 )  m .
03. (ENEM/2009) Considere um ponto P em uma
circunferência de raio r no plano cartesiano. Seja Q a
projeção ortogonal de P sobre o eixo x, como mostra a
295
CURSO DE MATEMÁTICA
Geometria Espacial de Posição
INTRODUÇÃO
É na idade da pedra que encontramos os primeiros
vestígios da geometria. Nessa época, pinturas, armas e
objetos em geral já mostravam simetria e harmonia nas
formas.
Na Mesopotâmia, por volta do ano 3000 a.C., já se
calculavam áreas de extensões de terras. Elas eram
subdivididas em triângulos e quadriláteros.
Na Grécia, entre 600 e 300 a.C., a geometria teve
notáveis avanços e tomou corpo como ciência. Nessa
época, destacaram Pitágoras e Tales de Mileto.
Mas foi Euclides o grande responsável pela
sistematização dos conceitos geométricos. Ele viveu entre
300 e 20 a.C.. Em sua obra “Os Elementos” Euclides
apresenta a geometria como um sistema lógico-dedutivo.
Até hoje, a geometria euclidiana é a teoria que melhor
explica as propriedades das figuras e descreve suas
formas, posição, relações e dimensões.
HAMILTON E ALEX
O plano é bidimensional ( tem comprimento e largura ) e
ilimitado, cresce infinitamente. Ele é representado por
letras minúsculas do alfabeto grego ( , , , ... ).
Postulados
Ponto, reta e plano ficam caracterizados através de uma
série de qualidades, essas qualidades, são chamadas de
postulados.
Os postulados ou axiomas são proposições da geometria
que são aceitas sem demonstração. Eles relacionam os
conceitos primitivos e são a base de toda a teoria.
Alguns Postulados e Definições
Postulado 1
P1 – Em uma reta e também fora dela,
existem infinitos pontos.
A
C B
A base da geometria é o conceito de ponto. Qualquer
conjunto não-vazio de pontos é uma figura geométrica.
Postulado 2
Neste capítulo, vamos começar o estudo da geometria
espacial. Para isso, vamos ampliar o nosso universo, com
o estudo das figuras espaciais ou tridimensionais.
P2 – Em um plano e também fora dele,
existem infinitos pontos.

Entes Geométricos Primitivos
Alguns conceitos geométricos não são definidos, eles são
o ponto de partida ou a matéria-prima de toda a teoria.Os
mais simples entes geométricos imaginados são: Ponto,
reta e plano.

r
A

( Ponto )
( reta )
( plano )
Por definição, reta e plano são entes ilimitados,
crescem infinitamente.
O ponto não tem dimensão ( adimensional ), ele é
representado por letras latinas maiúsculas ( A, B, C, ..., P,
Q, ... ).
A reta é unidimensional ( só tem comprimento ) e
ilimitada, cresce infinitamente. Ela é representada por
letras latinas minúsculas ( r, s, t, ... ).
Postulado 3
P33–Dois
uma
reta.
P
– Doispontosdistintosdeterminam
pontos distintos determinam
uma
reta.
A
B
Postulado 4
P4 – Por dois pontos distintos ( ou pela reta que
eles determinam ) passam infinitos planos
A
B
296
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Retas perpendiculares são retas concorrentes que
formam quatro ângulos retos ( 90º ).
Postulado 5
P
A reta
que possui dois pontos distintos
P53–
–Dois
pontosdistintosdeterminam
uma reta.
de um plano está contida neste plano.
A
São retas coplanares que não têm pontos comuns
(paralelas distintas) ou quando têm todos os pontos
comuns (paralelas iguais ou coincidentes).

B
Retas Paralelas
Retas paralelas distintas são retas coplanares que não
têm pontos comuns.
Postulado 6
P63–Dois
– Três
pontos (distintos) não alinhados
pontosdistintosdeterminam
uma reta.
determinam um plano.
retas

A
B
Retas paralelas iguais(coincidentes) são
coplanares que possuem todos os pontos comuns.
C
Retas Reversas
NOTA: Um ente geométrico está determinado
quando existe e é único.
Retas simplesmente reversas são retas não coplanares
que formam ângulos imaginários diferentes de 90º.
Retas reversas ortogonais são retas não coplanares que
formam ângulos imaginários medindo 90º.
Retas no Espaço
s
r
t
Duas retas do espaço podem ser coplanares ou
reversas.
a) Retas Coplanares
Quando existe um plano que as contém. As retas
coplanares são concorrentes ou paralelas.
Retas coplanares não são, necessariamente, retas que
estão em um mesmo plano. Duas retas são coplanares
quando “existe um plano que as contém”
r

s
As retas paralelas r e s não
estão no plano , mas são
coplanares, pois existe um
plano que as contêm.
b) Retas Reversas ou Não Coplanares
Na figura acima, as retas r e s são retas paralelas
distintas, as retas r e t são retas reversas ortogonais
e as retas
s
e
t
são retas concorrentes
perpendiculares.
Retas no Espaço ( Diagrama )
Distintas
Paralelas
Retas
Coplanares
Concorrentes
ou
Oblíquas
Retas Concorrentes
Retas oblíquas são retas concorrentes que formam
ângulos diferentes de 90º.
Coincidentes
ou
Perpendiculares
Quando não existe um plano que as contém. As retas
reversas são reversas ortogonais ou simplesmente
reversas.
Quando têm um único ponto comum. As retas
concorrentes podem ser oblíquas ou perpendiculares.
Ou
Reversas
Ortogonais
Retas
Reversas
Formam ângulo
imaginário de 90º
ou
Simplesmente
Reversas
Formam ângulo
imaginário
diferente de 90º
297
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Determinação de Planos
Posições Relativas
Um plano está determinado quando existe e é
único. A partir do postulado P6 podem ser
demonstrados mais três teoremas clássicos de
determinação de plano.
Reta e Plano
Quatro Maneiras
Existem quatro maneiras de verificar se um plano está
determinado. Essas maneiras são:
Uma reta r e um plano  do espaço podem ocupar as
seguintes posições relativas:
Reta paralela ao plano
Quando a interseção entre eles é um conjunto vazio. ( Não
têm pontos comuns).
r
r  = 

1ª Maneira
Três pontos (distintos) não colineares
determinam um plano

A
B
Reta contida no plano
Quando todos os pontos da reta são pontos do
r

Plano.
r  = r
C
Reta concorrente ( secante ) com o plano
Quando a reta e o plano têm um único ponto comum.
2ª Maneira
r
Duas retas concorrentes determinam um plano.
(Retas que possuem um único ponto comum )
P

r  = {P}

Plano e Plano
3ª Maneira
Uma reta e um ponto fora dela determinam um
plano.
P
Dois planos e  espaço podem ser classificados como:
planos paralelos iguais ( coincidentes ), planos
paralelos distintos ou planos secantes.
Paralelos iguais
Dois planos são paralelos iguais quando têm todos os
pontos comuns.
4ª Maneira
Duas retas paralelas distintas determinam um
plano.
=
Paralelos distintos
Dois planos são paralelos distintos quando não têm pontos
comuns, a intersecção desses planos é vazia.



298
CURSO DE MATEMÁTICA
Planos secantes
Dois planos são secantes quando têm apenas uma reta
em comum.

r
r

HAMILTON E ALEX
TEOREMAS
SOBRE
PARALELISMO
PERPENDICULARIDADE
E
 Se uma reta r está fora de um plano  e é paralela a
uma reta s contida em , então ela é paralela a este
plano .
r
s

Reta e Plano Perpendiculares
Uma reta “r“ e um plano ““ são perpendiculares quando a
reta r e o plano  são concorrentes, e r é perpendicular
com todas as retas que passam por P, sendo P o traço
de r em .
P, também é chamado de pé da perpendicular.
 Se um plano  contém duas retas concorrentes, ambas
paralelas a outro plano , então esses planos são
paralelos.(condição necessária e suficiente)


r

P
 Se dois planos 
 são perpendiculares e uma reta r
de um deles () é perpendicular à interseção dos
planos, então ela é perpendicular ao outro plano (  .
Teoremas
r
 Se uma reta
r,concorrente com um plano, for
perpendicular a pelo menos duas retas concorrentes
desse plano, então ela é perpendicular ao plano.


r

EXERCÍCIOS RESOLVIDOS
P
 Se uma reta r for perpendicular a um plano ,
qualquer reta paralela a r também será perpendicular a
esse plano.
r
s

Se r  e r // s  s 
1) Nas afirmativas abaixo, coloque V nas verdadeiras e
F nas falsas.
a) ( F ) Três pontos
distintos determinam um
plano.
Três pontos não colineares determinam um
plano.
b) ( V ) Por três pontos colineares passam infinitos
planos.
c) ( V ) Por dois pontos sempre passa uma reta.
Planos Perpendiculares
Um plano é perpendicular a outro se, e somente se, um
deles contém uma reta perpendicular ao outro.
r

Se r  e  r 

d) ( F ) Dois pontos determinam uma reta.
Dois pontos distintos determinam uma reta.
e) ( V ) Três retas paralelas duas a duas podem
determinar três planos.
f)
( F ) Se dois pontos de uma reta pertencem a um
plano, esta reta está contida nesse plano.
Os pontos têm que ser distintos.
299
CURSO DE MATEMÁTICA
HAMILTON E ALEX
2) Nas afirmativas abaixo, coloque V nas verdadeiras e
F nas falsas.
a) ( V ) Em dois planos paralelos distintos, todas as
retas de um são paralelas ao outro plano.
d) A reta t pode estar contida num plano
perpendicular a
e) todo plano que contém t é paralelo ao plano 
3)
(PUC – SP) – São dadas as proposições:
I – Uma reta é perpendicular a um plano quando ela é
perpendicular a todas as retas desse plano.
II – Se dois planos distintos são paralelos, então toda
reta de um é paralela ao outro.
III – Se um plano é perpendicular a outro, então ele é
perpendicular a qualquer reta desse outro.
É correto afirmar que:
a) Apenas II é verdadeira.
b) I, II e III são verdadeiras.
c) I, II e III são falsas.
d) Apenas II e III são verdadeiras.
e) Apenas III é verdadeira.
4)
( PUC – SP ) Se r e s são retas reversas, então
pode-se GARANTIR que:
a) todo plano que contém r também contém s.
b) o plano que contém r e é perpendicular a s.
c) existe um único plano que contém r e s.
d) existe um plano que contém r e é paralelo a s.
e) toda reta que encontra r encontra s.
b) ( F ) Em dois planos paralelos distintos, todas as
retas de um são paralelas às retas do outro plano.
As retas de um podem ser paralelas ou reversas
às retas do outro.
c) ( V ) Se uma reta é paralela a um plano, em tal
plano existe uma infinidade de retas paralelas àquela
reta.
d) ( F ) Se uma reta é paralela a um plano, é paralela
a todas as retas do plano.
A reta será paralela a infinitas retas do plano, mas
não a todas as retas do plano, algumas serão
reversas a ela.
e) ( V ) Se duas retas de um plano não são
paralelas elas são concorrentes.
f) ( F ) Se  e  são dois planos paralelos
distintos, toda reta paralela a  também será
paralela a .
Têm infinitas retas paralelas a  e que estão
contidas em .
EXERCÍCIOS
1) ( Unimontes – 2003 ) Sejam r, s e t três retas no
espaço. Analise as seguintes afirmações :
( ) Se r e s são paralelas, então existe um plano
que as contém.
( ) Se a interseção de r e s é o conjunto vazio,
então r é paralela a s.
( ) Se r, s e t são duas a duas paralelas, então
existe um plano que as contém.
( ) Se r  s =  e r não é paralela a s, então r
e s são reversas.
Considerando V para sentença verdadeira e F para
sentença falsa, a seqüência CORRETA que classifica
essas afirmações é :
a) V, V, V, V
b) F, V, V, F
c) V, F, F, V
d) V, V, F, F
2) ( UEL – PR ) Dados um plano  e uma reta t , tais
que  t = , então:
a) t 
b) t 
c) uma reta s, s tal que s // t.
5) Assinale a única alternativa FALSA.
a) Se uma reta é paralela a um plano, em tal plano
existe uma infinidade de retas paralelas àquela reta.
b)Se dois planos são paralelos distintos, toda reta de
um deles é paralela ao outro.
c) Se dois pontos de uma reta são pertencentes a um
plano , concluímos que esta reta está contida
nesse plano.
d)Uma reta e um ponto fora dela determinam um
plano.
6) Assinale a única alternativa VERDADEIRA.
a) Uma reta e um ponto determinam um plano.
b)Por um ponto passa uma única reta.
c) Se uma reta é paralela a um plano, é paralela a
todas as retas do plano.
d)Se dois planos forem paralelos a uma reta então são
planos paralelos entre si.
e) Por três pontos colineares passam infinitos planos.
7) (ITA – SP) Quais as sentenças falsas nos itens abaixo
?
I ) Se dois planos são secantes, todas as retas de um
deles sempre interceptam o outro plano.
II ) Dados dois planos, se num deles existem duas
retas distintas paralelas ao outro plano, os planos são
sempre paralelos.
III ) Em dois planos paralelos distintos, todas as retas
de um são paralelas ao outro plano.
IV ) Se uma reta é paralela a um plano, em tal plano
existe uma infinidade de retas paralelas àquela reta.
300
CURSO DE MATEMÁTICA
V ) Se uma reta é paralela a um plano, é paralela a
todas as retas do plano.
a) I, II e III
b) I, II e V
c) I, III e IV
d) II, III e IV
8) (CESCEM) – Sendo P um ponto qualquer, r uma reta
e  um plano, a alternativa correta é:
a) P , r   P r
b)P , r   P r
c) P r  P 
d)P r 
e) P r e r   P
9) (MACK-SP) – A reta r é perpendicular ao plano 
então:
a) Todas as retas de são paralelas a r.
b) A reta r não pode ser coplanar com nenhuma reta
de 
c) Existem em  retas paralelas e retas reversas a r.
d) Existem em  retas perpendiculares a r e também
existe em  retas reversas em relação a r.
e) Todo plano que contém r é paralelo a 
10) ( FEI – SP) Na determinação de um plano a
alternativa que corresponde às condições suficientes
é:
a) Duas retas concorrentes
b) Uma reta e um ponto
c) Duas retas distintas
d) Duas retas reversas
e) n.d.a
11) ( UFES ) Dados dois planos paralelos, se um outro
plano corta os dois dados, as interseções são retas :
a) concorrentes
b) perpendiculares
c) paralelas
d) reversas
e) não são retas
12) (ITA) – Sejam as afirmações:
I – Por um ponto passa uma única reta.
II – Um ponto e uma reta determinam um plano.
III– Se dois pontos de uma reta pertencem a um
plano, então a reta está contida neste plano.
IV – Por um ponto situado fora de uma reta existe
uma reta paralela à reta dada.
Podemos garantir que:
a) Apenas III é verdadeira
b)I e II são falsas
c) Apenas I é falsa
d)Apenas II e III são verdadeiras
e) Apenas II e IV são verdadeiras
HAMILTON E ALEX
13) (SANTO ANDRÉ) – Assinale a alternativa correta:
Dados um plano e um ponto P fora de :
a) Por P passa somente uma reta paralela a 
b) Por P passa mais do que uma reta paralela a ;
c) Por P não passa nenhuma reta paralela a ;
d) Toda reta que passa por P fura 
e) n.r.a
14) (MACK – SP) – A reta r é paralela ao plano . Então:
a) Todas as retas de são paralelas a r.
b) A reta r não pode ser coplanar com nenhuma reta
de 
c) Existem em  retas paralelas a r e também retas
reversas a r.
d) Existem em  retas paralelas e perpendiculares a
r.
e) Todo plano que contém r é paralelo a 
15) ( FCC – SP ) Se um plano e uma reta r são tais que
r    r , então :
a) existe um plano que contém r e não intercepta 
b) toda reta paralela a r está contida em  .
c) toda reta paralela a  é paralela a r.
d) existe uma reta em  que é concorrente com r.
e) toda reta perpendicular a  é perpendicular a r.
16) ( MACK – SP ) Sendo r e r’ retas reversas, o número
de planos paralelos a r, e que podem conter r’, é:
a) 2
b) 1
c) infinito
d) 0
e) n.d.a.
17) ( FMU – SP ) Dados um plano  e duas retas r e s
distintas a ele, tais que r  s e s  , podemos
afirmar que:
a) r  s = 
b) r e s são retas reversas
c) r//s
d) r//
e) n.d.a.
GABARITO
1) C
7) B
13) B
2) D
8) E
3) A
9) D
14) C
4) D
10) A
15) D
5) C
6) E
11) C
12) B
16) B
17) D
301
CURSO DE MATEMÁTICA
GEOMETRIA ESPACIAL
HAMILTON E ALEX
Propriedades
A soma dos ângulos das faces de um poliedro
convexo é dada por:
POLIEDROS
Sv = (v – 2). 360º
Poliedro convexo
Poliedro convexo é todo sólido cuja superfície é limitada
por polígonos convexos.
Onde v é o nº de vértices do poliedro.
Face do poliedro
Vértice do poliedro
Aresta do poliedro
Elementos do Poliedro
Número de Arestas
Convexo
de Um Poliedro
O número de arestas de um poliedro convexo pode ser
calculado a partir do número de lados das faces ou a
partir do número de arestas por vértices.
 Face – é cada polígono da superfície
 Aresta – é a interseção de duas faces
 Vértice – é a interseção de duas arestas
As faces de um poliedro convexo podem ser:
Triangulares – 3 arestas
Quadrangulares – 4 arestas
Pentagonais – 5 arestas
Hexagonais – 6 arestas,
Heptagonais – 7 arestas
Octogonais – 8 arestas
Eneagonais – 9 arestas
Decagonais – 10 arestas
E assim por diante.
A
N F .l F
2
O nome de um poliedro depende da quantidade de faces
que ele possui. O poliedro abaixo é um hexaedro, pois ele
possui seis faces .
O Poliedro ao lado possui 6 faces
triangulares, 2 vértices triédricos e
3 vértices tetraédricos.
A
N v .a v
2
Onde:
A é o nº de arestas do poliedro.
NF é o nº de faces do poliedro.
lF é o nº de lados de cada face.
NV é o nº de vértices do poliedro.
aV é o nº de arestas por vértice.
Teorema de Euler
Num poliedro convexo onde V é o número de vértices,
A é o número de arestas e F é o número de faces é
válida a relação:
F+V = A+2
Os vértices de um poliedro convexo podem ser:
Triédricos – 3 arestas por vértice
Tetraédricos – 4 arestas por vértice
Pentaédricos – 5 arestas por vértice
Hexaédricos – 6 arestas por vértice
ou
Exemplo:
Um poliedro convexo possui 3 faces quadrangulares,
5
faces hexagonais
e
8 faces triangulares.
Determine:
a) Quantos vértices tem esse poliedro;
b) A soma dos ângulos das faces desse poliedro.
302
CURSO DE MATEMÁTICA
HAMILTON E ALEX
POLIEDROS DE PLATÃO
POLIEDRO REGULAR
Um poliedro convexo é poliedro de Platão quando satisfaz
às três condições abaixo:
É todo poliedro convexo onde todas as faces são
polígonos regulares congruentes entre si, bem como todos
os ângulos poliédricos.
 Possui todas as faces com mesmo número de lados;
Todos os poliedros regulares são poliedros de Platão.
 Possui todos os vértices com o mesmo número de
arestas;
 Satisfaz o teorema de Euler ou seja, F + V = A + 2.
Tetraedro
Regular
Hexaedro
Regular
Octaedro
Regular
Exemplo:
Verifique se o sólido abaixo é um poliedro de Platão. Qual
o nome desse poliedro ?
Dodecaedro
Regular
Icosaedro
Regular
Propriedade
Os poliedros de Platão só podem assumir
as formas abaixo
Todo poliedro regular é poliedro de Platão, mas nem todo
poliedro de Platão é regular.
A tabela abaixo mostra o número de faces, arestas e
vértices dos poliedros regulares.
POLIEDROS
Nomes
Hexaedro
Tetraedro
Dodecaedro
Octaedro
Icosaedro
T etraedro ( 4 faces triangulares )

H exaedro ( 6 faces quadrangulares )

O ctaedro ( 8 faces triangulares )

D odecaedro ( 12 faces pentagonais )

I cosaedro ( 20 faces triangulares )
Os poliedros de PLATÃO têm apenas vértices
TRIÉDRICOS, TETRAÉDRICOS ou PENTAÉDRICOS.
faces
arestas
vértices
Tetraedro
4
6
4
Hexaedro
6
12
8
Octaedro
8
12
6
Dodecaedro
12
30
20
Icosaedro
20
30
12
Exercícios
1)

REGULARES
( ITA – SP ) Se um poliedro convexo possui 20 faces
e 12 vértices, então o número de arestas desse
poliedro é :
a) 28
b) 30
c) 12
d) 18
e) 32
2) ( Mack – SP ) Um poliedro convexo tem 3 faces
triangulares, 4 quadrangulares e 5 pentagonais. O
número de vértices desse poliedro é:
a) 15
b) 12
c) 25
d) 9
e) 13
303
CURSO DE MATEMÁTICA
3) ( Cesgranrio ) Um poliedro convexo é formado por 4
faces triangulares, 2 faces quadrangulares e 1 face
hexagonal. O número de vértices desse poliedro é de:
a) 6
b) 7
c) 8
d) 9
e) 10
4) (PUC-SP) O número de vértices de um poliedro
convexo constituído por doze faces triangulares é:
a) 4
b) 12
c) 8
d) 10
e) 6
5) ( Cesesp – PE ) Sabendo que num poliedro convexo
o número de arestas é igual ao número de vértices
somado com 12, assinale a alternativa que nos dá o
número de faces desse poliedro.
a) 12
b) 11
c) 10
d) 13
e) 14
6) ( PUC – PR ) Um poliedro é constituído de x faces
quadrangulares e quatro faces triangulares. Se o
número de arestas do poliedro é 16, qual o número de
vértices ?
7) ( UFPR ) Um poliedro convexo de 29 vértices possui
somente faces triangulares e faces hexagonais.
Quantas faces tem o poliedro se o número de faces
triangulares é a metade do número de faces
hexagonais ?
8) ( CEFET ) Um poliedro convexo possui duas faces
triangulares,
duas
quadrangulares
e
quatro
pentagonais. Logo, a soma dos ângulos internos de
todas as faces será:
a) 3240º
b) 3640º
c) 3840º
d) 4000º
e) 4060º
9) ( PUC – PR ) Um poliedro convexo tem três faces
pentagonais e algumas faces triangulares. Qual o
número de faces desse poliedro, sabendo-se que o
número de arestas é o quádruplo do número de faces
triangulares?
HAMILTON E ALEX
10) ( Fuvest – SP ) Quantas faces tem um poliedro
convexo com 6 vértices e 9 arestas ?
11) ( CEFET – PR ) Um poliedro convexo com 27 arestas
possui faces triangulares e hexagonais em igual
número. Calcule o número de vértices.
12) ( UNITAU – 95 ) A soma dos ângulos das faces de um
poliedro convexo vale 720°. Sabendo-se que o número
de faces vale 2/3 do número de arestas, pode-se dizer
que o número de faces vale.
a) 6.
b) 4.
c) 5.
d) 12.
e) 9.
13) ( ITA ) Um poliedro convexo tem 13 faces. De um dos
seus vértices partem 6 arestas: de 6 outros vértices
partem, de cada um, 4 arestas e, finalmente, de cada
um dos vértices restantes partem 3 arestas. O número
de arestas desse poliedro é:
a) 13
b) 17
c) 21
d) 24
e) 27
14) ( CEFET ) Num poliedro convexo, que só tem faces
triangulares e quadrangulares, há 20 vértices. O
número de faces triangulares é o dobro do número de
faces quadrangulares. Calcule o número de faces
desse poliedro.
15) ( UNIMONTES ) Quanto ao octaedro regular, é
incorreto afirmar que ele:
a) Possui 12 arestas
b) É um poliedro de Platão
c) Possui 8 faces triangulares
d) Possui 8 vértices
16) ( Puccamp – 96 ) Sobre as sentenças:
I - Um octaedro regular tem 8 faces quadradas.
II - Um dodecaedro regular tem 12 faces pentagonais.
III - Um icosaedro regular tem 20 faces triangulares.
É correto afirmar que APENAS
a) I é verdadeira.
b) II é verdadeira.
c) III é verdadeira.
d) I e II são verdadeiras.
e) II e III são verdadeiras.
304
CURSO DE MATEMÁTICA
17) ( UNIMONTES ) Dos desenhos apresentados em
cada opção, o único que não representa a
planificação de um poliedro regular é:
a)
b)
HAMILTON E ALEX
d) Qual a soma dos ângulos das faces desse poliedro ?
M
c)
N
d)
23) ( UFJF ) A figura a seguir representa a planificação de um
poliedro convexo. Determine o número de vértices desse
poliedro.
18) ( Cesesp – PE ) Considere os seguintes poliedros
regulares:
A1: tetraedro
A2: dodecaedro
A3: icosaedro
Assinale, entre as seguintes alternativas, a falsa:
a) O poliedro A1 tem as faces triangulares
b) O poliedro A2 tem as faces em forma de
dodecágono.
c) O poliedro A3 tem as faces triangulares
d) O poliedro A2 tem 12 faces
e) poliedro A3 tem 20 faces.
19) ( UFPR ) A soma do número de faces triangulares
dos cinco poliedros regulares é:
a) 28
b) 30
c) 32
d) 34
e) 36
20) ( UNIMONTES – 2002 ) O poliedro regular que tem
12 vértices e 30 arestas é o :
a) dodecaedro
b) tridecaedro
c) octaedro
d) icosaedro
21) ( PUC – SP ) Um poliedro de Platão não pode ter :
a) Faces triangulares
b) Faces quadrangulares
c) Faces pentagonais
d) Faces hexagonais
e) Ângulos pentaédricos
22) ( Unifesp / Adaptada ) Considere o poliedro abaixo cujos
vértices são os pontos médios das arestas de um cubo.
Observe esse poliedro e responda:
a) Quantas faces triangulares e quantas quadrangulares
tem esse poliedro ?
24. (FIP-2010) Observe a bola de futebol abaixo:
Sabendo-se que ela corresponde a um poliedro inflado,
que possui 32 faces, sendo 12 pentagonais e 20
hexagonais, qual o seu número total de vértices?
A) 120
B) 60
C) 48
D) 90
25. Sabe-se que a bola de futebol corresponde a um
poliedro criado por Arquimedes, que possui 32 faces,
sendo 12 pentagonais e 20 hexagonais. Se para costurar
dois lados comuns de uma dessas faces se gasta 10 cm
de linha, quantos centímetros de linha serão necessários
para costurar toda a bola ?
A) 800 cm
B) 900 cm
C) 1000 cm
D) 1200 cm
GABARITO
1) B
2) A
8) A
9) F = 6
c)
4) C
5) E
10) F = 5
13) D
14) F = 27
19) C
20) D
15) D
6) V = 9
11) V = 17
16) E
17) A
7) F = 18
12) B
18) B
21) D
22) a) 8 faces triangulares e 6 faces quadrangulares.
b) 24 arestas
b) Quantas arestas tem esse poliedro ?
3) C
23) V = 12
c) 12 vértices
24) B
d) S = 3600º
25) B
Quantos vértices tem esse poliedro ?
305
CURSO DE MATEMÁTICA
HAMILTON E ALEX
GEOMETRIA ESPACIAL
Prisma Regular
PRISMAS
É todo prisma reto que possui bases sendo polígonos
regulares.
É todo poliedro (sólido) constituído por faces planas, tendo
duas bases paralelas e congruentes e que possui faces
laterais sendo paralelogramos.
PARALELEPÍPEDO
É todo prisma
paralelogramos.
cujos
polígonos
das
faces
são
Elementos do Prisma
O prisma tem como elementos principais, as bases, a
face lateral, a aresta lateral e a aresta da base.
Paralelepípedo
Oblíquo
Paralelepípedo
Reto-retângulo
( Ortoedro )
Base
Face lateral
Aresta lateral
Aresta da base
Área Total do Paralelepípedo
É a soma das superfícies de todas as faces do
paralelepípedo.
Nomenclatura
Um prisma é classificado de acordo com o número de
arestas de uma base.
At = 2.( a.b ) + 2.( b.c ) + 2.( a.c )
c
At = 2 . ( a.b + b.c + a.c )
b
a
Volume
Prisma
quadrangular
Prisma
Triangular
Prisma
pentagonal
É o produto da
paralelepípedo.
área
da
base
pela
altura
do
c
Prisma Reto
Um prisma é reto, se suas arestas laterais são
perpendiculares aos planos das bases.
b
a
V = Ab . H
ou
V = ( a . b ) . c , Logo:
O volume será o produto das três dimensões.
H
V=a.b.c
No prisma reto a aresta lateral é a própria altura.
Diagonal do Paralelepípedo
Prisma Oblíquo
Um prisma é oblíquo, se suas arestas laterais não são
perpendiculares aos planos das bases.
D
c
D
c
d
d
b
a
2
H
2
2
2
2
2
D =(a +b )+c
a
2
2
D =d +c
d
b
2
2
d =a +b
D  a2  b2  c2
No prisma oblíquo a resta lateral será maior que a altura.
306
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Hexaedro Regular ( Cubo )
Prisma Regular ( Medidas )
É um paralelepípedo reto-retângulo que têm todas as
arestas com as mesmas medidas “a”.
Área de uma face Lateral
a
h
A face do cubo é um
quadrado de área
2
medindo a
a
Af = a . h
a
a
Área Lateral
Área Total do Cubo
É a soma das áreas das faces laterais.
É a soma das áreas de todas as faces do cubo.
Como o cubo possui 6 faces quadradas, a área total
será igual a soma das áreas dos 6 quadrados.
a
2
a
a
a2
2
a
a2
a2
2
a
Al = n.a.h onde n é o numero de faces laterais
É o produto da área da base pela altura do cubo.
V = Ab . H
V=(a.a).a
Área Total
É a soma da área lateral mais as áreas das duas bases,
ou seja, a soma das áreas de todas as faces.
a
Ab
a
V = a3
onde, 2p é o perímetro da
Base.
Al= 2p . H
Volume do Cubo
a
Ab
Diagonal do Cubo – ( D )
D
At = Al + 2 Ab
a
d
a
d
2
2
D =d +a
Volume
D2 = ( 2.a2 ) + a2
É o produto da área da base do prisma por sua altura.
2
d
a
2
2
D=
3.a 2
D = 3.a
d2 = a2 + a2
d2 = 2.a2
D=a 3
Nota: A diagonal de qualquer quadrado é:
a
onde, Ab é a área da base.
D
a
a
d
a
A área lateral pode ser expressa pelo perímetro da base
do prisma.
At = 6 . a

a
Al = 4. Af
a
a
h
a
a
2
a
a2
h
V = Ab . H

OBSERVAÇÕES
 Se o volume de um sólido for pedido em
“LITROS”, a melhor unidade a ser trabalhada é o
“decímetro” ( dm ).
d=a 2
a
307
CURSO DE MATEMÁTICA
 Se o volume de um sólido for pedido em
“MILILITROS” ( ml ), a melhor unidade a ser
trabalhada é o “centímetro” ( cm ).
dam
1 casa
m
1 casa
dm
1 casa
cm
1 casa
mm
1 casa
Km2
hm2
dam2
m2
dm2
2 casas 2 casas 2 casas 2 casas 2 casas
cm2
2 casas
mm2
2 casas
Volumes
3
3
3
3
3
3
Km
hm
dam
m
dm
3 casas 3 casas 3 casas 3 casas 3 casas
cm
3 casas
3
mm
3 casas
Exemplos
Ex.1 : Transforme 3,5 metros para cm.
hm
dam
m
3,5
Ex.2 : Transforme 2 m
Km3
hm3
dam3
3
dm
cm
35
350
mm
3
para dm .
m3
dm3
2
2000
cm3
mm3
Ex.3 : Transforme 1,3 dm 2 para dam2.
Km2
0,00013
2
c) 120 2 cm2
2
d) 150 cm
2) (PUC-SP) Um cubo tem área total igual a 72 m2 ; sua
diagonal vale:
Áreas
Km
 ( CESCEA ) A área total de um cubo cuja diagonal
b) 100 3
Comprimentos
hm
1 casa
EXERCÍCIOS
mede 5 3 cm é :
2
a) 140 cm
Transformando Unidades
Km
1 casa
HAMILTON E ALEX
hm2
0,013
dam2
m2
dm2
cm2
a) 2 6
b) 6
c)
6
d)
12
e)
24
3) (Cescea – SP) - Se a soma das medidas das arestas
de um cubo é igual a 60 cm, então o volume do cubo é
igual a :
a) 96 cm3
b) 116 cm3
c) 125 cm3
d) 140 cm3
e) 144 cm3
4) ( UFMG – 2002 ) Um reservatório cúbico, de 50 cm
de profundidade, está com água até a metade e
precisa ser totalmente esvaziado.
O volume de água a ser retirado desse reservatório é
de :
a) 62,5 litros
b) 125 litros
c) 250 litros
d) 25 litros
mm2
1,3
Princípio de Cavalieri
Consideremos um plano P sobre o qual estão apoiados
dois sólidos com a mesma altura. Se todo plano paralelo
ao plano dado interceptar os sólidos com seções de áreas
iguais, então os volumes dos sólidos também serão
iguais.
5) ( ACAFE – SC ) Uma caixa d’água tem o formato de
um cubo, cuja aresta mede 60 cm. Calcule quantos
2
litros há na caixa, ao preencher
de seu volume :
3
a) 216.000 litros
b) 144.000 litros
c) 216 litros
d) 144 litros
e) 72 litros
6) ( FEI – SP ) Determine o volume de um cubo de área
total igual a 96 cm2.
a) 44 cm3
b) 46 cm3
3
c) 54 cm
d) 64 cm3
e) 86 cm3
308
CURSO DE MATEMÁTICA
7) ( FGV – SP ) Um cubo tem 96 m2 de área total. Em
quanto deve ser aumentada a sua aresta para que
3
seu volume se torne igual a 216 m ?
a) 2 m
b) 3 m
c) 1 m
d) 0,5 m
e) 9 m
8) ( PUCCAMP – SP ) Usando uma folha de latão,
3
deseja-se construir um cubo com volume de 8 dm . A
área da folha utilizada para isso será no mínimo:
a) 20 cm2
b) 40 cm2
c) 240 cm2
2
d) 2000 cm
2
e) 2400 cm
9) (ENEM-2009) Considere um caminhão que tenha uma
carroceria na forma de um paralelepípedo retângulo,
cujas dimensões internas são 5,1 m de comprimento,
2,1 m de largura e 2,1 m de altura. Suponha que esse
caminhão foi contratado para transportar 240 caixas
na forma de cubo com 1 m de aresta cada uma e que
essas caixas podem ser empilhadas para o
transporte.
Qual é o número mínimo de viagens necessárias para
realizar esse transporte?
A) 10 viagens.
B) 11 viagens.
C) 12 viagens.
D) 24 viagens.
E) 27 viagens.
10) ( Unicamp ) Ao serem retirados 128 litros de água
de uma caixa d'água de forma cúbica, o nível da água
baixa 20 centímetros.
a) Calcule o comprimento, em dm, das arestas da
referida caixa.
b) Calcule a capacidade dessa caixa em litros (1 litro
eqüivale a 1 decímetro cúbico).
11) ( UFSC – 96 ) Na figura a seguir, que representa um
cubo, o perímetro do quadrilátero ABCD mede 8(1+
3
2 )cm. O volume do cubo em cm é:
a) 32
B
b) 32 2
A
c) 64
C
d) 64 2
e) 16
D
HAMILTON E ALEX
12) (Unesp) A área da superfície da Terra é estimada em
2
510.000.000km . Por outro lado, estima-se que se todo
vapor de água da atmosfera terrestre fosse
condensado, o volume de líquido resultante seria de
3
13.000km . Imaginando que toda essa água fosse
colocada no interior de um paralelepípedo retângulo,
cuja área da base fosse a mesma da superfície da
Terra, a medida que mais se aproxima da altura que o
nível da água alcançaria é
a) 2,54 mm.
b) 2,54 cm.
c) 25,4 cm.
d) 2,54 m.
e) 0,254 km.
13) ( Fuvest – SP ) Dois blocos de alumínio, em forma de
cubo, com arestas medindo 10 cm e 6 cm, são
levados juntos à fusão e em seguida o alumínio líquido
é moldado como um paralelepípedo reto-retângulo de
arestas 8 cm, 8 cm e x cm. O valor de x é:
a) 16
b) 17
c) 18
d) 19
e) 20
14) (ENEM – 2010) Uma fábrica produz barras de chocolates
no formato de paralelepípedos e de cubos, com o mesmo
volume. As arestas da barra de chocolate no formato de
paralelepípedo medem 3 cm de largura, 18 cm de
comprimento e 4 cm de espessura. Analisando as
características das figuras geométricas descritas, a
medida das arestas dos chocolates que têm o formato de
cubo é igual a
A) 5 cm
B) 6 cm
C) 12 cm
D) 24 cm
E) 25 cm
15) ( UNIMONTES ) Vários caixotes de plástico azul
ficaram armazenados ao ar livre, na posição indicada
na figura abaixo, na qual apenas um dos caixotes não
é visível. Com o tempo, o plástico exposto ao ar
perdeu sua cor, tornando-se cinza. Ao desfazer a
pilha, verificaremos que o número de caixotes com três
faces azuis e três faces cinzentas será :
a) 4
b) 5
c) 3
d) 2
e) 1
16) ( UNIMONTES – 99 ) Observe atentamente o sólido e
suas superfícies, formadas de cubos cujas arestas
medem 1 cm cada. A área da superfície visível e o
309
CURSO DE MATEMÁTICA
volume total do sólido medem, em cm
respectivamente:
a) 30, 50
b) 20, 30
c) 30, 20
d) 20, 50
2
HAMILTON E ALEX
3
e cm ,
17) ( CESGRANRIO ) Na figura , cada aresta do cubo
mede 3cm. Prolongando-se uma delas em 5cm,
obtemos o ponto M. A distância em cm, de M ao
vértice A é:
a) 2 21
b) 82
c) 8 3
e) 9
d) 8 2
18) ( Fuvest ) Qual é a distância entre os centros de duas
faces adjacentes de um cubo de aresta 4 ?
a) 2
b) 2 2
c) 4
d) 4 2
19) ( UEL – PR ) Um engenheiro deseja projetar um bloco
vazado cujo orifício sirva para encaixar um pilar. O
bloco, por motivos estruturais, deve ter a forma de um
cubo de lado igual a 80 cm e o orifício deve ter a
forma de um prisma reto de base quadrada e altura
igual a 80 cm, conforme as figuras seguintes. É
exigido que o volume do bloco deva ser igual ao
volume do orifício.
É correto afirmar que o valor "L" do lado da base
quadrada do prisma reto corresponde a:
a) 20 2 cm
b) 40 2 cm
c) 50 2 cm
d) 60 2 cm
e) 80 2 cm
20) ( UFPA ) Qual a área total de um paralelepípedo reto
cujas dimensões são 2 cm, 3 cm e 4 cm ?
2
a) 24 cm
2
b) 26 cm
c) 30 cm2
d) 40 cm2
e) 52 cm2
21) ( UFV – MG ) Se no paralelepípedo retângulo a = 1,
b = 2 e c = 3, o comprimento do segmento AC é :
C
a) 13
b) 11
c) 15
a
c
d)
14
A
b
e) 10
22) ( Unimontes – PAES) Um aquário aberto em cima, de
40 cm de altura, deve Ter uma capacidade de 140
litros. Sejam x o comprimento (em dm) e y a
largura (em dm) . A área total do vidro necessário para
a confecção desse aquário pode ser expressa pela
função f definida por :
280
a) f ( x ) = 3,5 + 80x +
x
280
b) f ( x ) = 35 + 80x +
x
280
c) f ( x ) = 35 + 8x +
x
280
d) f ( x ) = 3,5 + 8x +
x
23) ( DIAMANTINA) Uma caixa d’água, na forma de um
paralelepípedo retângulo, tem 1,5m de comprimento,
800mm de altura e 10dm de largura. Estando a caixa
vazia e começando a entrar à razão constante 20/3
litros por minuto, é correto afirmar que o total de horas
gastas para encher a caixa é igual a:
a) 3
b) 2
c) 4
d) 5
e) 8
24) ( UFF – 2001 ) Uma piscina tem a forma de um prisma
reto, cuja base é um retângulo de dimensões 15
metros e 10 metros. A quantidade necessária de litros
de água para que o nível de água da piscina suba 10
cm é:
a) 0,15 litros
b) 1,5 litros
c) 150 litros
d) 1500 litros
e) 15000 litros
25) ( UFMG ) A capacidade de um reservatório em forma
de um paralelepípedo retângulo, cujas dimensões são
50 cm, 2 m e 3 m é, em litros :
a) 3
b) 30
c) 300
d) 3000
e) 30000
26) ( FAFEOD – 2002 ) Observe a figura abaixo.
Um aquário de vidro, com a forma de um bloco
retangular, estava completamente cheio de água.
Depois que uma pedra foi retirada de dentro dele, o
nível de água baixou 5cm.
310
CURSO DE MATEMÁTICA
Admitindo-se que a espessura do vidro é desprezível,
é correto afirmar que o volume, em cm 3, da pedra
retirada desse aquário é igual a :
a) 18.000
5cm
b) 13.000
c) 15.000 45cm
50cm
d) 8.000
60cm
e) n.d.a
27) (Puccamp) Uma caixa-d'água, com a forma de um
paralelepípedo retângulo, tem capacidade para 1.000
litros. Qual é a capacidade de outra caixa, semelhante
à primeira, cujas medidas das arestas são 20%
maiores?
a) 1.728 litros
b) 1.800 litros
c) 1.836 litros
d) 1.900 litros
e) 1.948 litros
28) ( UFSC – 99 ) Usando um pedaço retangular de
papelão, de dimensões 12 cm e 16 cm, deseja-se
construir uma caixa sem tampa, cortando, em seus
cantos, quadrados iguais de
2 cm de lado e
dobrando, convenientemente, a parte restante. Qual a
terça parte do volume, em cm 3, dessa caixa ?
29) ( UNESP ) Considere um pedaço de cartolina
retangular de lado menor 10 cm e lado maior 20 cm.
Retirando-se 4 quadrados iguais de lados x cm (um
quadrado de cada canto) e dobrando-se na linha
pontilhada conforme mostra a figura, obtém-se uma
pequena caixa retangular sem tampa.
O polinômio na variável x, que representa o volume,
em cm¤, desta caixa é
a) 4x3 - 60x2 + 200x.
b) 4x2 - 60x + 200.
c) 4x3 - 60x2 + 200.
d) x3 - 30x2 + 200x.
e) x3 - 15x2 + 50x.
30) ( UFRJ ) A figura mostra uma placa retangular de
cartolina com comprimento igual ao dobro da largura.
Corta-se em cada canto um quadrado de lado 2 cm.
Em seguida, as abas são dobradas para cima, ao
longo das linhas pontilhadas, formando uma caixa
3
retangular sem tampa, de volume igual a 140 cm . A
2
área da cartolina , em cm , é ?
HAMILTON E ALEX
31) ( UFPE ) Um reservatório de forma cúbica tem aresta
medindo 3 m e é preenchido em três horas utilizando
uma bomba-d'água. Com a mesma bomba, em
quantas horas preenche-se um reservatório na forma
de um paralelepípedo reto de dimensões 4 m, 6 m e 9
m?
32) ( Fuvest – SP ) Um tanque em forma de um
paralelepípedo reto-retângulo tem por base um
retângulo horizontal de lados 0,8 m e 1,2 m. Um
indivíduo, ao mergulhar completamente no tanque, faz
o nível da água subir 0,075 m. Então o volume do
indivíduo, em metros cúbicos é:
a) 0,066
b) 0,072
c) 0,096
d) 0,600
e) 1,000
33) ( UNESP – 93 ) Uma piscina retangular de 10m x 15m
de fundo horizontal está com água até a altura de
1,5m. Um produto químico em pó deve ser misturado à
água à razão de um pacote para cada 4500 litros. O
número de pacotes a serem usados é:
a) 45
b) 50
c) 55
d) 60
e) 75
34) ( UFRRJ ) Observe o bloco retangular da figura 1, de
vidro totalmente fechado com água dentro. Virando-o,
como mostra a figura 2, podemos afirmar que o valor
de x é:
a) 12 cm.
b) 11 cm.
c) 10 cm.
d) 5 cm.
e) 6 cm.
35) ( Fatec – SP ) Temos na figura abaixo a planificação
de um sólido cujo volume é :
a) 6 3
3
3
b) 12 3
c) 24
d) 18 3
e) 72
8
3
3
311
CURSO DE MATEMÁTICA
36) ( UFPE ) O Tronco de prisma reto, figura abaixo, tem
por base um quadrado inscrito num círculo de raio 2
2 cm. A altura maior mede 10 cm e a altura menor
mede 7 cm. Podemos afirmar que:
2
a) A área lateral do tronco é 120 cm
2
b) A área total do tronco é de 158 cm
2
c) A área lateral do tronco é 162 cm
d) O volume do tronco é 160 cm 3
e) O volume do tronco é 136 cm3
37) ( UFMG ) Uma piscina tem 25 m de largura, 50m de
comprimento; 1,5 m de profundidade numa das
extremidades e 2,5 m na outra, sendo o fundo um
plano inclinado. O volume da piscina é:
3
a) 1875 m
3
b) 2000 m
c) 2300 m3
d) 2500 m3
e) 2800 m3
38) Um recipiente cúbico, inicialmente cheio, foi inclinado
conforme figura abaixo. Observando-se as medidas
indicadas, pode-se afirmar que o volume derramado e
o volume ainda contido no recipiente, nessa ordem,
são :
a) 37,5 litros e 87,5 litros
b) 37 litros e 88 litros
c) 36,5 litros e 88,5 litros
d) 36 litros e 89 litros
e) 35,5 litros e 89,5 litros
HAMILTON E ALEX
b) 4 m
c) 6 m
d) 8 m
41) ( PUC / SP – 2001) Na figura abaixo tem-se o prisma
reto ABCDEF, no qual DE =6 cm, EF = 8 cm e DE
 EF . Se o volume desse prisma é 120 cm 3, a sua
2
área total, em cm , é :
C
a) 144
A
b) 156
c) 160
F
d) 168
D
B
e) 172
E
42) Um prisma quadrangular regular, de altura H, tem a
aresta da base medindo 4 cm. Sabe-se que esse
prisma tem o mesmo volume que um prisma triangular
regular de aresta da base medindo 2 cm e altura
igual a 16 3 cm. Qual a medida da altura H desse
prisma ?
43) ( ITA – SP ) Dado um prisma hexagonal regular, sabese que sua altura mede 3 cm e que sua área lateral é o
dobro da área de sua base. Qual o volume desse
prisma em cm3 ?
30 cm
20 cm
39) ( UNIMONTES – 2001 ) Uma industria acondiciona
um de seus produtos em embalagens que têm a
forma de um prisma triangular regular, cuja
planificação está indicada no desenho abaixo.
Considerando que a aresta a da base mede 4 3 cm
e que a altura H do prisma mede 12 3 cm, é correto
afirmar que o volume de cada embalagem é ?
a
H
40) ( UFPA ) Num prisma regular de base hexagonal, a
2
área lateral mede 36 m e a altura é 3 m. A aresta da
base é:
a) 2 m
44) ( PUC – RS ) Se um prisma quadrangular regular tem
área total igual a 10 vezes a área da base, então a
razão( divisão ) entre sua altura e a aresta da base é :
a) 1/2
b) 1
c) 3/2
d) 2
e) 3
45) ( ITA – SP ) Considere P um prisma reto de base
quadrada, cuja altura mede 3m e com área total de
80m2. O lado dessa base quadrada mede:
a) 4 m
b) 16 m
c) 6 m
d) 8 m
e) 1 m
312
CURSO DE MATEMÁTICA
HAMILTON E ALEX
46) ( Cesgranrio – RJ ) De um bloco cúbico de isopor de
aresta 3a
recorta-se o sólido, em forma de H,
mostrado na figura. O volume do sólido é :
a) 27 a3
3
b) 21 a
a
3
c) 18 a
3
d) 14 a
3
a
e) 9 a
a a a
47) ( FAFEOD – 2002 ) Observe a figura a seguir, que
representa uma escada de concreto, compacta,
formada de três blocos retangulares, possuindo três
degraus, cada um medindo 25cm de altura, 30cm de
piso e 1m de largura.
Admitindo-se que o custo de cada metro cúbico de
concreto seja R$ 200,00 , é correto concluir que na
construção dessa escada, o gasto, em reais, relativo à
compra de concreto será igual a :
a) 80
b) 125
c) 90
d) 100
e) n.d.a
48) ( Mack – SP ) Um prisma regular triangular têm todas
as arestas congruentes e 48 m 2 de área lateral. Seu
volume vale :
a) 16 m3
b) 32 m3
c) 64 m3
O quarto do Cebolinha corresponde a um cubo perfeito.
Para cobrir todas as paredes laterais, foram necessários
17,64m² de papel de parede. Desse modo, pode-se afirmar
que a altura de cada parede é, em centímetros, igual a:
A) 220
B) 180
C) 210
D) 160
51.(FIP-2012) Algumas caixas cúbicas foram colocadas
dentro da caixa maior, conforme a figura abaixo. Para
preencher toda a caixa maior, quantas caixas cúbicas,
ainda precisam ser colocadas na caixa maior?
A) 420
B) 740
C) 568
D) 382
d) 4 3 m3
e) 16 3 m3
49) ( VUNESP ) O volume de ar contido em um galpão
com a forma e dimensões dadas pela figura abaixo é:
a) 288
b) 384
c) 480
d) 360
5
e) 768
3
12
4
4
50 .(FIP-2011) Observe a tirinha abaixo:
52.(FIP-2013) Num supermercado, o funcionário repositor
de estoque foi incumbido de colocar embalagens de leite,
com a forma de caixas retangulares de dimensões 6cm,
9cm e 15cm, sobre uma prateleira retangular de 42cm por
18cm. Todas as embalagens deverão ter uma de suas
faces totalmente apoiada na prateleira.
Nessas condições, o número máximo de embalagens que
poderão ser acomodadas é:
A) 12
B) 14
C) 13
D) 11
53.(FIP-2013)
Projeto de uma piscina que será construída num clube da
cidade
313
CURSO DE MATEMÁTICA
HAMILTON E ALEX
O arquiteto responsável pelo projeto resolveu revestir
o fundo da piscina com o menor número possível de
azulejos quadrados e fez as seguintes afirmativas:
I. O volume total da piscina é 156,6 m3
II. A área do fundo da piscina é 53,4 m2
III. O azulejo usado no fundo da piscina tem 30 cm
de lado.
É correto o que o arquiteto afirma em:
A)I e II somente.
B)II e III somente.
C)I, II e III.
D)III somente.
GABARITO
1) D
2) B
3) C
8) E
9) C
10) a) 80 dm
12) B
13)D 14) B
15) A
18) B
19) B 20) E
21)D
24) E 25) D
5) D
30) 162cm2
34) A
35) D
41) D
22) C
45) A
46) B
50) C
51) D(389)
7) A
11) C
17) B
23) A
28) 64 cm3
37) D
32) B
38) A
33) B
39) 432 cm2
43) 54 3
42) 3 cm
44) D
16) C
31) 24H
36) E
6) D
b) 512 litros
26) C 27) A
29) A
40) A
4) A
47) C
52) B
48) E
49) B
53) D
314
CURSO DE MATEMÁTICA
HAMILTON E ALEX
PIRÂMIDE
Demonstração do Volume da Pirâmide
Dados um polígono convexo P, contido em um plano  e
um ponto V (vértice) fora de , chamamos de pirâmide o
conjunto de todos os segmentos VA , com A P
(polígono P).
No prisma triangular ABCDEF abaixo, a aresta CF é a
altura H, e DEF é uma das bases.
A
B
C
C
v
Aresta Lateral
Face
D
D
Altura ( H )
Aresta da Base
E
E
F
F
Retirando-se a pirâmide DFEC do prisma ABCDEF, sobra
o sólido ABCDE, conforme figura abaixo.
A
B
C
Classificação
Pirâmide reta é quando a projeção ortogonal do vértice
coincide com o centro do polígono da base.
D
E
F
Seccionando
o sólido ABCDE acima, por um plano que
passa por ACE, obtemos a pirâmide ABCE abaixo.
C
B
A
C
D
Pirâmide regular é toda pirâmide reta cujo polígono da
base é regular.
O nome da pirâmide depende de sua base, ela pode ser
triangular, quadrangular, pentagonal, hexagonal, etc.
E
F
E
Perceba que as pirâmides ABCE e DFEC acima, têm
mesma altura e bases com áreas congruentes, logo elas
têm mesmo volume.
As pirâmides ADEC e ABCE abaixo, têm as bases ADE
e ABE congruentes, e como as alturas relativas a essas
bases também são congruentes, essas pirâmides têm o
mesmo volume.
A
D
Pirâmide
triangular
Pirâmide
quadrangular
Pirâmide
hexagonal
Relação entre Pirâmide e Prisma
Se uma pirâmide e um prisma têm as áreas das bases
congruentes e as alturas de mesma medida, a
1
pirâmide terá
do volume desse prisma.
3
LOGO :
1
V = Ab . H.
3
B
A
C
C
E
E
Como as pirâmides DEFC, ABCE e ADEC têm volumes
iguais e a soma de seus volumes resulta no volume do
prisma triangular ABCDEF, podemos concluir que o
volume de uma pirâmide é igual a um terço do volume do
prisma que possui mesma altura e mesma área da base
dessa pirâmide.
EXEMPLO
O volume do prisma quadrangular regular abaixo é 120
litros. Se “M” é ponto médio da aresta lateral, qual o
volume da pirâmide indicada na figura ?
M
V=?
315
CURSO DE MATEMÁTICA
Elementos de Uma Pirâmide Regular
Aresta lateral( f )
Apótema da pirâmide( g )
Altura ( H )
HAMILTON E ALEX
Volume da Pirâmide
O volume de uma pirâmide equivale a um terço do volume
do prisma que a contém.
V = Ab . H .
Apótema da base( m )
1
3
Aresta da base( a )
 Observe que o apótema da pirâmide também é a
altura de uma face.
 Observe os triângulos retângulos
g
H
g
m
f
a/2
g2 = H2 + m2
f 2 = g2 +(a/2)2
Exemplo
Ex1. : Na pirâmide regular quadrangular abaixo a aresta
da base mede 6 cm e a altura 4 cm. Determine:
a) O apótema da base;
b) O apótema da pirâmide;
c) A área da base;
d) A área de uma face lateral;
e) A área lateral;
f) A área Total;
g) O Volume.
Área de Uma Face Lateral
É a área de um dos triângulos isósceles que contornam a
pirâmide.
Af 
g
a.g
2
a
Área Lateral
É a soma das áreas dos triângulos laterais.
Al = n . Af
Onde “n” é o número
de triângulos
Área Total
Ex2. : Na pirâmide abaixo sabe-se que BC  CD , AC  BC
e AC  CD . Qual o volume dessa pirâmide se BC  3cm ,
CD  2cm e AC  6cm ?
A
É a soma da área lateral com a área da base.
D
B
C
At = Al + Ab
316
CURSO DE MATEMÁTICA
EXERCÍCIOS
1) ( PUC – RS ) Se uma pirâmide regular possui seis
faces, essa pirâmide será:
a) Uma pirâmide quadrangular regular.
b) Uma pirâmide pentagonal regular.
c) Uma pirâmide hexagonal regular.
d) Uma pirâmide heptagonal regular.
e) Uma pirâmide octogonal regular.
2) ( UFJF ) A planificação de uma pirâmide quadrangular
regular permite que se faça seu molde a fim de se
poder reproduzi-la novamente. O molde da pirâmide
quadrangular regular é composto por:
a) Cinco quadrados
b) Cinco triângulos
c) Três triângulos e dois quadrados
d) Um triângulo e quatro quadrados
e) Um quadrado e quatro triângulos
3) ( UFOP – MG ) A aresta lateral de uma pirâmide
quadrangular regular mede 10 m e a altura, 8 m . O
volume dessa pirâmide é :
a) 192
b) 192 2
c) 168
d)168 2
e) 144
4) ( Fuvest – SP ) Um telhado tem a forma da superfície
lateral de uma pirâmide regular de base quadrada. O
lado da base mede 8 metros e a altura da pirâmide
3 metros. As telhas para cobrir esse telhado são
vendidas em lotes que cobrem 1 m2. Supondo que
possa haver 10 lotes de telhas desperdiçadas (
quebras e emendas ), qual o número mínimo de lotes
de telhas a ser comprado ?
a) 90
b) 100
c) 110
d) 120
e) 130
5) ( UFPE ) Na figura a seguir o cubo tem aresta igual a
9 cm e a pirâmide tem um vértice no centro de uma
face e como base a face oposta. Se V cm3 é o
volume da pirâmide, determine (1/3)V.
a) 27 cm3
b) 36 cm3
3
c) 44 cm
9 cm
d) 64 cm3
e) 81 cm3
9 cm
9 cm
HAMILTON E ALEX
6) ( UFPA ) O apótema de uma pirâmide quadrangular
regular mede 8 cm e o apótema de sua base mede 5
cm. Qual a medida de sua área lateral ?
7) ( UFRN ) A altura de uma pirâmide regular de base
quadrada é o triplo do lado da base. Se o volume
dessa pirâmide é 27 cm3, o lado da base mede :
a) 27 cm
b) 9 cm
c) 33 cm
d) 3 cm
e) 1 cm
8) ( FEI ) É dado que, ABCDV é uma pirâmide reta,
ABCD é um quadrado cujo lado mede 6 cm e a altura
da pirâmide (segmento VO) mede 4 cm.
A superfície total da pirâmide, em cm2, é :
a) 96
V
b) 81
c) 51
d) 84
e) 72
C
B
O
D
9)
A
( UFMG ) Na figura, ABCD é um quadrado cujo lado
mede 1 cm e os triângulos VAB, VBC, VCD e VDA
são equiláteros. A área total da pirâmide VABCD, em
cm2, é :
V
a)
b)
c)
d)
e)
(1+ 3 )
( 1 + 23 )
( 1 + 33 )
( 1 + 43 )
N.D.A
D
A
C
B
10) ( UFPA ) A razão entre os volumes de um prisma e
de uma pirâmide de bases e alturas congruentes é :
a)
1
b)
3
3
4
c) 1
d)
4
3
e) 3
317
CURSO DE MATEMÁTICA
11) ( Conc. Público – 2001 / MG ) A figura abaixo mostra
a planificação de uma pirâmide quadrangular regular.
A área total da superfície dessa pirâmide é igual a:
a) 320 cm2
2
b) 340 cm
2
c) 360 cm
2
d) 400 cm
13 cm
10 cm
10 cm
12) ( Cesgranrio ) O volume da pirâmide de base
quadrada, cujas 8 arestas têm o mesmo comprimento
l, é:
a)
l3 3
2
l3
3
l3 3
e)
8
c)
b)
l3 2
6
d)
l3 3
4
13) ( MACK – SP ) Uma pirâmide cuja base é um
quadrado de lado 2a tem o mesmo volume que um
prisma cuja base é um quadrado de lado a. A razão
entre as alturas da pirâmide e do prisma, nessa
ordem, é:
a) 3/4
b) 3/2
c) a/3
d) 3 a
14) ( PUC – SP ) Determine o volume de uma pirâmide
hexagonal regular, cuja aresta da base tem 4m e a
altura mede 6m.
a) 36 m3
b) 56 3 m3
c) 64 m3
d) 48 3 m
e) 48m3
3
15) ( PUC – SP ) Determine o volume de uma pirâmide
hexagonal regular, cuja aresta lateral tem 8 m e o
raio da circunferência circunscrita à base mede 4m.
a) 168 m3
3
b) 58 3 m
3
c) 243 m
3
d) 144 3 m
3
e) 96m
16) ( Cesgranrio ) Uma folha de papel colorido, com a
forma de um quadrado de 20 cm de lado, será usada
para cobrir todas as faces e a base de uma pirâmide
quadrangular regular com altura de 12 cm e apótema
da base medindo 5 cm. Após se ter concluído essa
HAMILTON E ALEX
tarefa, e levando-se em conta que não houve
desperdício de papel, a fração percentual que sobrará
dessa folha de papel corresponde a:
a) 20 %
b) 16 %
c) 15 %
d) 12 %
e) 10 %
17) ( UNESP – SP ) O prefeito de uma cidade pretende
colocar em frente à prefeitura um mastro com uma
bandeira, que será apoiado sobre uma pirâmide reta
de base quadrada feita de concreto maciço, como
mostra a figura. Sabendo-se que a aresta da base da
pirâmide terá 6 m e que a altura da pirâmide será de
4 m, o volume de concreto (em m 3) necessário para a
construção da pirâmide será
a) 48
b) 36
c) 28
d) 12
e) 4
18) ( CESGRANRIO ) Em um cubo de aresta 3 6
considere o tetraedro VABC, como indicado na
figura. O volume do tetraedro é:
a) 2
V
b)
2
c)
3
3
d)
6 /3
e) 1

C
19) Um prisma quadrangular regular, com 240 cm3 de
volume, é seccionado nos pontos médios de suas
arestas como indicado na figura abaixo. O volume do
sólido restante indicado pela figura é :
a) 235 cm3
3
b) 230 cm
3
c) 225 cm
3
d) 220 cm
3
e) 215 cm
20) ( VUNESP ) Em cada um dos vértices de um cubo de
madeira se recorta uma pirâmide AMNP onde, M, N e
P são os pontos médios das arestas, como se mostra
na figura. Se V é o volume do cubo, o volume do
poliedro que resta é igual a:
a) V/2
b) 3V/4
c) 2V/3
N
d) 5V/6
e) 3V/8
M
P
A
318
CURSO DE MATEMÁTICA
21) ( Vassouras / 2001 ) Um cubo de faces opostas
ABCD e A’B’C’D’ é secionado por um plano que
contém o ponto médio da aresta AA’ e os vértices B
e D. O plano divide o cubo em dois sólidos cujos
volumes estão na razão :
D
C
a) 3
A
B
b) 4
c) 6
d) 11
C’
D’
e) 12
B’
HAMILTON E ALEX
Se o dono da fábrica resolver diversificar o modelo,
retirando a pirâmide da parte superior, que tem 1,5 cm
de aresta na base, mas mantendo o mesmo molde,
quanto ele passará a gastar com parafina para fabricar
uma vela?
3
A) 156 cm .
3
B) 189 cm .
3
C) 192 cm .
D) 216 cm3.
E) 540 cm3.
A’
25) ( UFPA ) Uma pirâmide regular, cuja base é um
quadrado de diagonal 6 6 cm e cuja altura é igual
22) (UFMG) Na figura, as pirâmides OABCD e O’ABCD
são regulares e têm todas as arestas congruentes. Se
o segmento OO’ mede 12cm, então a área da
superfície da figura é, em cm:
a) 24 3
O
d) 108 3
e) 144 3
D
A
C
B
2
do lado da base, tem área total igual a:
3
a) 96 6 cm
2
b) 252 cm
2
c) 288 cm
2
d) 84 3 cm2
e) 576 cm2
b) 36 3
c) 72 3
a
O’
23) Um corpo sólido é formado por duas pirâmides iguais
que têm por base comum um quadrado, sendo que os
vértices estão situados em semi planos opostos em
relação a essa base. Sabendo que o volume do sólido
é 96m3 e que o perímetro da base quadrada é 24m,
determinar a altura de cada pirâmide e a superfície
total do sólido.
24) (ENEM/2009) Uma fábrica produz velas de parafina
em forma de pirâmide quadrangular regular com 19
cm de altura e 6 cm de aresta da base. Essas velas
são formadas por 4 blocos de mesma altura — 3
troncos de pirâmide de bases paralelas e 1 pirâmide
na parte superior —, espaçados de 1 cm entre eles,
sendo que a base superior de cada bloco é igual à
base inferior do bloco sobreposto, com uma haste de
ferro passando pelo centro de cada bloco, unindo-os,
conforme a figura.
26) ( Unicamp – SP ) Dado um cubo de aresta a , qual é o
volume do octaedro cujos vértices são os centros das
faces do cubo ?
27) Um cubo foi truncado nos pontos médios de suas
arestas originando uma seção de área igual a 2 3
cm2. Pode-se afirmar que o volume do cubo original é
?
28) ( UFGO ) A base de uma pirâmide é um triângulo
equilátero, cujo lado mede 4 cm. Sendo a altura da
pirâmide igual à altura do triângulo da base, o volume
da pirâmide, em cm3, é :
a) 4
b) 6
c) 8
d) 10
319
CURSO DE MATEMÁTICA
HAMILTON E ALEX
29) ( UNICAMP – 2001 ) A base de uma pirâmide regular
é um triângulo eqüilátero de lado L = 6 cm e
arestas laterais das faces A = 4 cm. A altura dessa
pirâmide, em cm, é :
a) 1
b) 2
c) 3
d) 4
e) 5
30) ( UFRS ) A área total de um tetraedro regular é
A sua aresta vale :
a) 1
3
b)
2
12 .
c)
2
d) 2
31) ( UFPA ) A altura de um tetraedro regular é 4 2 cm.
O apótema do tetraedro mede :
a) 4 cm
b) 3 2
c) 4 3
d) 6
e) 6 2
GABARITO
1) B
2) E
3) A
4) A
8) A
9) A
10) E
15) E
16) E
11) B
17) A
21) D
22) E
25) C
26) a /6
30) C
31) D
3
6) 160cm 2
5) E
12) B
18) E
13) A
19) A
2
28) C
14) D
20) D
23) H = 4m e AT = 120m2
27) 64cm
7) D
24) B
29) B
320
CURSO DE MATEMÁTICA
HAMILTON E ALEX
CILINDRO CIRCULAR
Áreas de Um Cilindro
Conceito
Um cilindro é composto por três superfícies: a superfície
que o contorna lateralmente (área lateral) e as superfícies
de dois círculos (áreas das bases).
O sólido formado por todos os segmentos de reta de
medida m, paralelos à reta re que têm uma extremidade
na região circular C, denomina-se cilindro circular.
r
Ab
r
G
G ( ou H )
2..r
Ab
Elementos do Cilindro
Cilindro Reto
Área da Base (Ab)
É a área de um círculo de raio r.
Base
r
Ab = .r2
Geratriz (G) ou Altura (H)
r
Raio da Base ( r )
Área Lateral (AL)
É a área do retângulo de dimensões
contorna o cilindro.
Cilindro Oblíquo
Geratriz (G)
G
Altura (H)
Raio da Base ( r )
Cilindro Circular Reto ou Cilindro de
revolução
Um cilindro se diz Reto (ou de Revolução) quando as
geratrizes são perpendiculares às bases.
Ele é obtido pela rotação completa de um retângulo
em torno de um de seus lados.
Retângulo Gerador
2..r
G, que
AL = 2. .r.G
2..r
Área Total (At)
É a soma da área lateral com as áreas das duas bases.
Ab =.r
2
AL= 2..r.G
Ab =.r
At = AL + 2. Ab
2
Secção Reta ou Normal de um Cilindro
Volume de um Cilindro ( V )
É a secção que é feita perpendicularmente à geratriz do
cilindro.
É o produto da área da base pela altura.
Num cilindro circular reto, a
área da secção reta é igual
à área das bases.
e
V = Ab . H
ou
V =  . r2 . H
321
CURSO DE MATEMÁTICA
Secção Meridiana de um Cilindro
É a secção feita no cilindro reto por um plano que contém
o seu eixo.
2.r
A secção
meridiana
é um retângulo.
H
A área da secção meridiana é a área de um retângulo e é
obtida pela fórmula:
AS = 2. r. H
Cilindro Eqüilátero - ( G = 2r )
É todo cilindro reto que têm as geratrizes com a mesma
medida que o diâmetro da base (G = 2r).
G = 2r
2r
A secção meridiana de um cilindro eqüilátero é um
quadrado cuja área é:
2
2r
AS = 4. r
2r
Área Total do Cilindro Eqüilátero
A área total de um cilindro eqüilátero equivale a seis vezes
a área da base.
HAMILTON E ALEX
EXERCÍCIOS
1) ( UFPA ) Um cilindro circular reto tem o raio igual a
2cm, e altura de 3cm. Sua superfície lateral mede:
2
a) 9 cm
b) 6 cm2
2
c) 15 cm
d) 16 cm2
e) 12 cm2
2)
( PAES/ UNIMONTES – 2000 ) Um tonel com a forma
de cilindro circular reto foi seccionado, determinando
um troco de cilindro. Considerando as medidas
indicadas no desenho abaixo, o volume desse tronco
de cilindro é : ( considere  = 3,14 )
3
a) 565,20 m
3
b) 169,56 m
c) 282,60 m3
d) 395,64 m3 14m
3m
6m
3) (ENEM) Uma garrafa cilíndrica está fechada, contendo
um líquido que ocupa quase completamente seu corpo
conforme mostra a figura. Suponha que, para fazer
medições, você disponha apenas de uma régua
milimetrada.
Para calcular a capacidade total da garrafa, lembrando
que você pode virá-la, o número mínimo de medições
a serem realizadas é:
a) 1
b) 2
c) 3
d) 4
e) 5
4) ( UFBA ) O tonel representado abaixo está ocupado
em 60% de sua capacidade. A quantidade de água
nele contida, em litros, é de aproximadamente ?
AT = AL+ 2.Ab
AT = 2..r.G + 2..r2
60
Como G = 2r

cm
AT = 2..r.(2.r) + 2..r2
2
2
AT = 4..r + 2..r
2
AT = 6..r
50 cm
5) (PUC
–
SP)
Quantos
litros
comporta,
aproximadamente, uma caixa d’água cilíndrica com 2
metros de diâmetro e 70 cm de altura ?
A) 1250
B) 2200
C) 2450
D) 3140
E) 3700
6) (UNIMONTES) Uma caixa d’água cilíndrica tem raio e
altura de medidas respectivamente iguais a 5dm e
1,8m. Podemos afirmar que sua capacidade é, em
litros, aproximadamente:
322
CURSO DE MATEMÁTICA
A) 141,3
C) 282,6
B) 1413
D) 1430
7) ( UN. VIÇOSA ) Um cilindro tem altura igual a 7 e
raio da base igual a 2. Então a área da superfície
total do cilindro é :
A) 51
B) 22
C) 15
D) 36
E) 39
8) ( UF – AM ) Uma lata de cerveja tem a forma
cilíndrica, com 6 cm de diâmetro e 12 cm de altura.
Quantos ml de cerveja cabem nessa lata ?
A) 367,38
B) 339,12
C) 250,33
D) 150,72
E) 108,57
9) ( UFPR ) Uma montadora produz dois tipos de
caminhões. Um para carregar contêiner em forma de
paralelepípedo retângulo com 12 m de comprimento,
2 m de largura e 2,5 m de altura e outro para
transportar líquidos, com um tanque em forma de
cilindro circular reto com 12 m de comprimento e
diâmetro da base 2 m, como mostra a figura.
Considere  = 3,14.
Com base nesses dados, analise as afirmações:
I) O volume do contêiner é de 60 m 3.
II) O volume do tanque é de 75,36 m 3.
III) A área total do contêiner é de 118 m 2 e do tanque
2
é de 81,64 m .
Pode-se então afirmar que:
a) as afirmações I e II estão corretas.
b) as afirmações I e III estão corretas.
c) as afirmações II e III estão corretas.
d) as afirmações I, II e III estão corretas.
e) as afirmações I, II e III estão incorretas.
10) ( UFGO ) Um pedaço de cano, de 30 cm de
comprimento e 10cm de diâmetro(interno), encontrase na posição vertical e possui a parte inferior vedada.
Colocando-se dois litros de água em seu interior, a
água:
a) transborda
b) enche o cano até a borda
c) atinge exatamente o meio do cano
d) ultrapassa o meio do cano
e) não chega ao meio do cano .
11) ( UECE ) O volume de um cilindro circular reto é
36 6  cm3. Se a altura desse cilindro mede 6 6 cm,
2
então a área total desse cilindro, em cm , é:
a) 72 
HAMILTON E ALEX
b) 84 
c) 92 
d) 96 
12) ( UFV – MG ) Para se construir uma lata cilíndrica de
base circular, sem tampa, com 20 cm de diâmetro na
base e 25 cm de altura, são gastos x cm2 de
material. O valor de x é:
a) 400
b) 600
c) 300
d) 700
e) 500
13) ( UFPE ) Um contêiner, na forma de um cilindro
circular reto, tem altura igual a 3 m e área total (área
da superfície lateral mais áreas da base e da tampa)
2
igual a 20 m . Calcule, em metros, o raio da base
deste contêiner.
a) 2m
b) 2,5m
c) 3m
d) 3,5m
e) 4m
14) ( UEL – PR ) Certa peça de um motor é feita de aço
maciço e tem a forma de três cilindros retos, de alturas
iguais, um sobre o outro. Se a peça for seccionada por
um plano contendo os centros das bases dos cilindros,
tem-se a situação abaixo ilustrada. O volume dessa
peça, em centímetros cúbicos, é
a) 1.580
b) 1.330
c) 1.170
d) 970
e) 190
15) ( Cesgranrio ) Um recipiente com a forma de um
cilindro reto, cujo diâmetro da base mede 40 cm e
altura 100/ cm, armazena um certo líquido, que ocupa
40% de sua capacidade. O volume do líquido contido
nesse recipiente é, em litros, aproximadamente, igual
a:
a) 16
b) 18
c) 20
d) 30
e) 40
16) (UFPA) O reservatório “tubinho de tinta” de uma
caneta esferográfica tem 4mm de diâmetro e 10cm de
comprimento. Se você gasta 5 mm3 de tinta por dia, a
tinta de sua esferográfica durará:
a) 20 dias
b) 40 dias
323
CURSO DE MATEMÁTICA
HAMILTON E ALEX
c) 50 dias
d) 80 dias
e) 100 dias
17) ( UFMG ) Num cilindro de 5 cm de altura, a área da
base é igual à área de uma seção por um plano que
contém o eixo do cilindro, tal como a seção ABCD
na figura abaixo.
B
O volume desse cilindro é de :
A
250
500
A)
B)

625
C)


D)
125

C
D
18) ( UFSC ) Uma panela caseira tem a forma de um
cilindro; sua altura é 15 cm e o diâmetro, 20 cm.
Deve-se enchê-la com cubos de gelo de 2 cm de
aresta, de tal forma que não transborde ao derreter o
gelo. A quantidade máxima de cubos de gelo possível
é, aproximadamente:
a) 985
b) 859
c) 589
d) 598
e) 895
19) Uma lata cilíndrica, cujo volume é 128, foi colocada
dentro de outra lata cúbica de modo que elas
ficassem perfeitamente encaixadas (figura). Um
líquido foi colocado na parte interior da lata cúbica e
exterior da lata cilíndrica até atingir exatamente a
altura dessas latas. Se a lata cilíndrica for retirada,
qual a altura atingida pelo liquido na lata cúbica?
A) 2(4 – )
B) 2(6 – )
C) 4 – 
D) 6 – 
20) ( UFPE ) Um queijo tem a forma de um cilindro circular
reto com 40 cm de raio e 30 cm de altura. Retira-se
do mesmo uma fatia, através de dois cortes planos
contendo o eixo do cilindro e formando um ângulo de
60°. Se V é o volume, em cm 3, do que restou do
queijo (veja a figura a seguir), o valor de V é :
a) 45000
b) 40000
c) 38000
d) 36000
e) 32000
21) ( Unimontes / PAES 2002 ) Dois recipientes, um na
forma de prisma quadrangular regular e outro na
forma de cilindro circular reto, contêm água. Se a
aresta da base do prisma mede 4  metros e
sabendo-se que os níveis de água nos recipientes são
iguais, qual deve ser o raio do cilindro, para que os
volumes de água sejam também iguais ?
a) 16 m
b) 4 m
c) 16 m
d) 4 m
22) (ENEM-2010) Para construir uma manilha de esgoto,
um cilindro com 2 m de diâmetro e 4 m de altura (de
espessura
desprezível),
foi
envolvido
homogeneamente por uma camada de concreto,
contendo 20 cm de espessura. Supondo que cada
metro cúbico de concreto custe R$ 10,00 e tomando
3,1 como valor aproximado de , então o preço dessa
manilha é igual a
A) R$ 230,40
B) R$ 124,00
C) R$ 104,16
D) R$ 54,56
E) R$ 49,60
23) (PUCC-SP) Numa indústria, deseja-se utilizar
tambores cilíndricos para a armazenagem de um certo
tipo de óleo. As dimensões dos tambores serão 30cm
para o raio da base e 80cm para a altura.
O material utilizado na tampa e na lateral custa
R$100,00 o metro quadrado. Devido à necessidade de
um material mais resistente no fundo, o preço do
material para a base inferior é de R$200,00 o metro
quadrado. Qual o custo de material para a confecção
de um desses tambores sem contar as perdas de
material? (Em seus cálculos,considere  = 3,14 .)
a) R$235,50.
b) R$24250.
c) R$247,20.
d) R$249,20.
e) R$250,00.
24) Um fazendeiro pretende fazer em sua propriedade um
reservatório de água com formato cilíndrico, onde o
raio da base teria 1,5 metros e a altura teria 1,2
metros. Mas, devido à forte estiagem, ele resolveu
aumentar em 50 centímetros essas dimensões.
Com isso, esse fazendeiro irá aumentar a capacidade
do reservatório, aproximadamente, em:
A) 52%
B) 92%
C) 132%
D) 152%
GABARITO
1) E
2) C
9) B
10) D
3) C
4) 22,5 L
11) B
16) D 17) B 18) C
5) B
12) B
19) A
20) B
6) B
13) A
21) D
7) D
14) B
22) D
8) B
15) A
23) A
24) D
324
CURSO DE MATEMÁTICA
HAMILTON E ALEX
CONE DE REVOLUÇÃO
CONE CIRCULAR
O sólido geométrico constituído por todos os segmentos
que têm uma extremidade em um ponto v (fora do plano
da base) e a outra num ponto da região circular C (base)
denomina-se cone circular.
O cone circular reto também é chamado de cone de
revolução, pois é formado pela rotação completa de um
triângulo retângulo em torno de um de seus catetos.
v
Relação Entre Cone e Cilindro
2 .V
3
Elementos do Cone
V
3
Eixo
Vértice(v)
Geratriz (G)
Altura ( H )
Base
No triângulo retângulo formado pela altura, pela geratriz e
pelo raio podemos utilizar o teorema de Pitágoras para
determinar a medida de qualquer um desses elementos.
 Se um cone for retirado de um cilindro de volume
1
V , esse cone terá
do volume desse cilindro e
3
2
a parte restante terá
do volume V do
3
cilindro.
Áreas do Cone Circular Reto
V
G
2
2
G =H +r
H
2
G
G
G
AL
r
r
No cone, a altura e a geratriz são sempre diferentes.
r
2..r
Cone Circular Reto
Área Lateral ( Al )
Quando a projeção ortogonal do vértice sobre o plano da
base é o centro dessa base, o cone circular se diz RETO;
caso contrário, o cone se diz OBLÍQUO.
A área da superfície lateral de um cone é a área de um
setor circular. Por regra de três temos:
V
H
V
G
G
G
H
G
AL
G
G
AL
2..r
G
r
Cone Circular Reto
Cone Oblíquo
Observe que, num cone circular reto:
 O eixo é perpendicular à base e passa pelo seu centro.
 As geratrizes são todas de mesma medida
Observe que, num cone oblíquo, a altura H fica fora do
cone.
2..r
2..r
Área Lateral
Área do círculo
2r
2G
AL.G = .G .r
2
AL
G 2
2r
2G
AL = .r.G
325
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Área da Base (Ab)
EXERCÍCIOS
É a área de um círculo de raio r.
1) ( Fatec – SP ) A altura de um cone circular reto mede
o triplo da medida do raio da base. Se o comprimento
da circunferência dessa base é 8 cm, então o volume
do cone, em cm3, é :
a) 64
b) 48
c) 32
d) 16
e) 8
r
Ab =  .r2
Área Total ( At )
É a soma da área lateral com a área da base.
AT = AL + Ab
AL
Ab
Volume de um cone ( V )
O volume de um cone é igual a 1/3 do volume de um
cilindro que o contém.
1
V = Ab . H .
3
CONE EQÜILÁTERO
É todo cone reto que têm as geratrizes com a mesma
medida do diâmetro da base (G = 2r).
2r
2r
2r
2r
2r
2r
A altura de um cone eqüilátero pode ser encontrada
utilizando-se a fórmula da altura do triângulo eqüilátero.
H=
l 3

2
H=
( 2r ) 3
2
( Fórmula da altura do
triângulo eqüilátero)
H= r 3
A secção meridiana de um cone eqüilátero é um triângulo
eqüilátero cuja área é:
A
l2 3
4
A
(2r )2 . 3
4
A = r2.
3
2) ( UEL – PR ) Um cone circular reto tem altura de 8 cm
e raio da base medindo 6 cm. Qual é, em centímetros
quadrados, sua área lateral?
a) 20 
b) 30 
c) 40 
d) 50 
e) 60 
3) ( UE – CE ) Um cone circular reto de altura 3 2 cm
tem volume igual a 18 2 cm3. O raio da base desse
cone, em centímetros, mede:
a) 2
b) 2 2
c) 3
d) 3 2
4) ( UFMG ) Um cone circular reto tem raio da base igual
a 3 e altura igual a 6. A razão entre o volume e a área
da base é:
a) 2
b) 6
c)
2
d) 4
e) 1,5
5) (ENEM 2010) Um arquiteto está fazendo um projeto de
iluminação de ambiente e necessita saber a altura que
deverá instalar a luminária ilustrada na figura
Sabendo-se que a luminária deverá iluminar uma área
2
circular de 28,26m , considerando π(pi) = 3,14 , a
altura h será igual a
a) 3 m.
b) 4 m.
c) 5 m.
d) 9 m.
e) 16 m.
6) ( FEI – SP ) Um cone reto tem como base um círculo
de raio R = 3 cm e, de altura, H = 4 cm. Ao calcular
seu volume V, um aluno usou a fórmula errada
326
CURSO DE MATEMÁTICA
V
1
..R 2 .H . A diferença entre o volume achado e
2
o volume correto, em cm 3, é :
8
a)
b) 4
3
b) c) 5
d) 6
c) e) 18
7) ( UFMG ) O volume, em cm 3, da figura formada por
um cone e um cilindro circular reto, é :
a) 
b) 2
3cm
c) 3
d) 4
2cm
e) 5
HAMILTON E ALEX
d) 54
e) 81
11) ( Univali – SC ) Um cone de 3 cm de raio e 8 cm de
altura está completamente cheio. O raio, em cm, de
outro cone de mesma altura e com metade da
capacidade do primeiro é :
2 3
2 3
a) 3
b)
c)
2
3
d)
2 2
3
e)
3 2
2
12) ( PUC ) A área lateral de um cone reto é igual ao
dobro da área de sua base. Calcule o volume desse
cone, sabendo que sua geratriz mede 12 cm.
1cm
8) ( CESGRANRIO ) No desenho a seguir, dois
reservatórios de altura H e raio R, um cilíndrico e
outro cônico, estão totalmente vazios e cada um será
alimentado por uma torneira, ambas de mesma vazão.
Se o reservatório cilíndrico leva 2 horas e meia para
ficar completamente cheio, o tempo necessário para
que isto ocorra com o reservatório cônico será de:
a) 2 h
b) 1 h e 30 min
c) 1 h
d) 50 min
e) 30 min
9) ( ITA – SP ) Qual o volume, em cm3, de um cone
circular reto, se a área de sua superfície lateral é de
24 cm2 e o raio de sua base mede 4 cm ?
16
20
a)
3
b)
c)
d)
e)
24

4
24

3
8
24
3
20

3
10) ( UNIFOR – CE ) Em um cone reto, a área da base é
9 cm2 e a geratriz mede 3 10 cm. O volume desse
3
cone, em cm , é :
a) 27
b) 36
c) 48
13) ( PUC – RS ) Num cone de revolução a área da base é
2
2
36 m e a área total é 96 m . A altura do cone, em
metros, é igual a:
a) 4
b) 6
c) 8
d) 10
e) 12
14) ( UFOP – 98 ) Um reservatório de água com a forma
de um cone circular reto tem 8 m de altura e, sua
base, 3 m de raio. Se a água ocupa 40% da
capacidade total do reservatório, o volume de água
nele contido é:
a) 960 litros
b) 4800 litros
c) 2400 litros
d) 9600 litros
e) 96000 litros
15) ( Fuvest – SP ) O diâmetro da base de um cone tem
medida igual a geratriz. A razão da área total para a
área lateral do cone é :
3
1
a)
b)
2
2
3
2
c)
d)
3
4
e)
2
3
16) ( Unimontes ) A altura de um cone circular reto é igual
a 3 cm e o ângulo formado entre essa altura e a
geratriz é de 60º. O volume desse cone é igual a:
a) 27 cm3
327
CURSO DE MATEMÁTICA
b)
c)
d)
e)
32 cm3
3
36 cm
48 cm3
54 cm3
HAMILTON E ALEX
b) 96
c) 72
d) 80
17) ( ENEM – 2009 ) Um vasilhame na forma de um cilindro
circular reto de raio da base de 5 cm e altura de 30 cm
está parcialmente ocupado por 625 cm3 de álcool.
Suponha que sobre o vasilhame seja fixado um funil na
forma de um cone circular reto de raio da base de 5 cm
e altura de 6 cm, conforme ilustra a figura 1. O conjunto,
como mostra a figura 2, é virado para baixo, sendo H a
distância da superfície do álcool até o fundo do
vasilhame.
Considerando-se essas informações, qual é o valor da
distância H ?
A) 5 cm
B) 7 cm
C) 8 cm
D) 12 cm
E) 18 cm
20) ( UFRN – 2001 ) Dois sólidos de formatos cilíndricos
têm bases de mesmo raio
r . De um deles, foi
extraída uma parte cônica, que foi colada no outro,
conforme mostra a figura abaixo.
H
Aos dois sólidos resultantes, de mesma altura
H, chamamos de S1 e S2. Se V( S1 ) e V( S2 )
denotam, respectivamente, os volumes de S1 e S2 ,
pode-se afirmar que :
a) V( S1 ) > V( S2 )
b) V( S1 ) + V( S2 ) = 2  r2 H
c) V( S1 ) < V( S2 )
7
d) V( S1 ) + V( S2 ) =  r2 H
3
21) ( UFMG ) Observe a figura,
18) (UNIMONTES – 98) Considere o polígono ABCDEA
mais seus pontos interiores abaixo representados no
plano cartesiano RxR:
O volume, em cm3, do sólido gerado pela rotação
completa da figura ao lado, em torno da reta que
contém os pontos D e E, é:
a) 72
12 D
C
b) 640
c) 568
8 E
d) 712
2
A
2
B
8
10
Nessa figura, a base da pirâmide é um quadrado
inscrito no círculo da base do cone.
A razão entre o volume do cone e o volume da
pirâmide, nesta ordem, é:
a) /4
b) /2
c) 
d) 2
e) 2/3
22) (Fuvest – SP) Um cone circular reto está inscrito em
um paralelepípedo reto retângulo, de base quadrada,
como mostra a figura.
19) ( UEMG – 2001 ) Observe a figura.
g
y
b
8
a
6
0
a
2
x
Na figura, a região hachurada sofre uma rotação em
torno do eixo Y. Sendo V o volume do sólido de
revolução gerado, o valor de 3V é igual a:
a) 3( 24 + 8 )
A razão b/a entre as dimensões do paralelepípedo é
3/2 e o volume do cone é π. Determine o comprimento
g da geratriz do cone.
23) ( MACK – SP ) A área da secção meridiana de um
cone reto é igual à área de sua base. Se o raio da
base é 1, então a altura do cone é :

a)
2
328
CURSO DE MATEMÁTICA
b)
c) 84,8
d) 48,2
3
2
c)
d)
2
e)


24) ( UFMG – 2004 ) Um cone é construído de forma
que:
 Sua base é um círculo inscrito em uma face de um
cubo de lado a; e
 Seu vértice coincide com um dos vértices do cubo
localizado na face oposta àquela em que se
encontra a sua base.
Dessa maneira, o volume do cone é de :
 .a 3
a)
6
b)
c)
d)
HAMILTON E ALEX
 .a 3
12
 .a 3
9
 .a 3
3
25) ( PUC – SP ) A medida dos lados de um triângulo
eqüilátero ABC é a. O triângulo ABC gira em torno de
uma reta r do plano do triângulo, paralelo ao lado BC
e passando pelo vértice A. O volume gerado por esse
triângulo é :
a) a3 / 3
b) a3 / 2
c) a3
A
r
d) 3a3 / 2
e) a3 / 5
a
a
B
a
C
26) ( FAFEOD – 2000 ) Observe a figura abaixo:
27) ( FCC ) O volume do sólido gerado pela revolução de
um triângulo equilátero de lado a em torno de um de
seus lados é :
a 3
a 3
a)
b)
4
3
a
a 3
2
4 a 3
e)
3
c)
d)
3 a 3
4
28) ( UFOP ) Um triângulo retângulo possui catetos de
comprimentos a e b. Sejam Va e Vb os volumes dos
cones obtidos pela rotação do triângulo em torno,
respectivamente, dos catetos a e b. O quociente Va /
Vb vale:
ab
a)
2
a  b2
a
b)
a b
c)
b
a
d)
a 1
b 1
29) ( Mack – SP ) Um triângulo retângulo isósceles de
catetos unitários gira em torno da hipotenusa. O
volume do sólido gerado é :
 3
 6
 2
a)
b)
c)
2
2
6
d)
 2
3
e) n.d.a.
1
1
y (cm)
A (0, 3)
O (0, 0)
B (3, 3)
x (cm)
30) O setor circular abaixo é a planificação da área lateral
de um cone circular reto cujo raio da base mede 3 cm.
O volume desse cone, em cm3, é igual a:
a) 9 7
b) 8 7
c) 7 7
d) 6 7
Sendo S a região hachurada, é correto afirmar que o
volume aproximado do sólido gerado pela rotação de S
em torno do eixo x é, em centímetros cúbicos, igual a :
a) 28,2
b) 56,5
e) 3 7
270º
329
CURSO DE MATEMÁTICA
GABARITO
1) A
8) D
2) E
ESFERA
3) D
9) A
13) C
14) D
19) D
20) A
24) B
25) B
HAMILTON E ALEX
4) A
10) A
15) A
21) B
26) B
5) B
11) E
16) A
22)
27) A
6) D
7) C
12) 72 3
17)B
10
Esfera é um sólido gerado pela rotação completa de um
semicírculo em torno de um eixo que contém o seu
diâmetro.
18) C
23) D
28) C
R
29) A
30) E
Secção
Esférica
Área: AS =  r
2
CS = 2  r
Comprimento:
r
R
d
R
r
R
d
Círculo Área: A =  R
Máximo Comprimento: C = 2  R
2
R2 = r2 + d2
Área da superfície esférica
A área da superfície de uma esfera de raio R é
definida por:
Ae = 4..R2
Volume da esfera
O volume de uma esfera de raio R, ou região delimitada
pela esfera, é definido por:
Ve 
4 R 3
3
330
CURSO DE MATEMÁTICA
HAMILTON E ALEX
PARTES DA ESFERA
Volume da Cunha
FUSO ESFÉRICO
O volume da cunha pode ser obtido por uma regra de três
simples:
O fuso esférico é uma parte da superfície esférica que se
obtém ao girar uma semi-circunferência de um ângulo ,
0º <  < 360º em torno de seu eixo:
Fuso
esférico


R
AF

AF =

4..R 2 .
360º
VC



4 R 3
3
360°
VC

VC =
.R 3 .
270º
EXERCÍCIOS
A área do fuso esférico pode ser obtida por uma regra
de três simples:
360°
360°
4..R 3 .
VC =
3 . 360º
Área do Fuso
AE
VE

4R2
360°

AF

AF =
.R 2 .
90º
Obs.: O fuso esférico só possui área.
CUNHA ESFÉRICA
Parte da esfera que se obtém ao girar um semicírculo
em torno de seu eixo de um ângulo , 0º <  < 360º .
A cunha esférica possui área e volume.

R

Cunha
esférica
Área Total da Cunha
É a soma da área do fuso esférico com as áreas de dois
semicírculos.
ATC = AF + 2. ( Área do Círculo )
2
ATC = AF +  R2
1) ( PUC – MG ) Uma esfera de raio R = 3 cm tem
volume equivalente ao de um cilindro circular reto de
altura h = 12 cm. O raio do cilindro, em cm, mede:
a) 1
b) 2
c)
3
d) 3
e)
13
2) ( UFRS ) Uma panela cilíndrica de 20 cm de diâmetro
está completamente cheia de massa para doce, sem
exceder a sua altura de 16 cm. O número de doces,
em formato de bolinhas de 2 cm de raio, que se pode
obter com toda a massa é :
a) 300
b) 250
c) 200
d) 150
e) 100
3) ( UFMG ) O círculo máximo de uma esfera mede 6
cm. Qual o volume dessa esfera ?
3
a) 12 cm
3
b) 24 cm
3
c) 36 cm
3
d) 72 cm
e) 144 cm3
3
4) ( CFTMG ) Considere uma bola de sorvete de 36 cm
de volume e uma casquinha cônica de 3 cm de raio. A
altura da casquinha, para que o sorvete, ao derreter,
ocupe todo o seu espaço, em cm, é
a) 8
b) 9
c) 10
d) 12
331
CURSO DE MATEMÁTICA
5) ( UFMG ) Duas bolas metálicas (esferas), cujos raios
medem 1 cm e 2 cm, são fundidas e moldadas em
forma de um cilindro cuja altura mede 3 cm. Obtenha
a medida do raio da base do cilindro.
6) ( Fuvest ) Um recipiente cilíndrico cujo raio da base é
6 cm contém água até uma certa altura. Uma esfera
de aço é colocada no interior do recipiente ficando
totalmente submersa. Se a altura da água subiu 1 cm
então o raio da esfera é
a) 1 cm
b) 2 cm
c) 3 cm
1 cm
d) 4 cm
e) 5 cm
7) ( UEL –PR ) Considere um cone circular reto e um
cilindro circular reto, ambos com diâmetro da base
igual a 12 cm e também uma esfera com diâmetro de
12 cm, todos com volumes iguais. A altura do cone e
a altura do cilindro devem ser respectivamente iguais
a:
a) 12 cm e 4 cm
b) 30 cm e 10 cm
c) 24 cm e 8 cm
d) 9 cm e 3 cm
e) 18 cm e 6 cm
HAMILTON E ALEX
Nessa figura, ABC é um quadrante de círculo de raio
3 cm e ADEF é um quadrado, cujo lado mede 1 cm.
Considere o sólido gerado pela rotação de 360º, em
torno da reta AB, da região hachurada na figura.
Assim sendo, esse sólido tem um volume de :
a) 14 cm3
3
b) 15 cm
c) 16 cm3
3
d) 17 cm
10) ( Vunesp ) Um copinho de sorvete, em forma de cone,
possui 10cm de profundidade, e 4cm de diâmetro no
topo, tendo aí colocadas duas conchas semi-esféricas
de sorvete, também de 4 cm de diâmetro. Se o sorvete
derreter para dentro do copinho, podemos afirmar que:
a) não transbordará;
b) transbordará;
c) os dados são insuficientes;
d) os dados são incompatíveis;
e) as informações anteriores são falsas.
11) ( Unitau – SP ) Uma esfera de raio R está inscrita em
um cilindro. Qual a razão entre o volume do cilindro e
da esfera ?
12) ( Unimontes – PAES 2002 ) Se uma esfera está
inscrita em um cubo, podemos afirmar que a razão
entre o volume dessa esfera e o volume desse cubo é
igual a :
a)
8) ( UFRS ) São fundidas 300 esferas com 20 mm de
diâmetro para fabricar cilindros circulares retos com
20 mm de diâmetro e 200 mm de altura. O número
de cilindros resultantes é :
a) 2
b) 5
c) 20
d) 25
e) 30
9) ( UFMG – 2001 ) Observe esta figura:
B
D
A
E
F
C
b)
c)
d)
3
2

6
3
2
6

13) ( Fuvest – SP ) Uma superfície esférica de 13 cm de
raio é cortada por um plano situado a uma distância
de 12 cm de seu centro, determinando uma
circunferência. O raio desta circunferência, em
centímetros, é:
a) 1
b) 2
c) 3
d) 4
e) 5
332
CURSO DE MATEMÁTICA
14) ( CESCEM – SP ) A área da interseção de um plano
com uma esfera de raio 10 cm é 64 cm2. A distância
do plano ao centro da esfera é:
a) 1 cm
b) 5 cm
c) 6 cm
d) 12 cm
e) 25 cm
15) ( Unimontes – PAES 2002 ) Um plano intersecta uma
esfera, determinando um círculo de raio r igual à
metade do raio dessa esfera. Com base nessas
informações, é correto afirmar que a distância do
circulo ao centro da esfera é dada por:
a)
b)
3 r
r
2
c) 2r
d)
2r
16) ( UFOP / MG ) Um plano intercepta uma superfície
esférica formando uma circunferência de 6 3  cm
de comprimento. Sendo a distância do centro da
esfera ao centro da circunferência igual a 3 cm, o raio
da esfera é ?
a) 4 cm
b) 5 cm
c) 6 cm
d) 7 cm
e) 8 cm
17) ( UFMG ) A região delimitada por uma esfera é
interceptada por um plano a 3 cm do centro dessa
esfera. Se a área dessa interseção é 9 cm2, o
volume da região delimitada pela esfera, em cm 3, é :
a) 18 2
b) 36 2
c) 72 2
d) 144 2
e) 216 2
18) ( UFV – MG ) Em um recipiente que tem a forma de
um cilindro circular reto, com diâmetro da base igual a
16 cm, são colocadas duas esferas de chumbo de
raios iguais a 4 cm e 6 cm, conforme ilustra a figura
abaixo.
A altura, em cm, necessária para que um líquido
colocado no recipiente cubra totalmente as esferas é:
a) 15
b) 18
c) 16
d) 19
e) 17
HAMILTON E ALEX
19) ( UFMG ) Um recipiente cúbico, sem tampa, cujas
arestas medem 4 dm, contém 56 litros de água. Ao
lado desse recipiente, estão os seguintes sólidos,
todos de aço maciço:
• uma esfera de raio 3 2 dm ;
• um cilindro circular reto com raio da base 2 dm e
altura 2 dm ;
• um paralelepípedo retangular de dimensões 3 dm,
3 dm e
7 dm ; e
• uma pirâmide reta de altura
5 dm e de base
quadrada com lado 12 dm .
Qual desses sólidos, quando colocado no recipiente,
NÃO fará com que a água transborde?
a) A pirâmide
b) O cilindro
c) O paralelepípedo
d) A esfera
20) ( MACK – SP ) Seja 36 o volume de uma esfera
circunscrita a um cubo. Então, a razão entre o volume
da esfera e o volume do cubo é:
3
a)
2
8
b)
3
2
c)
3
d)
3
4
e)
3
21) ( MACK – SP ) Na figura, O é o centro de um de
círculo, e o volume gerado pela rotação da região
assinalada em torno da reta r é 18. Então, a área do
triângulo ABC é:
C
a) 6
b) 9
r
c) 4,5
A
O
B
d) 18
e) 27
22) ( Ufmt ) A região sombreada na figura a seguir sofre
uma rotação completa em torno do eixo y. Os pontos
indicados são: O = (0, 0); A = (1, 1); B = (0, 2); C =
(1, 3); D = (0, 3) e E = (0, 1). OAB é uma
semicircunferência com centro em E, conforme mostra
a figura a seguir. Faça o que se pede:
333
CURSO DE MATEMÁTICA
a) Desenhe o sólido de revolução gerado pela
rotação completa da figura em torno do eixo Y.
HAMILTON E ALEX
25) ( Fuvest – SP ) Para pintar a base plana de um
hemisfério maciço, gastamos doze galões de tinta.
Quantos galões serão necessários para pintar toda a
parte externa do hemisfério ?
hemisfério
b) Sendo V a medida do volume do sólido de
36
V.
revolução gerado, calcule o valor de
5
23) ( PUC – MG ) Uma esfera de raio r = 3 cm tem
volume equivalente ao de um cilindro circular reto de
altura h = 12 cm. A medida do raio desse cilindro é:
a) 1
b)
2
c) 2
26) ( Cescea – SP )
O volume da esfera inscrita no
cilindro equilátero de área lateral 36 cm2 é, em cm3,
igual a :
a) 4/3
b) 36
c) 12
d) 3
e) n.d.a
27) ( VUNESP ) Conta a lenda que Arquimedes pediu que
em sua lápide fosse gravada a figura de uma esfera
inscrita num cilindro porque ele descobriu um teorema
notável. Esse teorema está enunciado, a seguir, entre
4 proposições falsas.
d)
3
e) 3
24) ( UFJF ) Um reservatório de água tem a forma de um
hemisfério acoplado a um cilindro circular como
mostra a figura a seguir.
A medida do raio do hemisfério é a mesma do raio da
base do cilindro e igual a r = 3 m. Se a altura do
reservatório é h = 6 m, encontre:
a) A capacidade máxima, em
m 3, de água
comportada por esse reservatório.
Ele é :
a) A área da superfície da esfera é igual à soma das
áreas das bases do cilindro circunscrito.
b) A área da superfície da esfera é igual à área da
superfície lateral do cilindro circunscrito.
c) O volume da esfera é 1/3 do volume do cilindro
circunscrito.
d) A razão entre o volume da esfera e o volume do
cilindro circunscrito é um número irracional.
e) A área da superfície da esfera é igual à área da
superfície total do cilindro circunscrito.
28) ( UnB ) A região S hachurada é delimitada por 3
semi-circunferências, sendo o raio das duas menores
igual a 2 cm. Ao girar S em torno de AB obtém-se
3
um sólido de volume V (em cm ). Calcule V.
A
B
b) A superfície total externa desse reservatório,
sabendo que ele não tem tampa.
29) ( UnB ) Um sorveteiro vende sorvete de casquinha de
biscoito que tem a forma de cone de 3 cm de
diâmetro e 6 cm de profundidade. As casquinhas são
totalmente preenchidas de sorvete e , ainda, nelas é
superposta uma meia bola de sorvete de mesmo
334
CURSO DE MATEMÁTICA
diâmetro do cone. Os recipientes onde é armazenado
o sorvete tem forma cilíndrica de 18 cm de diâmetro e
5 cm de profundidade. Determine o número de
casquinhas que podem ser servidas com o sorvete
armazenado em um recipiente cheio.
30) ( PUC – SP ) Um cone circular reto, cujo raio da base
é 3 cm, está inscrito em uma esfera de raio 5 cm,
conforme mostra a figura a seguir. Observe a figura e
encontre:
a) A altura do cone
b) A razão entre o volume da esfera e o volume
do cone, nessa ordem.
31) ( UFRS ) Uma esfera de raio 2 cm é mergulhada num
copo cilíndrico de 4 cm de raio, até encostar no
fundo, de modo que a água do copo recubra
exatamente a esfera. Antes da esfera ser colocada no
copo, a altura da água era
a) 27/8 cm
b) 19/6 cm
c) 18/5 cm
d) 10/3 cm
H
e) 7/2 cm
32) (UFSM / Adaptada ) A área da superfície de uma
esfera e a área total de um cone circular reto são
iguais. Se o raio da base do cone mede 4 cm e o
volume do cone é 16 cm3, encontre o que se pede:
a) A medida da altura do cone
HAMILTON E ALEX
33) ( Mack – 2001 ) Bolas de tênis, normalmente, são
vendidas em embalagens cilíndricas contendo três
unidades que tangenciam as paredes internas da
embalagem. Numa dessas embalagens, o volume não
ocupado pelas bolas é 2, qual o volume dessa
embalagem ?
a) 4
b) 6
c) 8
d) 10
e) 12
34) ( Cesgranrio – RJ ) Uma laranja pode ser considerada
uma esfera de raio R, composta de 12 gomos
exatamente iguais. A superfície total de cada gomo
mede:
a) 2R2
b) 4R2
3R 2
c)
4
2
d) 3R
4R 2
e)
3
GABARITO
1) C
2) D
9) D 10) A
3) C
11)
16) C
17) C
22)a)
b) 12
3
2
29) 60 Casquinhas
5) R = 2
12) B
18) B
25) 36 Galões
31) D
4) D
13) E
19) C
23) D
26) B
14) C
20) A
24) a) 45 m
27) B
30) a) H = 9
32) a) H = 3cm
6) C
b) R = 3 cm
7) C 8) C
15) A
21) B
3
b) 36 m
2
28) 64
b) 500/81
33) B
34) E
b) A medida do raio da esfera
335
CURSO DE MATEMÁTICA
HAMILTON E ALEX
TRONCO DE PIRÂMIDE
PROPRIEDADES
Quando um plano intercepta uma pirâmide e este é
paralelo à base desta, obtém-se uma secção poligonal
denominada secção transversal da pirâmide.
Como as bases das duas pirâmides são paralelas,
pode-se afirmar que a pirâmide menor e a pirâmide maior
são semelhantes.
Utilizando semelhança de triângulo, temos:
A
h
h
H
B’
C’
B
O plano separa a pirâmide em dois sólidos, uma
pirâmide menor ( parte superior ) e um tronco de
Pirâmide ( parte inferior ).



As bases são polígonos regulares e semelhantes;
As faces laterais são trapézios isósceles;
A altura de um desses trapézios é chamada apótema
do tronco.
O apótema do tronco de pirâmide é encontrado
utilizando o teorema de Pitágoras.
apótema da base
menor ( m )
m
K
etc.
3
Onde :






h é a altura menor
H é a altura maior
Ab é a área da base menor
AB é a área da base maior
v é o volume da pirâmide menor
V é o volume da pirâmide maior
Área lateral do tronco de pirâmide regular
É a soma das áreas dos trapézios isósceles (faces
laterais)
f
Área total do tronco de pirâmide regular
M
apótema da base
maior ( M )
K
e
v
h
  
H
V
 
Face Lateral ( Trapézio )
Quando a pirâmide original é regular, o tronco de
pirâmide se diz regular. Nesse caso:
h B' C'

H
BC
2
Altura ( f ) de uma face ou
(apótema do tronco)
Base maior ( B )
ou
A
h
   b
AB
H
Base menor ( b )
Altura ( k )
do tronco
C
h AB'

H AB
NUM TRONCO DE PIRÂMIDE TEMOS:
H
É a soma da área lateral com a soma das áreas dos
dois quadrados (Base maior e base menor)
f
M–m
VOLUME DO TRONCO DE PIRÂMIDE
2
2
f = k + ( M – m)
2
É o volume da pirâmide maior menos o volume da
pirâmide menor.
336
CURSO DE MATEMÁTICA
EXERCÍCIOS
TRONCO DE CONE
Quando interceptamos um cone por um plano  que é
paralelo à base, determinamos dois sólidos: um deles é
outro cone (cone menor) e o segundo é denominado
tronco de cone de bases paralelas .
g
HAMILTON E ALEX
1) ( FCMMG ) Observe a figura :
h
G
Essa taça, cujo interior tem a forma de um cone,
contém suco até a metade da altura do cone interno. Se
o volume do cone interno é igual a V, então o volume
do suco nele contido é:
V
a)
16
V
b)
8
H
K
NUM TRONCO DE CONE DESTACAMOS:
c)
Área da base
menor :
Ab = .r
r
d)
2
K
Altura do tronco
R
Área da base
maior :
AB = .R
2)
( UFMG ) Um reservatório de água tem forma de um
cone circular reto, de eixo vertical e vértice para baixo.
Quando o nível de água atinge a metade da altura do
tanque, o volume ocupado é igual a . A capacidade
do tanque é:
a) 2
8
b)
3
c) 4
d) 6
e) 8
3)
( UnB – DF ) Um cálice tem a forma de um cone de
revolução, de altura igual a 100mm e volume V1.
Esse cálice contém um líquido que ocupa um volume
V2 , atingindo a altura de 25mm, conforme mostra a
V 
figura. O valor do quociente  1  é:
 V2 
a) 4
b) 8
100mm
c) 16
d) 32
e) 64
4)
( FCC – SP ) Uma pirâmide de altura 6 e área da
base 27 é interceptada por um plano, cuja distância
ao vértice é 2 e que é paralelo ao plano da base.
Qual o volume do tronco de pirâmide assim
determinado ?
a) 52
b) 48
Geratriz do
tronco
2
ÁREA LATERAL E ÁREA TOTAL DE UM TRONCO
DE CONE
r
Altura do tronco
K
R
ALT : Área lateral
do tronco ;
Ab
ALT
V
4
V
2
A l : Área lateral
do cone menor ;
AL : Área lateral
do cone maior ;
AT : Área total do
tronco ;
AB
ALT = AL – Al
AT = ALT + AB + Ab
337
CURSO DE MATEMÁTICA
c) 44
d) 40
e) 24
5)
( PUC – SP ) O recipiente abaixo, em forma de um
cone circular reto, tem raio com 12 cm e altura com
16 cm. O líquido ocupa
altura x do líquido é:
a) 1 cm
b) 2 cm
c) 4 cm
d) 6 cm
e) 8 cm
6)
7)
8)
1
do volume do recipiente. A
8
x
( UEPI – PI ) Uma pirâmide de base quadrangular
tem esta base com área de 64 cm2. Efetuando-se
nesta pirâmide um corte a 6 cm da base, obtém-se
uma secção transversal com área de 16 cm2. A
altura da pirâmide, então, é de :
a) 8 cm
b) 10 cm
c) 12 cm
d) 14 cm
6 cm
e) 16 cm
( PUC – SP ) Um quebra-luz é um cone de geratriz
medindo 17 cm e altura com 15 cm. Uma lâmpada
acesa no vértice do cone projeta no chão um círculo
de 2 metros de diâmetro. A que altura do chão se
encontra a lâmpada?
a) 1,50 metros
17
15
b) 1,87 metros
c) 1,90 metros
d) 1,97 metros
e) 2,00 metros
( UFAL ) Na figura abaixo tem-se, apoiado no plano
, um cone circular reto cuja altura mede 8 cm e
cujo raio da base mede 4 cm. O plano  é paralelo
a  e a distância entre os dois planos é de 6 cm. O
volume do cone que está apoiado no plano  é, em
centímetros cúbicos, igual a
a)  / 3
b)  / 2
c) 2 / 3
d) 3 / 4
e) 4 / 5
HAMILTON E ALEX
O volume do tronco de cone obtido dessa interseção
3
é, em cm :
a) 246
b) 312
c) 324
d) 348
e) 421
10) ( Cesgranrio ) Um tanque cônico, de eixo vertical e
vértice para baixo, tem água até a metade de sua
altura. Se a capacidade do tanque é de 1200 litros,
então a quantidade de água nele existente, em litros,
é de :
a) 600
b) 450
c) 300
d) 200
e) 150
11) ( Vunesp – SP ) Cortando um cone reto com um
plano paralelo à base e distante H/2 da base, onde
H é a altura do cone, obtemos um círculo de área A.
O volume V do cone é igual a:
a) (A.H)/3
b) (2.A.H)/3
c) A.H
d) (4.A.H)/3
e) (5.A.H)/3
12) ( Vunesp – SP ) É dada uma pirâmide de altura H, H
= 9 cm, e volume V, V = 108 cm3. Um plano paralelo
à base dessa pirâmide corta-a determinando um
tronco de pirâmide de altura h, h = 3 cm. Qual o
volume do tronco de pirâmide resultante ?
13) ( PUC – RS ) Uma secção paralela à base feita a 3 cm
do vértice de uma pirâmide tem área igual a 1/3 da
área da base. A altura da pirâmide é, em centímetros,
igual a:
a) 3 3
b) 5
c) 2 6
d) 2 3
e)
9)
( PUC – SP ) Um cone reto cuja geratriz mede 15 cm
e o raio da base mede 9 cm, é interceptado por um
plano paralelo à base, distando 4 cm de seu vértice.
3
14) ( Fuvest – SP ) Qual das expressões seguintes dá o
volume do tronco de cone circular de bases paralelas
em função de H, R, h, r ?
338
CURSO DE MATEMÁTICA
a)
b)
c)
d)
e)
/3[ HR2 + (H – h) r2 ]
2
2
/3[ HR – (H + h) r ]
2
2
/3[ HR – (H – h) r ]
/3[ HR2 + (H + h) r2 ]
n.r.a
r
H
h
R
15) ( UCMG ) A área lateral de um tronco de cone
circular reto de altura 4 cm, raio maior 8 cm e raio
menor 5 cm é, em cm2, igual a:
a) 45
b) 55
c) 65
d) 75
e) 85
16) ( PUC – RJ ) Um tanque subterrâneo tem a forma de
um cone circular invertido, de eixo vertical, e está
cheio até a boca ( nível do solo ) com 27000 litros de
água e 37000 litros de petróleo ( o qual é menos
denso que a água ). Sabendo que a altura total do
tanque é 8 m e que os dois líquidos não são
miscíveis, a altura da camada de petróleo é :
a) 6 metros
solo
b) 2 metros
c) 3 metros
d) 1 metro
e) 4 metros
HAMILTON E ALEX
19) ( Cesgranrio – RJ ) Uma ampulheta é formada por
dois cones de revolução iguais, com eixos verticais e
justapostos pelo vértice, o qual tem um pequeno
orifício que permite a passagem de areia da parte de
cima para a parte de baixo. Ao ser colocada para
marcar um intervalo de tempo, toda a areia está na
parte de cima e, 35 minutos após, a altura da areia na
parte de cima reduziu-se à metade, como mostra a
figura. Supondo que em cada minuto a quantidade de
areia que passa do cone de cima para o de baixo é
constante, em quanto tempo mais toda a areia terá
passado para a parte de baixo?
a) 5 minutos
b) 10 minutos
c) 15 minutos
d) 20 minutos
e) 30 minutos
20) ( Cesgranrio – RJ ) Um recipiente cônico, com altura
igual a 2, contém água até a metade de sua altura (
Fig. I ). Invente-se a posição do recipiente, como
mostra a figura II. A distância do nível da água ao
vértice, na situação da figura II é :
a)
b)
17) ( Unicamp – 95 ) Uma pirâmide regular, de base
quadrada, tem altura igual a 20 cm. Utilizando-se a
base dessa pirâmide constrói-se um cubo de modo
que a face oposta à base do cubo corte a pirâmide
em um quadrado de lado igual a 5 cm. O volume do
cubo nessas condições é:
a) 1000
b) 1728
c) 2197
d) 3375
18) ( Fuvest – SP ) Um copo tem a forma de um cone
com 8 cm de altura e 3 cm de raio da base.
Queremos enchê-lo com quantidades de água e suco
iguais. Para que isso seja possível a altura h atingida
pelo primeiro líquido colocado deve ser:
a) 8/3
b) 6
c) 4
3
2
3
2
3
c)
d)
3
7
e)
3
6
Figura I
Figura II
21) ( Fuvest – SP ) As bases de um tronco de cone
circular reto são círculos de raios 6 cm e 3 cm.
Sabendo que a área lateral do tronco é igual à soma
das áreas das bases, calcule:
a) a altura do tronco de cone
b) o volume do tronco de cone
d) 4 3
e) 4
3
4
339
CURSO DE MATEMÁTICA
22. Um cone oco, fechado e com 12 cm de altura, contém
água até a metade dessa altura (figura 1). Se esse cone
for colocado de forma invertida (figura 2), o valor da altura
da parte sem água é :
A) 6.3 7
B) 7.3 6
C) 6.3 4
h=?
12
D) 4.3 6
FIGURA 1
2) E
3) E
8) C
9) B
10) E
13) A
18) E
14) C
19) A
4) A
15) C
20) D
5) E
11) D
de peça feita nessa companhia tem o formato de um
paralelepípedo retangular, de acordo com as dimensões
indicadas na figura que se segue.
O produto das três dimensões indicadas na peça resultaria na
medida da grandeza
A) Massa
B) Volume
C) Superfície
D) Capacidade
E) Comprimento
FIGURA 2
GABARITO
1) B
HAMILTON E ALEX
6) C
7) B
12) 76 cm3
16) B
03. ( ENEM – 2010 ) Um porta-lápis de madeira foi construído
no formato cúbico, seguindo o modelo ilustrado a seguir. O
cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e
a do cubo menor, que é interno, mede 8 cm.
O volume de madeira utilizado na confecção desse objeto foi
de
17) A
21) a) k = 4 cm
b) 84 cm3
22) A
QUESTÕES DO ENEM
01. (ENEM-2009) Em uma padaria, há dois tipos de forma
de bolo, formas 1 e 2, como mostra a figura abaixo.
Sejam L o lado da base da forma quadrada, r o raio da
base da forma redonda, A1 e A2 as áreas das bases das
formas 1 e 2, e V1 e V2 os seus volumes, respectivamente.
Se as formas têm a mesma altura h, para que elas
comportem a mesma quantidade de massa de bolo, qual é
a relação entre r e L?
A) L=r
B) L=2r
C) L=  r
D) L=r 
2
E) L=(  r )/2
02. (ENEM - 2009) A siderúrgica “Metal Nobre” produz
diversos objetos maciços utilizando o ferro. Um tipo especial
04. (ENEM-2010) Certa marca de suco é vendida no mercado
em embalagens tradicionais de forma cilíndrica. Relançando a
marca, o fabricante pôs à venda embalagens menores,
reduzindo a embalagem tradicional à terça parte de sua
capacidade.
Por questões operacionais, a fábrica que fornece as
embalagens manteve a mesma forma, porém reduziu à
metade o valor do raio da base da embalagem tradicional na
construção da nova embalagem. Para atender à solicitação de
redução da capacidade, após a redução no raio, foi necessário
determinar a altura da nova embalagem.
Que expressão relaciona a medida da altura da nova
embalagem de suco (a) com a altura da embalagem tradicional
(h)?
05. (ENEM-2009) Considere um caminhão que tenha uma
carroceria na forma de um paralelepípedo retângulo, cujas
dimensões internas são 5,1 m de comprimento, 2,1 m de
largura e 2,1 m de altura. Suponha que esse caminhão foi
contratado para transportar 240 caixas na forma de cubo
com 1 m de aresta cada uma e que essas caixas podem
ser empilhadas para o transporte.
Qual é o número mínimo de viagens necessárias para
realizar esse transporte?
340
CURSO DE MATEMÁTICA
A) 10 viagens.
D) 24 viagens.
B) 11 viagens.
E) 27 viagens.
C) 12 viagens.
06. (ENEM-2009) Um artista plástico construiu, com certa
quantidade de massa modeladora, um cilindro circular reto
cujo de diâmetro da base mede 24 cm e cuja altura mede
15 cm. Antes que a massa secasse, ele resolveu
transformar aquele cilindro em uma esfera.
Volume da esfera: Vesfera = 4  r3/3
Analisando as características das figuras geométricas
envolvidas, conclui-se que o raio R da esfera assim
construída é igual a
A) 15
B) 12
C) 24
HAMILTON E ALEX
D) 3 3 60
E) 6 3 30
07. (ENEM-2009) Um vasilhame na forma de um cilindro
circular reto de raio da base de 5 cm e altura de 30 cm
está parcialmente ocupado por 625  cm3 de álcool.
Suponha que sobre o vasilhame seja fixado um funil na
forma de um cone circular reto de raio da base 5 cm e
altura de 6 cm, conforme ilustra a figura 1.O conjunto,
como mostra a figura 2, é virado para baixo, sendo H a
distância da superfície do álcool até o fundo do vasilhame.
Volume do cone: V cone=  r2h/3
Considerando-se essas informações, qual é o valor da
distância H?
A) 5cm. B) 7cm
C) 8cm
D) 12cm
E) 18cm
Se R = r 2 e h2 = h1/3 e, para encher o cilindro do meio,
foram necessários 30 minutos, então, para se conseguir
encher essa fonte e o segundo cilindro, de modo que fique
completamente cheio, serão necessários
A) 20 minutos
B) 30 minutos
C) 40 minutos
D) 50 minutos
E) 60 minutos
09. (ENEM-2010) Alguns testes de preferência por
bebedouros de água foram realizados com bovinos,
envolvendo três tipos de bebedouros, de formatos têm a
forma de um tronco de cone circular reto, de altura igual a
60 cm, e diâmetro da base superior igual a 120 cm e 60
cm, respectivamente. O bebedouro 3 é um semicilindro,
com 30 cm de altura, 100 cm de comprimento e 60 cm de
largura. Os três recipientes estão ilustrados na figura.
Considerando que nenhum dos recipientes tenha tampa,
qual das figuras a seguir representa uma planificação para
bebedouro 3?
08. (ENEM-2009) Em uma praça pública, há uma fonte
que é formada por dois cilindros, um der aio r e altura h1,
e o outro de raio R e altura h2. O cilindro de meio enche
e,após transbordar, começa a encher o outro.
341
CURSO DE MATEMÁTICA
10. (ENEM-2013) Num parque aquático existe uma
piscina infantil na forma de um cilindro circular reto, de 1
m de profundidade e volume igual a 12 m3, cuja base tem
raio R e centro O. Deseja-se construir uma ilha de lazer
seca no interior dessa piscina, também na forma de um
cilindro circular reto, cuja base estará no fundo da piscina
e com centro da base coincidindo com o centro do fundo
da piscina, conforme a figura. O raio da ilha de lazer será
r. Deseja-se que após a construção dessa ilha, o espaço
destinado à água na piscina tenha um volume de, no
3
mínimo, 4 m .
Considere 3 como valor aproximado para π.
Para satisfazer as condições dadas, o raio máximo da ilha
de lazer r, em metros, estará mais próximo de
A) 1,6.
B) 1,7.
C) 2,0.
D) 3,0.
E) 3,8.
HAMILTON E ALEX
B) Uma pirâmide de base quadrada tem 4 faces
triangulares e, quando um plano intercepta essa pirâmide,
divide cada face em um triângulo e um trapézio. Logo, um
dos polígonos tem 4 lados.
C) Uma pirâmide de base quadrada tem 5 faces e a
interseção de uma face com um plano é um segmento de
reta. Assim, se o plano interceptar todas as faces, o
polígono obtido nessa interseção tem 5 lados.
D) O número de lados de qualquer polígono obtido como
interseção de uma pirâmide com um plano é igual ao
número de faces da pirâmide. Como a pirâmide tem 5
faces, o polígono tem 5 lados.
E) O número de lados de qualquer polígono obtido
interceptando-se uma pirâmide por um plano é igual ao
número de arestas laterais da pirâmide. Como a pirâmide
tem 4 arestas laterais, o polígono tem 4 lados.
13. (ENEM/2010) No manejo sustentável de florestas, é
preciso muitas vezes obter o volume da tora que pode ser
obtida a partir de uma árvore. Para isso, existe um método
prático, em que se mede a circunferência da árvore à
altura do peito de um homem (1,30 m), conforme indicado
na figura. A essa medida denomina-se "rodo" da árvore. O
quadro a seguir indica a fórmula para se cubar, ou seja,
obter o volume da tora em m 3 a partir da medida do rodo e
da altura da árvore.
11. (ENEM-2013)Uma cozinheira, especialista em fazer
bolos, utiliza uma forma no formato representado na
figura:
Nela identifica-se a representação de duas figuras
geométricas tridimensionais.
Essas figuras são
A) um tronco de cone e um cilindro.
B) um cone e um cilindro.
C) um tronco de pirâmide e um cilindro.
D) dois troncos de cone.
E) dois cilindros.
12. (ENEM/2009) Um artesão construiu peças de
artesanato interceptando uma pirâmide de base quadrada
com um plano. Após fazer um estudo das diferentes peças
que poderia obter, ele concluiu que uma delas poderia ter
uma das faces pentagonal.
Qual dos argumentos a seguir justifica a conclusão do
artesão?
A) Uma pirâmide de base quadrada tem 4 arestas laterais
e a interseção de um plano com a pirâmide intercepta
suas arestas laterais. Assim, esses pontos formam um
polígono de 4 lados.
Um técnico em manejo florestal recebeu a missão de
cubar, abater e transportar cinco toras de madeira, de
duas espécies diferentes, sendo
 3 toras da espécie I, com 3 m de rodo, 12 m de
comprimento e densidade 0,77 toneladas/m 3;
 2 toras da espécie II, com 4 m de rodo, 10 m de
3
comprimento e densidade 0,78 toneladas/m .
Após realizar seus cálculos, o técnico solicitou que
enviassem caminhões para transportar uma carga de,
aproximadamente,
A) 29,9 toneladas. B) 31,1 toneladas.
C) 32,4 toneladas. D)35,3 toneladas.
E) 41,8 toneladas.
14. (ENEM/2010) Em um casamento, os donos da festa
serviam champanhe aos seus convidados em taças com
formato de um hemisfério (Figura 1), porém um acidente
na cozinha culminou na quebra de grande parte desses
recipientes. Para substituir as taças quebradas, utilizou-se
um outro tipo com formato de cone (Figura 2). No entanto,
os noivos solicitaram que o volume de champanhe nos
dois tipos de taças fosse igual.
342
CURSO DE MATEMÁTICA
HAMILTON E ALEX
sentido da ponta para a cauda, é formada pela seguinte
sequência de sólidos:
A) pirâmide, cilindro reto, cone reto, cilindro reto.
B) Cilindro reto, tronco de cone, cilindro reto, cone equilátero.
C) cone reto, cilindro reto, tronco de cone e cilindro equilátero.
D) cone equilátero, cilindro reto, pirâmide, cilindro
E) cone, cilindro equilátero, tronco de pirâmide, cilindro.
Considere:
4
1
Vesfera  R 3 e Vcone  R 2h
3
3
Sabendo que a taça com o formato de hemisfério é
servida completamente cheia, a altura do volume de
champanhe que deve ser colocado na outra taça, em
centímetros, é de
A)1,33.
B) 6,00.
C)12,00. D)56,52.
E)113,04.
15. (ENEM/2009) Uma empresa que fabrica esferas de
aço, de 6 cm de raio, utiliza caixas de madeira, na forma
de um cubo, para transportá-las.
Sabendo que a capacidade da caixa é de 13.824 cm 3,
então o número máximo de esferas que podem ser
transportadas em uma caixa é igual a
A) 4.
B) 8.
C) 16
D) 24.
E) 32.
16. (ENEM/2010) Uma fábrica produz barras de
chocolates no formato de paralelepípedos e de cubos,
com o mesmo volume. As arestas da barra de chocolate
no formato de paralelepípedo medem 3 cm de largura, 18
cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas
descritas, a medida das arestas dos chocolates que têm o
formato de cubo é igual a
A) 5 cm.
B) 6 cm.
C) 12 cm. D) 24 cm
E) 25 cm.
17. (ENEM–2010) Numa feira de artesanato, uma pessoa
constrói formas geométricas de aviões, bicicletas, carros e
outros engenhos com arame inextensível. Em certo momento,
ele construiu uma forma tendo como eixo de apoio outro
arame retilíneo e rígido, cuja aparência é mostrada na figura
seguinte
18. (ENEM-2010) Dona Maria, diarista na casa da família
Teixeira, precisa fazer café para servir as vinte pessoas que se
encontram numa reunião na sala. Para fazer o café, Dona
Maria dispõe de uma leiteira cilíndrica e copinhos plásticos,
também cilíndricos.
Com o objetivo de não desperdiçar café, a diarista deseja
colocar a quantidade mínima de água na leiteira para encher
os vinte copinhos pela metade. Para que isso ocorra, Dona
Maria deverá
A) encher a leiteira até a metade, pois ela tem um volume 20
vezes maior que o volume do copo.
B) encher a leiteira toda de água, pois ela tem um volume 20
vezes maior que o volume do copo.
C) encher a leiteira toda de água, pois ela tem um volume 10
vezes maior que o volume do copo.
D) encher duas leiteiras de água, pois ela tem um volume 10
vezes maior que o volume do copo.
E) encher cinco leiteiras de água, pois ela tem um volume 10
vezes maior que o volume do copo.
19. (ENEM 2011) É possível usar água ou comida para
atrair as aves e observá-las. Muitas pessoas costumam
usar água com açúcar, por exemplo, para atrair beijaflores, Mas é importante saber que, na hora de fazer a
mistura, você deve sempre usar uma parte de açúcar para
cinco partes de água. Além disso, em dias quentes,
precisa trocar a água de duas a três vezes, pois com o
calor ela pode fermentar e, se for ingerida pela ave, pode
deixá-la doente. O excesso de açúcar, ao cristalizar,
também pode manter o bico da ave fechado, impedindo-a
de se alimentar. Isso pode até matá-la.
ciência Hoje das crianças. FNDE; Instituto Ciência Hoje, ano 19, n.
166, mar. 1996.
Ao girar tal forma em torno do eixo, formou-se a imagem de
um foguete, que pode ser pensado como composição, por
justaposição, de diversos sólidos básicos de revolução.
Sabendo que, na figura, os pontos B, C, E e F são
colineares, AB = 4FG, BC = 3FG, EF = 2FG, e utilizando se
daquela forma de pensar o foguete, a decomposição deste, no
Pretende-se encher completamente um copo com
a mistura para atrair beija-flores. O copo tem
formato cilíndrico, e suas medidas são 10 cm de altura e 4
cm de diâmetro, A quantidade de água que deve ser
utilizada na mistura é cerca de (utilize π(pi) = 3)
a) 20 mL.
b) 24 mL.
343
CURSO DE MATEMÁTICA
HAMILTON E ALEX
c) 100 mL.
d) 120 mL.
e) 600 mL.
20. (ENEM-2006) Uma artesã confecciona dois diferentes
tipos de vela ornamental a partir de moldes feitos com cartões
de papel retangulares de 20 cm x 10 cm (conforme ilustram as
figuras abaixo). Unindo dois lados opostos do cartão, de duas
maneiras, a artesã forma cilindros e, em seguida, os preenche
completamente com parafina.
Supondo-se que o custo da vela seja diretamente proporcional
ao volume de parafina empregado, o custo da vela do tipo I,
em relação ao custo da vela do tipo II, será
A)
B)
C)
D)
E)
o triplo.
o dobro.
igual.
a metade.
a terça parte.
GABARITO
01. D
02. B
03. D
04. D
05. C
06. D
07. B
08. C
09. E
10. A
11. D
12. C
13. A
14. B
15. B
16. B
17. C
18. A
19. C
20. B
344
CURSO DE MATEMÁTICA
GEOMETRIA ANALÍTICA
EIXOS COORDENADOS
Consideremos uma reta r e uma unidade (u) de
comprimento com a qual mediremos os segmentos
contidos em r.
r
HAMILTON E ALEX
Importante
1º) A abscissa de origem é o número real zero ou o ponto
( 0, 0 ).
2º) Cada ponto de um eixo possui uma única abscissa, e
para cada abscissa existe um único ponto no eixo, isto é,
estabelecemos uma relação biunívoca entre o conjunto
dos números reais e o conjunto de pontos de uma reta
(eixo).
u
Consideremos também na reta r um ponto
arbitrário, que chamaremos de origem.
O
r
u
Sejam A e A' dois pontos de r tais que AO e OA e
tenham a mesma medida a, tomada com a unidade u, de
modo que A esteja à direita de O e A' à esquerda de O.
A’
A
O
y ( Eixo das ordenadas )
r
x
( Eixo das abscissas )
Vamos fixar o sentido de O para A como o sentido
positivo e representá-lo com uma ponta de seta.
A
O
a
Consideremos em um plano dois eixos X e Y
perpendiculares entre si e com a origem O comum.
Nessas condições, dizemos que X e Y formam um
sistema cartesiano ortogonal, e o plano dotado com tal
sistema será chamado de plano cartesiano.
a
a
A’
O SISTEMA CARTESIANO
r
a
Desta forma, dizemos que o ponto A está afastado a
unidades de O e que A' está afastado a unidades de O.
Podemos então associar aos pontos A e A' os números reais a e
a, respectivamente, que chamaremos de abscissas desses
pontos.
Para localizarmos um ponto P num plano dotado de
um sistema cartesiano ortogonal, traçamos por P duas
retas paralelas aos eixos x e y que encontram os
mesmos em P' e P", respectivamente.
y
P’’
P( x, y ) Coordenada do ponto P
P’
De um modo geral, podemos associar a cada ponto de
r um único número real que chamamos abscissa do
ponto, número esse que será positivo para pontos
marcados a partir da origem, no sentido positivo, e
negativo para pontos marcados no sentido contrário.
Exemplo:
P
O
–3
Q
r
4
abscissa de P = – 3
abscissa de Q = 4
 Observe que o ponto P deve ser representado
como P(– 3, 0 ) e o ponto Q, como Q( 4, 0 ) .
A reta orientada com um sentido positivo, com uma
origem arbitrada e uma unidade de medida
estabelecida, é chamada de eixo.
x
P
Abscissa de P’ = + 1
Abscissa de P’’ = + 3
Indicamos a abscissa de P' por xp e a abscissa de
P" por yp e o ponto P é localizado no plano pelo par
ordenado (xp, yp).
Para facilidade de linguagem, usamos as seguintes
denominações:
1º) A abscissa de P', a primeira abscissa de P, será
simplesmente a abscissa de P.
2º) A abscissa de P", a segunda abscissa de P, será a abscissa
ordenada de P, ou simplesmente ordenada de P.
3º) O par ordenado ( xp , yp ) será denominado coordenadas de
P.
4º) Os eixos x e y serão, respectivamente, o eixo das
abscissas e o eixo das ordenadas.
345
CURSO DE MATEMÁTICA
HAMILTON E ALEX
Exemplo:
P2) Se um ponto tem abscissa negativa, ele pertence ao
2º ou ao 3º quadrante do plano cartesiano ou ao semieixo negativo Ox .
Indicamos a seguir as coordenadas dos pontos
representados no plano cartesiano.
y
y
P1(–1, 3)
A(2, 3) ; B(4, 0)
A
F
C(3, – 2) ; D(0, – 3)
B
E
x
P2(–3, 0)
x
E(– 3, – 1) ; F(– 1, 2 )
P3(–2, –2)
C
D
P3) Se um ponto tem ordenada positiva, ele pertence ao
Observe
que
todos
os
representados na forma P(x, y ).
Abscissa do ponto
pontos
são
1º ou ao 2º quadrante do plano cartesiano ou ao semi-eixo
positivo Oy .
y
P2(0, 4)
Ordenada do ponto
P3(–1, 3)
P1(2, 2)
P(x, y) é a coordenada do ponto.
x
Os eixos x e y dividem o plano cartesiano em quatro
regiões que chamamos quadrantes (Q), que são
numerados conforme a figura abaixo:
y
( 2º QUADRANTE )
Abscissa negativa
Ordenada positiva
( 1º QUADRANTE )
Abscissa positiva
Ordenada positiva
x
( 3º QUADRANTE )
Abscissa negativa
Ordenada negativa
( 4º QUADRANTE )
Abscissa positiva
Ordenada negativa
P4) Se um ponto tem ordenada negativa, ele pertence ao
3º ou ao 4º quadrante do plano cartesiano ou ao semieixo negativo Oy .
y
x
P1(2, –2)
P3(–1, –2)
P2(0, – 4)
PROPRIEDADES DOS PONTOS DO PLANO
CARTESIANO
P1) Se um ponto tem abscissa positiva, ele pertence ao
1º ou ao 4º quadrante do plano cartesiano ou ao semieixo positivo Ox .
P5) Se um ponto tem abscissa nula, ele pertence ao eixo
y.
y
P1(0, 3)
P2(0, 2)
x
y
P3(0, –2)
P1(1, 3)
x
P2(3, 0)
P6) Se um ponto tem ordenada nula, ele pertence ao eixo
x.
y
P3(2, 2)
x
P1(–2, 0)
P1(4, 0)
346
CURSO DE MATEMÁTICA
P7) Se vários pontos têm a mesma abscissa a, eles
pertencem à reta paralela ao eixo y, traçada pela abscissa
a.
y
HAMILTON E ALEX
P12) Dois pontos simétricos em relação ao eixo Y têm a
mesma ordenada e abscissas opostas.
y
A’( 1, 2)
A(– 1, 2)
P1(a, 3)
P2(a, 1)
B’( 2, –1)
B(– 2, –1)
P3(a, –2)
P8) Se vários pontos têm a mesma ordenada a, ele
pertence à reta paralela ao eixo x, traçada pela ordenada
y
a.
P1(–2, a)
x
x
a
P13) Dois pontos simétricos em relação à origem têm
abscissas opostas e ordenadas opostas.
y
P3(3, a)
P2(1, a)
A(3, 1)
a
x
x
A’(–3, –1)
P9) Se um ponto tem coordenadas iguais, ele pertence à
reta bissetriz dos quadrantes ímpares.
y
P1(2, 2)
PONTOS ESPECIAIS DO PLANO
CARTESIANO
P2(1, 1)
x
PONTO PERTENCENTE AO EIXO “X”
P3(–3, –3)
Se um ponto do plano cartesiano pertencer ao eixo x,
este ponto sempre será representado por P(x, 0).
P10) Se um ponto tem coordenadas opostas, ele
pertence à reta bissetriz dos quadrantes pares.
y
y
P1(–2, 2)
x
P(x, 0)
P2(–1, 1)
P(x, 0)
x
P3(3, –3)
P11) Dois pontos simétricos em relação ao eixo x têm a
mesma abscissa e ordenadas opostas.
PONTO PERTENCENTE AO EIXO “Y”
Se um ponto do plano cartesiano pertencer ao eixo y,
este ponto sempre será representado por P(0, y).
y
A(–1, 2)
y
B(2, 1)
P(0, y)
x
x
B’(2, –1)
P(0, y)
A’(–1, –2)
347
CURSO DE MATEMÁTICA
PONTO PERTENCENTE À RETA BISSETRIZ DOS
QUADRANTES ÍMPARES
HAMILTON E ALEX
RETAS VERTICAIS
y
x = a ou x – a = 0
Se um ponto do plano cartesiano pertencer à reta
bissetriz dos quadrantes ímpares, este ponto sempre
será representado por P(a, a).
x
a
y
P(a, a)
x
RETA BISSETRIZ DOS QUADRANTES ÍMPARES
P(a, a)
y
Y = x ou y – x = 0
PONTO PERTENCENTE À RETA BISSETRIZ DOS
QUADRANTES PARES
x
Se um ponto do plano cartesiano pertencer à reta
bissetriz dos quadrantes pares, este ponto sempre será
representado por P(a, – a).
y
RETA BISSETRIZ DOS QUADRANTES PARES
P(a, – a)
y
x
Y = – x ou y + x = 0
P(a, – a)
PONTO PERTENCENTE A UMA RETA QUALQUER
Se um ponto do plano cartesiano pertencer a reta do tipo
y = mx + n, este ponto sempre será representado por
P(x, mx + n).
y
x
RETA MEDIATRIZ DE UM SEGMENTO AB
y = mx + n
É a reta que passa pelo ponto médio do segmento AB e é
perpendicular a esse segmento.
P(x, mx + n)
x
B
A
RETAS ESPECIAIS DO PLANO CARTESIANO
RETAS HORIZONTAIS
A reta mediatriz também pode ser definida como o lugar
geométrico do plano cartesiano dos infinitos pontos
eqüidistantes de dois pontos dados.
y
a
Reta mediatriz do segmento AB
Y = a ou Y – a = 0
B
x
A
348
CURSO DE MATEMÁTICA
DISTÂNCIA ENTRE DOIS PONTOS
HAMILTON E ALEX
2) Um ponto P(a, 2) é equidistante dos pontos A(3, 1) e
B(2, 4). Calcular a abscissa do ponto P.
Teorema de Pitágoras: Em um triângulo retângulo, o
quadrado da medida da hipotenusa a é igual à soma dos
quadrados das medidas dos catetos b e c, isto é,
a
b
a2 = b2 + c2
c
Dados os pontos A=(xA, yA) e B=(xB, yB) obtemos a
distância entre A e B, traçando as projeções destes
pontos sobre os eixos coordenados, obtendo um triângulo
retângulo e usando o Teorema de Pitágoras.
Y
B
YB
DAB
DAB
( YB – YA )
YA
( YB – YA )
COORDENADAS DO PONTO MÉDIO DE UM
SEGMENTO DE RETA
Se A(xA, yA) e B(xB, yB) são extremos de um segmento
de reta, as coordenadas do ponto médio M(xM, yM) desse
segmento é obtida com a média aritmética das
coordenadas dos pontos A e B.
A
( XB – XA )
XB
XA
Demonstração
X
B
( XB – XA )
M
2. xM = xA + xB
A
2
xM + xM = xA + xB
2
( DAB ) = ( XB – XA ) + ( YB – YA )
2
xA
DAB =
X B  X A 2  YB  YA 2
DAB =
 X 2   Y 2
Importante:
É fácil verificar que a fórmula para o cálculo da distância
entre dois pontos A e B continua válida quando AB for
paralelo a um dos eixos cartesianos, ou mesmo quando
A e B coincidem, caso em que DAB = 0.
EXEMPLOS
1) Prove que o triângulo com vértices A(– 2, 4), B(–5,1)
e C(–6,5) é isósceles.
xM
xB
(xM – xA)=(xB – xM)
xM =
x A  xB
2
O “yM” é obtido de forma análoga.
Logo as coordenadas do ponto médio M(xM, yM) é obtida
com a fórmula:
y A  yB
 x A  xB
,
2
2

M = 



EXEMPLOS
1) Os pontos A(1, 3), B( 6, 3) e C(7, 1) são os vértices
de um triângulo ABC. Encontre a medida da mediana
relativa ao lado AC desse triângulo.
349
CURSO DE MATEMÁTICA
2) Determinar o simétrico do ponto A(3,5) em relação ao
ponto Q(9,6).
HAMILTON E ALEX
ÁREAS DE POLÍGONOS
Consideremos um polígono convexo A1, A2, A3, A4, ...,
An, com vértices A1( x1, y1 ), A2( x2, y2 ), ... , An( xn, yn )
lidos no sentido anti-horário.
y
A5
A4
A6
A3
A7
COORDENADAS DO BARICENTRO DE UM
TRIÂNGULO
Em um triângulo qualquer, define-se baricentro como
o ponto de encontro das medianas. No plano cartesiano, o
par ordenado G(xG, yG) correspondente ao baricentro de
um triângulo de vértices A(xA, yA), B(xB, yB) e C(xC, yC)
possui coordenadas dadas por:
xG 
x A  xB  x c
3
e
yG 
y A  yB  y c
3
A2
An
A1
Para calcularmos a área da região limitada pelo polígono,
podemos dividi-lo em (n – 2) triângulos, conforme a figura.
y
A5
A4
A6
A3
An – 1
A2
An
Como o ponto G(xG, yG) é o baricentro, temos que:
 x A  x B  x C y A  yB  y C 
,

3
3


G= 
x
A1
x
Assim a área S do polígono será:
S = SA1,A2,A3 + SA1,A3,A4 + SA1,A4,A5 + ... + SA1,An-1,An
y
yB
yG
yC
yA
Desenvolvendo SA1,A2,A3, SA1,A3,A4, SA1,A4,A5e assim até
SA1,An-1,An, teremos que a área S será a metade do
B
módulo do determinante formado pelos vértices
do polígono.
G
C
A
xA
S
xB xG
xC
x
EXEMPLO
1) Se G é o baricentro de um triângulo cujos vértices
são os pontos A(– 2, 1 ), B( 6, 2 ) e C( 2, 6 ),
encontre a medida do segmento AG .
DET
2
Se o determinante for igual a zero é por que os pontos
que seriam os vértices do polígono, estão alinhados.
EXEMPLO
1) Achar a área do quadrilátero de vértices T( 0, 5 ), Q(3,
8), R(2, O) e P(4, 3).
350
CURSO DE MATEMÁTICA
2) Encontre as coordenadas dos pontos pertencentes à
reta y = 2x + 2 e que determinam com os pontos
A(2, 1) e B(3, 2) um triângulo de área 5.
HAMILTON E ALEX
Exercícios
1) ( Cesgranrio ) A distância entre os pontos M(4, – 5) e
N(–1, 7) do plano xoy vale:
a)
b)
c)
d)
e)
CONDIÇÃO PARA QUE
FIQUEM ALINHADOS
TRÊS
PONTOS
Observe o triângulo ABC e sua área.
B
A
C
Quando os vértices A, B e C tendem a ficarem
alinhados, a área do triângulo tende a zero.
B
A
A
A
B
B
C
C
C
Como a área tende a zero, conseqüentemente o
determinante também tenderá a zero.
DET = 0
Logo, a condição para que pontos fiquem alinhados é que
o determinante formado por esses pontos seja igual a
zero.
Observe que, para três pontos determinar um
triângulo, esses pontos não podem ficar alinhados,
logo DET ≠ 0.
EXEMPLO
1) O gráfico abaixo é de uma reta que relaciona o nível
de água em um reservatório em função do tempo. No
instante 5 horas, qual o nível da água no reservatório ?
Nível ( Metros )
3
4
14
13
12
9
8
2) ( UFF – RJ ) Os valores que r deve assumir para que
o ponto P(r, 2) diste 5 unidades do ponto K(0, –2)
são:
a) r = 2 e r = – 2
b) r = 3 e r = – 3
c) r = 1 e r = – 1
d) r = 4 e r = – 4
e) r = 5 e r = – 5
3) ( UFPR ) Suponha que duas partículas P e Q se
movem no plano cartesiano, de modo que em cada
instante t a partícula P está no ponto (2t, 3 – t) e
a partícula Q está no ponto (4t, 3t – 2). Com
base
nessas informações, avalie as seguintes
afirmativas:
I. As partículas colidem uma com a outra no instante
t = 5/4
II. Ambas as partículas passam pelo ponto (4, 1)
III. No instante t = 1, a distância entre as partículas é
5
Determine a alternativa correta
A) somente as afirmativas II e III são verdadeiras
B) somente a afirmativa II é verdadeira
C) somente a afirmativa III é verdadeira
D) somente a afirmativa I e II são verdadeiras
E) as três afirmativas são verdadeiras
4) ( U.C. Salvador ) Os vértices de um triângulo são
dados pelos pontos no plano cartesiano: A(–3, 4),
B(3, 12) e C(18, 4). O menor lado desse triângulo
mede:
a) 7
b) 9
c) 10
d) 13
5) ( Fuvest – SP ) O ponto do eixo das abscissas,
eqüidistante aos pontos P(–2, 2) e Q(2, 6) é:
a) (2, 0)
b) (5, 0)
c) (3, 0)
d) (0, 2)
e) (4, 0)
Tempo ( Horas )
351
CURSO DE MATEMÁTICA
6) Um grande vale é cortado por duas estradas retilíneas
E1
e
E2, que se cruzam perpendicularmente,
dividindo-o em quatro quadrantes. Duas árvores que
estão num mesmo quadrante têm a seguinte
localização: a primeira dista 300 metros da estrada
E1 e 100 metros da estrada E2, enquanto a segunda
se encontra a 600 metros de E1 e a 500 metros de
E2. A distância entre as duas árvores é:
A) 200 metros
B) 300 metros
C) 400 metros
D) 500 metros
E) 600 metros
7) ( UFES ) As coordenadas do ponto médio de um
segmento AB são (–1, 2). Sabendo-se que as
coordenadas do ponto A são (2, 5), então as
coordenadas de B são:
a) (4, 1)
b) (4, – 1)
c) (– 4, 1)
d) (– 1, – 4)
e) n.d.a
8)
(UFMG) Considere A(2, 1) e B(4, 0) dois pontos no
plano coordenado. As coordenadas do ponto C,
simétrico do ponto A em relação ao ponto B, são:
a) (6, –1)
b) (3, 1)
c) (2, –1)
d) (3, 1/2)
e) (1, 0)
9) (Cesgranrio – RJ) Os pontos M, N, P e Q do R2 são
vértices de um paralelogramo situado no primeiro
quadrante. Se M(3, 5), N(1, 2) e P(5, 1) então o
vértice Q é:
a) (7, 4)
b) (6, 5)
c) (9, 8)
d) (8, 6)
e) (6, 3)
10) ( Unimontes – PAES ) Considere o triângulo com
vértices nos pontos A(–1, 1), B(3, 2) e C(0, 5). Se M e
N são os pontos médios dos lados AC e BC,
respectivamente, então a medida do segmento MN é
igual a:
15
17
a)
b)
2
2
3
5
c)
d)
2
2
11) ( PUC – SP ) O triângulo
B(6, –2) e C(–11, –3) é:
de
vértices
HAMILTON E ALEX
a)
b)
c)
d)
e)
eqüilátero
isósceles
acutângulo
obtusângulo
retângulo
12) ( UFMT ) Os vértices de um triângulo são os pontos
A( 1, 4 ) , B( 4, 9 ) e C( 10, 15 ) . O comprimento
da mediana AM relativa ao lado BC é :
a) 17
b) 13
c) 10
d) 9
e) 8
13) ( MACK – SP ) No triângulo ABC, A(1, 1) é um dos
vértices, N(5, 4) é o ponto médio de BC e M(4, 2) é
o ponto médio de AB. Calcule as coordenadas dos
vértices B e C e o baricentro do triângulo.
14) ( Mack – SP ) Sabendo que os pontos A(6, 0), B(0,6)
e C(0, 0) são vértices do triângulo ABC, que M é
ponto médio do lado BC e que G é o baricentro do
triângulo, a área do triângulo GMB vale:
a) 6
b) 3
c) 3/2
d) 18
e) 12
15) ( FMU – SP ) Dados os pontos A(–1, 1), B(1, –1),
C(2, 1) e D(1, 2), a área do quadrilátero ABCD é
igual a:
a) 12
b) 10
c) 8
d) 9/2
e) 4
16) ( Unimontes – 2006 ) A área do pentágono, cujos
vértices são A( 0, 0 ), B( 3, 0 ), C( 5, 2 ), D( 5, 5 ) e E(
0, 3 ), é igual a :
a) 18
b) 36
c) 17
d) 35
A(4, 3),
352
CURSO DE MATEMÁTICA
HAMILTON E ALEX
25
e seus
2
vértices são ( 0, 1 ), ( 2, 4 ) e ( – 7, k ). Um possível
valor de k é :
a) 3
b) 2,5
c) 2
d) 4
e) 5
P, onde deve ocorrer a reflexão de um raio de luz que
vai do ponto A ao ponto B.
18) ( MACK – SP ) Dados os pontos A(2, 3), B(3, 4),
C(4, 6), D(2, 4), E(3, 8) e F(k, 1), se os triângulos
ABC e DEF têm mesma área, então um dos valores
de k é :
a) 0
b) 1
c) 2
d) 3
e) 4
23) ( PAES 2003 / Unimontes ) No jogo de bilhar, é
comum um jogador usar a tabela para atingir uma
bola. Nessas ocasiões, seu parceiro pode auxiliá-lo,
indicando o simétrico da bola que será atingida em
relação à tabela. Para isso, o parceiro mede a
distância dessa bola até a tabela e a repete da tabela
para fora da mesa, conforme figura abaixo.
17) ( Mack – SP ) A área de um triângulo é
19) ( PAES 2005 / Unimontes ) O gráfico abaixo nos
fornece o valor a ser pago pelo consumo de água, em
certa residência. Conforme o gráfico, para o consumo
de 28 m3, o valor a ser pago é de
a) R$ 36,80
Preço em R$
b) R$ 28,80 24
c) R$ 12,80
16
d) R$ 44,80
y
A
B
x
P
O jogador mira, então, o ponto indicado pelo parceiro e,
por tabela, acerta a bola que deseja.
8
3
Consumo em m
10
20
30
20) (Fatec – SP) Os pontos A(1, 4), B e C(5, –2) estão
numa mesma reta. Determine o ponto B, sabendo que
o mesmo é do eixo x.
21) ( FGV – SP ) Uma reta passa pelos pontos ( 3, 5 ) e
( 4, 8 ). Portanto, o valor da ordenada de um ponto
dessa reta cuja abscissa vale 10 é:
a) 17
b) –19
c) 19
d) – 26
e) 26
22) ( Unimontes – 2004 ) Considere, no plano cartesiano,
os pontos A(1, 4), B(6, 2) e P(x, y) como indicado
na figura abaixo. Determine as coordenadas do ponto
Agora, suponha que, colocando sobre a mesa um sistema
cartesiano, conforme a figura acima, e que nesse sistema
as coordenadas da bola lançada sejam (10,40) e as da
bola que se pretende atingir sejam (100,20), as
coordenadas do ponto onde a bola lançada deve bater na
tabela para depois acertar a bola que se quer atingir são
A) (60,0).
B) (70,0).
C) (90,0).
D) (80,0).
24) ( Unimontes – PAES / 2008 ) Um raio luminoso parte
do ponto A(3, 10) e reflete-se no ponto B(7, 0),
conforme a figura abaixo. A equação da reta suporte
do raio refletido é
y
A) 2x – 5y – 35 = 0.
A
B) 5x – 2y + 35 = 0.
10
C) 5x – 2y – 35 = 0.
D) 5x + 2y + 35 = 0.
3
B
x
353
CURSO DE MATEMÁTICA
HAMILTON E ALEX
25) ( Cesgranrio ) Uma barra de ferro com temperatura
inicial de –10°C foi aquecida até 30°C. O gráfico
anterior representa a variação da temperatura da
barra em função do tempo gasto nessa experiência.
Calcule em quanto tempo, após o início da
experiência, a temperatura da barra atingiu 0°C.
a) 1 min
Temperatura (ºC )
b) 1 min 5 seg
30
c) 1 min e 10 seg
d) 1 min e 15 seg
e) 1 min e 20 seg
Tempo (Min.)
5
8
5
5

8
8
5
b) 
c)
d)
4) ( Mack – SP ) A figura mostra os gráficos de y = x2 e
2
y = – x + P. A distância do ponto A até o ponto B
é:
y
a) 2 5
–10
A
b) 4 5
26) (Unimontes – PAES 2009 ) Na figura abaixo, MNOP
é um quadrado de lado 4 e OQRS é um quadrado
de lado 3. A abscissa do ponto T onde a reta
intercepta o eixo das abscissas é:
y
a) – 24/7
b) – 12
M
P
R
c) – 24
Q
d) – 32/7
S
O
N
c)
6
2
d) 3 6
MR
B
x
0
e) 5 2
GABARITO
x
1) B
2) B
3) A
4) C
7) E
8) A
9) A
10) B
EXERCÍCIOS EXTRAS
1) ( FEEQ – CE ) A distância entre os pontos A(cos a,
sen a) e B(sen a, – cos a) é:
a) 1
b)
2
c)
3
d) 2
2) ( ITA – SP ) Três pontos de coordenadas,
respectivamente (0, 0), (b, 2b) e (5b, 0), com b > 0,
são vértices de um retângulo. As coordenadas do
quarto vértice são dadas por
a) ( – b, – b )
b) ( 2b, – b )
c) ( 4b, – 2b )
d) ( 3b, – 2b )
e) ( 2b, – 2b )
13) B(7, 3); C(3, 5); G(
16) A
17) A
22) P(
25) D
26) C
13
, 0)
3
6) D
11) E
11
, 3)
3
18) B
21) E
5) E
19) A
23) B
14) B
12) C
15) D
20) B(11/3, 0)
24)C
Extras
1) B
2) C
3) B
4) A
3) ( UFMG ) Sejam A e B dois pontos da reta de
equação y = 2x + 2, que distam duas unidades da
origem.
Nesse caso, a soma das abscissas de A e B é:
a)
5
8
354
CURSO DE MATEMÁTICA
EQUAÇÃO DA RETA
DETERMINAÇÃO DE UMA RETA
Uma reta r fica determinada quando ela é única, ou seja,
quando as características apresentadas por essa reta são
suficientes para que se possa afirmar com exatidão qual é
a reta em questão. Existem, basicamente, duas formas de
se determinar uma reta:
HAMILTON E ALEX
determinante formado por esses pontos será igual a zero.
( DET = 0 )
EXEMPLO
1) Encontre a equação da reta
cartesiano abaixo.
y
r
indicada no plano
r
3
2
1ª forma: Dois pontos distintos determinam uma reta.
Se conhecermos dois pontos distintos de uma reta, em
um plano cartesiano, essa reta será única e, logo poderá
ser identificada por sua equação.
y
r
A
x
3
1
2) Encontre a área do triângulo ABO determinado pelos
eixos coordenados e pela reta r de equação y = – 2x
+ 6, indicado na figura abaixo.
B
y
x
B
2ª forma: Um ponto conhecido dessa reta e a inclinação
da mesma.
Se temos, no plano cartesiano, um ponto P de uma reta
e sabemos, de uma forma qualquer a inclinação dessa
reta, podemos encontrar a equação dessa reta.
Encontre, no plano cartesiano, a reta r que passa pelo
ponto P e é paralela à reta t que contém os pontos
distintos A e B, conforme a figura abaixo.
y
t
A
x
O
r
INCLINAÇÃO DE UMA RETA
Chamamos de inclinação de uma reta r com o eixo
horizontal a medida de um ângulo específico medido a
partir do referido eixo, no sentido anti-horário.
A
Observe abaixo alguns ângulos formados com o eixo Ox.
B
P
y
y
y
x
Fig. 1
Fig. 2
Observe que a reta r acima está determinada, pois
ela é única.
EQUAÇÃO DE UMA RETA QUANDO SE TÊM
DOIS PONTOS CONHECIDOS
B
r
x
x
O
y
Observe na figura abaixo que os pontos distintos A e B
determinam a reta r, e que essa reta é um conjunto de
infinitos pontos P(x, y) alinhados.
A



O
P
Fig. 3
Fig. 4
y
y
Fig. 5
Fig. 6

O
x

O
x
O
x

O
x
(x, y)
(xB, yB)
(xA, yA)
Se pegarmos os pontos A(xA, yA), B(xB, yB) e um ponto
P(x, y) qualquer dessa reta é fácil observar que esses
pontos estão alinhados e que, conseqüentemente, o
Observe que nas figuras acima, apenas nos gráficos 3 e
6, a abertura angular
 realmente corresponde à
inclinação da reta.
355
CURSO DE MATEMÁTICA
HAMILTON E ALEX
INCLINAÇÃO DA RETA
das ordenadas de A e B pela variação das abscissas
de A e B .
Seja
r
uma reta do plano cartesiano ortogonal
concorrente com o eixo Ox no ponto P(xp, 0) e que
passa pelo ponto Q(xQ, yQ), com yQ> 0. Seja M(xM, 0),
com xM> xp.
Y
r
B
YB
Chama-se inclinação da reta r à medida , com 0º ≤
< 180º do ângulo MPˆ Q orientado à partir do PM no
sentido anti-horário, como nos gráficos abaixo.
( XB – XA )

A
YA

XA
Q
Q

P
O

M
x
O
m = tg 
Quando conhecemos a
inclinação da reta
m = tg  
m=
m
1) Encontre a medida da inclinação, em graus, de cada
reta abaixo.
y
ou
c)
120º
O
45º
x
O
x
120º
y
O
x
C.O
C.A
yB  y A
xB  x A
y
b)
a)
x
x
M
P
EXEMPLO
y
XB
( XB – XA )
y
y
( YB – YA )

( YB – YA )
m
Quando conhecidos
dois pontos da reta
y
x
Atenção com o sentido das diferenças de x e y,
que devem ser o mesmo.
y
d)
EXEMPLOS
e)
1) Encontre o valor do coeficiente angular, de cada reta
abaixo.
O
x
O
x
y
a)
COEFICIENTE ANGULAR DE UMA RETA
Dados os pontos A(xA,yA) e B(xB,yB), com xA ≠ xB, o
coeficiente angular m da reta que passa por estes pontos
m = tg 
Analisando os pontos A(xA, yA) e B(xB, yB) de
uma reta r no plano cartesiano, pode-se verificar que o
coeficiente angular da reta r será a razão da variação
y
c)
120º
x
O
é o número real tal que m  tg  , onde é a inclinação
da reta.
Quando conhecido o
ângulo da inclinação
da reta
y
b)
d)
O
O
45º
y
e)
x
O
x
O
x
120º
y
x
356
CURSO DE MATEMÁTICA
2) Encontre o valor do coeficiente angular, das retas
abaixo.
y
a)
(1, 2)
(4, 3)
x
3
PONTOS ONDE CURVAS SE
INTERCEPTAM
y
b)
(3, 4)
O
HAMILTON E ALEX
x
O
Se duas curvas C1 e C2têm um ou mais pontos comuns,
isto é, se interceptam em um ou mais pontos, esses
pontos são obtidos encontrando-se os pontos onde essas
curvas são iguais, montando-se o sistema entre as
equações das curvas C1 e C2.
EXEMPLOS DE INTERSECÇÃO DE CURVAS
EQUAÇÃO DE UMA RETA QUANDO SE TÊM
UM PONTO E O COEFICIENTE ÂNGULAR
s Para se encontrar o ponto P(xP, yP), onde
Se uma reta passa por um ponto P(x0, y0) e possui um
coeficiente angular m, a equação dessa reta será obtida
através da fórmula do próprio coeficiente angular.
m
y  y0
y
m 
x
x  x0
P
r

r
B
Logo a equação fundamental da reta será
as retas r e s se interceptam,
 equação de r

monta-se o sistema 

equação de s
A
Para se encontrar os pontos A(xA, yA) e
B(xB, yB), onde a reta r e a parábola 
se interceptam, monta-se o sistema

 equação de r
equação de 


( y – y0 ) = m.( x – x0 )

Para se encontrar o ponto A(xA, yA), onde a
reta r e a parábola  se interceptam,
r
 equação de r

monta-se o sistema 

equação de 
EXEMPLOS
1) Encontre a equação da reta que passa pelo ponto P(
2
2, – 3 ) e cujo coeficiente angular é m =  .
5
A

B
A
2) Encontre a equação da reta
cartesiano abaixo.
r
indicada no plano
Para se encontrar os pontos A(xA, yA) e
B(xB, yB), onde a reta r e a circunferência 
r
se interceptam, monta-se o sistema
 equação de r

equação de 


y

r
(4, 3)
A
135º
O
x
Para se encontrar o ponto A(xA, yA), onde a
circunferência  se interceptam,
monta-se o sistema

 equação de r
equação de 


r reta r e a
357
CURSO DE MATEMÁTICA
EXEMPLO
1) Encontre as coordenadas dos pontos A e B onde a
2
reta ( r ) y – 2x + 6 = 0 e a parábola ( ) y = x – 5x
+ 4 se interceptam.
HAMILTON E ALEX
b) Equação Reduzida da Reta
Vimos que uma equação da reta r que passa pelo ponto
P(x0, y0) e tem coeficiente angular igual a m é y – y0=
m(x –xo). Isolando a variável y nessa equação, obtemos:
y = mx + y0 – m.x0
Fazendo y0 – m.x0= q, podemos escrever:
y = mx + q
FORMAS DA EQUAÇÃO DA RETA
Introdução
No plano cartesiano, a reta que passa pelo ponto P(x0,y0)
e tem coeficiente angular m pode ser representada pela
equação fundamental y–y0= m(x– x0); e a reta vertical
que passa pelo ponto P(x0,y0)pode ser representada pela
equação x = x0.
Embora essas equações sejam suficientes para a
representação de qualquer reta do plano, é útil conhecer
outras
formas
de
apresentação
dessas
equações.Veremos que cada uma dessas formas tem
uma utilidade específica; por exemplo, a equação geral
da reta pode representar qualquer reta do plano: oblíqua,
horizontal ou vertical - e, por isso, é chamada de geral; a
equação
reduzida
apresenta
explicitamente
o
coeficiente angular e o coeficiente linear da reta; a
equação segmentária apresenta explicitamente as
coordenadas dos pontos de intersecção da reta com os
eixos coordenados; e as equações paramétricas da reta
permitem o estudo da variação de cada variável em
função de um parâmetro.
Essa equação é chamada de equação reduzida da reta
r.
Note, que nesse formato, o coeficiente de x na equação
é exatamente o coeficiente angular m da reta. O termo
independente de x, o termo q, é o coeficiente linear da
reta.
O coeficiente angular é uma constante responsável pela
inclinação da reta, é ele quem determina se uma reta é
crescente ou decrescente.
O coeficiente linear é uma constante que indica o ponto
onde a reta intercepta o eixo das ordenadas ( eixo y).
Coeficiente Angular
Toda reta do plano cartesiano é gráfico de uma
equação da forma ax +by + c = 0 , em que x e y são
variáveis e a, b e c são números reais com a e b não
simultaneamente nulos. Essa equação é chamada de
equação geral da reta.
EXEMPLOS
1) Escreva as equações das retas abaixo na forma geral.
a) 2x – 3y = 4
b) y = 3x – 4
c)
Coeficiente Linear
Interpretação Geométrica
y
a) Equação Geral da Reta
Equação da reta
na forma reduzida
y = mx + q
y
r
r
y = mx + q
q
q
y = mx + q
x
Figura 1
x
Figura 2
Observe que na figura 1, a reta r é crescente porque o
coeficiente angular da reta é positivo(m > 0) e na figura 2,
a reta r é decrescente porque o coeficiente angular é
negativo( m < 0 )
Observe nas figuras 1 e 2, que o valor q
representa o ponto P( 0, q ) onde a reta intercepta o eixo
y.
2x y
 4
3 2
358
CURSO DE MATEMÁTICA
EXEMPLOS
d)
1) Escreva as equações das retas abaixo na forma
reduzida e identifique o coeficiente angular e o
coeficiente linear de cada uma delas.
a) 2x – 3y = 6
b)
HAMILTON E ALEX

x y
 1
2 5
2) Encontre a equação segmentária da reta r em cada
gráfico abaixo
y
a)
2x y
 2
3 2
y
b)
r
r
3
1
2) Escreva a equação da reta ( r ) x – 2y = 6 na forma
reduzida e faça a representação geométrica da
mesma.
c) Equação Segmentária da Reta
x
2
–2
x
3) Passe a equação da reta (r) 2x – y – 4 = 0 para a
forma segmentária e encontre as coordenadas dos
pontos onde essa reta intercepta os eixos
coordenados.
Consideremos a reta r que intercepta os eixos
coordenados nos pontos p( p, 0 ) e q( 0, q ) conforme a
figura abaixo.
y
r
q
x y
 1
p q
(0, q)
(p, 0)
p
x
x y
Observe que, na equação da reta na forma   1 , os
p q
números p e q são, respectivamente, os valores onde a
reta r intercepta os eixos x e y.
EXEMPLOS
1) Faça um esboço do gráfico de cada reta abaixo e
encontre as coordenadas dos pontos onde a reta
intercepta os eixos coordenados.
x y
a)
 1
2 4
d) Equação Paramétrica da Reta
São equações equivalentes à equação geral da reta,
da forma x = f( t ) e y = f( t ), que relacionam as
coordenadas x e y dos pontos da reta com um parâmetro
t.
 x  t1
Assim, por exemplo, 
, com t  R, são
y  t  3
equações paramétricas de uma reta r.
Para obter a equação geral dessa reta a partir das
paramétricas, basta eliminar o parâmetro t das duas
equações:
Isolando t na primeira equação, temos: t = x – 1
Substituindo esse valor em y = – t + 3, temos:
b)
x y
 1
2 3
y = –( x – 1 )+ 3
y=–x+1+3
c)

x y
 1
3 2
x+y–4=0
( equação geral de r)
359
CURSO DE MATEMÁTICA
EXEMPLOS
HAMILTON E ALEX
Retas Paralelas Iguais ( Coincidentes )
1) Encontre o coeficiente angular e o coeficiente linear
 x  t2
da reta r cuja equação paramétrica é 
.
 y  2 t  1
Se duas retas r e s, do plano cartesiano, possuem
mesma inclinação ( mesmo coeficiente angular ) e mesmo
coeficiente linear, elas são paralelas iguais
ou
coincidentes.
y
mr = ms ( Os coeficientes
angulares são iguais )
r=s
q1 = q2
2) Encontre uma equação paramétrica da reta r cuja
equação é 2x – y + 1 = 0
x
q1 = q2 ( Os coeficientes lineares
são iguais, pois são retas
coincidentes )
Na forma reduzida, as retas paralelas iguais, possuem a
mesma equação.
Ex.: As retas ( r ) y = 3x – 2 e ( s ) y = 3x – 2 são retas
coincidentes.
POSIÇÕES RELATIVAS ENTRE DUAS
RETAS
Retas Paralelas Distintas
Se duas retas distintas r e s, do plano cartesiano,
possuem mesma inclinação ( mesmo coeficiente angular )
elas são paralelas distintas.
y
q1
r
s
q2
x
Na forma geral, as retas paralelas iguais, são
caracterizadas por possuírem os coeficientes de x, os
coeficientes de y e os termos independentes iguais ou
múltiplos entre si.
Ex.: As retas ( r ) x – 3y + 2 = 0 e ( s ) 2x – 6y + 4 = 0
são coincidentes pois suas equações são múltiplas.
mr = ms ( Os coeficientes
angulares são iguais )
Retas Concorrentes
q1 ≠ q2 ( Os coeficientes lineares
são diferentes, pois são retas
distintas )
Se duas retas distintas r e s, do plano cartesiano,
possuem inclinações diferentes, elas se interceptam em
um único ponto desse plano e são chamadas de retas
concorrentes.
Como as inclinações das retas concorrentes são
diferentes, seus coeficientes angulares também são
diferentes.
Na forma reduzida, as retas paralelas distintas, são
caracterizadas por possuírem o mesmo coeficiente
angular e por terem os coeficientes lineares diferentes.
Ex.: As retas y = 2x – 3 e y = 2x – 1 são paralelas
distintas pois possuem o mesmo coeficiente angular e os
coeficientes lineares são diferentes.
As retas r e s abaixo são paralelas distintas:
y
r
s
x
mr ≠ ms ( Os coeficientes angulares
são diferentes )
“Se duas retas r e s possuem
coeficientes angulares diferentes elas
são concorrentes”
diferentes
y = mx + q
e
y = mx + n
Ex.: As retas ( r ) y = 5x – 2 e ( s ) y = 3x + 1 são retas
concorrentes.
iguais
360
CURSO DE MATEMÁTICA
Retas Concorrentes Perpendiculares
Se duas retas distintas r e s,do plano cartesiano, são
concorrentes e o ângulo formado por elas for igual a 90º,
elas são retas concorrentes perpendiculares.
Os
coeficientes
angulares
de
duas
retas
perpendiculares são diferentes, mas o produto desses
coeficientes é igual a “ – 1 ”.
y
mr ≠ ms ( Os coeficientes
angulares são diferentes )
r
s
HAMILTON E ALEX
EXERCÍCIOS
1) ( MACK – SP ) A equação da reta que passa pelos
pontos A( 3, 1 ) e B( – 2, 0 ) é:
a) – 5y + x – 2 = 0
b) 5y – x – 2 = 0
c) – x – 5y + 2 = 0
d) – 5y – x – 2 = 0
2) (UCS – RS) A figura contém a representação gráfica
y
da reta:
a) 2x – 3y + 6 = 0
4
b) 2x + 3y – 6 = 0
mr . ms = – 1
x
Quando duas retas distintas r e s são concorrentes
perpendiculares
pode-se dizer que o coeficiente
angular de uma é igual ao oposto do inverso do
coeficiente angular da outra.
mr . ms = – 1
mr =
1
ms
EXEMPLO
1) Sejam as retas ( r ) y = 2x – 3, ( s ) 2x – 3y = 6 e ( t
) 3x + 2y – 4 = 0. Qual a posição relativa entre essas
retas ?
2) Encontre a equação da reta que passa pelo ponto P(
– 1, 3 ) e é perpendicular à reta ( r ) 2x – 5y + 2 = 0.
c) 3x – 2y + 6 = 0
2
3
d) 2x – 3y – 2 = 0
x
3) ( MACK – SP ) A equação da reta r é dada por:
a) y – 2x – 2 = 0
y
r
b) y – x – 2 = 0
c) y + 2x + 2 = 0
x
d) y – 2x – 2 = 0
–1
e) y – 2x + 2 = 0
–2
4) ( PUC – SP ) Na figura a seguir tem-se representada,
em um sistema de eixos cartesianos ortogonais, a
rota de uma aeronave, de uma cidade M a uma
cidade N, passando sobre as pequenas cidades A e
B.
Se os quatro pontos pertencem à reta de equação
4x – 3y + 1200 = 0, a distância entre as cidades A e
B, em quilômetros, é de aproximadamente:
A) 50
B) 500
C) 800
D) 5000
E) 8000
5) (UFES) O valor de K para que a equação Kx –
y – 3K + 6 = 0 represente a reta que passa pelo
ponto P(5, 0) é:
a) 3
b) – 9
c) 9
d) –3
e) – 6
6) (PUC – SP) A equação geral da reta pelo ponto
P( –3, 2 ) e coeficiente angular m é:
a) mx + y + 3m = 0
b) mx – y + 2 + 3m = 0
361
CURSO DE MATEMÁTICA
c) x + my + 2 = 0
d) x – my + 3m = 0
7) ( UFRN ) O comandante de um barco resolveu
acompanhar a procissão fluvial do Círio – 2002,
fazendo o percurso em linha reta. Para tanto, fez uso
do sistema de eixos cartesianos para melhor
orientação. O barco seguiu a direção que forma 45º
com o sentido positivo do eixo x, passando pelo
ponto de coordenadas (3, 5). Este trajeto ficou bem
definido através da equação:
A) y = 2x – 1
B) y = – 3x + 14
C) y = x + 2
D) y = – x + 8
E) y = 3x – 4
8) ( UnB ) O Coeficiente angular da reta
é:
a)
b)
c)
d)
e)
3y  5
2
5x  5
3/5
1
3
5
10/3
9) ( UnB ) A reta que passa pelos pontos ( 1, 3 ) e
( 5, –1 ) intercepta o eixo y no ponto:
a) (0, 1)
b) (0, 2)
c) (0, 3)
d) (0, 4)
e) (0, 5)
10) ( UFRN ) Em termologia existem várias escalas
termométricas, isto é, escalas nas quais se pode
indicar a temperatura de um corpo ou ambiente.
Às vezes é necessário converter as unidades
indicadas nessas várias escalas. Sendo C os
valores das temperaturas dadas em graus Celsius
e F os valores das temperaturas dadas em graus
Fahrenheit. Sabendo que o ponto de fusão da água é
0ºC ou 32ºF sendo representado pelo ponto A(0, 32)
e o ponto de ebulição é 100ºC ou 212ºF sendo
representado pelo ponto B(100, 212), encontre a
equação de conversão de unidades Fahrenheit e
Celsius de temperatura, ou seja, a equação da reta
que passa pelos pontos A e B.
A) 9C – 5F + 160 = 0
B) 5C – 9F + 160 = 0
C) 9C – 9F – 160 = 0
D) 5C – 9F – 160 = 0
E) 5C + 9F – 160 = 0
HAMILTON E ALEX
11) ( Unimontes – PAES ) Duas formigas, F1e F2,
deslocam-se, no plano cartesiano, sobre as curvas de
equações y = 3x – 2 e y = x2 – 2x + 4,
respectivamente. Sabendo-se que essas formigas se
encontram em dois pontos dessas curvas, é correto
afirmar que esses pontos são
a) ( 2, 4 ) e ( 3, 4 )
b) ( 4, 2 ) e ( 3, 7 )
c) ( 2, 4 ) e ( 3, 7 )
d) ( 4, 2 ) e ( 7, 3 )
12) (UFRGS) As retas r e s da figura interceptam-se no
ponto de ordenada:
y
r
a) 3/2
s
3
b) 5/3
c) 7/4
1
d) 9/5
1
–
2
e) 11/6
x
13) ( UFBA ) Na figura, a distância de P ao eixo das
y
ordenadas é:
a) 1,5
6
b) 2,5
P
c) 3,5
d) 4
x
e) 5
1
6
–1
14) ( FMJ – SP ) Na figura, as retas r e s interceptamse no ponto A, sendo os pontos B e C as
interseções da reta t com os semi-eixos OY e OX,
respectivamente. Encontre o valor da área do
r
y
triângulo ABC.
s
A
a) 1
b) 1,5
c) 2
B
1
d) 2,5
C
e) 3
x
–2
1
–2
t
15) ( Esam – RN ) A equação da reta que tem
coeficientes angular e linear, respectivamente,
2
iguais a
e –1 é:
3
a) x + 3y – 5 = 0
b) 2x – 3y – 3 = 0
c) 2x – 3y + 3 = 0
2
d) y = – x +
3
2
e) y = x
3
362
CURSO DE MATEMÁTICA
16) ( ESPM ) Até o ano de 2000, a inflação num
certo
país
manteve-se
em
4% ao
ano,
aproximadamente. A partir daí sofreu aumentos
sucessivos de 2% ao ano, até 2002, declinando
novamente em 2003, conforme mostra o gráfico
abaixo. Segundo previsões otimistas de que esse
declínio se manterá constante pelos próximos anos,
pode-se esperar que a inflação volte ao patamar de
4% no ano de:
A) 2008
B) 2009
C) 2011
D) 2012
E) 2010
HAMILTON E ALEX
a equação da reta que passa por
perpendicular a AB.
a) 2x + y – 3 = 0
b) 2x – y – 3 = 0
c) 2x – y – 7 = 0
d) x + 2y – 3 = 0
e) x – 2y – 3 = 0
C
e
é
22) ( MACK – SP ) A reta r, determinada por A(2, –5) e
B(3, k), tem coeficiente angular 2k. A equação da
reta s paralela a r e que passa pela origem é:
a) 10x + y = 0
b) x – 10y = 0
c)10x – y – 25 = 0
d) y = 10x
e) y = x
17) ( UCB ) São dadas as retas r: 2x – 4y – 5 = 0, s:
– x + 2y – 3 = 0 e t:4x + 2y – 1 = 0, é correto afirmar
que :
a) r // s e s // t
b) r // s e s  t
c) s // t e r  s
d) r  s e s  t
e) r // t e r  s
23) ( UFES ) A equação da reta que passa pelo ponto
de intersecção das retas x + y – 1 = 0 e 2x – y = 0
e é paralela à bissetriz dos quadrantes ímpares é:
a) 3x – 3y – 3 = 0
b) 3x – 3y + 1 = 0
c) 3x – 3y – 1 = 0
d) 3x + 3y + 1 = 0
e) 3x – 3y + 3 = 0
18) ( PAES 2006 / Unimontes ) Ao traçar o mapa do bairro
da escola Delta, os alunos da 3ª série do ensino
médio nomearam as ruas com equações, conforme
suas posições. Qual a posição das ruas
representadas pelas equações r1 e r2, sendo r1: 3x
+ 2y – 1 = 0 e r2: 2x + 3y + 4 = 0 ?
a) Concorrentes
b) Paralelas
c) Reversas
d) coincidentes
24) ( PUC – RS ) Os pontos (2, 3) e (6, 7) são os
extremos da diagonal de um quadrado. A reta suporte
da outra diagonal é:
a) x – y + 9 = 0
b) x + y + 9 = 0
c) x – y – 9 = 0
d) x + y – 9 = 0
e) x – y + 1 = 0
19) ( UFRGS ) Dada a reta ( r ) = 2x – y + 1 = 0, a
equação da reta paralela a r pelo ponto P(1, 1) será:
a) 2x – y = 0
b) 2x – y + 2 = 0
c) 2x + y + 1 = 0
d) 2x + y – 1 = 0
e) 2x – y – 1 = 0
20) ( FEI – SP ) A equação da reta que passa pelo
ponto ( 1, 2 ) e é perpendicular a reta 3x – 2y + 2 = 0
é:
a) 2x – 3y + 5 = 0
b) 2x – 3y – 5 = 0
c) 2x – 3y – 4 = 0
d) 2x – 3y + 4 = 0
e) 2x + 3y – 8 = 0
25) ( Fuvest – SP ) Em relação a um sistema cartesiano
ortogonal, são dados os pontos A(3, 0) e B(1, 2). A
mediatriz do segmento AB é o conjunto dos pontos
P(x, y) cujas coordenadas satisfazem a equação:
a) x + y = 3
b) x + y = 0
c) x – y = 2
d) x + y = 2
e) x – y = 1
26) ( Unesp – 2001 ) Dada a reta r de equação 4x +
2y + 5 = 0 e o ponto P = (2, –1), determine :
a) O coeficiente angular de r ;
b) A equação da reta s que é perpendicular a r e
passa pelo ponto P.
21) ( Fuvest – SP ) No Plano cartesiano, são dados os
pontos A( –1, 2 ), B( 1, 3 ) e C( 2, –1). Determine
363
CURSO DE MATEMÁTICA
HAMILTON E ALEX
25
9
d) 4
c)
27) ( FEI – SP ) No gráfico abaixo, sabe-se que t  r e t
// s. Determine a equação da reta s e a equação da
reta t.
y
t
GABARITO
1) B 2) A 3) C 4) B 5) D 6) B 7) C 8) E 9) D
s
10) A 11) C 12) D 13) C 14) B 15) B 16) E
4
17) B 18) A 19) E 20) E 21) A 22) D 23) B
x
6
r
24) D
25) E
26) a) m = – 2; b) x – 2y – 4 = 0
27) (s) 3x – 2y = 18 e (t) 3x – 2y = 0
28) ( UFMG – 99 ) Observe a figura.
Nessa figura, ABCD é um paralelogramo, as
coordenadas do ponto C são (6, 10) e os lados AB e
AD estão contidos, respectivamente, nas retas de
x
equações y   14 e y = 4x – 2 .
2
28) D
Desafios
1) D
Nesse caso, as coordenadas do ponto B são:
y
a) (10, 19)
35
b) (7,
)
2
37
c)(9,
)
2
d) (8, 18
B
A
C
D
x
DESAFIO
1) ( Unimontes – PAES / 2007 ) Na figura abaixo, temos
esboço do gráfico da função logarítmica y =logax
e da reta r.
y
r
y =loga x
1
2
B
A
1
C
x
5
3
Se a inclinação da reta
segmento AB é
r é
7
, a medida do
10
8
e B está entre A e C, então o
21
valor de “a” é:
a) 2
b)
2
364
CURSO DE MATEMÁTICA
INEQUAÇÕES DO 1º GRAU NO PLANO
CARTESIANO
Chamamos de inequações do 1º grau às desigualdades
do tipo:
ax + by + c > 0 ; ax + by + c < 0 ; ax + by + c  0 ; ax
+ by + c ≤ 0
HAMILTON E ALEX
5º CASO: Inequação do tipo x ≤ k ou x – k ≤ 0
x≤k
y
x
Mas, para facilitar a análise geométrica, é melhor
representar as inequações na forma reduzida. Assim as
inequações serão do tipo :
y > ax + b ; y < ax + b ; y ax + b ; y ≤ ax + b
k
6º CASO: Inequação do tipo x  k ou x – k  0
xk
1º CASO: Inequação do tipo y ≤ k ou y – k ≤ 0
( onde k é um número real )
y
y
k
x
x
k
y≤k
2º CASO: Inequação do tipo y  k ou y – k  0
7º CASO: Inequação do tipo x < k ou x – k < 0
x<k
y
yk
y
k
x
3º CASO: Inequação do tipo y < k ou y – k < 0
k
x
y
k
x
y<k
8º CASO: Inequação do tipo x > k ou x – k > 0
x>k
4º CASO: Inequação do tipo y > k ou y – k > 0
y
y
y>k
k
x
k
x
365
CURSO DE MATEMÁTICA
HAMILTON E ALEX
9º CASO: Inequação do tipo y  ax + b
EXEMPLOS
y
y
y  ax + b
b
1) Faça a representação geométrica das inequações
abaixo:
a) y  0
y  ax + b
b
x
x
b) x ≤ 0
10º CASO: Inequação do tipo y > ax + b
y
y
y > ax + b
b
y > ax + b
b
c) x + y < 0
x
x
11º CASO: Inequação do tipo y ≤ ax + b
d) 2x – y > 4
y
b
y
x
b
x
y ≤ ax + b
2) Encontre um sistema de inequações que represente a
região indicada no plano cartesiano abaixo.
y
y ≤ ax + b
(4, 6)
3
x
12º CASO: Inequação do tipo y < ax + b
y
b
x
y
y < ax + b
b
x
y < ax + b
366
CURSO DE MATEMÁTICA
EXERCÍCIOS
1) ( Unimontes – 2005 ) Entre as regiões assinaladas nos
gráficos abaixo, marque a que melhor representa a solução
y4


do sistema de inequações 
x3
3x  4 y  37

a)
b)
y
7
4
4
c)
7
7
4
4
7
7
x
r
C
1
–1
x
y
7
B
2
A
3
d)
3
y
4
x
y
4) ( FCMSC – SP ) Considere os pontos A, B, C e D
que definem as retas r e s, conforme a figura.
Assinale a alternativa cujo conjunto de desigualdades
descreve a região indicada :
a) x ≥ 0 ; x – 2y + 3 ≥ 0 ; 2x + 3y ≥ 12
b) x ≥ 0 ; x – 2y + 3 ≤ 0 ; 2x + 3y ≤ 12
c) x ≥ 0 ; x + 2y – 3 ≤ 0 ; 2x – 3y ≤ 12
d) x ≥ 0 ; x – 2y + 3 ≤ 0 ; 2x – 3y ≥ 12
e) x ≤ 0 ; x – 2y + 3 ≥ 0 ; 2x + 3y ≤ 12
y
7
3
HAMILTON E ALEX
3
D
5 6
x
s
GABARITO
1) C
3
7
2) A
3) D
4) B
x
2) ( PUC – SP ) O semi-plano hachurado é o conjunto
dos pontos ( x, y ) tais que :
y
a) x ≥ 2y – 2
b) x ≥ – 2y – 2
c) y ≤ x + 2
1
d) x ≤ 2y + 2
x
e) y ≥ + 1
–2
x
2
3) A região sombreada no gráfico abaixo pode ser
representada pelo conjunto de inequações :
a) y  0 ; x  0 ; x  4 ; 3x + 2y  18
b) y  0 ; x  0 ; x  4 ; 3x + 2y  18
c) y  0 ; 2x  3x ; 3x + 2y  18
d) y  0 ; x  0 ; x  4 ; 3x + 2y  18
e) y  0 ; x  0 ; x  4 ; 3x + 5y  18
y
(4, 3)
0
4
6
x
367
CURSO DE MATEMÁTICA
DISTÂNCIA DE PONTO À RETA
A distância de um ponto P(xP, yP) à uma reta ( r ) ax +
by + c = 0, pode ser analisada como a distância desse
ponto P a um ponto específico P’ dessa reta r, onde
esse ponto P’ é a projeção ortogonal de P(xP, yP) sobre
a reta r.
HAMILTON E ALEX
2) Encontre a medida da altura relativa ao lado AB no
triângulo ABC abaixo.
B(3, 5)
A(1, 2 )
C(5, 0)
P’
( r ) ax + by + c = 0
P(xP, yP)
A distância de um ponto P(xP, yP) à uma reta ( r ) ax +
by + c = 0, também pode ser vista como o menor caminho
que liga o ponto P(xP, yP) à reta r.
DISTÂNCIA ENTRE DUAS RETAS
PARALELAS
FÓRMULA DA DISTÂNCIA DE UM PONTO “P” À
UMA RETA ( r )
Se ( r ) ax + by + k = 0 e ( t ) ax + by + w = 0, são duas
retas paralelas e distintas do plano cartesiano, a distância
entre essas retas é a mesma distância de um ponto
qualquer da reta ( r ) até a reta ( t ).
Dado um ponto P(xP, yP) e uma reta cuja equação geral
é ( r ) ax + by + c = 0, a fórmula que nos dá a distância do
ponto P à reta r está indicada baixo.
( r ) ax + by + k = 0
P
( t ) ax + by + w = 0
P’
( r ) ax + by + c = 0
( Equação geral )
P(xP, yP)
a.x P  b.y P  c
DP, r =
a2  b2
Encontrando um ponto P(xP, yP) qualquer, que pertença à
reta r, e calculando a distância desse ponto P à reta t,
encontramos, conseqüentemente, a distância entre as
retas r e t.
FÓRMULA DA DISTÂNCIA ENTRE DUAS RETAS
PARALELAS
Para encontrar a distância entre duas retas paralelas,
basta dividir a diferença em módulo das constantes das
equações pela raiz quadrada da soma dos quadrados dos
coeficientes dos termos de primeiro grau das equações.
EXEMPLO
1) Qual a distância do ponto P(1, –2) à reta r cuja
equação é y = –2x + 5?
( r ) ax + by +
P
( t ) ax + by +
D P,
r

k
=0
w
=0
w k
a2  b2
368
CURSO DE MATEMÁTICA
EXEMPLO
HAMILTON E ALEX
5) ( Ufac ) A distância entre as retas paralelas r e s
representadas no gráfico é :
1) Encontre o perímetro do quadrado ABCD abaixo,
sabendo que seus lados opostos estão contidos nas
retas r e s, conforme figura.
y
r
s
8
( r ) x + 2y + 8 = 0
B
A
( s ) x + 2y + 3 = 0
–6
x
7
C
D
EXERCÍCIOS
1) ( UFPA ) Qual é a distância da origem do sistema de
coordenadas à reta y = – x + 2 ?
a) 1
b)
c)
a)
b)
6) ( Mack – SP ) A equação da bissetriz de um dos
ângulos formados pelas retas r: x – y + 2 = 0 e
s: x + y – 2 = 0 é :
a) x = y
b) x = – y
c) x = 2
d) y = 2
e) y = 0
7) ( PUC – SP ) As equações das retas que contêm os
2
lados de um triângulo ABC são AB :x + y – 5 = 0,
3
BC :x + 7y – 7 = 0 e CA : 7x + y + 14 = 0.
A equação da bissetriz do ângulo interno em B é :
a) 3x + 6y – 4 = 0
b) 3x + 6y – 10 = 0
c) 3x + 6y – 16 = 0
d) 3x + 6y – 18 = 0
e) 3x + 6y – 20 = 0
2
3
2) ( Cesgranrio ) O ponto A(–1, –2) é um vértice de um
triângulo eqüilátero ABC, cujo lado BC está sobre
a reta de equação x + 2y – 5 = 0. Determine a
medida h da altura desse triângulo.
3) ( Fuvest – SP ) Seja r a reta que passa pelo ponto
P( 3, 2 ) e é perpendicular à reta s, de equação y =
– x+ 1. Qual é a distância entre o ponto A( 3, 0 ) e a
reta r ?
4) ( Mack – SP ) A equação da reta paralela a y = x ,
com distância 2 do ponto P( 1, 2 ) e que passa
pelo 2º quadrante é :
a) x – y + 3 = 0
b) x – y – 1 = 0
c) x – y – 2 = 0
d) x – y + 1 = 0
e) x – y + 2 = 0
8) ( UFPR ) A distância entre as retas paralelas 4x –
3y – 4 = 0 e 4x – 3y – 14 = 0 é:
a) 2
b) 4
c) 5
d) 10
e) 18
9) ( Fuvest – SP ) Calcule a distância entre a retar1, de
equação 3y = 4x – 2, e a reta r2, de equação 3y =
4x + 8, sabendo que r1 // r2.
10) A área de um quadrado de lado AB na reta r: x + y
+ 1 = 0 e lado CD na reta s: x + y + 3 = 0 é :
a) 2
b) 3
c) 4
d) 5
e) 6
369
CURSO DE MATEMÁTICA
GABARITO
1) B
2) h = 2 5
6) D
7) C
8) A
HAMILTON E ALEX
EQUAÇÃO DA CIRCUNFERÊNCIA
3)
2
9) 2 u.c
4) A
5) 5,6
10) 2 u.A
EQUAÇÃO REDUZIDA
Circunferência é o conjunto de todos os pontos de um
plano eqüidistantes de um ponto fixo, desse mesmo
plano, denominado centro da circunferência:
P
r
C
Assim, sendo C(xC, yC) o centro e P(x, y) um ponto
qualquer da circunferência, a distância de “C“ a “P“ é o
raio dessa circunferência. Então:
y
P(x, y)
y
r
( y - yC)
yC
C(xc, yc)
xC
x
x
(x - xC)
Onde:
“r“ é o raio da circunferência.
“xC“ é a abscissa do centro.
“yC“ é a ordenada do centro.
C(xC, yC) é a coordenada do centro.
P(x, y) é um ponto qualquer da circunferência.
r
(y - yC)
(x - xC)
2
2
r = (x – xC ) + (y – yC )
2
Equação reduzida de uma circunferência com centro
no ponto (xC, yC ) e com raio “r”
(x – xC )2 + ( y – yC )2 = r 2
Equação de uma circunferência com Centro
( 0, 0 ) “origem” e raio “r”
x 2 + y2 = r2
370
CURSO DE MATEMÁTICA
HAMILTON E ALEX
EXEMPLOS
EQUAÇÃO GERAL
1) Encontrar a equação reduzida de uma circunferência
A equação geral de uma circunferência é obtida à partir
do desenvolvimento de sua equação reduzida.
com centro no ponto (3, – 2) e com raio igual a
5.
Como sabemos, a equação reduzida de
circunferência é (x – xC )2 + ( y – yC )2 =
Desenvolvendo essa equação, temos:
uma
r 2.
x 2 – 2.xC.x + xC2 + y 2 – 2.yC.y + yC2 = r2
2) Encontrar a equação reduzida da circunferência de
centro “C” representada no plano cartesiano abaixo.
x 2 + y 2 – 2xC.x – 2yC.y + xC2 + yC2 – r2 = 0
k
y
x 2 + y 2 – 2xC.x – 2yC.y + k = 0
2
C
x
–3
Observe que as constantes
xC2, yC2 e
representadas por uma única constante k.
r2 serão
Onde : K = xC 2 + yC 2 – r2
3) Encontre as coordenadas do centro e a medida do
raio das circunferências cujas equações estão abaixo:
a) ( x – 2 )2 + ( y – 4 )2 = 9
2
2
2
r = xC + yC – k
r=
x C2  yC2  k
b) ( x + 5 )2 + ( y – 3 )2 = 3
EXEMPLOS
c) x2 + ( y – 1 )2 = 4
1) Encontre as coordenadas do centro e a medida do
raio das circunferências cujas equações estão abaixo:
a) x2 + y2 – 4x + 6y – 3 = 0
d) ( x + 7 )2 + y2 = 5
2
2
e) x + y = 8
4) Encontre a equação reduzida da circunferência com
centro no ponto (2, 1) e que passa pelo ponto (3, – 2).
2
2
b) x + y + 8x – 2y + 1 = 0
c) 2x2 + 2y2 – 8x + 4y – 8 = 0
d) – x2 – y2 – 8x + 4y + 13 = 0
2) Encontre o valor do raio da circunferência cuja
2
2
equação é x + y – 5x = 3.( x – 2y – 3 ).
371
CURSO DE MATEMÁTICA
HAMILTON E ALEX
2
3) Se R é o raio da circunferência cuja equação é x +
2
y – 2x = 16, então
a) 2
b) 4
c)
2
d)
4
17
e)
4
4
R é:
RECONHECENDO A EQUAÇÃO DE UMA
CIRCUNFERÊNCIA
2
2
Nem toda equação do tipo Ax + By + Cx + Dy + k = 0,
representa uma circunferência. Para que as equações
desse tipo possam representar uma circunferência temos
que verificar se ela satisfaz as condições abaixo.

Os coeficientes de x2e y2
diferentes de zero.( A = B )

Não pode existir o termo que possua xy.

devem ser iguais e
O raio não pode ser negativo nem nulo.
 x C2  yC2  k > 0
r>0
2) Encontre a soma dos possíveis valores naturais que
P pode assumir na equação x2 + y2 – 4x – 2y + P = 0
para que ela represente uma circunferência.
INEQUAÇÕES ENVOLVENDO
CIRCUNFERÊNCIAS
A equação de uma circunferência, quando representada
geometricamente, será a curva que nos dá o contorno de
um círculo no plano cartesiano. Já uma inequação de
uma
circunferência,
quando
representada
geometricamente, será uma superfície (área) do plano
cartesiano.
Teremos abaixo a representação geométrica de algumas
inequações de circunferências no plano cartesiano.
1º CASO: INEQUAÇÃO ( ≤ )
(x – xC )2 + ( y – yC )2 ≤ r 2
y
x C2  y C2 – k > 0
x
EXEMPLOS
1) Verifique se as equações abaixo representam ou não
equações de circunferências.
a) x2 – y2 + 2x – 6y – 2 = 0
2º CASO: INEQUAÇÃO ( < )
2
2
(x – xC ) + ( y – yC ) < r
2
y
2
2
b) x + 2y + 2x – 8y – 4 = 0
x
2
2
c) x + y – 2xy – 4y – 5 = 0
3º CASO: INEQUAÇÃO ( ≥ )
d) x2 – y2 + 2x – 6y – 2 = 0
2
2
(x – xC ) + ( y – yC ) ≥ r
2
y
e) x2 + y2 – 4x – 2y + 6 = 0
x
372
CURSO DE MATEMÁTICA
4º CASO: INEQUAÇÃO ( > )
y
HAMILTON E ALEX
3º CASO:( = ) O ponto pertence à circunferência
Observe que a distância do
centro C ao ponto P é
igual ao raio.
(x – xC )2 + ( y – yC )2 > r 2
C
DCP
P
C
DCP = raio
x
EXEMPLO
1) Verifique a posição dos pontos A( 1, 0), B(3, 2) e
C(2, –3) em relação à circunferência cuja equação é
2
2
x + y – 4x + 2y + 1 = 0.
EXEMPLO
1) Faça a representação geométrica da solução do
sistema de inequações abaixo:
(x  3)2  (y  4)2  1

(x  3)2  (y  4)2  4
POSIÇÕES DE UMA RETA EM RELAÇÃO À
UMA CIRCUNFERÊNCIA
POSIÇÕES RELATIVAS
POSIÇÕES DE UM PONTO EM RELAÇÃO À UMA
CIRCUNFERÊNCIA
Em relação a uma circunferência  de centro C(xC, yC) e
raio r, um ponto P(x, y) pode ser externo, interno ou
pertencer à circunferência.
Para identificar cada uma dessas posições, basta
substituir as coordenadas do ponto P na equação da
circunferência, obtendo assim uma desigualdade que
pode ser ( > ) ou ( < ), se for obtido uma igualdade é por
que o ponto pertence à circunferência.
Em relação a uma circunferência  de centro C(xC, yC) e
raio r, uma reta y = mx + n pode ser exterior, secante
ou tangente à circunferência.
Se um ponto P pertence à circunferência e à reta s, as
suas coordenadas satisfazem ao mesmo tempo, as
equações de e s. Por isso, para identificar essas
posições, basta resolver o sistema formado pelas
equações da circunferência e da reta s. Isolamos o valor
de x ( ou de y ) na equação da reta e o substituímos na
equação da circunferência. Obtemos uma equação do 2º
grau em y ( ou em x ) e, a seguir, analisamos o sinal do
seu discriminante .
1º CASO:( = 0 ) A reta é tangente
s
P
C
1º CASO:( > ) O ponto é exterior à circunferência
Observe que a distância
do centro C à reta “s” é
igualao raio.
C
C
DCP
P
C
Observe que a distância
do centro C ao ponto P é
maior que o raio.
DCP > raio
2º CASO:( < ) O ponto é interior à circunferência
C
P
C
DCP
Observe que a distância do
centro C ao ponto P é
menor que o raio.
DCP < raio
DCs
DCs = raio
=0
2º CASO:( < 0 ) A reta é exterior
s
P
C
C
DCs
< 0
Observe que a distância
do centro C à reta “s” é
maior que o raio.
DCs> raio
373
CURSO DE MATEMÁTICA
HAMILTON E ALEX
3º CASO:( > 0 ) A reta é secante
s
P
C
CIRCUNFERÊNCIAS TANGENTES INTERNAS
Observe que a distância
do centro C à reta “s” é
menor que o raio.
C
DCP
A distância entre os centros
das circunferências é igual
à diferença do raio maior
pelo raio menor.
R
r
D
DCs< raio
D=R–r
Observe que:
>0
D+r=R
Logo: D = R – r
CIRCUNFERÊNCIAS INTERIORES
EXEMPLO
1) Qual a posição relativa entre a reta y = 2x – 3 e a
circunferência x2 + y2 + 4x – 2y + 1 = 0 ?
A distância entre os centros
das circunferências é igual
à diferença do raio maior
pelo raio menor.
R
D
r
D<R–r
Observe que:
D+r<R
Logo: D < R – r
POSIÇÕES RELATIVAS
CIRCUNFERÊNCIAS
ENTRE
DUAS
CIRCUNFERÊNCIAS SECANTES
Considere uma circunferência  1, com equação (x – x1 )
+ ( y – y1 )2 = r12 e outra circunferência 2, com equação
(x – x2 )2 + ( y – y2 )2 = r22. Essas circunferências podem
ocupar as seguintes posições relativas: externas,
tangentes, internas e secantes.
2
R
r
D
A distância entre os centros
das circunferências é menor
que a soma e maior que a
diferença dos raios.
R–r<D<R+r
Para identificar essas posições, vamos considerar “ D
”como sendo a distância entre os centros de 1 e 2.
CIRCUNFERÊNCIAS EXTERNAS
R
r
D
A distância entre os centros
das circunferências é maior
que a soma dos raios.
D>r+R
CIRCUNFERÊNCIAS TANGENTES EXTERNAS
R
r
D
A distância entre os centros
das circunferências é igual
à soma dos raios.
D=r+R
374
CURSO DE MATEMÁTICA
EXERCÍCIOS
1) Faça a representação geométrica das circunferências
cujas equações são:
2
2
a) ( x – 1 ) + ( y + 4 ) = 1
b)
2
6) ( PUC – RS ) O ponto P(–3, b) pertence à
circunferência de centro C(0, 3) e raio r = 5. Quais
os valores de b ?
a) –14 e 20
b) –20 e 14
c) 8 e 2
d) –7 e 1
e) 7 e –1
7)
2
(x+1) +(y–3) =9
2
HAMILTON E ALEX
( UFMG ) Determine a equação da circunferência na
qual os pontos A(2,  3 )
diametralmente opostos.
e
B(0,
3 ) são
2
c) x + ( y – 2 ) = 4
8) ( Mack – SP ) Determine o centro e o raio da
circunferência x2 + y2 – 6x – 16 = 0 .
2) ( Unifor – CE ) O centro e o raio de uma
2
2
circunferência de equação (x – 2) + (y – 3) = 4
são, respectivamente:
a) ( 4, 9 ) e 2 b) (–2, –3 ) e 2
c) ( 2, 3 ) e 4
d) (–2, –3 ) e 4
e) ( 2, 3 ) e 2
3) ( UFBA ) Sendo M(–5, 0) e N(1, 0), a equação da
circunferência abaixo é:
y
a) (x + 2)2 + y2 = 9
b) (x – 2)2 + y2 = 9
c) x + (y – 2)2 = 9
2
2
d) (x – 2) + y = 4
x
2
2
M
N
C
e) x + y = 4
2
4) ( PUC – SP ) O ponto da circunferência (x – 2) + (y +
4)2 = 4 que tem ordenada máxima é:
a) (2, – 4)
b) (2, – 2)
c) (2, – 6)
d) (– 4, 2)
e) (– 4, 4)
5) ( Cesgranrio – RJ ) Uma equação da circunferência
de centro (– 3, 4) e que tangencia o eixo x é:
a) ( x – 3 )2 + ( y – 4 )2 = 16
b) ( x – 3 )2 + ( y – 4 )2 = 9
2
2
c) ( x + 3 ) + ( y + 4 ) = 16
2
2
d) ( x + 3 ) + ( y – 4 ) = 9
e) ( x + 3 )2 + ( y – 4 )2 = 16
9) ( Fuvest – SP ) O segmento AB é diâmetro da
circunferência de equação x2 + y2 – 10y = 0. Se A é
o ponto (3, 1), então B é o ponto:
a) (– 3, 9)
b) (3, 9)
c) (0, 10)
d) (– 3, 1)
e) (1, 3)
10) ( UFPA ) O raio da circunferência x2 + y2 – 2x
= 3 é:
a) 2
d) 3
b) 3 e) 4
c) 2
11) ( FEI – SP ) Qual é o centro e o raio da circunferência
de equação x2 + y2 = 2( x – y ) + 1 ?
12) ( OSEC – SP ) Qual é a equação da circunferência
que passa pela origem e tem o ponto C( – 1, – 5
) como centro ?
a) x2 + y2 + 2x + 10y + 2 = 0
b) x2 + y2 – 2x – 10y = 0
2
2
c) x + y – 26 = 0
2
2
d) x + y + 2x + 10y = 0
e) n.d.a
375
CURSO DE MATEMÁTICA
13) ( FGV – SP ) Dado o ponto P(5, 4) e a circunferência
de equação x2 + y2 – 2x – 2y – 1 = 0. A equação da
circunferência concêntrica com a circunferência dada
que passa por P é:
2
2
a) x + y – 2x – 2y – 20 = 0
2
b) x + y2 – 2x – 2y – 21 = 0
c) x2 + y2 – 2x – 2y – 22 = 0
d) x2 + y2 – 2x – 2y – 23 = 0
2
2
e) x + y – 2x – 2y – 24 = 0
14) ( UECE ) A distância do ponto
P(–3, 8) à
circunferência x2 + y2 – 10x – 4y + 13 = 0 está
compreendida entre:
a) 7 e 9
b) 5 e 7
c) 3 e 5
d) 1 e 3
15) ( UFPA ) Qual das equações abaixo é equação de
uma circunferência ?
a) x2 + y2 + 1 = 0
b) x2 + y2 + 2x + 2y + 4 = 0
2
2
c) x + y + 2xy + 2x + 4y = 64
2
d) x + y2 + 2x – 4y = – 4
e) x2 +2xy + y2 = 32
16) ( UFPA ) O maior valor inteiro de P para que a
equação x2 + y2 – 6x + 4y + P = 0 represente uma
circunferência é :
a) 8
b) 10
c) 11
d) 12
e) 15
HAMILTON E ALEX
y
y
a)
b)
1
–1
1
0
1
2
x
–1
–1
0
2
1
2
x
–1
y
y
c)
d)
1
1
–1
1
0
1
2
x
–1
–1
0
x
–1
20) ( Unimontes – 2004 ) O esboço que melhor
representa a região do plano complexo dada por 1 ≤
|z −i | < 2, onde z = x + y i, com x e y em R, é
b)
a)
i
i
d)
c)
i
i
17) ( UFU – MG ) A condição para que x2 + y2 – 6x +
4y + 17 – m2 = 0 represente uma circunferência é:
a) m  – 2 ou m  2
b) m < – 2 ou m > 2
c) – 2 < m < 2
d) – 2 ≤ m ≤ 2
e) A equação não pode representar uma
circunferência
21) ( PUC – Campinas ) Sejam o ponto P(–3, 0), a reta r
de equação y = x + 6 e a circunferência C de
equação x2 + y2 – 4y = 0. É verdade que:
a) P pertence ao interior de C
b) P pertence a r
c) r e C não têm pontos em comuns
d) r e C interceptam-se em um único ponto
e) r e C interceptam-se em dois pontos
18) Represente no plano cartesiano a solução da
inequação x2 + y2 – 6x + 5 < 0.
22) ( UGF – RJ ) Qual deve ser o valor de K de modo
que o ponto P( 1, 0 ) pertença ao interior da
circunferência cuja equação é x2 + y2 – 2x – 2y – k =
0 ?
a) K = – 2
b) K > – 1
c) K < 1
d) K > 3
e) K = 5
19) ( Unimontes – 2005 ) Sejam os conjuntos A ={(x, y)
IR × IR | x2 + y2 ≥ 1} e B ={(x, y)  IR × IR | (x −1)2 +
y2 < 1}. A região hachurada, no plano cartesiano, que
melhor representa A∩B é :
23) ( F. Eng. Lorena ) O ponto P( 2 , 1 ), em relação à
2
2
circunferência 4x + 4y = 9, é:
376
CURSO DE MATEMÁTICA
a)
b)
c)
d)
e)
Externo
Pertencente
Interno
Centro
N.d.a
24) ( FEI – SP ) A reta x + y = 2 , em relação à
circunferência x2 + y2 = 1, é:
a) Secante sem possuir o centro
b) Secante passando pelo centro
c) Tangente
d) Exterior
e) nda
25) ( Uece – CE ) A equação da reta tangente à
circunferência x2 + y2 – 6x + 10y + 29 = 0 no ponto (
2, – 3 ) é:
a) x – 3y – 11 = 0
b) 2x + y – 1 = 0
c) x – 2y – 8 = 0
d) x + y + 1 = 0
e) nra.
26) ( Mackenzie – SP ) A curva x2 + y2 – 2x – 2y + 1 = 0
tem um único ponto comum com a reta x + y = k, k
 R. A soma dos possíveis valores de k é:
a) 4
b) – 2
c) – 4
d) 2
e) 0
27) ( UFPA ) As circunferências x2 + y2 – 4x + 3 = 0 e
2
2
x + y – 8x + 12 = 0, são:
a) exteriores
b) tangentes exteriores
c) tangentes interiores
d) concêntricas
e) secantes
28) ( Cesgranrio – RJ ) As circunferências x2 + y2 + 8x +
2
2
6y = 0 e x + y – 16x – 12y = 0, são:
a) exteriores
b) secantes
c) tangentes internamente
d) tangentes externamente
e) concêntricas
29) Na figura abaixo, a reta r intercepta os eixos
coordenados nos pontos ( 2, 0 ) e ( 0, 4 ). Encontre
a equação da circunferência indicada sabendo que
HAMILTON E ALEX
ela possui centro na origem e que é tangente à reta r
no ponto P.
EXERCÍCIOS EXTRAS
1) ( FGV – SP ) A equação da circunferência que passa
pelos pontos (3, 3) e (–1, 3) e cujo centro está no
eixo das abscissas é:
a) x2 + y2 = 1
b) x2 + y2 + 4x = 46
c) (x – 1)2 + y2 = 25
d) x2 + y2 – 2y = 10
e) x2 + y2 – 2x = 12
2) ( UFBA ) A intersecção da reta y + x – 1 = 0 com a
circunferência x2 + y2 + 2x+ 2y – 3 = 0, determina
uma corda cujo comprimento é:
a) 3 2
b) 2 3
c) 2 2
d)
2
3) ( UFJF – MG ) A corda determinada pelo eixo das
abscissas sobre a circunferência de equação x2 + y2
– 5x – 7y + 6 = 0 tem como medida:
a) 1 u.c
b) 3 u.c
c) 5 u.c
d) 9 u.c
e) 18 u.c
4) ( Unifor – CE ) Uma circunferência  é tangente
aos eixos coordenados e à reta de equação x =
3. Se o centro de  pertence ao quarto quadrante, a
equação de é :
a) 4 x2 + 4 y2 – 12x – 12y – 9 = 0
b) 4 x2 + 4 y2 + 12x – 12y – 9 = 0
c) 4 x2 + 4 y2 – 12x + 12y – 9 = 0
2
2
d) 4 x + 4 y + 12x – 12y + 9 = 0
2
e) 4 x + 4 y2 – 12x + 12y + 9 = 0
5) (ITA – SP) Num sistema de coordenadas cartesianas
ortogonais, considere a circunferência de equação
377
y
4
CURSO DE MATEMÁTICA
2
2
2x + 2y – 11x + 6y – 8 = 0. Qual é a equação da
circunferência tangente ao eixo das abscissas e com
o mesmo centro da circunferência dada ?
HAMILTON E ALEX
GABARITO
Equação da Circunferência
y
y
1) a)
1
b)
x
3
–4
x
–1
y
c)
2
6) ( Fuvest – SP ) Qual a equação da circunferência
tangente ao eixo dos x na origem e que passa pelo
ponto (3, 4) ?
x
2) E
3) A
4) B
7) ( x – 1 )2 + y2 = 4
9) A
7) ( Cesgranrio – RJ ) Faça o gráfico, no plano
complexo, do conjunto dos pontos z = x + yi, tais que
|z|≤1 e y0.
6) E
8) C( 3, 0 ) e R = 5
11) C( 1, – 1 ) e R =
10) C
12) D
5) E
13) D
14) B
15) D
3
16) D
17) B
y
18)
19) B
1
5
20) A
x
21) C
22) B
23) A
24) C
25) C
26) A
27) E
28) D
29) 5x 2 + 5y2 – 16 = 0
Exercícios Extras
8) ( Mack – SP ) Encontre as equações das retas que
passam pelo ponto P(2, 3) e que são tangentes à
circunferência de centro C( 0, 0 ) e raio 2.
1) E
2) D
3) A
2
4) E
2
11 
3
9

5)  x     y   
4 
2
4

2
2
6) 4x + 4y – 25y = 0
1
7)
–1
1
8) 5x – 12y + 26 = 0
e
x–2=0
378
CURSO DE MATEMÁTICA
QUESTÕES DO ENEM
01. (ENEM-2011) Um bairro de uma cidade foi planejado
em uma região plana, com ruas paralelas e
perpendiculares, delimitando
quadras
de
mesmo
tamanho. No plano de coordenadas cartesianas
seguinte, esse bairro localiza-se no segundo quadrante,
e as distâncias nos eixos são dadas em quilômetros.
HAMILTON E ALEX
A seguir, o professor representa corretamente os cinco
conjuntos sobre uma mesma malha quadriculada,
composta de quadrados com lados medindo uma unidade
de comprimento, cada, obtendo uma figura.
Qual destas figuras foi desenhada pelo professor?
A reta de equação y = x + 4 representa o planejamento
do percurso da linha do metrô subterrâneo que
atravessará o bairro e outras regiões da cidade. No
ponto P = (-5, 5), localiza-se um hospital público. A
comunidade solicitou ao comitê de planejamento que
fosse prevista uma estação do metrô de modo que sua
distância ao hospital, medida em linha reta, não fosse
maior que 5 km.
Atendendo ao pedido da comunidade, o comitê
argumentou corretamente que isso seria automaticamente
satisfeito, pois já estava prevista a construção de uma
estação no ponto
A) (–5, 0).
B) (–3, 1).
C) (–2, 1).
D) (0, 4).
E) (2, 6).
02. (ENEM-2013)Durante uma aula de Matemática, o
professor sugere aos alunos que seja fixado um sistema
de coordenadas cartesianas (x, y) e representa na lousa a
descrição de cinco conjuntos algébricos, I, II, III, IV e V,
como se segue:
I — é a circunferência de equação x2 + y2 = 9;
2
II — é a parábola de equação y = − x − 1, com x
variando de −1 a 1;
III — é o quadrado formado pelos vértices (−2, 1), (−1, 1),
(−1, 2) e (−2, 2);
IV — é o quadrado formado pelos vértices (1, 1), (2,1), (2,
2) e (1, 2);
V — é o ponto (0, 0).
379
CURSO DE MATEMÁTICA
HAMILTON E ALEX
03. (ENEM-2013) Nos últimos anos, a televisão tem
passado por uma verdadeira revolução, em termos de
qualidade de imagem, som e interatividade com o
telespectador. Essa transformação se deve à conversão
do sinal analógico para o sinal digital. Entretanto, muitas
cidades ainda não contam com essa nova tecnologia.
Buscando levar esses benefícios a três cidades, uma
emissora de televisão pretende construir uma nova torre
de transmissão, que envie sinal às antenas A, B e C, já
existentes nessas cidades. As localizações das antenas
estão representadas no plano cartesiano:
A torre deve estar situada em um local equidistante das
três antenas.
O local adequado para a construção dessa torre
corresponde ao ponto de coordenadas
A) (65 ; 35).
B) (53 ; 30).
C) (45 ; 35).
D) (50 ; 20).
E) (50 ; 30).
GABARITO
01. B
02. E
03. E
380
NÚMEROS COMPLEXOS
INTRODUÇÃO
Sabe-se que o conjunto dos números reais (IR) é o
mais amplo que conhecemos até então. Sendo assim,
surge o seguinte questionamento: “como resolver em IR
equações do tipo”:
x2 + 1 = 0;
x2 + 4 = 0;
2
x + 9 = 0,
onde Δ < 0 ?
Até o presente momento, afirmava-se que para
equações deste tipo, não havia solução no campo dos
números reais. E durante muitos séculos essa resposta foi
aceita, até que, em 1572 o matemático Raffaelli Bombeli
publicou seu tratado de Álgebra, que falava a respeito de
raiz quadrada de números negativos.
Desta forma surgia um novo e maravilhoso conjunto, o
dos NÚMEROS COMPLEXOS (C), com todos os
elementos de IR e nos quais as equações acima
passaram a ter solução.
Criaram-se então os NÚMEROS IMAGINÁRIOS ou
UNIDADADES IMAGINÁRIAS, simbolizados pela letra “i”,
que substituiria a  1 .
i=
1
Exemplo
Encontre, em C, o conjunto solução da equação:
x2 + 1 = 0
• Quando a parte imaginária de um número complexo
for nula (b = 0), este número é chamado de Real.
Exemplo
Determine o valor de k, para que o número
complexo
z = (k - 3) + 6i
seja imaginário puro.
Lembre: Img. Puro ⇔ Re(z) = 0 e Im(z) ≠ 0
k-3=0 ⇒ k=3
CONJUGADO
Dado um número complexo z na forma algébrica
z = a + bi, em que a ∈ IR e b ∈ IR, define o complexo
conjugado de z como sendo:
z = a – bi
Exemplos
Z = 3 – 4i ⇒ z = 3 + 4i
Z = –1 + 6i ⇒ z = – 1 – 6i
OPERAÇÕES
Vamos acompanhar aqui as operações com os
números complexos.
São elas: Adição, Subtração, Multiplicação e Divisão.
Vamos acompanhar em forma de exemplos práticos a
explicação destas operações.
Consideremos os seguintes complexos que
chamaremos de:
*** como i =
 1 , i2 = – 1
FORMA ALGÉBRICA
Todo número complexo pode ser escrito na forma
z = a + bi, com a, b ∈ IR, denominada forma algébrica.
O número real a é denominado parte real de z, e o
número real b é denominado parte imaginária de z.
Assim temos que:
ATENÇÃO!!!
• Quando a parte real de um número complexo é nula (a =
0) e sua parte imaginária é não-nula (b ≠ 0) este número
complexo é chamado de Imaginário puro.
381
E agora vejamos a divisão de dois complexos como
ficaria.
b)
Obs: Para efetuar a divisão de dois complexos, devemos
multiplicar o numerador e o denominador pelo conjugado
do complexo do denominador.
EXERCÍCIOS
01.(UFBA) O número complexo z que satisfaz a
Igualdade
é:
OBSERVE QUE Z .
(Z.
z
z
2
= a +b
2
é chamado de NORMA de Z )
POTÊNCIAS DE BASE i
n
Estudando as potências de i (i , n ∈ IN), temos:
02.(ILHÉUS) O número complexo z = 6.i25 + (2i)6 + (i)–3
é igual a:
Então pode-se concluir que:
Portanto, para determinarmos uma potência de base i
superior a 4, basta dividirmos o expoente de i por 4 e
considerarmos apenas i elevado ao resto dessa divisão.
Exemplos
Calcule as potências:
a)
382
O PLANO COMPLEXO
O plano cartesiano quando é utilizado para representar
números complexos é denominado plano de ArgandGauss.
***Cada ponto P(a, b) desse plano é a imagem ou afixo
do número complexo a + bi
MODULO DE UM NÚMERO COMPLEXO
ARGUMENTO DE UM NÚMERO COMPLEXO
Sendo z = a + bi um número complexo não-nulo e P
afixo de z no plano de Gauss de origem O, chamamos
argumento do número complexo z a medida do arco com
centro em O tomado a partir do semi-eixo real positivo até
a semi-reta OP no sentido anti-horário.
Da trigonometria concluímos que:
Assim:
383
em que
é o módulo de z. Em particular quando:
Exercícios resolvidos
1. Dar a forma trigonométrica dos seguintes números
complexos:
a) z = – 1 + i
b) z = –3i
Exercícios resolvidos
1. Calcular o argumento do número complexo z = 2 - 2i.
2. Calcular o argumento de z = -4i.
FORMA TRIGONOMÉTRICA DE UM NÚMERO
COMPLEXO
Vimos, anteriormente, que:
Substituindo (I) e (II) em z = a + bi, temos:
Portanto:
Essa expressão é a forma trigonométrica ou forma
polar do número complexo z = a + bi, de módulo ρ e
argumento θ.
384
Multiplicação de Números Complexos
Consideremos os números complexos não-nulos:
A multiplicação será dada por :
Exemplo
Calcular o produto dos números complexos:
2. Escrever, na forma algébrica, os seguintes números
complexos:
Divisão de Números Complexos
Consideremos os números complexos não-nulos:
A divisão será dada por :
OPERAÇÕES NA FORMA TRIGONOMÉTRICA
Adição de Números Complexos
Sejam os números complexos Z1 e Z2 na forma
trigonométrica:
Potenciação
Sendo
natural não-nulo, temos:
em n um número
385
Radiciação
2) (UFU-MG) Sejam os complexos z = 2x – 3i e t =
2 + yi, onde x e y são números reais. Se z = t,
então o produto x.y é
A) 6
B) 4
C) 3
D) – 3
E) – 6
Exemplo:
3) (UCMG) Qual o número complexo 2z, tal que 5z +
z = 12 + 6i ?
4) ( UFPA ) O número complexo z = x + ( x 2 – 4 ) i é
real se, e somente se :
a) x = 0
b) x  0
c) x =  2
d) x   2
e) x  0 e x   2
Observe que a 1ª raiz sempre será obtida por:



Z 0  n   cos  i.sen 
n
n

5) ( PUC – MG ) O produto ( a + bi ) . ( 3 + 2i ) é um
número real. O valor de 2a + 3b é :
a) - 3
b) - 2
c) 0
d) 2
e) 3
6) (UFPA) Qual o valor de m, real, para que o
produto (2 + mi).(3 + i) seja um imaginário puro?
A) 5
B) 6
C) 7
D) 8
E) 10
Geometricamente teríamos as distribuições destas
raízes da seguinte forma:
7) ( PUC – SP ) O número complexo z que verifica a
equação iz + 2 z + 1 – i = 0 é :
a) – 1 + 2i
b) – 1 + i
c) 1 – i
d) 1 + i
e) – 1 – i
8) ( UEL – PR ) Seja o número complexo z = x + yi,
2
no qual x, y  IR. Se z . (1 – i) = (1 + i) , então
a) x = y
b) x – y = 2
c) x . y = 1
d) x + y = 0
e) y = 2x
9) ( Fuvest – SP )
Determine OS NÚMEROS
complexos z tal que z  z  4 e z. z = 13, em
que z é o conjugado de z .
Nota-se que estes 3 pontos são vértices de um
triângulo eqüilátero.
10) ( Cefet – PR ) A expressão
1 i
2i

, na qual i
1  i 1  3i
é a unidade imaginária, é igual a :
EXERCÍCIOS
3  6i
5
3i
b)
2
a) 
2
1) ( FMU – SP ) A solução da equação x + 2x + 5 = 0
no conjunto dos números complexos é dada por :
a)  i
b)  2i
c) – 1  2i
d) 2  i
e) n.d.a
c) 1 + 2i
d) – 1 – 2i
e)
2  4i
5
386
11) ( Santa Casa – SP ) O valor de
a)
3 4
 i
5 5
c) 1 + 9i
d) – 8 + 6i
e) – 8 – 6i
é igual a:
b) 3 – 4 i
c) 4 + 3 i
e)
2i
2i
d)
20) ( Mack – SP ) Se u = 3 + 2 i e v = 1 + i , então
|u+v| é:
a) 5
b) 26
2 4
 i
3 3
3 4
 i
5 5
c) 29
e) 15
d) 7
12) ( FEI – SP ) Escrevendo o número complexo z =
21) ( UFRN ) Se z é um número complexo, tal que z
z = 12, então o módulo de z é :
a) 2 3
b) 3
c) 3
1
1

na forma algébrica, temos:
1 i 1 i
a) 1 – i
c) 1 + i
e) 1
b) i – 1
d) i
d) 3 2
13) (MACK-SP) O conjugado de
A) 1 – 2i
C) 1 + 3i
E) 2 – i
2i
vale
i
B) 1 + 2i
D) –1 + 2i
14) ( F. C. Chagas ) Se i é a unidade imaginária, então
i15  i16
e) 3 3
22) ( Cesgranrio – RJ ) O
4
complexo ( 1 + 3 i ) é :
a) 256
b) 100
c) 81
d) 64
e) 16
2
i 31  i110
15) ( UFSC ) A expressão
i13
é eqüivalente a :
i 3  3i 8  2i
i15  i18
a) 2 – 3i
c) 243i
e) 243
é:
B) 2 – i
D) 3
48
17) (UCSal) O valor da expressão y = (1 + i) – (1 + i)
a) 1 + i
b) –224 . i
c) –1 + i
d) 224 . i
49
é:
18) Calcular o valor da expressão Y = i2 + i3 + i4 + ... + i
103
.
19) ( UFJF ) Se z = 2 + 4i e w = 1 – i são números
2
z
complexos, então   é igual a :
w
a) 8 – 6i
b) – 1 + 3i
5+ 7i e w=1–
números complexos, então
b) – 1 + i
d) – 1 – i
A) – 2 + i
C) – 1 – 2i
número
 1 i 

 é:
 1  2i 
6
2
a)
b)
5
5
3
4
c)
d)
5
5
24) ( UFOP ) Se z =
16) ( CEFET ) O valor de
do
23) ( FEI – SP ) O módulo do número complexo z =
é igual a :
i17  i18
a) – 1
b) – i
c) 1 + i
1 i
d)  
2 2
1 i
e)  
2 2
a) 1 – i
c) 1 + i
módulo
z
w
2 i são
5
é igual a :
b) 32i
d) 32
25) ( UEL – PR ) Seja o número complexo z = x + yi,
no qual x, y  IR. Se z . (1 – i) = (1 + i)2, então
a) x = y
b) x – y = 2
c) x . y = 1
d) x + y = 0
e) y = 2x
26) (FEI – SP) O módulo do número complexo (1 + i)
é:
a) 2
b) 1
c) – 3
d) 2 /4
e) 0
–3
27) ( Fatec – SP ) O conjugado do número complexo
387
c)
3
d) 3 /2.
e) 1/2.
é igual a
a) 1 + i
b) 1 – i
c) (1/2) (1 – i)
d) (1/2) (1 + i)
e) i
n
2n
28) (ITA) O número natural n tal que (2i) + (1 + i) = –
16i, em que i é unidade imaginária do conjunto dos
números complexos, vale:
a) n = 6
b) n = 3
c) n = 7
d) n = 4
e) não existe n nestas condições
29) (UNIMONTES) Se i é a unidade imaginária, para que
a  bi
seja um número real, a relação entre a, b, c e
c  di
d deve satisfazer:
b a
A)

c d
B) b + d = 0 e a + c ≠ 0
ab
C)
cd
b d
D)

a c
30) (UFV-MG) Dadas às alternativas abaixo
2
2
I. i = 1
II. (i + 1) = 2i
III. |4 + 3i| = 5
IV. (1 + 2i).(1 – 2i) = 5
pode-se dizer que
a) todas as alternativas acima estão corretas
b) todas as alternativas acima estão erradas
c) as alternativas I e III estão erradas
d) as alternativas II, III e IV estão corretas
e) as alternativas I e III estão corretas
31) (UNIMONTES) O inverso do número complexo 2 + 3i
é o número
2
3
A)

i
13 13
1 1
B)
 i
2 3
2
3
C)

i
13 13
1 1
D)
 i
2 3
33) ( FGV – SP ) Admita que o centro do plano
complexo Argand-Gauss coincida com o centro de
um relógio de ponteiros, como indica a figura
abaixo. Se o ponteiro dos minutos tem 2 unidades
de comprimento, às 11h55 sua ponta estará sobre
o número complexo
a) –1 +
3i
b) 1 +
3i
c) 1 –
3i
d)
3 –i
e)
3 +i
34) ( Ufsm ) Dado z = x + yi um número complexo,
as soluções da equação | z – 2i | = 5 são
representadas graficamente por
a) uma reta que passa pela origem.
b) uma circunferência com centro (0, 2) e raio 5.
c) uma reta que passa por (0, 2).
d) uma circunferência com centro (2, 0) e raio 5.
e) uma circunferência com raio igual a 5 e que
passa por (2, 0).
35) ( UEG ) O conjunto dos números complexos que
satisfazem a condição |z – 3i| = |z – 2| é
representado no plano cartesiano por uma reta
a) cuja inclinação é positiva.
b) que contém a origem do sistema.
c) que não intercepta o eixo real.
d) cuja inclinação é negativa.
36) ( UFU ) A representação geométrica do conjugado
2
do número complexo (2i + 2) /(3i – 2), em que i é
a unidade imaginária, encontra-se no
a) primeiro quadrante.
b) segundo quadrante.
c) terceiro quadrante.
d) quarto quadrante.
32) ( UNIFESP ) Os números complexos z1, z2 = 2i e z3
37) ( UFRS ) Sendo z um número complexo e w o
seu conjugado, a representação geométrica do
conjunto solução da equação w = z – 1 é
a) um segmento de reta.
b) uma reta.
c) um arco de círculo.
d) um círculo.
e) uma parábola.
= a 3 + ai, onde a é um número real positivo,
representam no plano complexo vértices de um
triângulo eqüilátero. Dado que |z2 – z1| = 2, o valor de
a é:
a) 2.
b) 1.
38) ( FGV – SP ) Seja o número complexo z = (x –
2i)2, no qual x é um número real. Se o argumento
principal de z é 90°, então 1/z é igual a
a) –i/8
b) –8i
c) 4i
d) –1 + 4i
e) 4 – i
388
39) ( FEI – SP ) Escrevendo o número complexo z = 1/(1 –
i) + 1/(1 + i) na forma algébrica obtemos:
a) 1 – i
b) i – 1
c) 1 + i
d) i
e) 1
40) ( UEL – PR ) Seja z um número complexo de módulo
2 e argumento principal 120°. O conjugado de z é
a) 2 - 2i 3
c) –1 – i 3
b) 2 + 2i 3
41) ( UFPA ) O número complexo z =
forma trigonométrica é :


a) 2.  cos  i sen 
6
2+
2 i , na


b) 2.  cos  i sen 
6



c) 2.  cos  i sen 
3
3
5
5

e) 2.  cos  i sen 
4
4 


P


c) 2.  cos  i sen 
4



2  cos  i sen 
2
2

b)
d)



2  cos  i sen 
4
4



e) 2.  cos  i sen 
2
2 3
 i, a
3 5
representação trigonométrica de z1  z2 é:
a)

 7 
 7 
2 cos
  i sen

 4 
 4 

b)

 5 
 5 
2 cos
  i sen

4


 4 

c)
2 cos
d)
2 cos   i sen 

 3 
 3 
  i sen 
4
 
 4 


  
 4 

4

48) ( UEL – PR ) O número real positivo K que torna o
módulo do número complexo z =
é:
a) 1
c) 3
e) 5
49) Se
z1 = 5.  cos 2 + i sen 2 


a) seu argumento e seu módulo;
5
e
5 
5
z2 = 2.  cos 3 + i sen 3 
5 
são dois números
complexos, o produto z1 . z2 vale:
a) 10
b) – 10
c) 10 3
d) – 10 3
3 .  cos 4 + i sen 4
50) Se z1 = 2
4  3i
, determine:
3  4i
K i
5
igual a
3i
5
b) 2
d) 4
2
44) ( FEI – SP ) Dado z 
z2  
e
em um sistema de coordenadas
8+ i
cartesianas xOy. Determine o número complexo
b, de módulo igual a 1, cujo afixo M pertence ao
quarto quadrante e é tal que o ângulo LOM é reto.
43) ( FEI – SP ) A representação trigonométrica do
número complexo z = 1 + i é :
a) 2 ( cos 0º + i sen 0º )
1 2
 i
3 5
3
3 
 i sen

4
4 
2 3

z1 
47) ( UNESP ) Seja L o afixo do número complexo a =
42) ( Med. Jundiaí – SP ) Na figura, o ponto P é o afixo
de um número complexo Z no plano de ArgandGauss. A forma trigonométrica de Z é:
a) 4( cos 300º + i sen 300º )
b) 4( cos 60º + i sen 60º )
2
c) 16( sen 330º + i cos 330º)
d) 2( sen 300º + i cos 300º)
e) cos( – 60º ) + i sen (–60º)
4
46) ( UFBA ) Sendo
4
4
d) 2.  cos


d) 4
d) –1 + i 3
e) 1 + i 3

c) – 2 + i 2
e) – 4i
z2 =
9




3 .  cos + i sen 
9
9



 e
9 
são dois números
complexos, encontre o complexo w =
b) a forma trigonométrica de z.
z1
z2
51) Se w = 2  cos  + i sen   é um número complexo,
45) ( UEL – PR ) Se z ={ 2 [cos(/4) + i sen(/4)] }, então
o conjugado de z2 é igual a
a) 2 – i 2
b) – 2 – i 2

6
6 
encontre o número complexo w8
389
52) ( FIPMOC ) Numa aula de Matemática, o tema era
Números Complexos. Inicialmente, o professor definiu a
unidade imaginária como sendo uma das soluções da
equação x2 + 1 = 0. Após a explicação, o professor sugeriu
a seguinte questão:
Qual o valor da soma dos “n” primeiros elementos da
sequência
( i2006 + i2007 + i2008 + i2009 + ... ) ?
Na tentativa de acertar a questão proposta, quatro alunos
fizeram as seguintes afirmações:
• ANA: A soma será –1 se n ∈ { 2 , 6 , 10 , ...};
• BETO: A soma será (–1 – i ) se n ∈ { 4 , 8 , 12 , ...};
• CAIO: A soma será –i se n ∈ { 3 , 7 , 11 , ...};
• DANIEL: A soma será 0 se n ∈ { 1, 5, 9, ...};
Considerando-se as respostas apresentadas, qual aluno
acertou a questão?
A) Beto.
B) Ana.
C) Daniel.
D) Caio.
GABARITO
1) C
2) D
8) D
9) z = 2 + 3i ou z = 2 – 3i
12) E
3) 4 + 3i
13) D
18) – 1 – i
4) C
14) B
19) E
15) D
20) A
26) D
5) C
7) E
10) A
11) E
16) D
17) B
21) A
22) B
25) D
30) D
31) C
32) B
33) A
34) B
35) A
36) A
37) D
38) A
39) E
40) C
41) B
42) A
43) D
44)
50) 1 + i 3
51)
45) E
48) A
28) B
23) B
24) D
47) b = (1 – i 8 )/3
27) D
6) B
29) D
46) A
49) B
52) D
390
POLINÔMIOS
VALOR NUMÉRICO
DEFINIÇÃO
Chama-se polinômio toda expressão algébrica
constituída de um monômio ou de uma soma de
monômios.
Exemplos


seja, do maior grau (n) até o menor grau (zero).
O monômio –5x3y é um polinômio de variáveis x e y.
3
2
A expressão 6x – 2x + 5 é um polinômio de variável
x e contém três termos.
Um polinômio que possui dois termos não semelhantes
é chamado binômio: um polinômio que possui três termos
não semelhantes é denominado trinômio.
Exemplos
 6x2y – 2x é um binômio de variáveis x e y.
 x3 – 4x + 6 é um trinômio de variável x.
GRAU DE UM POLINÔMIO
Grau de um polinômio é o expoente máximo que ele
possui.
Exemplos:
O valor numérico de um polinômio P(x) para x=a, é o
número que se obtém substituindo x por a e efetuando
todas as operações indicadas pela relação que define o
polinômio. Exemplo:
Se P(x) = x3 + 2x2 + x - 4, o valor numérico de P(x),
para x=2, é:
P(x)= x3+2x2+x-4
3
2
P(2)= 2 +2.2 +2-4
P(2)= 14
Obs: Se P(a ) = 0, o número a chamado raiz ou zero
de P(x).
Exemplo
Sendo P(x) = x3 – 5x2 + 4x + 6, temos:
3
2
P(3) = 3 – 5.3 + 4.3 + 6 = 27 – 45 + 12 + 6 = 0.
Então 3 é raiz ou zero de P(x).
Um polinômio P(x) que se anula para todo valor real
de x é chamado polinômio nulo. Na prática, um
polinômio só é nulo se, escrito na forma canônica, tem
todos os coeficientes iguais a zero.
OPERANDO COM POLINÔMIOS
1.
P(x)  5 ou P(x)  5.x é um polinômio
constante, ou seja, grau é 0.
2.
P(x)  3x  5 é um polinômio do 1º grau, isto é, o
0
grau é 1.
POLINÔMIOS DE UMA VARIÁVEL REAL
A adição e a subtração de polinômios, bem como a
Multiplicação de um polinômio por uma constante
são operações simples.
Exemplo
 Sendo A(x) = 5x 2 – x + 3 e B(x) = – x2 + 2x – 1,
calcule os polinômios 2A + B .
2
2
2
2A + B = (10x – 2x + 6 )+ (– x + 2x – 1) = 9x + 5
Sendo x urna variável real, n  IN e ao, a1, a2, ...,an,
constantes reais, chama-se polinômio de variável real x
toda expressão algébrica do tipo
P(x)  a 0 x n  a 1 x n 1  a 2 x n -2  ...  a n
As constantes a o , a 1 , a 2 , ..., a n são os coeficientes do
n
n–1
n–2
polinômio. Cada uma das parcelas aox , a1x , a2x , ... ,
an é um termo do polinômio. Em particular, an é o termo
independente do polinômio, pois ele independe da
variável x. Sendo a n  0 , o polinômio é de grau n.
Exemplo:
 P(x) = x4 – 6x3 + 3x + 5 é um polinômio de variável x.
Seus coeficientes são 1, – 6, 3 e 5.
Ele possui 4 termos, sendo + 5 o termo independente.
Na definição que acabamos de apresentar, observe
que o polinômio P(x) aparece de tal forma que:
a) não há termos semelhantes;
b) os termos estão dispostos de forma ordenada, ou
A multiplicação de dois polinômios se baseia na
propriedade distributiva da multiplicação em relação à
adição. Multiplica-se cada termo de um dos polinômios
por cada termo do outro. Em seguida, reduzem-se os
termos semelhantes, caso existam.
Exemplo
 Calcule AB sendo A(x) = 3x 2 – 1 e B(x) = x2 – 2x +
3.
(3x2 – 1) (x2 – 2x + 3)
= 3x4 – 6x3 + 9x2 – x2 + 2x – 3 =
= 3x4 – 6x3 + 8x2 + 2x – 3
Divisão de polinômios
Sejam dois polinômios P(x) e D(x), com D(x) não
nulo.
Efetuar a divisão de P por D é determinar dois
polinômios Q(x) e R(x), que satisfaçam as duas
condições abaixo:
391
1ª) Q(x).D(x) + R(x) = P(x)
2ª) gr(R) < gr(D) ou R(x)=0
Nessa divisão:
P(x) é o dividendo.
D(x) é o divisor.
Q(x) é o quociente.
R(x) é o resto da divisão.
P( x)
D( x )
R( x)
Q( x)
Obs: Quando temos R(x)=0 dizemos que a divisão é
exata, ou seja, P(x) é divisível por D(x) ou D(x) é divisor de
P(x).
Se D(x) é divisor de P(x)  R(x)=0
Exemplo:
Determinar o quociente de P(x)=x 4+x3-7x2+9x-1 por
D(x)=x2+3x-2.
Aplicando o método da chave, temos:
dividendo ordenadamente na parte de cima da
“cerquinha”.
2º) O primeiro coeficiente do dividendo é repetido
abaixo.
3º) Multiplicamos a raiz do divisor por esse coeficiente
repetido abaixo e somamos o produto com o 2º
coeficiente do dividendo, colocando o resultado abaixo
deste.
4º) Multiplicamos a raiz do divisor pelo número
colocado abaixo do 2º coeficiente e somamos o
produto com o 3º coeficiente, colocando o resultado
abaixo deste, e assim sucessivamente.
5º) Separamos o último número formado, que é igual
ao resto da divisão, e os números que ficam à
esquerda deste serão os coeficientes do quociente.
Observe que o grau de Q(x) é uma unidade inferior
ao de P(x), pois o divisor é de grau 1.
Resposta:Q(x)=3x2+x+3 e R(x)=4.
TEOREMA DO RESTO
O resto da divisão de um polinômio P(x) pelo binômio
 b
ax + b é igual a P   .
 a
Note que -
b
é a raiz do divisor.
a
Exemplo:
Calcule o resto da divisão de x2 + 5x – 1 por x + 1.
1°- Achamos a raiz do divisor:
x + 1=0 => x = – 1
O dispositivo de Briot-Ruffini
Serve para efetuar a divisão de um polinômio P(x) por
um binômio da forma (ax+b).
Exemplo: Determinar o quociente e o resto da divisão do
polinômio P(x) = 3x3 – 5x2 + x –2 por (x – 2).
Resolução:
2°- Pelo teorema do resto sabemos que o resto é igual
a
P(-1)
P(-1)=(-1)2+5.(-1)-1 => P(-1) = -5 = R(x)
Resposta: R(x) = -5.
EXERCÍCIOS
Para a resolução desse problema no dispositivo de BriotRuffini seguimos os seguintes passos:
1º) Colocamos a raiz do divisor e os coeficientes do
01. (PUC-SP) Os valores de A e B tais que
1 x
A
B
, são respectivamente:
 
2
x 1 x
xx
a) 2 e 1
b) 3 e 2
c) 1 e 2
d) 2 e 3
e) 1 e 3
392
02. (UFMG) Considerem-se os polinômios
–
–
–
O conjunto de todos os valores reais de a, para os quais a
soma P(x) + Q(x) sejam um polinômio do 2º grau, é:
a) {1}
b) {2}
c) {7}
d) {1, 2}
e) {1, 2, 7}
03. (UNIMONTES) Seja o polinômio
, no qual n ∈ IN. Dividindo esse
polinômio por x + 1, obtém-se o resto
a) 0
b) 4
c) –2
d) 5
04. (DIAMANTINA)
I. Sendo o polinômio
ao polinômio
igual a 7.
–
idêntico
, então a + b + c + d é
II. Não existe valor de m tal que o polinômio
–
seja de grau 2.
III. Sendo P(x) um polinômio de grau 100, Q(x) = x – 3 e
P(3) = 0, é possível concluir que a divisão de P(x) por Q(x)
não é exata.
IV. Sendo P1(x), P2(x), P3(x) três polinômios de graus 4, 7
e 7, respectivamente, podemos afirmar que o grau do
polinômio P1(x)+ P2(x) + P3(x) é 7.
Assinale a alternativa CORRETA.
a) Todas as afirmativas são falsas.
b) Todas as afirmativas são verdadeiras.
c) Apenas a afirmativa IV é falsa.
d) Apenas a afirmativa II e IV são falsas.
e) Apenas as afirmativas I e II são verdadeiras.
05. (UFMG) O quociente da divisão de
por
é:
a) x - 5
b) x - 1
c) x + 5
d) 4x-5
e) 4x – 8
06. (Fuvest-SP) Dividindo-se o polinômio P(x) por
, obtem-se quociente
e resto –x+2.
Nessas condições , o resto da divisão de P(x) por x-1 é
a) 2
b) 1
c) 0
d) -1
e) -2
07. (UFMG) O polinômio P(x) = x 4 + mx2 + n é divisível
por x2 – 4 e também por x2 – 3. O valor do produto m.n
é
a) – 84
b) – 12
c) – 1
d) 12
e) 14
08. (Ufal) O polinômio
, com
∈
, é tal que P(2) = 14. Sendo i a unidade
imaginaria, tem-se que P(2i) é igual a:
a) 8-18i
b) -18i
c) -14i
d) 14i
e) 8
09. (U. São Judas-SP) Se o polinômio
é identicamente
nulo, então a+b+c vale:
a) 2
b) 1
c) 0
d) -1
e) -2
10. (Uepa) Se o numero 1 é uma das raízes do
polinômio
, entao P(-1) é igual a:
a) 2
b) -2
c) 3
d) -3
e) -4
11. (UFMG) Consideram-se
e
. o conjunto de
todos os valores reais de a, para que a soma P(x) +
Q(X) seja um polinômio do 20 grau, é:
a) {1}
b) {2}
c) {7}
d) {1,2}
e) {1,2,7}
12. (Cesgranrio) Sendo Q(x) o quociente da divisão de
podese afirmar que Q(-1) é igual a:
a) 0
b) 2
c) 4
d) 6
e) 8
13. (Faap-SP) Se
divide
exatamente (isto é, o resto da divisão do segundo
polinômio pelo primeiro é zero), então o valor da
constante q é:
a) 5
b) 2
c) 25
393
d) -18
e) 16
C) 1, -1 e 2.
D) 1, -1 e 0.
14. (FGV-SP) O resto da divisão do polinômio
por
é:
a) -1
b) 1
c) 2
d) -1
e) 0
20.(Unimontes) O valor de P(x) 
2
3
1
1
1
1
1
x1
para x = a é
3
2
15.(UFMG) Sendo P(x) = 2b x – bx e Q(x) = a x + 2ax ,
o valor de P(a) – Q(b) é
2
a) 2ab
3
b) – 2a b
c) ab(a – b)
d) ab(a + b)
e) 4ab2 – 2a3b
16.(OSEC) Se os polinômios ax 3 + bx2 + cx + d e x(x –1)(x
– 2) são idênticos, então:
a) a = 0
b) b = 1
c) c = 2
d) d = 3
e) n.d.a.
21.(Unimontes)Os valores de A, B e C, de forma que
x5
Ax  b
C
são, respectivamente,


x3  x2  x  1 x2  1 x  1
A) 2, 7 e 8.
B) –5, 2 e 1.
C) –2, 4 e –1.
D) –3, –2 e 3.
17.(ITA) Dividindo P(x) = x3 + x2 + x + 1 por Q(x) obtemos
23. (CFO/PM) Sejam a, b, c, d números reais que
aparecem no dispositivo de Briot- Ruffini
quociente S(x) = 1 + x e resto R(x) = x + 1. O polinômio
Q(x) satisfaz:
a) Q(2) = 0
b) Q(3) = 0
c) Q(0)  0
d) Q(1)  0
e) n.d.a.
Sendo :
2
3
K = { [( a + b ) – ( c – d ) ]. [( 2acd -
c.d
b
)] } , o valor
de K é :
2
3
2
18.(UFMG) Sejam P(x) = x – 4 e Q(x) = x – 2x + 5x + a,
onde Q(2) = 0. O resto da divisão de Q(x) por P(x) é
a)
b)
c)
d)
e)
–x–2
9x – 18
x+2
0
– 9x + 18
23.(CTSP-2010) Dada a expressão
2
A
B
C
. O valor de A.B.C. é:
 

3
x
x

1
x
1
x x
19.(Unimontes) Os valores de M, N e P, tais que
para todo x real, x ≠ 1, x ≠
0e
x ≠ −1, são, respectivamente,
A) -1, 2 e 0.
B) -1, 1 e 1.
A) - 549
B) - 836
C) 1054
D) 990
A) 4
B) -2
C) -4
D) 6
24.(UNIFESP)A divisão de um polinômio p(x) por um
3
2
polinômio k(x) tem q(x) = x + 3x + 5 como quociente e
2
r(x) = x + x + 7 como resto. Sabendo-se que o resto da
394
divisão de k(x) por x é 2, o resto da divisão de p(x) por x é
a) 10.
b) 12.
c) 17.
d) 25.
e) 70.
21.
22.
23.
24.
25.
26.
27.
D
D
B
C
A
C
A
25.(FMTM-MG) Dividindo-se o polinômio P(x) por 3x – 2
obtém-se quociente Q(x) = x2 - 2x + 5 e resto r. Se P(2) =
20, então o valor de r é:
A) 0
B) 2
C) 4
D) 5
E) 20
26.(UNIMONTES-2010) As raízes do polinômio
3
2
P(x) = x + mx + nx + p são 1, 2 e 3. O quociente de P(x)
por x − 3 é
A) x2 + 2.
B) x2 − 2x +1.
C) x2 − 3x + 2.
D) x2 + 3x − 2.
27.(UNIMONTES) Considere a e b números reais não
nulos. Se o polinômio P(x) = bx 3 + ax2 − bx + b é divisível
por x – 1, é INCORRETO afirmar que
GABARITO
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
C
D
B
A
B
B
A
A
B
E
A
E
C
B
B
C
D
B
B
D
395
EQUAÇÕES POLINOMIAIS
A obra Al-jabr wa’l muqãbalah, escrita no século IX pelo
matemático árabe Mohammed ibu-Musa al-Khowarizmi é
um dos trabalhos pioneiros a respeito da Teoria das
Equações, no qual são estudadas as equações do 1º e do
2º grau. A partir da mesma, al-Khowarizmi inspirou os
tratados posteriores até o Renascimento, quando os
matemáticos buscavam uma fórmula resolutiva para
equações polinomiais de qualquer grau, o que já haviam
conseguido para equações até o 4º grau. Os matemáticos
Évariste Galois e Niels Henrik Abel finalizaram esta busca,
demonstrando que equações de grau superior a 4 não
podem ser resolvidas por radicais e combinações de
coeficientes. Desta forma, não há uma fórmula geral que
resolva equações polinomiais de grau maior que 4.
EQUAÇÕES POLINOMIAIS
TEOREMA FUNDAMENTAL DA ÁLGEBRA
A demonstração desse teorema foi a tese de
doutoramento de Carl Friedrich Gauss, apresentada no
ano de 1798. Embora outros matemáticos já tivessem
tentado fazer essa demonstração, Gauss foi o primeiro
a realizá-la com perfeição.
Toda equação algébrica P(x) = 0 de grau n ≥ 1
admite, pelo menos, uma raiz complexa.
TEOREMA DA DECOMPOSIÇÃO
Decomposição Em Fatores Do 1º Grau
Com o auxílio do teorema fundamental da álgebra, é
possível mostrar que um polinômio de grau n ≥ 1 pode
ser decomposto em um produto de fatores do 1º grau.
Equação Polinomial ou Equação Algébrica é toda
equação do tipo P(x) = 0:
P(x) =an.xn + an-1.xn-1 + ... + a3.x3 + a2.x2 + a1.x + a0 = 0
Em que:
an, an-1, ..., a3, a2, a1, a0 são os coeficientes;
n é número natural;
x é a variável complexa;
Exemplo :
O grau da equação polinomial é o grau do polinômio
P(x);
1. Considere o polinômio P(x) = 2x3 – 8x2 – 2x + 8,
cujas raízes são x1 = -1, x2 = 1 e x3 = 4. Colocando
P(x) na forma fatorada, tem-se:
O grau é dado pelo maior expoente da variável x.
P(x) = 2(x + 1). (x – 1). (x – 4)
Exemplos :
1. A equação x3 + 3x2 – 5x + 4 = 0 é polinomial, tendo:
- Coeficientes: 1, 3, -5, 4; e Grau 3.
2
2. A equação x + 4 = 0 é polinomial, tendo:
- Coeficientes: 1, 0, 4 e Grau: 2.
RAIZ DA EQUAÇÃO POLINOMIAL
MULTIPLICIDADE DE UMA RAIZ
Ao fatorarmos um polinômio P(x), pode acontecer
que um fator (x – x1) apareça exatamente m vezes.
Dizemos, então, que o número z é a raiz de
multiplicidade m do polinômio P(x) ou da equação P(x)
=0
Assim, no polinômio
Raiz da equação polinomial P(x) = 0 é todo número
complexo α, tal que P(α) = 0.
P(x) = x4 .(x – 2)3 .(x + 1)2 .(x – 5), dizemos que:
Exemplos:
• o número zero é a raiz de multiplicidade 4 (ou raiz
quádrupla);
1. O valor 6 é raiz da equação polinomial 2x – 12 = 0,
pois 2.6 – 12 = 0. Então P(6) = 0.
• o número 2 é raiz de multiplicidade 3 (ou raiz tripla);
2. Os valores 2 e 5 representam as raízes da equação
polinomial x2 – 7x + 10 = 0,
pois 22 – 7.2 + 10 = 0 e 52 –7.5 + 10 = 0.
Então P(2) = 0 e P(5) = 0.
• o número –1 é raiz de multiplicidade 2 (ou raiz dupla);
• o número 5 é raiz de multiplicidade 1 (ou raiz
simples).
396
Exemplos:
Conseqüências do teorema
1. Dada a equação algébrica (x – 5)(x + 3)4(x – 1)2=0,
vamos determinar o que se pede.
1.. Se uma equação algébrica de coeficientes reais
admite a raiz z = a + bi (b ≠ 0) de multiplicidade m,
então admite também como raiz o conjugado z = a – bi
de mesma multiplicidade.
Resolução:
a) O grau da equação
Somando os graus de cada fator, obtemos o grau da
equação: 1 + 4 + 2 = 7
Logo, o grau é 7.
b) O conjunto solução nos complexos
(x – 5)(x + 3)4(x – 1)2 = 0
x–5=0⇒x=5
(x + 3)4 = 0 ⇒ x + 3 = 0 ⇒ x = –3
(x – 1)2 = 0 ⇒ x – 1 = 0 ⇒ x = 1
2. Toda equação algébrica de coeficientes reais e
grau ímpar admite pelo menos uma raiz real, pois o
número de raízes não-reais é sempre par.
Exemplos:
1. Vamos ver qual é o menor grau que pode ter uma
equação de coeficientes reais que admita as raízes 2,
3i e 1 + i.
Resolução:
A equação algébrica terá no mínimo 5 raízes:
Logo, o conjunto solução é:
S = {–3, 1, 5}
c) A multiplicidade da raiz –3
A raiz –3 tem multiplicidade quatro, pois o polinômio x +
3 aparece quatro vezes na forma fatorada da equação.
2. Vamos resolver a equação
x4 – 10x3 + 32x2 – 38x + 15 = 0, sabendo que
1 é raiz de multiplicidade 2.
2, 3i, – 3i, 1 + i, 1 – i.
Logo, o menor grau da equação é 5.
RAÍZES RACIONAIS
Resolução:
A seguinte propriedade possibilitar-nos-á determinar
todas as raízes racionais de uma equação algébrica de
coeficientes inteiros.
Se p/q com p e q primos entre si é uma raiz racional
da equação algébrica de coeficientes inteiros
Se 1 é raiz de multiplicidade 2, então podemos escrever:
anxn + an–1xn–1+....+ a2x2 + a1x + a0 = 0,
P(x) = (x – 1)2 . Q(x)
Para obtermos Q(x), devemos dividir P(x) por (x – 1) duas
vezes seguidas:
Então p é divisor de a0 e q é divisor de an (com
an ≠ 0 e a0 ≠ 0)
Exemplo:
4
3
Vamos encontrar as raízes da equação 6x – 11x –
2
6x + 9x – 2 = 0.
Solução:
A equação tem coeficientes inteiros.
Logo, Q(x) = x2 – 8x + 15.
Resolvendo a equação Q(x) = 0, encontramos as outras
raízes: 3 e 5.
Logo, o conjunto solução é: S = {1, 3, 5}.
RAÍZES COMPLEXAS
Teorema:
Se um número complexo z = a + bi (b ≠ 0) é raiz de
uma equação algébrica de coeficientes reais, então o
conjugado de z, = a – bi, também é raiz da equação.
397
Relações de Girard para uma equação de grau 4
A equação a0x4 + a1x3 + a2x2 + a3x + a4=0 possui
como raízes os termos r1, r2, r3 e r4, nesse caso:
Exemplos:
RELAÇÕES DE GIRARD
Relações de Girard para uma equação de grau 2
A equação a0x2 + a1x + a2=0 possui como raízes os
termos r1 e r2, nesse caso:
Relações de Girard para uma equação de grau 3
A equação a0x3 + a1x2 + a2x + a3 = 0 possui como
raízes os termos r1, r2 e r3, nesse caso:
TEOREMA DE BOLZANO
Seja
P(x)=0
uma equação polinomial de
coeficientes reais e [a, b] um intervalo fechado.

Se P(a) . P(b) < 0, então existe um número
ímpar de raízes reais entre a e b.
398
3. CALCULE o comprimento da diagonal desse
paralelepípedo.
02. (UFP–RS) A soma dos inversos das raízes da
equação x3– 2x2 + 3x – 4 = 0 é igual a:

Se P(a) . P(b) > 0, então existe um número par de
raízes reais entre a e b.
a) –3/4
b) –1/2
c) 3/4
d)4/3
e) 2
03.(UNIMONTES-2010) Para a equação
, onde
, as afirmações abaixo
verdadeiras, EXCETO
são
A) A soma das raízes é 2.
B) O discriminante é 9.
C) As raízes são imaginárias.
D) As raízes podem ser encontradas por fatoração,
usando-se números imaginários.
04. (UNIMONTES – PAES) O volume de um
paralelepípedo é V(x) = x3 – 6 x2 + 11x – 6 e sua altura
é 3. A soma das outras dimensões desse
paralelepípedo é
a) 3.
b) 2.
c) 6.
d) 4.
EXERCÍCIOS
01.( UFMG) As dimensões a, b e c, em cm, de um
paralelepípedo retângulo são as raízes do polinômio
GABARITO
01. 1. 77/6
02. C
03. A
04. A
2. 103/3
3.
p (x) = 6x3 – 44x2 + 103x – 77
1. CALCULE o volume desse paralelepípedo.
2. CALCULE a soma das áreas das faces desse
paralelepípedo.
399
QUESTÕES DO ENEM
LÓGICA E ROTAÇÃO E TRANSLAÇÃO DE FIGURAS
01. (ENEM-2009) Um decorador utilizou um único tipo de
transformação geométrica para compor pares de
cerâmicas em uma parede. Uma das composições está
representada pelas cerâmicas indicadas por I e II.
Utilizando a mesma transformação, qual é a figura que
compõe par com a cerâmica indicada por III?
02. (ENEM-2009) Um dos diversos instrumentos que o
homem concebeu para medir o tempo foi a ampulheta,
também conhecida como relógio de areia. Suponha que
uma cozinheira tenha de marcar 11 minutos, que é o
tempo exato os biscoitos que ela colocou no forno.
Dispondo de duas ampulhetas, uma de 8 minutos e outra
de 5, ela elaborou 6 etapas, mas fez o mesmo esquema,
representando a seguir, somente até a 4ª etapa, pois é só
depois dessa etapa que ela começa a contar os 11
minutos.
03. (ENEM-2009) Uma das expressões artísticas mais
famosas associada aos conceitos de simetria e
congruência é, talvez, a obra de Maurits Comelis
Escher, artista holandês cujo trabalho é amplamente
difundido. A figura apresentada, de sua autoria, mostra
a pavimentação do plano com cavalos claros e cavalos
escuros, que são congruentes e se encaixam sem
deixar espaços vazios.
Realizando procedimentos análogos aos feitos por
Escher, entre as figuras abaixo, aquela que poderia
pavimentar um plano, utilizando-se peças congruentes
de totalidades claras e escuras é
A opção que completa o esquema é
400
04. (ENEM-2013)Um programa de edição de imagens
possibilita transformar figuras em outras mais complexas.
Deseja-se construir uma nova figura a partir da original. A
nova figura deve apresentar simetria em relação ao ponto
O.
pontos A e B são equidistantes do pivô:
A projeção ortogonal da trajetória dos pontos A e B,
sobre o plano do chão da gangorra, quando esta se
encontra em movimento, é:
A imagem que representa a nova figura é:
06.(ENEM/2009) As figuras a seguir exibem um trecho
de um quebra-cabeças que está sendo montado.
Observe que as peças são quadradas e há 8 peças no
tabuleiro da figura A e 8 peças no tabuleiro da figura B.
As peças são retiradas do tabuleiro da figura B e
colocadas no tabuleiro da figura A na posição correta,
isto é, de modo a completar os desenhos.
qBittorrent.lnk
05. (ENEM-2013)Gangorra é um brinquedo que consiste
de uma tábua longa e estreita equilibrada e fixada no seu
ponto central(pivô). Nesse brinquedo, duas pessoas
sentam-se nas extremidades e, alternadamente,
impulsionam-se para cima, fazendo descer a extremidade
oposta, realizando,assim, o movimento da gangorra.
Considere a gangorra representada na figura, em que os
401
e)
Disponível em: http://pt.eternityii.com. Acesso em: 14 jul. 2009.
É possível preencher corretamente o espaço indicado pela
seta no tabuleiro da figura A colocando a peça
a)1 após girá-la 90° no sentido horário.
b)1 após girá-la 180° no sentido anti-horário.
c)2 após girá-la 90° no sentido anti-horário.
d)2 após girá-la 180° no sentido horário.
e)2 após girá-la 270° no sentido anti-horário.
GABARITO
01. B
02. C
03. D
04. E
05. B
06. C
07. E
07.(ENEM/2009) Em Florença, Itália, na Igreja de Santa
Croce, é possível encontrar um portão em que aparecem
os anéis de Borromeo. Alguns historiadores acreditavam
que os círculos representavam as três artes: escultura,
pintura e arquitetura, pois elas eram tão próximas quanto
inseparáveis.
Scientific American, ago. 2008.
Qual dos esboços a seguir melhor representa os anéis de
Borromeo?
a)
b)
c)
d)
402
PROVA DO ENEM - 2015
403
404
405
406
407
408
409
410
411
412
413
414
PROVA DO ENEM APLICADA NAS UNIDADES PRISIONAIS E SOCIOEDUCATIVAS ( 2015 )
415
416
417
418
419
420
421
422
423
424
425
426
427
GABARITO - ENEM 2015
GABARITO - ENEM 2015 (UNIDADES PRISIONAIS)
428