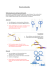Binäre Bäume

Binäre Bäume
Binäre Bäume
Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.B.
die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben
Organisationshierarchien in Unternehmen oder die Aufrufstruktur eines Divide-and-ConquerAlgorithmus.
Ein Nachteil beim Suchen von Komponenten in linearen Listen ist, dass man sich, beginnend
beim Listenkopf, linear durch die.Liste bewegen muss.
Idee: Wenn wir beim Kopfknoten zwei Referenzen verfolgen können, sind die Teillisten
kürzer.
Dies nutzen wir beim Suchen aus:
kopf
5
Eine Datenstruktur mit Schlüsselwerten 1 bis 10
wurzel
3
4
9
Suchschritte (Mittelwert s)
Suche von 5: 1 Vergleich
Suche von 2: 7 Vergleiche
Suche von 7: 10 Vergleiche
......
6
s = (1 + 2+ ....... + 10) / 10 = 5,5
5
3
9
4
6
2
10
1
8
10
2
8
1
Mittelwert
s = (1+2+3+4+5+ 2+3+4+5+6) / 10 = 3,5
7
Bei geeigneter Fortführung erhalten wir einen Baum.
© Wagner, 14. Apr. 2011 Seite 1
7
Binäre Bäume
Binärbaum
Stufe (level)
der Knoten
0
innerer
Knoten
6
1
9
3
2
8
5
2
li. Teilb.
3
1
Die maximale Stufe
des Baums heißt Höhe:
h=3
Wurzel
4
7
10
Die Zahl der Kanten
von der Wurzel bis
zu einem Knoten
heißt Weglänge.
re. Teilb.
Blatt
= äußerer Knoten
Ein Knoten auf der
Stufe i hat die
Weglänge i
Der Knoten (node) ohne Vorgänger heißt Wurzel (root).
Knoten mit Nachfolgern heißen innere Knoten.
Knoten ohne Nachfolger heißen Blätter (leaf, leaves).
Jedem Knoten ist eine Stufe (level) zugeordnet: Die Stufe ist die Länge des Pfades bis zur
Wurzel.
Die Höhe (height) des Baums ist die maximale Stufe.
Der leere Baum hat die Höhe -1.
Suchaufwand
Schlüssel
6
3, 9
2, 5, 8, 10
1, 4, 7
Zahl der Vergleiche
1
2
3
4
© Wagner, 14. Apr. 2011 Seite 2
Binäre Bäume
Damit erhalten wir einen mittleren Suchaufwand
s = (1 + 2*2 + 4*3 + 3*4)/ 10 = 2,9.
Bei z.B. 1023 Schlüsseln beträgt s = 9.
Definition
Ein binärer Baum (binary tree) vom Knotentyp T (Klassentyp) ist entweder
1. die leere Struktur oder
2. ein Knoten (Wurzel) vom Typ T, der mit zwei verschiedenen binären (Teil-)Bäumen
vom Typ T verknüpft ist: linker und rechter Teilbaum der Wurzel.
Anmerkungen
Auf Grund dieser rekursiven Definition ist ein Baum eine rekursive Datenstruktur.
Falls linker und rechter Teilbaum leer sind, besteht der Baum nur aus der Wurzel.
Bäume
Baum mit 6 Knoten
Leerer Baum
∅
Baum mit 1 Knoten
null
Nur der
Handle
Bemerkung: Die lineare Liste ist ein Sonderfall eines Baums,
wobei jeder Knoten nur einen Nachfolger hat.
© Wagner, 14. Apr. 2011 Seite 3
Binäre Bäume
Definition
Ein binärer Baum heißt voll, wenn alle inneren Knoten 2 Nachfolger haben.
Ein voller Binärbaum heißt vollständig, falls alle Blätter die gleiche Tiefe haben.
Eigenschaften
Wie viele Blätter b hat ein binärer Baum der Höhe h maximal?
-> b ≤ 2h
Wie viele Knoten n hat ein binärer Baum der Höhe h maximal?
-> n ≤ 2h+1 - 1
Wie viele Kanten (edges) e hat ein binärer Baum mit n Knoten? -> e = n - 1
Wie hängen bei einem vollständigen Binärbaum Blattzahl und die Zahl der inneren Knoten
zusammen?
Bäume finden bei arithmetischen Ausdrücken als Strukturbäume (parse trees) eine
Anwendung. In den inneren Knoten sind die Operatoren, in den Blättern werden die
Operanden gespeichert.
© Wagner, 14. Apr. 2011 Seite 4
Binäre Bäume
Strukturbäume (parse trees)
a+b*c
(a + b)*c
+
*
*
a
+
c
b
b
a
Weitere Beispiele:
(( a + b ) / c ) * (d - e*f)
( a + b*c )*d
Aufgabe: Welche der obigen Strukturbäume sind vollständig?
Für einen vollständigen binären Baum der Höhe h gilt:
Höhe
Knoten n
0
1
2
1 = 20+1 -1
3 = 21+1-1
7 = 22+1-1
Blätterzah
l
1= 20
2= 21
4= 22
h
n = 2h+1 -1
2h
n = 2h+1 -1
à n + 1 = 2h+1 | lg
à lg(n + 1) = (h + 1)* lg 2
à h = lg(n+1) /lg 2 - 1
© Wagner, 14. Apr. 2011 Seite 5
c
Binäre Bäume
Eigenschaften
Falls der Baum vollständig ist, gibt es
1 Knoten mit der Weglänge 0
2 "
"
"
1
4 "
"
"
2
8 "
"
"
3
.............
2k "
"
k
Für einen vollständigen Binärbaum der Höhe h = 3 gilt für die mittlere Weglänge:
laenge = (1*0 + 2*1 + 4*2 + 3*8 ) /15 = 2,3
Aufgaben
Berechne Knoten- und Blattzahl, sowie die mittlere Weglänge bei einem vollständigen Baum
der Höhe h = 4, 5, 6, 10, 20.
Die Höhe eines vollständigen binären Baums wächst nur logarithmisch mit der Knotenzahl:
n = 10000 ⇒ h ≈ 13; n=106 ⇒ h ≈ 19
© Wagner, 14. Apr. 2011 Seite 6
Binäre Bäume
Vollständig ausgeglichene Bäume
Konstruktion eines Baums mit minimaler Höhe
(vollständig ausgeglichener Baum)
Beispiel: n = 10
5
nli = [ n / 2]
2
nre = n -1 - [ n / 2]
4
2
nli = [2 div 2]
2
nre = 0
Der komplette Baum
© Wagner, 14. Apr. 2011 Seite 7
1
usw.
Binäre Bäume
Aufgaben:
Erstelle vollständig ausgeglichene Bäume mit n = 5, 6, 7, 8, 9, 11 Knoten.
Lösung (für n = 8)
Vollständig ausgeglichener Baum
(n = 8)
5
7
3
2
4
6
8
1
Definition: Ein binärer Baum heißt vollständig ausgeglichen, wenn sich für jeden Knoten
die Anzahlen der Knoten im linken und rechten Teilbaum um höchstens 1 unterscheiden.
Anmerkung (nicht im Lehrplan)
Eine schwächere Definition gilt für den AVL-Baum:
Definition: Ein binärer Baum heißt ausgeglichener Baum (AVL-Baum: Adelson-Velskij;
Landis), wenn sich für jeden Knoten die Höhen der beiden Teilbäume um höchstens 1
unterscheiden.
© Wagner, 14. Apr. 2011 Seite 8
Binäre Bäume
Algorithmus Voll_Ausgeglichener_Baum
· Erzeuge Knoten für die Wurzel
· Erzeuge linken Teilbaum mit nli = n / 2 Knoten (ganzzahlige Division)
· Erzeuge rechten Teilbaum mit nre = n - nli - 1 Knoten
© Wagner, 14. Apr. 2011 Seite 9
Binäre Bäume
Traversierungsarten
Traversieren eines Baums
(tree traversal)
W
L
R
Preorder: Betrachte (bearbeite) die Wurzel, dann in gleicher Weise
den linken Teilbaum, dann den rechten Teilbaum
Preorder: WLR
Inorder:
LWR
Postorder: LRW
Rekursive Traversierung eines Baums mit n Knoten
Jede Kante wird zweimal durchlaufen: Beim Absteigen und beim Aufsteigen.
Dies ergibt 2n -2 Kantentraversierungen (Schritte), d.h. S(n) = O(n)
© Wagner, 14. Apr. 2011 Seite 10
Binäre Bäume
Fülle einen vollständig ausgeglichenen Baum mit n Knoten gemäss Inorder mit den Zahlen 1
bis n: Gib die Knotenreihenfolge für die Traversierungsarten Preorder und Postorder an: n= 7
( n= 9)
Beispiel: n = 8
Vollständig ausgeglichener Baum
(n = 8)
5
7
3
2
4
6
8
1
Aufgaben
1.1 Erstelle "von Hand" einen vollständig ausgeglichenen binären Baum derart, dass bei
Preorder-Traversierung das Wort ALGORITHMUS gelesen wird.
1.2 Schreibe die Besuchsreihenfolge bei Inorder- und Postorder-Traversierung auf.
1.3 Bei Postorder-Traversierung eines Baumes wird das Wort POSTORDER ausgegeben.
Gib den Baum an.
© Wagner, 14. Apr. 2011 Seite 11
Binäre Bäume
Anwendung: Strukturbäume
Im Elternknoten steht das Operatorsymbol, die Kindknoten sind die Wurzeln der zu dem
Operator gehörenden Terme.
Traversieren eines Strukturbaums
c * (b + a)
*
+
c
b
Preorder
*c+ba
Inorder
c*b+a
Postorder
cba+*
Der Postorderdurchlauf
liefert die Postfixnotation.
Sie kommt ohne Klammern
aus und hält die Operatorprioritäten ein!
a
// jBaum09
Postorder-Traversierung
(a + b)*c
*
a b+ c *
+
a
b
c
© Wagner, 14. Apr. 2011 Seite 12
Binäre Bäume
Aufgaben
Erstelle für folgende Terme den Strukturbaum und gib den Term in Postfixnotation an:
a) a*(b+c) - d
b) 3* a + c/ 5
c) a * b + c - d
d) a * b +( c - d)
e) (a - c) / (e - 11)
f) ((a + b) /c)*(d - e*f)
g) ((a + b) /c) * (d - e + f)
Gib die Strukturbäume an
( a + b*c )*d
(( a + b ) /c )*(d - e * f)
(( a + b) + c) +d
a*(b + c) - d
Welche Ausgaben liefert ein Postorderdurchlauf?
Levelorder-Durchlauf
Durchlaufe den Baum Schicht für Schicht, beginnend mit der Wurzel.
Levelorder-Durchlauf
Start
1
3
2
4
8
6
5
9
7
10
© Wagner, 14. Apr. 2011 Seite 13
Gewinnpositionen
Ende ?
Binäre Bäume
Der Baum stellt Spielpositionen dar. Levelorder sucht Gewinnpositionen, die mit möglichst
wenig Zügen (Kanten) erreichbar sind.
Aufgabe: Wie groß ist die Maximalzahl der Knoten in einer Schicht, wenn der Baum aus n
Knoten besteht?
Lösung:
© Wagner, 14. Apr. 2011 Seite 14