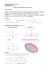a utilização do geogebra no ensino de equações diferenciais

Transcrição

CADERNO DE FÍSICA DA UEFS 12 (02): 57-71, 2014
A UTILIZAÇÃO DO GEOGEBRA NO ENSINO DE EQUAÇÕES
DIFERENCIAIS
THE UTILIZATION OF GEOGEBRA IN TEACHING OF DIFFERENTIAL EQUATIONS
Sonia Barbosa Camargo Igliori, Marcio Vieira de Almeida
Pontifícia Universidade Católica de São Paulo, [email protected]; [email protected]
Este artigo trata do ensino de equações diferenciais com o uso do software GeoGebra. Nele é apresentada uma
abordagem fundamentada em teoria elaborada por Tall e colaboradores visando favorecer a aprendizagem do Cálculo
Diferencial e Integral. Na perspectiva de Tall,os autores deste artigo escolheram um software adequado, o GeoGebra, e
definiram uma estratégia de resolução da equação diferencial, a forma (gráfica), ou qualitativa. Essas escolhas são parte
da pesquisa e por isso, os autores incluem no artigo todos os comandos e ferramentas disponíveis no software para
esboçar campo de direções associado a uma equação diferencial.Como resultado é esperado trazer aos docentes e
pesquisadores,envolvidos com ensino de conceitos de Cálculo,contribuições, tanto no que se refere à utilização de
elementos de uma teoria que favoreça esse ensino quanto a construção de uma atividade referenciada nela.
Palavras-chave:Educação Matemática, Equações Diferenciais, Tecnologia, Campos de Direção, David Tall.
This paper deals with the teaching of differential equations with the use of the GeoGebra software. The approach was
elaborated by Tall and contributing writers, aiming at favoring the learning of Differential and Integral Calculus. From
Tall’s perspective, the authors of this paper have chosen an adequate software, the GeoGebra and defined a strategy of
resolution of differential equations, the graphic form, or qualitative. These choices are part of the research and that is why
the authors include, in the paper, all the commands and tools which are available in the software in order to draw the field
of directions associated to a differential equation. We hope to contribute to teachers and researchers who are involved in
teaching concepts of Calculus. Not only do these contributions refer to the use of elements of a theory that benefits the
teaching, but also to the building of an activity referring to it.
Keywords: Mathematical Education, Differential Equations, Technology, Fields of Direction, David Tall.
INTRODUÇÃO
Este artigo tem por alvo apresentar uma abordagem de ensino para as equações diferenciais ordinária
de 1ª ordem com a utilização do computador.
A potencialidade da utilização dos computadores no ensino dos tópicos avançados da Matemática no
que se refere à aprendizagem é indicada por Tall quando diz:
[…] utilizar os computadores para visualizar conceitos matemáticos de maneira útil no
Cálculo e em Análise. A utilização criativa dos softwares, que plotam gráficos, e das
calculadoras gráficas tem permitido aos estudantes lidar de maneira significativa com
conceitos como a diferenciação por meio da noção de “retidão local”, integração por meio
da soma de áreas, e resolver equações diferenciais (de 1.ª ordem) por meio da visualização
da construção das curvas solução com um gradiente dado. Durante esse tempo, me tornei
cada vez mais consciente do conceito imagem limitado oferecido por gráficos plotadores
de gráficos que só desenhar gráficos razoavelmente suaves dados por fórmulas (TALL,
1993, p. 2, tradução nossa).
Na perspectiva desse pesquisador, o computador munido de um software adequado, pode ser utilizado
“para propiciar imagens que auxiliarão no desenvolvimento de tópicos do Cálculo e da Análise”
(ALMEIDA, 2013, p. 114).
No artigo (TALL, 2000) é apresentada uma característica, que determinados ambientes
computacionais possuem, e que pode ser utilizada para o desenvolvimento cognitivo dos sujeitos. Segundo o
pesquisador, os computadores:
[...] podem executar quaisquer algoritmos de forma rápida e eficiente, além de exibir o
resultado final com uma gama de diferentes representações. Por exemplo, os resultados
57
Igliori e Almeida
podem ser representados visualmente e manipulados fisicamente.Utilizando um mouse é
possível ao estudante construir relações corporificadas que fazem parte de uma estrutura
conceitual mais rica e ampla (TALL, 2000, p. 10, tradução nossa, grifo do autor).
Softwares que provêm um retorno imediato às alterações realizadas pelo usuário são denominados
pelo pesquisador como organizadores genéricos1, que é “um ambiente (ou micromundo2) que permite ao
aprendiz manipular exemplos e (se possível) contra exemplos de um conceito matemático específico ou de
um sistema de conceitos relacionados” (TALL, 2000, p. 10, tradução nossa, grifo do autor).
Tall sugere a apresentação da equação diferencial por meio da seguinte situação problema:
Considere o problema inverso da diferenciação (Não, esse não é a integração!). O
problema é o seguinte – se você conhece a inclinação de uma função em cada ponto de
seu domínio, como poderíamos construir seu gráfico? (TALL, 2000, p. 14, tradução
nossa).
E Tall atribui um significado corpóreo para esse conceito:
Se eu apontar meu dedo em um ponto (x, y) qualquer do plano, então eu posso calcular a
inclinação da curva solução naquele ponto como m = F(x, y) e traçar um segmento de reta
pequeno com inclinação igual a m através do ponto (x, y) (TALL, 2000, p. 14, tradução
nossa).
As equações diferenciais foram escolhidas para esta pesquisa levando - se em conta que seu estudo faz
parte de um instrumental matemático importante na resolução de problemas da de várias áreas do
conhecimento, como ressaltam Boyce e DiPrima,
A importância das equações diferenciais está no fato de que mesmo as equações mais
simples correspondem a modelos físicos úteis, como por exemplo, o decaimento de
substâncias radioativas, o comportamento de sistemas de massas e molas e o
comportamento de circuitos elétricos (BOYCE; DIPRIMA, 1999, prefácio).
Bassanezi (2013) destaca a importância das equações diferenciais como um tópico vasto da
Matemática e que pode ser abordado de maneiras diversas, dependendo do objetivo proposto. Esse
pesquisador destaca o papel desse conceito para modelar um problema, quando diz que:
Um problema real não pode ser representado de maneira exata em toda sua complexidade
por uma equação matemática ou um sistema de equações. Um modelo deve ser
considerado apenas como um retrato ou uma simulação de um fenômeno e sua validação
depende muito da escolha das variáveis e das hipóteses formuladas. É muito frequente em
se tratando de modelar um fenômeno ou um experimento, obtermos equações para
descrever as ‘variações’das quantidades (variáveis de estado) presentes e consideradas
essenciais. Desta forma, as leis que regem tal fenômeno são traduzidas por equações de
variações. Quando estas variações são instantâneas, a dinâmica do fenômeno se
desenvolve continuamente e as equações matemáticas são denominadas equações
diferenciais (BASSANEZI, 2013, p. 61 – 62).
Tomando por base os componentes teóricos apresentados por Tall no que se refere ao uso do
computador no ensino da Matemática, escolheu-se o software GeoGebra. No decorrer deste artigo, são
apresentados comandos e ferramentas disponíveis nesse software para a construção da aplicação pretendida,
qual seja esboçar um campo de direções associado a uma equação diferencial dada.
Esse software de Geometria Dinâmica foi escolhido porque além de ser gratuito possui interface
simples e intuitiva, e, possibilita o desenvolvimento de atividades que unem a Geometria, a Álgebra e o
1 Tradução do termo original generic organisers.
2Esse termo é utilizado pelo pesquisador no sentido que Papert (1980, p. 117 apud TALL, 1986) como “um mundo autossuficientes no
qual certas questões são relevantes e outras não”.
58
A Utilização do Geogebra...
Cálculo. Há a possibilidade de elaborar e modificar applets, tanto para uso em sala de aula quanto para
disponibilizar em web sites da internet.
Esse software possui todas as ferramentas e comandos que possibilitam a construção dos campos de
direção. Com isso, pretende-se destacar que o GeoGebra pode ser utilizado na introdução de conceitos
avançados do Cálculo Diferencial e Integral.
O que motivou a forma de abordagem por meio da exploração dos campos de direção associado a uma
equação diferencial, foi tratar-se de uma abordagem qualitativa e possibilitar o estudo no registro de
representação geométrico (ARTIGUE, 1994).
Além disso, porque livros de Cálculo, editados atualmente, como Stewart (2005) e Anton, Bivens e
Davis (2007) indicam o uso da abordagem por meio dos campos de direção.
Em Stewart (2005), por exemplo, após apresentar a definição de uma equação diferencial, a ordem de
uma equação diferencial e dois exemplos de modelagem, cujo modelo é uma equação diferencial, são
apresentados os campos de direção, como uma maneira pela qual é possível “aprender muito sobre a solução
[de uma equação diferencial] através de uma abordagem gráfica (campos de direção)” (STEWART, 2005,
p. 586, adaptado). Nós completaríamos, mesmo quando não é possível obter uma solução analítica.
Este artigo está dividido assim:campo de direções; ferramentas e comandos do software, que
possibilitam a construção do campo de direções; um exemplo da Física. Para finalizar serão apresentadas
considerações sobre as contribuições esperadas.
CAMPO DE DIREÇÕES
Se f é uma função definida em um aberto
A⊂
2
assumindo valores em
.
A equação
dy
= f ( x, y ) ou y ' = f ( x , y ) ,
dx
(1)
é uma equação diferencial ordinária de primeira ordem.
A função diferenciável y=y(x) será chamada uma solução de (1) em um intervalo aberto I de
se e
somente se y e sua derivada y’satisfazem (1).
A interpretação gráfica das soluções de uma equação diferencial com em (1) é a seguinte: se um
ponto ( x0 , y 0 ) pertence a uma solução y = y(x) então f ( x 0 , y 0 ) é a inclinação
da reta tangente ao gráfico
de y nesse ponto.
Chama-se campo de direções de uma equação diferencial, como em (1), nos pontos (x, y) do aberto Ao
conjunto dos segmentos de retas com um vértice em (x,y) e com inclinação f(x,y). Exemplo:
59
Igliori e Almeida
Figura 1: A representação do campo de direções associado à equação diferencial. Fonte: Os autores.
Os segmentos de reta indicam a direção da curva solução em dado ponto. Esse campo auxilia a
visualizar a família de curvas solução da equação diferencial. No caso do campo de direções associados à
equação y '= 2 x é possível vislumbrar que a família de soluções e a família de parábolas dadas pela
sentença y = x 2 + c (com c ∈ ). Por exemplo, a curva solução no ponto (0,1) é a apresentada na Figura 2:
Figura 2: O esboço da curva solução da equação diferencial no ponto (0,1). Fonte: Os autores.
A abordagem das equações diferenciais por meio do campo de direção possibilita propiciar um
significado à solução da equação diferencial, o qual pode auxiliar a compreensão dessa noção.
A CONSTRUÇÃO DO CAMPO DE DIREÇÕES NO GEOGEBRA
60
Nesta seção serão apresentados comandos e ferramentas, disponíveis no software GeoGebra que
possibilitam a construção de um campo de direções associado a uma equação diferencial y ' = f ( x, y ) , no
seguinte conjunto do plano { ( x, y ) ∈
2
− 5 ≤ x ≤ 5 e − 5 ≤ y ≤ 5 }3.
Para a construção de um campo de direções é necessário esboçar um conjunto dos segmentos de retas
com um dos extremos em (x,y) e inclinação igual a f(x, y).
Inicialmente é apresentada a ferramenta Campo de Entrada4 a qual possibilita ao usuário digitar a
sentença f (x, y), segundo membro da equação diferencial. Após isso o software esboçará o campo de
direções.
Após clicar no ícone Campo de Entrada clique em Janela de Visualização com o objetivo de
posicionar o campo. Após esse clique aparece uma janela, que possui dois campos: Legenda e Objeto
Vinculado. No campo Legenda deve ser colocada a identificação associada a esse campo. Neste artigo, por
exemplo, a legenda adotada foi: “Digite o segundo membro da equação y’=f(x,y)”. No campo Objeto
Vinculado, deve ser selecionado um objeto, já construído no arquivo GeoGebra, que será associado ao
Campo de Entrada, e receberá como parâmetro o que foi digitado nesse Campo. No caso deste artigo, por
exemplo,o objeto é uma função real de duas variáveis
f(x,y) = x + y.
(2)
O segundo é o comando “Segmento [<Ponto>, <Ponto>]” (HOHENWARTER, 2009, p. 49) que
constrói um segmento de reta cujos extremos são as coordenadas dos pontos digitados no comando. Para
inserir um ponto no GeoGebra é necessário digitar, entre parênteses, a abscissa e a ordenada do ponto e
separá-los por vírgulas. Por exemplo, para construir o segmento com extremos (1, 2) e (3, 4) basta digitar, no
campo Entrada, o seguinte comando: Segmento [(1,2), (3,4)].
Na Janela de Visualização, é desenhado o segmento:
Figura 3: Segmento de reta com extremos nos pontos (1, 2) e (3, 4). Fonte: Os autores.
Para esboçar o segmento de reta, com as condições necessárias, para a construção do campo de
direções, será utilizado o seguinte procedimento:
3O procedimento exposto neste artigo pode ser aplicado a outros conjuntos do plano, foi fixado esse exemplo, para ilustrar o método de
construção apresentado.
4 O ícone desse campo, na versão 4.4 do GeoGebra, é o seguinte
.
61
Igliori e Almeida
Seja (a,b) um ponto do plano e y’ = f(x, y) uma equação diferencial. A equação da reta que passa
por (a,b)e tem coeficiente angular f(a, b)é:
y − b = f ( a, b ) ⋅ ( x − a ) .
(3)
Para esboçar um segmento de reta com as condições necessárias para a construção do campo de
direções deve-se determinar os extremos de cada um dos segmentos que comporão o campo. Para possibilitar
a construção considera-se que cada segmento possua o mesmo comprimento; Assim é possível determinar as
coordenadas dos extremos encontrando os pontos de interseção de uma reta que passa por (a, b) com a
circunferência, com centro em (a, b) e raio igual à metade do comprimento do segmento, conforme a Figura 4.
Figura 4: Os extremos de um segmento, como comprimento fixo, e inclinação igual a f(a, b). Fonte: Os autores.
Para obter as coordenadas dos extremos do segmento de reta, com comprimento igual a s, que vai
compor o campo de direções, é necessário resolver o seguinte sistema de equações:

( y − b) = f (a, b) ⋅ ( x − a )

.

s2
2
2
x
a
y
b
(
−
)
+
(
−
)
=


4
(4)
Resolvendo o sistema obtém-se as abscissas das coordenadas dos extremos dos segmentos de reta que
vão compor, a saber, o campo de direções:
x1 = a −
s
2
2 1 + [ f ( a, b)]
e x2 = a +
s
2
2 1 + [ f (a, b)]
.
(5)
.
(6)
E as ordenadas dos extremos dos segmentos de reta serão:
y1 = b −
s ⋅ f ( a, b)
2
2 1 + [ f (a, b)]
e y2 = b +
s ⋅ f ( a, b)
2
2 1 + [ f (a, b)]
Logo, as coordenadas dos extremos de um segmento de reta com medida igual a s são os pontos
( x1 , y1 ) e ( x 2 , y 2 ) .
O terceiro comando é o comando Sequência. Segundo o manual do software (HOHENWARTER,
2009, p. 60–61), para utilizá-lo é necessário digitar o seguinte no Campo Entrada: “Sequência[<Expressão>,
<Variável>, <Valor inicial>, <Valor Final>, <Incremento>]”, tal comando fornece a lista dos objetos
criados usando a “Expressão” dada, em função da “Variável”, determinada pelo usuário e que deve fazer
parte da “Expressão” digitada, que varia a partir do “Valor inicial”, com a soma do “Incremento”, até o
“Valor final”.
62
Para a construção do campo de direções, associado à equação diferencial y ' = f ( x, y ) passando por
(a,b) é necessário construir uma sequência de segmentos levando-se em conta as coordenadas dos pontos
extremos do segmento de reta, cujas coordenadas são ( x1 , y1 ) e ( x 2 , y 2 ) , e a inclinação desse segmento de
reta é a igual a f(a,b).
Após ter definido, no GeoGebra, a função real de duas variáveis reais e o comprimento de cada
segmento de reta, neste artigo 0,2 u. c., será construída uma sequência de segmentos de reta, cada um com a
inclinação necessária para a construção do campo de direções e de modo que a ordenada, dos pontos médios
dos extremos, seja zero.
Para construir essa sequência é necessário digitar os seguintes comandos, no campo Entrada:
Sequência [Segmento[(d - 0.1 / sqrt(1 + f(d, 0)²), 0 + f(d, 0) (-0.1) / sqrt(1 + f(d, 0)²)), (d + 0.1 (1 /
sqrt(1 + f(d, 0)²)), 0 + f(d, 0) 0.1 (1 / sqrt(1 + f(d, 0)²)))], d, -5, 5, 0.2].
Destrinchando o código exposto anteriormente: o comando “Segmento[(d - 0.1 / sqrt(1 + f(d, 0)²), 0 +
f(d, 0) (-0.1) / sqrt(1 + f(d, 0)²)), (d + 0.1 (1 / sqrt(1 + f(d, 0)²)), 0 + f(d, 0) 0.1 (1 / sqrt(1 + f(d, 0)²)))]” cria
um segmento de reta, cujo extremos são as coordenadas ( x1 , y1 ) e ( x 2 , y 2 ) , definidas pelas expressões (5)
e (6). O valor “0.1” presente no código é referente à metade do comprimento de cada um dos segmentos, que
neste exemplo é 0,2 u.c.. Os valores iniciais e finais estão relacionados à região do plano, na qual o campo de
direções será esboçado. Caso se considere outra região do plano, basta alterar os valores Inicial e Final desse
código.O incremento, fixado nesta linha de código em “0.2”, está relacionado ao valor da abscissa do
próximo termo da sequência, que será o valor inicial somado a “0.2”. Logo, com valor inicial igual a – 5 e
inicial igual a 5, serão esboçados cinquenta segmentos de reta. Caso seja necessário alterar o espaçamento
entre cada segmento de reta, basta aumentar, ou diminuir, o incremento.
Como resultado, do código anterior, é obtida a seguinte sequência de segmentos, na Janela de
Visualização:
Figura 5: Uma sequência de segmentos de reta do campo de direções da equação diferencial em que o
ponto médio dos extremos tem ordenada zero. Fonte: Os autores.
Ao substituir o valor 0, no código anterior, por 15, será obtida a seguinte sequência de segmentos cujos
pontos médios dos extremos possuem ordenada igual a 1. Na Figura 6 está a representação dessa outra
sequência de segmentos, na Janela de Visualização:
5Após essa alteração, o código resultante será o seguinte: Sequência[Segmento[(d - 0.1 / sqrt(1 + f(d, 1)²), 1 + f(d, 1) (0.1) / sqrt(1 + f(d, 1)²)), (d + 0.1 (1 / sqrt(1 + f(d, 1)²)), 1 + f(d, 0) 0.1 (1 / sqrt(1 + f(d, 1)²)))], d, -5, 5, 0.2].
63
Igliori e Almeida
Figura 6: Uma sequência de segmentos de reta do campo de direções da equação diferencial, em que os
pontos médios dos extremos têm ordenada igual a 1. Fonte: Os autores.
Assim,
{ ( x, y ) ∈
2
para
construir
o
campo
de
direções,
no
conjunto
− 5 ≤ x ≤ 5 e − 5 ≤ y ≤ 5 }, é necessário “encaixar” dois comandos Sequência, um
responsável pela variação da ordenada e o outro construirá uma “fileira” de segmentos de reta do campo de
direções. Com isso, o código final será o seguinte:
Sequência[Sequência[Segmento[(d - 0.1 / sqrt(1 + f(d, e)²), e + f(d, e) (-0.1) / sqrt(1 + f(d, e)²)), (d +
0.1 (1 / sqrt(1 + f(d,e)²)), e + f(d, e) 0.1 (1 / sqrt(1 + f(d, e)²)))], d, -5, 5, 0.2], e, -5, 5, 0.2].
Os elementos destacados em negrito, no código acima, dizem respeito aos acréscimos e alterações, em
relação ao código anterior. Essas alterações produzem: com o acréscimo de outro comando Sequênciaa
construção de uma sequência em que cada elemento é uma “fileira” do campo de direções, e a variável
associada a essa sequência é “e”. O primeiro “elemento” dessa sequência é composto por segmentos, cujos
pontos médios dos extremos possuem ordenada igual a – 5; o outro termo é composto por segmentos cujos
pontos médios dos extremos segmentos possuem ordenada igual a “– 4,8”, por causado incremento
especificado no código6. Esse processo é repetido até que a soma dos incrementos seja igual a cinco.
Ao realizar essas alterações no código, o resultado final na Janela Visualização é:
Figura 7: O campo de direções da equação diferencial y'= 2 x representado no conjunto
{ ( x, y ) ∈
2
− 5 ≤ x ≤ 5 e − 5 ≤ y ≤ 5 }. Fonte: Os autores.
Com todas as ferramentas e comandos apresentados neste artigo tem-se como resultado os seguintes
elementos na Janela de Visualização: um Campo de Entrada para que o usuário digite a sentença da função
de duas variáveis, associadas à equação diferencial, e o campo de direções, associado a essa equação
diferencial, no seguinte conjunto do plano cartesiano
{ ( x, y ) ∈
2
− 5 ≤ x ≤ 5 e − 5 ≤ y ≤ 5 }.
6 Note que para colocar o número decimal 0,2, no software GeoGebra, é necessário digitar no campo Entrada: 0.2, com
um ponto final, ao invés de uma vírgula.
64
Figura 8: O resultado final das construções desenvolvidas neste artigo. Fonte: Os autores.
Da maneira como o arquivo foi desenvolvido, basta que o usuário digite, no campo de Entrada (parte
superior da Figura 8), existente na Janela de Visualização, para que o software trace o campo de direções
associados à equação diferencial.
A seguir, são apresentados outros exemplos de campos de direção:
Figura 9: Os campos de direções associados às equações diferenciais (figura da direita) e da (figura da
esquerda). Fonte: Os autores.
EXEMPLO DE APLICAÇÃO À FÍSICA
Nesta seção é apresentado um exemplo de uma situação problema relacionada à Física, modelada por
uma equação diferencial, e que com o estudo do campo de direções é possível investigar o comportamento
das soluções de forma não algébrica, ou seja, sem a necessidade de uma resolução analítica.
Esse exemplo encontra-se no capítulo introdutório do livro de Boyce e Di Prima (1999), na seção
“Um objeto em queda”.
65
Igliori e Almeida
A situação é a seguinte: suponha que um objeto está caindo na atmosfera, perto do nível do mar. Esse
movimento é governado pela segunda Lei de Newton, que diz que o módulo da força resultante sobre um
objeto é igual ao produto da massa do objeto pela sua aceleração.
Fresul tan te = m ⋅ a .
(7)
Sendo que m é massa do objeto (em kg), a sua aceleração (m/s2) e F a força resultante que age sobre o
objeto, em Newtons (N).
É possível relacionar a aceleração e a velocidade do objeto, pela seguinte equação:
a=
dv
.
dt
(8)
Com isso, a equação (7) é reescrita do seguinte modo:
Fresul tan te = m ⋅
dv
.
dt
(9)
Após essa primeira análise, considere as forças que agem sobre um objeto em queda. Na Figura 10,
são exibidas essas forças:
Figura 10: Esquema com as forças que agem num objeto em queda livre. Fonte: Boyce e Di Prima
(1999, p. 2).
Uma dessas forças é a força peso do objeto, cujo módulo é dado por mg (considerando g, a aceleração
da gravidade sendo aproximadamente igual a 9,8
m/s2, nas proximidades da superfície da Terra). A outra
força indicada é devido à resistência do ar. É admitido que a resistência do ar seja proporcional à velocidade
do objeto. Dessa maneira, a força de resistência do ar tem módulo igual a γ
⋅ v , sendo que γ é uma
constante chamada de coeficiente de resistência do ar, que varia de acordo com o objeto, e v a velocidade do
objeto em queda livre.
Para exemplificar, será considerado que a massa do objeto é 10 kg,
γ = 2 kg/s e a aceleração da
2
gravidade 9,8 m/s . Então pela equação (9) tem-se:
dv
v
= 9,8 − .
dt
5
Na equação diferencial (10),
(10)
v
f (t , v ) = 9,8 − . Independente de não ser conhecida acurva solução,
5
é possível tirar algumas conclusões como: se o ponto (t 0 , v 0 ) pertencer à curva solução, então
v
dv
(t 0 ) = 9,8 − 0 . Isso é equivalente a dizer que a inclinação da reta tangente à curva solução em
dt
5
66
(t 0 , v 0 ) é 9,8 −
de
v0
. No exemplo apresentado neste artigo, é possível inferir que independentemente do valor
5
t, o valor da inclinação no ponto (t , v 0 ) é o mesmo. Logo, o campo de direções associados à equação
diferencial (10) possuirá nos pontos do plano, cujas abscissas são iguais, segmentos com mesma inclinação.
Para exemplificar serão fixados dois valores de v: se v1
= 30 então
dv
= 3,8 ; e se v1 = 60 então
dt
dv
= − 0, 2 .
dt
Com auxílio da aplicação construída neste artigo, é possível esboçar o campo de direções da equação
(10) no conjunto { ( x , y ) ∈
2
0 ≤ x ≤ 10 e 30 ≤ y ≤ 60 }. Para isso devem ser alterados os seguintes
parâmetros: o primeiro é o tamanho de cada um dos segmentos, que compõe o campo de direções, pois um
segmento com
0,2 u. c. deixaria a representação do campo, muito “poluída” e não auxiliaria no estudo
pretendido. Em virtude do conjunto que será representado, os valores iniciais e finais do código tiveram que
ser alterado e também o incremento, que foi alterado para 1 u. c.. O código está em 7.
No exemplo em questão deve ser digitado no Campo de Entrada o comando: “9.8 - y/5”: O campo
representado é o que segue:
Figura 11: O campo de direções associados à equação diferencial. Fonte: Os autores.
Por meio da representação do campo de direções é possível fazer outras deduções qualitativas sobre o
comportamento das soluções da equação diferencial. Uma dessas seria que se a velocidade de queda do
objeto (v) fosse menor que determinado valor, então todos os segmentos de reta possuem coeficientes
angulares positivos, e a velocidade de queda aumenta enquanto o objeto cai. Pela observação da Figura 11,
isso acontece para valores de v menores que 49 m/s.
7Sequência[Sequência[Segmento[(d - 0.5 / sqrt(1 + f(d, e)²), e + f(d, e) (-0.5) / sqrt(1 + f(d, e)²)), (d + 0.5 (1 / sqrt(1 + f(d,
e)²)), e + f(d, e) 0.5 (1 / sqrt(1 + f(d, e)²)))], d, 0, 10, 1], e, 30, 60, 1]
67
Igliori e Almeida
Por outro lado é possível observar que os coeficientes angulares das retas que compõem o campo de
direções, são negativos,se os valores de v fossem maiores do que 49 m/s.Isso significa que a velocidade do
objeto em queda vai diminuindo à medida que ele cai.
No campo de direções para v = 49 m/s, parece que os segmentos formam uma reta. Considere a função
real
v, dada pela sentença v(t) = 49, é uma solução da equação diferencial, descrita em (10). Essa solução
não varia de acordo com o tempo, essa é a chamada solução de equilíbrio (BOYCE, DI PRIMA, 1999, p. 2).
Uma interpretação física dessa solução é que ela corresponde ao equilíbrio entre a gravidade e a resistência
do ar.
Com o campo de direções representado (Figura 10), é possível notar que todas as outras soluções, da
equação diferencial considerada, parecem estar convergindo para a solução de equilíbrio quando
t tende a
infinito.
Outra sugestão é após expor a maneira analítica de resolver a equação diferencial que modela a
situação, uma equação diferencial linear de 1ª ordem, esboçar junto do campo de direções, uma das curvas
soluções da equação diferencial. Para o problema proposto no artigo, a solução geral é a seguinte:
v (t ) = 49 + k ⋅ e
1
− t
5
, sendo
k∈ .
(11)
Definas duas condições iniciais e esboce duas curvas soluções da equação diferencial que modela o
nosso problema. Para exemplificar, serão esboçadas as seguintes curvas soluções da equação:
v1 (t ) = 49 − 9 ⋅ e
1
− t
5
e v 2 (t ) = 49 + 11 ⋅ e
1
− t
5
. Isso tem o objetivo de mostrar que as inferências feitas na
abordagem qualitativa estão de acordo com a solução analítica. Na Figura 12, estão as duas curvas e o campo
de direções.
Figura 12: O campo de direções e duas soluções particulares da equação diferencial y ' = 9,8 − y . Fonte:
5
Os autores.
CONSIDERAÇÕES FINAIS
Neste artigo apresentou-se uma atividade com o uso do GeoGebra para o ensino das equações
diferenciais ordinárias,a ser utilizada por professores e pesquisadores envolvidos com cursos superiores que
68
têm Cálculo, como disciplina do currículo. O objetivo da atividade é evidenciar as vantagens do uso da
tecnologia para o ensino dessa área. A atividade envolve a escolha de uma abordagem para a resolução da
equação, a gráfica ou qualitativa. Para tanto é construído e explorado o campo de direções, associado à
solução.
A vantagem da utilização do computador para ampliar a potencialidade da aprendizagem está
sustentada pela teoria de Tall sobre a atribuição do significado corporificado ao conceito matemático. Para
obter essa corporificação Tall desenvolveu um software que constrói a solução gráfica de uma equação
diferencial de 1ª ordem do seguinte modo: o mouse é utilizado para mover um segmento, cuja inclinação é
definida pela equação diferencial, dada pelo usuário, e com um clique sobre o plano cartesiano, esse
segmento é fixado (BLOKLAND, GIESSEN, TALL, 2000 apud TALL, 2001, p. 211). Na Figura 13 está
representado esse software:
Figura 13: Exemplo de software que explora a solução de uma equação diferencial. Fonte: Blokland,
Giessen e Tall (2000 apud TALL, 2001, p. 211).
Uma parte deste estudo foi analisar se os comandos do GeoGebra preenchiam as condições exigidas
pelo software construído por Tall (Figura 13). Verificou-se que com o GeoGebra era necessário construir o
campo de direções, diferentemente do software da Figura 13 que possibilita o aparecimento das tangentes
com a movimentação do mouse. Deixamos para outra pesquisa a verificação se é possível conseguir com o
GeoGebra essa mesma funcionalidade. Mesmo assim achamos interessante apresentar uma atividade com o
uso do GeoGebra, pois com isso é possível propiciar a um número maior de pessoas a utilização da teoria de
Tall.
Destacamos também que há no software GeoGebra, desde a versão 4.4, o comando: ResolverEDO e
suas variações8, com os quais podemos construir um lugar geométrico, e então apresentar a solução da
8 As variações desse comando são as seguintes: ResolverEDO[<f’(x,y)>]; ResolverEDO[<f’(x,y)>, <Ponto de f>];
ResolverEDO[<f’(x,y)>, <Valor de x Inicial>, <Valor de y Inicial>, <Valor de x Final>, <Passo>]; ResolverEDO[<y’>,
<x’>, <Valor de x Inicial>, <Valor de y Inicial>, <Valor de t Final>, <Passo>].
69
Igliori e Almeida
equação e ser adendada ao campo associado a ela, ampliando assim as possibilidades de exploração dos
conceitos envolvidos.
Para finalizar queremos destacar que a abordagem qualitativa tem sido defendida em pesquisas como
é o caso de Javaroni (2007) e em Artigue (1994).
REFERÊNCIAS
ALMEIDA, M. V. Um panorama de artigos sobre a aprendizagem do cálculo diferencial e integral na
perspectiva de David Tall. 2013. 155 f. Dissertação (Mestrado em Educação Matemática) –
Pontifícia Universidade de São Paulo, São Paulo, 2013.
ANTON, H.;BIVENS, I.; DAVIS, S. Cálculo. Volume I. Tradução Claus Ivo Doering. Bookman, 8ª
ed.PortoAlegre: Bookman, 2007.
ARTIGUE, M. Didactical engineering as a framework for the conception of teaching products. In:
BIEHLER, R. E. A. (Ed.). Didactics of Mathematics as a Scientific Discipline.Netherlands:
KluwerAcademicPublishers, p.27 – 39, 1994.
BASSANEZI, R. C. Temas & Modelos. Santo André: UFABC, 2013.
BOYCE, W. E.; DIPRIMA, R. C. Equações Diferenciais Elementares e Problemas de Valores de
Contorno. Tradução de Horácio Macedo. 6. ed. rev. Rio de Janeiro: LTC, 1999.
HOHENWARTER, J.; HOHENWARTER, M. Ajuda GeoGebra: Manual Oficial da Versão 3.2. Tradução e
adaptação
para
português
(de
Portugal)
de
António
Ribeiro.
2009.
Disponível
em:
<http://www.geogebra.org/help/docupt_PT.pdf >. Acesso em: 25 jun. 2014.
JAVARONI, S. L. Abordagem geométrica: possibilidades para o ensino e aprendizagem de Introdução
às Equações Diferenciais Ordinárias. 2007. 231f. Tese (Doutorado em Educação Matemática) –
Universidade Estadual Paulista Júlio de Mesquita Filho, Rio Claro, 2007. Disponível em:
http://www.rc.unesp. br/gpimem/downloads/teses/javaroni_tese.pdf. Acesso em: 28 jun. 2014.
STEWART, J. Cálculo. Vol. II. 4 ed. São Paulo: Pioneira Thomson Learning, 2005.z
TALL, D. O. Building and Testing a Cognitive Approach to the Calculus Using Interactive Computer
Graphics.1986. 505 f. Tese (Doutorado em Educação Matemática) – Universityof Warwick,
Inglaterra, 1986.
__________. Concept Images, Generic Organizers, Computers and Curriculum Change.For the
Learning
of
Mathematics,
9(3):
70
37-42,
1989.
Disponivelem:
<http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.377.2004&rep=rep1&type=pdf>.
Acesso em: 25jun. 2014.
__________.Real Mathematics, Rational Computers and Complex People. In: ANNUAL
INTERNATIONAL CONFERENCE ON TECHNOLOGY IN COLLEGE MATHEMATICS
TEACHING,
5.,
1993,
Procedings…,
Addison-Wesley,
Disponívelem:<http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/
p.
243-258,
1993.
dot1993h-real-rat-
cmplx.pdf>.Acessoem: 25 jun. 2014.
__________.Biological Brain, Mathematical Mind & Computational Computers (how the computer
can support mathematical thinking and learning). In: ASIAN TECHNOLOGY CONFERENCE
IN MATHEMATICS, 5, 2000, Chiang Mai. Proceedings... Blackwood: ATCM Inc, 2000.
Disponível em: <http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/ dot2000h-plenaryatcm2000.pdf>. Acesso em: 25jun. 2014.
___________. Cognitive development in advanced mathematics using technology.Mathematics
Education
Research
12
Journal,
(3),
p.
210
–
230,
2001.Disponívelem<http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2001b-merjamt.pdf>.Acesso em: 25jun. 2014.
71

a utilização do geogebra no ensino de equações diferenciais

Transcrição

Documentos relacionados

CÁLCULO DE RAÇÃO PELO MÉTODO ALGÉBRICO

2. Função Linear 2.1 Função linear e sua representação gráfica

EM 524 – aula 04

Derivada Implícita

Alg I - Glencoe

Superfícies Quádricas (Resumo)

e4-SOLICITACAO ADJUNTO-FISICA APLICADA

y - Webnode

Imprimir os dados deste veículo

Prova/Gabarito