T rajectory - trackingand P ath - following C ontrollersfor C

T rajectory - trackingand P ath - following C ontrollersfor C

T r a je c to r y -tr a c k in g a n d P a th -fo llo w in g C o n tr o lle r s fo r C o n s tr a in e d
U n d e r a c tu a te d V e h ic le s u s in g M o d e l P r e d ic tiv e C o n tr o l*
A n d re a A le s s a n d re tti1
2
, A . P e d ro A g u ia r
A b s tr a c t— T h is p a p e r a d d r e s s e s th e d e s ig n o f M o d e l P r e d ic tiv e C o n tr o l (M P C ) la w s to s o lv e th e tr a je c to r y -tr a c k in g
p r o b le m a n d th e p a th -fo llo w in g p r o b le m fo r c o n s tr a in e d u n d e r a c tu a te d v e h ic le s . B y a llo w in g a n a r b itr a r ily s m a ll a s y m p to tic
tr a c k in g e r r o r , w e d e r iv e M P C la w s w h e r e th e s iz e o f th e
te r m in a l s e t is o n ly lim ite d b y th e s iz e o f th e s y s te m c o n s tr a in ts .
I n fa c t, fo r th e c a s e o f u n c o n s tr a in e d in p u ts , th e te r m in a l s e t
c a n b e n e g le c te d a n d th e r e s u ltin g M P C c o n tr o lle r s p r o v id e
a g lo b a l s o lu tio n to th e a d d r e s s e d c o n s tr a in e d m o tio n c o n tr o l
p r o b le m s . S im u la tio n r e s u lts a r e p r e s e n te d w h e r e th e p r o p o s e d
M P C c o n tr o lle r s a r e a p p lie d to 2 -D a n d to 3 -D m o v in g v e h ic le s .
I. IN T R O D U C T IO N
T h e m o tio n c o n tro l o f u n d e ra c tu a te d v e h ic le s h a s b e e n
a lo n g th e y e a r s a n a ttr a c tiv e to p ic b e c a u s e o f th e w id e
ra n g e o f p ra c tic a l a p p lic a tio n s a n d th e th e o re tic a l c h a lle n g e s
a s s o c ia te d w ith th e c o n tro l p ro b le m .
In s p ite o f th a t a n d th e n u m e ro u s re s u lts p u b lis h e d in
th e te c h n ic a l lite ra tu re , w h e re a la rg e s e t o f th e p ro p o s e d
c o n tro l a lg o rith m s a re o b ta in e d v ia L y a p u n o v -b a s e d d e s ig n
te c h n iq u e s , o n ly fe w m e th o d s e x p lic itly c o n s id e r th e c a s e o f
c o n s tra in e d in p u ts s ig n a ls . T h is re s u lts in c o n tro l la w s th a t,
in p ra c tic e , a re o n ly a p p lic a b le in a lim ite d re g io n w h e re
th e c o n tro l a c tio n , d e s ig n e d fo r th e u n c o n s tra in e d v e h ic le ,
d o e s n o t v io la te th e s y s te m c o n s tra in ts . W e re fe re n c e [1 ]– [5 ]
fo r s e m i-g lo b a l a n d g lo b a l s o lu tio n s to th e (u n c o n s tra in e d )
tra je c to ry -tra c k in g p ro b le m .
M o d e l p r e d ic tiv e c o n tr o l, g iv e n its a b ility to e x p lic itly h a n d le c o n s tra in ts , re p re s e n ts a n a tu ra l d ire c tio n fo r th e c o n tro l
o f c o n s tra in e d s y s te m s . A c o m m o n a p p ro a c h to s o lv e th e
tra je c to ry -tra c k in g a n d th e p a th -fo llo w in g p ro b le m c o n s is ts
in re w ritin g th e m a s s ta b iliz a tio n p ro b le m in a c o n v e n ie n tly
d e fi n e d e r r o r s p a c e , a n d t h e n u s e t h e c l a s s i c t o o l s f o r t h e
d e s ig n o f s ta b iliz in g M P C la w s , e .g ., [ 6 ] – [ 1 0 ] . H o w e v e r,
s in c e th e e rro r d y n a m ic s a re o fte n tim e -v a ry in g , s o lv in g th is
c o n t r o l p r o b l e m r e m a i n s a d i f fi c u l t t a s k a n d o n l y f e w r e s u l t s
h a v e b e e n p re s e n te d in th e lite ra tu re . F o r a n o v e rv ie w o n
t h e t o p i c s e e , f o r i n s t a n c e , t h e w o r k [ 1 1 ] . I n [ 1 2 ] , s u f fi c i e n t
c o n d itio n s fo r s ta b ility a re p re s e n te d a n d in [1 3 ]– [1 5 ] a lo c a l
s o lu tio n to th e tra je c to ry -tra c k in g p ro b le m c a n b e fo u n d .
* T
[P T D
F C T
S F R H
(F C T
1
h is
C /E E
[P E s
/B D
), P o
E´ c o l e
w o rk
A C R O
t-O E /E
/5 1 0 7 3
rtu g a l.
P o ly te
w
/1 1 3
E I/L
/2 0 1
a s
8 2 0 /2
A 0 0 0
0 o f
su p p o
0 0 9 ],
9 /2 0 1 1
th e F
rte
M
].
o u
d
b y
O R P H [E
T h e fi r s t
n d a tio n fo
p ro je c ts
C O N A V
F P 7 IC T 2 8 8 7
a u t h o r b e n e fi t e d f r
r S c ie n c e a n d T e
U
/F C T -P T
0 4 ], a n d
o m g ra n t
c h n o lo g y
c h n i q u e F e´ d e´ r a l e d e L a u s a n n e ( E P F L ) , L a u s a n n e , S w i t z e r -
3
a n d C o lin N . J o n e s
1
M o r e o v e r , f o r t h e s p e c i fi c c a s e o f u n i c y c l e m o d e l s e e a l s o
[1 6 ]. A s m a in d ra w b a c k o f th e s e a p p ro a c h e s , th e p ro p o s e d
t e r m i n a l s e t a n d t h e t e r m i n a l c o s t a r e o n l y l o c a l l y d e fi n e d ,
re s u ltin g in a p o te n tia lly lim ite d re g io n o f th e a ttra c tio n .
M o tiv a te d b y th e s e o b s e r v a tio n s , in th is p a p e r w e a d d re s s th e tra je c to ry -tra c k in g p ro b le m a n d th e p a th -fo llo w in g
p ro b le m fo r u n d e ra c tu a te d v e h ic le s w ith c o n s tra in e d in p u ts ,
w h e re th e m o tio n is c o n s id e re d in b o th 2 -D a n d 3 -D c a s e s .
A llo w in g a n a rb itra rily s m a ll a s y m p to tic tra c k in g e rro r, w e
d e r iv e M P C c o n tr o lle r s u s in g th e r e s u lts f r o m [ 1 7 ] to g e th e r
w ith a n o n lin e a r a u x ilia ry c o n tro l la w p ro p o s e d in [1 ]. T h e
re s u ltin g te rm in a l s e t is o n ly lim ite d b y th e s iz e o f th e
s y s te m c o n s tra in ts , le a d in g to g lo b a l s o lu tio n s fo r th e c a s e
o f u n c o n s tra in e d s y s te m s .
T h e re m a in d e r o f th is p a p e r is o rg a n iz e d a s fo llo w s . In
S e c t i o n I I t h e a d d r e s s e d m o t i o n c o n t r o l p r o b l e m s a r e d e fi n e d .
In S e c tio n III w e re c a ll s o m e re s u lts fro m th e lite ra tu re ,
w h ic h a re u s e d in S e c tio n III fo r th e d e s ig n o f th e M P C
c o n tro l la w s . N u m e ric a l re s u lts a re s h o w n in S e c tio n V ,
w h e re a m o d e l o f a w h e e le d ro b o t (2 -D c a s e ) a n d a m o d e l o f
a n a e ro v e h ic le (3 -D c a s e ) a re c o n s id e re d . S e c tio n V I c lo s e s
th e p a p e r w ith s o m e c o n c lu s io n s .
II. P R O B L E M
S T A T E M E N T
T h is s e c tio n d e s c rib e s th e m o d e l o f a n u n d e ra c tu a te d v e h ic le a n d fo rm u la te th e m o tio n c o n tro l p ro b le m s a d d re s s e d .
L e t I b e a n in e rtia l c o o rd in a te fra m e a n d B b e a
b o d y c o o rd in a te fra m e a tta c h e d to th e v e h ic le . T h e p a ir
( p ( t ) , R ( t ) ) ∈ S E ( 3 ) 1 d e n o t e t h e c o n fi g u r a t i o n o f t h e
v e h ic le , p o s itio n a n d o rie n ta tio n , w h e re R ( t) is th e ro ta tio n m a trix fro m b o d y to in e rtia l c o o rd in a te s . N o w , le t
(v (t), Ω (ω (t)))
∈
s e ( 3 ) 1 b e t h e t w i s t t h a t d e fi n e s t h e
v e lo c ity o f th e v e h ic le , lin e a r a n d a n g u la r, w h e re th e m a trix
Ω ( ω ( t) ) is th e s k e w -s y m m e tric m a trix a s s o c ia te d to th e
a n g u l a r v e l o c i t y ω ( t ) : = ( ω 1 ( t ) , ω 2 ( t ) , ω 3 ( t ) ) , d e fi n e d a s


0
− ω 3 (t)
ω 2 (t)
0
− ω 1 (t) ∈ R 3× 3 .
Ω ( ω ( t ) ) :=  ω 3 ( t )
− ω 2 (t)
ω 1 (t)
0
T h e k in e m a tic
s a t i s fi e s
˙p ( t ) =
m o d e l o f a
R (t)v (t),
R˙ (t)
v e h ic le
=
m o v in g
in
R (t)Ω (ω (t)).
3 D
sp a c e
(1 a )
la n d .
2 I n s titu te f o r S y s te m s a n d R o b o tic s ( I S R ) , I n s titu to S u p e r io r T e c n ic o
(IS T ), L is b o n , P o rtu g a l.
3 F a c u lty o f E n g in e e r in g , U n iv e r s ity o f P o r to ( F E U P ) , P o r tu g a l.
1 F o r a g iv e n n ∈ N , S E ( n ) d e n o te s th e C a r te s ia n p r o d u c t o f R n w ith th e
g ro u p S O ( n ) o f n × n ro ta tio n m a tric e s a n d s e ( n ) d e n o te s th e C a rte s ia n
p ro d u c t o f R n w ith th e s p a c e s o ( n ) o f n × n s k e w -s y m m e tric m a tric e s .
In th is p a p e r w e c o n s id e r c o n s tra in e d u n d e ra c tu a te d v e h ic le s w h e re th e c o n tro l in p u t


v 1 (t) ω (t) ∈ U ,
u ( t) :=
(1 b )


v 1 (t) 0
0
w ith v ( t)
:=
∈
R 3 , c o n s is ts o f
o n ly th e fo rw a rd a n d th e a n g u la r v e lo c ity , a n d is c o n s tra in e d to lie in s id e th e c o m p a c t in p u t c o n s tra in t s e t
U
⊂
R 4 th a t, e .g , r e p r e s e n ts th e p h y s ic a l lim its o f th e
a c tu a to rs . F o r th e s a k e o f s im p lic ity , w e d ro p th e e x p lic it
d e p e n d e n c e o n tim e w h e re v e r c le a r fro m th e c o n te x t. F o r
th e 2 -D c a s e th e s a m e m o d e l (1 ) a p p lie s , w h e re d iffe re n tly , ( p , R )
∈
S E ( 2 ) , ( v , Ω ( ω ) )
∈
s e ( 2 ) w ith


0
− ω
v 1 , 0
v :=
a n d Ω ( ω ) :=
∈ R 2× 2 , a n d
ω
0


v 1 ω
u :=
∈ U ⊂
R 2 . W e c o n s id e r th e fo llo w in g
tra je c to ry -tra c k in g a n d p a th -fo llo w in g p ro b le m s :
P ro b le m 1 (C o n s tr a in e d T r a je c to r y -tr a c k in g ): C o n s id e r a
c o n s tra in e d v e h ic le d e s c rib e d b y (1 ) a n d le t p d ( t) , w ith
t ∈ [0 , ∞ ) , b e a d iffe re n tia b le d e s ire d tra je c to ry . D e s ig n a
c o n t r o l l a w s u c h t h a t , a s t g o e s t o i n fi n i t y , t h e p o s i t i o n o f t h e
v e h ic le c o n v e rg e s a n d re m a in s in s id e a tu b e , c e n te re d a ro u n d
p d ( ·) , th a t c a n b e m a d e a r b itr a r ily th in , i.e ., p ( t ) − p d ( t )
c o n v e rg e s to a n e ig h b o rh o o d o f z e ro th a t c a n b e m a d e
a rb itra rily s m a ll.
P ro b le m 2 (C o n s tr a in e d P a th -fo llo w in g ): C o n s id e r
a
c o n s tra in e d v e h ic le d e s c rib e d b y (1 ) a n d le t p d ( γ ) b e a
d iffe re n tia b le d e s ire d p a th p a ra m e triz e d w ith th e p a ra m e te r
γ
∈
[ 0 , ∞ ) . M o r e o v e r , l e t ˙γ
∈
G b e a v irtu a l in p u t
c o n s tra in e d in s id e a c o m p a c t s e t G ⊂ R . D e s ig n a c o n tro l
l a w f o r u a n d ˙γ s u c h t h a t , a s t g o e s t o i n fi n i t y , i ) t h e
p o s itio n o f th e v e h ic le c o n v e rg e s a n d re m a in s in s id e a tu b e ,
c e n te re d a ro u n d p d ( γ ) , th a t c a n b e m a d e a rb itra rily th in a n d
i i ) t h e p a r a m e t e r γ a s y m p t o t i c a l l y s a t i s fi e s a d e s i r e d s p e e d
a s s i g n m e n t γ ˙ d ∈ G , i . e . , ˙γ ( t ) − γ ˙ d ( t ) g o e s t o z e r o .
III. B A C K G R O U N D
T h is
tio n p ro
to d e s ig
la w th a
A . M P C
se c
b le
n a
t e x
tio n c o
m a n d
s ta b le
p o n e n
n ta in
o u r p
M P C
tia lly
s th
re v
c o
s ta
e d e fi n i t i o n o f t h e M P C o p t i m i z
io u s re s u lt [1 7 ] th a t illu s tra te s h o
n tro lle r u s in g a n o n lin e a r a u x ilia
b iliz e s th e u n c o n s tra in e d s y s te m
a w
ry
.
o p tim iz a tio n p ro b le m
C o n s id e r th e d y n a m ic a l s y s te m
˙x ( t ) =
f (x (t), u (t)),
x (0 ) =
x
0
t ≥
,
0
(2 a )
c o n d i t i o n x¯ ( 0 ) = z . T h e o p e n l o o p M P C p r o b l e m d e n o t e d
b y P T ( z ) c o n s i s t s o f fi n d i n g t h e o p t i m a l c o n t r o l s i g n a l
u¯ ∗ ( [ 0 , T ] ) t h a t s o l v e s t h e f o l l o w i n g o p t i m i z a t i o n p r o b l e m
∗
J
(z ) =
T
m in
x¯ ˙ ( τ ) =
f ( x¯ ( τ ) , u¯ ( τ ) )
x¯ ( 0 ) =
z , x¯ ( T ) ∈ X
n
R
n
,
u (t) ∈ U
⊆
m
R
m
,
t ≥
0
(3 a )
∀ τ ∈ [0 , T ]
(3 b )
(3 c )
f
x¯ ( τ ) ∈ X , u¯ ( τ ) ∈ U
∀ τ ∈ [0 , T ]
(3 d )
T

w i t h J T ( z , u¯ ( [ 0 , T ] ) ) : =
l ( x¯ ( τ ) , u¯ ( τ ) ) d τ + F ( x¯ ( T ) )
0
T h e n o t a t i o n u¯ ∗ ( [ 0 , T ] ; z ) i s u s e d w h e r e v e r w e w a n
m a k e th e d e p e n d e n c e to th e in itia l s ta te z e x p lic it.
fi n i t e h o r i z o n c o s t J T ( · ) i s c o m p o s e d o f t h e s t a g e
l : X × U →
R ≥ 0 a n d th e te r m in a l c o s t F : X f →
R
T h ro u g h o u t th is p a p e r w e d e n o te b y k f : X f →
U
a u x i l i a r y c o n t r o l l a w d e fi n e d o v e r t h e t e r m i n a l s e t X f .
s ta te fe e d b a c k s a m p le d -d a ta M P C fra m e w o rk th e o p tim
tio n p ro b le m P T ( z ) is re p e a te d ly s o lv e d a t d is c re te s a m p
in s ta n ts ti = iδ , i ∈ N 0 , w ith z = x ( ti) a n d 0 < δ ≤
w h e r e δ i s t h e s a m p l i n g t i m e o f t h e M P C l a w d e fi n e d a
u (t) =
k
M
u¯ ∗ ( t −
( x ) :=
P C
B . S ta b le M P C
ti; x ( t i) ) , ∀ t ∈ [t i, t
).
i + 1
.
t to
T h e
c o st
.
≥ 0
a n
In a
iz a lin g
T ,
s
(4 )
u s in g a p re -e x is tin g A u x ilia r y C o n tro l L a w
W e c o n s id e r th e fo llo w in g a s s u m p tio n s [1 7 ]:
A s s u m p tio n 1 : f ( ·) is lo c a lly L ip s c h itz c o n tin u o u s in th e
r e g i o n o f i n t e r e s t a n d s a t i s fi e s f ( 0 , 0 ) = 0 .
A s s u m p tio n 2 : T h e s e t U ⊂ R m is c o m p a c t, X ⊆ R n is
c o n n e c te d , a n d ( 0 , 0 ) ∈ in t ( X ) × in t ( U ) 2 .
A s s u m p t i o n 3 : T h e s t a g e c o s t l ( · ) s a t i s fi e s l ( 0 , 0 ) = 0
a n d is lo w e r b o u n d e d b y a K ∞ - c la s s f u n c tio n 3 w ( ·) , i.e .,
w ( x ) ≤ l(x , u ), ∀ (x , u ) ∈ X × U .
A s s u m p tio n 4 : T h e re
e x is t a
k n o w n
c o n tro l la w
k f
: X D
→
R m c o n tin u o u s a ro u n d th e o rig in a n d
a c o n tin u o u s ly d iffe re n tia b le L y a p u n o v fu n c tio n V ( ·) , a n d
th e p o s itiv e c o n s ta n ts k 1 , k 2 , k 3 , a n d a s u c h th a t
k
∀ x
1
a
x
≤
V (x ) ≤
∈
X
k
a
x
2
∂ V
f (x , k
∂ x
se t X D
,
,
fo r so m e
0 ∈ in t ( X D ) ⊆ R n .
A s s u m p tio n 5 : T h e c o n tro l la w
a n d th e s ta g e c o s t l( ·) s a tis fy
D
k
f
f
(x )) ≤
− k
⊆
R
( ·) fro m
n
3
x
a
w ith
A s s u m p tio n 4
v
l(x , k
⊆
( z , u¯ ( [ 0 , T ] ) )
T
s .t.
w ith
x (t) ∈ X
J
u¯ ( [ 0 , T ] )
f
(x )) ≤

a
i
x
i
,
∀ x ∈ X
l
(5 )
i = 1
(2 b )
w h e re x (t) ∈ R
a n d u (t) ∈ R
a re th e s ta te a n d th e
in p u t a t tim e t , r e s p e c tiv e ly , a n d X ⊆ R n a n d U ⊆ R m
a r e th e s ta te a n d in p u t c o n s tr a in t s e ts , r e s p e c tiv e ly . F o r a
g e n e ric tra je c to ry x ( ·) w e d e n o te b y x ( [0 , T ]) th e tra je c to ry
c o n s id e re d in th e tim e in te rv a l [0 , T ]. T h e M P C o p tim iz a tio n
p r o b l e m i s d e fi n e d a s f o l l o w s :
D e fi n i t i o n 1 ( M P C P r o b l e m ) : L e t T ∈ ( 0 , ∞ ) b e a g i v e n
h o r i z o n l e n g t h a n d x¯ ( [ 0 , T ] ) a n d u¯ ( [ 0 , T ] ) b e a p a i r o f s t a t e
a n d in p u t p re d ic te d tra je c to rie s th a t s a tis fy (2 ) w ith in itia l
fo r so m e se t
w ith v ≥ 1 ,
a a r e p o s itiv
N o te th a t A
c a se o f a q
w ith Q
∈
2
G iv e n a s e
A c o n tin u o
if it is s tric tly
if a = ∞ a n d
3
X l ∈ R n w ith 0
a n d a i ∈ R , i =
e c o n s ta n ts .
s s u m p tio n 5 is
u a d ra tic s ta g e
R n × n , Q
=
t A
u s
in
w
, w
fu n
c re a
( r )
e d e n o te
c tio n w :
s in g a n d
→ ∞ a s
∈ in t ( X l) a n d c o n s ta n ts v ∈ N ,
1 , . . . , v , w h e re k 1 , k 2 , k 3 , a n d
t r i v i a l l y v e r i fi e d f o r t h e c l a s s i c
c o st l(x , u ) =
x Q +
u R ,
Q T 
0 a n d R
∈ R m × m ,
b y in t ( A ) th e in te rio r o f s u c h s e t.
[0 , a ) → [0 , ∞ ) is s a id to b e lo n g to c la s s K
w ( 0 ) = 0 . It is s a id to b e lo n g to c la s s K ∞
r → ∞ .
= R T  0 , a n d a lin e a r a u x ilia ry c o n tro l la w u = K x ,
w i t h K ∈ R m × n , w h e r e , f o r a g i v e n m a t r i x A , λ m in ( A )
a n d λ m ax ( A ) d e n o te th e s m a lle s t a n d la rg e s t re a l p a rt o f th e
e ig e n v a lu e s o f A , r e s p e c tiv e ly , a n d f o r a g iv e n v e c to r a o f
s u i t a b l e d i m e n s i o n , w e u s e t h e n o t a t i o n a 2A = a A a . I n
fa c t l(x , K x ) ≤
x 2 λ m a x ( Q + K R K ) , w h i c h s a t i s fi e s ( 5 )
w ith v = 2 , a 1 = 0 , a 2 = λ m ax ( Q + K R K ) , a n d X l = R n .
M o re o v e r, it g e n e ra liz e s to th e c a s e w h e re l( ·) is u p p e r
b o u n d e d b y a p o ly n o m ia l (w ith o u t th e c o n s ta n t te rm ) in
th e s ta te a n d in th e in p u t, a n d k f ( ·) is u p p e r b o u n d e d b y
a p o ly n o m ia l (w ith o u t a c o n s ta n t te rm ) in th e s ta te .
T h e o re m 1 : C o n s id e r th e c o n s tra in e d s y s te m (2 ) a n d th e
o p tim iz a tio n p ro b le m P T ( ·) w ith

 i/ a
 v
k 2
a k 2
F (x ) =
a i
x i
(6 )
k
i
k
1
3
i = 1
X f = { x : V (x ) ≤ α } ⊆ X¯f ,
(7 )
th is c a s e , th e p ro p o s e d a lg o rith m w o u ld re tu rn th e la rg e s t
le v e l s e t o f V ( ·) c o n ta in e d in th e in n e r a p p ro x im a tio n .
w h e re X¯ f := { x : x ∈ X ∩ X D ∩ X l, k f ( x ) ∈ U } a n d
α > 0 . If A s s u m p tio n s 1 -5 h o ld a n d P T ( x ( t) ) is fe a s ib le fo r
t = 0 , th e n th e o rig in o f th e re s u ltin g c lo s e d lo o p s y s te m (2 )
w ith (1 2 ) is a s y m p to tic a lly s ta b le , w ith re g io n o f a ttra c tio n
c o n s is tin g o f th e s e t o f s ta te s x ∈ X fo r w h ic h P T ( x ) a d m its
a fe a s ib le s o lu tio n .
1 ) C o m p u ta tio n o f th e T e r m in a l S e t: F ro m [1 7 ], w e re c a ll
a p ro c e d u re to s y s te m a tic a lly c o m p u te th e te rm in a l s e t fo r
th e M P C s c h e m e in tro d u c e d a b o v e .
L e t R [x ] a n d Σ [x ] d e n o te th e s e t o f p o ly n o m ia l a n d s u n o f - s q u a r e s f u n c t i o n s o n x , r e s p e c t i v e l y , w i t h r e a l c o e f fi c i e n t s .
A s s u m p tio n 6 : S u p p o s e th a t th e fu n c tio n V ( ·) is a p o ly n o m ia l fu n c tio n o n x a n d th e s e t X¯ f is a b a s ic s e m i-a lg e b ra ic
s e t, i.e ., it c a n b e r e w r itte n in th e f o r m
C o n s id e r th e e
g iv e n n o n z e r o a r b
d im e n s io n . N o te
p o s itio n c o n v e rg e
c e n te re d a ro u n d p
It is p o s s ib le to
R
n
{ x ∈ R
fo r s
n q ∈
It c a
c o n d
o f-sq
: q i(x ) ≥
o m e p o ly n
N .
n b e sh o w
itio n (7 ) is
u a re s o p tim
α
∗
s .t.
q
:=
i
o m ia ls q
i
i
∈
∈ R [x ], i =
R [x ], i
1 , . . . , n
=
q
} ,
1 , . . . , n
q
(8 )
w ith
n th a t, th e la rg e s t le v e l v a lu e α s u c h th a t
s a t i s fi e d i s t h e s o l u t i o n t o t h e f o l l o w i n g s u m iz a tio n p ro b le m :
α ,s
−
i
s
0 , q
m a x
1,
...,s
α
(α − V )s
∈ Σ [x ],
(9 a )
nq
i
∈ Σ [x ],
i =
1 , . . . , n
q
(9 b )
i =
1 , . . . , n
q
(9 c )
w ith d e g ( V s i ) = d e g ( q i ) , i = 1 , . . . , n q , w h e r e f o r a g iv e n
p o ly n o m ia l fu n c tio n f ∈ R [x ], d e g ( f ) d e n o te s th e d e g re e
o f th e p o ly n o m ia l f . A lth o u g h th e o p tim iz a tio n p ro b le m (9 )
c a n n o t b e d ire c tly s o lv e d u s in g c o n v e x o p tim iz a tio n m e th o d s ,
d u e to th e p ro d u c t α s i in (9 b ) th a t m a k e s th e p ro b le m
n o n c o n v e x , it c a n b e s o lv e d v ia b is e c tio n o v e r th e s c a la r
v a r i a b l e α . I n f a c t , f o r a n y fi x e d α , ( 9 ) b e c o m e s a c o n v e x
f e a s i b i l i t y p r o b l e m , w h i c h c a n b e e f fi c i e n t l y s o l v e d u s i n g
a v a ila b le to o lb o x e s f o r s u m - o f - s q u a r e s p r o g r a m m in g ( e .g .
S e D u M i [1 8 ], S D P T 3 [1 9 ], Y A L M IP [2 0 ]).
R e m a r k 1 : T h e re p re s e n ta tio n (8 ) is q u ite g e n e ra l, a lth o u g h , if th e s e t X¯ f c a n n o t b e re w ritte n a s (8 ), o n e c o u ld
c h o o s e th e s e t (8 ) to b e a n in n e r a p p ro x im a tio n o f X¯ f . In
IV . M A IN R E S U L T S
In th is s e c tio n , s im ila rly to [1 ], w e c o m p u te a tra je c
tra c k in g c o n tro lle r fo r th e u n c o n s tra in e d m o d e l (1 a ), w
is th e n u s e d , to g e th e r w ith T h e o re m 1 , to d e s ig n th e d e
M P C tra je c to ry -tra c k in g a n d p a th -fo llo w in g c o n tro l la w
S in c e w e w is h to c o n tro l a v e h ic le w ith c o n s tra in e d in
s o m e a s s u m p tio n s o n th e c o n s tra in t s e ts U a n d G a n
th e d e s ire d v e h ic le v e lo c ity v d ( t) a re e x p e c te d in o rd
g u a ra n te e th a t a s o lu tio n to th e c o n tro l p ro b le m e x is ts .
A s s u m p tio n 7 (B o u n d e d D e s ire d V e lo c ity ): T h e
d e
v e h ic le v e lo c ity is b o u n d e d a s v d ( t) ≤ β , ∀ t ≥ 0 ,
β ∈ R ≥ 0 .
to ry h ic h
s ire d
s.
p u ts ,
d o n
e r to
s ire d
w ith
A . A u x ilia r y C o n tro l L a w
rro r e
itra rily
th a t a s
s to a
( ·) , i.e
sh o w
:= R ( p − p d
s m a ll c o n s ta n t
th e e rro r g o e s
n a rb itra rily th
., p − p d →
th a t
− Ω e +
˙e =
u −
) −
,
v e c to r
to z e
in tu b
a s
R
˙p
w
o f
ro
e ,
e
h e
a p
th
th
→
re
p ro p
e v e
e 0 .
is
ria
h ic
tu b
a
te
le
e ,
(1 0 )
d
w ith

1
=
fo r th e
th e ith
P ro p
th e s y s
2
−
0


=
o r
1
2 -D c a se
c o m p o n e
o s itio n 1
te m (1 a )
u =
1
 0
−
c a s
e v e
to r y
d -lo
e , r
c to
-tr a
o p
k ( R , e , ˙p d ) =
r
3
2
1

2
−
0
3
0
o r 3 -D
n t o f th
(T r a je c
in c lo s e
−
0
1

0
e s p e c tiv e ly , w h e r e i d e n o te s
.
c k in g c o n tro lle r ): C o n s id e r
w ith
¯ (R
˙p
d
−
K e ) ,
(1 1 )
w h e re ¯ :=
(
) , K i s a g i v e n p o s i t i v e - d e fi n i t e
m a trix w ith s u ita b le d im e n s io n s , a n d
is s u c h th a t
is fu ll
ra n k . T h e n , th e o rig in e = 0 o f th e c lo s e d -lo o p (1 0 ) w ith
(1 1 ) is a g lo b a l e x p o n e n tia lly s ta b le e q u ilib riu m p o in t.
P ro o f: C o n s id e r th e fu n c tio n V = ( 1 / 2 ) e e . C o m b in in g
i t s d e r i v a t i v e V ˙ = e ˙e = e ( − Ω e +
u − R ˙p d ) w i t h t h e
c o n tro l in p u t (1 1 ) w e o b ta in V˙ = − e ( Ω + K ) e = − e K e ,
w h e re w e u s e d th e fa c t th a t Ω is a s k e w -s y m m e tric m a trix fo r
w h ic h x Ω x = 0 , ∀ x h o ld s , w h ic h u s in g s ta n d a rd L y a p u n o v
th e o ry , c o n c lu d e s th e p ro o f.
N o te th a t A s s u m p tio n 7 im p lie s k ( ·, e , ·) ∈ V ( e ) w ith
 


b 1 k¯ 1




.
¯
.
V ( e ) := c o n v
K e , b 1 , . . . , b n u ∈ { ± 1 }

 −
.


b n k¯ n
− 1
u
w h e
sp a c
[A ]i
re sp
r e k¯ i
e a n
d e n
e c tiv
:=
d ,
o te
e ly
u
.
β [ ¯ ]i , n u d e n o te s th e d im e n s io n o f th e in p u t
f o r a g iv e n s e t A a n d m a tr ix A , c o n v A a n d
th e c o n v e x h u ll o f A a n d th e ith ro w o f A ,
A s s u m p tio n 8 (F e a s ib ility o f th e A u x ilia r y L a w ): T h e
c o n tr o l la w ( 1 1 ) is f e a s ib le in a n e ig h b o r h o o d o f e = 0 , i.e .,
k ( R ( t ) , 0 , v d ( t ) ) ∈ in t ( U ) , ∀ t ∈ [0 , ∞ ) .
A s s u m p tio n 8 g u a r a n te e s th a t o n c e e = 0 , i.e ., th e v e h ic le
e n te re d th e -tu b e a ro u n d th e p a th , a fe a s ib le in p u t th a t k e e p s
th e e rro r e q u a l z e ro a lw a y s e x is ts . S in c e , d u e to th e tim e v a ry in g n a tu re o f k ( R ( t) , 0 , v d ( t) ) , th is a s s u m p tio n c a n b e
d i f fi c u l t t o b e a p r i o r i v e r i fi e d , l a t e r i n t h i s S e c t i o n I V - D a n
a lte r n a tiv e v e r s io n is p r e s e n te d .
B . M P C
J
t r
(z , ti) =
P ro b le m 1 is s o lv e d u s in g T h e
o n tro l la w fro m P ro p o s itio n 1 .
C fo r T r a je c to r y -tr a c k in g ): C o n s
(1 ) a n d th e c o n tro l p ro b le m P ro
th e s o lu tio n to th e o p tim
i ) b e
d e s c rib e d b y
m in
u¯
J
( [0 ,T ])
tr
R¯ ( τ )
R¯ ( τ )

e¯ ( T ) ∈ E f ,
e¯ ( τ ) = R ¯ ( τ )

v¯ 1 ( t
u¯ t r ( τ ) =
p¯ ˙ ( τ ) =
R ¯˙ ( τ ) =
( z , t i , u¯
t r
t r
o re m
+
(
u¯
t r
P C ,t r
(t) =
u¯
∗
t r
R¯
(t −
J
( z , u¯
p f
( [0 ,T ])
R ¯ ( τ ) v¯ ( τ )
R ¯ ( τ ) Ω ( ω¯ )

p¯ ( 0 ) R ¯
E f ,
R ¯ ( τ ) ( p¯ ( τ ) − p

v¯ 1 ( t ) ω ¯ ( t )

v¯ 1 ( t ) ω ¯
G ,

=
z
∀ τ ∈ [0 , T ]
∀ τ ∈ [0 , T ]
d
O K
)
)
τ )
∀ τ ∈ [0 , T ]
∀ τ ∈ [0 , T ]
(0 )
γ¯ ( 0 )

=
z
d ( γ ( τ ) ) ) −

γ¯ ˙ ( τ )

(t)
∈ U
∀ τ ∈ [0 , T ]
∀ τ ∈ [0 , T ]
∀ τ ∈ [0 , T ]
∀ τ ∈ [0 , T ]
w ith
T

J
( z , u¯
p f
u
T
p f
( [0 , T ]) ) :=
e¯
γ¯ ˙ −
˙γ
d
2
o
d τ +
a
2
e¯ ( T )

2
+
Q
M
P C ,p f
(t) =
u¯
∗
p f
(t −
2


u¯


p f
∂ p d 
− R¯
γ¯ ˙
∂ γ 
O
2
O a r e a p o s itiv e e fi n i t e m a t r i x , r e o
∈
R > 0 , a n d
y p o s itiv e c o n s ta n t
a trix K
s u c h th a t
t ∈ [0 , ∞ ) . If A s p ro b le m P p f ( z ( t) ) ,
s ib le a t in itia l tim e
l a w d e fi n e d b y
ti; z ( ti) ) , ∀ t ∈ [ti, t
i + 1
),
(1 2 )
2
e¯
˙p ( t i +
( [0 , T ]) )
p f
O K )
m a x ( Q + K
w h e re a 2 =
, Q a n d
2 λ m in ( K )
d e fi n i t e m a t r i x a n d a p o s i t i v e - s e m i d
s p e c tiv e ly , w ith s u ita b le d im e n s io n s ,
E f (α ) =
{ e : (1 / 2 )e e ≤ α } , fo r a n
α
∈
R ≥ 0 a n d p o s i t i v e - d e fi n i t e m
k (R (t), e , v (t)) ∈ U , ∀ e ∈ E f (α ), ∀
s u m p t i o n s 7 - 8 h o l d a n d t h e o p t i m i z a t i o n
p ( t) R ( t) γ ( t) , is fe a
w ith z ( t) =
t = 0 , th e n s a m p le d -d a ta M P C fe e d b a c k
∀ τ ∈ [0 , T ]
R¯ ( 0 )
( p¯ ( τ ) − p d ( t i + τ ) ) −

) ω¯ ( τ )
∈ U
K
pf
0
∀ τ ∈ [0 , T ]
p¯ ( 0 )
w h e r e a 2 = λ m a x 2 ( λQ m + i n K (
m a tr ix a n d a p o s itiv e
s u ita b le d im e n s io n s ,
p o s itiv e c o n s ta n t α
th a t k ( R ( t) , e , v ( t) )
If A s s u m p tio n s 7 -8
P tr ((p (t), R (t)), t)
th e s a m p le d -d a ta M P
(τ ) =
γ¯ ˙ ( τ ) ∈
id e r th e
b le m 1 .
iz a tio n
( [0 , T ]) )
Ω ( ω¯ )
−
p f
m in
u¯
e¯ ( T ) ∈
+
v¯ ( τ )
( z , t i , u¯ ( [ 0 , T ] ) ) : =
t r
(z ) =
s .t.
˙p ¯ ( τ ) =
R ¯˙ ( τ ) =
u¯
Q
0
O
2
d τ + a
2
, Q a n d O a re a p
- s e m i d e fi n i t e m  a t r i x , r e s
a n d E f (α ) =
e : 12 e e
a n d p o s i t i v e - d e fi n i t e m
∈ U , ∀ e ∈ E f (α ),
h o ld a n d th e o p tim iz
is fe a s ib le a t in itia l tim
C f e e d b a c k l a w d e fi n e d
e¯ ( T )
2
o s i t i v e - d e fi n i t e
p e c t i v e l y , w i t h
≤ α , fo r a n y
a trix K
su c h
∀ t ∈ [0 , ∞ ) .
a tio n p ro b le m
e t = 0 , th e n
b y
t i; ( p ( ti) , R ( t i) ) , ti) , ∀ t ∈ [t i, t
i + 1
)
s o lv e s P ro b le m 1 a n d th e re g io n o f a ttra c tio n c o in c id e s w ith
th e s e t o f in itia l p o s itio n s a n d h e a d in g s o f th e v e h ic le fo r
w h ic h P tr ( ( p ( 0 ) , R ( 0 ) ) , 0 ) a d m its a fe a s ib le s o lu tio n .
D u e to s p a c e c o n s tra in ts th e fu ll p ro o f is o m itte d , a lth o u g h
n o te th a t th e tra je c to ry -tra c k in g p ro b le m c a n b e s e e n a s a
s p e c i a l i z a t i o n o f t h e p a t h - f o l l o w i n g p r o b l e m w h e r e ˙p d =
p d( γ ( t ) )
˙γ d a n d t h e p r o o f o f C o r o l l a r y 1 f o l l o w s s i m i l a r l y
γ
to th e p ro o f o f C o ro lla ry 2 .
C . M P C
∗
p f
J
λ

M
p f
1
w ith
u
( [0 , T ]; z ) b e th e s o lu tio n to th e o p tim iz a tio n p ro b le m
( z ) d e s c rib e d b y
p f
e¯ ( τ ) =
s .t.
J
∗
fo r T r a je c to r y -tr a c k in g
In th is s e c tio n
to g e th e r w ith th e c
C o ro lla r y 1 (M P
c o n s tra in e d s y s te m
L e t u ¯ ∗t r ( [ 0 , T ] ; z , t
p ro b le m P tr ( z , ti)
∗
P
u¯
fo r P a th -F o llo w in g
C o ro lla r y 2 (M P C fo r p a th -fo llo w in g ): C o n s id e r th e c o n s tra in e d s y s te m (1 ) a n d th e c o n tro l p ro b le m P ro b le m 2 . L e t
s o lv e s P ro b le m 1 a n d th e re g io n o f a ttra c tio n c o in c id e s w ith
th e s e t o f z fo r w h ic h P tr ( z ) a d m its a fe a s ib le s o lu tio n .
P r o o f : I n t h i s p r o o f w e fi r s t r e w r i t e t h e e r r o r s y s t e m
(1 0 ), a n d th e a s s o c ia te d in p u t c o n s tra in t s e t, in a n e w
in p u t c o o rd in a te s s y s te m , th e n T h e o re m 1 w ith th e a u x ilia ry
c o n tro l la w o b ta in e d fro m k ( ·) , is a p p lie d to s ta b iliz e th e
r e d e fi n e d e r r o r s y s t e m . P e r f o r m i n g t h e i n p u t c o o r d i n a t e s
p d
tra n s fo rm a tio n v = φ ( u ) :=
u − R
γ ( t ) ˙γ t h e e r r o r s y s t e m ( 1 0 ) b e c o m e s ˙e = − Ω ( t ) e + v , t ∈ [ 0 , ∞ ) , w h i c h s a t i s fi e s
A s s u m p tio n 1 , a n d th e in p u t c o n s tra in t s e t U a n d th e c o n tro l
l a w k ( · ) b e c a m e U e : = { v : u ∈ i n t ( U ) , ˙γ ∈ G } =
p d
¯ (v + R
{ v
:
∈
i n t ( U ) , ˙γ ∈
G } a n d
γ ˙γ )
v = k e ( e ) :=
− K e , r e s p e c t i v e l y . D e fi n i n g t h e a u x i l i a r y
c o n t r o l l a w a s v = k e ( e ) a n d ˙γ = ˙γ d , w h i c h i s f e a s i b l e i n
a n e ig h b o rh o o d o f e = 0 b y A s s u m p tio n 8 , w e h a v e th a t
0 ∈ i n t ( U e ) a n d , t h u s , A s s u m p t i o n 2 i s s a t i s fi e d . M o r e o v e r ,
t h e s t a g e c o s t l ( e , v , ˙γ ) : =
e 2Q +
v 2R +
˙γ − ˙γ d 2o
s a t i s fi e s A s s u m p t i o n 3 a n d t h e a u x i l i a r y c o n t r o l l a w w i t h
t h e L y a p u n o v f u n c t i o n V ( · ) s a t i s fi e s A s s u m p t i o n 4 w i t h
k 1 = k 2 = 0 . 5 , a = 2 , k 3 = λ m in ( K ) , a n d X D = R 2 o r , f o r
th e 3 -D c a s e , X D = R 3 . N o te th a t, a lth o u g h th e a u x ilia ry
c o n t r o l l a w i d e n t i c a l l y s e t s ˙γ = ˙γ d , t h i s d o e s n o t a p p l y t o
th e re s u ltin g M P C c o n tro lle r, w h ic h w ill o p tim a lly c h o o s e
t h e i n p u t ˙γ . C o m b i n i n g s t a g e c o s t w i t h t h e a u x i l i a r y c o n t r o l
l a w , A s s u m p t i o n 5 i s s a t i s fi e d w i t h a 2 = λ m a x ( Q + K O K ) ,
v =
2 , a n d X l =
R 2 o r, fo r th e 3 -D c a s e , X l =
R 3 .
o b ta in C o ro lla ry 2 , w h e re w e
o n th e v e h ic le m o d e l.
1 a n d C o ro lla ry 2 s till h o ld
r e to lie in s id e a c o n n e c te
its in te rio r. T h is c a n b e o f in
h e re w e w o u ld lik e to e n fo rc
f th e p o s itio n o f th e v e h ic le
tu b e a ro u n d th e d e s ire d p a th .
m a d e
Position Trajectories
if
d
te
e
to
w e
se t
re st
th e
b e
In o rd e r to v e rify th e fe a s ib ility o f th e a u x ilia ry c o n tro l la w
in A s s u m p tio n 8 a lo n g a ll th e tim e t, w e u s e th e b o u n d fro m
A s s u m p tio n 7 , a n d w e in tro d u c e th e fo llo w in g a s s u m p tio n :
A s s u m p tio n 9 : T h e in p u t c o n s tra in t s e t U is a c lo s e d b a s ic
s e m i-a lg e b ra ic s e t th a t c o n ta in s V ( 0 ) in its in te rio r.
N o te th a t A s s u m p tio n 9 im p lie s A s s u m p tio n 8 a n d c a n b e
c o n s i d e r e d i t s r o b u s t i fi e d v e r s i o n , t h u s m o r e c o n s e r v a t i v e .
M o re o v e r, n o te th a t { e
:
V B (e )
⊆
U
}
is a b a s ic s e m i-a lg e b ra ic s e t th a t in n e r a p p ro x im a te s
{ e : k tr ( e ) =
− K e ∈ U e } = { e : k ( R , e , ˙p d ) ∈ U } ,
w h ic h fro m A s s u m p tio n 9 , is n e v e r e m p ty a n d , fo llo w in g
R e m a r k 1 , i t c a n b e u s e d t o e f fi c i e n t l y s o l v e t h e o p t i m i z a t i o n
p ro b le m (9 ) a n d to c o m p u te th e d e s ire d te rm in a l s e t.
R e m a r k 3 : It is w o rth n o tin g th a t, fo r th e c a s e o f v e h ic le s
w ith u n c o n s tr a in e d in p u ts , i.e . U = R n , a n y c h o ic e o f
α > 0 is a fe a s ib le . T h u s , th e te rm in a l s e t c a n b e n e g le c te d ,
re s u ltin g in M P C c o n tro lle rs th a t g lo b a lly s o lv e th e a d d re s s e d
m o tio n c o n tro l p ro b le m s .
A . 2 -D
8
uMPC,tr(.)
kf(.)
2
0
−2
−4
−6
−2
0
u(t)
2
4
x [m]
4
20
2
10
0
6
8
ω(t)
0
−2
−10
0
2
4
time t [s]
b(t)
0
2
4
time t [s]
|e(t)|
0
2
4
time t [s]
6
0.5
4
0
2
−0.5
0
V . S IM U L A T IO N R E S U L T S
s th e p re v io u s re s u lts w ith
) a n d o f a n a e ro v e h ic le (
d i f f e r e n t i n i t i a l c o n fi g u r a
e c lo s e d -lo o p tra je c to rie s o
s e d c o n tr o lle r s , i.e ., th e a u x
M P C tra je c to ry -tra c k in g
th e M P C p a th -fo llo w in g
uMPC,pf(.)
4
D . C o m p u ta tio n o f th e T e r m in a l S e t
T h is s e c tio n illu s tra te
o f a w h e e le d ro b o t (2 -D
e a c h v e h ic le a n d fro m
s im u la te a n d c o m p a re th
te m w ith th e th re e p ro p o
fro m P ro p o s itio n 1 , th e
fro m C o ro lla ry 1 , a n d
fro m C o ro lla ry 2 .
10
6
y [m]
A p p ly in g T h e o re m 1 w e
e x p lic it th e d e p e n d e n c e
R e m a r k 2 : C o ro lla ry
e n fo rc e th e e rro r v e c to
c o n ta in in g th e o rig in in
fo r s o m e a p p lic a tio n s w
c lo s e d -lo o p tra je c to ry o
b o u n d e d in s id e a n o u te r
0
a m
3 -D
tio n
f th
ilia
c o n
c o n
o d e ls
). F o r
s, w e
e sy sry la w
tro lle r
tro lle r
2
4
time t [s]
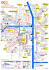
F ig . 1 .
T ra je c to rie s o f th e p o s itio n o f th e w h e e le d ro b
w ith th e p ro p o s e d c o n tro l la w s fo r d iffe re n t in itia l p o s itio
w h ic h a re b y th e a rro w s . T h e b la c k d o tte d lin e re p re s e n ts
O n e i n i t i a l c o n fi g u r a t i o n , i d e n t i fi e d w i t h t h e d o t t e d c i r c l e ,
d e ta ils o n c o n tro l in p u ts , tra c k in g e rro r, a n d v e lo c ity o f
a re d is p la y e d . In o rd e r to e m p h a s iz e th e d ire c tio n o f th e
w e d e fi n e b ( t ) : = s i g n ( p ˙ d ( t ) [ 1 , 0 ] ) p ˙ d ( t ) .
o t in c lo s e d -lo o p
n s a n d h e a d in g s ,
th e d e s ire d p a th .
is c h o s e n a n d th e
th e d e s ire d p o in t
d e s ire d p o s itio n
c a s e : W h e e le d R o b o t
C o n s id e r  th e

u
=
c o n s t r a i n e d u n i c y c l e m o d e l ( 1 ) w i t h

ω
U
: u ∈ [− 3 , 3 ], ω ∈ [− 1 0 , 1 0 ] . T h e


0 .4 t s in 0 .4 t
d e s i r e d t r a j e c t o r y i s d e fi n e d a s p d ( t ) =
a n d t h e a u x i l i a r y c o n t r o l l a w  f r o m
P ro p o s itio n 1 is
0 .2
0
c h o s e n w ith
=
a n d K
=
0 .8 I 2 × 2 ,
w h e r e f o r a g iv e n n
∈
N > 0 , w e d e n o te b y
I n × n
∈
R n × n
th e
id e n tity
m a trix
w ith
g iv e n
d i m e n s  i o n s . T h e t r  a j e c t o r  y s a t i s fi e s A s s u m p t  i o n 7 w i t h
 
 
 
 
0 .4  ≥
0 .4 c o s 0 .4 t  =
β =
˙p d .
 0 .4
 0 .4
U s in g
β
th e  c h o s e n
w e
o b t a i n
w ith
b 1 0 .5 6 5 7
¯
V (e ) = c o n v
−
0 .8 e , b 1 , b 2 ∈ { − 1 , + 1 }
b 2 2 .8 2 8 4
w h i c h s a t i s fi e s A s s u m p t i o n s 8 - 9 . T h e s t a g e c o s t f u n c t i o n
is c h o s e n w ith Q = 1 0 I 2 × 2 a n d O = 0 .1 I 2 × 2 , a n d th e
te rm in a l s e t E f = { e : e e ≤ 3 .1 8 } is c o m p u te d fo llo w in g
th e p ro c e d u re p ro p o s e d in S e c tio n IV -D .
F o r t h e p a t h - f o l l o w i n g c o n t r o l l e r , t h e t r a j e c t o r y  i s
γ
s in γ ,
p a ra m e triz e d w ith th e p a ra m e te r γ a s p d ( γ ) =
a n d w e c h o s e t h e d e s i r e d p a r a m e t e r s p e e d ˙γ d = 0 . 4 ∈ G ,
w ith G = [− 1 , 1 ]. S im ila rly to th e tra je c to ry -tra c k in g c a s e ,
A s s u m p tio n s 7 -9 h o ld a n d th e M P C p a th -fo llo w in g a n d
th e s ta g e c o s t is c h o o s e w ith Q = 1 0 I , O = 0 .1 I 2 × 2 ,
o = 2 . N u m e ric a l re s u lts a re p re s e n te d in F ig . 1 w h e re ,
fo r s im u la tio n p u rp o s e s , th e s y s te m is d is c re tiz e d w ith a
d is c re tiz a tio n s te p o f 0 .1 5 s e c o n d s . T h e h o riz o n le n g th is
c h o s e n a s T = 1 .5 s e c o n d s . N o te th a t, c o n tra rily to th e
a u x ilia ry c o n tro l la w a n d to th e M P C tra je c to ry -tra c k in g
c o n t r o l l e r u t r ( · ) w h e r e ˙p d ( t ) i s a p r i o r i fi x e d , i n t h e M P C
p˙ d
p a t h - f o l l o w i n g l a w w e h a v e ˙p d ( t ) =
˙γ w h e r e ˙γ i s a n
γ
in p u t th a t c a n b e c o n tro lle d . A s e ffe c t, d u rin g th e in itia l
p h a s e , th e d e s ire d p o s itio n g o e s in th e d ire c tio n o f th e
Position Trajectories
c e n te re d a ro u n d th e d e s ire d p
a n a s y m p to tic tra c k in g e rro r,
te rm in a l s e t a n d th e te rm in a
p ro c e d u re s . T h is re s u lts in M
g iv e n h o r iz o n le n g th , th e s iz e
o n ly lim ite d b y th e s iz e o f th e
s o lu tio n s fo r th e c a s e o f u n c o n
uMPC,pf(.)
uMPC,tr(.)
40
kf(.)
30
20
10
R E F E R E N C E S
0
−10
10
0
z [m]
F ig . 2 .
U
re p re s e n te d
in c lo s e d -lo o
d o tte d lin e w
s in g d
b y th e
p w ith
e id e n
iffe re n
a rro w
th e p r
tify th
−10
−10
0
−5
5
10
x [m]
t in itia l p o s itio n s a n d h e a d in g s o f th e v e h ic le ,
s , th e tra je c to rie s o f th e p o s itio n o f th e v e h ic le
o p o s e d c o n tro l la w s a re d is p la y e d . W ith th e b la c k
e d e s ire d p a th .
n e g a tiv e x in o r d e r to d e c r e a s e th e e r r o r e “ w a itin g ” f o r
th e v e h ic le to a p p ro a c h th e d e s ire d p a th .
B . 3 -D c a s e : A e ro V e h ic le
C o n s i d e r t h e c o n s t r a i n e d A e r o V e h i c l e m o d e l ( 1 )


u
ω
w ith
U
=
: u ∈ [ − 3 , 3 ] , − ω¯ ≤ ω ≤ ω¯ ,


1 0 1 0
0 , w h e re w e a re a b le to o n ly
ω¯
=
c o n tr o l f o r w a r d v e lo c ity , r o ll a n d p itc h ( i.e . th e y a w
i s i d e n t i c a l l y s e t t o z e  r o ) . T h e d e s i r e d t r a j e c t o r y i s
d e fi n e d a s p d ( t )
=
5 s in ( 0 .0 8 t) c o s ( 0 .0 8 t ) 0 .0 8 t
a n d
th e
a u x ilia ry
la w
f r o m
P ro p o s itio n  1
is
− 0 .2 0
− 0 .2
c h o se n
w ith
=
a n d
K
=
I  3  × 3 . T h e t r a j e c  t  o r y s a t i s fi e s A s s u m p t i o n 7
 0 .4 0 .4 0 .4  . U s in g β a n d th e c h o s e n
w ith β =
 

b 1 1 .4 1 4 2
b 2 2 .5
b 3 5
w e o b ta in V ( e ) =
c o n v
− ¯ e ,
b 1 , b 2 , b 3 ∈ { − 1 , + 1 } } w h i c h s a t i s fi e s A s s u m p t i o n s 8 - 9 .
T h e s ta g e c o s t fu n c tio n is c h o s e n w ith Q = 1 0 I 3 × 3 a n d
O = I 4 × 4 , a n d th e te rm in a l s e t E f = { e : e e ≤ 1 .7 } is
c o m p u te d fo llo w in g th e p ro c e d u re p ro p o s e d in S e c tio n IV -D .
F o r
th e
p a th -fo llo w in g
c o n tro lle r
th e
tra je c to ry
is
p a ra m e triz e d
w ith
th e
p a ra m e te r
γ
a s
p d (γ )
=
( c o s γ , − s in γ , γ ) , a n d w e c h o s e th e
d e s i r e d s p e e d ˙γ d = 0 . 0 8 ∈ G , w i t h G = [ − 1 , 1 ] .
S im ila rly to th e tra je c to ry -tra c k in g c a s e , A s s u m p tio n s 7 9 . T h e s ta g e c o s t fu n c tio n is c h o s e n w ith Q = 1 0 I 3 × 3 ,
O = I 4 × 4 , o = 1 . N u m e ric a l re s u lts a re p re s e n te d in F ig . 2
w h e re , fo r s im u la tio n p u rp o s e s , th e s y s te m is d is c re tiz e d w ith
a d is c re tiz a tio n s te p o f 0 .1 s e c o n d s . T h e h o riz o n le n g th is
c h o se n a s T = 1 se c o n d s.
T h
is a d
tra c k
to tic
e m
d re s
in g
c o n
a th a re p re s e n te d . A llo w in g
w e a re a b le to c o m p u te th e
l la w a v o id in g lin e a riz a tio n
P C s tra te g ie s w h e re , fo r a
o f th e re g io n o f a ttra c tio n is
c o n s tra in ts le a d in g to g lo b a l
s tra in e d s y s te m s .
o tio
se d
a n d
v e rg
n
c o
a n d
o n e
e n c e
V I. C O
n tro l p ro b
tw o M P C
fo r p a th -fo
o f th e p o
[
[
[
[
[
[
[
[
[
[
N C L U S IO N
le m
c o n
llo w
s itio
o f u
tro lle
in g ,
n o f
n d e ra
rs, o n
th a t g
th e v
c tu a
e fo
u a ra
e h ic
te d v e h ic le
r tra je c to ry
n te e a s y m p
le to a tu b
s
e
-
[
[1 ] A . A g u ia r a n d J . H e s p a n h a , “ P o s itio n tra c k in g o f u n d e ra c tu a te d
v e h i c l e s ,” i n P r o c . o f t h e A m e r i c a n C o n t r o l C o n f . , v o l . 3 , p p . 1 9 8 8 –
1 9 9 3 , IE E E , 2 0 0 3 .
[2 ] R . F ie rro a n d F . L e w is , “ C o n tro l o f a n o n h o lo n o m ic m o b ile ro b o t:
b a c k s t e p p i n g k i n e m a t i c s i n t o d y n a m i c s ,” i n P r o c . o f t h e 3 4 t h I E E E
C o n f. o n D e c is io n a n d C o n tr o l, v o l. 4 , p p . 3 8 0 5 – 3 8 1 0 , IE E E , 1 9 9 5 .
[3 ] B . D ’A n d re a -N o v e l, G . B a s tin , a n d G . C a m p io n , “ D y n a m ic fe e d b a c k
l i n e a r i z a t i o n o f n o n h o l o n o m i c w h e e l e d m o b i l e r o b o t s ,” i n P r o c . I E E E
In te r n a tio n a l C o n f. o n R o b o tic s a n d A u to m a tio n , p p . 2 5 2 7 – 2 5 3 2 , IE E E
C o m p u t. S o c . P re s s , 1 9 9 2 .
[4 ] G . O rio lo , A . D e L u c a , a n d M . V e n d itte lli, “ W M R c o n tro l v ia d y n a m ic
fe e d b a c k lin e a riz a tio n : d e s ig n , im p le m e n ta tio n , a n d e x p e rim e n ta l v a li d a t i o n ,” I E E E T r a n s a c t i o n s o n C o n t r o l S y s t e m s T e c h n o l o g y , v o l . 1 0 ,
p p . 8 3 5 – 8 5 2 , N o v . 2 0 0 2 .
[5 ] C . S a m s o n a n d K . A it-A b d e rra h im , “ F e e d b a c k c o n tro l o f a n o n h o lo n o m i c w h e e l e d c a r t i n C a r t e s i a n s p a c e ,” i n P r o c . I E E E I n t e r n a t i o n a l
C o n fe re n c e o n R o b o tic s a n d A u to m a tio n , p p . 1 1 3 6 – 1 1 4 1 , IE E E C o m p u t. S o c . P re s s , 1 9 9 1 .
[ 6 ] H . C h e n a n d F . A l l g o ¨ w e r , “ A Q u a s i - I n fi n i t e H o r i z o n N o n l i n e a r M o d e l
P r e d i c t i v e C o n t r o l S c h e m e w i t h G u a r a n t e e d S t a b i l i t y ,” A u t o m a t i c a ,
v o l. 3 4 , p p . 1 2 0 5 – 1 2 1 7 , O c t. 1 9 9 8 .
[7 ] D . M a y n e , J . R a w lin g s , C . R a o , a n d P . S c o k a e rt, “ C o n s tra in e d m o d e l
p r e d i c t i v e c o n t r o l : S t a b i l i t y a n d o p t i m a l i t y ,” A u t o m a t i c a , v o l . 3 6 ,
p p . 7 8 9 – 8 1 4 , Ju n e 2 0 0 0 .
[8 ] F . A . F o n te s , “ A g e n e ra l fra m e w o rk to d e s ig n s ta b iliz in g n o n lin e a r
m o d e l p r e d i c t i v e c o n t r o l l e r s ,” S y s t e m s & C o n t r o l L e t t e r s , v o l . 4 2 ,
p p . 1 2 7 – 1 4 3 , F e b . 2 0 0 1 .
[ 9 ] R . F i n d e i s e n a n d F . A l l g o ¨ w e r , “ T h e q u a s i - i n fi n i t e h o r i z o n a p p r o a c h t o
n o n l i n e a r m o d e l p r e d i c t i v e c o n t r o l . ,” N o n l i n e a r a n d A d a p t i v e C o n t r o l ,
2 0 0 3 .
1 0 ] R . F in d e is e n , L . Im s la n d , F . A llg o w e r, a n d B . A . F o s s , “ S ta te a n d
o u t p u t f e e d b a c k n o n l i n e a r m o d e l p r e d i c t i v e c o n t r o l : A n o v e r v i e w ,”
E u ro p e a n jo u r n a l o f c o n tro l, v o l. 9 , n o . 2 -3 , p p . 1 9 0 – 2 0 6 , 2 0 0 3 .
1 1 ] T . F a u lw a s s e r, O p tim iz a tio n -b a s e d
S o lu tio n s
to
C o n s tr a in e d
T r a je c to r y -tr a c k in g a n d P a th -fo llo w in g P ro b le m s .
P h D th e s is ,
O t t o - v o n - G u e r i c k e - U n i v e r s i t a¨ t M a g d e b u r g , 2 0 1 2 .
1 2 ] T . F a u lw a s s e r a n d R . F in d e is e n , N o n lin e a r M o d e l P r e d ic tiv e P a th F o llo w in g C o n tro l, v o l. 3 8 4 o f L e c tu re N o te s in C o n tro l a n d In fo r m a tio n S c ie n c e s . S p rin g e r B e rlin / H e id e lb e rg , 2 0 0 9 .
1 3 ] L . M a g n i a n d R . S c a tto lin i, “ T ra c k in g o f n o n -s q u a re n o n lin e a r c o n tin u o u s t i m e s y s t e m s w i t h p i e c e w i s e c o n s t a n t m o d e l p r e d i c t i v e c o n t r o l ,”
J o u r n a l o f P ro c e s s C o n tro l, v o l. 1 7 , p p . 6 3 1 – 6 4 0 , S e p t. 2 0 0 7 .
1 4 ] L . M a g n i, G . D e N ic o la o , a n d R . S c a tto lin i, “ O u tp u t fe e d b a c k a n d
t r a c k i n g o f n o n l i n e a r s y s t e m s w i t h m o d e l p r e d i c t i v e c o n t r o l ,” A u t o m a tic a , v o l. 3 7 , p p . 1 6 0 1 – 1 6 0 7 , O c t. 2 0 0 1 .
1 5 ] S . Y u , X . L i , H . C h e n , a n d F . A l l g o¨ w e r , “ N o n l i n e a r M o d e l P r e d i c t i v e
C o n t r o l f o r P a t h F o l l o w i n g P r o b l e m s ,” i n P r o c . o f t h e N o n l i n e a r M o d e l
P re d ic tiv e C o n tro l C o n fe re n c e , 2 0 1 2 .
1 6 ] D . G u a n d H . H u , “ R e c e d in g h o riz o n tra c k in g c o n tro l o f w h e e le d
m o b i l e r o b o t s ,” I E E E T r a n s a c t i o n s o n C o n t r o l S y s t e m s T e c h n o l o g y ,
v o l. 1 4 , p p . 7 4 3 – 7 4 9 , J u ly 2 0 0 6 .
1 7 ] A . A le s s a n d re tti, M . N . Z e ilin g e r, A . P . A g u ia r, a n d C . N . J o n e s ,
“ A N o n lin e a r M o d e l P r e d ic tiv e C o n tr o l S c h e m e w ith G u a r a n te e d
S t a b i l i t y u s i n g a G i v e n E x p o n e n t i a l l y S t a b i l i z i n g L a w ,” t e c h . r e p . , u r l :
w e b .is t.u tl.p t/a n d r e a .a le s s a n d r e tti/te c h m p c e s 1 3 .p d f , 1 0 1 2 .
1 8 ] J . S tu r m , “ U s in g S e D u M i 1 .0 2 , a M a tla b T o o lb o x f o r O p tim iz a tio n
o v e r s y m m e t r i c c o n e s ,” O p t i m i z a t i o n m e t h o d s a n d s o f t w a r e , 1 9 9 9 .
1 9 ] R . T u ¨ t u ¨ n c u ¨ , K . T o h , a n d M . T o d d , “ S o l v i n g s e m i d e fi n i t e - q u a d r a t i c l i n e a r p r o g r a m s u s i n g S D P T 3 ,” M a t h e m a t i c a l p r o g r a m m i n g , p p . 1 – 3 1 ,
2 0 0 3 .
2 0 ] J . L o fb e rg , “ Y A L M IP : a to o lb o x fo r m o d e lin g a n d o p tim iz a tio n in
M A T L A B ,” I E E E I n t e r n a t i o n a l C o n f . o n R o b o t i c s a n d A u t o m a t i o n ,
p p . 2 8 4 – 2 8 9 , 2 0 0 4 .