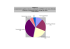Usando os números como ferramentas - MDMat

Usando os números como ferramentas
Neste módulo, vamos retomar conceitos que foram explorados nos módulos anteriores.
Nosso foco será os números decimais. Por que, afinal de contas, estamos insistindo no
estudo desses números? Um dos motivos é que eles são ferramentas importantes para
representar quantidades e resolver problemas.
Quando os números decimais aparecem? Quando precisamos medir uma quantidade,
inventamos uma unidade de medida. Por exemplo, usamos a hora como unidade de
medida do tempo. Em muitas épocas e ainda hoje, em muitos lugares, as pessoas não
têm necessidade de medir a passagem do tempo: se orientam pelo nascer e pôr-do-sol,
pela passagem das estações.
Nós precisamos dessa medida; e como muitas coisas diferentes podem acontecer
durante uma hora, precisamos de minutos. Por exemplo, se um ônibus porte às 7 horas e
15 minutos e você chegar na rodoviária às 7 horas e 25 minutos, perdeu o ônibus!
Usamos o relógio, então, para medir as horas e os minutos. Mas há situações em que o
minuto torna-se longo! Então dividimos o minuto em segundos e os segundos em décimos
em centésimos de segundo. Por exemplo, quando comparamos o tempo de dois atletas
ou carros de Fórmula Um.
Do mesmo modo como dividimos o dia em horas, as horas em minutos, os minutos em
segundos, os segundos em décimos, os décimos em centésimos, também podemos
dividir qualquer unidade de medida em duas metades, ou em quatro quartos, ou em
sessenta partes ou em dez décimos, em cem centésimos, em mil milésimos e assim por
diante.
Podemos dividir a unidade de medida em partes porque a unidade de medida é
uma invenção e porque desenvolvemos instrumentos de medida (por exemplo, o relógio
ou o cronômetro) de maior precisão.
O metro é uma unidade que inventamos para medir comprimento; dividindo o metro em
mil partes, temos os milímetros. Na fábrica metalúrgica o milímetro é a unidade de medida
mais usada para comprimentos. Mas em muitas situações é necessário usar o décimo de
milímetro ou até o centésimo de milímetro para falar da espessura de uma peça ou de um
acabamento. Uma régua comum pode medir milímetros; mas para medir décimos de
milímetro, precisamos pelo menos de um paquímetro.
O real é uma unidade que mede os valores pelos quais são trocadas as mercadorias, ou
são pagos os serviços. Mas em muitas situações o real torna-se uma unidade grande: é
preciso dividir o real em centavos. Uma passagem custando R$ 0,65 é diferente de uma
passagem custando R$ 0,90; mas ambas custam menos de um real. Há outras situações
em que até o centavo torna-se muito grande e então precisamos dividir o real em partes
ainda menores que um centavo. Por exemplo, para calcular alguns impostos, ou para
realizar câmbios de moeda.
Os números decimais também aparecem em muitas outras situações. Quando calculamos
médias, porcentagens ou quando realizamos divisões com resultados não inteiros. Neste
módulo, vamos desenvolver atividades onde os números decimais tornam-se necessários.
Além de estudar essas diferentes situações, estamos propondo que você desenvolva o
manejo dos decimais, através das operações e estimativas.
No final do módulo, estamos propondo alguns desafios com números e figuras para você
e os colegas "quebrarem a cabeça". Convidamos você e os colegas a inventar outros!
Estaremos aguardando...
Fazendo compras
Num supermercado, alguns legumes e frutas têm preço unitário e outros precisam ser
pesados.
Banana
kg
0,58
Batata
kg
0,98
Batata (pacote 2 kg)
1,28
Beringela
kg
1,58
Beterraba
molho
0,98
Cebola
kg
0,98
Couve-flor
unid
1,58
Maçã
kg
1,98
Mamão
kg
1,48
Vagem
kg
0,78
No balança eletrônica do supermercado, aparecem informações como a do desenho
abaixo:
Peso (kg)
Preço/kg
Preço total (R$)
1,350
1,58
2,13
Que cálculo devemos fazer para conferir se o preço a ser pago está correto?
Se você comprar 1 quilo de beringela, vai pagar R$ 1,58.
Se comprar um quilo e meio, vai pagar uma vez e meia R$ 1,58, isto é, R$ 1,58 + R$ 0,79
= R$ 2,37.
Então você pode imaginar que comprando 1,350 kg de beringela vai pagar mais do que
R$ 1,58 e menos do que R$ 2,37. Isto é uma estimativa, uma aproximação do que você
vai pagar.
Compare a estimativa com o seu cálculo.
E o que acontece quando você compra menos de um quilo? Quanto você pagaria por
0,850kg de cebola? E a mesma quantidade de maçã?
Na tabela abaixo, deixamos alguns espaços em branco para que você complete.
Peso (kg)
1,150
2,350
1,700
3,150
Preço por kg
0,78
1,48
0,58
0,98
Preço total (R$)
2,30
3,55
Estimando quantidades pequenas
Qual a espessura de uma folha de papel do seu caderno?
Você pode fazer uma estimativa dessa espessura sem usar a paquímetro. Como?
Compare a espessura da folha do caderno com a espessura de outros tipos de papel (por
exemplo, jornal ou cartolina).
Uma torneira pingando pode desperdiçar muita água. Como você poderia calcular o
volume de água de uma gota? Faça a experiência.
Calculando áreas e preços
No segundo módulo, usamos papel milímetro do para calcular áreas. Você observou que
1 centímetro equivale a 10 milímetros, mas 1 centímetro quadrado não equivale a 10
milímetros quadrados.
Quantos milímetros quadrados temos em 1 centímetro quadrado?
Da mesma forma, 1 metro equivale a 100 centímetros, mas 1 metro quadrado não
equivale a 100 centímetros quadrados.
Quantos centímetros quadrados temos em 1 metro quadrado? Muito mais do que 100.
Como você pode chegar a esse resultado?
Imagine uma montadora com 5.000 automóveis no pátio. Você pode ter uma idéia da área
que esses automóveis ocupam? São mais ou menos do que 1.000 metros quadrados?
Uma manifestação de desempregados lotou uma praça que tem 100 metros em cada
lado. Você pode ter uma idéia de quantas pessoas estavam lá?
Compare suas estimativas com as dos seus colegas.
Agora vamos calcular o preço de uma persiana. Preciso de uma persiana de 1,80 metros
de largura por 1,25 de altura. Se o metro quadrado da persiana custa R$ 56,00, quanto
vou pagar?
Quero azulejar uma parede com 2,5 metros de altura e 4,3 metros de comprimento. Se o
metro quadrado do azulejo custa R$ 5,90, quanto vou gastar?
Médias
Para calcular a média das idades de duas pessoas, somamos as duas idades e dividimos
por dois. Como podemos calcular a média das idades de dez pessoas?
Calcule a média das idades dos alunos e alunas da turma.
No Brasil, em 1970, as mulheres em idade de ter filhos tinham, em média, 7,5 filhos.
Como isso e possível? Afinal, uma mulher pode ter 7 filhos ou 8 filhos, mas nenhuma terá
7,5 filhos.
Em 1980, essa média caiu para 4,3 filhos. Imagine, com seus colegas, uma situação onde
a média de filhos por mulher e 4,3.
Calcule a média de filhos dos alunos e alunas da turma.
Contas de energia elétrica
As contas de energia elétrica apresentam várias informações: em que mês se consumiu
mais, qual é o consumo diário (em quilowatts-hora kWh), quanto se gasta por dia com
energia (em reais - R$).
Vamos conferir algumas das informações que estão na conta apresentada abaixo.
O relógio fez uma leitura do consumo em 32 dias. Qual o consumo nesse período? Como
podemos calcular o consumo diário?
Qual foi o consumo diário de energia na sua casa? Compare sua conta com a dos
colegas.
Quanto você gostou, por dia, com energia elétrica? Quanto você e seus colegas gastaram
com energia elétrica, em média, no último mês?
Câmbio
A tabela abaixo nos dá a cotação de diferentes moedas estrangeiras pelo Banco Central,
no dia 18 de dezembro de 1997.
Dólar (EUA)
1,11330
Lira (Itália)
0,0006384
Marco (Alemanha)
0,627144
Peso (México)
0,137902
Quantos reais eram necessários, nesse dia, para comprar 100 dólares? E 100 liras?
Com 100 reais, quanto de cada moeda se podia comprar?
Altura e peso
O índice de massa corporal (IMC) é uma maneira através da qual se mede a relação entre
a altura e o peso de uma pessoa. Para achar este índice se faz o seguinte cálculo:
Calcule o seu IMC e compare com os índices que seus colegas acharam.
Idade
Peso
Necessidade diária
Necessidade
diária/kg
80 a 100
3 dias
3,0
250 a 300 ml
10 dias
3,2
400 a 500 ml
3 meses
5,4
750 a 850 ml
6 meses
7,3
950 a 1100 ml
9 meses
8,6
1100 a 1250 ml
1 ano
9,5
1250 a 1300 ml
2 anos
11,8
1350 a 1500 ml
4 anos
16,2
1600 a 1800 ml
6 anos
20,0
1800 a 2000 ml
10 anos
28,7
2000 a 2500 ml
14 anos
45,0
2200 a 2700 ml
18 anos
54,0
2200 a 2700 ml
40 a 50
Olhando para a tabela podemos ver que o total de água que uma pessoa precisa beber
durante um dia vai aumentando com a idade e o peso.
Mas esse total não aumenta da mesma maneira que o peso! Uma criança de 10 anos,
pesando três vezes o que pesa uma criança de 1 ano, não bebe o triplo do que bebe a
criança menor.
Na última coluna da tabela temos a relação entre a necessidade diária de água e o peso,
de acordo com as idades. Complete a coluna.
Podemos notar que a necessidade diário de água por quilo vai diminuindo. Por que você
acho que isso acontece?
Estrutura fundiária do Brasil
Na figura abaixo, temos a distribuição dos estabelecimentos agrícolas pelas suas
dimensões e a área ocupada.
Qual é a porcentagem dos estabelecimentos que têm até 100 hectares?
Que parte da área ocupam esses estabelecimentos?
Qual é a porcentagem dos estabelecimentos que têm mais de 1000 hectares?
Que parte da área ocupam esses estabelecimentos?
Na figura abaixo, temos dados sobre o uso da terra no Brasil.
Quantas vezes a área de pastos é maior que a de lavouras?
Obtenha a porcentagem de cada tipo de uso em relação ao total da área.
Nas regiões Sul e Sudeste, a pecuária ocupa, em média, 5 hectares por boi. Como
podemos comparar a produção de alimentos nas áreas de pasto e de lavoura?
DESAFIOS
Jogo com letras e números
Você quer participar de um jogo? Neste jogo cada letra vale um número. Por exemplo: a
letra A vale 23, a letra B vale 22, o C vale 21, e assim por diante.
Quanto vai valer a letra P? E a letra Z?
Que regra podemos inventar para descobrir o valor numérico de uma palavra?
E se você usar a regra que inventou, que palavra tem maior valor numérico: BRASIL ou
AMÉRICA?
Você sabe qual o valor numérico do seu nome?
Que tal encontrar uma palavra com valor numérico maior que 100?
Tangran
O tangran, um quebra-cabeças chinês, é formado por
sete peças recortadas de um mesmo quadrado,
conforme a figura ao lado. Com as sete peças, muitas
formas diferentes podem ser construídas.
Será possível construir um quadrado usando duas peças? Três peças? Quatro?
Construa o seu tangran seguindo o esquema da figura.
Tente construir as figuras desenhadas usando as sete peças, sem colocá-las umas sobre
as outras.
Moedas no tabuleiro
Desenhe um tabuleiro quadrado (como um tabuleiro de xadrez) com 36 casas.
O desafio é: colocar 18 moedas no tabuleiro, de modo que nenhuma casa tenha mais de
uma moeda e que cada linha ou coluna tenha exatamente três moedas.
Compare sua resposta com a dos colegas.
Para não afundar
Um veleiro está afundando e nele estão sete pessoas que poderão se salvar usando dois
botes salva-vidas. Você pode ajudá-las a se organizar nos botes? Para ajudá-las você
deve levar em consideração que:
a) cada bote pode levar no máximo 300 quilos;
b) três pessoas pesam 70 quilos cada uma;
c) duas pessoas pesam 80 quilos cada uma
d) duas pessoas pesam 110 quilos cada uma.
Jogo com números
Na figura abaixo, cada símbolo está no lugar de um algarismo entre 3 e 7; cada símbolo
igual corresponde número igual. Os números no final de cada linha ou coluna indicam a
soma dos algarismos representados. Você pode descobrir quais são os algarismos?
Referências bibliográficas
ANDRADE Filho, O. Vademecum Pediátrico Glória. Constantes biológicas e dados de utilidade em
prática pediátrica .
BASSO, M.V.A. Desafios matemáticos na comunicação via rede. Porto Alegre: UFRGS.
Laboratório de Estudos Cognitivos, 1992 [mimeo].
PEREIRA, D, ed. Geografia: ciência do espaço: o espaço brasileiro. São Paulo: Atual, 1994.
PERELMAN, Y. Problemas y experimentos recreativos. Moscou: MIR, 1975.
SNOPE, C. & SCOTT, H. Enigmas maternáticos. Lisboa: Gradiva, 1994.
Texto elaborado com a colaboração do professor Marcus Vinicius de Azevedo Basso.