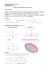3a- SÉRiE

Transcrição

3a- SÉRiE

caderno do
ensino médio
a
3 - SÉRIE
volume 1 - 2009
matemática
PROFESSOR
Coordenação do Desenvolvimento dos
Conteúdos Programáticos e dos Cadernos
dos Professores
Ghisleine Trigo Silveira
Linguagens, Códigos e suas Tecnologias
AUTORES
Educação Física: Adalberto dos Santos Souza,
Jocimar Daolio, Luciana Venâncio, Luiz Sanches
Neto, Mauro Betti e Sérgio Roberto Silveira
Ciências Humanas e suas Tecnologias
Filosofia: Paulo Miceli, Luiza Christov, Adilton
Luís Martins e Renê José Trentin Silveira
Geografia: Angela Corrêa da Silva, Jaime Tadeu
Oliva, Raul Borges Guimarães, Regina Araujo,
Regina Célia Bega dos Santos e Sérgio Adas
Governador
José Serra
História: Paulo Miceli, Diego López Silva,
Glaydson José da Silva, Mônica Lungov Bugelli e
Raquel dos Santos Funari
Vice-Governador
Alberto Goldman
Sociologia: Heloisa Helena Teixeira de Souza
Martins, Marcelo Santos Masset Lacombe,
Melissa de Mattos Pimenta e Stella Christina
Schrijnemaekers
Secretária da Educação
Maria Helena Guimarães de Castro
Secretária-Adjunta
Iara Gloria Areias Prado
Chefe de Gabinete
Fernando Padula
Coordenadora de Estudos e Normas
Pedagógicas
Valéria de Souza
Coordenador de Ensino da Região
Metropolitana da Grande São Paulo
José Benedito de Oliveira
Coordenadora de Ensino do Interior
Aparecida Edna de Matos
Presidente da Fundação para o
Desenvolvimento da Educação – FDE
Fábio Bonini Simões de Lima
EXECUÇÃO
Coordenação Geral
Maria Inês Fini
Concepção
Guiomar Namo de Mello
Lino de Macedo
Luis Carlos de Menezes
Maria Inês Fini
Ruy Berger
GESTÃO
Fundação Carlos Alberto Vanzolini
Presidente do Conselho Curador:
Antonio Rafael Namur Muscat
Presidente da Diretoria Executiva:
Mauro Zilbovicius
Diretor de Gestão de Tecnologias
aplicadas à Educação:
Guilherme Ary Plonski
Coordenadoras Executivas de Projetos:
Beatriz Scavazza e Angela Sprenger
COORDENAÇÃO TéCNICA
CENP – Coordenadoria de Estudos e Normas
Pedagógicas
Ciências da Natureza e suas Tecnologias
Biologia: Ghisleine Trigo Silveira, Fabíola Bovo
Mendonça, Felipe Bandoni de Oliveira, Lucilene
Aparecida Esperante Limp, Maria Augusta
Querubim Rodrigues Pereira, Olga Aguilar Santana,
Paulo Roberto da Cunha, Rodrigo Venturoso
Mendes da Silveira e Solange Soares de Camargo
Ciências: Ghisleine Trigo Silveira, Cristina
Leite, João Carlos Miguel Tomaz Micheletti Neto,
Julio Cézar Foschini Lisbôa, Lucilene Aparecida
Esperante Limp, Maíra Batistoni e Silva, Maria
Augusta Querubim Rodrigues Pereira, Paulo
Rogério Miranda Correia, Renata Alves Ribeiro,
Ricardo Rechi Aguiar, Rosana dos Santos Jordão,
Simone Jaconetti Ydi e Yassuko Hosoume
Física: Luis Carlos de Menezes, Sonia Salem,
Estevam Rouxinol, Guilherme Brockington, Ivã
Gurgel, Luís Paulo de Carvalho Piassi, Marcelo de
Carvalho Bonetti, Maurício Pietrocola Pinto de
Oliveira, Maxwell Roger da Purificação Siqueira
e Yassuko Hosoume
Química: Denilse Morais Zambom, Fabio Luiz de
Souza, Hebe Ribeiro da Cruz Peixoto, Isis Valença
de Sousa Santos, Luciane Hiromi Akahoshi,
Maria Eunice Ribeiro Marcondes, Maria Fernanda
Penteado Lamas e Yvone Mussa Esperidião
Arte: Geraldo de Oliveira Suzigan, Gisa Picosque,
Jéssica Mami Makino, Mirian Celeste Martins e
Sayonara Pereira
LEM – Inglês: Adriana Ranelli Weigel Borges, Alzira
da Silva Shimoura, Lívia de Araújo Donnini Rodrigues,
Priscila Mayumi Hayama e Sueli Salles Fidalgo
Língua Portuguesa: Alice Vieira, Débora Mallet
Pezarim de Angelo, Eliane Aparecida de Aguiar,
José Luís Marques López Landeira e João Henrique
Nogueira Mateos
Matemática
Matemática: Nílson José Machado, Carlos
Eduardo de Souza Campos Granja, José Luiz
Pastore Mello, Roberto Perides Moisés, Rogério
Ferreira da Fonseca, Ruy César Pietropaolo e
Walter Spinelli
Caderno do Gestor
Lino de Macedo, Maria Eliza Fini e Zuleika de
Felice Murrie
Equipe de Produção
Coordenação Executiva: Beatriz Scavazza
Assessores: Alex Barros, Antonio Carlos
Carvalho, Beatriz Blay, Carla de Meira Leite, Eliane
Yambanis, Heloisa Amaral Dias de Oliveira, José
Carlos Augusto, Luiza Christov, Maria Eloisa Pires
Tavares, Paulo Eduardo Mendes, Paulo Roberto da
Cunha, Pepita Prata, Renata Elsa Stark, Solange
Wagner Locatelli e Vanessa Dias Moretti
Equipe Editorial
Coordenação Executiva: Angela Sprenger
Assessores: Denise Blanes e Luís Márcio Barbosa
Projeto Editorial: Zuleika de Felice Murrie
Edição e Produção Editorial: Conexão Editorial,
Edições Jogos de Amarelinha, Jairo Souza Design
Gráfico e Occy Design (projeto gráfico)
APOIO
FDE – Fundação para o Desenvolvimento da
Educação
CTP, Impressão e Acabamento
Imprensa Oficial do Estado de São Paulo
A Secretaria da Educação do Estado de São Paulo autoriza a reprodução do conteúdo do material de sua titularidade pelas demais
secretarias de educação do país, desde que mantida a integridade da obra e dos créditos, ressaltando que direitos autorais protegidos*
deverão ser diretamente negociados com seus próprios titulares, sob pena de infração aos artigos da Lei nº 9.610/98.
* Constituem “direitos autorais protegidos” todas e quaisquer obras de terceiros reproduzidas no material da SEE-SP que não
estejam em domínio público nos termos do artigo 41 da Lei de Direitos Autorais.
Catalogação na Fonte: Centro de Referência em Educação Mario Covas
S239c
São Paulo (Estado) Secretaria da Educação.
Caderno do professor: matemática, ensino médio - 3a série, volume 1
/ Secretaria da Educação; coordenação geral, Maria Inês Fini; equipe, Carlos
Eduardo de Souza Campos Granja, José Luiz Pastore Mello, Nílson José
Machado, Roberto Perides Moisés, Walter Spinelli.– São Paulo : SEE, 2009.
ISBN 978-85-7849-188-8
1. Matemática 2. Ensino Médio 3. Estudo e ensino I. Fini, Maria Inês. II. Granja,
Carlos Eduardo de Souza Campos. III. Mello, José Luiz Pastore. IV. Machado,
Nílson José. V. Moisés, Roberto Perides. VI. Spinelli, Walter. VII. Título.
CDU: 373.5:51
Prezado(a) professor(a),
Dando continuidade ao trabalho iniciado em 2008 para atender a uma das
prioridades da área de Educação neste governo – o ensino de qualidade –, encaminhamos a você o material preparado para o ano letivo de 2009.
As orientações aqui contidas incorporaram as sugestões e ajustes sugeridos
pelos professores, advindos da experiência e da implementação da nova proposta em sala de aula no ano passado.
Reafirmamos a importância de seu trabalho. O alcance desta meta é concretizado essencialmente na sala de aula, pelo professor e pelos alunos.
O Caderno do Professor foi elaborado por competentes especialistas na área
de Educação. Com o conteúdo organizado por disciplina, oferece orientação
para o desenvolvimento das Situações de Aprendizagem propostas.
Esperamos que você aproveite e implemente as orientações didático-pedagógicas aqui contidas. Estaremos atentos e prontos para esclarecer dúvidas ou
dificuldades, assim como para promover ajustes ou adaptações que aumentem
a eficácia deste trabalho.
Aqui está nosso novo desafio. Com determinação e competência, certamente iremos vencê-lo!
Contamos com você.
Maria Helena Guimarães de Castro
Secretária da Educação do Estado de São Paulo
SuMário
São Paulo faz escola – uma Proposta Curricular para o Estado
Ficha do Caderno
5
7
orientação geral sobre os Cadernos
Situações de Aprendizagem
8
12
Situação de Aprendizagem 1 – A Geometria e o método das coordenadas
Situação de Aprendizagem 2 – A reta, a inclinação e a proporcionalidade
Situação de Aprendizagem 3 – Problemas lineares – máximos e mínimos
12
20
32
Situação de Aprendizagem 4 – Circunferências e cônicas: significados, equações,
aplicações 42
Orientações para Recuperação
57
Recursos para ampliar a perspectiva do professor e do aluno para
a compreensão do tema 58
Considerações finais
60
Conteúdos de Matemática por série/bimestre do Ensino Médio
4
61
Matemática – 3ª- série, 1o bimestre
São PAulo FAz ESColA – uMA ProPoStA
CurriCulAr PArA o EStAdo
Prezado(a) professor(a),
É com muita satisfação que apresento a todos a versão revista dos Cadernos do
Professor, parte integrante da Proposta Curricular de 5a a 8a séries do Ensino Fundamental – Ciclo II e do Ensino Médio do Estado de São Paulo. Esta nova versão
também tem a sua autoria, uma vez que inclui suas sugestões e críticas, apresentadas
durante a primeira fase de implantação da proposta.
Os Cadernos foram lidos, analisados e aplicados, e a nova versão tem agora a medida
das práticas de nossas salas de aula. Sabemos que o material causou excelente impacto
na Rede Estadual de Ensino como um todo. Não houve discriminação. Críticas e sugestões surgiram, mas em nenhum momento se considerou que os Cadernos não deveriam
ser produzidos. Ao contrário, as indicações vieram no sentido de aperfeiçoá-los.
A Proposta Curricular não foi comunicada como dogma ou aceite sem restrição.
Foi vivida nos Cadernos do Professor e compreendida como um texto repleto de significados, mas em construção. Isso provocou ajustes que incorporaram as práticas e
consideraram os problemas da implantação, por meio de um intenso diálogo sobre o
que estava sendo proposto.
Os Cadernos dialogaram com seu público-alvo e geraram indicações preciosas para
o processo de ensino-aprendizagem nas escolas e para a Secretaria, que gerencia esse
processo.
Esta nova versão considera o “tempo de discussão”, fundamental à implantação
da Proposta Curricular. Esse “tempo” foi compreendido como um momento único,
gerador de novos significados e de mudanças de ideias e atitudes.
Os ajustes nos Cadernos levaram em conta o apoio a movimentos inovadores, no
contexto das escolas, apostando na possibilidade de desenvolvimento da autonomia
escolar, com indicações permanentes sobre a avaliação dos critérios de qualidade da
aprendizagem e de seus resultados.
5
Sempre é oportuno relembrar que os Cadernos espelharam-se, de forma objetiva,
na Proposta Curricular, referência comum a todas as escolas da Rede Estadual, revelando uma maneira inédita de relacionar teoria e prática e integrando as disciplinas
e as séries em um projeto interdisciplinar por meio de um enfoque filosófico de Educação que definiu conteúdos, competências e habilidades, metodologias, avaliação e
recursos didáticos.
Esta nova versão dá continuidade ao projeto político-educacional do Governo de
São Paulo, para cumprir as 10 metas do Plano Estadual de Educação, e faz parte das
ações propostas para a construção de uma escola melhor.
O uso dos Cadernos em sala de aula foi um sucesso! Estão de parabéns todos os que
acreditaram na possibilidade de mudar os rumos da escola pública, transformando-a
em um espaço, por excelência, de aprendizagem. O objetivo dos Cadernos sempre será
apoiar os professores em suas práticas de sala de aula. Posso dizer que esse objetivo foi
alcançado, porque os docentes da Rede Pública do Estado de São Paulo fizeram dos
Cadernos um instrumento pedagógico com vida e resultados.
Conto mais uma vez com o entusiasmo e a dedicação de todos os professores, para
que possamos marcar a História da Educação do Estado de São Paulo como sendo
este um período em que buscamos e conseguimos, com sucesso, reverter o estigma que
pesou sobre a escola pública nos últimos anos e oferecer educação básica de qualidade
a todas as crianças e jovens de nossa Rede. Para nós, da Secretaria, já é possível antever
esse sucesso, que também é de vocês.
Bom ano letivo de trabalho a todos!
Maria inês Fini
Coordenadora Geral
Projeto São Paulo Faz Escola
6
FiCHA do CAdErno
o plano de descartes: a parceria entre a álgebra e a geometria
nome da disciplina:
Matemática
área:
Matemática
Etapa da educação básica:
Série:
Período letivo:
temas e conteúdos:
Ensino Médio
3ª1º- bimestre de 2009
Geometria Analítica Plana
O plano cartesiano
A equação da reta
A equação da circunferência
As equações das cônicas
7
oriEntAção GErAl SobrE oS CAdErnoS
Os temas escolhidos para compor o conteúdo disciplinar de cada bimestre não se afastam,
de maneira geral, do que é usualmente ensinado
nas escolas ou do que é apresentado nos livros
didáticos. As inovações pretendidas referem-se
à forma de abordagem desses temas, sugerida
ao longo dos Cadernos de cada um dos bimestres. Em tal abordagem, busca-se evidenciar os
princípios norteadores do presente currículo,
destacando-se a contextualização dos conteúdos, as competências pessoais envolvidas, especialmente as relacionadas com a leitura e a
escrita matemáticas, bem como os elementos
culturais internos e externos à Matemática.
Em todos os Cadernos, os conteúdos estão
organizados em oito unidades mais ou menos
do mesmo tamanho, que podem corresponder a
oito semanas de trabalho letivo. De acordo com
o número de aulas disponíveis por semana, o
professor explorará cada assunto com mais ou
menos aprofundamento, ou seja, escolherá uma
escala adequada para o tratamento dos temas
escolhidos. A critério do professor, em cada situação específica, o tema correspondente a uma
das unidades pode ser estendido para mais de
uma semana, enquanto o de outra unidade pode
ser tratado de modo mais simplificado.
É desejável que o professor tente contemplar todas as oito unidades, uma vez que, juntas, compõem um panorama do conteúdo do
bimestre, e, muitas vezes, uma das unidades
contribui para a compreensão das outras. Insistimos, no entanto, no fato de que somente
8
o professor, em sua circunstância particular, e
levando em consideração seu interesse e o dos
alunos pelos temas apresentados, pode determinar adequadamente quanto tempo dedicará
a cada uma das unidades.
Ao longo dos Cadernos são apresentadas,
além de uma visão panorâmica do conteúdo do
bimestre, quatro Situações de Aprendizagem
(1, 2, 3 e 4), que pretendem ilustrar a forma de
abordagem sugerida, instrumentando a ação
do professor na sala de aula. As atividades são
independentes e podem ser exploradas pelos
professores com mais ou menos intensidade,
segundo seu interesse e de sua classe. Naturalmente, em razão das limitações de espaço dos
Cadernos, nem todas as unidades foram contempladas com Situações de Aprendizagem,
mas a expectativa é de que a forma de abordagem dos temas seja explicitada nas atividades
oferecidas.
São apresentados também em cada Caderno, sempre que possível, materiais diversos (textos, softwares, sites e vídeos, entre
outros), que estejam em sintonia com a forma de abordagem proposta, e que possam
ser utilizados pelo professor para o enriquecimento de suas aulas.
Compõem o Caderno ainda algumas considerações sobre a avaliação a ser realizada, bem
como o conteúdo considerado indispensável ao
desenvolvimento das competências esperadas
no presente bimestre.
Conteúdos básicos do bimestre
O conteúdo básico do 1º- bimestre da
3ª- série é Geometria Analítica Plana. Mesmo quando o professor dispõe de poucas
aulas por semana, tal tema costuma ser contemplado nessa série. E mesmo quando ele é
apenas parcialmente ensinado, a equação da
reta é apresentada aos alunos. Neste Caderno, sugerimos uma abordagem da Geometria
Analítica que privilegia a equação da reta,
apresentada de um modo peculiar e que destaca certa classe de problemas cuja solução
depende apenas de uma compreensão adequada da ideia de proporcionalidade subjacente. São os chamados problemas lineares,
entre os quais estão alguns problemas de máximos e mínimos muito interessantes.
De acordo com os princípios gerais
que norteiam todos os Cadernos, espera-se que os demais assuntos sejam contemplados, com maior ou menor ênfase, segundo
o interesse do professor e as condições efetivas da classe. Mas consideramos que a parte
correspondente às retas, suas equações, suas
propriedades e suas aplicações pode ser especialmente representativa do significado da
Geometria Analítica como um método de
abordagem dos problemas geométricos que
contempla o ideal cartesiano – ou o “plano”
de Descartes, que buscava uma aproximação
efetiva entre a Geometria e a Álgebra.
A Geometria Analítica Plana é apresentada
como um método de abordagem dos problemas geométricos em que os pontos do plano
são representados por coordenadas (x; y);
retas e curvas de diversos tipos são representadas por equações; e regiões do plano são
representadas por inequações, possibilitando,
assim, a solução de um grande número de problemas envolvendo distâncias, comprimentos,
relações, áreas, etc.
Para o tratamento dos temas, sugere-se
uma organização dos trabalhos em oito unidades. O primeiro passo, na unidade 1, seria
o da consolidação do uso do sistema de coordenadas cartesianas XOY, já iniciado em séries anteriores, tanto no Ensino Fundamental
quanto no Ensino Médio. Tal sistema será utilizado para representar pontos do plano, determinando-se, por exemplo, a distância entre
dois pontos, o ponto médio e a inclinação do
segmento determinado pelos dois pontos.
A ideia de inclinação de um segmento
pode ser explorada de modo muito fecundo,
tanto na caracterização de segmentos paralelos quanto na condição de alinhamento de
três pontos, uma vez que para três pontos A,
B e C estarem alinhados, as inclinações de AB,
BC e AC devem ser iguais. Com base nessas
noções iniciais, é possível propor e resolver
uma série de problemas geométricos simples,
em que a aprendizagem do método analítico
situa-se no centro das atenções. Uma atividade para a sala de aula, incluindo questões
cujas respostas podem depender ou não do
sistema de coordenadas escolhido, será apresentada na Situação de Aprendizagem 1.
O segundo passo, na unidade 2, após a exploração inicial do plano, seria a representação
de curvas por equações, iniciando-se com a
9
reta. Os casos particulares das retas paralelas
aos eixos coordenados são tratados diretamente, de modo simples. Para as retas inclinadas em
relação aos eixos OX e OY, a qualidade comum
a todos os seus pontos é o fato de que, qualquer
que seja o par de representantes que escolhamos, a inclinação do segmento correspondente
é sempre a mesma: tal inclinação constante é a
inclinação da reta. Assim, facilmente se chega
à equação y = mx + h, em que o coeficiente m
representa a inclinação da reta, e h representa
o ponto em que a reta corta o eixo OY. A caracterização de retas concorrentes e paralelas,
com base nas inclinações correspondentes, é
uma consequência natural.
Na unidade 3, o passo seguinte a ser dado
é o estudo da condição de perpendicularidade de duas retas, com base em suas inclinações m1 e m2. Uma maneira simples de
compreender que se as inclinações são tais
que m1 . m2 = –1 então as retas serão perpendiculares será apresentada neste Caderno.
A forma geral da equação da reta, bem
como a representação de regiões do plano
por meio de desigualdades, servirá de conclusão dessa etapa. Uma atividade referente à equação da reta e à representação de
regiões por meio de inequações será apresentada na Situação de Aprendizagem 2.
Na unidade 4 poderá ser feita uma exploração dos estudos sobre as retas, tendo
em vista a resolução de alguns problemas
lineares, ou seja, problemas que, em última
instância, envolvem apenas relações de proporcionalidade direta. Uma coleção deles,
incluindo-se alguns problemas de máximos
10
e mínimos, será apresentada na Situação de
Aprendizagem 3. Apesar de problemas como
esses não serem usualmente apresentados no
Ensino Médio, pedimos ao professor que os
leia com atenção, pois certamente perceberá
que constituem situações simples em contextos interessantes.
Na unidade 5, seria apresentada a equação
da circunferência com centro na origem do
sistema de coordenadas. O tempo disponível
pelo professor deverá determinar o nível de
exploração de tal equação, deixando-se à escolha do professor o estudo das translações
da equação ou da forma geral da equação da
circunferência, que pode ser apenas sugerido
ou deslocado para o estudo das funções, no
3º- bimestre.
y
P
r
O
y
x
x
C: x2 + y2 = r2
C: x2 + y2 = r2
A unidade 6 poderia ser utilizada para a
apresentação de uma maneira simples de efetuar o cálculo da distância de um ponto a
uma reta, baseado apenas na inclinação m da
reta. Complementando tal cálculo, poderá
ser feito um estudo simplificado das posições
relativas entre retas e circunferências.
Na unidade 7, as cônicas são apresentadas e
caracterizadas por meio de propriedades de diversas maneiras. Além de constituírem interseções de um plano com uma superfície cônica, o
que lhes garante a denominação, a elipse é uma
circunferência “achatada”; a hipérbole surge na
representação de grandezas inversamente proporcionais; e a parábola, na representação de uma
grandeza que é proporcional ao quadrado de
outra. Complementarmente, as cônicas também
são apresentadas pelas suas importantes propriedades características em relação aos focos.
Quadro geral de conteúdos
do 1º- bimestre da 3ª- série
do Ensino Médio
unidade 1 – O plano cartesiano. Distância entre dois pontos. Ponto médio de
um segmento. Condição de alinhamento
de três pontos.
unidade 2 – A equação da reta. Significado dos coeficientes. Retas paralelas.
Na unidade 8 são apresentadas as equações
da elipse, da hipérbole e da parábola, em posições convenientes em relação aos eixos de
coordenadas, de modo a simplificar os cálculos. Uma extensão de tal estudo, conduzindo a
equações mais gerais, pode ser dispensada ou
adiada para o terceiro bimestre, na parte referente a funções. Uma atividade exploratória das
caracterizações das cônicas, de suas equações
em situações simples e de algumas aplicações é
apresentada na Situação de Aprendizagem 4.
unidade 3 – Retas perpendiculares. Regiões
do plano.
Sinteticamente, as oito unidades que compõem o presente bimestre são apresentadas
a seguir:
unidade 8 – Equações da elipse, da hipérbole e da parábola.
unidade 4 – Problemas lineares.
unidade 5 – A equação da circunferência.
unidade 6 – Distância de ponto a reta.
Posições relativas entre reta e circunferência.
unidade 7 – Cônicas. Apresentação e
propriedades da elipse, da hipérbole e da
parábola.
11
SituAçõES dE APrEndizAGEM
SITUAçãO DE APRENDIzAGEM 1
A GEOMETRIA E O MÉTODO DAS COORDENADAS
tempo previsto: 1 semana e meia.
Conteúdos e temas: coordenadas cartesianas no plano; cálculo de distâncias, coordenadas do
ponto médio, inclinação de segmentos usando coordenadas; escolha de sistemas de coordenadas convenientes para a solução de problemas geométricos.
Competências e habilidades: compreensão da linguagem algébrica na representação de situações e
problemas geométricos; expressão de resultados geométricos por meio da linguagem algébrica.
Estratégias: retomada do uso de sistemas de coordenadas já iniciado na 6a série do Ensino
Fundamental e apresentação de problemas geométricos simples, que podem ser resolvidos
por meio da linguagem das coordenadas.
roteiro para aplicação da Situação
de Aprendizagem 1
Na Geometria Analítica Plana, representamos os pontos de um plano por coordenadas (x; y) e fazemos cálculos relativos a
y
y
B
yB
figuras geométricas por meio de operações
algébricas sobre os pares de coordenadas.
Cálculo de distância entre dois pontos da inclinação de um segmento, por exemplo, podem ser realizados conforme as expressões
indicadas a seguir:
y
B
yB
mBC
dAB
yA
A
yA
0
xA
xB x
d AB = distância entre A e B
d AB =
12
E
C
√ (xB – xA)2 + (yB – yA)2
0
mAB
mAB
A
A
mDE
B
D
1
xA
xB
mAB = inclinação de AB
m AB =
yB – yA
xB – x A
x
0
x
A, B, C não alinhados: mAB ≠ mBC
BC paralelo a DE: mBC = mDE
Também é possível escrever de modo simples as equações de retas paralelas aos eixos
coordenados:
y
h
1
m
y
y = mx + h
(m < 0)
y=h
(h > 0)
0
x
h
0
Comparando as inclinações das retas, podemos identificar as que são paralelas e as que
são concorrentes, e particularmente a relação
entre as inclinações de retas perpendiculares:
x
h
y=h
(h < 0)
y
x=h
(h < 0)
x=h
y
(h > 0)
r1: y = m1x + h1
0
x
Para as retas inclinadas em relação aos eixos, lembrando dos gráficos das funções do
1o grau, temos as equações indicadas a seguir:
r2: y = m2x + h2
m1 ≠ m2
r1 e r2 concorrentes
x
y
y
y = mx + h
(m > 0)
y2 = m2x + h2
m
1
h
0
y1 = m1x + h1
x
m1 = m2
x
r1 e r2 paralelas
13
y
y
P
yP
r2
m1 = 0
r1
r : y = mx + h
d (P, r)
yp – yr
m
1
yr
yr = mxp+h
não existe m2
x
xp
r1 e r2 perpendiculares
(caso particular)
x
1
d( P; r )
=
yp – y r
1 + m2
y
r2
y2 = m2x + h2
d( P; r ) =
r1
x
d( P; r ) =
yp – y r
1 + m2
yp – m . xr – h
1 + m2
y1 = m1x + h1
r1 e r2 perpendiculares: m1 . m2 = –1
Para calcular a distância de um ponto a
uma reta, deixando de lado o caso mais simples, em que a reta é paralela a um dos eixos,
podemos explorar a semelhança de triângulos indicada na figura:
14
Para continuar nosso estudo de Geometria
Analítica, três lembretes são importantes.
Em primeiro lugar, trata-se de uma retomada de modo mais sistemático de um uso dos sistemas de coordenadas que, de fato, já se iniciou
bem anteriormente, na solução de sistemas de
equações lineares e no estudo das funções.
Em segundo lugar, o que aqui se buscará
desenvolver é um novo método de abordar problemas geométricos já conhecidos, ou seja, a
novidade está na forma de tratamento dos problemas, não no seu conteúdo.
unidades de comprimento. Utilizando os
sistemas de coordenadas XOY e X’MY’, determine:
E em terceiro lugar, é importante lembrar
que, muitas vezes, temos a liberdade de escolher
o sistema de coordenadas que será utilizado na
resolução dos problemas. Nesses casos, convém
notar que, embora as coordenadas dos pontos
representados dependam do sistema escolhido, existem informações relativas aos pontos
que podem depender ou não do sistema. Por
exemplo, fixados três pontos A, B, C, quando
escolhemos um sistema de coordenadas para
representá-los:
b) a inclinação dos segmentos FE, DC,
BC, AM, FA, ED, AC, FB;
a) as coordenadas dos pontos A, B, C, D,
E, F, M;
c) as coordenadas do ponto médio dos
segmentos AB, FC, FM, AE, BC, DC.
AD.
Y’
E
D
M
F
C
X’
f as coordenadas dos pontos A, B e C dependem do sistema XOY escolhido;
f a distância entre dois desses pontos não
depende do sistema escolhido;
A
f a inclinação do segmento AB depende
do sistema escolhido;
B
Y
E
D
f a área do triângulo ABC não depende
do sistema escolhido;
f a medida do ângulo BAC não depende do
sistema escolhido, e assim por diante.
Para praticar o uso das informações citadas anteriormente, são apresentadas as atividades seguintes.
Atividade 1
O hexágono regular ABCDEF tem centro M,
como mostra a figura, e cada lado tem dez
M
F
C
X
O
A
B
Será necessário calcular a altura de um
triângulo equilátero de lado 10, que é igual
a 5 ∙∙∙
3 .
15
h2 + 52 = 102
10
h
h2 = 75
5
A partir desse resultado, para o sistema XOY,
temos:
a) A (5; 0); B (15; 0); C (20; 5∙∙∙
3);
∙∙∙
∙∙∙
D (15; 10 3); E (5; 10 3);
F (0; 5∙∙∙
3); M (10; 5∙∙∙
3).
b) FE: ∙∙∙
3; DC: –∙∙∙
3; BC: ∙∙∙
3; AM: ∙∙∙
3;
∙∙∙
∙∙∙
3
3
; FB: –
.
FA: –∙∙∙
3; ED: 0; AC:
3
3
c) AB: (10; 0); FC: (10; 5∙∙∙
3);
FM: (5; 5∙∙∙
3); AE: (5; 5∙∙∙
3);
∙∙∙
5 3
); DC: (17,5; 7,5∙∙∙
3);
BC: (17,5;
2
AD: (10; 5∙∙∙
3).
Professor!
É importante notar que os segmentos
FE e BC são paralelos, assim como
também o são os segmentos FA e DC,
AB e ED, AM e FE etc. Esse é o significado da igualdade das inclinações,
nesses casos.
Para o sistema X'MY', as coordenadas são
as seguintes:
a) A (–5; –5∙∙∙
3); B (5; –5∙∙∙
3); C (10; 0);
∙∙∙
∙∙∙
D (5; 5 3); E (–5; 5 3); F (–10; 0); M (0; 0).
b) FE: ∙∙∙
3; DC: –∙∙∙
3; BC: ∙∙∙
3; AM: ∙∙∙
3;
∙∙∙
∙∙∙
3
3
FA: –∙∙∙
3; ED: 0; AC:
; FB: –
.
3
3
16
c) AB: (0; –5∙∙∙
3); FC: (0; 0); FM: (–5; 0);
AE: (–5; 0); BC: (7,5; –2,5∙∙∙
3);
DC: (7,5; 2,5∙∙∙
3); AD: (0; 0).
Muitos outros exercícios semelhantes à
Atividade 1 podem ser apresentados aos alunos, tendo em vista recordar fatos e relações da
Geometria Plana, expressando-os por meio das
coordenadas cartesianas. Triângulos, quadrados, losangos, retângulos, pentágonos, entre
outros, poderiam ser representados no plano
por meio de coordenadas, calculando-se comprimentos de lados, de medianas, baricentro,
etc. O destaque a ser dado é ao reconhecimento
do fato de que muitos problemas de Geometria Plana já conhecidos podem ser abordados
em outra perspectiva, com a parceria entre a
Álgebra e a Geometria. A escolha do sistema
de coordenadas mais simples em cada situação
concreta também pode ser explorada. Os exercícios seguintes ilustram o que se sugere.
Atividade 2
Em um sistema de coordenadas cartesianas, represente os pontos:
A (1; 2); B (3; 8); C (–2; 8); e D (–4; 2).
a) Mostre que os pontos A, B, C, D são os
vértices de um paralelogramo.
b) Calcule o comprimento do lado maior
do paralelogramo ABCD.
c) Calcule o comprimento da diagonal
menor de ABCD.
d) Determine as coordenadas do ponto M
em que as duas diagonais de ABCD se
encontram.
e) Calcule a área do triângulo AMD.
C
Logo, a diagonal menor é AC.
y
8
B
M
∙
2
D
A
-4
-2
0
1
d) Basta lembrar que as diagonais do paralelogramo se cruzam no ponto médio de cada
uma delas e achar o ponto médio de AC, que
1
é – ;5 .
2
e) Por inspeção direta, a base de AMD tem
comprimento 5 e a altura mede 3; logo, a
área de AMD é igual a 7,5.
3
x
Vamos representar os pontos indicados para
orientar a resposta aos diversos itens. No
entanto, poderíamos responder a cada uma
das questões apenas com as informações do
enunciado, sem qualquer figura.
a) Calculando as inclinações dos segmentos
AB e CD, notamos que elas são iguais:
8–2
=3
mAB =
3–1
2–8
–6
mCD =
=3
=
–4 – (–2)
–2
Logo, AB e CD são paralelos. De modo análogo, mostramos que AD e BC também são
paralelos. Resulta, então, que o quadrilátero
ABCD é um paralelogramo.
b) Calculando as distâncias entre A e B, e
entre B e C, obtemos:
∙
Atividade 3
Represente os pontos A (0; 0), B (3; 7),
C (–2; 13) em um sistema de coordenadas.
Sendo M o ponto médio de AC e N o ponto
médio de BC:
a) Determine as coordenadas de M e N.
b) Calcule as inclinações dos segmentos
AB e MN, verificando que tais segmentos são paralelos.
c) Calcule as distâncias dAB e dMN, verificando que dAB = 2 . dMN.
Como no exercício anterior, vamos fazer um
esboço da figura, para orientação da solução.
y
C
13
(8 – 2)2 + (3 – 1)2 = ∙∙∙
40 ;
dAB = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
N
(8 – 8)2 + (–2 – 3)2 = 5
dBC= ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
Logo, o lado AB é maior, valendo 2∙∙∙
10 .
c) Calculando as distâncias entre A e C e
entre B e D, obtemos as diagonais:
M
(8 – 2)2 + (–2 – 1)2 = ∙∙∙
45;
dAC = ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
(2 – 8)2 + (–4 – 3)2 = ∙∙∙
85 .
dBD= ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
B
7
x
A
-2
0
3
17
a) As coordenadas de M, ponto médio de
AC, são a média aritmética das coordenadas
correspondentes de A e C:
x + xC
y + yC
13
= –1 yM = A
=
xM = A
2
2
2
13
1
. Analogamente, N =
M = –1;
; 10 .
2
2
∙
∙
∙
∙
b) Calculando a inclinação de AB, temos:
y + yA
7
mAB = B
=
xb + xA
3
y + yN
7
=
Analogamente, mMN = M
xM + xN
3
Como as inclinações são iguais, concluímos
que os segmentos AB e MN são paralelos.
c) Calculando as distâncias entre A e B e
entre M e N, obtemos:
∙∙∙
58
58 e dMN =
dAB = ∙∙∙
2
dAB
ou seja, dMN = 2
Para que três pontos A, B e C estejam alinhados, é necessário e suficiente que as inclinações
dos segmentos AB, BC (e em consequência, AC)
sejam iguais, ou seja, que os três pontos constituam uma única rampa ABC.
y
C C
yC
mAB � mBC
B
A
18
xA
B
yB
mAB = mBC = mAc
yA
0
A
xA
xB
xC
x
a) Determine o valor de k para que os pontos A (1; 3), B (3; 7) e C (4; k) estejam
alinhados.
b) Determine o valor de k para que a área
do triângulo ABC seja igual a zero.
xB
a) Devemos ter mAB = mBC ; resulta daí que
7–3
k–7
=
, e, então, k = 9.
3–1
4–3
b) A área de ABC será nula quando os três
pontos estiverem alinhados, ou seja, quando
k = 9. É interessante aproximar essas duas
informações: sempre que três pontos estão
alinhados, a área do triângulo formado por
eles é nula e vice-versa.
c) Vamos construir uma figura para
orientar a solução.
yA
0
C
c) Sendo k = 3, calcule a área do triângulo
ABC.
Atividade 4
yB
y
yC
xC
x
Por inspeção direta na figura, verificamos
que a base AC mede 3 e a altura relativa
mede 4; logo, a área é igual a 6.
É interessante associar esse fato ao resultado da Atividade 3, notando que os lados do
paralelogramo são os segmentos que unem os
pontos médios dos lados dos triângulos em que
o quadrilátero inicial se divide quando são traçadas as suas diagonais.
y
B
7
3
C
A
x
1
3
Atividade 6
4
Atividade 5
Em um sistema de coordenadas qualquer,
represente quatro pontos de modo a formarem um quadrilátero ABCD. Pode escolher as
coordenadas à vontade. Analisando o quadrilátero formado:
Calcule a distância do ponto P de coordenadas (2; 15) à reta r nos casos indicados
a seguir:
a) r: y = 3
b) r: x = 9
c) y = 3x + 1
Vamos fazer uma figura para orientar a solução:
a) Calcule os pontos médios dos lados AB,
BC, CD e DA.
y = 3x + 1
b) Mostre que os quatro pontos médios
obtidos formam um paralelogramo.
Basta seguir os passos do enunciado: calcular os
pontos médios dos quatro segmentos determinados pelos pontos escolhidos arbitrariamente,
calcular as inclinações dos segmentos determinados por esses quatro pontos médios, e verificar que elas são iguais duas a duas. Converse
com seus colegas e procure verificar que isso vale
para qualquer quadrilátero. Em outras palavras,
os pontos médios dos lados de um quadrilátero
qualquer sempre formam um paralelogramo.
y

10
N
P
15
3
Q
1
d
M
B
15 – 7 = 8

10
x=9
A
7
D
y2 = 3 . 2 + 1 = 7
y=3
3
A
1
C
0
2
9
x
B
19
a) Por inspeção direta, notamos que a distância de P até a reta y = 3 é igual a 15 – 3 = 12.
b) Analogamente, notamos que a distância
de P até a reta x = 9 é 9 – 2 = 7.
c) Para calcular a distância d de P até a reta
y = 3 . x + 1, observando na figura a semelhança entre os triângulos PAB e MNQ, tePB
PA
=
.
mos:
QM QN
8
8∙∙∙
10
d
= ∙∙∙ , de onde obtemos d =
.
Logo,
10
10
1
Considerações sobre a avaliação
Ao final desta primeira unidade, a expectativa é que a Geometria Analítica tenha sido assimilada como um método
novo para a abordagem de problemas já
conhecidos, como foi registrado anteriormente. Nos exercícios apresentados, a colaboração entre a Álgebra e a Geometria
pode ser notada e, a partir disso, ela deve
ser ampliada continuamente.
Considera-se que o desenvolvimento da
Situação de Aprendizagem foi bem-sucedido
se os alunos consolidaram o uso do sistema
de coordenadas cartesianas, tendo aprendido
a determinar o ponto médio de um segmento, calcular a distância entre dois pontos e a
inclinação de um segmento, bem como verificar se dois segmentos dados pelas coordenadas de seus pontos são ou não paralelos,
além de outros resultados que o professor
considerar viáveis no contexto de sua sala de
aula, sempre associados à representação de
pontos por coordenadas.
A RETA, A INCLINAçãO E A PROPORCIONALIDADE
tempo previsto: 2 semanas.
Conteúdos e temas: equação da reta: proporcionalidade, inclinação constante; relação entre
as inclinações de retas paralelas e de retas perpendiculares; inequações lineares e regiões do
plano cartesiano; problemas envolvendo equações da reta.
Competências e habilidades: compreensão da linguagem algébrica na representação de situações
e problemas geométricos; expressão de situações envolvendo proporcionalidade por meio de
equações e inequações envolvendo retas.
Estratégias: caracterização da reta tendo por base a inclinação constante do segmento formado por qualquer par de seus pontos; enfrentamento de situações-problema envolvendo
proporcionalidade, tendo como recurso a equação da reta.
20
de Aprendizagem 2
A partir de agora, vamos procurar representar curvas por equações com base na expressão algébrica das propriedades que tais
curvas apresentam. E vamos iniciar com a
mais simples das "curvas", ou seja, com a reta,
que é como uma "curva sem imaginação", pois
segue sempre na mesma direção.
Para determinar a equação de uma reta, ou
seja, a relação entre as coordenadas x e y que
deve satisfazer todos os seus pontos, basta estar
atento ao fato de que todos os segmentos nela
contidos têm a mesma inclinação. Deixemos
de lado os casos particulares das retas paralelas aos eixos coordenados, cujas equações são
do tipo:
y
x = constante = m, ou seja, y = mx, que
representa uma reta de inclinação m, pas-
sando pela origem. Se a reta não passar pela origem, mas cortar o eixo y no
y–h
= m.
ponto de ordenada h, temos:
x–0
Logo, todo ponto da reta satisfaz a equação y = mx + h, sendo:
f h: ordenada do ponto em que a reta corta o eixo OY;
f m: inclinação da reta, ou seja, a variação na ordenada y por unidade a
mais de x.
x = constante = k, para todo y (reta paralela ao eixo OY);
ou então:
y = constante = h para todo x (reta paralela ao eixo OX).
Consideremos agora as retas que cortam
os eixos. Se uma reta corta o eixo OY no ponto P0 (0; h), tendo como inclinação comum a
todos os seus segmentos o valor m, então um
ponto qualquer P (x; y) da reta deve ser tal que
a inclinação do segmento P0P é igual a m.
A inclinação constante de todos os segmentos de uma reta pode ser associada à
representação de grandezas diretamente proporcionais. De fato, se uma grandeza y é diretamente proporcional a outra grandeza x, então
Reiteramos então que, se a partir de certo valor h, y varia de modo diretamente proporcional
a x, então temos: y – h = mx, ou seja, y = mx + h.
A inclinação m representa a constante de proporcionalidade, e é interessante notar que m corresponde à variação no valor de y quando o valor de
x aumenta de uma unidade:
x ⇒ y = mx + h
x’ = x + 1 ⇒ y’ = m(x + 1) + h =
mx + m + h = y + m
x’ – x = 1 ⇒ y’ – y = m
21
Ou seja, quando x aumenta de uma unidade, a variação de y será y’ – y = m.
y
Exemplo ilustrativo
Sem qualquer necessidade de cálculo, na
reta de equação y = 473,5x + 12,879, se x variar de uma unidade passando, por exemplo,
de 2008 para 2009, o valor de y aumentará
de 473,5 que é o coeficiente de x na equação
y = mx + h.
y=h
(h < 0)
x
Nestes casos m = 0
x=k
k<0
Muitos exemplos de retas com diferentes
valores e sinais para m e h são apresentados
a seguir, e é muito interessante acostumar-se a
associar a cada uma das retas representadas o
pequeno triângulo correspondente ao significado da inclinação.
y
x=k
k>0
0
x
Nestes casos não existe m
Se duas retas são paralelas, então elas têm
a mesma inclinação; se são concorrentes, então suas inclinações são diferentes. As figuras
seguintes podem colaborar para a compreensão de tais afirmações:
y
y = mx + h
m
0
(h > 0)
0
os sinais dos coeficientes m e h
h
y=h
1
y
r1
x
y = m1x + h1
Retas paralelas ao eixo OX, que têm equação do tipo y = h, podem ser consideradas
retas de inclinação m = 0. Retas que passam
pela origem do sistema de coordenadas têm
equação do tipo y = mx, uma vez que h = 0.
Para as retas paralelas ao eixo OY, não se define inclinação.
22
r2
y = m2x + h2
x
0
m1 = m2
r1 e r2 paralelas
r1
y
h
m
r3
–3
–2
r4
–1
∙∙∙
5
r5
∙∙∙
3
–7
r6
– ∙∙∙
5
6,4
r7
π
0
r8
–0,5
– ∙∙∙
7
r9
–0,8
π
y = m1 . x + h1
y = m2 . x + h2
r2
0
x
m1 ≠ m2
r1 e r2 concorrentes
Para a familiarização com tais fatos são
apresentados a seguir alguns exercícios. As
questões formuladas são simples, mas representam conhecimentos fundamentais. Com
os valores de h e m, podemos escrever diretamente a equação da reta (Atividade 1). Também podemos facilmente escrever a equação
da reta que passa por um ponto dado, com
inclinação dada, ou que passa por dois pontos
dados (Atividades 2 e 3).
Um esboço das nove retas, destacando-se os
valores relativos dos coeficientes m e h, é
indicado a seguir:
y
r6
y = – 
5 + 6,4x
r9
y = – 0,8 + πx
y = –1 + 
5x
r4
Atividade 1
Represente no plano cartesiano as retas
r1 a r9 correspondentes aos valores de h e m
tabelados abaixo:
r7
y=π
x
h
r1
r2
m
0
5
3
–2
r3
y = – 3 – 2x
r2
y = 3 – 2x
r1
y = 5x
r5
y = 
3 – 7x
y = – 0,5 – 
7x
r8
23
Atividade 2
1ª- solução
Determine a equação da reta que passa
pelo ponto A (2; 5) e tem inclinação m = 3.
Y
a equação é da forma y = mx + h.
Substituindo as coordenadas dos pontos, temos:
P
y
Sendo a reta inclinada em relação aos eixos,
7=m.1+h
16 = m . 4 + h
3
5
Resolvendo o sistema, temos: m = 3 e h = 4.
1
2
x
Logo, a equação é y = 3x + 4.
X
2ª- solução
seja, é y = 3x + h
16 – 7
= 3.
4–1
E já sabemos que a equação é do tipo
Como o ponto (2; 5) pertence à reta, devemos
y = 3x + h.
1ª- solução
A equação da reta é do tipo y = mx + h, ou
ter: 5 = 3 . 2 + h
Se ela passa pelo ponto A (1; 7), temos:
Logo, h = –1, e a equação é y = 3x –1
7=3.1+h
2ª- solução
Sendo (x; y) um ponto genérico da reta,
y–5
devemos ter: m =
= 3.
x–2
Logo, y – 5 = 3(x – 2), e segue que y = 3x –1
de onde segue que h = 4. Logo, a equação é
y = 3x + 4.
Professor, uma sugestão!
Atividade 3
Escreva a equação da reta que passa pelos
pontos A (1; 7) e B (4; 16).
y
16
A inclinação da reta é m =
B
Apresente exercícios de fixação sobre os
fatos básicos explorados nas atividades
anteriores. Proponha aos alunos a determinação de diversas equações de retas a
partir de diferentes informações:
f Reta passando por dois pontos dados.
f Reta passando por um ponto dado, sendo fornecida a inclinação.
A
7
A atividade pode ficar ainda mais interessante e significativa se forem incluídos os casos de retas paralelas aos eixos
coordenados.
0
24
1
4
x
Atividade 4
y
Considere o quadrado ABCD cujo lado
mede cinco unidades e o triângulo equilátero
EFG, cujo lado mede dez unidades.
A
B
B
A
0
D
5
D
x
C
C
5
E
y
E
10
G
M
10
F
a) Escolha um sistema de coordenadas que
considere mais adequado e escreva as
equações das retas AB, BC, CD, DA,
AC e BD.
b) Escolha um sistema de coordenadas que
considere mais adequado e escreva as
equações das retas EF, FG, GE e OM,
onde M é o ponto médio do lado EF e
O é o ponto médio do lado GF.
F
G
0
x
a) reta AB: y = 5 reta DC: y = 0
reta AD: x = 0
reta CB: x = 5
reta DB: y = x
reta AC: y = –x + 1
b) reta FG: y = 0
Naturalmente, existem muitas respostas distintas para a questão. São indicados a seguir
alguns exemplos de sistemas de coordenadas
que poderiam ser escolhidos:
f calculando a altura do triângulo equilátero, obtemos h = 5∙∙∙
3; logo, as retas
EF e EG têm equações do tipo
y = mx + 5∙∙∙
3;
25
f como a reta EF passa pelo ponto F(5;
0), concluímos que 0 = m . 5 + 5∙∙∙
3, ou
∙∙∙
seja, m = – 3; a equação de EF é
y = – x + 5∙∙∙
3;
f analogamente, como EG passa pelo ponto (–5; 0), concluímos que sua inclinação
5∙∙∙
3
, ou seja, é igual a ∙∙∙
3; sua equaé
5
ção é y = ∙∙∙
3 x + 5∙∙∙
3;
f a reta OM terá equação do tipo y = m . x,
uma vez que passa pela origem.
Como as coordenadas do ponto M são
3
5 5∙∙∙
, calculamos o valor de M e ob,
2
2
temos m = ∙∙∙
3; portanto, a equação de OM
∙∙∙
é y = 3 x.
∙
∙
a outra deverá ter inclinação negativa. Além
disso, podemos mostrar que, existindo as
inclinações m1 e m2 de duas retas perpendiculares, então seu produto sempre será igual
a –1:
Se m1 e m2 são as inclinações de r1 e r2
r1 e r2 são perpendiculares
então, m1 . m2 = –1
Para justificar tal fato, basta observar a figura:
y
h2
y = m1x + h1
Professor:
Outros sistemas de coordenadas poderiam ser escolhidos. Em sala de aula, essa
diversidade possibilita algumas comparações interessantes sobre quais resultados dependem e quais não dependem de
tal escolha. Nesse momento também é
interessante analisar qual o sistema mais
conveniente, no sentido de simplificar as
equações a serem obtidas.
Atividade 5
Se duas retas inclinadas em relação aos
eixos coordenados r1 e r2 são perpendiculares, então suas inclinações m1 e m2 têm sinais
opostos, ou seja, m1 . m2 < 0. É possível convencer os alunos de tal fato representando retas em diferentes situações e notando que se
uma tem inclinação positiva, então certamente
26
m1
1
h1
0
m2
y = m2x + h2
x
Pode-se notar que, no triângulo retângulo
formado pelas duas retas e pelo segmento em
que estão representadas as inclinações m1 e m2,
a altura relativa à hipotenusa é igual a 1; logo,
o produto dos comprimentos dos segmentos
representados por m1 e m2 é igual a 1, uma vez
que o quadrado da medida da altura relativa à
hipotenusa é igual ao produto das medidas das
projeções dos catetos sobre ela. Como as inclinações têm sinais opostos, concluímos que:
–1
m1 . m2 = –1, ou seja, m1 =
.
m2
Um outro modo de comprovar tal relação
é aplicar o teorema de Pitágoras no triângulo retângulo anteriormente referido, notando que um dos catetos é ∙∙∙∙∙∙∙∙
1 + m12, o outro
é ∙∙∙∙∙∙∙∙
1 + m22 , e a hipotenusa é m1 – m2 (lembrar
que m2 é negativo; logo, o comprimento do
segmento representado pelas duas inclinações
é m1 – m2).
Isso significa que:
(m1 – m2)2 = 1 + m12 + 1 + m22, de onde
segue que m1. m2 = –1.
Conhecendo esse fato, vamos resolver
alguns exercícios em que se escreve a equação da reta que passa pelo ponto A e é perpendicular à reta r em diversos casos, como
os seguintes:
A
r
(0; 0)
y = 4 – 3x
(0; 4)
y = 2x – 5
(0; –3)
y = 0,2x + 7
(0; 7)
y = –∙∙∙
3x+2
(1; 2)
y = 3x + 7
Em cada caso, buscamos a equação da reta
que passa pelo ponto dado e é perpendicular à
reta dada. Para obter a inclinação m’ da reta
procurada, basta tomar a inclinação m da
reta dada, inverter e trocar o sinal, pois sabemos que o produto m.m’ deve ser igual a – 1.
Assim, temos a seguinte tabela:
A
r
m
m'
(0; 0)
y = 4 – 3x
–3
1
3
(0; 4)
y = 2x – 5
2
(0; –3)
y = 0,2x + 7
0,2
–5
(0; 7)
3x+2
y = –∙∙
–∙∙∙
3
1
∙∙∙
3
=
∙∙∙
3
3
(1; 2)
y = 3x + 7
3
–
–
1
2
1
3
As retas perpendiculares são, portanto:
y = m’ . x + h, com o m’ calculado acima e
com o h calculado a partir do fato de que elas
passam pelo ponto indicado.
No primeiro caso, teríamos:
1
x + h; como a reta passa pela ori3
1
x.
gem (0; 0), h = 0, e temos y =
3
No segundo caso:
1
x + h; como a reta passa pelo
y=–
2
ponto (0; 4), temos:
–1
∙ 0 + h segue que h = 4, e temos
4=
2
1
x+4.
y=–
2
Nos demais casos, temos, sucessivamente:
1
7
1
y = –5x –3 y =
x+7 y= – x+
∙∙∙
3
3
3
y=–
27
Atividade 6
Já vimos que a equação y = mx + h representa os pontos de uma reta inclinada em relação aos eixos coordenados. Uma reta divide o
plano em dois semiplanos. Em um deles, o que
y
y = mx + h
se situa acima da reta, os pontos são tais que
y > mx + h; no outro, abaixo da reta, temos
y < mx+h. Se os semiplanos incluem os pontos da reta, temos y ≥ mx + h para os pontos acima da reta ou na reta, e y ≤ mx + h
para os ponto abaixo da reta ou na reta.
y
y = mx + h
y � mx + h
y � mx + h
y � mx + h
0
0
x
y � mx + h
x
Observação sobre a notação:
y > mx + h: pontos do semiplano situado acima da reta y = mx + h.
y ≥ mx + h: pontos do semiplano situado acima da reta, mais os pontos da reta y = mx + h.
y < mx + h: pontos do semiplano situado abaixo da reta y = mx + h.
y ≤ mx + h: pontos do semiplano situado abaixo da reta, mais os pontos da reta y = mx + h.
Para exercitar a associação de regiões
do plano a inequações, associe cada uma
das regiões hachuradas A, B, C, D, E, F
y
a uma inequação, ou a um sistema de inequações do tipo y > mx + h, ou então,
y < mx + h:
y
y = 3x + 5
A
y = 5 – 0,5x
B
0
28
x
x
y
y
y = 5 + 2x
C
D
y = 7 – 0,5x
x
0
x
y = 4 – 0,9x
y
y=4+x
y
F
E
y = π – 
2x
x
0
7
A: y ≥ 3x + 5
B: y < 5 – 0,5x
C: –3 + 2x ≤ y ≤ 5 + 2x
D: 4 – 0,9x ≤ y < 7 – 0,5x
E: 4 ≤ y ≤ 4 + x para 0 ≤ x ≤ 7
F: π – ∙∙∙
2 x < y ≤ π para 0 ≤ x ≤ 5
A equação da reta em sua forma geral
ax + by = c não foi especialmente contemplada na apresentação das ideias neste texto.
Entretanto, consideramos importante que o
professor explore em alguns exercícios o fato
de que tal equação sintetiza adequadamente
os dois casos aqui estudados em separado: as
0
5
x
retas paralelas aos eixos coordenados e as retas inclinadas em relação aos eixos. Particularmente importante nesse caso é reconhecer
a inclinação da reta apresentada na forma
geral ax + by = c. Sendo b ≠ 0, a reta não
será paralela ao eixo OY e podemos encontrar sua inclinação. Explicitando o valor de y,
–a
c
x +
e notamos que
escrevemos y =
b
b
–a
a inclinação da reta é m =
. Seria interesb
sante praticar tal reconhecimento em variados
exercícios. Para dedicar mais espaço neste Caderno à exploração de temas menos frequentemente abordados, deixamos tal tarefa a cargo
do professor.
29
Atividade 7
Uma pessoa deve fazer uma dieta em que
deve ingerir no mínimo 75g de proteínas por
dia, servindo-se apenas de certo alimento A.
a) Se cada grama de A fornece 0,15g de
proteína, quantos gramas de A deverão
ser ingeridos por dia, no mínimo?
Sendo x a quantidade de gramas de A, a ser
ingerida, devemos ter x.0,15 ≥ 75.
Concluímos, então, que x ≥ 500, ou seja, devem ser ingeridas no mínimo 500 g do alimento A.
b) Represente algebricamente a relação
entre a quantidade x de A em gramas a
ser ingerida e a quantidade y de proteínas correspondentes.
A quantidade y em gramas de proteína ingerida é uma função da quantidade x em gramas ingerida do alimento A. Então, temos:
y = 0,15x.
y
c) Represente no plano cartesiano os pontos
correspondentes aos pares (x; y) para os
quais a prescrição da dieta é atendida.
Os pares (x; y) do plano cartesiano que correspondem ao atendimento à prescrição da
dieta são os pontos da reta y = 0,15x, tais
que x ≥ 500, ou seja, são os pontos da reta
y = 0,15x à direita da reta x = 500.
d) Represente no plano cartesiano a região
em que a dieta estaria igualmente satisfeita, porém com alimentos mais ricos
em proteínas do que o alimento A.
Os pares (x; y) que correspondem a alimentos mais ricos em proteínas do que A são tais
que y > 0,15x, ou seja, ingerindo-se x gramas, a quantidade y de proteínas será maior
do que 0,15x: trata-se da região acima da
reta y = 0,15x; como devemos ter a ingestão
de, no mínimo, 75g de proteína, então y ≥ 75,
e devemos considerar, na região y > 0,15x,
apenas os pontos acima da ou na reta y = 75.
x = 500
y = 0,15x
y = 75
x
30
Atividade 8
Um fazendeiro dispõe de 18 alqueires para
plantar milho e alfafa. Chamando de x a área a
ser plantada de milho e de y a área a ser plantada de alfafa, e sabendo-se que o fazendeiro
pode optar por deixar uma parte das terras sem
plantar qualquer uma das culturas, responda
às seguintes questões:
a) Represente a relação algébrica que deve
existir entre os valores de x e y.
Sendo x a quantidade de alqueires plantados de milho e y a quantidade de alqueires
plantados de alfafa, e sabendo-se que existe
a opção de não plantar todos os 18 alqueires,
devemos ter, então, a soma x + y menor ou
igual a 18, ou seja, x + y ≤ 18.
b) Represente a região A do plano cartesiano que corresponde à relação entre x
e y anteriormente referida.
Representando no plano cartesiano, obtemos
o semiplano abaixo da reta x + y = 18, e
mais os pontos da reta x + y = 18; naturalmente, somente faz sentido no problema
em questão os pares (x; y) em que temos
x ≥ 0 e y ≥ 0.
região B do plano correspondente aos
pares (x; y) que satisfazem as condições
formuladas?
Sabendo que devem ser plantados no mínimo 5 alqueires de milho, temos, então, x ≥ 5;
no plano, teremos a região à direita da reta
x = 5, e abaixo da reta, x + y = 18.
d) Sabendo-se que devem ser plantados
no mínimo 5 alqueires de milho e no
mínimo 3 alqueires de alfafa, qual a região C do plano que corresponde aos
pares (x; y) que satisfazem as condições
formuladas?
Sabendo que devem ser plantados no mínimo
5 alqueires de milho e no mínimo 3 alqueires de alfafa, devemos ter, simultaneamente,
x + y ≤ 18, x ≥ 5 e y ≥ 3; no plano, trata-se da região acima da, ou na reta y = 3,
à direita da, ou na reta x = 5, e abaixo da,
ou na reta x + y = 18 (incluindo-se os pontos
das duas retas).
y
18
Para obtermos a representação dos pontos
da reta x + y = 18, basta escolhermos os
pontos em que x = 0 (e, portanto, y = 18), e
em que y = 0 (e, portanto, x = 18).
c) Sabendo-se que devem ser plantados
no mínimo 5 alqueires de milho, qual a
A
0
x + y = 18
18
x
31
y
18
Ao final desta Situação de Aprendizagem, é
fundamental que as equações de retas estejam
naturalmente associadas à variação proporcional entre x e y, tanto a partir da origem quanto
a partir de outros valores: y = kx, y – h = kx,
ou ainda, y – y0 = k(x – x0).
x + y = 18
B
0
18
5
x
y
18
x + y = 18
C
3
0
5
18
x
Espera-se que os alunos compreendam que retas paralelas aos eixos têm equações simples, e que
retas inclinadas em relação aos eixos têm equações
na forma y = mx + h e ainda que saibam interpretar o significado dos coeficientes m e h. Especial
atenção deve ser dada ao pequeno triângulo que
determina a inclinação de cada reta, em decorrência das múltiplas informações que ele propicia.
Também faz parte das expectativas de aprendizagem o reconhecimento de regiões do plano determinadas por desigualdades do tipo
y < mx + h, ou y > mx + h, bem como de suas
variações, envolvendo igualdade e desigualdade.
PROBLEMAS LINEARES – MÁXIMOS E MÍNIMOS
tempo previsto: 2 semanas.
Conteúdos e temas: equação da reta em diferentes contextos: problemas lineares; representação de retas e regiões do plano cartesiano: problemas de máximos e mínimos.
Competências e habilidades: capacidade de recorrer à linguagem da Geometria Analítica para
enfrentar situações-problema em diferentes contextos; reconhecimento da importância da ideia
de proporcionalidade e de sua relação direta com as equações das retas.
Estratégias: apresentação de uma coleção de problemas lineares, alguns deles envolvendo
situações de máximos ou mínimos, como motivação para uso das equações e inequações associadas a retas e regiões do plano.
32
de Aprendizagem 3
De maneira geral, situações que envolvam
grandezas diretamente proporcionais, ou cujas
variações, a partir de certo valor inicial, traduzam uma proporcionalidade direta, resultam
em equações de retas, quando traduzidas algebricamente. Vamos examinar, nos problemas
que seguem, algumas situações concretas desse tipo. Os enunciados dos problemas podem
não parecer usuais no conteúdo de Geometria
Analítica, mas os requisitos para a solução de
todos eles são apenas o conhecimento básico
que já foi apresentado envolvendo equações de
retas ou inequações correspondentes a regiões.
Alguns dos problemas examinam situações de
otimização, ou seja, em que se busca a solução
de um problema de máximo ou de mínimo. As
perguntas iniciais de cada problema são simples e servem de degraus para facilitar a compreensão e a solução das últimas questões.
Atividade 1
Em uma fábrica que produz um só tipo
de produto, o custo C da produção de x unidades é a soma de um custo fixo C0 com um
custo variável C1, que é proporcional a x.
Se o processo de produção for tal que cada
unidade produzida a mais custe sempre a
mesma quantia, independentemente do valor de x, então C1 = kx, onde k representa o
custo de cada unidade do produto. Em uma
fábrica como a descrita anteriormente, tem-se:
C = 3 000 + 150x (x é o número de artigos;
C é o custo da produção em reais).
a) Esboce o gráfico de C em função de x.
O gráfico de C = 3 000 + 150x é uma reta de
inclinação m = 150, cortando o eixo OY, em
que está representado o custo C, no ponto
(0; 3 000):
C
150
1
3 000
C = 3 000 + 150x
x
b) Para qual valor de x o custo fixo se iguala ao custo variável?
O custo fixo é 3 000 e o custo variável é 150x;
eles são iguais quando x = 20.
c) A partir de qual valor de x o custo fixo
passa a representar menos de 10% do
custo total da produção?
O custo fixo passará a corresponder a 10%
do custo total quando:
3 000 = 10% de (3 000 + 150x), ou seja, quando
3 000 = 0,1(3 000 + 150x), e então x = 180.
C = 3 000 + 150x
C
150
C1 = 150x
1
3 000
20
x
33
Atividade 2
Uma fábrica produz dois tipos de produtos,
A e B. A quantidade produzida diariamente
de A é igual a x, e a quantidade diária de B
é igual a y. O processo de produção é tal que
cada unidade produzida de A custa sempre 5
reais, e cada unidade de B custa 8 reais, sendo,
portanto, o custo da produção conjunta de A
e B igual a C = 5x + 8y (C em reais).
Sendo C = 3 200, então temos:
5x + 8y = 3 200. Os pares (x; y)
correspondentes situam-se sobre a reta
5x + 8y = 3 200 (que é paralela à reta
5x + 8y = 2 400).
Quando y = 0, x assume o valor máximo
possível: x = 640.
Quando x = 0, y assume o valor máximo
possível: y = 400.
a) Sendo o valor de C, certo dia, igual a
2 400 reais, determine dois pares de valores possíveis para x e y.
y
400
Para termos 2400 = 5x + 8y, podemos ter
x = 0 e y = 300, ou então, y = 0 e x = 480,
ou ainda, x = 400 e y = 50. Existem infinitos pares de valores de x e de y que satisfazem
a relação dada: são os correspondentes aos
pontos da reta cuja equação 5x + 8y = 2 400
é representada a seguir:
300
5x + 8y = 3 200
5x + 8y = 2 400
0
480
640 x
c) Represente em um sistema de coordenadas no plano, os pares (x; y) para os
quais se tem C ≤ 3 200.
y
300
Teremos o custo C menor ou igual a 3 200 na
região do primeiro quadrante situada na reta
5x + 8y = 3 200 ou abaixo dela:
5x + 8y = 2 400
y
400
50
480
0
400
5x + 8y = 3200
x
b) Sendo o máximo valor admissível para
C igual a 3 200 reais, qual o valor máximo possível para x? E qual o valor
máximo possível para y? (devemos ter,
naturalmente, x ≥ 0, y ≥ 0).
34
0
640
x
Atividade 3
Uma pessoa deve fazer uma dieta que forneça pelo menos 6 mg de vitamina B2 alimentando-se exclusivamente dos alimentos I e II,
oferecidos em pacotes de 100 g. Cada pacote
do alimento I fornece 1,2 mg de B2, e cada
pacote do alimento II fornece 0,15 mg de B2.
Sendo x o número de pacotes do alimento I
a ser ingeridos e y o número de pacotes do
alimento II:
a) Escreva a relação que deve existir entre
x e y para que a dieta seja satisfeita.
Como cada pacote do alimento I fornece
1,2 mg de vitamina B2, x pacotes de I fornecerão x . 1,2 mg de vitamina B2; se cada
pacote de II fornece 0,15 mg de B2, então
y pacotes de II fornecerão 0,15y mg de B2.
Logo, ingerindo x pacotes de I e y pacotes de
II, a quantidade ingerida de B2 será igual a
1,2x + 0,15y. Para a dieta ser satisfeita, devemos ter 1,2x + 0,15y ≥ 6.
b) Represente graficamente os pares (x; y)
que satisfazem essa relação (lembrese de que devemos ter, naturalmente,
x ≥ 0, y ≥ 0).
y
40
Os pontos (x; y) que satisfazem a relação
1,2x + 0,15y ≥ 6 são os pontos do primeiro
quadrante que se situam acima da, ou na reta
1,2x + 0,15y = 6. Essa reta corta o eixo OX no
ponto (5; 0) e o eixo OY no ponto (0; 40).
Atividade 4
Retome o enunciado do exercício anterior.
Considere que cada pacote de 100g do alimento I custa 5 reais, e que cada pacote do alimento II custa 2 reais.
a) Expresse o custo C da alimentação, se
forem utilizados x pacotes de I e y pacotes de II.
Como cada pacote de I custa 5 reais, e cada pacote de II custa 2 reais, o custo C será igual a
5x + 2y, ou seja: C = 5x + 2y (C em reais).
b) Represente graficamente no plano cartesiano os pares (x; y) que correspondem
ao custo C1 = 40 reais, notando que eles
correspondem a uma reta r1.
Sendo o custo C1 = 40, os pares (x; y) que
satisfazem a relação 40 = 5x + 2y são os
pontos da reta r1, representada a seguir.
Para representar tal reta, basta notar que
quando x = 0, y = 20, e que quando y = 0,
x = 8, ou seja, os pontos (0; 20) e (8; 0)
pertencem a r1.
y
20
1,2x + 0,15y = 6
r1
C1 = 40
5x + 2y = 40
0
5
x
0
8
x
35
c) Represente os pontos que correspondem
ao custo de C2 = 60 reais e C3 = 80 reais,
notando que eles correspondem às retas
r2 e r3, paralelas à reta r1 do item anterior.
Os pontos que correspondem ao custo C2 = 60
e C3 = 80 são pontos, respectivamente, das
retas r2 : 5x + 2y = 60 e r3 : 5x + 2y = 80,
representadas a seguir.
e) Para qual dos pares (x; y) tem-se a dieta
satisfeita e o custo da alimentação o mínimo possível?
y
40
1,2x + 0,15y ≥ 6
Para representar r2, basta notar que:
se x = 0, então y = 30;
se y = 0, então x = 12.
Para representar r3, analogamente, temos:
x = 0, y = 40; y = 0, x = 16.
∙As retas r
2
e r3 são paralelas, pois têm a
mesma inclinação m, determinada pelos co5
eficientes 5 e 2: m = – .
2
∙
d) Mostre que quanto menor o custo, menor a ordenada do ponto em que a reta
que o representa corta o eixo y.
Para cada valor fixado de C, a reta C = 5x + 2y
C
; assim, quanto
corta o eixo OY no ponto 0;
2
C
menor o custo, menor o valor de . Podemos
2
observar esse fato nos exemplos dos itens anteriores, para C igual a 40, 60 e 80.
∙
∙
y
r3
30
C3 = 80
r2
r1
C2 = 60
36
Recordemos, da Atividade 3, que para a dieta
ser satisfeita, os pares (x; y) devem pertencer à região do primeiro quadrante situada na
reta 1,2x + 0,15y = 6, ou acima dela. Estamos, agora, procurando o par (x; y) que corresponde ao custo mínimo entre os pontos da
região em que 1,2x + 0,15y ≥ 6.
Vamos observar como as retas que traduzem
os custos da alimentação, representadas anteriormente, situam-se na região que corresponde à satisfação da dieta.
Notamos que:
f para os diversos valores do custo, as retas
representativas são paralelas (inclinação
5
;
igual a –
2
f quanto mais baixa for a reta que representa o custo, menor é esse custo (seu valor determina o ponto em que a reta corta
C
.
o eixo y, que é 0;
2
f o ponto mais baixo a que se pode chegar
sem sair da região que satisfaz a dieta
∙
C1 = 40
0
x
5
∙
40
20
0
8
12
16 x
∙
(acima ou na reta 1,2x + 0,15y = 6), é o
ponto (5; 0);
f nesse ponto, o custo será
C = 5 . 5 + 2 . 0 = 25, que é o custo mínimo.
Todos esses fatos estão reunidos na figura a
seguir:
y
30
20
1,2x + 0,15y ≥ 6
12,5
C = 60
C = 40
0
5
fora da região
de satisfação
da dieta
8
Cmínimo
C = 25
12
a) Como se pode representar, em termos
de x e y, o rendimento total R a ser recebido pelo fazendeiro, supondo que venda a totalidade de sua produção?
Cada alqueire de milho renderá 20 000; logo,
se plantar x alqueires, o rendimento será
20 000x. Cada alqueire de cana renderá
15 000; logo, se plantar y alqueires de cana,
o rendimento será 15 000y. O rendimento total será R = 20 000x + 15 000y.
C = 5x + 2y
40
irrigação, e cada alqueire de cana requer
somente 10 000L de água, sendo que, no período correspondente, a quantidade de água
disponível para tal fim é 120 000L.
C = 80
16
x
Portanto, o custo mínimo, nas condições do
enunciado, ocorre com 5 pacotes do alimento
I e nenhum pacote do alimento II; tal custo
corresponde a 25 reais.
b) Qual a relação entre x e y que traduz
a exigência de que o total de alqueires
plantados não pode ser maior do que 8?
Represente no plano cartesiano os pontos (x; y) que satisfazem essa relação.
Sendo x a quantidade de alqueires a ser
plantados de milho e y a quantidade de alqueires plantados de cana, a soma x + y não
pode ultrapassar os 8 alqueires disponíveis,
ou seja: x + y ≤ 8.
Atividade 5
Um pequeno fazendeiro dispõe de 8 alqueires para plantar milho e cana. Ele deve
decidir quanto plantar de milho e de cana, em
alqueires, de modo que seu rendimento total
seja o maior possível. Cada alqueire de milho
plantado deve resultar em um rendimento líquido de 20 000 reais, e cada alqueire de cana
deverá render 15 000 reais. No entanto, cada
alqueire de milho requer 20 000L de água para
y
8
x+y≤8
8
x
37
c) Qual a relação entre x e y que traduz a
exigência de que o total de água a ser
utilizado não pode superar os 120 000L?
Represente no plano cartesiano os pontos (x; y) que satisfazem essa relação.
Como cada alqueire de milho requer 20 000L
de água, x alqueires requererão 20 000x L; da
mesma forma, y alqueires de cana utilizarão
10 000y L de água. Assim, o total de litros
de água utilizados será 20 000x + 10 000y, e
não poderá ultrapassar o limite de 120 000,
ou seja: 20 000x + 10 000y ≤ 120 000. Isso
corresponde aos pontos situados abaixo da
reta ou na reta 20 000x + 10 000y = 120 000.
Confira a representação:
Os pontos do plano que satisfazem simultaneamente as duas restrições são os pontos
situados abaixo ou na reta x + y = 8, e abaixo ou na reta 2x + y = 12. Formam o quadrilátero ABCD indicado na representação
a seguir.
y
12
2x + y = 12
8A
y
B
12
x+y=8
2x + y = 12
D
0
2x + y ≤ 12
0
6
8
x
Para representar a reta, podemos simplificar
os coeficientes, obtendo 2x + y = 12.
f para x = 0, temos y = 12;
f para y = 0, temos x = 6.
d) Represente no plano cartesiano o conjunto dos pontos que satisfazem simultaneamente as duas exigências expressas
nos itens b e c (lembrando que devemos
ter x ≥ 0, y ≥ 0).
38
C
6
8
x
e) Determine o conjunto dos pontos
(x; y) do plano que correspondem
ao rendimento R1 = 75 000 reais e os
que correspondem ao rendimento
R2 = 120 000 reais.
Os pontos (x; y) que correspondem ao rendimento R1 = 75 000 reais são os pontos da reta
r1 de equação 75 000 = 20 000x + 15 000y,
ou seja, simplificando os coeficientes,
4x + 3y = 15.
Os pontos que correspondem ao rendimento
R2 = 120 000 são os pontos da reta r2 de equação 120 000 = 20 000x + 15 000y, ou seja,
simplificando os coeficientes, 24 = 4x + 3y.
As duas retas são paralelas e estão representadas a seguir:
sem sair da região de viabilidade corresponde
à reta que passa pelo ponto de interseção das
retas x + y = 8 e 2x + y = 12. Calculando tal
ponto, obtemos x = 4 e y = 4. No ponto (4; 4),
portanto, o valor de R é o maior possível, respeitadas as condições de x + y ≤ 8 e 2x + y ≤ 12.
Calculando o valor de R nesse ponto, obtemos:
R = 20 000.4 + 15 000.4, ou seja, R = 140 000
reais. Acompanhe o raciocínio que foi feito na
figura abaixo:
y
12
R2 = 120 000
A
2x + y = 12
R1 = 75 000
5
B
x+y=8
C
D
0
15
___
4
6
8
x
fora da região
da viabilidade
Rmáximo
r1: 4x + 3y = 15
x=0⇒y=5
15
y=0⇒x=
4
r2: 4x + 3y = 24
x=0⇒y=8
R2 = 120 000
y=0⇒x=6
f) Mostre que, quanto maior o rendimento
R, maior a ordenada do ponto em que a
reta que o representa corta o eixo OY.
Para cada valor fixado do rendimento R, a
reta R = 20 000x + 15 000y corta o eixo
OY no ponto em que x = 0, ou seja, em que
R
. Isso significa que quanto maior o
y=
15 000
rendimento, mais alta a ordenada do ponto em
que a reta que o representa corta o eixo y.
g) Determine o ponto da região do item
d que corresponde ao rendimento total
máximo.
Buscamos agora o ponto da região de viabilidade do problema, ou seja, que foi determinado no item d, no qual o rendimento total
R é o maior possível. O mais alto possível para
a reta R = 20 000x + 15 000y cortar o eixo y
y
12
A
2x + y = 12
R1 = 75 000
5
4
B
x+y=8
D
0
4
15
___
4
C
6
8
x
Atividade 6
Uma fábrica utiliza dois tipos de máquinas,
M1 e M2, para produzir dois tipos de produtos,
P1 e P2. Cada unidade de P1 exige 2 h de trabalho de M1 e 2 h de M2; cada unidade de P2
exige 1 h de trabalho de M1 e 4 h de M2. Sabese que as máquinas M1 e M2 podem trabalhar
no máximo 10 h por dia e 16 h por dia, respectivamente, e que o lucro unitário, na venda de
P1, é igual a 40 reais, enquanto na venda de P2,
o lucro unitário é de 60 reais. Representando
39
b) Qual a relação entre x e y de modo que o
tempo de utilização da máquina M2 não
ultrapasse as horas diárias permitidas?
Represente os pontos correspondentes
no plano cartesiano.
por x a quantidade diária a ser produzida de
P1 e por y a quantidade a ser produzida de P2,
responda às questões seguintes:
a) Qual a relação entre x e y de modo que o
tempo de utilização da máquina M1 não
ultrapasse as horas diárias permitidas?
Represente os pontos correspondentes
no plano cartesiano.
Analogamente ao item anterior, cada unidade de P1 utiliza 2 h de M2 , e cada unidade
de P2 utiliza 4 h de M2. Logo, x unidades
de P1 e y unidades de P2 utilizarão 2x + 4y
horas de M2, e devemos ter 2x + 4y ≤ 16.
O gráfico foi está representado anteriormente.
Cada unidade de P1 utiliza 2 h de M1; cada
unidade de P2 utiliza 1 h de M1; logo, produzindo-se x unidades de P1 e y unidades de P2,
a máquina M1 ficará ocupada x . 2 + y . 1
horas. Como M1 poderá trabalhar no máximo 10 h, devemos ter 2x + 1y ≤ 10. Corresponde à região do plano abaixo da ou na reta
2x + y = 10 (ver a seguir).
c) Represente a região do plano cartesiano
que corresponde aos pontos (x; y) que
satisfazem simultaneamente as duas
restrições dos itens a e b.
Trata-se da região do primeiro quadrante situada abaixo das ou nas retas
y
2x + y = 10 e 2x + 4y = 16; é o quadrilátero
A de vértices (0; 0), (5; 0), (0; 4) e (4; 2).
10
Para encontrar o vértice (4; 2), basta achar a
interseção das retas 2x + y = 10 e 2x + 4y = 16
2x + y ≤ 10
y
5
10
x
y
4 2x + y ≤ 10
4
2
A
2x + 4y ≤ 16
2x + 4y ≤ 16
8
40
x
5
8
x
d) Qual a expressão do lucro total L que
resulta da venda de todas as unidades
produzidas de P1 e P2?
viabilidade para o problema. Para descobrir tal ponto, vamos relacionar o lucro L
com a região A.
O lucro total L, que resulta da venda de todas
as x unidades produzidas de P1 e y unidades
produzidas de P2, é igual a 40x + 60y, pois
cada unidade de P1 gera um lucro de 40, e
cada unidade de P2 gera um lucro de 60. Assim, temos L = 40x + 60y.
e) Represente os pontos do plano que correspondem a um lucro total igual a 120
reais.
Se o lucro L for igual a 120 reais, temos:
120 = 40x + 60y. Os pontos que satisfazem
a essa relação pertencem a uma reta, representada a seguir:
y
Lucro crescente
10
2x + y ≤ 10
Lmáximo
L = 240
L = 120
2
A
2x + 4y ≤ 16
3
2
120 = 40x + 60y
0
y
3
x
f) Qual o ponto da região do item c que
corresponde ao lucro total máximo?
Queremos agora encontrar o ponto da região A, indicada no item c, para o qual o
lucro total L seja máximo. A região A é
formada pelos pares (x; y), que obedecem às duas restrições inicialmente apresentadas, constituindo, assim, a região de
4
5
6
8
x
Para cada valor de L, a expressão L = 40x
+ 60y representa uma reta; para valores
diferentes de L, as retas correspondentes
são todas paralelas. Por exemplo, para
L = 240, temos 240 = 40x + 60y, que é uma
reta que intercepta o eixo x no ponto (6;
0), e o eixo y no ponto (0; 4).
Para encontrar o lucro máximo, basta
procurar entre as retas paralelas L = 40x +
60 . y aquela que corta o eixo y o mais alto
possível, sem sair da região de viabilidade
do problema. Tal reta é a que passa pelo
ponto (4; 2); o valor de L correspondente é
L = 40 . 4 + 60 . 2 = 280. O lucro total máximo é, portanto, 280 reais.
41
Nesta presente Situação de Aprendizagem,
foram explorados problemas lineares, envolvendo exclusivamente equações de retas, em alguns
dos quais o que estava em foco era uma questão
de otimização (de máximo ou de mínimo). Tais
problemas, apesar de seus enunciados relativamente longos, não são especialmente difíceis, exigindo apenas uma leitura atenta das informações
apresentadas. Eles podem se prestar muito bem
à realização de pequenos projetos de estudo ou
de investigação sobre os temas abordados, como
as dietas ou a organização do trabalho em uma
fábrica, por exemplo.
Os objetivos da Situação de Aprendizagem
estarão garantidos se os alunos conseguirem
explorar de modo analítico, com consciência,
todas as informações constantes em pelo menos um dos problemas de otimização apresentados, compreendendo o fato de que a solução
do mesmo somente exige apenas conhecimentos iniciais de Geometria Analítica. Não é necessário o professor ter a preocupação de resolver todos os exercícios, mas é preciso que
estabeleça como meta explorar muito bem pelo
menos uma das modelagens apresentadas para
problemas práticos.
Sobre a forma de avaliação, consideramos que
o assunto favorece uma utilização de múltiplos
instrumentos, não se limitando às provas. Trabalhos de modelagem matemática e equacionamento de problemas lineares, como os apresentados,
incorporando-se outras variáveis ou condições,
além das referidas, podem ser realizados, explorando-se centros de interesse dos alunos.
CIRCUNFERÊNCIAS E CÔNICAS: SIGNIFICADOS,
EQUAçÕES, APLICAçÕES
tempo previsto: 2 semanas e meia.
Conteúdos e temas: caracterização da circunferência e das cônicas (elipse, hipérbole e parábola) por
meio de propriedades; equações da circunferência e das cônicas em situações simples, com centro
na origem; utilização das equações das circunferências e das cônicas em diferentes contextos.
Competências e habilidades: capacidade de expressar por meio da linguagem algébrica as propriedades características de curvas muito frequentes na natureza, como as circunferências
e as cônicas; capacidade de reconhecer, em diferentes contextos, a presença das circunferências e das cônicas, expressas por meio de suas equações; capacidade de lidar com as equações das circunferências e das cônicas para resolver problemas simples, em diferentes contextos.
Estratégias: apresentação de uma coleção de situações em que as circunferências e as cônicas
estão presentes, explorando suas propriedades tendo em vista a representação de tais curvas
por meio de equações; apresentação de alguns exercícios exemplares, para sinalizar aos professores os principais centros de interesses dos temas estudados.
42
de Aprendizagem 4
Nas três Situações de Aprendizagem anteriores, a ênfase foi dada à abordagem algébrica de problemas geométricos envolvendo as
retas e suas equações. A partir de agora, outras curvas serão estudadas com os métodos
da Geometria Analítica. Também aqui não
se trata de apresentar curvas e propriedades
desconhecidas, mas sim de abordar de uma
maneira nova uma série curvas e de problemas já conhecidos, aumentando dessa forma ,
assim, nossa capacidade de enfrentar situações-problema.
As circunferências e as cônicas (elipses, hipérboles e parábolas) são as curvas cujas equações apresentaremos a seguir. A circunferência
e a elipse podem ser vistas a partir de seções
de um cilindro circular; a elipse não passa de
uma circunferência alongada em uma de duas
direções perpendiculares.
circunferência
elipse
circunferência
elipse
Os quatro tipos de curvas podem ser vistos como seções de uma superfície cônica.
hipérbole
circunferência
elipse
parábola
43
A caracterização dessas curvas pode ser
feita com mais vagar pelo professor, sendo interessante, inclusive, a observação das mesmas
colocando-se água em recipientes cilíndricos,
cortando-se um salame, ou construindo materiais para ser usados ema aula com madeira
e serrote.
No que segue, buscaremos mostrar as
equações de tais curvas, quando situadas em
um plano cartesiano convenientemente escolhido. Começaremos com a circunferência.
y
P
y
r
0
x
x
y
Circunferência
A propriedade característica da circunferência é a de que seus pontos são todos
equidistantes de um ponto interior chamado
centro; a distância comum de cada um de seus
pontos ao centro é o raio da circunferência.
Assim, se o centro for a origem do sistema de
coordenadas e P (x; y) um ponto de uma circunferência de raio r, a equação que relaciona
as coordenadas de um ponto qualquer da circunferência é:
d(P; O) = r,
Ou seja, ∙∙∙∙∙∙∙
x2 + y2 = r ,
Ou, ainda, x2 + y2 = r2.
Se o centro C for o ponto (xo; yo), então da
igualdade característica d(P; C) = r resultará:
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
(x – xo)2 + (y – yo)2 = r.
Ou seja, (x – xo)2 + (y – yo)2 = r2.
44
P
y
r
y0
0
C
x0
x
x
Exemplo ilustrativo
a) A equação x2 + y2 = 10 representa uma
circunferência com centro na origem e
raio igual a ∙∙∙
10.
b) A equação (x – 3)2 + (y – 5)2 = 16 representa uma circunferência de centro no
ponto (3; 5) e raio igual a 4.
c) A equação x2 + (y – 1)2 = 25 representa
uma circunferência de centro no ponto
(0; 1) e raio igual a 5.
d) A equação (x + 7)2 + y2 = 13 representa
uma circunferência de centro no ponto
(–7; 0) e raio igual a ∙∙∙
13.
Atividade 1
d) Calcule a distância entre P1 e P2.
Considere a circunferência de centro (4; 4)
e de raio 4.
a) Represente-a no plano cartesiano e determine sua equação.
A equação da circunferência é
(x – 4)2 + (y – 4)2 = 16; ver figura a seguir.
y
P1
Calculando a distância entre P1 e P2, encontramos 8, que é o diâmetro da circunferência.
Professor:
Outros exercícios poderiam ser propostos, articulando o reconhecimento da
equação da circunferência e os resultados já conhecidos sobre retas. Em virtude da limitação do espaço do Caderno,
deixamos tal tarefa para o discernimento
e a disponibilidade do professor.
S
Elipse
4
P2
0
4
4
x
b) Determine a equação da reta s que passa pela origem e pelo centro da circunferência.
A reta s que passa pela origem e pelo centro
da circunferência tem inclinação igual a 1;
logo, sua equação é y = x.
c) Calcule as coordenadas dos pontos P1 e
P2, de interseção da reta s com a circunferência dada.
Os pontos de interseção da reta s com a circunferência são as soluções do sistema formado
pelas equações y = x e (x – 4)2 + (y – 4)2 =
16. Substituindo y por x na segunda equa2 e x2 = 4 – 2∙∙∙
2.
ção, obtemos x1 = 4 + 2∙∙∙
2 ; 4 + 2∙∙∙
2 ) e
Logo, P1 = (4 + 2∙∙∙
2 ; 4 – 2 ∙∙∙
2 ).
P2 = (4 – 2∙∙∙
As curvas chamadas cônicas – a elipse, a
hipérbole e a parábola – ocorrem com muita
frequência na natureza e no dia-a-dia. Vamos
conhecer suas principais características, iniciando pela elipse.
Quando inclinamos um recipiente cilíndrico aberto, de seção circular, contendo água em
repouso, o contorno da superfície da água é
uma elipse. Também é uma elipse a sombra
projetada de uma circunferência situada em
um plano vertical, quando a luz do Sol, ou
outra luz qualquer, incide obliquamente.
Foi Kepler (1571-1630), em seus estudos de
Astronomia, quem associou às trajetórias dos
planetas ao redor do Sol não mais circunferências, mas sim elipses, ou seja, circunferências
“achatadas”. Nessas elipses, Kepler destacou
45
a existência de dois pontos simetricamente
opostos em relação ao centro, chamados focos, em um dos quais o Sol se situava.
A partir desses dois pontos, uma propriedade fundamental pode ser utilizada para caracterizar uma elipse: qualquer ponto da elipse é tal
que a soma das distâncias até esses dois pontos
fixados, que são os focos, é constante. Jardineiros
utilizam frequentemente essa propriedade para
construir canteiros elípticos: fincando-se duas
estacas, uma em cada foco, e deslocando-se um
estilete, com um barbante de comprimento L
(maior do que a distância entre os focos) esticado, obtém-se uma elipse.
Um coador de café de plástico pode ilustrar o fato de que as elipses podem ser consideradas como curvas intermediárias entre a
circunferência e o segmento de reta:
Uma elipse apresenta dois eixos de simetria: o semieixo maior costuma ser representado por a, o menor por b. Assim, os dois
eixos são 2a e 2b.
Como já foi dito anteriormente, a elipse é
como uma circunferência "achatada". Com
isso em mente, vamos obter a equação da elipse
com centro na origem na atividade seguinte.
y
�
F1
F2
d(P, F1) + d(P, F2) = constante
46
–a
Semieixos
b
0
–b
a
x
Atividade 2
Exemplo ilustrativo
Usando o fato de que a elipse é uma circunferência “achatada”, ou seja, é a curva obtida
quando reduzimos (ou ampliamos) na mesma
proporção todas as cordas perpendiculares a
um diâmetro dado, mostrar que a equação da
elipse de centro na origem e com os semieixos
x2
y2
a e b é 2 + 2 = 1.
a
b
De fato, se os pontos (x; y’) de uma circunferência de centro na origem e raio a satisfazem a equação x2 + y´2 = a2, os pontos (x; y)
da elipse obtida reduzindo todas as ordenadas
na proporção de a para b (a > b > 0) são tais
y'
a
a
= , ou seja, y’ = y ∙ .
que
y
b
b
y
a
l
–a
(x; y’)
b
(x; y)
0
a
–b
x
Elipse
x2 y2
+ =1
a2 b2
Circunferência x2 +(y`)2 = a2
Substituindo esse valor de y’ na equação
da circunferência x2 + y’2 = a2, obtemos
y.a 2 2
x2 y2
= a , de onde resulta: 2 + 2 = 1,
x2 +
a
b
b
que é a equação da elipse.
∙
y2
= 1 representa uma
5
elipse de semieixos 1 e ∙∙∙
5 , com centro
na origem.
b) A equação x2 +
c) A equação 4x2 + 9y2 = 36 representa
uma elipse, pois pode ser escrita na forx2
y2
ma equivalente
+
= 1; tem cen9
4
tro na origem e semieixos 3 e 2.
Professor:
Aqui seria interessante apresentar muitos
exercícios de identificação dos dois semieixos de elipses dadas por equações na
x2
y2
forma 2 + 2 = 1, com a correspona
b
dente representação no plano cartesiano, bem como exercícios de escrita das
equações de elipses já representadas no
plano, com o centro na origem do sistema e com os valores dos semieixos indicados sobre os eixos coordenados.
Atividade 3
–a
∙
x2
y2
+
= 1 representa uma
9
7
elipse de semieixos 3 e ∙∙∙
7, com centro
na origem.
a) A equação
Em uma elipse com centro na origem e semieixo maior a no eixo OX, os pontos (0; b) e
(0; –b) distam do centro menos do que a. Os
pontos do eixo OX que estão a uma distância
a de (0; b) e (0; –b) têm coordenadas (c; 0) e
(–c; 0). Eles são particularmente importantes,
sendo chamados de focos da elipse. O valor c
é chamado distância focal da elipse. Por construção, a soma das distâncias dos pontos (0; b)
47
e (0; –b) até os focos é igual a 2a. É possível
mostrar que para todo ponto P:(x; y) do plax2
y2
no, se 2 + 2 = 1, então a soma das distâna
b
cias de P até os focos (c; 0) e (–c; 0) é igual a
2a. A razão c/a é chamada excentricidade da
elipse e, sendo representada pela letra e.
y
Observação:
No caso da órbita da Terra, que Kepler
concluiu ser uma elipse com o Sol em
um dos focos, a excentricidade e é igual a
0,01675, ou seja, a órbita é quase uma circunferência. Os semieixos, nesse caso, são,
aproximadamente, a = 153 493 000 km e
b = 153 454 000 km.
b
a
–a
–c
Atividade 4
a
c
0
a
x
Considere a elipse de centro na origem e
semieixos a = 13 e b = 5.
–b
a) Mostre que, entre a, b e c, vale a relação
a2 = b2 + c2.
y
5
13
F1
c
13
F2
x
Observando o triângulo retângulo formado
na figura, de hipotenusa a e catetos b e c,
concluímos que a2 = b2 + c2.
b) Mostre que, fixado o valor de a, quanto menor for o valor de b, mais a excentricidade se aproxima de 1, e a elipse
se aproxima de um segmento de reta;
quanto mais próximo de a for o valor
de b, mais a excentricidade se aproxima
de zero, e a elipse se aproxima de uma
circunferência.
Como c = ∙∙∙∙∙∙∙∙
a2 – b2 , notamos que, sendo fixado o valor de a, quanto maior for o valor de b, menor será c, e portanto, menor a
excentricidade, e mais a elipse se aproxima
de uma circunferência; quanto menor o valor de b, mais próximo de a é o valor de c,
e portanto, maior é a excentricidade, que se
aproxima do valor 1.
48
Determine:
a) a equação da elipse, representando-a no
plano cartesiano;
A equação da elipse é
x2
y2
+
=1
132 52
b) a excentricidade da elipse;
c
, sendo
a
c = ∙∙∙∙∙∙∙∙
132 – 52 = 12. Calculando o valor de e,
12
temos: e =
= 0,923.
13
c) os focos da elipse;
A excentricidade da elipse é e =
Os focos da elipse são os pontos de coordenadas (c; 0) e (–c; 0), ou seja, são os pontos
(12; 0) e (–12; 0).
d) o valor de k para que o ponto P (5; k), do
primeiro quadrante, pertença à elipse;
Para que o ponto (5; k) pertença à elipse,
52
k2
devemos ter 2 + 2 = 1 , de onde obtemos
13
5
60
que k = ± . Sendo P do primeiro quadran13
60
te, segue que k = .
13
y
x.y=k
y1
x3
0
y3
y2
x1
x2
x
e) a soma das distâncias de P aos focos
da elipse.
Podemos calcular a soma das distâncias do
60
até os focos obtidos no item
ponto P 5;
13
c); sabemos, no entanto, que tal valor será
igual a 2a, ou seja, a 26.
∙
∙
eixos oblíquos
x1 . y1 = x2 . y2 = x3 . y3 = constante = k
Hipérbole
Quando representamos graficamente pares (x;y) de grandezas que são inversamente
proporcionais, isto é, cujo produto x . y é constante, a curva obtida é uma hipérbole:
y
y1
xy = k
y2
x3
0
x1
x2
y3
x
Como já vimos anteriormente, a hipérbole
surge, ainda, quando seccionamos um cone
circular reto com um plano que forma com o
plano da base um ângulo maior do que aquele
formado por uma geratriz do cone com a base.
Quando um avião se desloca a certa altura
com velocidade maior do que a do som, um
problema importante consiste em determinar a região da superfície da Terra de onde
se pode escutar o barulho de seus motores.
Essa região é chamada zona de audibilidade
e se desloca com o avião. É possível mostrar
que, em cada instante, seu contorno é uma
hipérbole.
eixos perpendiculares/sistema ortogonal
49
Uma propriedade característica da hipérbole é a seguinte: existem dois pontos fixados
F1 e F2 tais que a diferença entre as distâncias
de qualquer ponto da curva até esses dois pontos é constante. A partir dessa propriedade, é
possível traçar hipérboles da forma indicada
na figura a seguir:
P
Para escrever a equação da hipérbole,
podemos partir da representação de grandezas inversamente proporcionais. No caso
de um sistema XOY, em que os eixos cartesianos são ortogonais, a hipérbole é chamada equilátera e os dois ramos da curva
aproximam-se indefinidamente dos eixos
coordenados, nunca neles encostando. A
origem é um centro de simetria, e os eixos
coordenados são chamados, nesse caso, de
assíntotas da hipérbole.
Exemplos ilustrativos
As curvas formadas pelos pontos cujas
coordenadas satisfazem as relações abaixo são
hipérboles, tendo como assíntotas os eixos coordenados (ver figura).
a) xy = 7
F1
b) xy = –5
F2
y
xy = 7
elipse
d(P, F2) + (d(P, F1) = constante
0
x
P
F1
y
F2
xy = –5
0
hipérbole
d(P, F2) – (d(P, F1) = constante
50
x
A equação x2 – y2 = 1 pode ser escrita
(x + y).(x – y) = 1, ou seja, X.Y = 1, sendo
Y = (x – y) e X = (x + y); podemos, então,
verificar que os pontos (x; y) que satisfazem
a equação x2 – y2 = 1 são os mesmos que satisfazem a equação X . Y = 1. Podemos reconhecê-los, no sistema cartesiano, notando
que quando X = 0, ou seja, no eixo Y, temos
y = x, o que significa que o eixo Y é a bissetriz
dos quadrantes ímpares, y = x. Analogamente, vemos que Y = 0 quando y = – x, ou seja, o
eixo X é a bissetriz dos quadrantes pares. Temos, então, a representação a seguir. Dizemos
que as assíntotas da hipérbole são as retas
y = x e y = – x.
Atividade 5
Obtenha a equação de uma hipérbole com
centro na origem, passando pelo ponto (a; 0)
b
x e
e tendo como assíntotas as retas y =
a
b
y= –
x.
a
∙
∙ ∙
∙
Em relação ao sistema de eixos XOY, em
b
que o eixo Y corresponde à reta y =
x e
a
–b
o eixo X corresponde à reta y =
x, a equaa
ção da hipérbole seria : X.Y = K (constante).
y
y=
b
x
a
Y
Y (y = x)
y
x 2 – y2 = 1
–a
0
XY = 1
a
x
0
x
y= –
b
x
a
X
X (y = x)
Analogamente, a equação 4x 2 – 9y 2 = 36
pode ser vista como uma hipérbole. Basta fatorar o primeiro membro, obtendo (2x – 3y) .
(2x + 3y) = 36, ou seja, X . Y = 36. Nesse
caso, as assíntotas são as retas 2x – 3y = 0 e
2x + 3y = 0, conforme a representação a
seguir:
y
Y (2x – 3y = 0)
0
4x2 – 9y2 = 36
x
X (2x + 3y = 0)
Em relação ao sistema ortogonal xOy, é posy = constante
sível mostrar que ao produtox . X.Y
= K corresb
b
ponde o produto yy –
x ∙ y+
x = k.
a
a
x
Um indício de tal fato é a correspondência:
b
Y=0
corresponde a
y–
x=0
a
(eixo X)
(assíntota da hipérbole)
b
x =0
X=0
corresponde a y + –
a
(eixo Y)
(assíntota da hipérbole)
∙
∙∙
∙
Calculando o produto indicado, temos:
X.Y = K corresponde a
∙y –
b
b
x ∙ y+–
x = k.
a
a
∙ ∙
∙
51
b2
Ou seja, y – 2 x2 = k.
a
Como a curva passa pelo ponto (a; 0), podemos calcular o valor de k:
b2
02 – 2 a2 = k, ou seja, k = – b2
a
Logo, a equação da hipérbole é
b2
y2 – 2 x2 = – b2, de onde obtemos:
a
x2
y2
–
=1
a2
b2
2
entre as distâncias de um ponto qualquer da hipérbole até F1 e até F2 é constante e igual a 2a.
y
b
y= a x
b
F2
–c
–a
c
0
F1
5
a c
x
Exemplo ilustrativo
x2
y2
–
= 1 é uma hi9
16
pérbole que passa pelo ponto (3; 0) e tem como
4
4
assíntotas as retas y =
xey=–
x.
3
3
A curva de equação
Professor:
Neste ponto, seria interessante apresentar diversos exercícios de representação
no plano cartesiano de hipérboles dadas por equações na forma apresentada
acima, sempre destacando as assíntotas, que podem ser obtidas pela simples
fatoração da diferença de quadrados,
característica da equação da hipérbole
nessa forma.
–b
y= a x
Para cada uma das hipérboles a seguir, determine os focos e calcule o valor constante da diferença das distâncias entre um ponto qualquer
da hipérbole e os focos. Confira o valor obtido
fazendo os cálculos diretamente para um ponto
da hipérbole arbitrariamente escolhido.
a)
y
3
0
4
x
Atividade 6
b
–b
xey=
x , com a e b posia
a
tivos, as assíntotas de uma hipérbole que passa
por (a; 0), os pontos F1: (c; 0) e F2: (–c; 0), tais
que c2 = a2 + b2, são chamados focos da hipérbole.
Na figura a seguir, são mostrados os focos da
hipérbole. É possível mostrar que a diferença
Sendo y =
52
Temos a = 4, b = 3; logo, c = ∙∙∙∙∙∙∙
a2 + b2 = 5.
Os focos são os pontos (5; 0) e (–5; 0).
A diferença entre as distâncias de um ponto qualquer da hipérbole até os dois focos é
igual a 2a, ou seja, é 8.
b)
c)
y
y
12
5
x
x
5
5
Analogamente, a = 5, b = 12 e c = 13.
Focos: (13; 0) e (–13; 0). A diferença entre
as distâncias de um ponto qualquer da hipérbole até os dois focos é 2a = 10.
Um dos sistemas utilizados para a localização de automóveis utiliza a propriedade característica da hipérbole anteriormente referida, ou seja, a diferença das distâncias de um
ponto P qualquer da hipérbole a dois pontos
fixados F1 e F2 , que são seus focos, é constante, ou seja, o valor absoluto da diferença PF1 –
PF2 = constante. Se um auto situado no ponto
P enviar um sinal para cada uma das centrais
F1 e F2, considerando a diferença dos tempos
de recepção dos sinais, e consequentemente,
das distâncias entre P e F1 e P e F2, pode-se
concluir que o ponto P situa-se em um dos
ramos de uma hipérbole H12. Se outro sinal
for enviado do auto para uma terceira central F3, combinando-se os dados de F2 e F3 ,
pode-se concluir que o ponto P situa-se sobre
outra hipérbole H32. Os pontos de interseção
das duas hipérboles fornecem as posições possíveis para o auto.
Neste caso, os eixos estão invertidos, e os focos estão no eixo y. Temos c = 5∙∙∙
2 e os focos
(0; 5∙∙∙
2) e (0; –5∙∙∙
2). A diferença entre as
distâncias de um ponto qualquer da hipérbole
até os dois focos é 2a = 10.
H12
F1
P
F3
H12
H32
F2
P
??
H32
53
Parábola
Em geral, quando representamos graficamente pares (x; y) de grandezas tais que y é
diretamente proporcional ao quadrado de x
(y = kx2, k constante e k ≠ 0), a curva correspondente no plano cartesiano é uma parábola.
y
A parábola tem certas propriedades características que podem ser utilizadas para defini-la. Uma delas é a existência de um ponto
F, fixado, e de uma reta r, fixada, tais que a
distância de cada ponto P da parábola até F
é igual à distância de P até r. F é o foco da
parábola e r é sua diretriz.
PII
y = kx2
P'
d(P, F) = d(P,r)
d(P', F) = d(P',r)
d(PII, F) = d(PII,r)
x
0
P
É o que ocorre, por exemplo, quando uma
pedra é abandonada e registramos a relação
entre a distância percorrida verticalmente e o
tempo de queda livre. Também é uma parábola a trajetória de todos os projéteis lançados obliquamente em relação à superfície da
Terra, desconsiderados os efeitos do ar.
Além disso, quando, de um ponto fixado no
solo, lançamos projéteis sempre com a mesma
velocidade inicial vo, em todas as direções possíveis, em um plano vertical dado, o contorno
da região determinada pelos pontos que podem
ser atingidos pelos projéteis é também uma parábola, chamada parábola de segurança.
Como registramos no início desta Situação
de Aprendizagem, quando seccionamos um
cone circular reto por um plano que forma
com a base um ângulo exatamente igual ao
que uma geratriz do cone forma com a base,
obtemos também uma parábola.
0
54
F
Outra propriedade interessante das parábolas é a seguinte: sendo P um ponto qualquer da parábola, a reta que passa pelo foco F
e por P forma com a tangente à parábola em
P um ângulo igual ao formado pela tangente
com a reta paralela ao eixo da parábola passando por P (ver figura).
F
Isso explica a razão de os faróis dos automóveis serem envolvidos por uma superfície que é
um paraboloide, ou seja, é a superfície gerada
por uma parábola que dá uma volta completa
em torno de seu eixo. Se a lâmpada situar-se exatamente no foco, os raios de luz formarão um
feixe paralelo ao eixo, como é desejável, para
uma maior concentração da luz.
Na atividade seguinte, vamos procurar
aproximar a parábola que resulta da proporcionalidade direta entre uma grandeza y e o
quadrado de outra grandeza x com a parábola definida por meio de um foco F e de uma
diretriz r, a partir da propriedade da equidistância de um ponto da parábola entre o foco
e a diretriz.
Substituindo y por kx2 e efetuando os cálculos, obtemos:
x2 + (kx2 – c)2 = (kx2 + c)2
x2 + k2x4 + c2 – 2kx2.c = k2x 4 + c2 + 2kcx2
x2(1 – 4kc) = 0
Daí segue que, para a igualdade valer para
1
todo x, devemos ter c =
4k
1
Logo, o foco é o ponto 0;
4k
1
é a reta y = –
.
4k
∙
∙ , e a diretriz
y
y = kx2
1
F (0; 4k )
Atividade 7
Determine o foco e a diretriz das parábolas.
a) y = kx2
x
0
b) x = ky2
c) y = kx2 + h
r
1
y = – 4k
Consideremos a parábola y = kx2.
Se o foco for o ponto F(0; c), então a diretriz
r será a reta y = – c, pois o ponto (0; 0) pertence à parábola e a distância dele ao foco deve
ser a mesma que a distância dele à diretriz.
Sendo P (x; y) um ponto qualquer da parábola, a distância de P ao foco deve ser
igual à distância até a diretriz, ou seja:
d (P; F) = ∙∙∙∙∙∙∙∙∙∙∙
x2 + (y – c)2 = y + c = d(P; r).
Logo, x2 + (y – c)2 = (y + c)2 .
Analogamente, se a parábola fosse x = ky2,
teríamos:
foco
∙
1
;0
4k
∙
e diretriz: x = –
1
4k
Para uma parábola de equação y = kx2 + h,
o foco e a diretriz seriam transladados na
direção do eixo OY de um valor h, ou seja,
teríamos:
55
1
F 0; h +
4k
∙
∙
1
r: y = h –
4k
e
Na grade de conteúdos proposta para
as três séries do Ensino Médio, pressupõese que muitos dos temas se apóiam mutuamente, sendo mais fácil interessar os alunos
quando se apresenta um cenário de conteúdos mais abrangente do que quando se lhes
subtrai a possibilidade de contato com alguns dos temas. Na presente proposta, reservou-se apenas um bimestre para a Geometria
Analítica Plana. Dependendo do número de
aulas disponíveis para o professor, nem
todos os temas podem ser tratados com a
mesma profundidade, cabendo ao professor
mesmo selecionar as ideias que serão mais
ou menos contempladas.
y
r
x = ky2
0
x
1
4k
x=–
1
4k
y
y = kx2 + h
1
F (0; h + 4k )
1
4k
1
4k
h
0
r
x
Professor:
Em função do tempo disponível, exercícios
de identificação do foco e da diretriz de diversas parábolas, expressas por meio de
equações do tipo y = ax2 + bx + c, podem
ser propostos. Para achar o foco, é fundamental antes achar o vértice; a partir daí,
determina-se a equação da diretriz.
56
Na apresentação das circunferências e
das cônicas, buscou-se destacar mais o significado e as ocorrências de cada uma delas
em diferentes contextos do que as manipulações algébricas com as equações. Trata-se,
naturalmente, de uma escolha, em razão das
limitações do tempo disponível. Sugere-se,
portanto, que a avaliação concentre-se na caracterização da circunferência, da elipse, da
hipérbole e da parábola em situações simplificadas, escrevendo as equações das curvas com
centro na origem, e adiando-se ou omitindose uma exploração algébrica mais detida dos
casos mais gerais.
Quanto à forma de avaliação, também
aqui consideramos que o assunto favorece
uma utilização de múltiplos instrumentos,
não não devendo se limitar às provas. No
caso das cônicas, o reconhecimento destas
mesmas em situações como as indicadas no
texto (seção de cones, sombras de circunferências, cortes ou inclinações de cilindros etc.)
pode ser simples e motivador. A construção
de instrumentos para desenhá-las no plano,
como alguns sugeridos no texto, também
pode ser muito interessante. A verificação da
propriedade citada das parábolas nas superfí-
cies cromadas dos faróis dos automóveis, por
meio da construção efetiva de uma superfície parabólica com uma lâmina de alumínio,
fixada em uma tábua, com uma pequena
lanterna no foco da parábola, pode ser uma
atividade especialmente significativa, a ser
levada em consideração no processo de avaliação (ver figura seguinte).
ORIENTAçÕES PARA RECUPERAçãO
Ao término da Situação de Aprendizagem 1, caso o professor avalie que as metas
estabelecidas não foram satisfatoriamente atingidas, pode optar por estendê-la por
mais uma semana, propondo novos exercícios de determinação de pontos por coordenadas e novas ações simples sobre os
pontos, por meio de operações algébricas sobre as coordenadas. Por exemplo, é possível
estender o que foi feito na Atividade 1 com o
hexágono, para outros polígonos, como, por
exemplo, o quadrado, o que seria mais simples para começar. Cada uma das atividades
propostas presta-se a uma espécie de duplicação, trocando-se os polígonos envolvidos ou
as propriedades indicadas.
Outra estratégia para recuperação poderia
ser recorrer a folhas de papel quadriculado
para a representação de pontos por coordenadas e para a realização inicial de cálculos como
o do ponto médio de dois pontos, da distância
57
entre pontos ou da inclinação de segmentos.
Após tal abordagem mais simples, que certamente já foi utilizada em séries anteriores, na
apresentação dos sistemas de coordenadas, o
professor poderia retomar a perspectiva proposta na Situação de Aprendizagem 1.
Já na Situação de Aprendizagem 2, o processo de recuperação pode concentrar-se na
exploração dos fatos apresentados sobre as
equações das retas em estreita sintonia com
o estudo já realizado em séries anteriores da
função do primeiro grau f(x) = ax + b, destacando o significado geométrico dos coeficientes, ou ainda, dos sistemas de duas equações
linea-res com duas incógnitas, associando-se
as posições relativas das retas às diversas possibilidades de soluções do sistema. Essa retomada pode ser interessante para destacar o
fato de que, na Geometria Analítica, não estamos estudando conteúdos novos, mas apenas
uma forma nova de abordar velhos conteúdos,
conforme já se mencionou neste Caderno, em
diferentes momentos.
Caso considere que os alunos não tenham
se interessado por qualquer um dos problemas
propostos na Situação de Aprendizagem 3, ou
então, não tenham entendido perfeitamente as
soluções apresentadas, sugerimos que o professor retome os enunciados desses mesmos
problemas, escolhendo um deles e conversando mais detidamente sobre a situação examinada. Após despertar o interesse, é muito
importante destacar o fato de que o problema
pode ser perfeitamente resolvido apenas com
os conhecimentos sobre retas, presentes na Situação de Aprendizagem. Somente um exercício de leitura atenta pode levar à compreensão
plena do problema proposto e ao consequente
interesse na resolução.
Uma estratégia alternativa pode ser a seguinte: reunir todos os elementos de Geometria Analítica presentes no problema – as equações de retas, as inequações correspondentes a
regiões, os sistemas correspondentes aos pontos de interseção de retas etc. – e propor questões envolvendo tais elementos de modo direto... ("represente a reta de equação 45 = 4x +
5y..."; “ache a interseção das retas 3x + 4y = 24
e 2x + 5y = 20...", ..."; "determine a região do plano correspondente à inequação
x + y < 8..." etc., somente depois associando
tais questões parciais à solução do problema
maior apresentado.
RECURSOS PARA AMPLIAR A PERSPECTIVA DO PROFESSOR
E DO ALUNO PARA A COMPREENSãO DO TEMA
Existem diversos softwares disponíveis
que podem ser utilizados para a exploração
dos conteúdos de Geometria Analítica Plana.
CABRI e GEOMETRIA DINÂMICA são
58
dois deles, sendo possível recorrer a muitos
outros, em uma pesquisa na internet. Consideramos, no entanto, que, em um primeiro momento, a construção efetiva por parte
dos alunos das figuras representativas das
equações estudadas é muito importante.
Após esse contato inicial, a utilização de o
recurso a softwares que facilitem a construção gráfica das curvas e das regiões do pla-
no é, sem dúvida, conveniente e relevante.
É importante ressaltar que a não-disponibilidade de tais softwares não impede a efetivação de qualquer das atividades propostas
no presente texto.
59
CONSIDERAçÕES FINAIS
Ao final deste Caderno, podemos resumir as
expectativas de aprendizagem referentes às quatro Situações de Aprendizagem apresentadas:
Geometria Analítica
f Usar de modo sistemático sistemas de
coordenadas cartesianas para representar pontos, figuras, relações, equações.
f Reconhecer a equação da reta, o significado de seus coeficientes, as condições
60
que garantem o paralelismo e a perpendicularidade entre retas.
f Representar graficamente inequações
lineares por regiões do plano; resolver
problemas práticos associados a equações e inequações lineares.
f Identificar as equações da circunferência e das cônicas na forma reduzida,
com centro na origem, bem como propriedades características das cônicas.
ContEúdoS dE MAtEMátiCA Por SériE/biMEStrE
4o bimestre
3o bimestre
2o bimestre
1o bimestre
do EnSino Médio
1a série
2a série
3a série
NÚMEROS E SEQUÊNCIAS
- Conjuntos numéricos.
- Regularidades numéricas:
sequências.
- Progressões aritméticas, progressões geométricas; ocorrências em
diferentes contextos; noções de
Matemática Financeira.
TRIGONOMETRIA
- Arcos e ângulos; graus e radianos.
- Circunferência trigonométrica:
seno, cosseno, tangente.
- Funções trigonométricas e fenômenos periódicos.
- Equações e inequações trigonométricas.
- Adição de arcos.
GEOMETRIA ANALÍTICA
- Pontos: distância, ponto médio e
alinhamento de três pontos.
- Reta: equação e estudo dos coeficientes, retas paralelas e perpendiculares, distância de ponto a reta;
problemas lineares.
- Circunferências e cônicas: propriedades, equações, aplicações em
diferentes contextos.
FUNçÕES
- Relação entre duas grandezas.
- Proporcionalidades: direta,
inversa, direta com o quadrado.
- Função do 1o grau, função do 2o
grau; significado e ocorrência em
diferentes contextos.
MATRIzES, DETERMINANTES E SISTEMAS LINEARES
- Matrizes: significado como tabelas, características e operações.
- A noção de determinante de uma
matriz quadrada.
- Resolução e discussão de sistemas lineares: escalonamento.
EQUAçÕES ALGÉBRICAS,
POLINÔMIOS, COMPLEXOS
- Equações polinomiais: história,
das fórmulas à análise qualitativa.
- Relações entre coeficientes e
raízes de uma equação polinomial.
- Polinômios: identidade, divisão
por x - k e redução no grau de
uma equação.
- Números complexos: significado
geométrico das operações.
FUNçÕES EXPONENCIAL E
LOGARÍTMICA
- Crescimento exponencial.
- Função exponencial: equações e
inequações.
- Logaritmos: definição, propriedades, significado em diferentes
contextos.
- Função logarítmica: equações e
inequações simples.
ANÁLISE COMBINATÓRIA E
PROBABILIDADE
- Raciocínio combinatório: princípios multiplicativo e aditivo.
- Probabilidade simples.
- Arranjos, combinações e permutações.
- Probabilidades; probabilidade
condicional.
- Triângulo de Pascal e Binômio de
Newton.
ESTUDO DAS FUNçÕES
- Panorama das funções já estudadas: principais propriedades.
- Gráficos: funções trigonométricas, exponenciais, logarítmicas e
polinomiais.
- Gráficos: análise de sinal, crescimento, decrescimento, taxas de
variação.
- Composição: translações, reflexões, inversões.
GEOMETRIATRIGONOMETRIA
- Razões trigonométricas nos
triângulos retângulos.
- Polígonos regulares: inscrição,
circunscrição; pavimentação
superfícies.
- Resolução de triângulos não
retângulos: lei dos senos e lei dos
cossenos.
GEOMETRIA MÉTRICA
ESPACIAL
- Organização do conhecimento
geométrico: conceitos primitivos,
definições, postulados, teoremas.
- Prismas e cilindros: propriedades,
relações métricas.
- Pirâmides e cones: propriedades,
relações métricas.
- A esfera e suas partes; relações
métricas; a esfera terrestre.
ESTATÍSTICA
- Cálculo e interpretação de índices estatísticos.
- Medidas de tendência central:
média, mediana e moda.
- Medidas de dispersão: desvio
médio e desvio-padrão.
- Elementos de amostragem.
O sombreado assinala os conteúdos relacionados aos trabalhados neste bimestre.
61

3a- SÉRiE

Transcrição

Documentos relacionados

Alg I - Glencoe

y - Webnode

Matemática – 3ª Série

2. Função Linear 2.1 Função linear e sua representação gráfica

anexo i – conteúdo programático

Números Reais ‒ Localização na reta numérica

CIPA Informa: dicas para manter uma postura correta

Derivada Implícita

PLANO CARTESIANO ou SISTEMA DE COORDENADAS O Plano

Números Reais – Localização na reta numérica