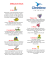O Código de Pascal Série Matemática na Escola

O Código de Pascal
Série Matemática na Escola
Objetivos
1. Introduzir sequência de números naturais;
2. Mostrar os coeficientes do Binômio de
Newton;
3. Motivar algumas propriedades aritméticas
dos números naturais;
4. Apresentar o famoso Triângulo de Pascal.
O Código de
Pascal
Série
Matemática na Escola
Conteúdos
Conjuntos dos números naturais,
Sequências numéricas.
Duração
Aprox. 10 minutos.
Objetivos
1. Introduzir sequência de
números naturais;
2. Mostrar os coeficientes do
binômio de Newton;
3. Motivar algumas propriedades
aritméticas dos números
naturais;
4. Apresentar o famoso
Triângulo de Pascal.
Sinopse
Um jovem encontra um
manuscrito com vários números
quem parece código. Ao tentar
decifrar o código, o grande
matemático Pascal aparece para
ajudá-lo. A ajuda é mútua em
algum sentido.
Material relacionado
Áudios: Triângulo Ímpar;
Experimentos: Geometria do
Taxi; Quadrado de Koch;
Softwares: Corrida ao cem;
Vídeos: Uma dinâmica de grupos;
Naturalmente.
VÍDEO
O Código de Pascal 2/10
Introdução
Sobre a série
A série Matemática na Escola aborda o conteúdo de matemática do
ensino médio através de situações, ficções e contextualizações. Os
programas desta série usualmente
usualmente são informativos e introdutórios de
um assunto a ser estudado em sala de aula pelo professor. Os
programas são ricos em representações gráficas para dar suporte
sup
ao
conteúdo mais matemático e pequenos documentários trazem
informações interdisciplinares.
interdisciplinares
Sobre o programa
O programa vai abordar o triângulo conhecido como sendo de Pascal.
Na ficção, um surfista descobre um velho manuscrito com muitos
números naturais
urais distribuídos em uma forma triangular. O surfista fica
curioso e, com o auxílio da imaginação, conversa com o próprio
Pascal, que fica satisfeito com alguém que finalmente tenha
encontrado o seu código.
Os números que aparecem no triângulo aritmético têm muitas
propriedades interessantes. O vídeo apresenta de maneira gráfica
VÍDEO
O Código de Pascal 3/10
algumas destas propriedades.
É bem provável que a disposição dos números no Triângulo de Pascal
tenha sido apenas para facilitar a consulta para o cálculo da expressão
expandida de potências de binômios. Isto é
௡
ሺ‫ ݔ‬+ ‫ ݕ‬ሻ ௡ = ෍
௣ୀ଴
݊!
‫ ݔ‬௡ି௣ ‫ ݕ‬௣
‫ !݌‬ሺ݊ − ‫݌‬ሻ!
Os números que aparecem nas linhas do Triângulo são os coeficientes
binomiais, a saber:
݊!
‫ !݌‬ሺ݊ − ‫݌‬ሻ!
Onde n estará associado à linha e p varia de 1 a n em cada linha. Por
exemplo:
Tabela 1 Triângulo de Pascal até n=6
1
1
1
1
1
1
1
2
3
4
5
6
1
3
6
10
15
1
1
4
10
20
1
5
15
1
6
1
O famoso divulgador de matemática Martin Gardner cita o também
famoso pesquisador em algoritmos computacionais Donald Knuth com
a seguinte frase:
VÍDEO
O Código de Pascal 4/10
Existem tantas relações [matemáticas] no Triângulo de Pascal que
ninguém mais se admira quando alguém descobre uma nova relação,
exceto o próprio descobridor.
Pascal tinha um encanto especial e religioso pela matemática. O
programa mostra um pouco desta característica de Pascal.
O professor pode enfatizar o aspecto algorítmico associado à
construção do triângulo aritmético e sequência de Fibonacci.
Nem tudo que parece um fractal é um fractal
O vídeo menciona a conexão entre o Triângulo de Pascal e o fractal de
Sierpinski. Os fractais, do ponto de vista matemático, têm várias
propriedades e uma delas é chamada de autossimilaridade - a forma
(ou aparência, ou outra característica) do todo é semelhante à de uma
parte do fractal. Em simples palavras, se você olhar de perto, com
alguma lupa ou de longe vai ver a mesma forma. Todos estes
conceitos têm definições precisas e são bem elaborados, mas não é
propósito deste vídeo nem desse guia o aprofundamento no assunto.
No entanto, vale ressalvar os exemplos que o vídeo mostra como
fractais da natureza: Ondas do mar, flocos de neves e esqueleto de
moluscos (Figura 1). Estes exemplos exibem estruturas autossimilares
em algumas escalas, mas não são matematicamente fractais.
Figura 1 Este exemplo dado no vídeo não é um fractal, mas tem algumasVÍDEO
características em comum.
O Código de Pascal 5/10
Apesar de não serem rigorosamente fractais, os exemplos da natureza
dados no vídeo e outros que os alunos podem pesquisar revelam
Figura 2 Imagem fractal criada por KaCey97007 disponível sob licença CC (2008).
estruturas que lembram algumas propriedades dos fractais.
Os computadores modernos conseguem gerar fractais belíssimos a
partir de algoritmos de fórmulas matemáticas recursivas, como da
Figura 2.
Sugestões de atividades
Antes da execução
Desenvolver explicitamente algumas as seguintes expressões:
VÍDEO
O Código de Pascal 6/10
ሺ‫ ݔ‬+ ‫ݕ‬ሻଶ = ሺ‫ ݔ‬+ ‫ݕ‬ሻሺ‫ ݔ‬+ ‫ݕ‬ሻ = ‫ ݔ‬ଶ + 2‫ ݕݔ‬+ ‫ ݕ‬ଶ
ሺ‫ ݔ‬+ ‫ݕ‬ሻଷ = ሺ‫ ݔ‬+ ‫ݕ‬ሻଶ ሺ‫ ݔ‬+ ‫ݕ‬ሻ = ‫ ݔ‬ଷ + 3‫ ݔ‬ଶ ‫ ݕ‬+ 3‫ ݕݔ‬ଶ + ‫ ݕ‬ଷ
ሺ‫ ݔ‬+ ‫ݕ‬ሻସ = ሺ‫ ݔ‬+ ‫ݕ‬ሻଷ ሺ‫ ݔ‬+ ‫ݕ‬ሻ =?
E chamar a atenção para os coeficientes numéricos que multiplicam os
vários termos.
Depois da execução
Desafiar os alunos a apresentarem a expansão explícita dos seguintes
binômios: ሺ‫ ݔ‬+ ‫ݕ‬ሻସ =?, ሺ‫ ݔ‬+ ‫ݕ‬ሻହ =? , ሺ‫ ݔ‬+ ‫ݕ‬ሻ଺ =?
Calcular com a ajuda de uma calculadora, ou não, os seguintes
números: 112, 113, 114
Mostre aos alunos a correspondência com as linhas do Triângulo de
Pascal. A expansão do binômio:
ሺ1 + 10
ሻ௡
௡
=෍
௣ୀ଴
݊!
10௣
‫ !݌‬ሺ݊ − ‫݌‬ሻ!
Isto é, os números do Triângulo de Pascal correspondem aos valores
da unidade, dezena, centena, milhar e dezena de milhar.
Por que o número 115 não é associado à linha n=5 do triângulo de
Pascal como são os casos de 110, 111, 112, 113, 114?
Desafios Algébricos
O vídeo menciona também os números de Fibonacci que formam uma
sequência recursiva.
Definição A sequência de Fibonacci {un , n=0,1,2,3...}, é tal que u0=0,
u1 =1 e
VÍDEO
O Código de Pascal 7/10
‫ݑ‬௡ାଵ = ‫ݑ‬௡ + ‫ݑ‬௡ିଵ
para ݊ ≥ 1.
O professor pode propor o seguinte teorema.
Teorema. Considerando a sequência de Fibonacci para ݊ ≥ 1 temos
que
‫ݑ‬௡ଶ − ‫ݑ‬௡ିଵ ‫ݑ‬௡ାଵ = ሺ−1ሻ௡ାଵ
Isto é, a diferença entre o quadrado de um número da sequência de
Fibonacci e o produto de seus dois vizinhos é um, se n for ímpar e
menos um se n for par.
Professor. Desafie os alunos com qualquer número de Fibonacci e
verifique com eles a veracidade do teorema. A demonstração é simples
e deve-se enfatizar a metodologia que empregamos, isto é, usamos
apenas as definições, as hipóteses, a lógica e a álgebra, para
demonstrarmos a tese do teorema.
Demonstração. Os principais passos para a demonstração são os
seguintes. Vamos definir a função auxiliar
݂ሺ݊ሻ ≡ ‫ݑ‬௡ଶ − ‫ݑ‬௡ିଵ ‫ݑ‬௡ାଵ
Pela definição da sequência de Fibonacci calculamos imediatamente
f(1)=1 e f(2)=-1. Vamos usar então a indução, assumindo que vale
para n qualquer, então mostrar que vale para n+1.
݂ሺ݊ሻ = ሺ−1ሻ௡ାଵ
ଶ
− ‫ݑ‬௡ ‫ݑ‬௡ାଶ
݂ ሺ݊ + 1ሻ ≡ ‫ݑ‬௡ାଵ
ଶ
= ‫ݑ‬௡ାଵ
− ‫ݑ‬௡ ሺ‫ݑ‬௡ାଵ + ‫ݑ‬௡ ሻ
ଶ
= ‫ݑ‬௡ାଵ
− ‫ݑ‬௡ ‫ݑ‬௡ାଵ − ‫ݑ‬௡ଶ
= ‫ݑ‬௡ାଵ ሺ‫ݑ‬௡ାଵ − ‫ݑ‬௡ ሻ − ‫ݑ‬௡ଶ
VÍDEO
O Código de Pascal 8/10
= ‫ݑ‬௡ାଵ ሺ‫ݑ‬௡ିଵ ሻ − ‫ݑ‬௡ଶ
= −݂ሺ݊ሻ
Nos passos do desenvolvimento acima, a relação de recorrência foi
usada duas vezes ‫ݑ‬௡ାଶ = ሺ‫ݑ‬௡ାଵ + ‫ݑ‬௡ ሻ e ሺ‫ݑ‬௡ାଵ − ‫ݑ‬௡ ሻ = ሺ‫ݑ‬௡ିଵ ሻ. Concluímos
então que ݂ ሺ݊ + 1ሻ = ሺ−1ሻ௡ାଶ como era de se esperar pela hipótese de
indução. CQD.
Combinatória
O professor pode usar este vídeo quando tratar de combinatória, mais
especificamente de combinação. Os números do triângulo aritmético
são exatamente a quantidade de combinações que podemos fazer
considerando n objetos em grupos de p objetos, que é o número
‫ܥ‬௣௡ =
௡!
.
௣!ሺ௡ି௣ሻ!
Sugestões de leitura
J.F. Porto da Silveira, O triângulo de Pascal é de Pascal?
http://athena.mat.ufrgs.br/~portosil/histo2.html (2001). Página
visualizada em 11/Abril/2010.
AZEVEDO, A.. Sequencias de Fibonacci. Revista do Professor de
Matematica, 45, p. 44-47, (2001).
Élvia Mureb Sallum, Fractais no ensino médio. Revista do Professor de
Matematica 57, p. 1-8, (2005).
KaCey97007, Fractal for Kaleidospheres & Kaleifractals
http://www.flickr.com/photos/kacey/2569739192/ (2008) . Página
visualizada em 21/Abril/2010.
Ficha técnica
Autor: Samuel Rocha de Oliveira
Revisora: Laura L.R. Rifo
Coordenador de audiovisual Prof. Dr. José Eduardo Ribeiro de Paiva
Coordenador acadêmico: Samuel Rocha de Oliveira
Universidade Estadual de Campinas
Reitor Fernando Ferreira Costa
VÍDEO
O Código de Pascal 9/10
Vice-reitor Edgar Salvadori de Decca
Pró-Reitor de Pós-Graduação Euclides de Mesquita Neto
Instituto de Matemática, Estatística e Computação Científica
Diretor Jayme Vaz Jr.
Vice-diretor Edmundo Capelas de Oliveira
VÍDEO
O Código de Pascal 10/10