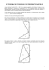FT36. Razão das áreas e dos perímetros

Escola Secundária de Lousada
Matemática do 7º ano – FT nº_______ Data: ___ / ____ / 2012
Assunto: Semelhança de figuras: Razão das áreas e dos perímetros
Lição nº ____ e ____
Relação entre perímetros e áreas de polígonos semelhantes
1. Observa a figura.
a)
b)
c)
d)
Qual é a razão de semelhança que transforma o triângulo A no triângulo B?
Qual é a razão entre o perímetro do triangulo B e o perímetro do triângulo A?
Qual é a razão entre a área do triângulo B e a área do triângulo A?
Compara cada uma das razões obtidas nas alíneas b) e c) com a razão de semelhança determinada
em a). O que podes concluir?
Propriedades:
Dados dois polígonos X e Y semelhantes e com razão de semelhança de X para Y igual a r, tem-se:
•
A razão entre o perímetro do polígono Y (PY) e o perímetro do polígono X (PX) é igual à razão
de semelhança, ou seja,
PY
=r
PX
•
A razão entre a área do polígono Y (AY) e a área do polígono X (AX) é igual ao quadrado da
razão de semelhança, ou seja,
AY
= r2
AX
2. Os perímetros de dois triângulos semelhantes são 12,4cm e 37,2cm. Calcula a área do segundo
triângulo, sabendo que a área do primeiro é 7,2cm2.
3. Da figura sabe-se que:
[
]
2
[
]
2
- a área do triângulo APQ é 99 cm e a área do triângulo ABC é 11cm ;
____
- BC//PQ ; - PQ = 12 cm
____
Calcula BC , explicando o teu raciocínio.
4. A área de um quadrado é 144 m 2 . Quanto mede o lado de um quadrado semelhante a este, de razão
de semelhança
1
6
?
5. Dois quadrados têm de áreas 9 cm 2 e 144 cm 2 . Qual é a razão de semelhança, considerando-a como
uma ampliação?
6. Num triângulo, os lados são 10,4 cm, 12 cm e 9,6 cm. Determina o comprimento dos lados de um
triângulo semelhante com 80 cm de perímetro.
7. Sabe-se que as áreas de dois triângulos semelhantes são 25 cm2 e 9 cm2. Qual é a razão de
semelhança dos perímetros?
8. Os perímetros de dois triângulos semelhantes são 36 cm e 24 cm. Determina a área do triângulo
maior, sabendo que a área do outro é 24 cm2.
9. A D. Maria tem um terreno de forma triangular. No seu interior, existe um canteiro semelhante ao
terreno. Sabe-se que a razão entre os comprimentos dos respectivos lados é
1
.
3
9.1. Sabendo que a D. Maria gastou 714 m de rede para vedar o terreno, que quantidade de rede
necessita para vedar o canteiro?
9.2. Sabendo que o canteiro tem de área 12 m2, qual a área do terreno? E a área compreendida
entre o terreno e o canteiro?
10. Na figura, estão representados dois hexágonos regulares.
Sabe-se que:
♦ O comprimento do lado do hexágono exterior é cinco vezes maior que o lado
do hexágono interior;
♦ A área do hexágono interior é 23 cm2.
10.1. Determina a área do da parte sombreada a cinzento, mostrando
como chegaste à resposta.
11. Considera um triângulo equilátero que tem 6 cm de lado. Recorrendo a material de desenho e de
medição, constrói a ampliação, de razão 1,5, deste triângulo. Efectua a construção a lápis. Não
apagues as linhas auxiliares que traçares para construíres o triângulo.
12. Dois triângulos equiláteros são semelhantes? Justifica.
13. Dois triângulos isósceles quaisquer são semelhantes? Justifica.