Propriedade das cevianas e algumas consequências
Transcrição
Propriedade das cevianas e algumas consequências
Propriedade das cevianas e algumas consequências imediatas. Professor: Isaac Pimentel. Assunto: Teorema de Menelaus-Ceva. Teorema de Menelaus. Três pontos distintos, um cada reta suporte dos segmentos de um triângulo, serão colineares, se, e somente se: 1 , onde a medida de um segmento AB é representada por: m AB . m BP m CP m AP P m CP 3 m AP 2 m BP 1 3 2 1 1 A P1 A P2 P3 B P2 B C C Demonstração. . (Se os três pontos distintos, um em cada reta suporte são colineares, então vale a relação.) Trace por C, uma reta r paralela a AB . P3 r P1 A r P1 A P2 M M P3 B P3 B C m CM m MP . m BP m BP m P P m P P m AP m AP 2) Dos triângulos semelhantes P AP e CP M: . m MP m CM m CP m CP m CM m CP .m BP m CM 3) Da proporção (1) . m BP m BP m BP m AP m AP m CP .m AP m CM 4) Da proporção (2) . m CM m CP m AP m CP .m AP .m BP 1. 5) Dividindo (1) por (2), membro a membro: m BP .m CP .m AP 1) Dos triângulos semelhantes CMP3 e BP1P3: m CP3 3 3 1 1 2 C 1 3 1 1 3 2 2 3 2 3 3 3 1 1 2 1 3 1 2 2 2 3 2 1 3 2 1 MATCONC – MATEMÁTICA E CONCURSOS http://www.matconc.co.cc P2 . (Se vale a relação, então os três pontos distintos nas retas suportes de cada segmento são colineares.) 1. m BP m CP m AP m CP3 m AP2 m BP1 Três pontos distintos, um cada reta suporte, são tais que: 3 2 1 Vamos tomar, dois pontos, P2 ' e P2 , com P2 colinear com P1 e P3 , tais que a relação seja verdadeira, então: 1 , cancelando os termos equivalentes de cada lado da m BP m CP ' m AP m BP m CP m AP m AP ' m AP igualdade, , como o P AC e o ponto divisor de um segmento numa razão dada é único, então P ' P . m CP ' m CP m CP3 m AP2 ' m BP1 m CP3 m AP2 m BP1 3 2 1 2 2 2 2 3 2 1 2 2 2 (cqd) Teorema de Ceva. Ceviana: Reta determinada pelo vértice e um ponto pertencente à reta suporte do lado oposto, num triângulo. (Se as cevianas se encontram num único ponto, então vale a relação.) As cevianas de um triângulo se encontram em um único ponto, se, e A somente se 1. m CP m BP m AP m AP2 m CP1 m BP3 2 P3 1 3 Demonstração. . P2 (Se as cevianas se encontram num único ponto, então vale a relação.) O m BO m AP 1 . m BP m OP m AC m BP m OP m AC 1. 2) Por Menelaus, no triângulo BAP : C P m AP m BO m CP m CP m BO m AP m BP m OP m AC 1 , resulta em: Multiplicando, membro a membro, (1) e (2): m BP m OP m AC m AP m BO m CP m AP m CP m BP 1. 3) m CP m BP m AP m CP1 1) Por Menelaus no triângulo BCP2: B 2 1 2 3 2 2 1 3 1 2 1 2 1 3 2 1 3 3 2 2 2 3 2 . (Se vale a relação, então as cevianas se encontram num único ponto.) Retomando (1), observa-se que a relação de Menelaus, para o triângulo BCP2, é feita com as cevianas BP2 e AP1 , valendo a relação m AC 1 . m CP m BO m AP m BP1 m OP2 1 2 Retomando (2), observa-se que a relação de Menelaus, para o triângulo BAP2, é feita com as cevianas BP2 e CP3 , valendo a m BO' m CP 1 , supondo que tenham um ponto comum O’. m BP m O' P m AC m BP m OP m AC m AP m BO' m CP 1. Multiplicando (1), (2) e cancelando m AC : 4) m CP m BO m AP m BP m O' P m AC m AP m CP m BP m OP m BO' 1 Reordenando (4): m BP m AP m CP m BO m O' P m OP m BO' m OP m O' P 1 Ou seja: , mas B, O, O’ e P , são colineares, e o ponto que divide um m BO m O' P m BO m BO' relação m AP3 2 3 2 1 2 1 3 2 1 3 2 1 2 2 3 2 3 2 2 2 2 2 2 2 segmento numa razão dada é único, portanto, O O' . (cqd). MATCONC – MATEMÁTICA E CONCURSOS http://www.matconc.co.cc O Baricentro, o incentro e o ortocentro. O Baricentro é o ponto comum às três medianas do triângulo. Mediana é o segmento que vai do vértice ao ponto médio do lado oposto, no triângulo. Baricentro é o ponto comum às medianas do triângulo. A Considerações. M2 Prova. Por ceva e pelas considerações acima: O 1. m CM m BM m AM m AM2 m CM1 m BM3 2 1 3 (cqp) B M1 C O incentro é o ponto comum às três bissetrizes do triângulo. Bissetriz é o segmento que vai do vértice ao lado oposto, dividindo o ângulo do vértice de origem ao meio. Incentro é o ponto comum às bissetrizes do triângulo. Considerações. Pela propriedade da bissetriz: A m BA . m CP m AC m CP m CB 2) . m AP m BA m AP m AC 3) . m BP m CB 1) m BP1 1 P3 P2 2 O 2 3 3 B P1 C Prova. Multiplicando (1), (2) e (3), membro a membro: m BA m CB m AC . m CP m AP m BP m AC m BA m CB m BP1 m CP 2 m AP3 1 2 3 Observe que é possível cancelar todos os termos do 2º membro da igualdade, então: 1. m CP m AP m BP m BP1 m CP 2 m AP3 1 m AM3 m BM3 ;m AM2 m CM2 ;m BM1 m CM1 . M3 2 3 (cqp). MATCONC – MATEMÁTICA E CONCURSOS http://www.matconc.co.cc O ortocentro é o ponto comum às três alturas do triângulo. Altura é o segmento que vai do vértice ao lado oposto formando um ângulo reto com o lado oposto. Ortocentro é o ponto comum às alturas do triângulo. A Considerações. 1) Os triângulos AOP2 e BOP1 são semelhantes, ou seja: m AO . m BP m BO m AP2 P3 1 2) Os triângulos AOP3 e COP1 são semelhantes, ou seja: P2 O m AO . m CP m CO m AP3 1 3) Os triângulos BOP3 e COP1 são semelhantes, ou seja: B P1 m BO . m CP m CO m BP3 C 2 Prova. Multiplicando (1), o inverso de (2) e (3), membro a membro: m CP m BP m AO m CO m BO m AP m CP m BP 1 . m BP m AP m CP m BO m AO m CO m CP m BP m AP m AP2 1 3 2 1 3 1 3 2 2 1 3 (cqp). Razão de divisão do baricentro. O baricentro divide cada mediana na razão de 1 para 2. A Considerações. Pelo conceito de mediana. M3 2) m AC 2m AM 2m CM ; 3) m BC 2m BM 2m CM . M2 1) m AB 2m AM3 2m BM3 ; O B M1 2 2 1 1 C Prova. m AO m BM 1 m AO 1 m AO 2m OM . m AM m OM m BC 2m OM m CM m BO m AM m BO 1 1 m BO 2m OM . Para o triângulo BCM , por (2) e (3): m BM m OM m AC 2m OM m BM m CO m AM m CO 1 1 m CO 2m OM . Para o triângulo BCM , por (1) e (3): m CM m OM m AB 2m OM Para o triângulo ACM1, por (2) e (3): m CM 2 1 1 2 1 1 1 2 2 2 1 2 1 2 3 3 3 1 3 3 (cqp). MATCONC – MATEMÁTICA E CONCURSOS http://www.matconc.co.cc
Documentos relacionados
1. Considere o triângulo abaixo, ache os pontos equidistantes dos
 1. Considere o triângulo abaixo, ache os pontos equidistantes dos lados AC e BC; e distantes 1,5
cm de C
1. Considere o triângulo abaixo, ache os pontos equidistantes dos lados AC e BC; e distantes 1,5
cm de C




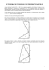


 1. (Udesc) Observe a figura.
1. (Udesc) Observe a figura.

