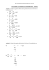Umwandeln eines gemeinen Bruches in einen Dezimalbruch

Umwandeln eines gemeinen Bruches in einen Dezimalbruch
Dividiere den Zähler durch Nenner.
•
Rest Null tritt auf
⇒
•
Rest Null tritt nie auf
⇒
5
8
=
5
:
0
5
4
0
8
2
1
8
=
0
6
4
4
0,
6
2
endlicher Dezimalbruch
periodischer Dezimalbruch
13
6
5
=
1
3
1
2
1
:
6
0
6
4
3
0
6
4
3
0
0
0
Ergebnis:
=
0
6
4
13
=
6
2,
1
6
1
6
6
6
0
…
2,
Dezimalbrüche, die irgendwann abbrechen, heißen endliche Dezimalbrüche.
Beispiele:
23,784
53,5
0,37756842
Dezimalbrüche, bei dem sich bestimmte Zifferngruppen nach dem Komma ständig wiederholen,
heißen periodische Dezimalbrüche.
Die sich wiederholende Zifferngruppe heißt Periode.
Die Anzahl der Zahlen, die sich ständig wiederholen, ist die Periodenlänge.
2,16 = 2,1666... hat die Periode 6 und die Periodenlänge 1
Beispiele:
„Zwei Komma Eins Sechs Periode Sechs“
54, 22334 = 54, 22334334334... hat die Periode 334 und die Periodenlänge 3
„Vierundfünfzig Komma Zwei Zwei Drei Drei Vier Periode Drei Drei Vier“
0,15 = 0,151515... hat die Periode 15 und die Periodenlänge 2
„Null Komma Eins Fünf Periode Eins Fünf“
Beginnt die Periode sofort nach dem Komma, ist es ein rein periodischer Dezimalbruch.
2, 6 = 2, 666...
Beispiele:
32,115 = 32,115115115...
Treten Vorziffern auf, die nicht zur Periode gehören, ist es ein gemischt periodischer
Dezimalbruch.
5,1234 = 5,12343434...
Beispiele:
335,88973 = 335,88973973973...
Forme in einen Dezimalbruch um.
a)
7
5
b)
7
8
c)
4
3
d)
14
3
e)
15
4
f)
12
5
g)
11
6
h)
6
5
5
4
i)
j)
k)
11
11
22
7